blog di a_magaro

Nel documento PDF allegato abbiamo voluto approfondire il comportamento di una struttura in acciaio su due livelli sottoposta all' azione di forze orizzontali come possono essere quelle sismiche.

Abbiamo preso spunto da una parte dell' edificio che stiamo progettando come tema del semestre e abbiamo provato a disporre i controventi tipici della tecnologia dell' acciaio, in modo da valutare il centro delle rigidezze di ciascuno dei due impalcati, la sua relazione con il centro di massa e come questa influisce sul comportamento dell' edificio.

Abbiamo fatto alcune considerazioni su come converrebbe agire per avvicinare centri delle rigidezze e centri di massa, tenedo conto dei vincoli che la struttura e il progetto impongono.

Abbiamo completato l' esercitazione verificando su SAP la struttura, non prima di aver effettuato un predimensionamento di travi e pilastri, trovando conferma delle nostre previsioni (a meno di lievi margini di errore nei valori) sugli andamenti di spostamenti e rotazioni.

Effettuerò la verifica a deformabilità di strutture simili a quelle utilizzate nell’ esercitazione per il dimensionamento di travi in un telaio, in cui una campata è a sbalzo.

Lo scopo dell’ esercitazione è quello di valutare le differenze tra le due strutture e verificare come sbalzi di notevoli dimensioni sono difficili da gestire e spesso richiedono, oltre ad un incremento delle dimensioni, ad una modulazione della sezione lungo l’asse, anche un cambio di tecnologia.

Per portare a termine l’esercitazione utilizzerò un foglio di calcolo preimpostato per le tre tecnologie al quale è aggiunta una verifica a deformabilità di massima, in cui è necessario valutare che lo spostamento massimo non superi il rapporto di 1 a 250 con la luce dello sbalzo.

I telai su cui andrò a valutare la deformabilità in presenza dello sbalzo sono 2, molto simili tra loro nelle dimensioni, ma che vedono invertite luci e interassi, provocando una volta uno sbalzo di 4 metri ed un’ altra di 6 metri.

L' esercitazione è svolta nel documento PDF allegato.

Questa struttura presenta alcune complicazioni che impongono di procedere con cautela, si tratta infatti di una struttura iperstatica priva di simmetrie e con una singolarità in mezzeria dovuta alla presenza di una cerniera che non interrompe la continuità della trave.

Possiamo comunque fare alcune ipotesi preliminari e poi valuteremo, applicando l’equazione della linea elastica, che queste ipotesi siano corrette.

LA DEFORMATA

Dal momento che la cerniera non interrompe la continuità della trave dobbiamo immaginare che localmente la deformata sia una curva continua, senza singolarità. Passando concettualmente dal modello di Bernoulli ad un modello tridimensionale, dobbiamo immaginare quello che fa la sezione in corrispondenza della cerniera B. Dal momento che la struttura non è simmetrica, dobbiamo immaginare che la sezione in B non stia ferma, ma ruoti dalla parte che è meno vincolata, quindi verso BC, verso destra, ovvero in senso orario.

Viceversa nell’ incastro A la rotazione è inibita dal vincolo ed invece è libera in C.

La deformata potrebbe essere quella di figura, poco proporzionata e molto accentuata.

IL MOMENTO

Alcune cose si possono dire anche del momento. Innanzitutto il carico è distribuito su entrambi i tratti della trave (tratti che definiamo non perché vi sia una discontinuità geometrica, ma vi è una discontinuità dovuta alla reazione vincolare in B) per questo motivo il momento sarà parabolico sia sul tratto AB che su quello BC. Le due parabole saranno diverse.

Entrambe si annulleranno nei punti di flesso (individuati in figura con delle X) poiché in essi cambia la curvatura della deformata. Dire che cambia la curvatura significa dire che la curvatura CAMBIA DI SEGNO. Il che vuol dire che in quel punto la curvatura si annulla. Visto che il momento è proporzionale alla curvatura (a meno del prodotto EJ che è costante e diverso da 0) nei punti dove si annulla la curvatura si annulla anche il momento.

Inoltre il momento si annulla anche nella cerniera C, mentre ha un valore nel punto B, in cui si trasmette momento per la continuità della trave. Nel punto B si ha un punto angoloso poiché in esso vi è una forza concentrata (la reazione vincolare) essa determinerà una irregolarità anche nel taglio.

IL TAGLIO

Il carico distribuito determina il fatto che il momento sia parabolico ed il taglio sia lineare, su entrambi i tratti, ma con inclinazioni ed andamenti diversi.

Quel che è certo è che in corrispondenza di B così come vi è un punto angoloso del momento, vi è un SALTO del taglio, salto che sarà uguale alla reazione vincolare della cerniera in B.

Infine il taglio si annullerà con certezza in due punti che sono i punti di vertice delle due parabole del momento, quella del tratto AB e quella del tratto BC. In questi punti infatti, la funzone momento, ha tangente orizzontale, il che equivale a dire che la derivata della funzione momento è nulla, ma la derivata della funzione momento è proprio la funzione taglio cambiata di segno, per cui in quei punti il taglio è nullo.

CONDIZIONI AL BORDO E DI CONTINUITA’

Innanzitutto dobbiamo chiederci di quante condizioni al bordo abbiamo bisogno. Per capirlo dobbiamo ricordarci che abbiamo diviso la trave idealmente in due tratti che si comportano in maniera diversa. A ciascuno dei due dobbiamo applicare l’Equazione della Linea Elastica, che integrata 4 volte presenterà 4 costanti di integrazione per tratto per un totale di 8.

E’ proprio di 8 condizioni che cerchiamo, e saranno sia di natura statica che cinematica.

BORDO A

In A c’è un incastro, è immediato dire che gli spostamenti sono inibiti, quindi anche quello verticale, come anche le rotazioni per cui:

PUNTO B (condizioni di continuità)

In B, come abbiamo già visto, la continuità della trave è garantita, per cui, nonostante la presenza di una cerniera IL MOMENTO viene trasmesso e quindi NON E’ NULLO. Quel che è certo però è che esso è lo stesso sia a sinistra che a destra del vincolo.

Certamente sono inibiti gli spostamenti e quindi anche quelli verticali, e questa è una condizione doppia, poiché vale sia per il tratto AB che per quello BC.

Altra cosa che possiamo dire è che la continuità della trave ci dice che la ROTAZIONE RELATIVA è nulla, per cui la rotazione a destra e a sinistra è la stessa

Abbiamo quindi 4 condizioni, quelle sugli spostamenti e sulle rotazioni sono di natura cinematica, mentre quella sui momenti è di natura statica.

BORDO C

Nella cerniera sono libere le rotazioni quindi su di esse non possiamo dire nulla, sono inibiti gli spostamenti e quindi anche quelli verticali, ed è nullo il momento per cui:

EQUAZIONE DELLA LINEA ELASTICA

L’ equazione della linea elastica è:

Essa va applicata ai due tratti, separatamente se le condizioni al bordo sono separate, e contemporaneamente quando le condizioni al bordo lo richiedono.

TRATTO AB	TRATTO BC

 

 

 

 

 

 

 

 

Ora passiamo ad applicare alle giuste equazioni le condizioni al bordo:

PUNTO A

Dire che c’è un incastro in quel punto a sinistra, da dove iniziamo a contare le ascisse, equivale a dire che lo spostamento e la rotazione sono nulli, il che significa che le costanti c3 e c4 sono nulle.

PUNTO B

Nel punto B avremo delle equazioni che comprendono sia le costanti c del primo tratto sia le costanti d del secondo tratto, mettendole in relazione tra loro, ma iniziamo con le equazioni che mantengono separate le costanti, che sono quelle riguardanti gli spostamenti:

Vi sono poi le equazioni miste relative alle uguaglianze tra momenti e rotazioni. Per quanto riguarda il momento, stiamo considerando una trave continua, ma essa potrebbe essere continua anche se presentasse diversa sezione o se fosse di un diverso materiale nel primo e nel secondo tratto. Basterebbe infatti che fosse giuntata con continuità. Avremmo quindi dovuto considerare nei due tratti E1 e J1 ed E2 e J2 per diversi materiali e per diverse sezioni. Per semplificare però immaginiamo una trave continua per sezione e per materiale. Questo comporta che uguagliare i momenti significa in definitiva uguagliare le curvature, dal momento che nell’ uguaglianza dei momenti posso dividere a destra e a sinistra per EJ (che sono uguali nei due tratti).

Infine passiamo all’ uguaglianza delle rotazioni (condizione inerente alla nullità della rotazione relativa).

PUNTO C

Nel punto C abbiamo una condizione cinematica che riguarda la nullità dello spostamento e una condizione statica che riguarda la nullità del momento, a cui corrisponde la nullità della curvatura dal momento che EJ è sempre diverso da 0.

RIASSUMENDO

Ci ritroviamo con un sistema di 8 equazioni in 8 incognite, anzi, equazioni ed incognite sono di meno dal momento che alcune sono state definite come nulle. Indico con A il rapporto q/EJ.

Se non avessi già apportato delle semplificazioni per l, quando necessario, mi accorgerei da dove proviene ciascuna delle equazioni, quelle di 4° grado in l derivano dagli spostamenti, quelle di 3° dalle rotazioni, quelle di 2° dai momenti.  Avendo abbassato di grado in alcuni casi non posso più determinarlo ad occhio.

E’ necessario risolvere il sistema:

Sostituiamo il d₂ della 8° equazione nella 5° equazione e troviamo d₁ in funzione di c₁ e c₂

Sostituiamo il d₁ appena trovato ed i d₂ e d3 della 7° ed 8° equazione nella 4° equazione e troviamo c₂ in funzione di c₁

Sostituiamo il c₂ appena trovato nella 6° equazione e troviamo c₁:

Sostituiamo il c₁ appena trovato nelle altre costanti che sono scritte in sua funzione e avremo tutte le costanti a cascata:

Ora che abbiamo tutte le costanti, riscriviamo le equazioni della linea elastica:

TRATTO AB	TRATTO BC

 

 

 

 

 

 

 

 

Adesso che abbiamo tutte le funzioni possiamo descrivere il comportamento della struttura in ogni punto.

TAGLIO

Iniziamo dal taglio: valutare i punti dove si annulla significa trovare i punti di vertice delle parabole del momento. Calcoliamo il Taglio nei punti notevoli e poi vediamo dove si annulla:

Se prima avevamo ipotizzato un andamento, ora possiamo disegnarlo quantitativamente:

MOMENTO

Per quanto riguarda il momento, nei punti dove si annulla il taglio avremo i vertici delle parabole, ma ci servono altri due punti notevoli, che sono quelli dove si annullano le curvature della deformata nei due tratti. Ci calcoliamo prima questi e poi il momento nei punti notevoli, iniziamo dal tratto AB

E poi il tratto BC:

Calcoliamo il momento nei vincoli A e B (in C è 0) e nei punti di vertice delle parabole che sono quelli per cui si annulla il taglio:

Ora è possibile disegnare il grafico del momento:

REAZIONI VINCOLARI

In ultimo, possiamo indicare i valori delle reazioni vincolari. Esse infatti sono le azioni di contatto che si trasformano in reazioni vincolari sui bordi, appena fuori dalle travi:

Come si vede, la reazione vincolare della cerniera in B è pari al salto che c’è nel taglio poiché essa si comporta, per il taglio e per il momento, come un carico concentrato, determinando un salto ed un punto angoloso. Essa è diretta verso l’alto, a dimostrazione del fatto che quel vincolo “lavora” per contrastare il desiderio della trave di inflettersi in quel punto.

Il sistema è equilibrato infatti le tre reazioni sono concordi e bilanciano alla traslazione verticale il carico così come accade per il momento.

Avremmo potuto praticare degli opportuni tagli di Cauchy per verificare che le reazioni vincolari sono esattamente queste, tenendo sempre conto della corretta convenzione di segno.

Per un dimensionamento di massima delle travi nelle diverse tecnologie, possiamo determinare all' interno di un telaio quale sia la trave che debba sopportare il maggior carico ed eventualmente riferirci ad essa per dimensionare le altre.

Mi avvalgo dell' ausilio di un foglio di calcolo per determinare i carichi, in funzione di essi e della lunghezza della trave il momento massimo, la sigma ammissibile, e quindi l'altezza della trave una volta fissata una base.

Proverò a valutare le differenze su due telai simili, in cui è invertita l'orditura, nelle tre tecnologie, quella del legno, quella dell' acciaio e quella del calcestruzzo.

Vediamo i due telai:

Nel primo caso la luce della trave principale è di 4m, e l' interasse è di 6m, viceversa nel secondo caso la trave principale ha una luce di 6m, mentre l'interasse tra le travi principali è di 4m. L' area di influenza di ciascuna trave è la medesima, pari a 24mq e su di essa insistono quindi gli stessi carichi calcolati a spanne.

Prima di iniziare un cenno sui carichi. Essi sono di tre tipi:

 

• CARICHI STRUTTURALI: sono i carichi derivanti dal peso degli elementi strutturali secondari come i travetti di un solaio. Si devono calcolare.
• SOVRACCARICHI PERMANENTI: sono quei carichi che gravano permanentemente sulla struttura, ma non costituiscono struttura. Anche essi devono essere calcolati.
• SOVRACCARICHI ACCIDENTALI: sono di diverso tipo, e si riferiscono a quei carichi che gravano in maniera non permanente, ma che comunque hanno una alta probabilità di incidere sul carico complessivo. Essi sono dati dalla normativa.

La loro somma determina il carico complessivo su un solaio, ma a noi interessa il carico al metro quadro che poi verrà moltiplicato per l'interasse e ci darà il carico al metro lineare che insiste sulla nostra trave.

Per ottenere il carico al metro quadro basta moltiplicare, per ciascuno strato della tecnologia scelta, il peso specifico del materiale da cui è composto lo strato, per lo spessore dello strato.

Se lo strato non è omogeneo valuterò quanta materia omogenea c'è in ciascuno strato e la sommerò di conseguenza. Sarà ad esempio il caso dei travetti.

In altri casi è comunque più agevole avvalersi delle garanzie del produttore quando si utilizzano elementi prefabbricati.

SOLAIO IN LEGNO

Inizio con il solaio in legno. Quello che utilizzerò è di questo tipo:

Nel disegno è già riportata la trave principale, con una base di 23 cm e un' altezza di 25, è quasi certo che alla fine del processo di dimensionamento questa sezione andrà cambiata.

Inizio dai carichi strutturali. Essi, escludendo ovviamente la trave che non è ancora dimensionata, sono costituiti esclusivamente dai travetti. La loro base ha dimensioni 9 x 11 cm e sono posti a 18 cm l' uno dall' altro. Nello spazio di un metro ho quindi 3 travetti.

Il volume dei travetti sul metro quadrato è di

Il loro peso al metro quadro dipende dal peso specifico del materiale impiegato. Utilizzerò per i travetti legno massello (di rovere) per un peso specifico di 750 Kg/m³. Il carico strutturale è dato dal prodotto del volume dei travetti su un metro quadro e il peso specifico del materiale usato per cui:

Passo ai sovraccarichi permanenti. Inizierò a valutare strato per strato, partendo dall' alto, moltiplicando il peso specifico del materiale usato per lo spessore dello strato. Per fare questo velocemente mi avvalgo di Excel.

Per i sovraccarichi accidentali mi affido alla normativa e computo l' incidenza degli impianti che è 0,5 KN/m2, l' incidenza tramezzi che p 1 KN/m2 e il carico dovuto alla destinazione d' uso che per quella domestica è 2 KN/m2.

Posso riportare questi valori appena calcolati in tabella insieme all' interasse delle travi principali nei due casi che sto valutando e la loro combinazione lineare tramite dei coefficienti anch'essi dati dalla norma mi darà il valore del carico sulla trave che sto esaminando.

Aggiungendo il valore della luce, avrò il momento massimo di una trave doppiamente appoggiata che è in mezzeria ed è QL²/8

Gli altri valori riguardano la classe di resistenza del legno scelto (il numero rappresenta la resistenza a flessione in Mpa) ed il coefficiente di sicurezza

In tabella alcuni altri tentativi oltre i primi due raccontati in cui vario la conformazione del telaio (interasse/luce), la base della trave, e la classe di resistenza del legno.

SOLAIO IN ACCIAIO

Il solaio in acciaio che utilizzo è di questo tipo

In esso il carico strutturale è quello dei travetti che sono dei profili IPE 80, la trave ipotizzata è una IPE 160, vedremo al termine dei calcoli se andrà bene o dovrà essere dimensionata diversamente. Per il carico dato dai travetti basta guardare sui profilari. Il peso però è espresso al metro lineare, per cui sarà necessario moltiplicare per la lunghezza di un travetto (in realtà sono le sue mezze lunghezze) per il numero dei travetti che troviamo in un metro quadro di superficie di solaio. (Essendo larghi 4,6 cm ipotizzo ve ne siano 7 ogni metro di trave)

Per quanto riguarda i carichi permanenti procedo come nel legno, con la differenza che per i solai in acciaio alcuni elementi sono standardizzati, così il peso della lamiera grecata al metro quadro è dato dal produttore ed è 0,11 KN/m². Per La rete elettro saldata il discorso è lo stesso 0,0063 KN/m², e per il controsoffitto anche lì ci rivolgiamo alle garanzie del produttore (28 Kg/m²). Restano da calcolare il peso della pavimentazione, dello strato di malta per la posa e del massetto (tenendo conto della sua morfologia)

Ancora una volta utilizzo Excel

Per i carichi accidentali mi rivolgo alla normativa, la destinazione d' uso è ancora quella residenziale e l' incidenza impianti e tramezzi è sempre quella data.

Posso inserire i carichi nella tabella Excel e valutare il Momento massimo in relazione alla luce

Inserendo la classe di resistenza dell' acciaio (per il momento la stessa intermedia S275) ottengo la Sigma Ammissibile che è la stessa ovviamente poichè essa è relativa solo al materiale utilizzato, ed il modulo di resistenza a flessione Wx. Approssimando per eccesso questo valore trovo di nuovo sul profilario quale sia la IPE che mi serve per sostenere questo carico

Nel primo caso prenderò una IPE 300 (Wx = 557,1 cm3), nel secondo, la prima approssimazione per eccesso è molto più grande, dovrei usare una IPE 360 (Wx = 903,6 cm3), sarà il caso di cambiare tecnologia o basterà solo cambiare il profilo?

In ogni caso la dimensione del disegno è errata.

SOLAIO IN LATEROCEMENTO

Il solaio in laterocemento che utilizzerò è quello nel disegno

Gli ammorsamenti continui dei vari elementi nel solaio in laterocemento lo rendono molto performante, ma è per questo che il calcolo sarà un pò più complesso, proprio per la disomogeneità degli strati, ma anche per il fatto che il solaio in laterocemento è generalmente gettato in opera e quindi le sue caratteristiche possono essere molto variabili.

Il calcolo dei carichi è lo stesso di quello visto per gli altri tipi di solaio, al solito per gli strati omogenei moltiplicherò lo spessore dello strato per il peso specifico del materiale, mentre per gli strati non omogenei, come l'alternanza travetto/pignatta, mi baserò sui dati del produttore per la pignatta e sul calcolo specifico per i travetti, impostando una tabella sul foglio di calcolo.

I carichi strutturali sono costituiti dai travetti gettati in opera. Il travetto ha un fondello in laterizio, che però non ha una funzione strutturale, ma è solo la cassaforma a perdere del travetto che si forma con il getto di completamento.

Per il carico strutturale calcolo il volume su un metro lineare di ciascun travetto e lo moltiplico per il peso specifico del calcestruzzo armato (per tener conto anche dei ferri di armatura) e moltiplico ancora tutto per il numero dei travetti in un metro quadrato di solaio:

Per i sovraccarichi permanenti utilizzo il foglio di calcolo per gli strati omogenei e sommo i valori certificati dai produttori

Infine vado a compilare la tabella con i valori dei sovraccarichi accidentali dati dalla norma, con i valori di luce e interasse, I valori riguardanti la classe dell' acciaio per i ferri d'armatura (in realtà la Fy, la tensione allo snervamento), la RCK che è la resistenza caratteristica del Calcestruzzo, ed una volta inserita la dimensione della base ho il valore di altezza utile, ovvero quella al di sopra dei ferri inferiori d'armatura, alla quale va sommato il "copriferro" (che in realtà è il copriferro dato dalla norma in funzione delle condizioni ambientali sommato al raggio della sezione del ferro d'armatura) per ottenere l'altezza totale della trave e di conseguenza una serie di altri dati deducibili dalle grandezze che abbiamo, come l'area della sezione della trave, il rapporto altezza luce e molto importante il peso della trave, che nel calcestruzzo è da tenere sotto controllo da subito essendo un materiale "intrinsecamente" pesante.

 

Due diversi metodi

Questo tipo di semplice trave reticolare può essere assimilata ad una qualsiasi trave appoggiata, come se tra i vincoli esterni vi fosse un unico corpo rigido.

Assegnati i carichi, è immediato determinare le reazioni vincolari, che devono reagire ad un carico complessivo di 3F. Il sistema è simmetrico e caricato simmetricamente, per cui le reazioni saranno equamente distribuite sui vincoli, saranno dirette verso l'alto e pari a 3F/2

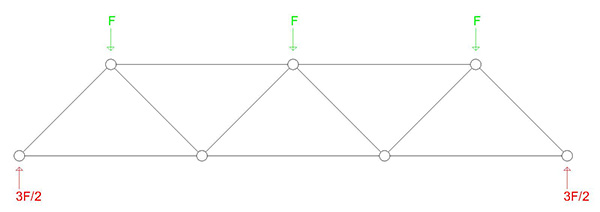
La particolarità della trave reticolare, intesa come modello, quindi intendendo che per ciascuna asta sia trascurabile il peso proprio, e che tutte le aste siano incernierate tra loro per non trasmettersi momento, è che ciascuna asta è sottoposta o a compressione o a trazione, è quindi da considerarsi o un puntone o un tirante.

Una volta assegnati i carichi quindi le travi reticolari piane sono di semplice risoluzione secondo due metodi: il metodo dell' equilibrio dei nodi, che accennerò, ed il metodo delle sezioni di Ritter, che è quello che invece approfondirò.

RISOLUZIONE CON IL METODO DELL' EQUILIBRIO DEI NODI

Il metodo dell' equilibrio dei nodi si basa sul concetto che i nodi, nella struttura reticolare, devono essere tutti equilibrati.

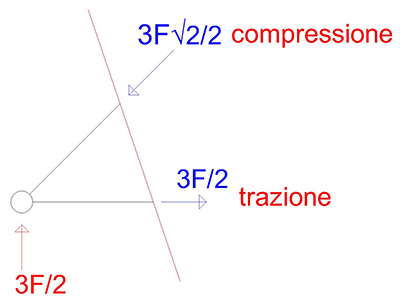
Iniziamo quindi con il nodo A. su di esso agiscono certamente la reazione vincolare che conosciamo e le azioni delle due aste ad esso collegate che per convenzione prendiamo uscenti dal nodo, in modo che corrispondano alla reazione di trazione sull'asta che, sempre per convenzione, è positiva.

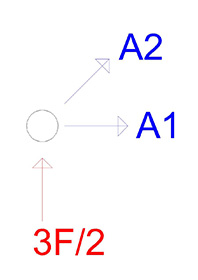
Un sistema di 3 forze che, per come le abbiamo disegnate, hanno le linee d'azione che si intersecano in un punto, è risolvibile graficamente, a patto che si chiuda il triangolo delle forze. L' unico modo affinchè questo accada, dal momento che conosciamo gli angoli che tra di loro formano le forze (che sono gli stessi che formano le aste), è il seguente:

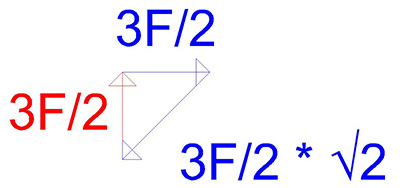
Queste sono le azioni sul nodo, che corrispondono a sforzi sulle aste che hanno lo stesso modulo ma verso opposto

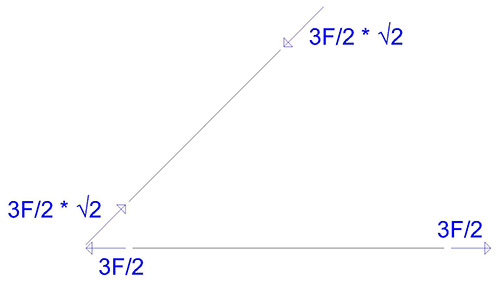
Per questo motivo possiamo affermare che l' asta 1 è un puntone e l' asta 2 è un tirante.

Si prosegue in maniera analoga per tutti gli altri nodi, tenendo presente che di volta in volta ci si può ritrovare non con triangoli delle forze, ma con poligono delle forze, ma in strutture semplici come questa sono facili da risolvere anche graficamente.

In ogni modo, si può porre anche l' equilibrio e risolvere le equazioni per la traslazione.

Bisogna procedere con ordine però perchè avendo a disposizione solo 2 equazioni, devono esserci solo 2 incognite, per cui gli altri sforzi devono essere sempre determinati nel nodo precedente.

RISOLUZIONE CON IL METODO DELLE SEZIONI DI RITTER

Il metodo delle sezioni di Ritter si basa sul fatto che una parte del sistema reticolare, ottenuta operando una sezione, che tagli al massimo 3 aste deve essere equilibrata.

Anche qui bisogna fare attenzione a come procedere, infatti, se si inizia sezionando le aste 1 e 2 non si riesce immediatamente a determinare gli sforzi sulle due aste. Iniziamo quindi facendo una sezione sulle aste 2, 3 e 4.

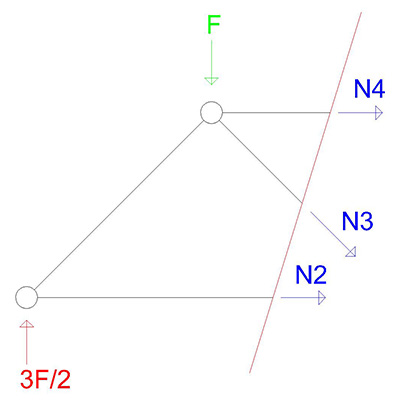
Imponendo l'equilibrio a questo pezzetto di sistema, otteniamo il seguente sistema di equazioni.

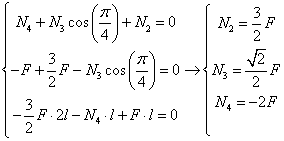
Ho imposto l' equilibrio alla rotazione in un punto che ho ritenuto conveniente, dal momento che annulla i momenti di 2 sforzi.

Considerando i segni negativi per la compressione e i segni positivi per la trazione ottengo che gli sforzi sono quindi diretti secondo la figura

Ora possiamo ritornare a sezionare le aste 1 e 2, per trovare lo sforzo sull' asta 1, visto che conosciamo la reazione vincolare e lo sforzo sull' asta 2. Anche qui potremmo procedere graficamente, o mediante equazioni di equilibrio.

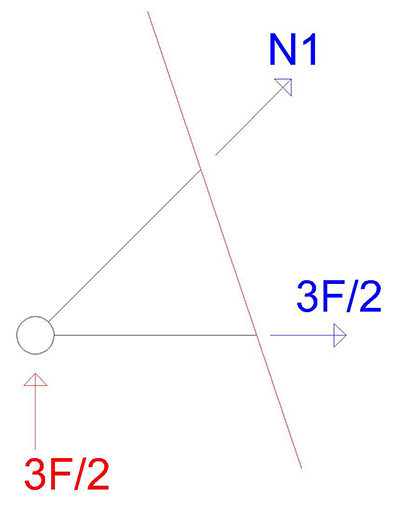
Ho posto per convenzione N1 con il verso positivo. Scrivo le equazioni di equilibrio (me ne basta una perchè ho una sola incognita da determinare)

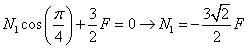
Risulta che  l'asta 1 sia compressa.

Procedo con un' ulteriore sezione che taglia le aste 4, 5 e 6 e ho come incognite gli sforzi sull' asta 5 e sull' asta 6

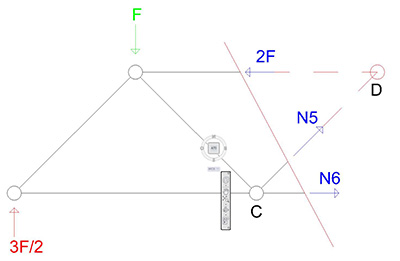
Se imponiamo l'equilibrio è necessario prestare attenzione al punto attorno al quale effettuare l' equilibrio a rotazione, infatti, se si facesse attorno al punto C si eliminerebbero dall' equazione entrambe le incognite, rendendo di fatto l'equazione un' identità. Farlo attorno a qualsiasi altro punto che non sia il punto D lascerebbe 2 incognite nell' equazione, complicandola inutilmente.

CI bastano comunque le sole due equazioni di equilibrio alla traslazione avendo 2 incognite.

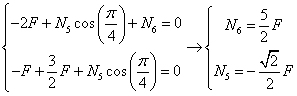
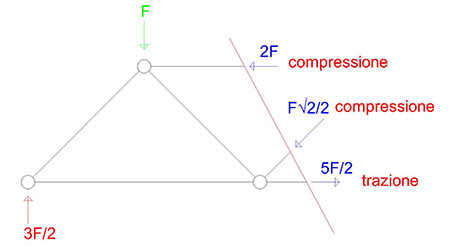
La trave reticolare è risolta perchè è simmetrica e caricata simmetricamente rispetto ad un' asse verticale passante per il punto D

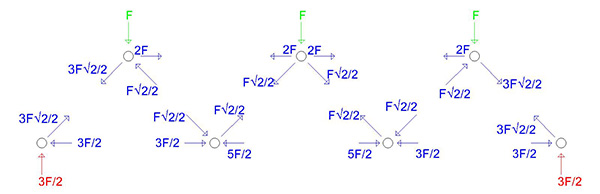
I grafici dello sforzo normale sono i seguenti

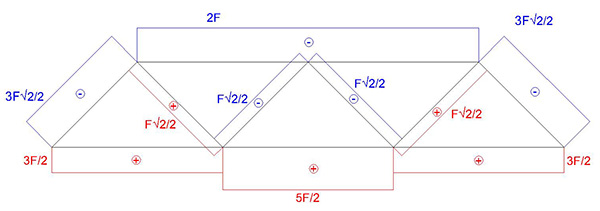
RISOLUZIONE CON SAP 2000

E' certamente possibile disegnare, sia in SAP che in AutoCAD o in Rhinoceros, la trave che ci interessa, ma essendo una trave particolarmente semplice, possiamo utilizare lo strumento predefinito di SAP.

Clicchiamo su NUOVO (classica icona di windows con il nuovo documento) e dalla finestra che si apre è necessario stabilire le unità di misura (nel nostro caso KN,m,C) e scegliere lo strumento RETICOLARI.
 

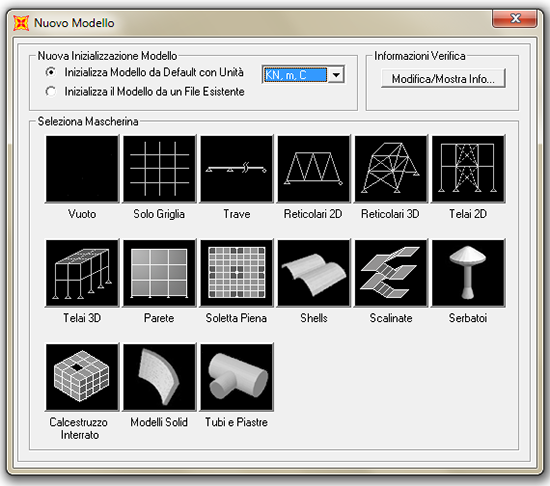
Dalla successiva finestra andiamo a scegliere il numero di parti di cui si compone il reticolo (nel nostro caso 3) e le dimensioni del passo. Se vogliamo un angolo di 45° è necessario scegliere 2 di lunghezza e 1 di altezza.

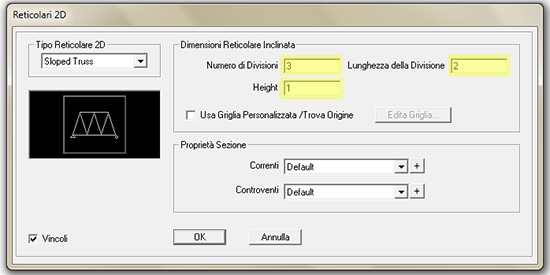
La trave reticolare apparirà sullo schermo, possiamo chiudere la finestra 3D che non ci serve.

Quella che è stata disegnata però non è una trave reticolare intesa come la intendiamo noi, infatti tra le aste sono presenti degli incastri interni, che però noi non vogliamo. E' necessario infatti che i vincoli interni siano tutte cerniere affichè non vi sia trasmissione di momento da un' asta all' altra.

Per apportare questa modifica selezioniamo tutti i nodi interni (in realtà ci basta selezionare tutto poichè la modifica he andremo a fare agirà sui nodi e non sulle aste) e clicchiamo su

ASSEGNA -> FRAME -> RILASCI,RIGIDEZZE PARZIALI

Si apre una finestra di dialogo in cui possiamo andare a selezionare la sollecitazione che non si deve trasferire nè all' inizio nè alla fine dell' asta.
 

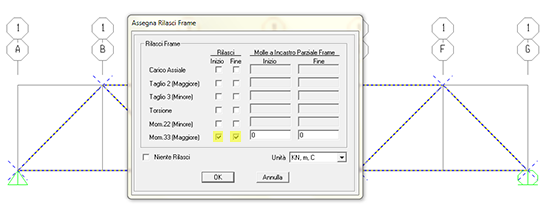
Selezioniamo MOMENTO 3-3 tenendo conto del sistema di riferimento locale di SAP, che è quello legato alla singola asta e che ha l'asse 1 sull' asse dell' asta e le altre orientate secondo la regola della mano destra.

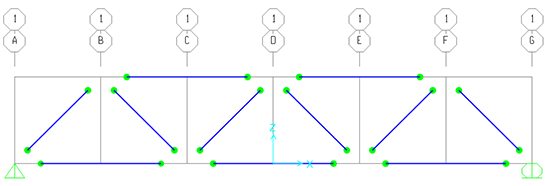
Fatto questo passiamo ad assegnare i carichi

Potremmo creare dei casi di carico e poi applicarli, oppure passare all' applicazione dei carichi e definire da lì il nuovo caso di carico, è la stessa cosa.

Selezioniamo i 3 nodi superiori dove vogliamo che agisca il carico e clicchiamo su

ASSEGNA -> CARICHI NODO -> FORZE

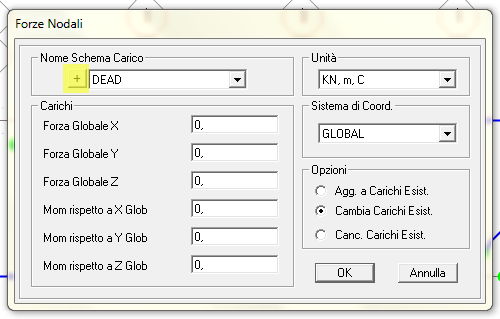
Da questa finestra è possibile cliccare sul + per aggiungere un nuovo caso di carico direttamente da qui

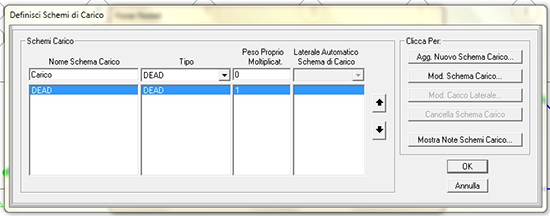
Diamo un nome univoco al nuovo caso di carico (l' ho chiamato "carico") e ho assegnato come moltiplicatore del peso proprio (DEAD) il valore 0 in modo da non considerarlo nei calcoli. Fatto questo andiamo a cliccare su Agg. Nuovo Schema Carico e torneremo alla finestra precedente dopo aver cliccato OK

Nel menu a tendina affianco alla + troveremo il caso di carico appena creato.

Ad esso dobbiamo assegnare un valore (ed una direzione) siccome è una forza concentrata diretta verso il basso assegneremo a FORZA GLOBALE Z il valore -100 (KN si intende)

Dopo aver dato l' OK questa è la configurazione della nostra trave

Un passo fondamentale è quello di assegnare una sezione alle aste. Per farlo è necessario selezionarle tutte e poi cliccare su

ASSEGNA -> FRAME -> SEZIONI FRAME

Dalla finestra che si apre diamo un nome alla sezione che stiamo creando (io l' ho chiamata sezione di prova) e poi clicchiamo su AGG. NUOVA PROPRIETA' e si aprirà una finestra dalla quale sarà possibile scegliere il tipo di sezione. Scegliamo il TUBO

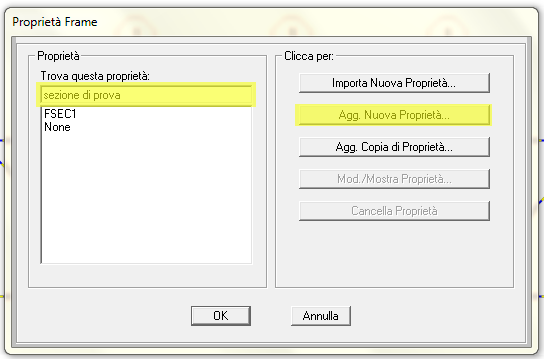
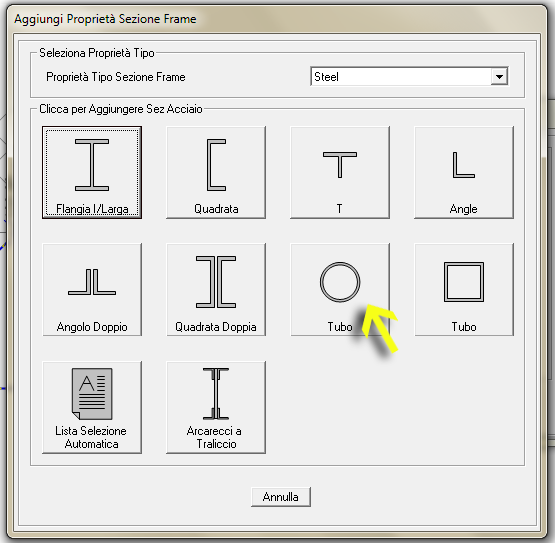
si apre una ulteriore finestra nella quale possiamo assegnare un nome alla sezione che stiamo creando, un diametro esterno ed uno spessore della parete, ed un materiale (quello di default è l'acciaio A992Fy50)

Selezoniamo la sezione appena creata e diamo l' OK. su tutte le aste apparirà il nome della sezione che gli abbiamo assegnato

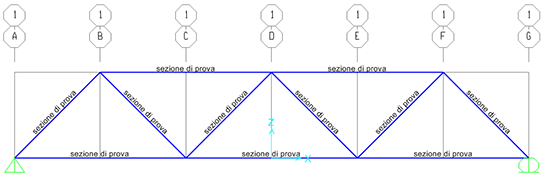
A questo punto il modello è pronto e possiamo andare ad effettuare i calcoli

Clicchiamo su ANALIZZA e vediamo che SAP apre una finestra con tutti i casi di carico creati. a noi interessa solo quello che abbiamo creato noi e quindi mettiamo in NOT RUN gli altri e poi clicchiamo su Esegui ORA

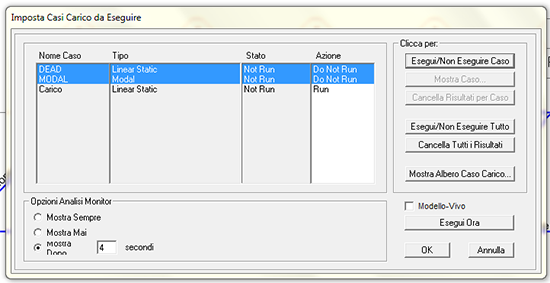
Ci verrà chiesto di salvare il file se non l'abbiamo già fatto e dopo pochi secondi apparirà la configurazione deformata

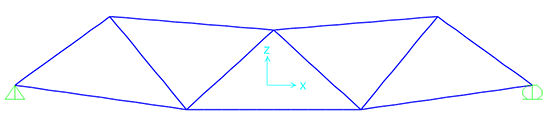
Ora possiamo andare a vedere tutti i risultati che sono stati ottenuti: per prima cosa la deformata in relazione alla configurazione indeformata. Per una struttura così semplice è poco interessante e per nulla stupefacente
 

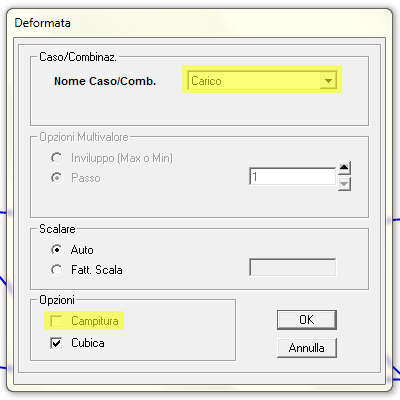
Dobbiamo selezionare il caso di carico per il quale vogliamo vedere la deformata e spuntare la voce campitura in modo da vedere che i nodi si sono spostati verticalmente ed orizzontalmente (per la presenza del carrello)

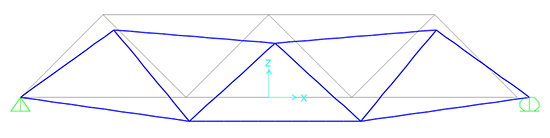
Ovviamente possiamo vedere i grafici delle sollecitazioni, cliccando sull' icona MOSTRA SOLLECITAZIONI / TENSIONI si apre un menu a tendina e scegliamo FRAME/CAVI/TIRANTI

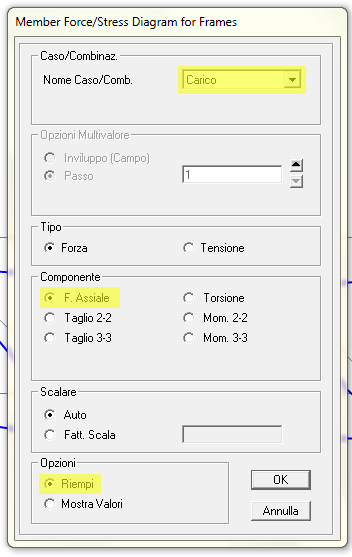
Lasciamo selezionata la forza assiale e clicchiamo su MOSTRA VALORI e poi su OK

Scegliamo il MOMENTO 3-3 per verificare che i valori siano nulli

E' chiaro che l'analisi appena fatta deve portarci a delle considerazioni sulle deformazioni e sugli spostamenti che subisce una struttura così modellata, per cui dobbiamo avere dei numeri a disposizione per verificare che siano accettabili ed eventualmente intervenire.

Esportiamo quindi tutti i dati raccolti in formato Excel o Access cliccando su VISUALIZZA -> MOSTRA TABELLE

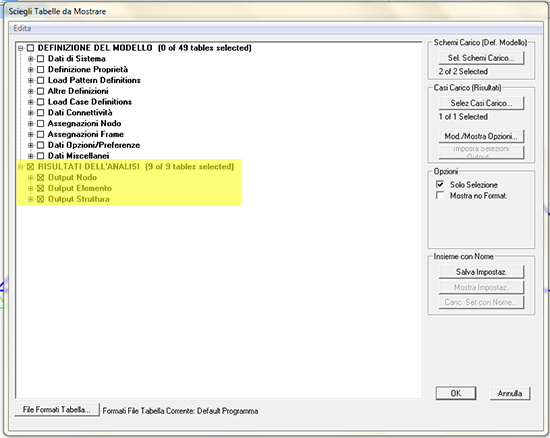
Diamo l'OK e appaiono le tabelle. Possiamo salvare quella che ci interessa o tutte quante, ma lo vedremo meglio nella struttura 3D

TRAVE RETICOLARE SPAZIALE

La struttura reticolare nello spazio che intendo analizzare è un anello costituito dalla ripetizione di un modulo costituito da tre campate reticolari a piramide ripetuto attorno ad un centro posto a circa 40 metri di distanza. La struttura è composta da 50 ripetizioni di questo modulo.

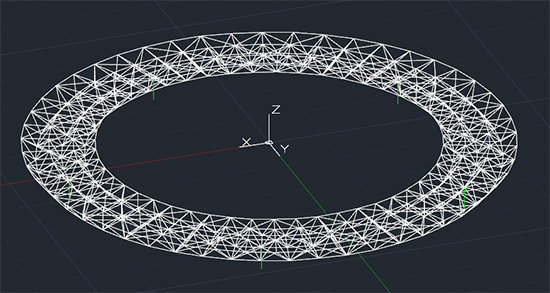
Nel disegnare questa struttura occorre prestare grande attenzione alle controventature delle basi delle piramidi che nel modulo adiacente devono essere specchiate.

Dal momento che vorrei che questo anello fosse sostenuto da 5 pilastri (in corrispondenza dei quali posizionerò delle cerniere) per facilitarmi la vita in SAP, creerò in AutoCAD delle aste "segnaposto" che individueranno i nodi su cui inserire le cerniere e che eliminerò appena apposti i vincoli esterni.

Per l' importazione in SAP ho avuto cura di posizionare tutto su un livello diverso dal livello 0 e soprattutto, dal momento che ho fatto largo uso per la modellazione di questa struttura del comando SERIE POLARE, è stato necessario esplodere le serie create in modo da avere ogni asta come elemento separato. Viceversa SAP non leggerà gli elementi non esplosi.

Il salvataggio del file nel formato DXF non comporterà problemi nell' importazione in SAP

Scelto il tipo di file da importare (AutoCAD DXF) in SAP mi si apre la finestrella in cui specificare la direzione dell' asse verso l'alto (lascerò Z di default) e le unità di misura

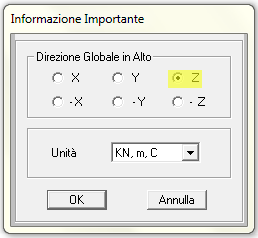
Mi si apre quindi la finestra in cui devo scegliere cosa importare e da quale livello di AutoCAD. Importerò i telai dal livello "anello reticolare".

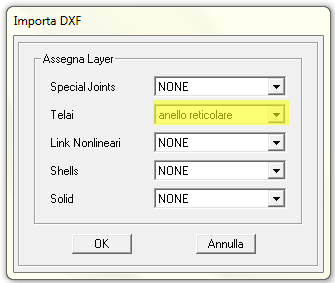
L' importazione non ha comportato grossi problemi

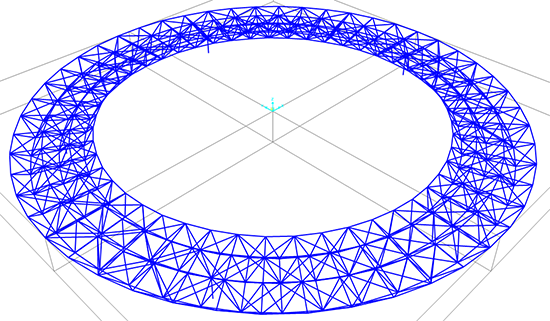
ora andrò a selezionare i nodi dai quali pendono delle aste con estremo libero che mi servivano da "segnaposto" e gli assegno i vincoli esterni cliccando su
ASSEGNA -> NODI -> VINCOLI ESTERNI

All' apertura della finestra posso selezionare il vincolo di cerniera e vedrò che vengono inibite le traslazioni sui tre assi del sistema di riferimento locale. Premo OK e procedo a cancellare le aste "segnaposto".

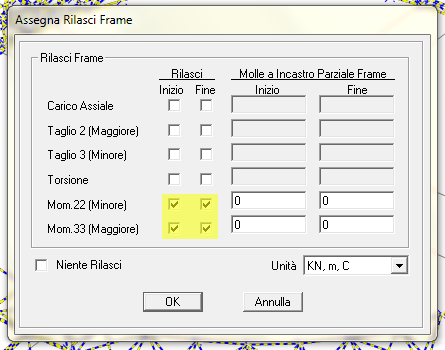
Il prossimo passo è quello di definire i vincoli interni tra le aste. Come visto prima per la trave piana selezionerò tutto (le modifiche avranno efficacia solo sui nodi) e andrò su ASSEGNA -> FRAME -> RILASCI,RIGIDEZZE PARZIALI e nella finestra di dialogo che si apre devo spuntare oltre a MOMENTO 3-3 INIZIO e FINE anche MOMENTO 2 - 2 INIZIO E FINE, perchè altrimenti le cerniere sarebbero delle cerniere cilindiriche.

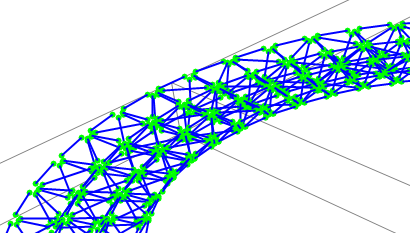
Vado ora a fissare i carichi sui nodi. Immaginiamo che questa struttura costituisca il sostegno di un edificio ad un piano a forma di corona circolare il cui corpo è di 15 metri ed il raggio è di 40. Su ciascun nodo grava il carico ripartito su un'area che è pari a circa 5 mt x 5 mt ovvero 25 mq il prodotto di quest' area per la somma dei carichi permanenti e dei carichi accidentali mi darà il valore in KN del carico puntuale su ciascun nodo (non sto volutamente considerando il peso proprio della struttura).

Supponiamo che il carico sia di 10 KN/Mq, il carico puntuale sarà 250 KN.

Associare il carico puntuale ai nodi è facile in questo caso perchè tutti i nodi su cui grava il carico sono sul piano superiore, passo quindi alla vista XY e seleziono tutto e poi vi associo un carico come ho fatto nella trave reticolare piana

Il carico è puntuale diretto come z e verso il basso di 250 KN.

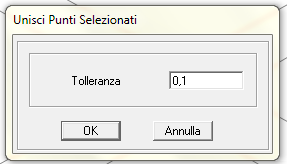
Prima di procedere, per evitare problemi nel calcolo, visto che il modello è stato importato da un software esterno, seleziono tutto e saldo i nodi con la tolleranza di default, in modo che se ci sono stati dei problemi di disegno si risolvano. Per farlo vado su EDITA -> EDITA PUNTI -> UNISCI NODI

Ora è fondamentale associare a ciascuna asta una sezione ed un materiale

Vado su ASSEGNA -> FRAME -> SEZIONI FRAME

e aggiungo una nuova proprietà, le do un nome (sezione) e scelgo il tubo. COme diametro darò 30 cm e lo spessore sarà di 2,5 cm. Il materiale è l'acciaio di default.
 

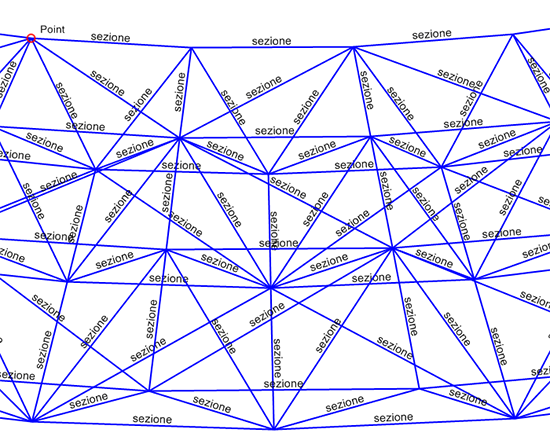
Posso effettuare i calcoli andando su ANALIZZA ed eseguendo solo il caso di carico che ho creato io.

QUesta è la geometria deformata rispetto alla geometria indeformata.

Prima di passare alle tabelle dei dati vediamo i diagrammi

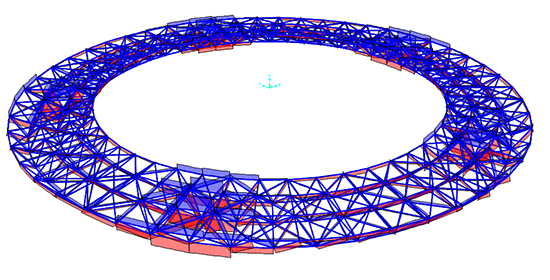
Le più sollecitate in sforzo normale sembrano essere le aste più vicine ai pilastri (ai vincoli)

Facendo i diagrammi dei momenti si rileva che non ve ne sono sulle aste, il che la conferma come una struttura reticolare.

Con la scorciatoia CTRL+T passo alla visualizzazione delle tabelle dei dati.

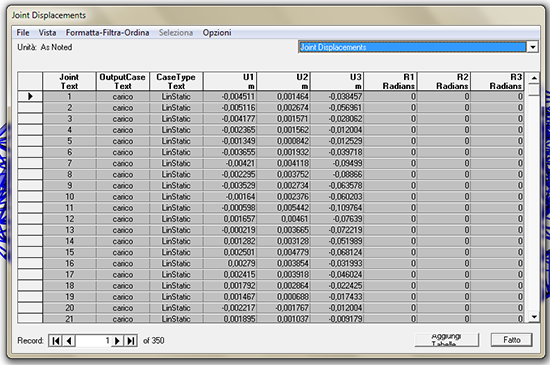
Uno dei dati che mi interessa di più è valutare se sono tollerabili gli spostamenti verticali massimi dei nodi, dal momento che, se questa trave deve sostenere un corpo di fabbrica, se in alcuni punti essa si imbarca troppo è chiaro che questo avrebbe delle ripercussioni su quanto è sostenuto.

Esporto quindi la tabella JOINT DISPLACEMENT in excel e la riordino in senso crescente poichè è plausibile che gli spostamenti maggiori si avranno in senso negativo
 

vi sono 10 nodi che si spostano di 10 cm ed è questo il massimo spostamento verticale verso il basso. Diciamo che su una struttura dal raggio di 40 metri composta da aste di 5 metri circa può essere accettabile (???), c'è da tenere conto che sto trascurando il peso proprio, che in una struttura di tubolari di 5 metri per 30 centrimetri di diametro, con una parete del tubolare dello spessore di 2 cm di acciaio probabilmente non è trascurabile.

Se volessi migliorare il comportamento di questa struttura, diminuendo lo spostamento di questi nodi potrei aumentare la sezione o lo spessore della parete dei tubolari.

Per ora mi fermo qui, rendo disponibili le tabelle per il download a chi fosse interessato.

FILE EXCEL

RESISTENZA DELLE ASTE ALLA TENSIONE (A SPANNE)

Esportando la tabella ELEMENT STRESSES - FRAMES possiamo vedere tra i valori le tensioni massime per ciascun' asta in diversi punti.

Il valore massimo della tensione riguarda alcuni elementi 243645,64 N/m² . L' acciaio utilizzato da SAP è contrassegnato da un codice, che termina con Y50 che dovrebbe indicare la resistenza del materiale espressa in KSI che è l'unità di misura nel sistema anglosassone.

Un pò di equivalenze, sperando che siano corrette:

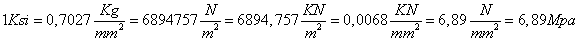
Per cui quel tipo di acciaio ha una resistenza di 50 x 6,89 Mpa = 344737,85 KN/m² che è superiore alla tensione massima individuata da SAP.

La tensione massima si riscontra ancora nelle vicinanze dei pilastri