STRUTTURA IN CEMENTO ARMATO
Innanzitutto disegniamo la carpenteria, andando ad individuare la trave più sollecitata:
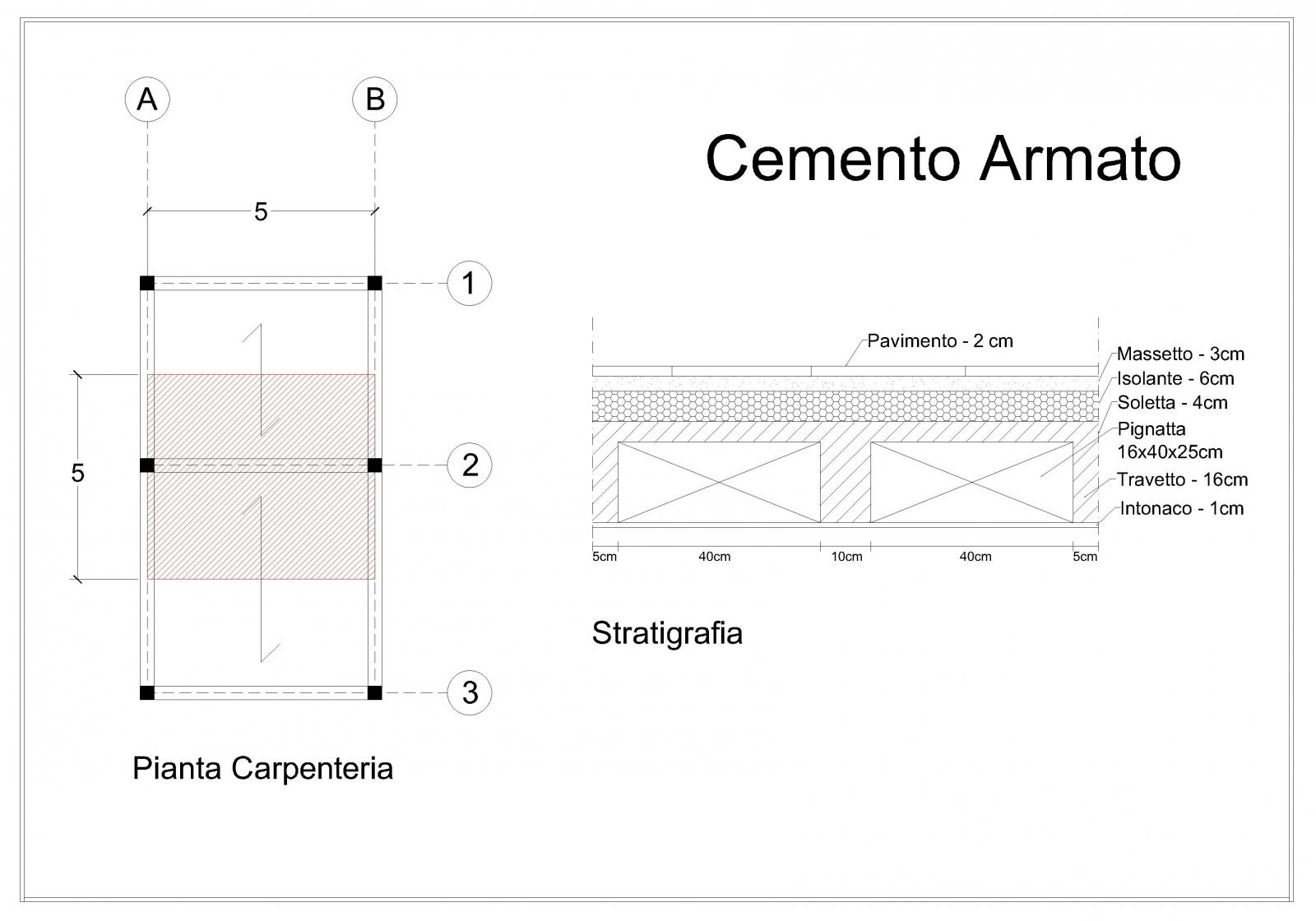
La zona tratteggiata in rosso è l’area di pertinenza della trave che abbiamo individuato, con un valore di interasse pari a 5 metri.
Apriamo adesso il nostro file Excel e selezioniamo il foglio destinato al dimensionamento delle strutture in cemento armato.
Il foglio è strutturato in modo che le celle in cui vanno inseriti i dati siano azzurrine, mentre quelle di calcolo automatico bianche.
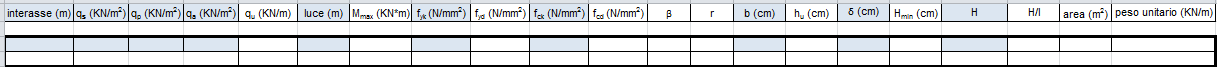
Il primo dato da inserire è proprio l’interasse.
Successivamente ci vengono richiesti i carichi agenti sul solaio:
qs: carico strutturale, ovvero il carico dovuto al peso proprio della parte strutturale del solaio;
qp: carico permanente, ovvero il carico dovuto agli ulteriori strati componenti il solaio che non hanno funzione strutturale, ai tramezzi, agli impianti, a tutto ciò in sostanza che grava in modo permanente sulla parte strutturale;
qa: carico accidentale, sono regolati dalla normativa, e possono comprendere i carichi di esercizio, il sisma etc.
Per l’analisi dei carichi prendiamo in considerazione un metro quadro di solaio, di cui nell’immagine di sopra riportiamo la sezione con gli spessori dei vari strati.
Per calcolare il peso su un metro quadro di ogni materiale, dobbiamo conoscere il suo peso specifico, solitamente espresso in KN/m3, e moltiplicarlo per il suo volume contenuto in un metro quadro (m3/m2).
Iniziamo con il carico strutturale: nel caso del cemento armato, la funzione strutturale è svolta dalla soletta in cls, dalle pignatte, e dai travetti.
I pesi specifici che adesso ci servono sono dunque:
Calcestruzzo: 24 KN/m3
Pignatta 16x40x25: 8 kg/cad
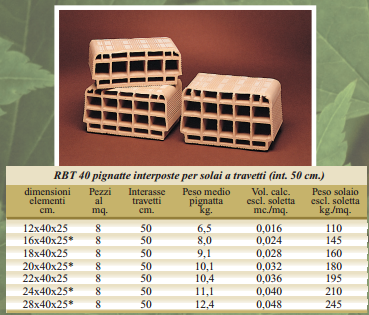
Calcoliamo [volume/m2 x peso specifico]:
qs Soletta: (0.04m x 1m x 1m)/m2 x 24 KN/m3 = 0.96 KN/m2
qs Pignatte: 2 x 4 x 8 kg/m2 = 64 kg/m2 x 10-2= 0.64 KN/m2
qs Travetti: (0.16m x 0.2m x 1m)/m2 x 24 KN/m3 = 0.768 KN/m2
qs Tot= 0.96 KN/m2 + 0. 64 KN/m2 + 0.768 KN/m2= 2.368 KN/m2
Andiamo dunque ad inserire il dato ottenuto nella tabella Excel, sotto il valore qs.
Calcoliamo ora i carichi permanenti. In questa categoria, come già detto, ricadono tutti i pesi fissi agenti sulla parte strutturale, come gli intonaci, le mattonelle, i massetti di livellamento, gli impianti e i tramezzi divisori interni. Di questi ultimi due in particolare non andremo a fare un calcolo esatto, ma aggiungeremo al totale raggiunto 1kN/m2 per i tramezzi e 0,5 kN/m2 per gli impianti, poiché sono dati difficili da calcolare e , come nel caso dei tramezzi, possono mutare nel tempo.
Per i carichi permanenti, i pesi specifici di cui necessitiamo sono:
Mattonelle in ceramica: 31,250 KN/m3
Massetto: 2000 Kg/m3= 2000 x 10-2 KN/m3 = 20 KN/m3
Isolante: 30 Kg/m3 = 30 x 10-2 KN/m3 = 0.3 KN/m3
Intonaco: 18 KN/m2
Calcoliamo:
qp Pavimento: (0.02m x 1m x 1m)/m2 x 31.250 KN/m3 = 0.625 KN/m2
qp Massetto: (0.03m x 1m x 1m)/m2 x 20 KN/m3 = 0.6KN/m2
qp Isolante: (0.06m x 1m x 1m)/m2 x 0.3 KN/m3 = 0.018 KN/m2
qp Intonaco: (0.01m x 1m x 1m)/m2 x 18 KN/m3 = 0.18 KN/m2
qp Tot= 0.625 KN/m2 + 0.6KN/m2+ 0.018 KN/m2 = 1.423 KN/m2 (+ 1 KN/m2 + 0.5 KN/m2) = 2.923 KN/m2
Per quanto riguarda i carichi accidentali qa, la normativa per il residenziale prevede 2 KN/m2.
Inseriamo questi ultimi due dati nella tabella, e il valore della luce che è pari a 5m.

Il foglio di calcolo ci ha calcolato il q ultimo come somma dei tre carichi (strutturale, permanente e accidentale) moltiplicati ognuno per un coefficiente di sicurezza dettato dalle normative, il tutto moltiplicato per l’interasse; inoltre viene calcolato anche il Momento massimo tenendo in considerazione che la trave è una trave appoggiata e che quindi Mmax= ql2/8.
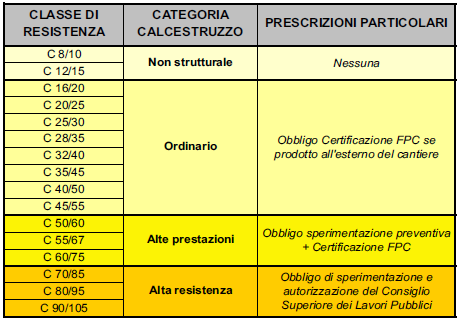
Il secondo passo è introdurre le tensioni caratteristiche del calcestruzzo e dell’acciaio fyk (N/mm2) e fck (N/mm2) in base alla tipologia che scegliamo.
Nel nostro caso, scegliamo l’acciaio da armatura B450A con fyk=450 e il calcestruzzo di classe C45/55 (C di Concrete) in cui il primo numero individua il valore caratteristico di resistenza cilindrica a compressione monoassiale fck =45 mentre il secondo identifica quella cubica Rck = 55.
Una volta inseriti i dati nella tabella Excel, otteniamo la resistenza di progetto dell’acciaio fyd come il rapporto tra fyk e il coefficiente parziale di sicurezza relativo all’acciaio da armatura di valore 1,15; mentre la resistenza di progetto del calcestruzzo fcd viene calcolata come il rapporto tra fck e il coefficiente parziale di sicurezza per il calcestruzzo (pari a 1,5) il tutto moltiplicato per α= 0.85 (coefficiente riduttivo per le resistenze di lunga durata).
I valori β ed r vengono calcolati anche loro automaticamente in base ai risultati ottenuti; l’ultimo dato da inserire è la base, ipotizzando di mantenere un δ (copriferro dell’armatura inferiore) uguale a 5cm.

Ipotizziamo dunque una b= 25cm. Automaticamente, il foglio di calcolo trova l’altezza utile Hu e dunque, sommandoci il δ, l’altezza minima Hmin in cm. In base a questo valore, andiamo ad ingegnerizzare la trave inserendo il valore di H come la decina subito superiore di Hmin e controllando che il foglio di calcolo dia “Verificato”.
La sezione così progettata risulta effettivamente verificata se oltre ai carichi già calcolati, è in grado di sopportare anche il peso proprio, di cui troviamo il valore alla fine della riga sui cui abbiamo lavorato fino ad ora.
Nella riga sottostante infatti, come possiamo notare, non vi sono presenti caselle azzurre, ovvero quelle modificabili, ma solo caselle di calcolo bianche. Proprio in questa riga, nella casella del carico ultimo, viene aggiunto al valore precedentemente calcolato il peso proprio moltiplicato per un fattore di sicurezza 1.3 e in base al risultato vengono rieffettutati tutti i calcoli fino ad arrivare ad una nuova Hmin. Se il risultato di questi calcoli automatici porta ad una Hmin comunque inferiore al valore ingegnerizzato, la trave è verificata.
(Questi calcoli con il peso proprio si effettuano solo sul cls in quanto le travi in legno e in acciaio hanno un peso proprio più piccolo tale da non far incrementare troppo il momento flettente.)
Proviamo a fare il calcolo adesso su una struttura in legno.
STRUTTURA IN LEGNO
Innanzitutto, notiamo dopo una prima occhiata al foglio di calcolo dedicato al legno, che i dati in questo caso da calcolare (ovvero le celle bianche) sono di meno rispetto al cemento armato, poiché andiamo a lavorare con un solo materiale. Avremo però dei coefficienti differenti, perché nel caso del legno bisogna tenere conto di determinati valori come l’umidità del luogo in cui opererà, o l’effetto della durata del carico.

I dati di cui necessitiamo sono quindi i seguenti:
- Interasse
- Carichi strutturali
- Carichi permanenti
- Carichi accidentali
- Luce
- fm,k ovvero la resistenza caratteristica a flessione del legno scelto
- kmod ovvero il coefficiente che tiene conto di umidità e tempo e che viene dato dalla normativa
- γ m ovvero il coefficiente parziale di sicurezza dipendente dal materiale
- Base
Ipotizzando questa pianta di carpenteria e questa sezione di solaio, iniziamo a calcolare i carichi strutturali seguendo il procedimento utilizzato per il cemento armato:
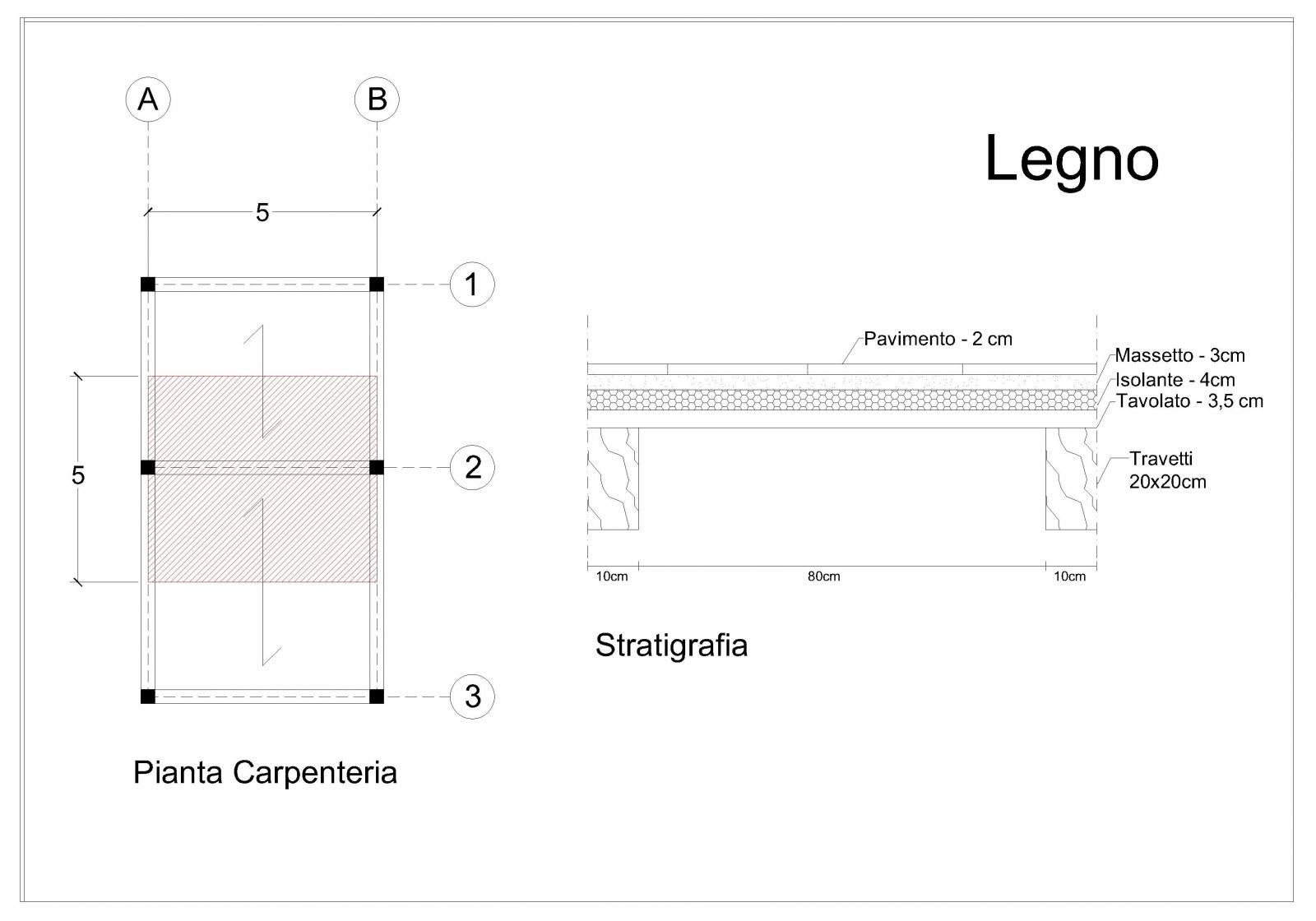
Per trovare il peso specifico del legno, devo sceglierne una classe: utilizzo in questo caso il legno lamellare GL24C, il più comunemente usato, che ha un peso specifico = 350kg/m3= 350 x 10-2 KN/m3 = 3,5 KN/ m3 e una fm,k = 24.
qs Travetti: 2(0.2m x 0.1m x 1m)/m2 x 3,5 KN/m3 = 0.14 KN/m2
qs Tavolato: 0.035m x 0.1m x 1m/m2 x 3,5 KN/m3 = 0.1225 KN/m2
qs Tot: 0.14 KN/m2 + 0.1225 KN/m2 = 0.2625 KN/m2
Per i carichi permanenti, i pesi specifici di cui necessitiamo sono:
Isolante: 30 Kg/m3 = 30 x 10-2 KN/m3 = 0.3 KN/m3
Massetto alleggerito: 11 KN/m3
Pavimento legno duro: 850 kg/m3= 850 x 10-3 KN/m3= 8,5 KN/m3
Calcoliamo:
qp Isolante: (0.04m x 1m x 1m)/m2 x 0.3 KN/m3 = 0.012 KN/m2
qp Massetto: (0.03m x 1m x 1m)/m2 x 11 KN/m3 = 0.33 KN/m2
qp Pavimento legno duro: (0.02m x 1m x 1m)/m2 x 8.5 KN/m3 = 0.17 KN/m2
qp Tot= 0.012 KN/m2 + 0.33 KN/m2 + 0.17 KN/m2= 0.512 KN/m2 (+ 1 KN/m2 + 0.5 KN/m2) = 2.012 KN/m2
Inseriamo nel foglio Excel interasse, carichi strutturali, carichi permanenti, carichi accidentali, luce e fm,k = 24 (dato dalla normativa in base alla classe scelta).
Rimangono tre dati da inserire: Kmod, γ m e la base.
Per quanto riguarda i primi due, essi sono dettati dalle normative; Kmod tiene conto della durata del carico a cui dovrà essere sottoposta la trave tramite le cinque “Classi di durata del carico” e delle condizioni climatiche in cui dovrà agire tramite le tre “Classi di Servizio” ; γ m invece è il coefficiente parziale di sicurezza relativo al materiale scelto.
Per quanto riguarda la base ipotizziamo b=30.
Nel foglio di calcolo otterremo quindi questi risultati, con una Ingegnerizzazione di H= 55cm.

STRUTTURA IN ACCIAIO
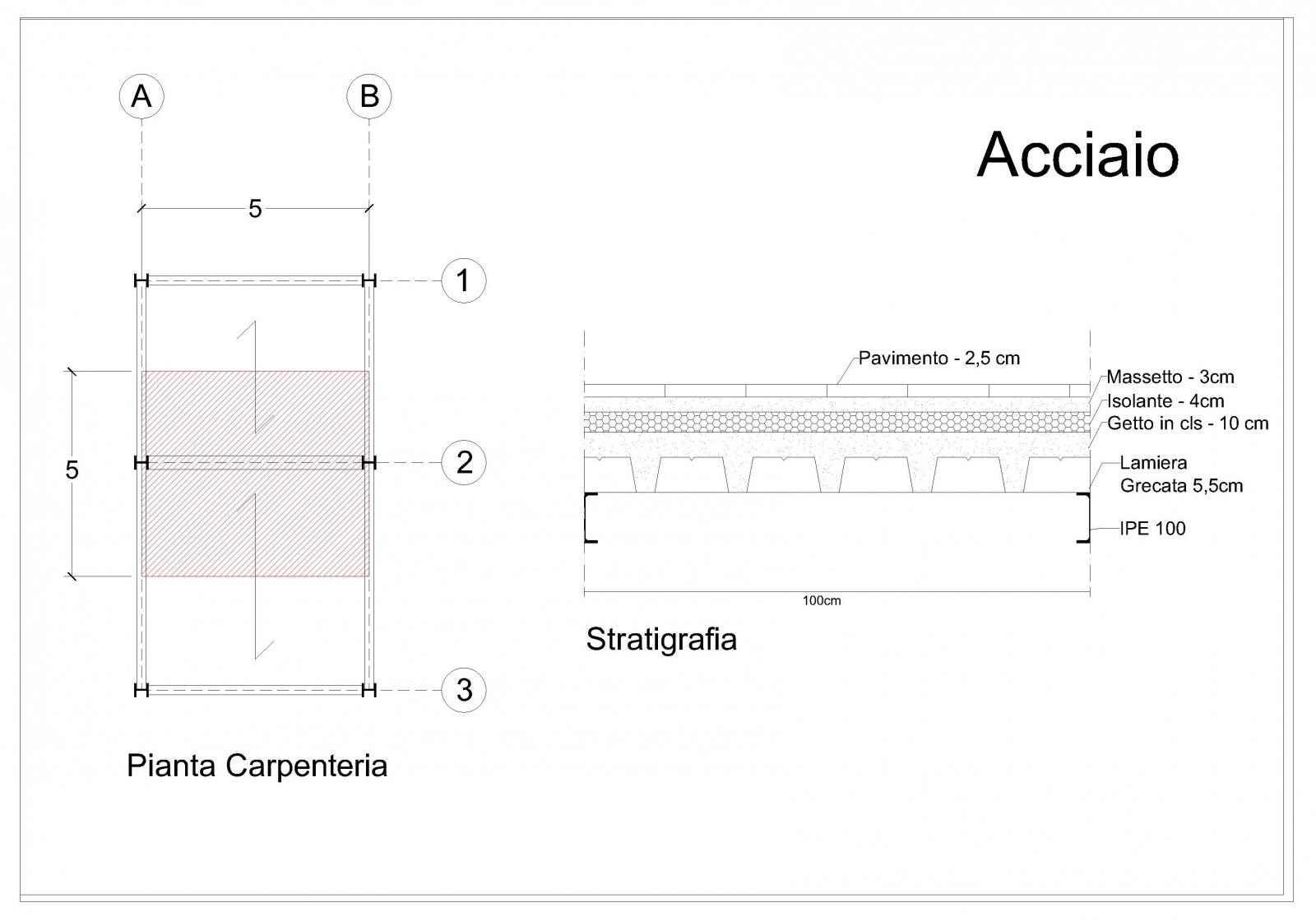
Utilizziamo il procedimento fino ad ora seguito ed andiamo a calcolare i carichi strutturali e permanenti, sapendo che il peso specifico dell’acciaio è 78 KN/m3
qs IPE 100: (0.00103 m2 x 1m) /m2 x 78 KN/m3 = 0.08 KN/m2
qs Lamiera Grecata + Soletta: 9.16 Kg/m3 + 190 kg/m2 = 199.16 Kg/m2= 1.9916 KN/m2
qs tot: 0.08 KN/m2 + 1.9916 KN/m2= 2.07194 KN/m2
qp Isolante: (0.04m x 1m x 1m)/m2 x 0.3 KN/m3 = 0.012 KN/m2
qp Massetto: (0.03m x 1m x 1m)/m2 x 11 KN/m3 = 0.33 KN/m2
qp Pavimento : (0.025m x 1m x 1m)/m2 x 8.5 KN/m3 = 0.21 KN/m2
qp Tot= 0.012 KN/m2 + 0.33 KN/m2 + 0.21 KN/m2= 0.5545 KN/m2 (+ 1 KN/m2 + 0.5 KN/m2) = 2.0545 KN/m2
Dopo aver inserito i carichi, l’interasse e la luce all’interno della tabella Excel, viene calcolato il Momento ql^2/8 e non ci rimane altro che scegliere la nostra classe di resistenza.
Nel nostro caso, proviamo ad utilizzare la classe più bassa, ovvero l’acciaio S235 con una resistenza caratteristica fy,k = 235.
Andando ad inserire questo valore, ci viene calcolata subito la tensione di progetto fd = fy,k / γ s , in cui γ s è il coefficiente parziale di sicurezza (simile a quello che abbiamo trovato nella tensione di progetto del legno) che in questo caso è = 1.05; viene calcolato inoltre il Modulo di resistenza a flessione Wxmin, che è uguale al rapporto tra il Momento massimo e la tensione di progetto fd.

Controlliamo dunque nella tabella dei profilati IPE quale abbia un valore di Wxmin superiore a quello ottenuto e scopriamo così quale profilo è il più adatto alla situazione, nel nostro caso l’IPE 330.
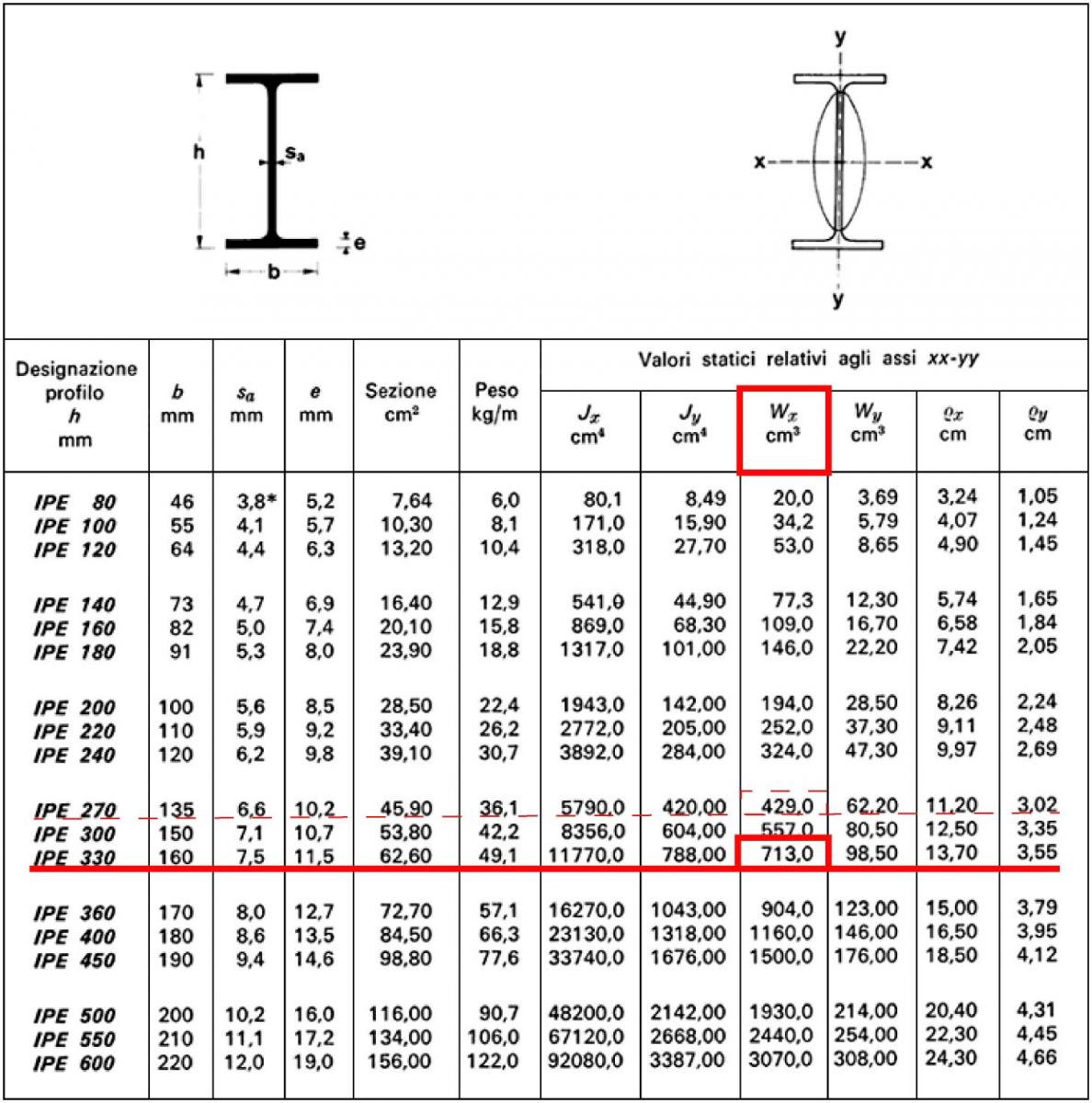
Ovviamente, andando a scegliere una classe di resistenza dell’acciaio più alta, come ad esempio la S355, il modulo di resistenza a flessione risulterà più piccolo, essendo loro inversamente proporzionali, e potremmo scegliere un profilato con dimensioni più piccole, in questo caso sarebbe sufficiente una IPE 270 (tratteggiato nella tabella).

Commenti recenti