Terza Esercitazione - Dimensionamento di una Trave a Sbalzo e verifica a Deformabilità

In questa terza esercitazione andremo a dimensionare una trave a sbalzo, comunemente detta mensola, nelle tre principali tecnologie (Legno, Acciaio, Cemento Armato).

La prima parte di dimensionamento ha un procedimento simile a quello utilizzato nella prima esercitazione, rimando dunque QUI per il calcolo di :

• carichi
• momento massimo (ricordando però che in questo caso ci troviamo in uno schema statico differente e che quindi il Momento nell'incastro sarà ql²/2 e non più ql²/8)
• altezza minima (e conseguente ingegnerizzazione della sezione).

Una volta terminata questa prima fase, dobbiamo controllare che nell'estremo libero la mensola non si abbassi troppo, operando non più dunque allo SLU (Stato Limite Ultimo), ma allo SLE (Stato Limite d'Esercizio) in modo da controllare che gli spostamenti non impediscano l'utilizzo della costruzione.

Operiamo:

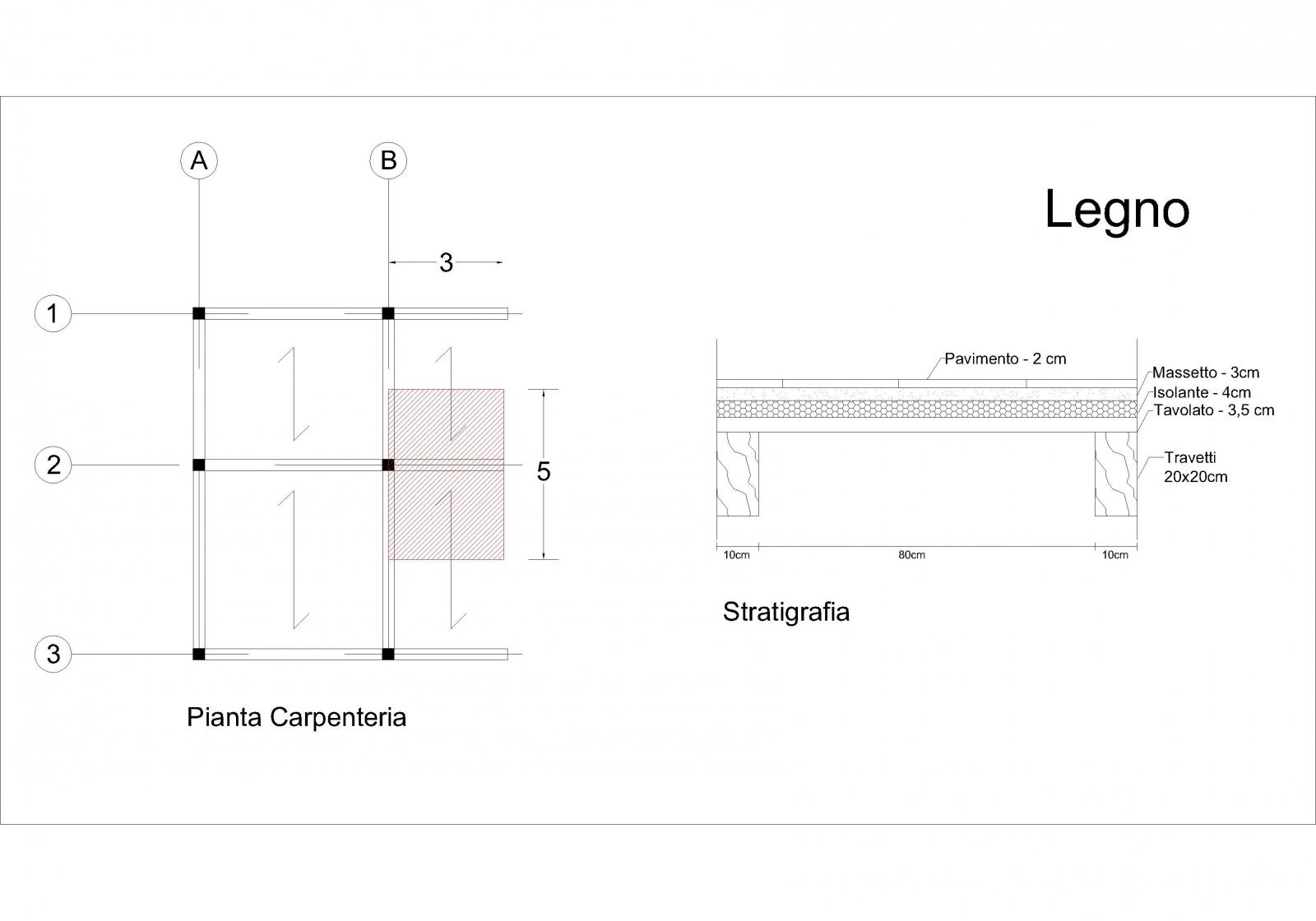
• Abbiamo l'altezza della sezione ingegnerizzata con una base di 30cm: 50cm
• Inseriamo informazioni sul materiale : E (modulo elastico di Young) = 8000 N/mm2
• Viene calcolata l'inerzia come b x h³/12= 312500 cm⁴
• Viene calcolato il carico di esercizio q_e=(q_s+q_p+ ψ₁₁xq_a) x interasse = 16KN/m
• Una volta ottenuto il carico totale allo SLE e specificato il modulo elastico E e il momento d'inerzia I_x, possiamo calcolare lo spostamento massimo per la mensola V_max = ql⁴/8EI_x = 0,66cm

La sezione risulta verificata in quanto il rapporto tra la luce e lo spostamento massimo per le travi deve essere maggiore di 250.

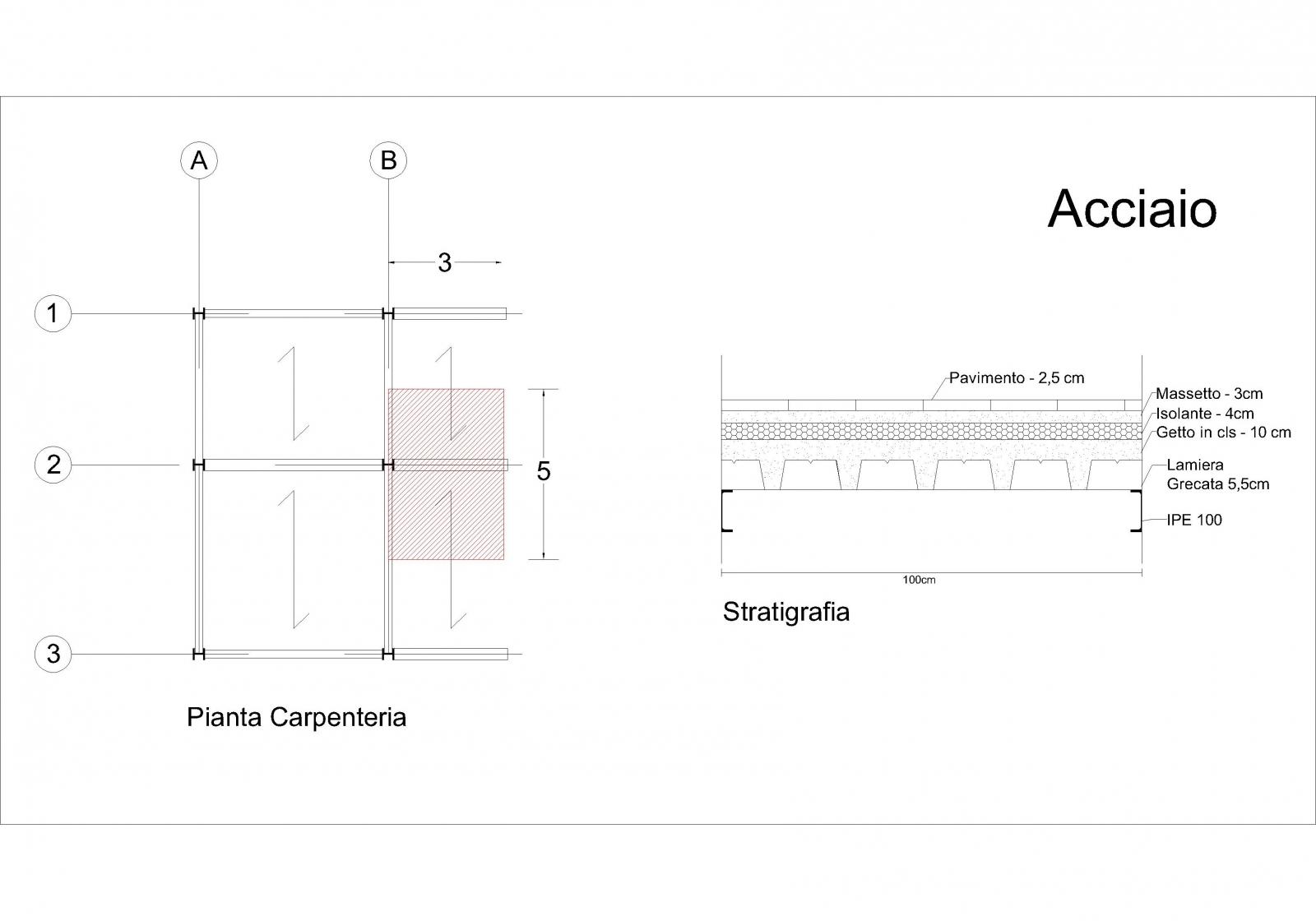
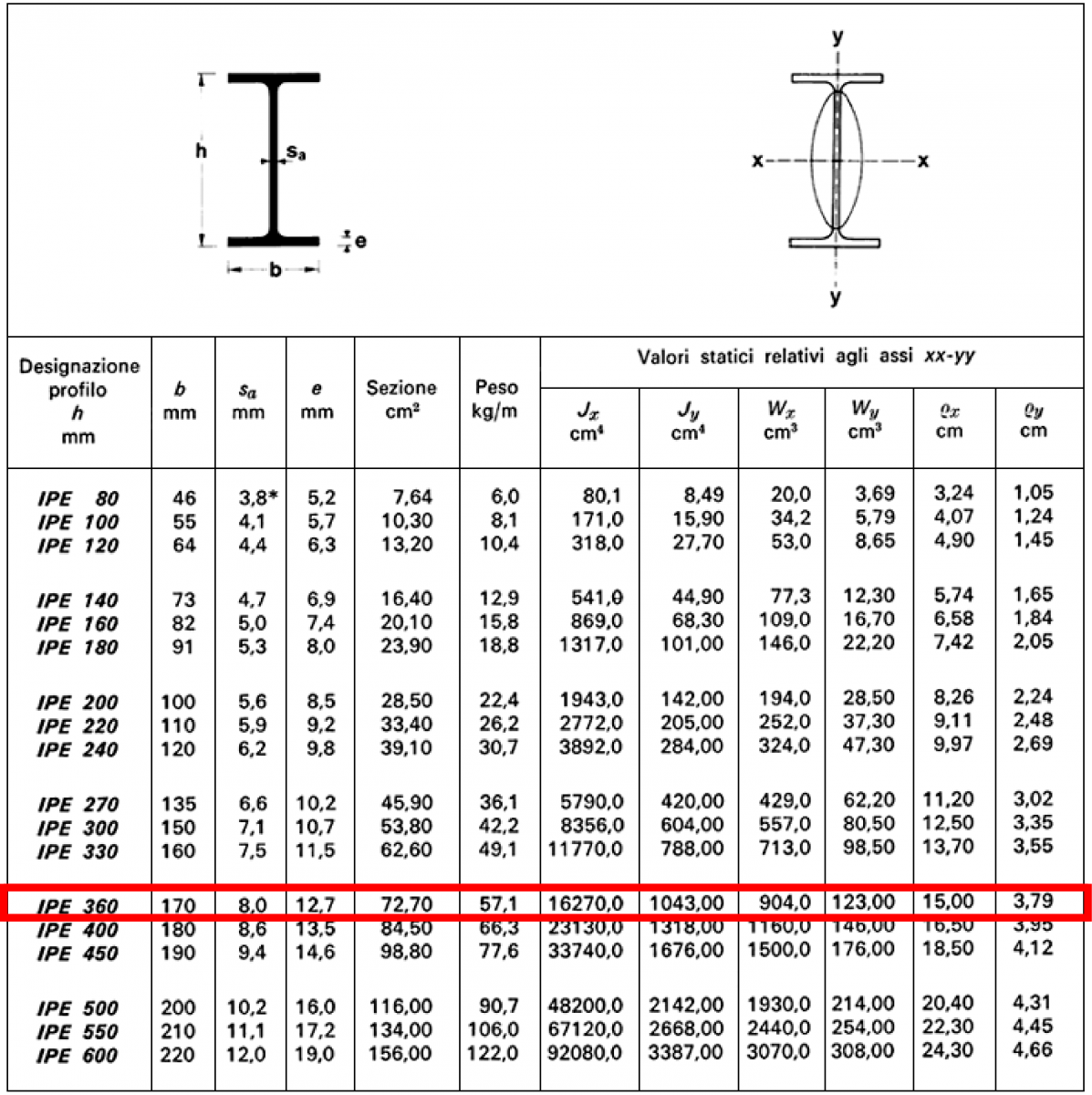
• Con i calcoli della prima esercitazione abbiamo ottenuto il modulo di resistenza a flessione W_x e ingegnerizzato la sezione come IPE 360.
• Inseriamo nel foglio il relativo modulo di inerzia I ricavato dalla tabella dei profilati.
• Sempre dalla tabella dei profilati ricaviamo anche il peso proprio e lo inseriamo nel foglio, stando attenti a portare i kg/m in kN/m
• Il foglio calcola il carico di esercizio q_e=(q_s+q_p+ ψ₁₁xq_a) x interasse + peso = 26,2032KN/m
• Inseriamo il modulo elastico dell'acciaio E=210000N/mm²
• Una volta ottenuto il carico totale allo SLE e specificato il modulo elastico E e il momento d'inerzia I_x, possiamo calcolare lo spostamento massimo per la mensola v_max= ql⁴/8EI_x = 0,77cm

La sezione è verificata in quanto il rapporto tra la luce e lo spostamento massimo per le travi risulta maggiore di 250.

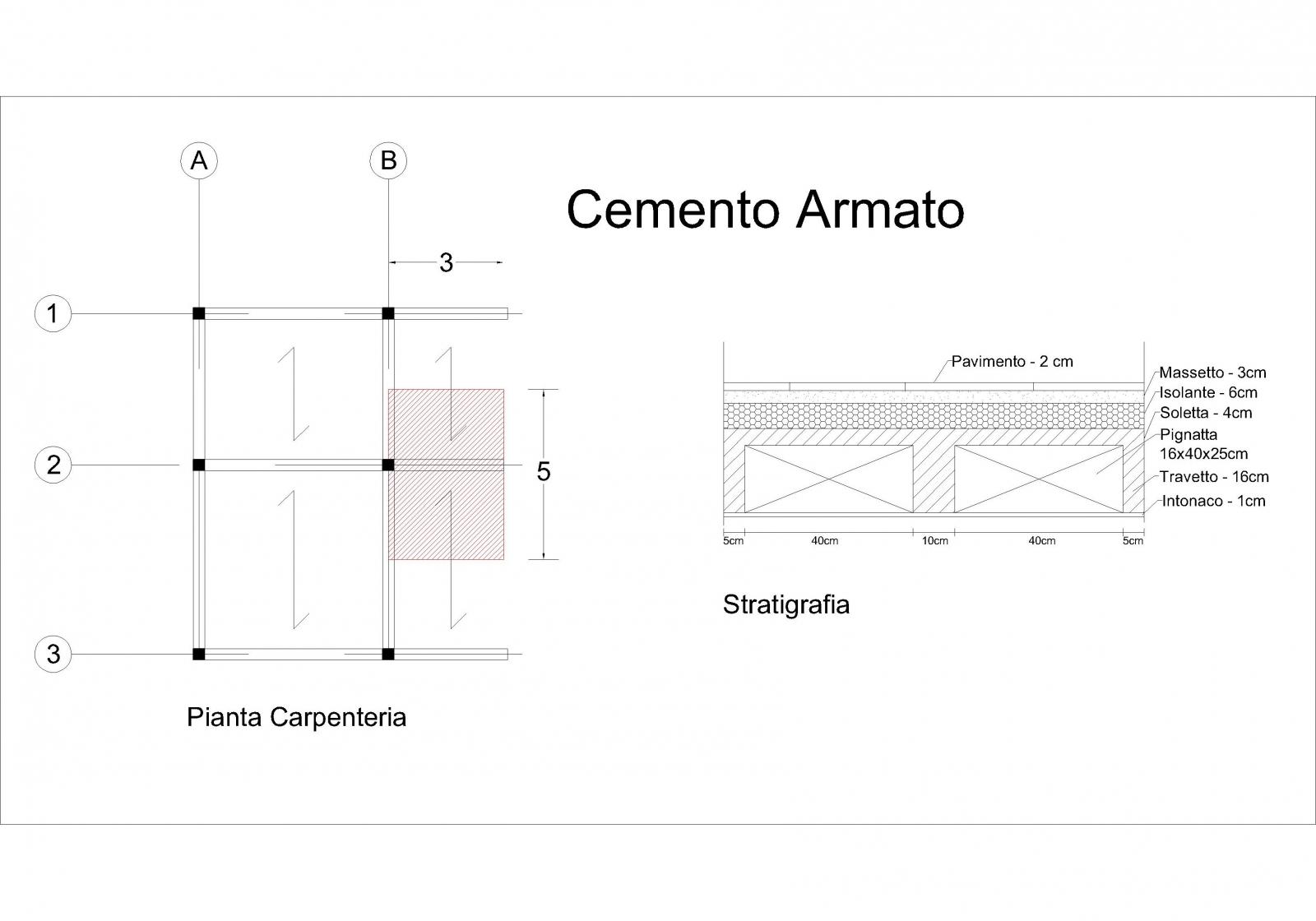
• Con la prima esercitazione avevamo ingegnerizzato l'altezza tenendo già in considerazione il peso proprio della trave.

Inseriamo adesso le ultime informazioni che sono necessarie:

• Area = b x h = 0.18m²
• Peso= b x h x peso specifico del CLS (2500kN/m³) = 4.38 kN/m
• Carico d'esercizio  q_e=(q_s+q_p+ ψ₁₁xq_a) x interasse + peso = 35.83 kN/m
• Inseriamo il modulo elastico del CLS E=21000 N/mm²
• Il foglio calcola l'inerzia I_x= b x h³/12= 714583 cm⁴
• Una volta ottenuto il carico totale allo SLE e specificato il modulo elastico E e il momento d'inerzia I_x, possiamo calcolare lo spostamento massimo per la mensola v_max= ql⁴/8EI_x = 0,24cm

La sezione è verificata in quanto il rapporto tra la luce e lo spostamento massimo risulta maggiore di 250.