blog di Giovanna

 

 

 

 

 

 

 

L’esercitazione prevede il dimensionamento di una mensola nelle tre tecnologie: legno, acciaio e cls armato.

Osservando la struttura è evidente che la mensola su cui grava più carico è quella centrale e la sua area è pari a 6 m², con Luce = 2m e Interasse = 3m

Iniziamo il calcolo prendendo come riferimento gli stessi carichi dell’ Esercitazione 1 - Dimensionamento di una trave in Legno, Acciaio e Cls Armato

(vedi collegamento Esercitazione 1 - Dimensionamento Trave)

Legno

Scelta degli elementi di calcolo

• Carico strutturale: qs = 0,438 kN/m²
• Carico permanente: qp = 2,69 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 15,2088 kN/m

Inserendo la luce l=2 m, possiamo ricavare il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

Dobbiamo scegliere:

1– La tipologia di legno: Legno lamellare GL 24h con

     resistenza a flessione caratteristica fm,k = 24 MPa    

2 – coefficiente della durata del carico kmod = 0,8 (fornito dalla normativa)

3 – coefficiente parziale di sicurezza del materiale γm = 1,45 (legno lamellare) con questi dati possiamo calcolare la tensione ammissibile f_d c (N/mm²) = fm,k x kmod / γm

4 – impostando la base b= 20 cm, ricaviamo l’altezza hmin:

hmin è il valore minimo che deve avere l’altezza della sezione, tale va ingegnerizzata cioè va scelto un valore di altezza superiore ad hmin, cioè H= 35 cm quindi non avendo considerato il peso proprio della trave è giusto scegliere la sezione con un profilo pari a 20 x 35 cm

5 – determiniamo il valore del modulo elastico E = 8.000 N/mm²

6 – il foglio excel ci determina il momento d’inerzia I_x = b x h³/12 e i carichi incidenti come q_e = (q_s + q_p + q_a x 0,5) x i come vediamo non inseriamo il peso proprio del trave perché è materiale leggero (mentre verrà inserito per l’acciaio e il cls)

7– avendo ottenuto il carico totale q_e, specificato E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce:

Fase di verifica _ Limiti Di Deformabilità:

1 – la verifica è molto semplice dobbiamo determinare che il rapporto tra la luce e l’abbassamento sia maggiore o uguale a 250, quindi l/ v_max ≥ 250:

                                                                                La sezione 20 x 35 cm è stata verificata!

2- definiamo un altro esempio di sezione con base b=30 cm e poniamo un H=35 cm, come si vede dalla tabella il rapporto tra la luce e l’abbassamento è minore di 250 quindi la mensola supera i limiti di deformabilità:

                                                                                La sezione 30 x 35 cm non è verificata!

Acciaio

                                  

Scelta degli elementi di calcolo

• Carico strutturale: qs =  2,01 kN/m²
• Carico permanente: qp = 2,84 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 29,619 kN/m

Inseriamo la luce l= 2 m ricaviamo il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

1 - la tensione di snervamento del Fe 430/ S275 è fy,k = 275 MPa quindi otteniamo un modulo di resistenza pari a W_x,min = 226,18 cm³:

Dopo aver ottenuto il modulo di resistenza, per ingegnerizzare la sezione si inserisce nella colonna affianco il valore del momento d’inerzia I_x del profilo, che ha come modulo di resistenza W_x,min un valore maggiore di quello trovato:

Il profilo scelto è un IPE 220 con:

• Ix=2772 cm⁴;
• Peso=26,2 kg/m = 0,262 kN/m

2- Al carico totale q_e si inserisce il peso proprio dell’elemento strutturale e otteniamo:

3 – determiniamo il valore del modulo elastico E = 210.000 N/mm²

4– avendo ottenuto il carico totale q_e, specificato la luce l, E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce:

Fase di verifica _ Limiti Di Deformabilità

1 – Determiniamo che  il rapporto tra la luce e l’abbassamento deve essere maggiore o uguale a 250, quindi l/ v_max ≥ 250:

                                                                           Il profilo IPE 220 è stato verificato!

CLS

 

Scelta degli elementi di calcolo

• Carico strutturalo: qs =  2,368 kN/m²
• Carico permanente: qp = 2,654 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 30,18 kN/m

Inseriamo la luce l= 2 m ricaviamo il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

1 - acciaio per il cls: B450C avremo come tensione di snervamento fyk = 450 MPa, con queste scelte è possibile ricavare la tensione di progetto con la formula:           

fyd = fyk / γs

2 –tensione di progetto del cls fcd = αcc x fck/γc quindi fck = 60 MPa

3 – β = 0,53 e r = 2,14

4 – consideriamo una base b = 15 cm

otteniamo un Hmin pari a 28,29 cm, quindi ingegnerizzando possiamo scrivere H = 30 cm.

Quindi la sezione finale della trave in cls sarà 15 x 30 cm.

5 - Al carico totale q_e si inserisce il peso proprio dell’elemento strutturale

6 – determiniamo il valore del modulo elastico E = 21000 N/mm²

7 – avendo ottenuto il carico totale q_e, specificato la luce l, E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce l/ v_max ≥ 250:

Fase di verifica _ Limiti Di Deformabilità

1- Calcoliamo il peso unitario:

p = (0,15 x 0,30x 1) m³/m² x 25 kN/m³ = 1,125 kN/m²

quindi il carico totale con l’aggiunta del peso proprio del cls moltiplicato per 1,3 è

qu = 31,64 kN/m

                                                                             La sezione 15 x 30 cm è stata verificata!

 

 

Disegniamo la geometria 

SAP2000 è un programma che utilizza il metodo degli elementi finiti e si basa sulla Teoria di Eulero-Bernoulli. Per le unità di misura lavora con gruppi prestabiliti e  per questa esercitazione utilizzeremo kN,m,°C.

Per quanto riguarda gli assi utilizzeremo come ordinata z = gravità mentre come gli assi locali si decide tramite regola della mano destra:

                                                                       

Il programma ci permette di creare una struttura reticolare cubica o piramidale. Noi disegneremo quella cubica con:

1. New Model – Grid Only

Assi Locali:

X =3 m

Y =5 m

Z =2 m

Spazio Griglia:

X =2 m

Y =2 m

Z =2 m

           

2. Tasto Frame (per disegnare i lati e le diagonali del cubo)

Importante

-Prima di andare avanti con la struttura bisogna verificare che le aste non siano doppie:

Selezionare struttura – Edit –Merge Duplicates – OK

-Controllare che tutti i nodi siano uniti:

Selezionare la struttura – Edit – Edit Points - Merge Joints – 0,1 - OK

(0,1 = raggio entro cui tutti i nodi vicini coincidono nello stesso nodo)

Vincoli esterni

Vincoliamo esternamente la struttura con quattro cerniere agli spigoli esterni e assegniamo i vincoli interni alle aste:

-Assign – Joint – Restraints – selezionare la cerniera – OK

-Selezionare la struttura - Assign – Frame – Releases (accendere Moment 2-2 e 3-3) e ricontrollare l’unità di misura

          

          

Scelta del Profilo:

Selezionare la struttura – Assign – Frame – Frame Sections – Add New Property – Pipe Section – OK

           

 

Forze Concentrate

Dopo aver deciso di realizzare la struttura con dei tubolari in acciaio, l’ho caricata superiormente, con carichi di 50kN:

- Creare F ed eliminare il peso proprio:

Define – Load Patterns – “F” – (non considerare il peso proprio quindi scrivere 0 su "Self Weight Multiplier”) - cliccare su Add New Load Pattern – Selezionare il carico “F” – OK

- Assegnare il Carico 50kN:

Selezionare la parte superiore sella struttura – Assign – Joint Loads – Forces – Scegliere il carico F – Force Global Z – inserire –50kN – OK

          

 

Analisi della struttura - deformata

A questo punto, clicco Play per far partire l’analisi della struttura. Come vediamo dall’immagine la struttura si è deformata a causa del carico che ho ipotizzato dato che non ho considerato il peso proprio della struttura:

           

Analisi della struttura – sforzi normali

       

Tabella

Il programma SAP2000 riassume in una tabella tutti i valori che ho inserito e i relativi risultati. Il valore che ci interesserà  è lo Sforzo Normale (N) di ogni singola asta. Con SAP è possibile estrarre la tabella in formato Excel, così da facilitare i calcoli in seguito:

Display – Show Tables – Analysis Results – selezionare Select Load Patters, il carico F –Ok – Element Forces – Frames – File – Export Curren Table –To Excel – Labels – OK

Il sistema della tabella è molto semplice bisogna eliminare i valori che non vengono impiegati per il calcolo e lasciare:

lo sforzo normale = N

il numero delle aste = n°

le lunghezze delle aste = L

Dato che abbiamo scelto un cubo dobbiamo considerare solo le lunghezze di

 L=2 m (lati)

 L=2,82843 m (diagonali)

 

Dividiamo le Aste

Aste Tese _ Fase di Progetto

Prima cosa da fare è scegliere il tipo di acciaio dalla Normativa Tecnica per le costruzione – del 2008 ed identificare:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Il Coefficiente di sicurezza del materiale γm = 1,05
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ

Calcolare l’area minima che deve avere l’elemento: A_min = N/fd

Scegliamo dalla Tabella Profilati metallici (scaricabile dal sito Profili Acciaio) i profili con:

A_design > A_min

Per le aste a trazione ho scelto 3 tipi di profilati in acciaio:

A=2,54 cm² - 33,7 x 2,6 mm

A=3,94 cm² - 42,4 x 3,2 mm

A=5,74 cm² - 60,3 x 3,2 mm

Fase di verifica _ σ<fd o N/A<fd

Consideriamo l’asta più sollecitata:

N/A = 126130 N / 574 mm² = 219,73 N/mm²   

fd = 223,81MPa

                                                                              N/A≤fd è VERIFICATA!

Asta Compressa _ Fase di Progetto

1 Fase di Progetto _ I calcoli per trovare A_min in un asta a compressione sono uguali come per l’asta a trazione:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Coefficiente di sicurezza del materiale γm=1,05;
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ
• Calcolare l’area minima che deve avere l’elemento: A_min=N/fd

Per l’asta a compressione non basta la verifica dell’A_min, anzi bisogna considerare oltre alla rottura dell’asta anche lo sbandamento.

2 Fase di Progetto  _ Per questo bisogna considerare:

• Il modulo di elasticità del materiale E = 210000 MPa (acciaio);
• Lunghezza dell’asta l = 2m;
• Coefficiente del vincolo β= 1;
• Coefficiente di sicurezza del materiale γm=1,05;
• Sforzo Normale di progetto euleriano (kN) N_ed = N x γ
• Momento d’inerzia minimo (cm⁴) I_min = N_ed x (β x l)²/ π² x E

1-2 Fase di progetto_ Scegliere dalla Tabella dei Profili metallici:

• L’area di Progetto (cm²) A_design > A_min;
• Momento d’inerzia di progetto (cm⁴) I_design > I_min;
• Scrivere il raggio d’inerzia (cm)  ρ_design del profilo;
• Nell’asta di compressione bisogna conoscere la SNELLEZZA λ

Fase di Verifica  _ N/A < fd e λ ≤ 200

Asta n°67 più sollecitata

1- Come per l’asta a trazione verifichiamo anche per quella a compressione la più sollecitata:

N/A = -157445 N / 820 mm² = 192,0 N/mm²   

fd = 223,81MPa

                                                                             N/A≤fd è VERIFICATA!

2- Verifichiamo la snellezza λ ≤ 200 considerando sempre la stessa asta:

λ = 110,06

                                                                             λ ≤ 200 è VERIFICATA!

                                                                  ESERCITAZIONE

 

                                      

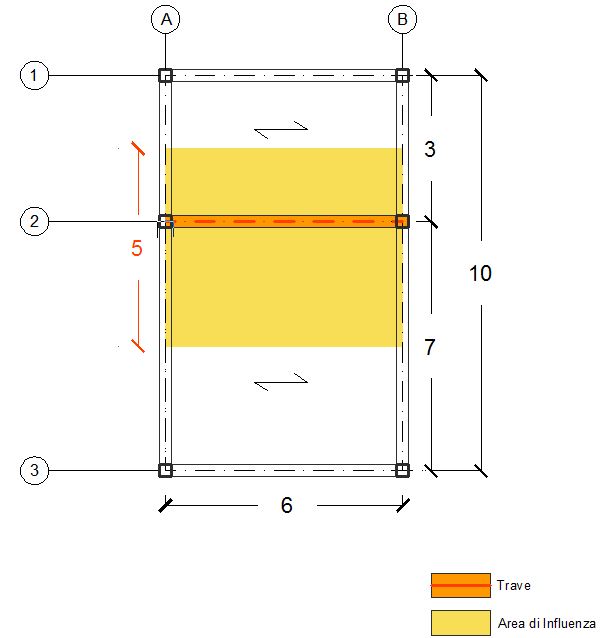
La prima esercitazione prevede il dimensionamento della trave più sollecitata del telaio nelle tre tecnologie: legno, acciaio e cls armato. 

Osservando la struttura è evidente che la trave su cui grava più carico è quella centrale poiché la sua area è pari a 30 m², cioè:

Luce = 6m - Interasse = 5m

Trave in Legno

                    

• Carichi strutturali della trave:

Travetto con sezione 12x22 cm e peso specifico pari a 6 kN/m³

                  q₁= (0,12 x 0,22 x 1) m³/m² x 6kN/m³ = 0,158 kN/m²

Tavolato con spessore 4 cm e peso specifico pari a 7 kN/m³

                  q₂= (0,04 x 1 x 1) m³/m² x 7kN/m³ = 0,28 kN/m²

calcoliamo il carico strutturale qs escludendo il peso proprio della trave principale:

qs = q₁ + q₂ = 0,158 kN/m² + 0,28 kN/m² = 0,438 kN/m²

• Carichi permanenti della trave:

Caldana alta 4 cm e peso specifico pari a 0,28 kN/m²

                               q₁ = 0,28 kN/m²

Isolante spessore 3,5 cm e peso specifico pari a 30 Kg/m³ =  0,3 kN/m³

                               q₂ = (0,035 x 1 x 1) m³/m² x 0,3 kN/m³ = 0,0105 kN/m²

Sottofondo alto 3 cm e peso specifico pari a 0,54 kN/m²

                               q₃ = 0,54 kN/m²

Pavimento in cotto spesso 2 cm e peso specifico pari a 18 kN/m³

                               q₄ = (0,02 x 1 x 1) m³/m² x 18 kN/m³ = 0,36 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,28 kN/m² + 0,0105 kN/m² + 0,54 kN/m² + 0,36 kN/m² =

         1,19 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,69 kN/m²

• Carichi accidentali qa della trave possono variare nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008.

Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(0,438 x 1,3) + (2,69 x 1,5) + (2,00 x 1,5)] x 5 = 38,02 kN/m

Inserendo la luce che è uguale a 6 m, possiamo ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Nella fase progettuale dobbiamo scegliere:

1– La tipologia di legno: Legno lamellare GL 24h con

     resistenza a flessione caratteristica fm,k = 24 MPa    

2 – coefficiente della durata del carico kmod = 0,8 (fornito dalla normativa)

3 – coefficiente parziale di sicurezza del materiale γm = 1,45 (legno lamellare)

Con questi dati possiamo calcolare la tensione ammissibile f_d (N/mm²) = fm,k x kmod / γm

4 – impostando la base b= 35 cm, ricaviamo l’altezza hmin

hmin è il valore minimo che deve avere l’altezza della sezione, tale va ingegnerizzato cioè va scelto un valore di altezza superiore ad hmin, cioè H= 50 cm

quindi non avendo considerato il peso proprio della trave è giusto scegliere la sezione con un profilo pari a 35 x 50 cm

Nella fase di verifica dobbiamo:

1 – dimensionare il carico della trave p (kN/m) e sommarlo al carico totale:

p = (0,35 x 0,50 x 1) m³/m x 6kN/m³ = 1,05 kN/m

Il nuovo carico qu, che comprende il peso della trave, può essere sostenuto da una trave con h = 47,90 cm con profilo rettangolare 35 x 50 cm.

                                               La sezione 35 x 50 cm è stata verificata!

Trave in Acciaio

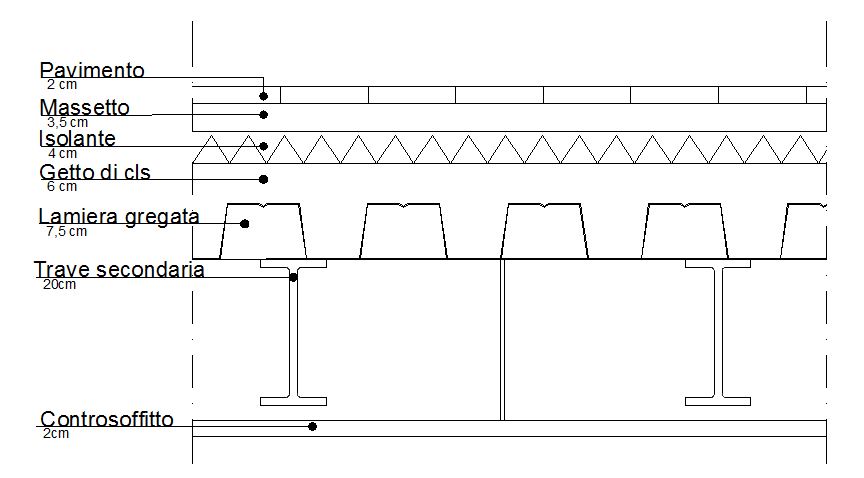
• Carichi strutturali della trave:

Trave secondaria area della sezione 0,00285 m² e peso specifico pari a 78,5 kN/m³ (IPE 200)                  

                               q₁ = (0,00285 m² x 1 m) x  78,5 kN/m³ = 0,224 kN/m²

Lamiera gregata altezza 7,5 cm e peso specifico pari a 11 Kg/m² =  0,11 kN/m²

                               q₂ = 0,11 kN/m²

Getto di cls volume 0,07 m³ peso specifico pari a 24 kN/m³

                               q₃ = 0,07 m³/m² x  24 kN/m³ = 1,68 kN/m²

calcoliamo il carico strutturale qs:

qs = q₁ + q₂  +q₃ = 0,224 kN/m² + 0,11 kN/m² +  1,68 kN/m² = 2,01 kN/m²

• Carichi permanenti della trave:

Controsoffitto peso specifico pari a 0,3 kN/m²

                               q₁ = 0,3 kN/m²

Isolante altezza 4 cm e peso specifico pari a 35 Kg/m³ =  0,35 kN/m³

                               q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto spessore 3,5 cm e peso specifico pari a 18 kN/m³

                               q₃ = (0,035 x 1 x 1) m³/m² x 18kN/m³ = 0,63 kN/m²

Pavimento in ceramica peso specifico pari a 0,4 kN/m²

                               q₄ = 0,4 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,3 kN/m² + 0,014 kN/m² + 0,63 kN/m² + 0,4 kN/m² =

         1,34 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,84 kN/m²

• Carichi accidentali qa della trave possono essere variabili nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008. Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(2,01 x 1,3) + (2,84 x 1,5) + (2,00 x 1,5)] x 5 = 49,37 kN/m

Inseriamo la luce che è uguale a 6 m, così da ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Fase progettuale:

la tensione di snervamento del Fe 430/ S275 è fy,k = 275 MPa quindi:

dai risultati ottenuti con modulo di resistenza pari a Wx,min = 848,18 cm³ è opportuno selezionare come profilo un IPE 360.

Fase di verifica:

calcoliamo il carico q della trave aggiungendo il peso della trave p moltiplicandolo per 1,3.

Sezione della Trave IPE 360 = 72,70 cm²

p = (0,00727 x 1) m³/m² x 78,5 kN/m³ = 0,57 kN/m

Il nuovo carico qu, che comprende il peso della trave, può essere sostenuto da una trave IPE 360 dato che il valore di Wx,min non supera quello Wx scelto.

                                            Il profilo IPE 360 è stato verificato!

Trave in CLS armato

 

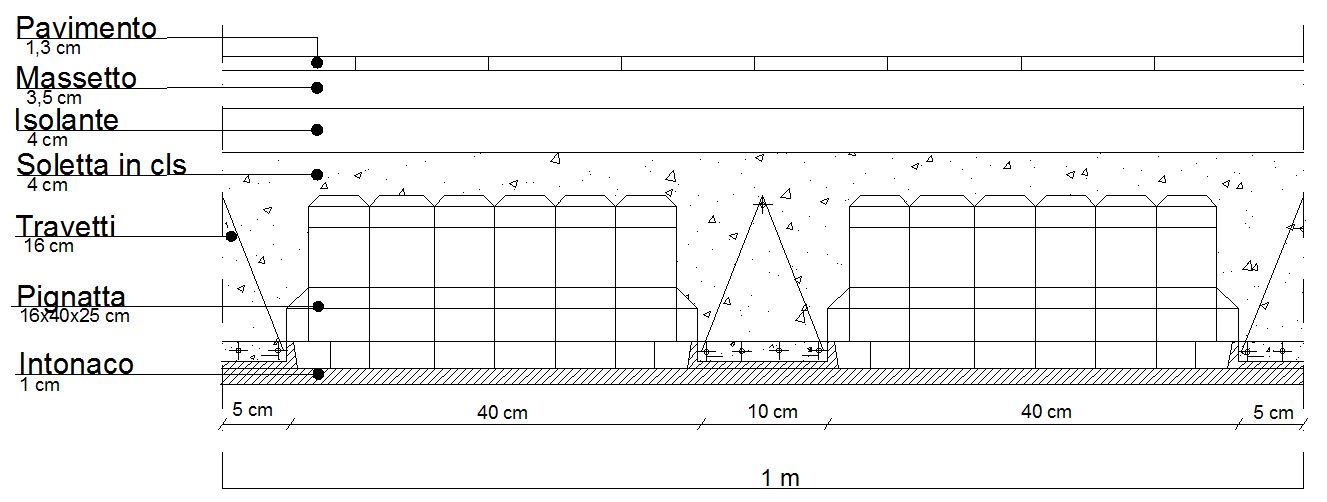
• Carichi strutturali della trave:

Pignatta n°8 di pignatte e peso specifico pari a 8 Kg

                               q₁ = 8 x 8 Kg/m² = 64 Kg/m² = 0,64 kN/m²

Soletta in cls altezza 4 cm e peso specifico pari a 24 kN/m³

                               q₂ = (0,04 x 1 x 1) m³/m² x 24 kN/m³ = 0,96 kN/m²

Travetti altezza 16 cm e peso specifico pari a 24 kN/m³

                               q₃ = 2 x(0,16 x 0,1 x1)m³/m² x  24 kN/m³ = 0,768 kN/m²

calcoliamo il carico strutturale

qs = q₁ + q₂  +q₃ = 0,64 kN/m² + 0,96 kN/m² +  0,768 kN/m² = 2,368 kN/m²

• Carichi permanenti della trave:

Intonaco spessore 1cm e peso specifico pari a 16 kN/m³

                              q₁ = (0,01 x 1 x 1)m³/m² x 16 kN/m³ = 0,16 kN/m²

Isolante altezza 4 cm e peso specifico pari a 35 Kg/m³ =  0,35 kN/m³

                              q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto spessore 3,5 cm e peso specifico pari a 2000 Kg/m³ =  20 kN/m³

                              q₃ = (0,035 x 1 x 1) m³/m² x 20 kN/m³ = 0,7 kN/m²

Pavimento in cotto  peso specifico pari a 28 Kg/m²

                              q₄ = 0,28 kN/m²

calcoliamo il carico permanente qp aggiungendo l’incidenza degli impianti e dei tramezzi:

qp = q₁ + q₂ + q₃ + q₄ = 0,16 kN/m² + 0,014 kN/m² + 0,7 kN/m² + 0,28 kN/m² =

         1,154 kN/m² + 0,5 kN/m² + 1 kN/m² = 2,654 kN/m²

• Carichi accidentali qa della trave possono essere variabili nel tempo e sono regolati dalle Norme Tecniche per le costruzione – del 2008.

Per questa esercitazioni consideriamo un edificio ad uso residenziale quindi:

qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico in un foglio excel darà come risultato il carico totale qu (kN/m) considerando che:

qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse =

   = [(2,368 x 1,3) + (2,654 x 1,5) + (2,00 x 1,5)] x 5 = 50,30 kN/m

Inseriamo la luce che è uguale a 6 m, così da ricavare il Momento massimo di una trave appoggiata  Mmax = ql²/8

Fase progettuale:

1 - acciaio per il cls: B450C avremo come tensione di snervamento fyk = 450 MPa, con queste scelte è possibile ricavare la tensione di progetto con la formula:           

fyd = fyk / γs

2 –tensione di progetto del cls fcd = αcc x fck/γc

3 – β = 0,53 e r = 2,14

4 – consideriamo una base b = 30 cm

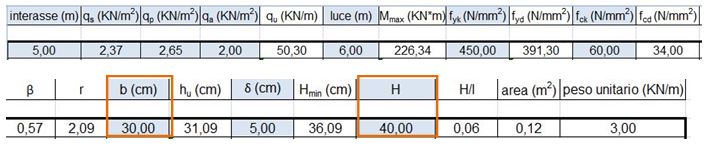
otteniamo un Hmin pari a 36,09 cm, quindi ingegnerizzando possiamo scrivere H = 40 cm.

Quindi la sezione finale della trave in cls sarà 30 x 40 cm.

Fase di verifica:

Come per la trave in legno e in acciaio è opportuno calcolare il carico q della trave in cls, quindi calcoliamo il peso unitario:

p = (0,30 x 0,40 x 1) m³/m² x 25 kN/m³ = 3 kN/m²

quindi il carico totale con l’aggiunta del peso proprio del cls moltiplicato per 1,3 è

qu = 54,20 kN/m.

                                  La sezione 30 x 40 cm è stata verificata!

Ciao!!!