ESERCITAZIONI
Le strutture reticolari sono strutture formate da aste rettilinee connesse da cerniere interne (3gdl) in cui le forze esterne sono applicate sui nodi e per questo sono soggette a solo sforzo assiale. In queste strutture gli elementi tesi prendono il nome di tiranti, e quelli compressi puntoni. Riportiamo due esempi di strutturreticolari ( simmetrica e asimmetrica) svolti utilizzando il metodo delle sezioni di Ritter i il metodo dei nodi.
STRUTTURA RETICOLARE SIMMETRICA
I vincoli esterni della struttura in esame sono una cerniera(3gdl) e un carrello(2gdl).
Verifichiamo l'isostaticità della struttura: n° gradi di libertà= n° gradi di vincolo
Ve + a = 2 nodi (vincoli esterni+num aste=2*num nodi)
3 + 11 = 2 x 7 --> 14=14 verificato! Oppure
V=L dove V = Ve + Vi --->33 L= 3 x num aste --->33 isostaticità verificata
Calcolo delle reazioni vincolari: una volta verificata l'isostaticità si calcolano le reazioni vincolari con l'equilibrio allo sforzo verticale. In seguito con il metodo di Ritter eseguiamo delle sezioni virtuali su tre aste e studiamo l'equilibrio alla rotazione rispetto ad un polo.



Verifica su Sap2000:
Partendo da una griglia in xz di 7x2 campate disegnamo la struttura reticolare. Selezioniamo le aste una ad una e impostiamo momento nullo alla fine e all'inizio dell'asta poichè queste sono soggette solo a sforzi assiali. Selezioniamo i nodi in cui abbiamo dei vincoli ( nodo A e nodo H) e con il comando Assing -> Joint -> Restraint assegnamo rispettivamente una cerniera e un carrello. Definiamo le forze e le assegnamo ai tre nodi B,D,G. A questo punto possiamo far partire l'analisi che ci mostrerà i diagrammi degli sforzi agenti sulle aste e la deformata.

STRUTTURA RETICOLARE ASIMMETRICA

Eseguiamo l'equilibrio del corpo
Σv = 0 RvA-10KN-10KN=0 ---> RvA=20
Σu = 0 RuA=RuH
ΣMA= 0 -10KN*1m - 10KN*2m + RuH ---> RuH=30KN=RvA
Metodo dei nodi: effettuiamo l'equilibrio al nodo e determiniamo lo stato di trazione o compressione delle aste che convergono in quel nodo
Partiamo dal nodo H
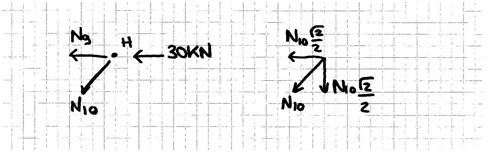
Σu = 0 -N9-30KN-N10 √2/2=0 ---> N9=-30KN (il verso ipotizzato era sbagliato) l'asta è compressa.
Come unica forza verticale ho la componente verticale di N10
Σv = 0 N10√2/2=0 ne segue che l'asta è scarica.
Continuiamo ad analizzare gli altri nodi partendo sempre da quelli dove abbiamo meno incognite


Non serve verificare l'equilibrio verticale del nodo poichè non ho incognite da trovare.
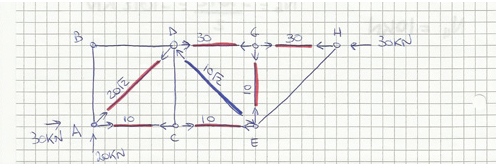
Conosciamo gli sforzi normali a cui sono sottoposte le aste della struttura; possiamo disegnare la struttura evidenziando puntoni, tiranti e aste scariche.


TRAVE CON INCASTRO CARRELLO E CERNIERA INTERNA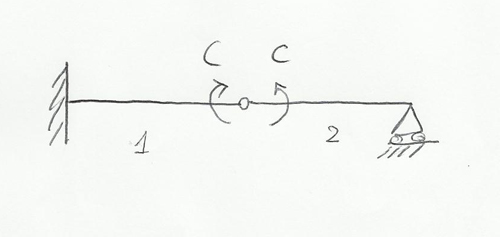
Analisi qualitativa
Osservando la struttura possiamo affermare che non ci sono salti nel grafico dello sforzo normale poiché non vi sono forze concentrate normale. (dN/dS)+q=0 non essendoci il carico la derivata della normale è nulla, ovvero la tangente al grafico è orizzontale, quindi N è costante; ora capiamo quanto vale. Vado al bordo e vedo che Ruc=0 quindi N è costante e pari a 0.
Ripetiamo il ragionamento per il taglio: (dT/dS)+q=0 sulla struttura non agisce nessun carico ripartito trasversale quindi il taglio è costante. Per calcolare il valore del taglio consideriamo il due corpi separatamente: il momento C deve essere equilibrato da una coppia di forze che dia un momento uguale ed opposto. Il taglio è costante e vale C/L.
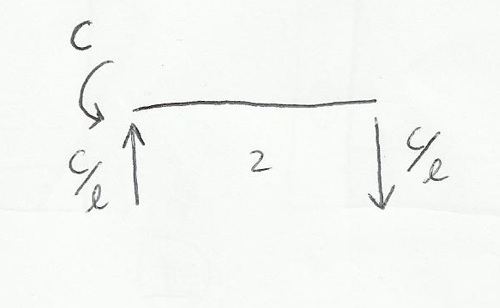
Ricordiamo che taglio e momento sono legati dalla seguente relazione :
(dM/dS) + T = 0
Se il taglio è costante il momento è lineare. La forza C/l con braccio 2l genera un momento pari a 2C, per cui all’incastro devo avere un momento uguale ed opposto.

Verifichiamo su Sap
Disegnamo la struttura ricordando di impostare:Assing--> Releases--> Moment 3-3 alla fine del primo segmento e all'inizio del secondo per configurare la cerniera interna. Definiamo il carico, che in questo caso è una coppia che ruota attorno all'asse y e la assegnamo ai due corpi in prossimità della cerniera.

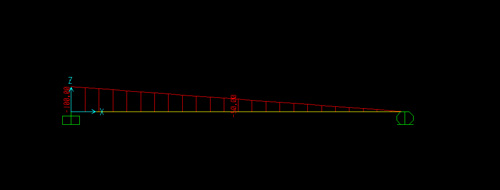
ARCO A TRE CERNIERE CON CARICO DISTRIBUITO
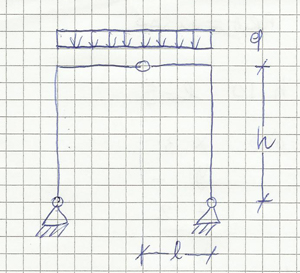
Analizziamo il nodo
La struttura è simmetrica e la cerniera interna si trova sull'asse di simmetria---> le forze a e -a, non essendo simmetriche, non possono esistere.
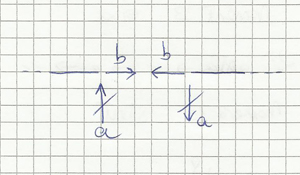
Calcoliamo le reazioni vincolari
Il carico distribuito ha risultante -2ql, le reazioni vincolari verticali saranno simmetriche e avranno valore ql.

Analizziamo metà struttura (sempre per le proprietà della simmetria il ragionamento fatto per un corpo vale anche per il secondo), c deve equilibrare b; per conoscere b svolgo l'equilibrio alla rotazione attorno al nodo c: Mc=0--> b*h+(ql)2/2=0--> b=-(ql)2/2h. Cambio il verso assegnato a b mentre c=(ql)2/2h
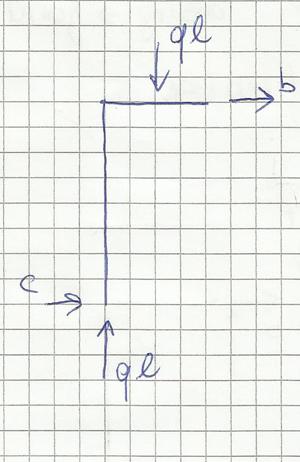
Per disegnare i diagrammi di taglio e momento guardo i bordi: il taglio sul primo elemento verticale è costante e di valore ql2/2h, mentre nel tratto centrale è lineare; il momento è lineari nei tratti in cui il taglio è costante e vale ql2/2(M= fb ql2/2h * h) e parabolico nel tratto orizzontale, con valore nullo in cerniera.

ARCO A TRE CERNIERE CON CARICO CONCENTRATO

Osservando il portale possiamo subito affermare che la forza concentrata viene equilibrata dalle reazioni verticali in cerniera. Analizziamo i due corpi separatamente
Corpo 1 Corpo 2 Cerniera
Σu=0 --> RuA = b Σu=0 ---> b' = Ruc Σu=0 ---> b' = b
Σv=0 --> a =F/2 Σv=0 --> a' =F/2 Σv=0 --> a' + a = F
ΣMA=0 --> bh-F/2*l --->b= Fl/2h ΣMA=0 --> -b'h+F/2*l ---> b= Fl/2h
Disegnamo i diagrammi degli sforzi di normale, taglio e momento
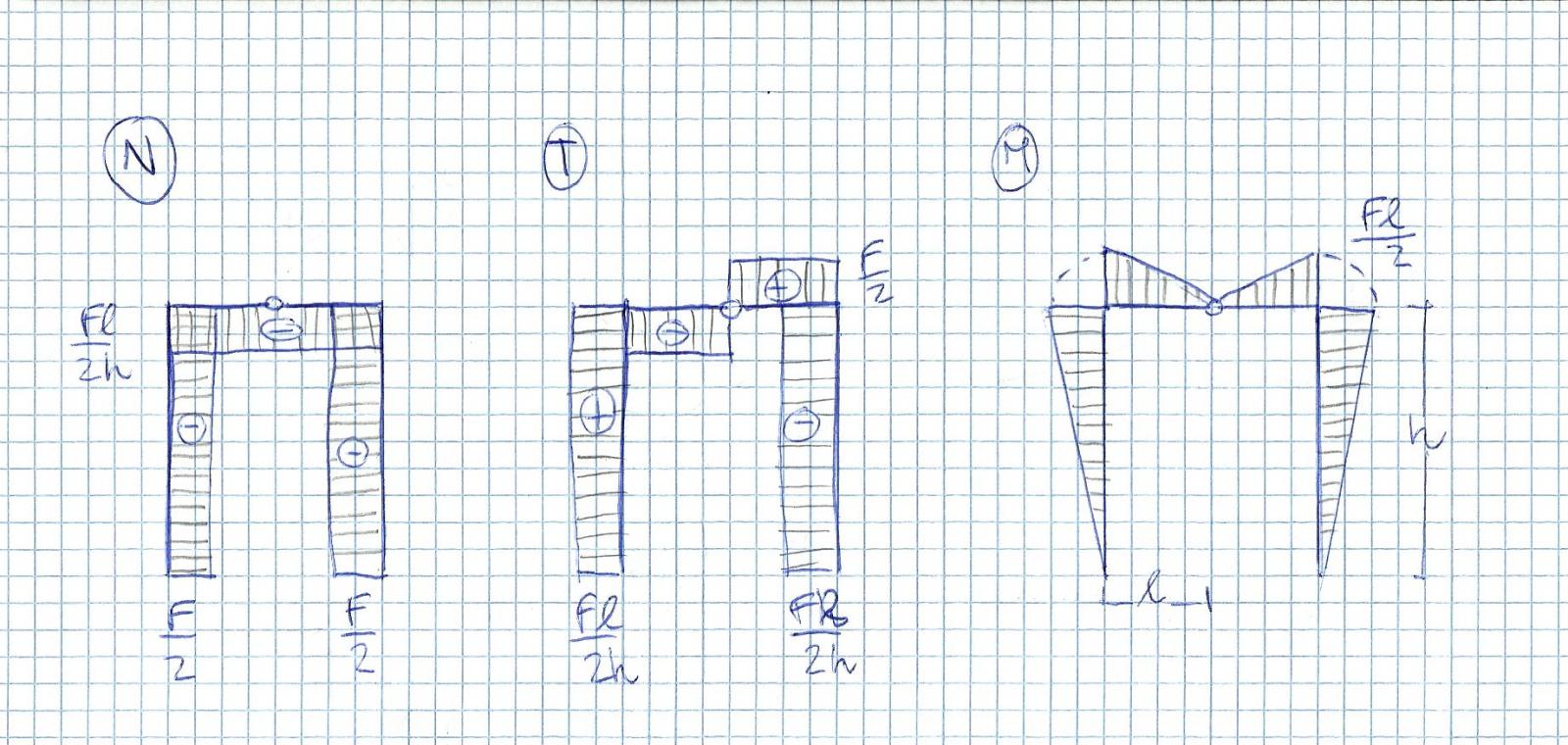
Osserviamo come, in corrispondenza di un carico concentrato ci sia un salto nel grafico del taglio e conseguente spigolo nel diagramma del momento. Portiamo la struttura su Sap e verifichiamo quanto ottenuto con il calcolo delle reazioni vincolari.


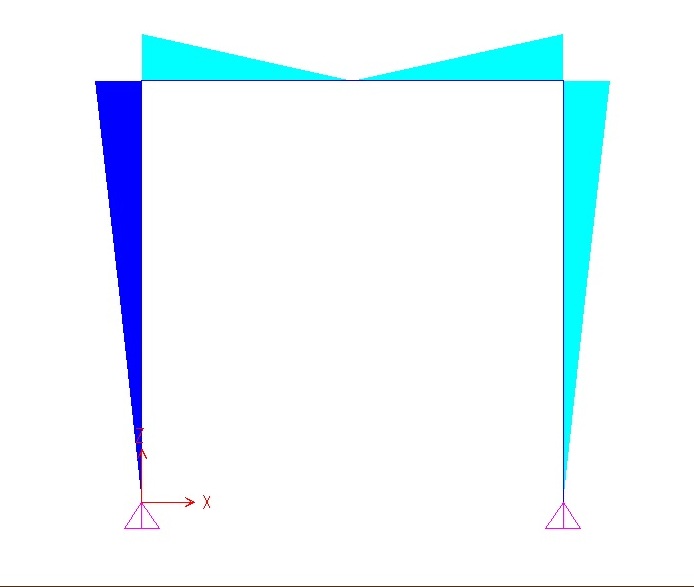
deformata taglio momento
ARCO A TRE CERNIERE CON CARICO DISTRIBUITO SULL'ELEMENTO VERTICALE

Corpo 1 Corpo 2
Σu=0 --> RuA + qh= b Σu=0 ---> b' = Ruc
Σv=0 --> a = Rva Σv=0 ---> a' = Rvc
ΣMA=0 --> -qh2 /2 -al+bh ΣMA=0 --> -b'h-a'l ---> a'= -bh/l
Mettendo a sistema le due equazioni dei momenti dei corpi 1 e 2, e sapendo che la cerniera è equilibrata, ottengo:
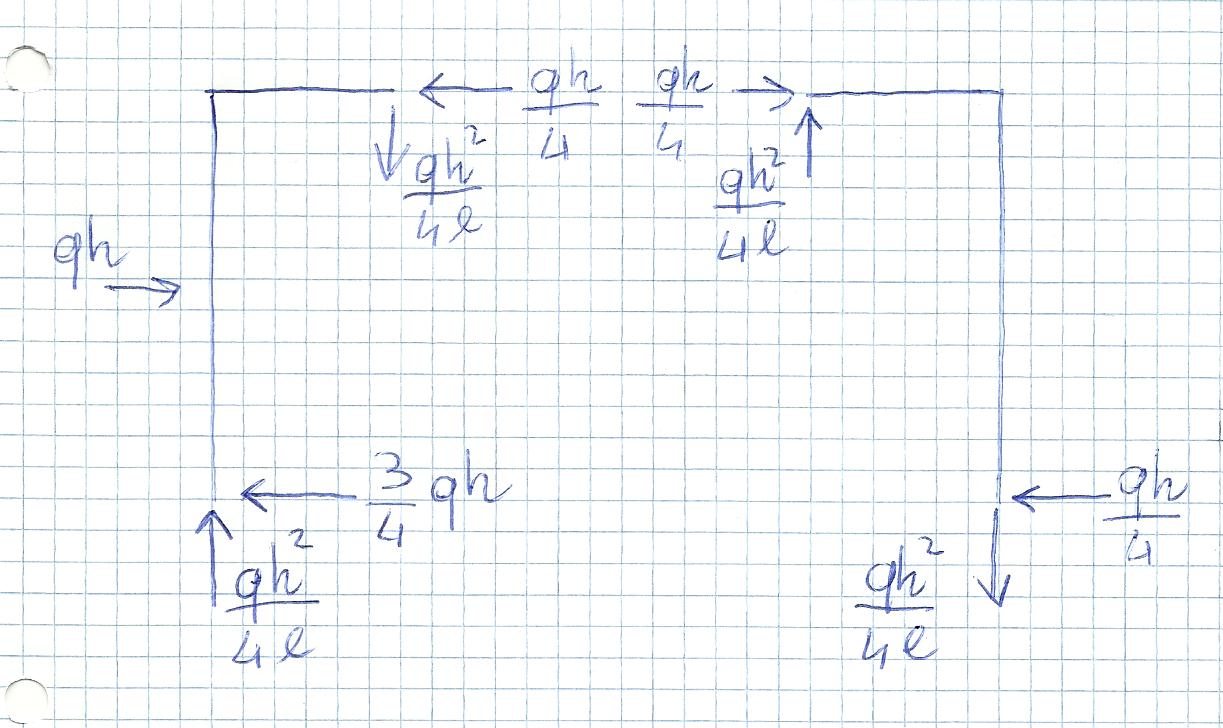
Ora possiamo disegnare i diagrammi osservando ai bordi le sollecitazioni a cui sono sottoposte le aste
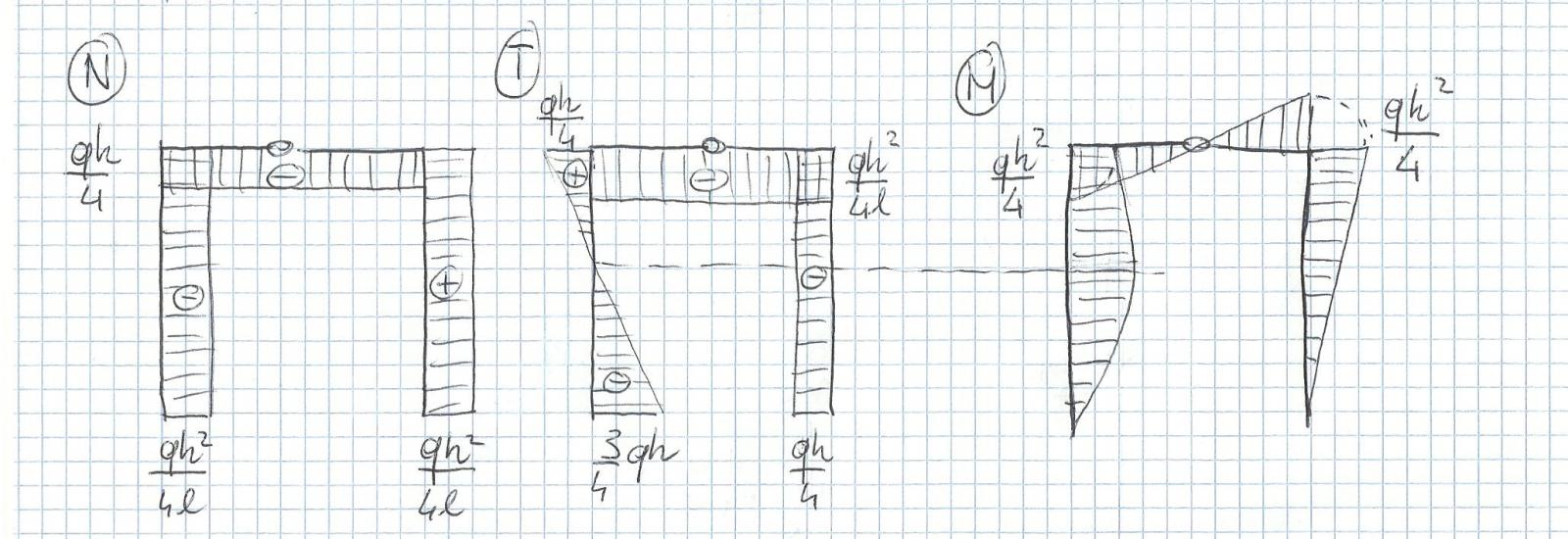
La presenza del carico distribuito comporta un andamento lineare del taglio che si annulla nel punto di massimo del momento dT/ds+q = 0 dM/ds + T = 0
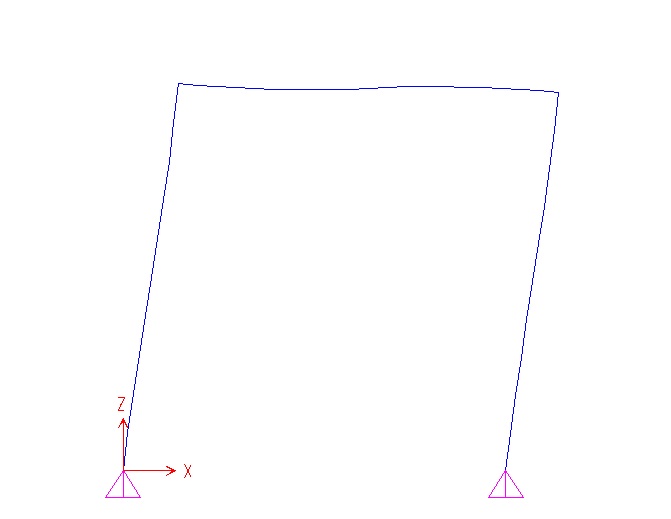
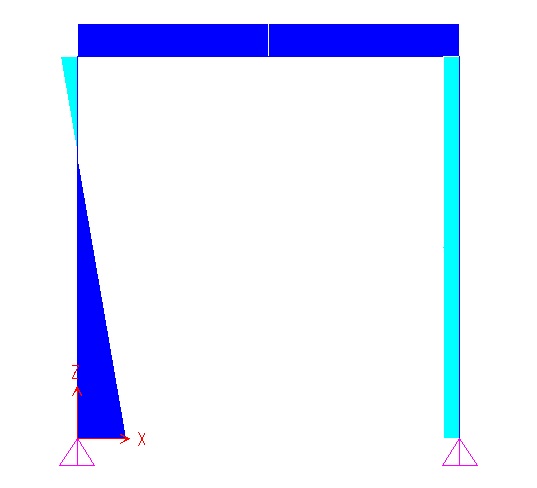

deformata taglio momento
PROGETTO DI UNA TRAVE
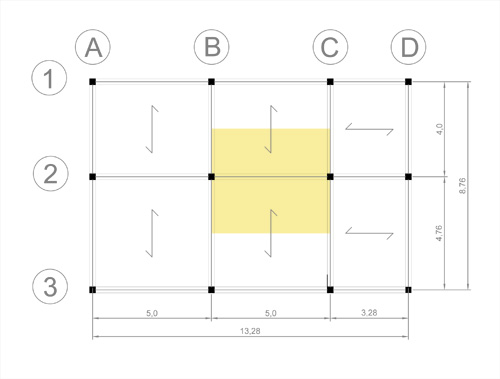
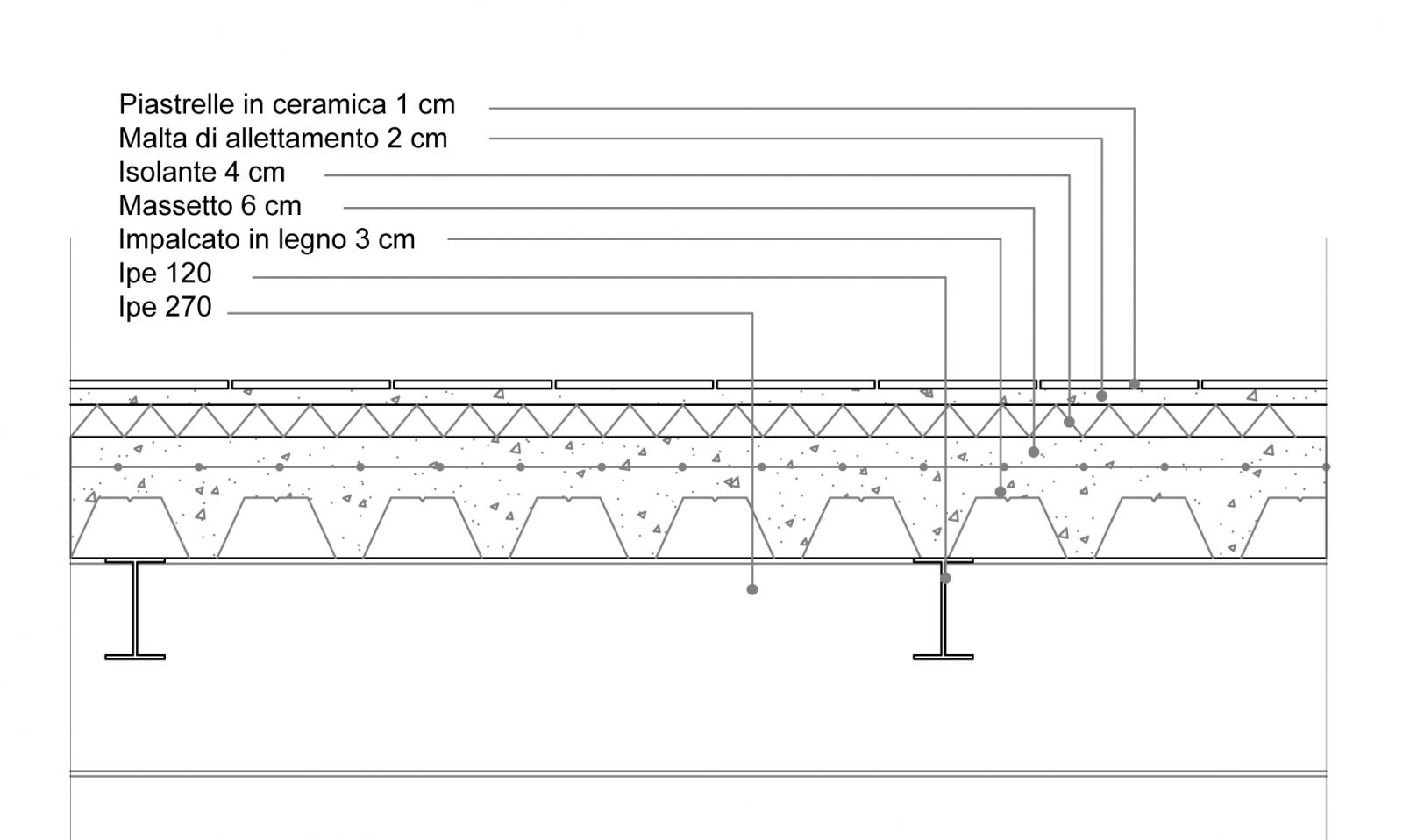
Rappresentiamo un impalcato di una abitazione unifamiliare e progettiamo la trave B2-C2.
Per il progetto della trave dobbiamo conoscere quali sono i carichi che gravano su di essa. Il progetto verrà ripetuto ipotizzando l’utilizzo di tre materiali diversi: legno, acciaio e cemento armato e servendoci di un foglio di calcolo Excel. I carichi che distinguiamo sono di tre tipi:
-carico strutturale: carico dovuto agli elementi con funzione strutturale;
-carico permanente-non strutturale:carico dovuto agli elementi non strutturali che fanno parte del solaio o che poggiano su di esso ( tramezzi, impianti, pavimentazione, isolante…)
-carico accidentale: carico che dipende dalla funzione dell’edificio, è un valore tabellato. In questo caso, trattandosi di una civile abitazione il carico è di 2KN/mq.
Legno GH32
PROGETTO TRAVETTI: progettiamo i travetti che sostengono l’orditura del solaio
Interasse 1 mt luce 4,38 mt
-Calcolo dei carichi incidenti sui travetti:
Carico strutturale (impalcato in legno)
P = V*gamma=(0,03*1*1)m* 6KN/mc=0, 18KN--> calcolo il peso unitario dell’impalcato moltiplicando il volume per il peso specifico del legno
qs= P/A= 0,18KN/mq-->divido il peso per l’area di un m2 ed ottengo il carico
Carichi permanenti non strutturali
definisco la stratigrafia del solaio, individuo il peso specifico dei diversi materiali e lo moltiplico per il loro spessore
· pavimento in gress porcellanato 0.2KN/mq
· malta in cls alleggerito 20KN/mc*0.02m= 0, 4KN/mq
· isolante (lana di vetro) 0,4KN/mc* 0,04m= 0,016 KN/mq
· massetto 22KN/mc*0,04m= 0,88KN/mq
· Impianti e tramezzi 0,5KN/mq+1KN/mq= 1,5KN/mq
qp= 0,2+0,4+0,016+0,88+1,5=2,99KN/mq
Carico accidentale
qa= 2KN/mq
-Dimensionamento del travetto:
Inserisco i dati nel foglio Excel ed ottengo il carico al metro lineare(q) e, partendo da una base ipotizzata di 12 cm, trovo un altezza di 23,51cm che arrotondo per eccesso a 25cm.

-Aggiungo il carico dei travetti:
(0,12*0,25*6KN/mc)*i =0,18KN/m
modificando il foglio Excel includo questo dato nel calcolo del carico al metro lineare e verifico che la dimensione trovata per i travetti vada bene.

Verificato.
PROGETTO DELLA TRAVE:
Interasse 4,38m Luce 5m
q’s=qs+qtr= 0,18+ 0,18=0,36KN/mq
qp=2,99KN/mq (gli elementi che costituiscono il pacchetto dei carichi permanenti sono gli stessi)
qa=2KN/mq
Carico totale al metro lineare: (q’s+qp+qa)*i=23,43KN/m
DIMENSIONAMENTO DELLA TRAVE:
Inserisco i dati nel foglio Excel ed ottengo il dimensionamento della trave 25*40 cm

Aggiungo il carico della trave stessa nel foglio Excel e verifico che la sezione scelta vada bene. qtr=(0,25*0,40*6KN/mc)/4,38m=0,13KN/mq

La trave scelta va bene.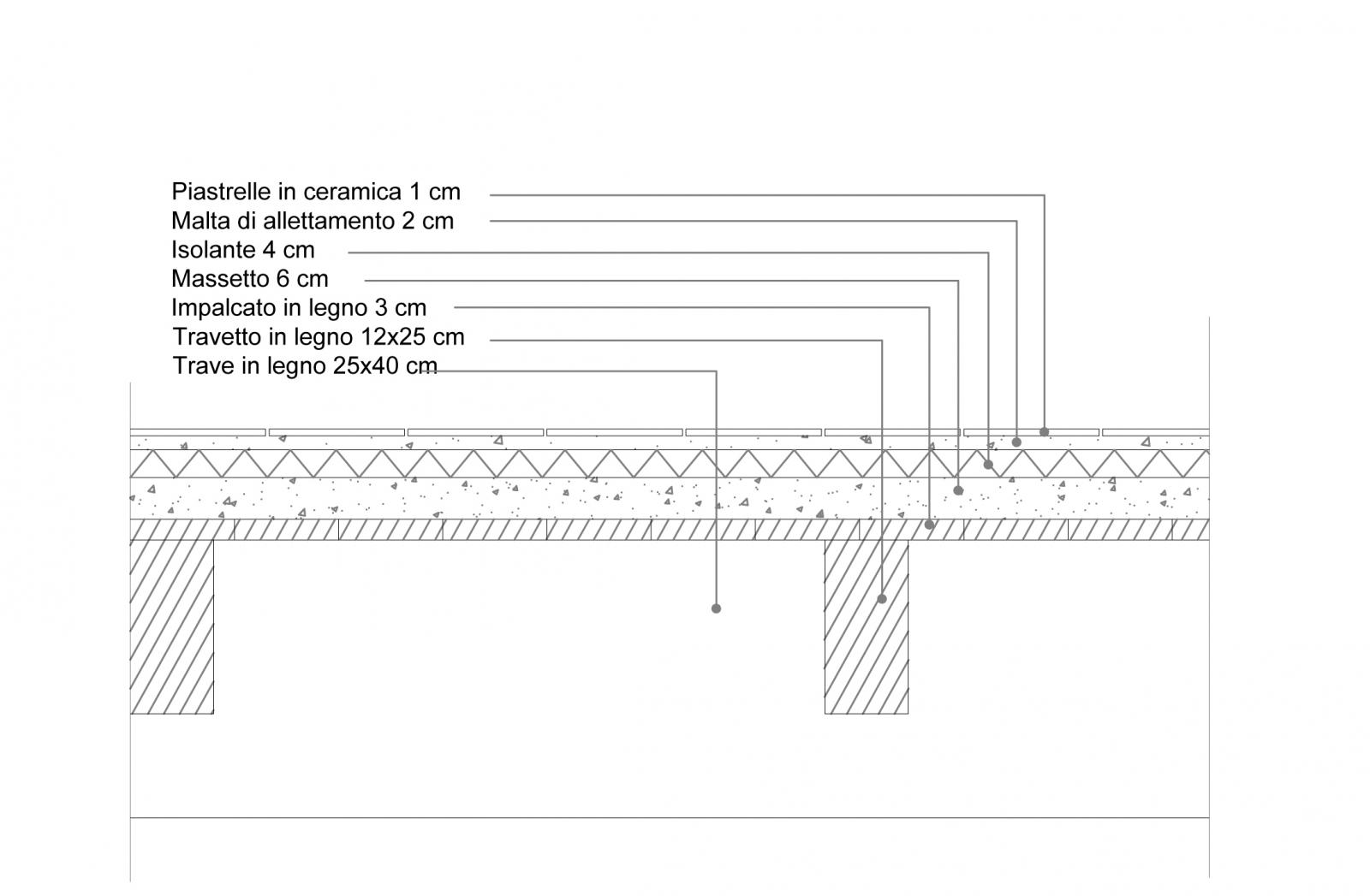
Acciaio Fe360 S235
PROGETTO TRAVETTI:
Interasse 1 m luce 4,38 m
-Calcolo dei carichi incidenti sui travetti:
Carico strutturale
Lamiera grecata e getto in cls: per la mia luce la normativa impone una lamiera di tipo A75/P600, h lamiera 75mm e una altezza totale della soletta di 15cm.
qs= 2,5 KN/mq
Carico accidentale (civile abitazione)
qa= 2KN/mq
Carichi permanenti
· pavimento in gress porcellanato 0.2KN/mq
· malta in cls alleggerito 20KN/mc*0.02m= 0, 4KN/mq
· isolante (lana di vetro) 0,4KN/mc* 0,04m= 0,016 KN/mq
· pannello in cartongesso Vaccaro 0,1KN/mq
· Impianti e tramezzi 0,5KN/mq+1KN/mq= 1,5KN/mq
qp=0,2+0,4+0,0160,1+1,5=2,21KN/mq
DIMENSIONAMENTO DEL TRAVETTO:
Inserisco i dati nelle caselle corrispondenti del foglio Excel e determino il modulo di resistenza a flessione Wx .

Tramite un profilario trovo la Ipe corrispondente (si prende il valore di Wx maggiore o uguale a quello trovato). Ipe 140 h 14cm b 7,3cm
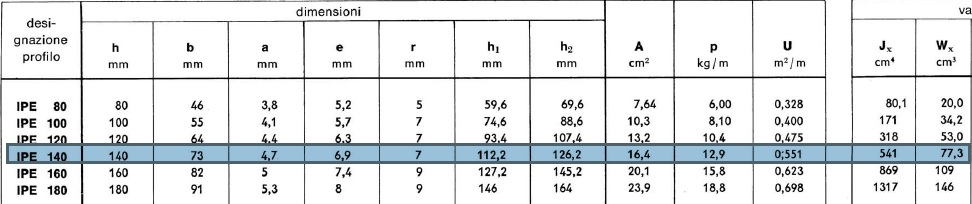
peso tabellato della trave 0,13KN/mà al mq diventa qtr=0,13/i= 0,13KN/mq
q’s= qs+qtr= 2,5+0,13=2,63KN/mq
Imposto questo nuovo carico nel foglio di calcolo e verifico che la Ipe scelta supporti anche il peso proprio. La trave scelta va bene.
PROGETTO TRAVE:
Interasse 4,38m Luce 5m
-Calcolo dei carichi incidenti sui travetti:
Carico strutturale
Lamiera grecata, getto in cls e travetti:
qs=2,63KN/mq
Carico accidentale (civile abitazione)
qa= 2KN/mq
Carichi permanenti
qp=2,21KN/mq
Carico totale al metro lineare: (q’s+qp+qa)*i=28,77KN/m
DIMENSIONAMENTO DELLA TRAVE:
Ripeto lo stesso procedimento fatto per il dimensionamento dei travetti ed ottengo:
Ipe 270

 Aggiungo il peso della trave al carico totale al metro lineare
Aggiungo il peso della trave al carico totale al metro lineare
peso tabellato della trave 36kg/m-->al metro quadro diventa (0,3KN/m)/i= 0,3/4,38=0,068KN/mq
q’s= qs+qtr=2,63+ 0,068=2,69KN/mq Aggiornando i dati su Excel ottengo ilnuovo Wx, pari a 421,98 cm3, e verifico tramite il profilario che la trave scelta vada bene.
Verificato.
Cemento Armato
PROGETTO TRAVE:
Interasse 4,38m Luce 5m
-Calcolo dei carichi incidenti sui travetti:
Carico strutturale
Solaio in latero - cemento gettato in opera di tipo “Bausta” :

qs=2,66KN/mq
Carichi permanenti
· pavimento in gress porcellanato 0.2KN/mq
· malta in cls alleggerito 20KN/mc*0.02m= 0, 4KN/mq
· isolante (lana di vetro) 0,4KN/mc* 0,04m= 0,016 KN/mq
· pannello in cartongesso Vaccaro 0,1KN/mq
· Impianti e tramezzi 0,5KN/mq+1KN/mq= 1,5KN/mq
qp=0,2+0,4+0,0160,1+1,5=2,21KN/mq
Carico accidentale
qa= 2KN/mq
Carico totale al metro lineare: (qs+qp+qa)*i=30KN/mq
Calcolo del momento massimo
Trattandosi di una trave doppiamente appoggiata il valore del momento massimo è ql2/8
M=30 *52/8=93,75KN*m
DIMENSIONAMENTO DELLA TRAVE:
Ipotizzando una base di 25cm ottengo una altezza di 46,25 cm (H=hu+d) che approssimo a 50 cm


Aggiungo il carico della trave e verifico che il dimensionamento sia corretto.
qtr=A*Peso specifico =(0,25*0,5)*33,3KN/mc=4,16KN/m
qtr al metro quadro=qtr/i=0,54KN/mq
Aggiungo il carico della trave e verifico che il dimensionamento sia corretto

Verificato

STRUTTURA RETICOLARE SPAZIALE
Disegno della struttura su Autocad
Costruiamo il modulo di base della struttura reticolare tramite una polilinea con punto di partenza nell’origine degli assi (0,0,0);

ruotiamo il modulo per una visualizzazione frontale
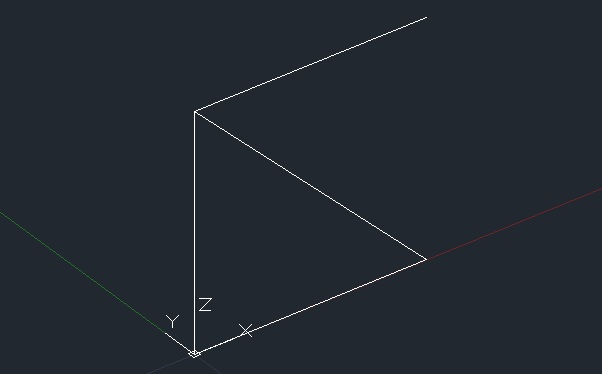
con il comando “serie” costruiamo passo passo il reticolo spaziale, impostando ogni volta il numero di righe e colonne esatte e mantenendo sempre una spaziatura pari a 2 (misura del modulo). Nel procedere fate attenzione a non duplicare le linee.
.jpg)
disegniamo il nuovo modulo da ripetere lasciandolo aperto
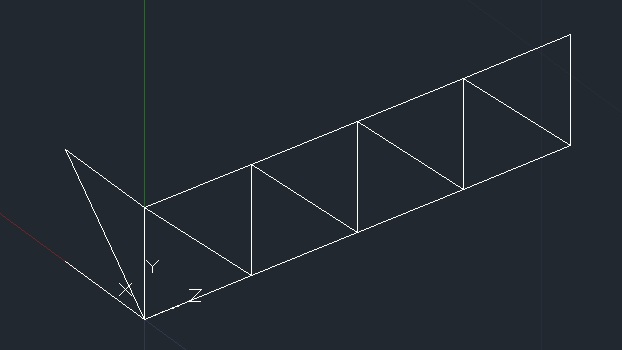
ruotiamo l'orientamento degli assi con il comando "ucs" per tre punti
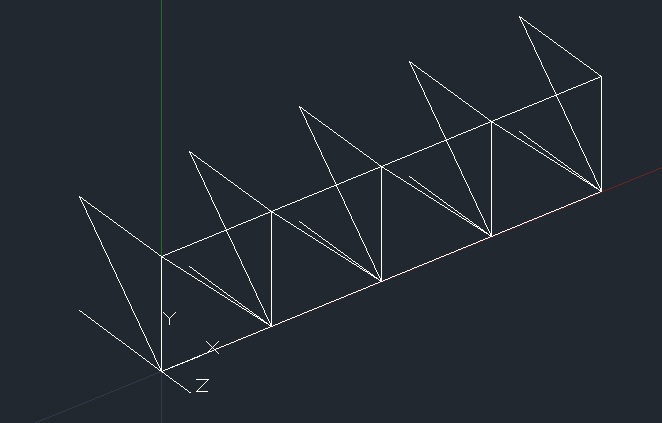
completiamo con le aste diagonali superiori e inferiori

ripetiamo il modulo con il comando serie e chiudiamo la struttura ruotando la vista per non sbagliare punti di ancoraggio. Ottengo una reticolare spaziale di 4x6 campate

una volta completata la struttura esplodiamo tutte le polilinee, verifichiamo che siano tutte su un unico layer che possiamo chiamare "aste" e salviamo in Autocad dxf 2000.
Analizziamo la struttura su Sap 2000
Quando importiamo il file su Sap si apre una finestra di dialogo in cui dovremo impostare Frame -> aste. In questo modo Sap riconosce tutte le aste come elementi strutturali e potremo assegnare caratteristiche di materiale e sezione uguali per tutte. Assegniamo i carrelli sui quattro nodi di appoggio (il reticolo spaziale ci consentirebbe di disporre gli appoggi anche in modo più casuale)

sottoponiamo le aste a solo sforzo assiale andando a spuntare, nella finestra "frame releases" le caselle Moment 2-2 Moment 3-3 all'inizio e alla fine dell'asta.
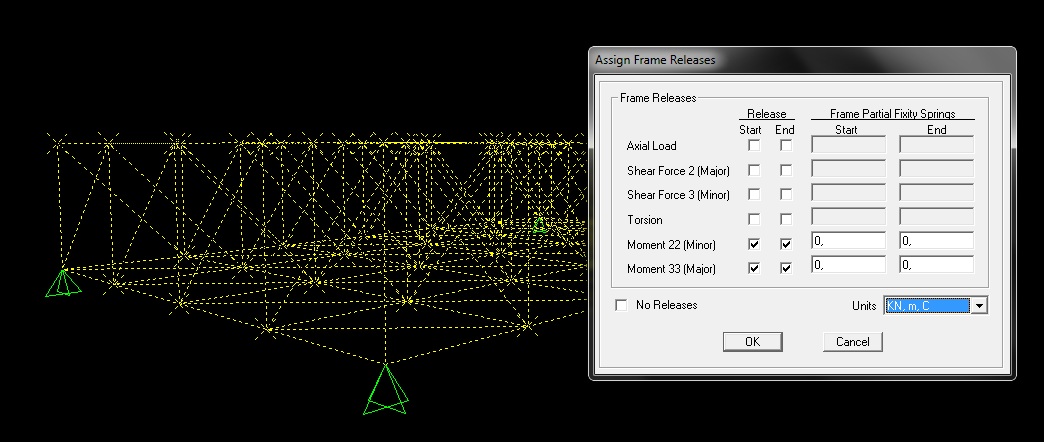
Definiamo un nuovo materiale e gli assegniamo una sezione:
Assing-> frame-> frame section-> add new properties-> pipe/acciaio
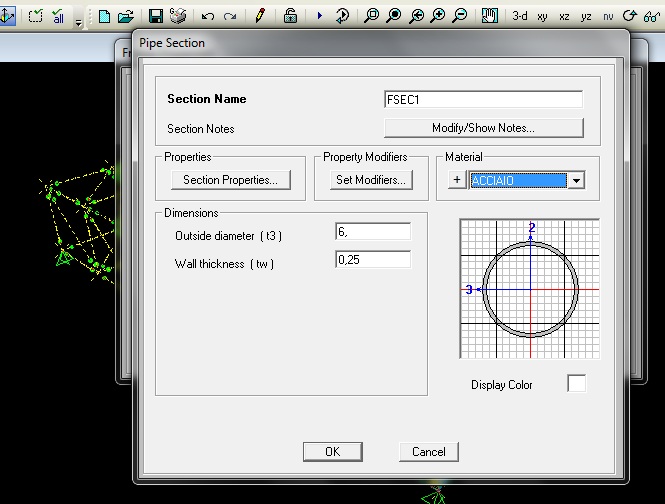
Definiamo un carico concentrato verticale di 40KN


Spuntiamo la voce che rende invisibili le aste e selezioniamo i nodi superiori su cui assegneremo il carico concentrato; a questo punto possiamo far partire l’analisi e vedere come si deforma la struttura
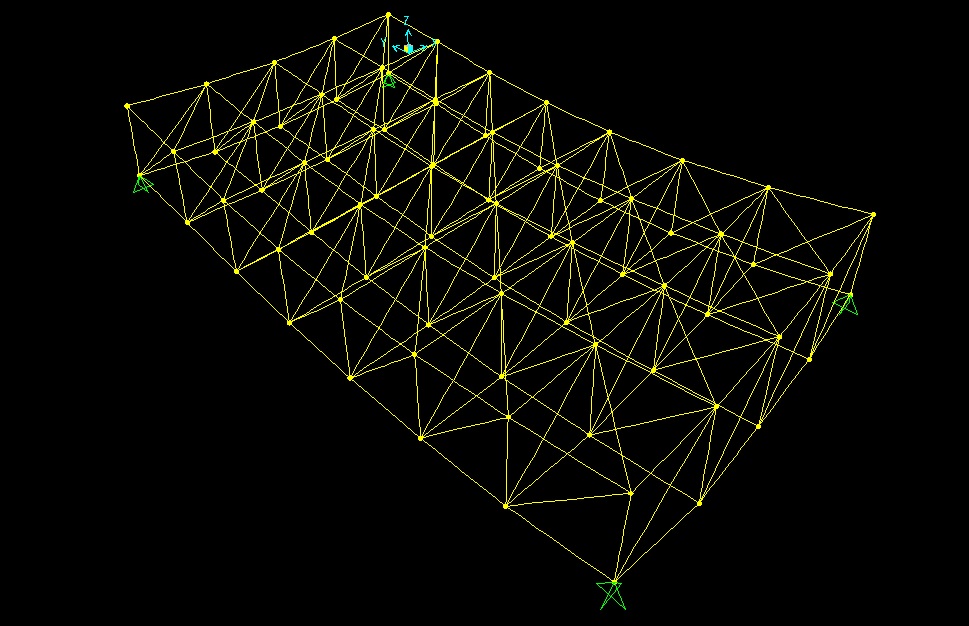
La visualizzazione degli sforzi sul diagramma risulta poco leggibile per cui attiviamo il comando "label" che numera le aste e apriamo una tabella che riporta i valori di sforzo assiale a cui sono sottoposte le singole aste:
Display-> show tables-> analysis result-> element output

Dall'analisi della tabella individuiamo le aste più tese e più compresse, utili per il dimensionamento del profilo
Progetto dell’asta maggiormente tesa
Dalla tabella rilevo uno sforzo massimo a trazione di 259,16KN; con la formula di Navier dimensiono l’asta (scegliendo l’asta più tesa mi tengo in sicurezza anche rispetto alle altre)
A=N/fd dove fd= fyk*1,05 scegliendo un acciaio Fe360 S235 trovo un’area pari a:
A=259167/ (235*1.05)=1158mm2 --> 11,58cm2
Sul profilario trovo un tubolare che abbia una sezione con area maggiore a quella minima trovata

Sezione A’=12,5cm2
Verifica a resistenza
(N/A’)< fd 259167N/1250mm2=207,33Mpa<223,8Mpa
il progetto è verificato.
Progetto dell’asta maggiormente compressa
Le aste compresse possono essere soggette a carico critico euleriano che porta a una inflessione dell’asta fino al collasso della stessa. Rispetto a ciò molto importante è il fattore snellezza (rapporto h/l). Per progettare la struttura eseguiremo una verifica a resistenza, a snellezza e a stabilità.
Il maggior sforzo a compressione è di 307,25 KN, dimensioniamo l’asta utilizzando l’acciaio Fe360 S275 e tramite la formula di Navier troviamo l’area minima che resiste a tale sforzo.
A=N/fd dove fd= fyk*1,05
A=307250/ (275*1.05)=1064mm2--> 10,64cm2
Verifica a resistenza
Dal profilario il primo valore che trovo è 10,7 cm2 ma preferisco scegliere un’area di 12,5cm2 Jx 192cm4 e verifico che fd ≤ fyk tramite la formula:
fd=N/A= (307.25*1000)/(12,5*100)=245,8MPa< 275MPa Asta verificata a resistenza
Verifica a snellezza
l<200 dove l=lo/ρ
lo è la luce libera di inflessione che dipende dal tipo di vincolo dell’asta. Nel caso di un asta doppiamente incernierata lo=b*l=1*l; ρ lo leggo dalla tabella
l=283/3,92=72,19<200 Asta verificata a snellezza
Verifica a stabilità
Per prima cosa trovo il carico critico euleriano e verifico che lo sforzo assiale Nd sia minore della resistenza alla stabilità Nd<Nbdr
Ncr=(ρ2E Jmin)/lo2= (3,14²* 210000MPa*192 cm⁴ *10000/283²cm*10)/1000 = 496,4KN
Ora calcoliamo Nbdr
Nbdr=χ*A*fyk/g1 dove:
χ = 1/Φ+√(Φ²-λ ²)≤1
λ=√ (A*fyk/Ncr)
Φ= 0,5[1+α(λ – 0,2)+λ²] α coeff. di imperfezione (0,21)
Nbdr=(0,68 x 12,5cm²x 100 x 275MPa/1,05)/1000 = 222,62KN
Nd=307,25KN > Nbdr non verificato.
Scegliamo un profilo con un'area maggiore:
A 15,5cm2 J=234 cm4 41cm3 ρ=3,89 cm
Verifica a resistenza
fd=N/A= (307.25*1000)/(15,5*100)=198,22MPa< 275MPa Asta verificata a resistenza
Verifica a snellezza
l=283/3,89=72,75<200 Asta verificata a snellezza
Verifica a stabilità
Calcoliamo il carico critico euleriano
Ncr = (3.14)2 x 210000 N/mm2 x 2340000 mm4 / (2830 mm)2 = 604,95 KN
λ=√ (A*fyk/Ncr)= √1550*275/604952= 0,83
Φ = 0.5[1 + 0.21 ( 0.83 - 0.2) + (0.83)2] = 0,91
X = 1 / 0.9106 + √(0.9106)2 - (0.83)2 = 0,77<1
Nbrd = 0,77 x 1550 mm2 x 275 N/mm2 / 1.05 = 312,5KN < 545 KN
Nd=307,25< 312,5 KN Asta verificata a stabilità
RIPARTIZIONE DELLE FORZE SISMICHE
Studiamo la ripartizione delle forze sismiche (forze orizzontali) sui telai che compongono l'impalcato, calcolando anzitutto le diverse rigidezze K dei controventi. Possiamo considerare l'impalcato come un corpo rigido e i controventi come delle molle che reagiscono alle forze orizzontali secondo la legge di Hook F= kd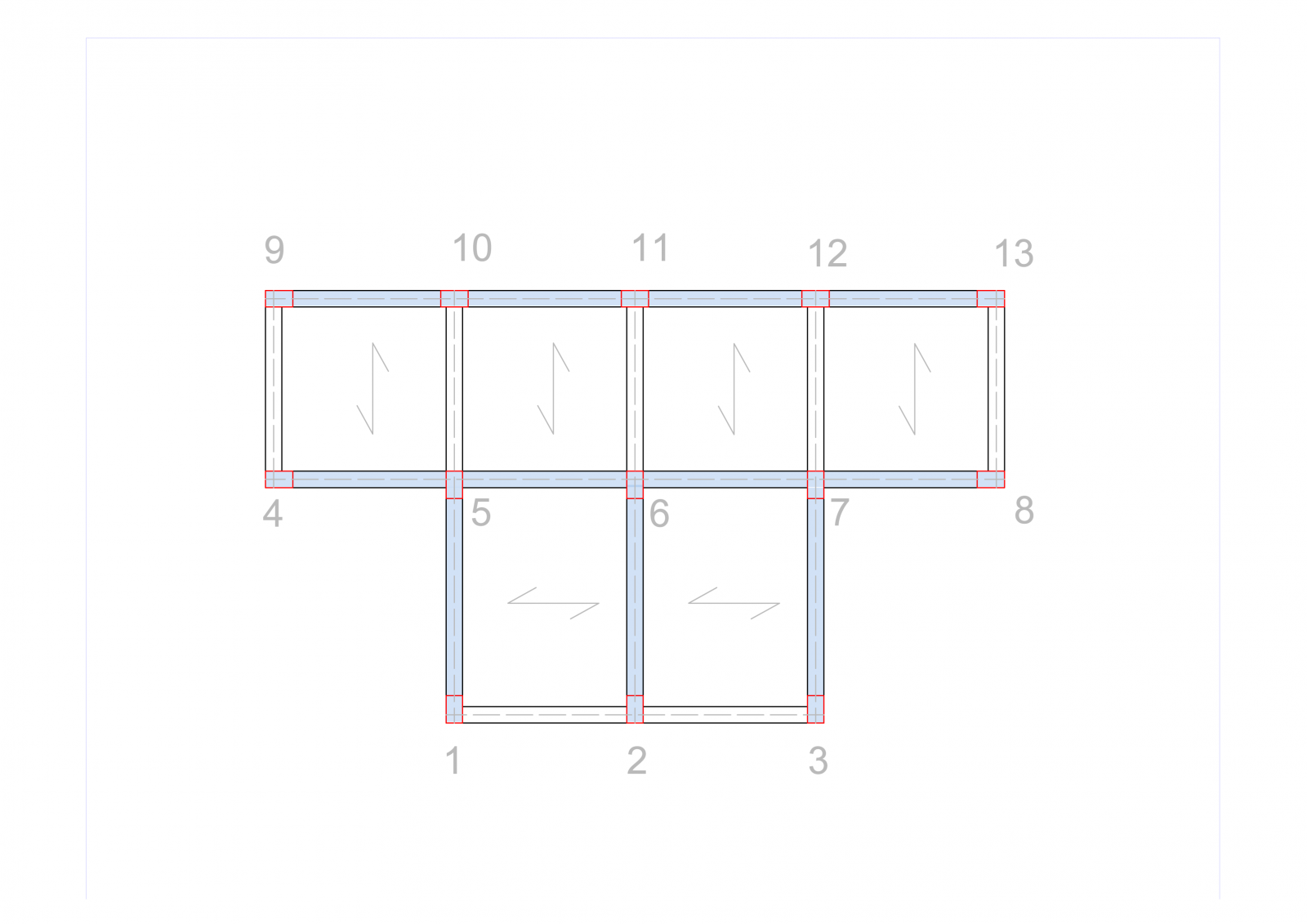
Disegnamo l'orditura dei solai in base alla luce minore della maglia ed evidenziamo di conseguenza quali travi portano il solaio. Queste sono le travi che si inflettono di più, e per continuità del nodo, anche i pilastri si inflettono. I pilastri vanno quindi disposti in modo da sfruttare il loro momento d'inerzia maggiore, nel caso in cui un pilastro appartenga a due telai ( come per i pilastri 5,6,7), si favorisce il telaio con luce maggiore. Scegliamo una struttura in cemento armato (E=21000) e dei pilastri rettangolari con sezione 30x50 cm.
Mx=bh3/12=312500cm4 My=b3h/12=112500cm4
Calcolo delle rigidezze dei controventi

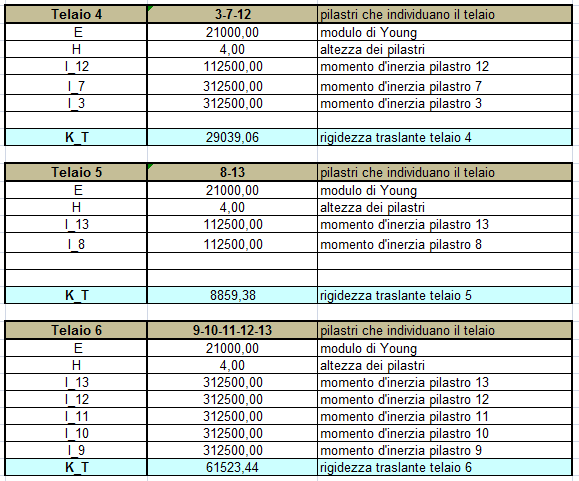

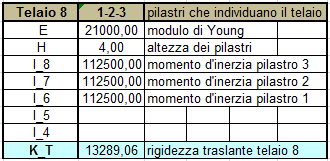
Ipotizziamo un centro O attorno al quale facciamo agire f ed effettuiamo il bilancio dei momenti. Inseriamo nel foglio Excel le distanze dei controventi da questo punto O
Tabella sinottica dei controventi e delle loro distanze dal centro di massa

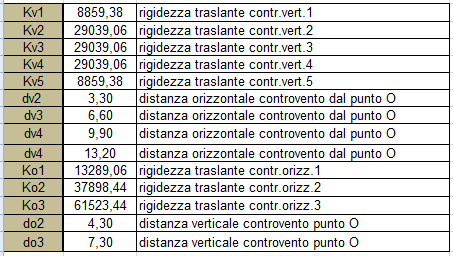
Calcolo del centro di massa
Dividiamol'impalcato in due aree, calcoliamo i rispettivi baricentri ed infine troviamo la posizione del centro di massa G dell'impalcato, punto in cui sono applicate le forze (in questo caso forza sismica).
Xg = Area1 Xg1 + Area2 Xg2 / Area1+Area2
Yg = Area1 Yg1 + Area2 Yg2 / Area1+Area2

Calcolo del centro delle rigidezze e delle rigidezze globali
Il centro delle rigidezze è il punto di applicazione della risultante delle reazioni dei controventi. Per una buona progettazione in zona sismica è bene far coincidere il più possibile il centro delle masse con il centro delle rigidezze, in modo da non creare momenti e quindi rotazioni.
Xc = Kvi dvi /Kvtot
Yc = Koi doi /Kotot

Analisi dei carichi sismici
La forza sismica imprime un'accelerazione all'edificio F=ma, questa accelerazione dipende dalla classificazione della zona sismica a= cg c <1 coeff. di intensità sismica. Possiamo quindi riscrivere allora il principio d'inerzia come:
F = mcg = c P Questo peso viene chiamato peso sismico W ed è espresso come la somma dei carichi permanenti e strutturali e i carichi accidentali moltiplicati per un coefficiente di contemporaneità.
W= (G+Q)Ψ G= ( qs+qp)A tot
Q= qa A tot
Ψ = 0,8

Ripartizione della forza sismica lungo x
La forza orizzontale non viene assorbita solo dai controventi orizzontali e viceversa poichè questa spesso ha un braccio rispetto a C e fa ruotare il corpo ---> Momento torcente= Forza sismica*braccio

Traslazione orizzontale μ0 = F/ Kotot ; Rotazione rigida dell'impalcato ψ = Fb/ Kψtot
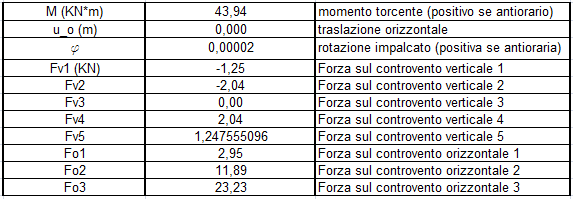
Ripartizione della forza sismica lungo y



Commenti
Flavia.Valdarnini
Ven, 23/03/2012 - 11:17
Collegamento permanente
Metodo dei nodi Partiamo
Metodo dei nodi
Partiamo dal nodo H...
Flavia.Valdarnini
Ven, 23/03/2012 - 11:24
Collegamento permanente
Equilibrio
Equilibrio orizzontale
-N9-30KN-N10 √2/2=0 ---> N9=-30KN (il verso ipotizzato era sbagliato)l'asta è compressa