esercitazione2_soluzione di struttura iperstatica tramite linea elastica + verifica SAP
Esercitazione 2
Soluzione di una struttura iperstatica tramite le equazioni della linea elastica
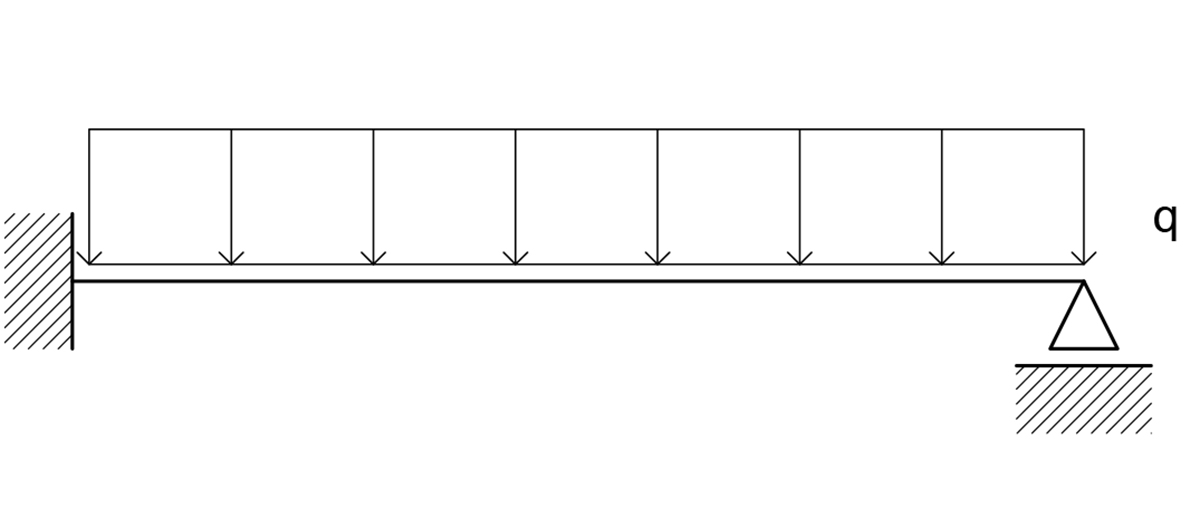
Dato che la struttura ha un grado di iperstaticità, mi accingo a risolverla per mezzo della soluzione della linea elastica.
Questa viene ottenuta (usando il modello di trave di Eulero-Bernoulli) tramite la messa in relazione di quelle cinque equazioni che riguardano il taglio e il momento nei tre sistemi de
- le equazioni di equilibrio
- le equazioni di compatibilità
- i legami costitutivi
ovvero:
⎧(dT/ds) + q₂ = 0
⎪(dM/ds) + T = 0
⎨M = EJχ
⎪χ = (dφ/ds)
⎩φ = (dv/ds)
N.B. le altre tre equazioni riguardano i carichi e le sollecitazioni assiali.
Questo sistema ha cinque equazioni e cinque incognite, tutte tra l’altro legate da rapporti di derivazione:
ciò permette di esprimere tali incognite tutte come derivate della legge dello spostamento verticale.
v(s) = ( q₂ s⁴ / 24 EJ) + c₁ (s³ / 6) + c₂ (s² / 2) + c₃ s + c₄
A questa equazione si giunge attraverso una progressiva integrazione a partire dall’equazione che descrive il carico, ovvero:
q(s) = (d⁴v/ds⁴) EJ
Supponendo infatti la legge del carico una funzione lineare costante, possiamo giungere a descrivere la legge v(s) come un polinomio del tipo:
p(x) = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴
(compatibile con la funzione espressa in precedenza)
Si noti che per arrivare alla legge di v(s) è stata fatta un’altra ipotesi, ovvero quella di considerare costante il prodotto EJ: ciò equivale a considerare costanti la dimensione, la forma ed il materiale delle sezioni lungo l’asse della trave.
Incognite del nostro sistema sono divenute ora le quattro costanti di integrazione presenti nella legge dello spostamento verticale. Per rendere il sistema risolvibile, serve quindi ora analizzare i caratteri dei vincoli della struttura per avere alcune informazioni sulle condizioni al bordo.
Da osservazioni sui vincoli deduco infatti alcuni fatti certi:
- lo spostamento verticale in 0 e in l sono nulli dato che si è in presenza di un incastro e di un carrello orizzontale
v(0) = 0
v(l) = 0
da cui si deduce che il coefficiente c₄ è anch’esso nullo
c₄ = 0
- In 0, dato che siamo in presenza di un incastro, avremo una rotazione nulla
φ(0) = 0
da ciò deduciamo che anche il coefficiente c₃ è nullo
c₃ = 0
- In l, dato che siamo in presenza di un carrello, sappiamo che la sollecitazione a momento (e quindi anche χ) sarà nulla.
(d²v/dv²)(l) = 0
Siamo ora a conoscenza di sufficienti informazioni per impostare un sistema in due equazioni con c₁ e c₂ come incognite:
⎧v(l) = ( q₂ l⁴/24 EJ) + c₁ (l³/6) + c₂ (l²/2) = 0
⎨
⎩(d²v/dv²)(l) = (q₂ l²/2 EJ) + c₁s + c₂ = 0
da cui si ottiene che :
c₁ = -5 ql/8 EJ
c₂ = ql/8 EJ
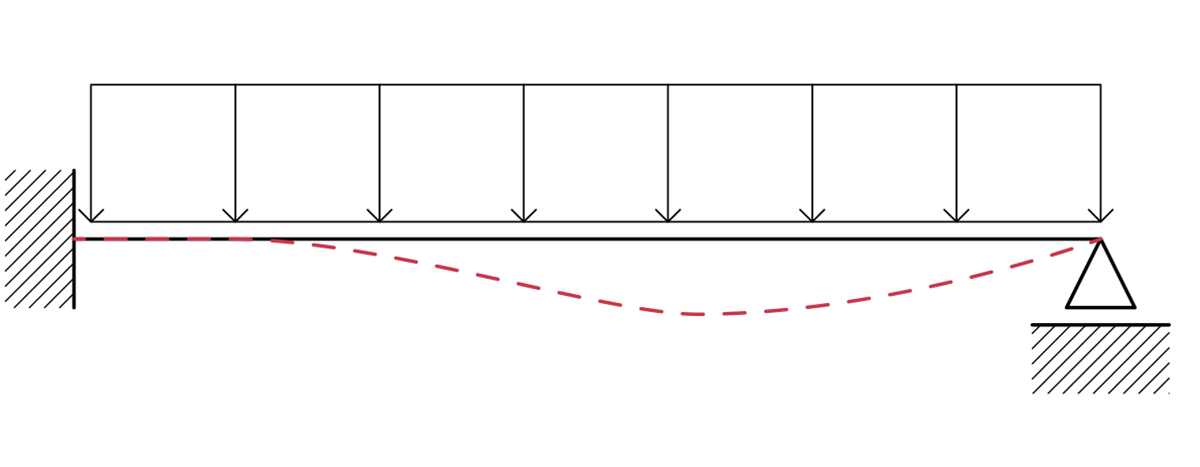
Ora, l’esercitazione richiedeva di individuare il valore dello spostamento verticale massimo della trave. Questo si troverà sicuramente dove la curva della deformata avrà un minimo, ovvero dove φ = 0.
(disegno deformata)
risolvendo questa equazione di terzo grado
φ = dv/ds = (q₂ s³/6 EJ) + c₁(s²/2) + c₂ s = 0
Dato che in tutti i termini è presente s, come prima soluzione avrà per certo s=0, come era facilmente deducibile dalla presenza dell’incastro.
Le altre due soluzioni si ottengono mediante formula risolutiva.
Cadendo una delle due soluzioni fuori dal tratto della trave, l’unica soluzione accettabile risulta:
s = 0,578 ql
ovvero lo spostamento verticale massimo si verificherà poco più a destra della metà della trave.
N.B. si può notare che la presenta del vincolo a momento generato dall’incastro a sinistra sposti dal centro verso destra il punto di vmax, che in un sistema isostatico di trave appoggiata si sarabbe trovato perlappunto in l/2.
Possiamo ora esplicitare il valore di vmax come v(0,578ql) = 0,0054 (q²l⁴/EJ)
Si possono graficare ora le leggi del taglio e del momento in modo qualitativo, usando le informazioni ottenute nell’esercizio, ovvero che il taglio è nullo, e quindi la parabola del momento ha un minimo, nel punto 0,578 l.
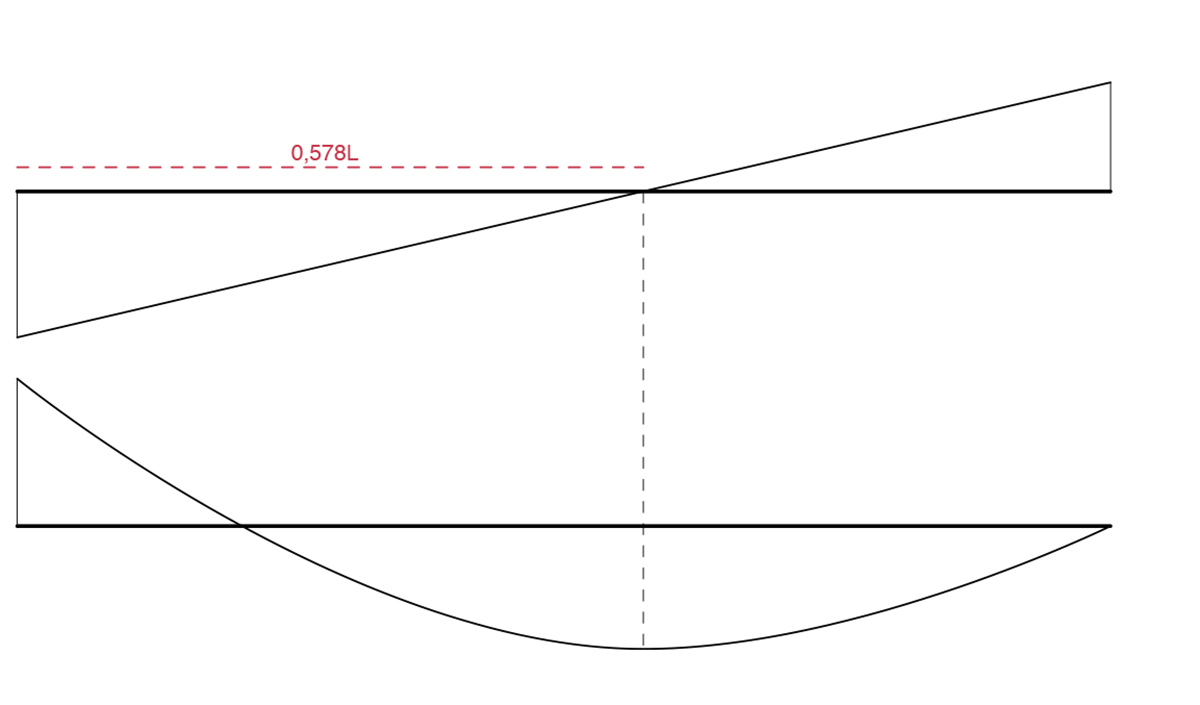
N.B. i diagrammi delle sollecitazioni della struttura iperstatica possono essere visti come sovrapposizione (o somma) di due diagrammi di strutture isostatiche (trave appoggiata con carico uniformemente distribuito + trave incastrata con carico puntuale in corrispondenza del carrello) per il principio di sovrapposizione degli effetti.
Ora si può assegnare una lunghezza alla trave e una densità di carico, nonché un materiale (E), una dimensione ed una forma (J) alla sezione e verificare il risultato ottenuto sul software SAP2000.
Verifica_SAP2000
creare un nuovo file con una griglia utile al disegno dell'asta:
FILE>NEW MODEL

QUICK GRID LINES > impostare due assi lungo la direzione x, uno lungo y e uno in direzione z > impostare come GRID SPACING la dimensione che vorremo dare alla lunghezza della trave.
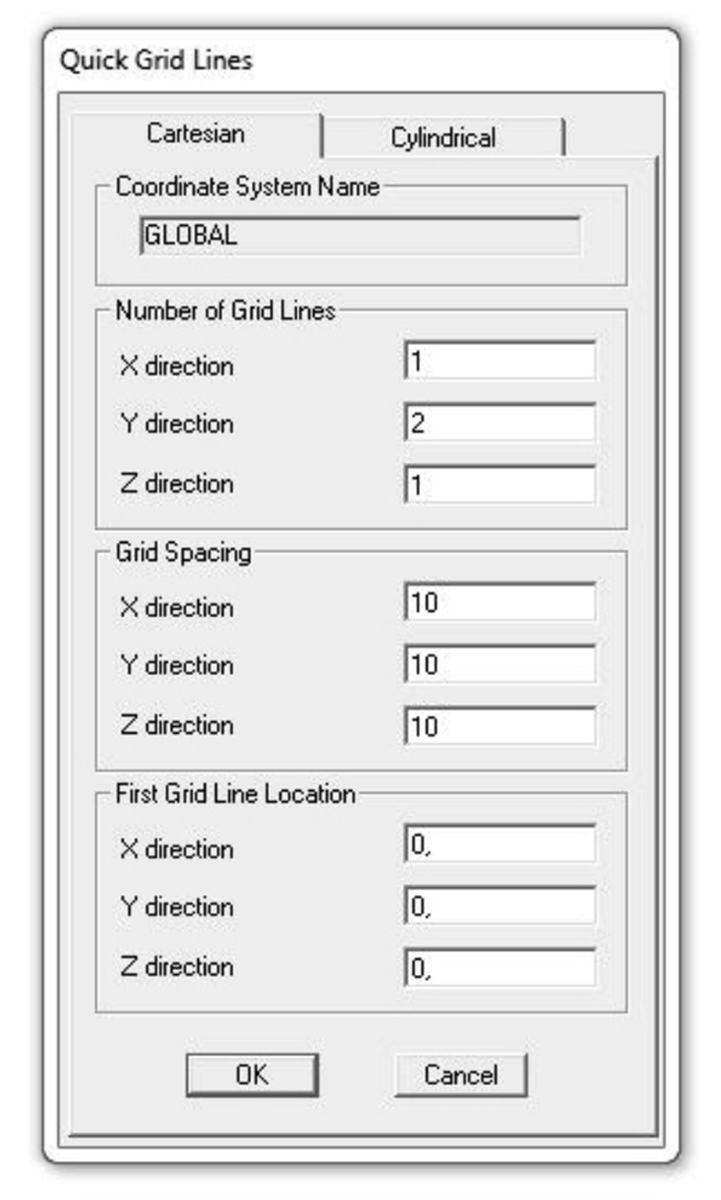
le impostazioni date alla griglia dovrebbero produrre una condizione analoga alla seguente:

Disegnare un'asta seguendo la spaziatura della griglia preimpostata.

assegnare i vincoli:
selezionare il punto > ASSIGN > JOINT RESTRAINTS > spuntare le sollecitazioni che il vincolo da posizionare trattiene.
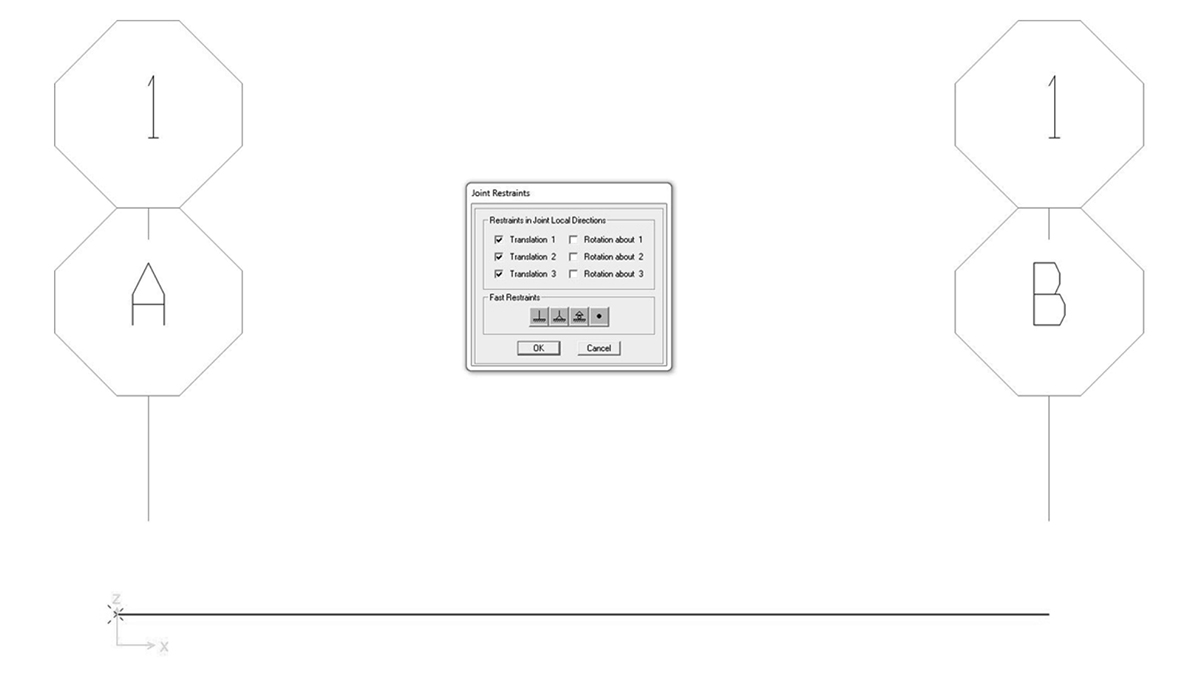
assegnare un incastro a sinistra ed un carrello a destra.

assegnare un carico uniformemente distribuito:
selezionare l'asta > ASSIGN > FRAME LOADS > DISTRIBUTED > impostare l'unità di misura voluta (nel nostro caso N,m, °C) > nella casella UNIFORM scrivere (ad es.) - 10 KN (carico verso l'alto considerato positivo)

rendere visibile il carico impostato:
DISPLAY > VIEW LOADS
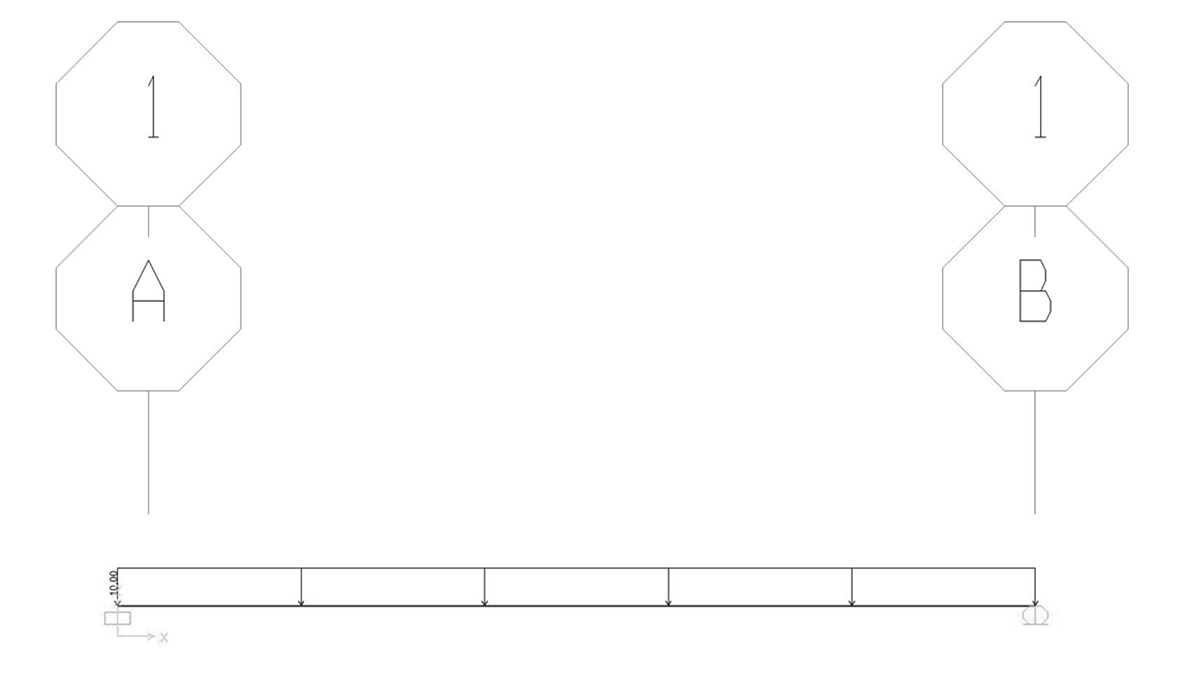
eliminare il contributo del peso proprio della struttura dall'analisi:
DEFINE > LOAD PATTERNS > SELF WEIGHT MULTIPLER = 0 > nominare il load pattern "peso_nullo" > ADD NEW LOAD PATTERN
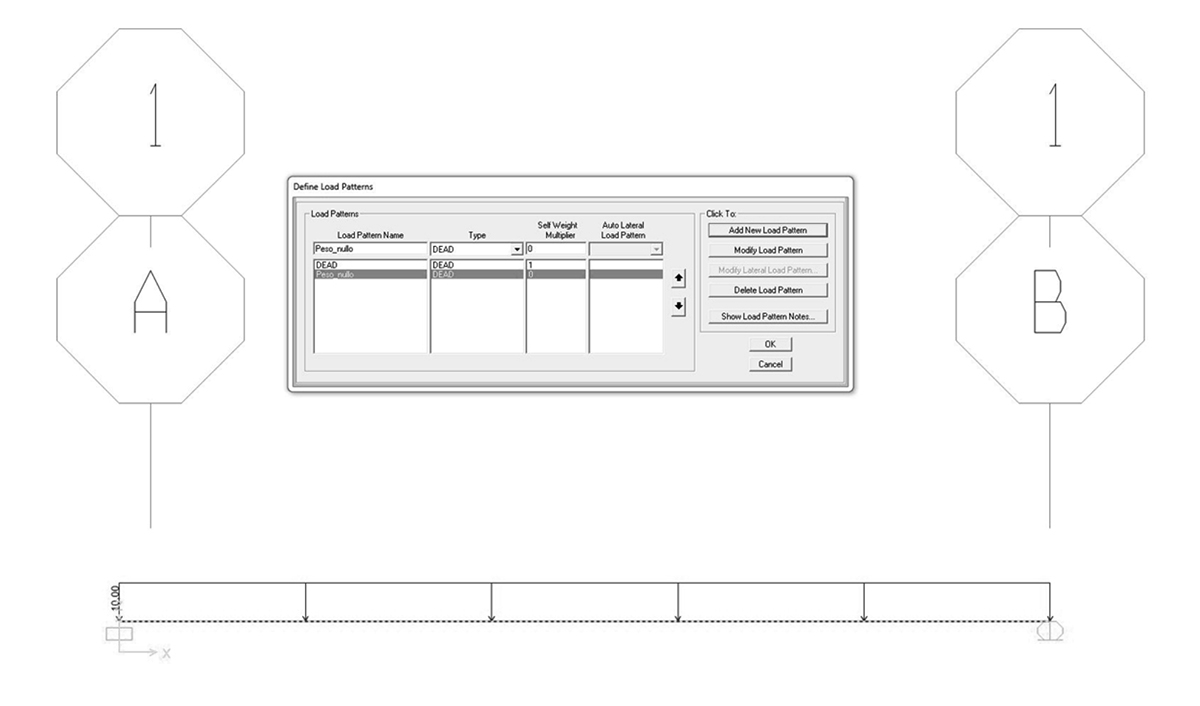
eliminare MODAL dall'analisi:
selezionare il load pattern MODAL > se nella colonna ACTION c'è RUN, premere il pulsante RUN/DO NOT RUN CASE per disattivare l'analisi
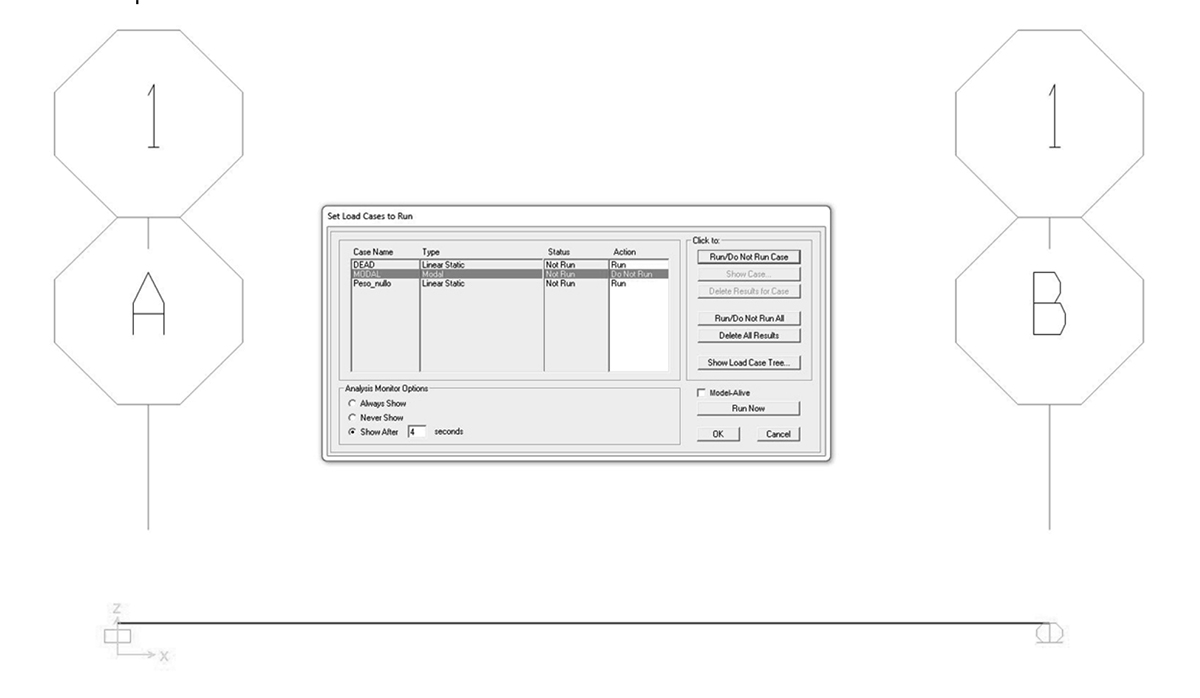
visualizzare la curva della deformata e confrontarla qualitativamente con quella ipotizzata:
RUN ANALYSIS

visualizzare le reazioni vincolari:
RUN ANALYSIS > JOINT REACTIONS

visualizzare il grafico del taglio e confrontarlo qualitativamente con quello ipotizzato:
RUN ANALYSIS > SHEAR 2-2

visualizzare il grafico del momento e confrontarlo qualitativamente con quello ipotizzato:
RUN ANALYSIS > MOMENT 3-3 > spuntare START e END

impostare il materiale, la forma e la dimensione della sezione:
ASSIGN > FRAME > FRAME SECTION > (nel nostro caso impostare acciaio a doppia T > impostare le misure desiderate (nel nostro caso quelle di una IPE500) > rinominare la sezione
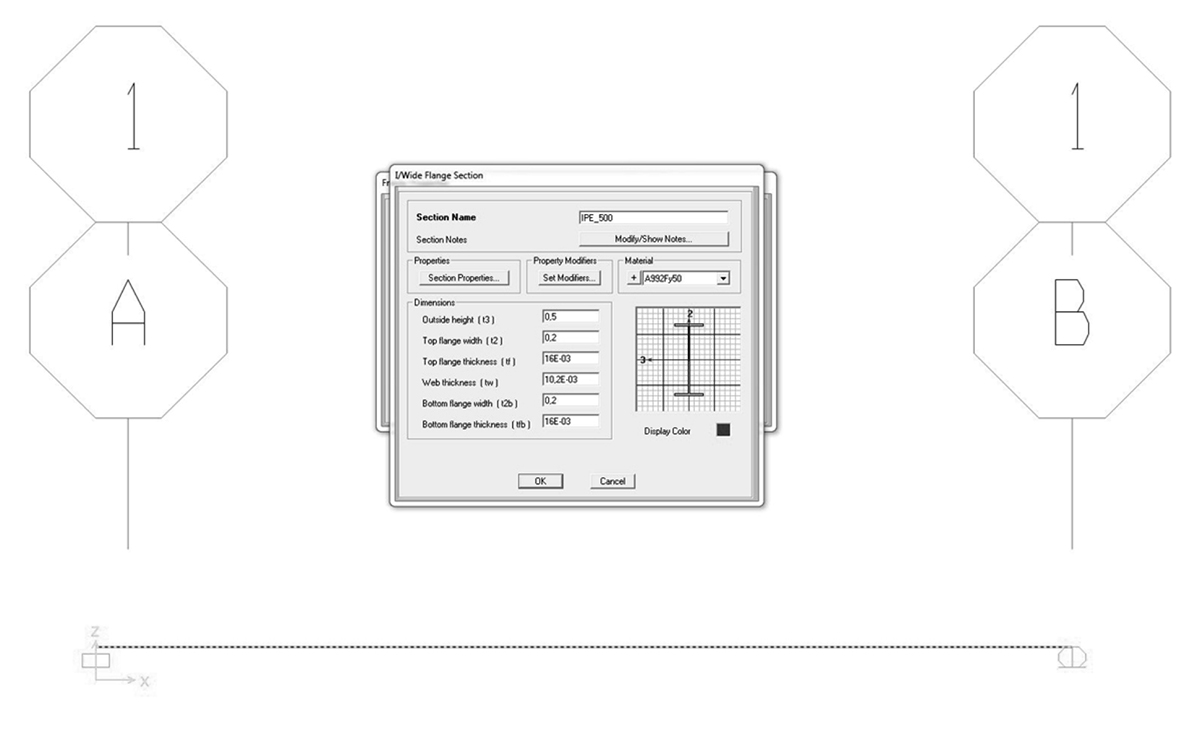
visualizzare le tabelle relative ai dati dell'analisi:
DISPLAY > SHOW TABLES > spuntare la parte ANALYSIS RESULTS

visualizzare gli spostamenti dovuti alle deformazioni per confrontare quello verticale con quello ottenuto nell'esercizio:
dal menù a tendina scegliere JOINT DISPLACEMENT > trovare il dato in R2
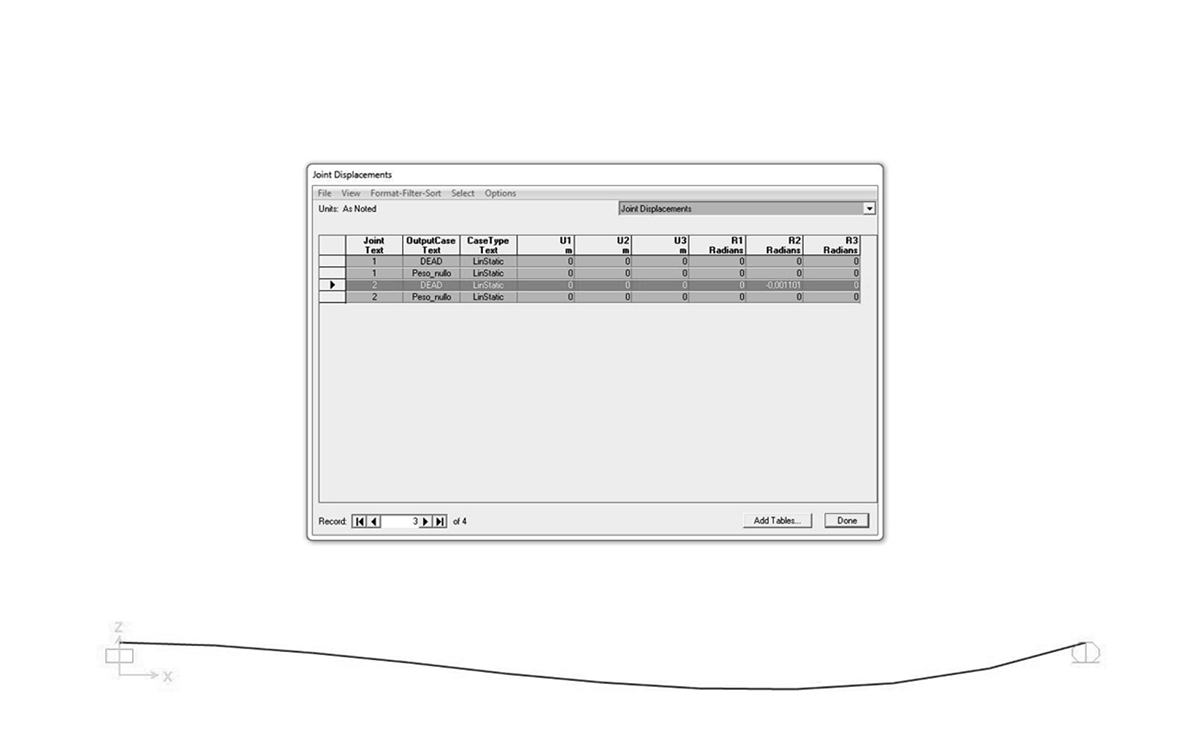
esportare i dati in formato EXCEL per riorganizzarli:
finestra delle tabelle > FILE > EXPORT > EXCEL FILE > SAVE
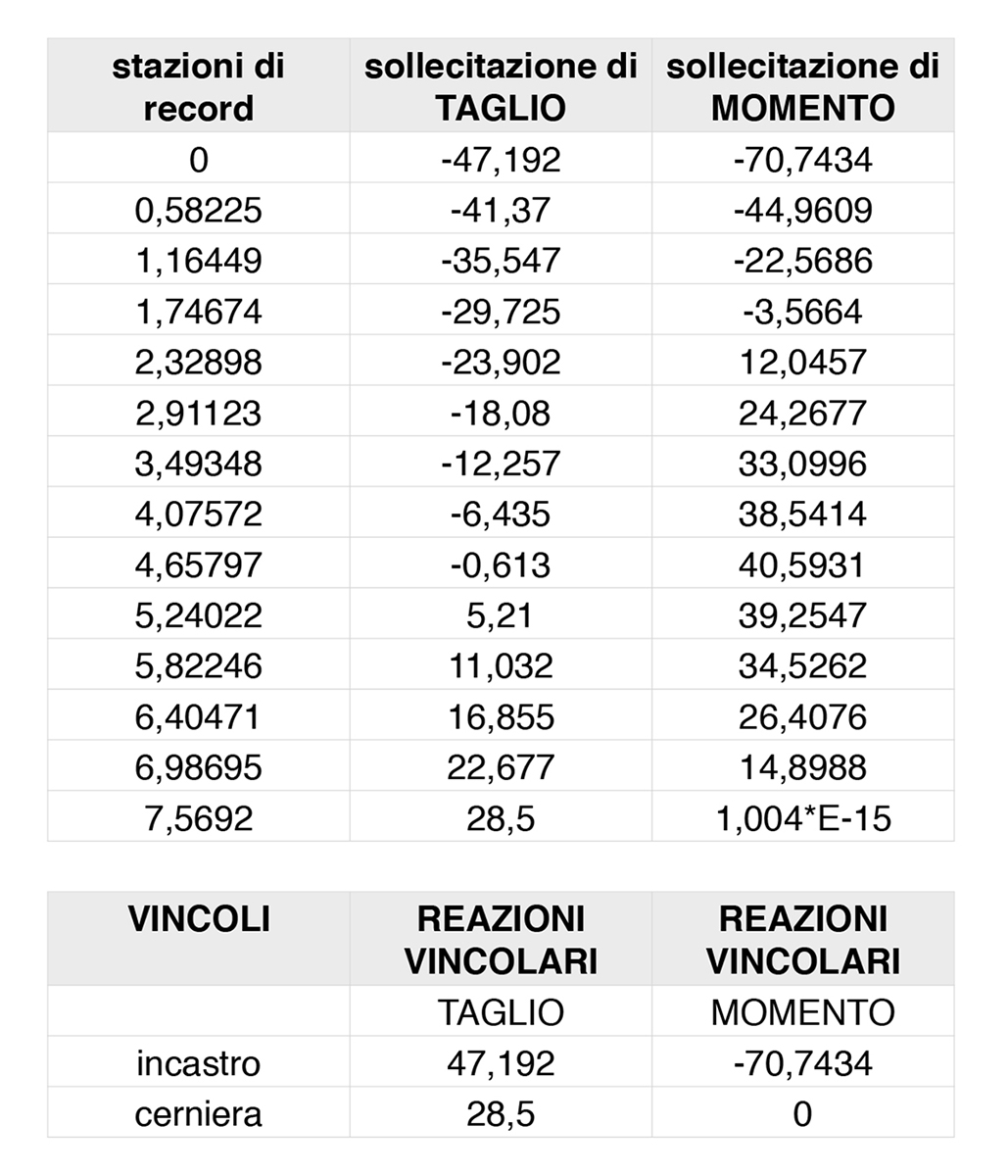

Commenti
erica.agnelli
Ven, 05/04/2013 - 11:13
Collegamento permanente
precisazione
Il file allegato contiene la versione intera dell'esercitazione, ovvero completa di immagini esplicative e della verifica in SAP2000