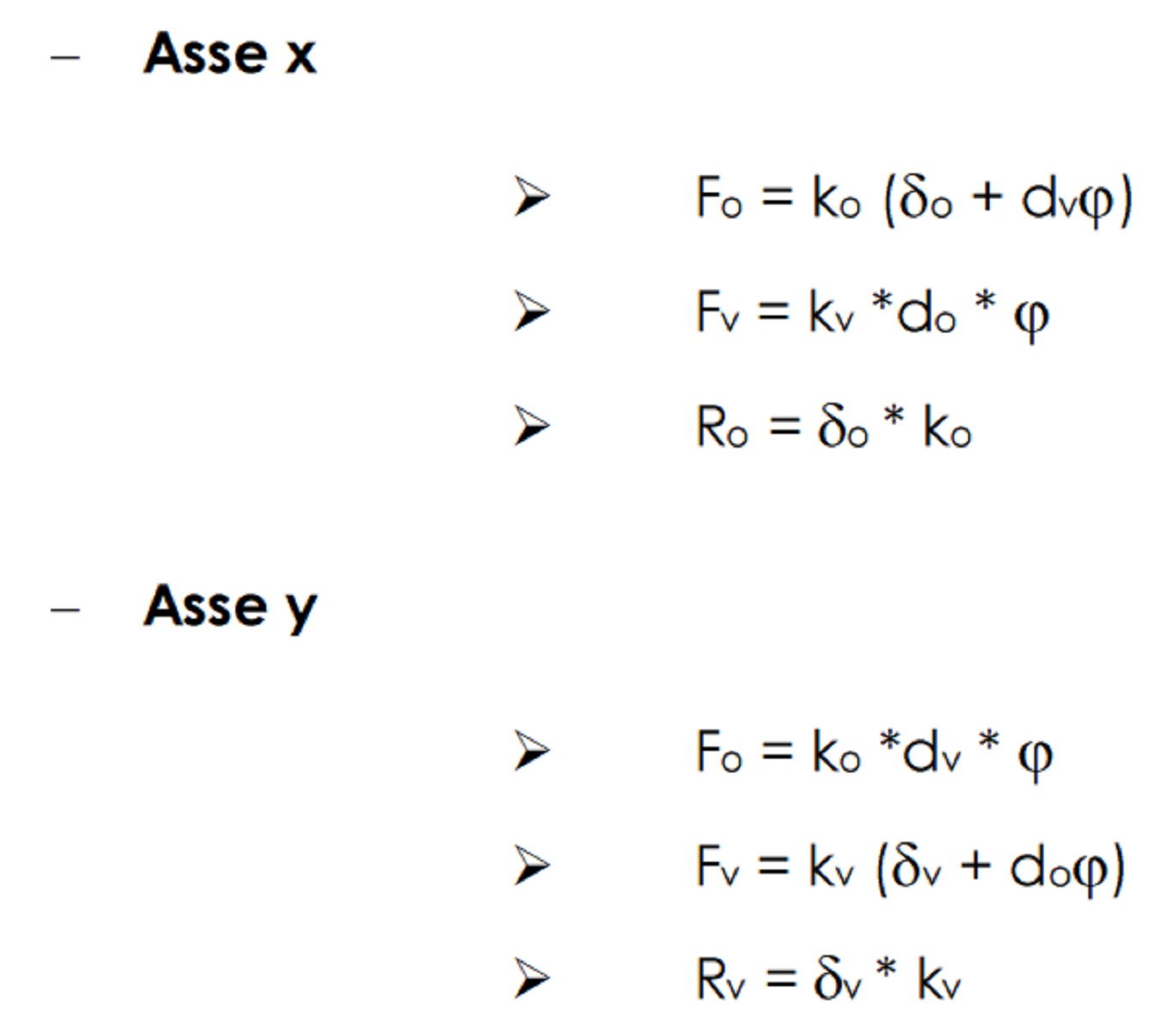9_RIPARTIZIONE DELLE FORZE ORIZZONTALI_11-05-2013

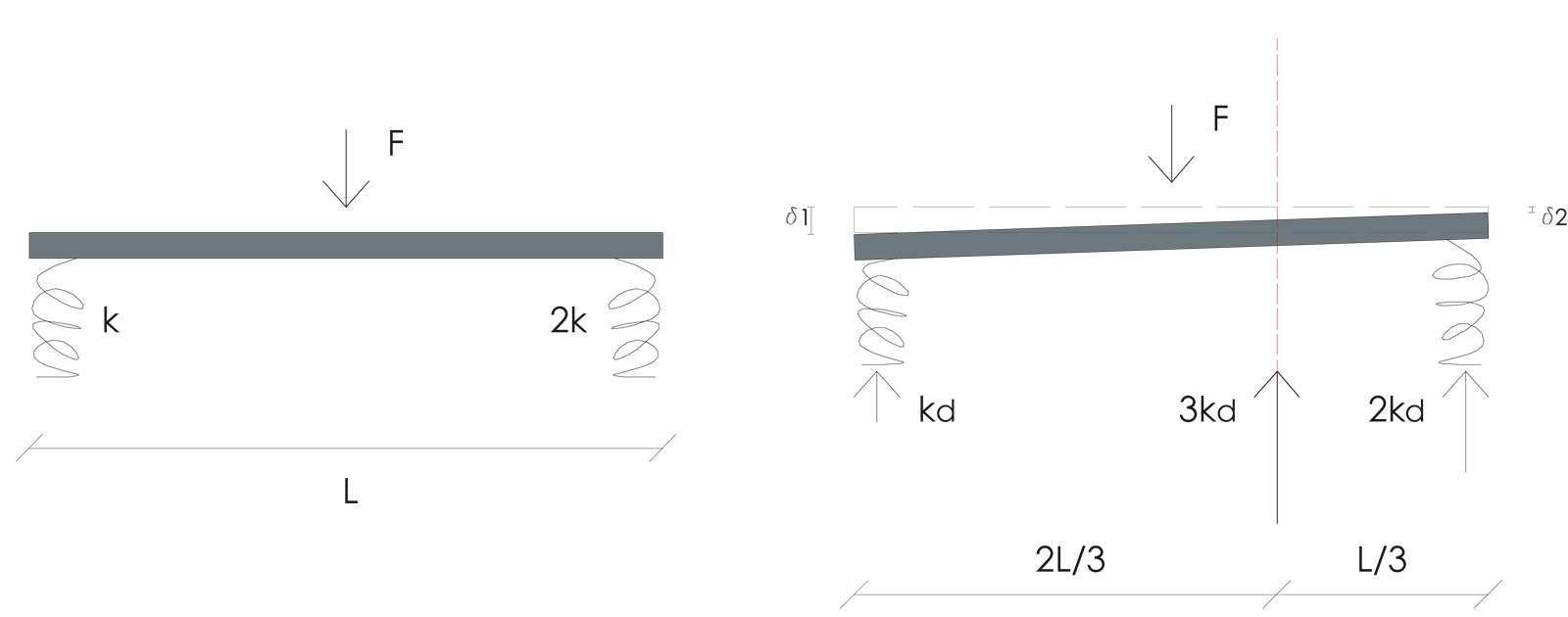
Analizzando il telaio shear-type abbiamo assimilato il concetto di rigidezza: essa può essere espressa come la forza necessaria ad imprimere uno spostamento unitario, dal momento che la forza F è pari alla rigidezza K per lo spostamento d. In sostanza è ciò che lega la causa (forza) all’effetto prodotto (spostamento): maggiore è la rigidezza, maggiore dovrà essere la forza necessaria a produrre un medesimo spostamento.

Trattando il tema dei controventi e, di conseguenza, della risposta alle azioni orizzontali di varia natura (sisma, vento, ecc.) che una struttura deve necessariamente essere in grado di sopportare, è opportuno fare una precisazione: l’efficacia di un sistema di controventi risiede nella possibilità di considerare l’impalcato in questione come un corpo infinitamente rigido sul piano orizzontale. Esso, quindi, è incapace di deformarsi se soggetto a forze agenti lungo il suo medesimo piano e si inflette nel caso dell’azione di forze verticali che qui però non trattiamo. I controventi, dunque, possono essere considerati vincoli elastici cedevoli, i quali contrastano le forze agenti sul loro stesso piano. La loro elasticità consente al corpo rigido degli spostamenti indotti dalla forza agente, alla quale corrisponde una reazione proporzionale alla rigidezza (vedi telaio shear-type). 

Nel caso più semplice di controventi con eguale rigidezza avremo una medesima ripartizione della forza agente e il corpo rigido traslerà.

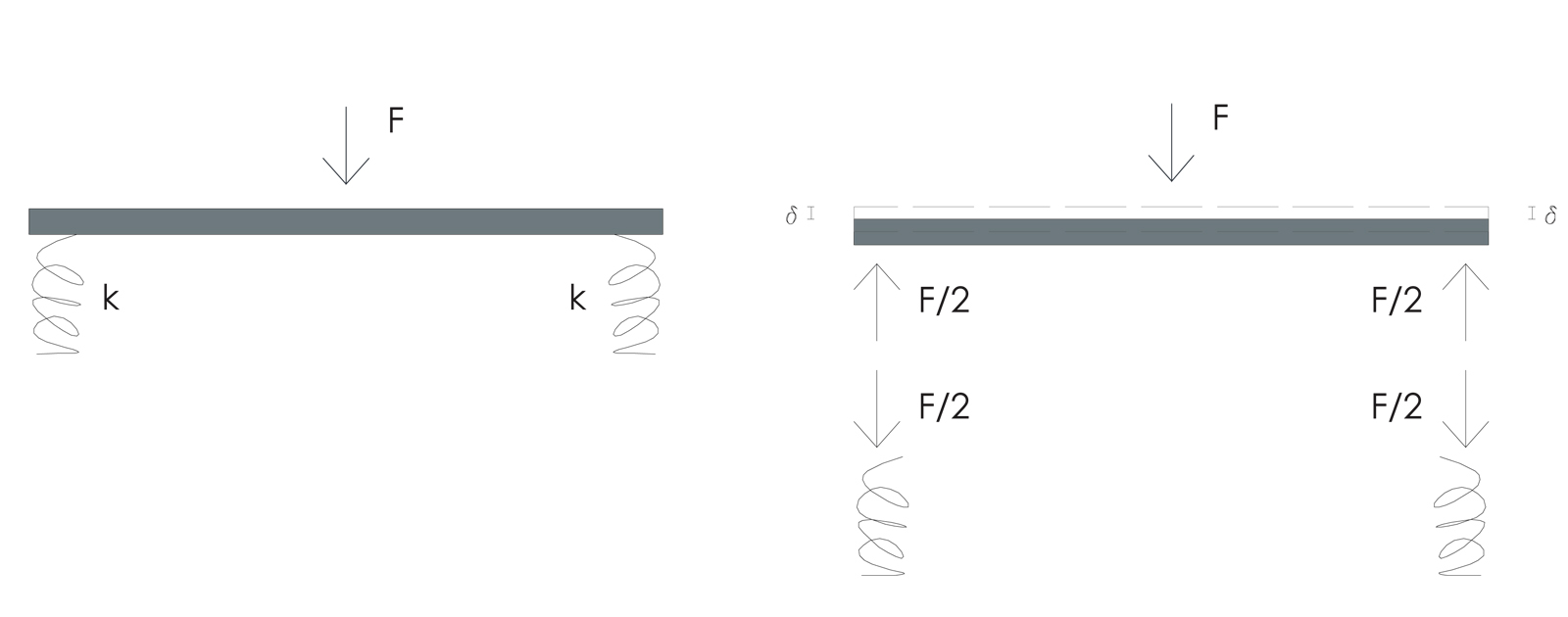
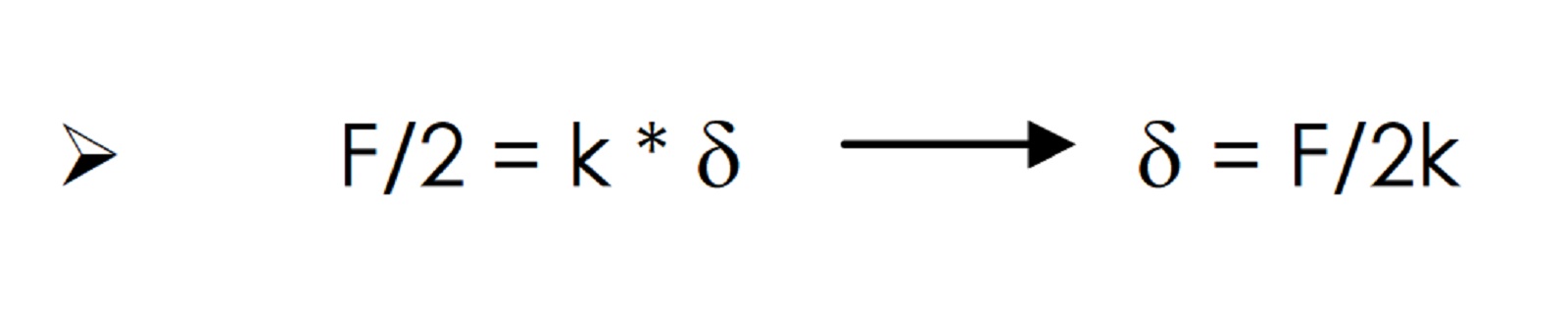
Quando, invece, abbiamo controventi con rigidezze tra loro differenti sappiamo che la forza agente verrà ripartita in proporzione alle rigidezze appunto, quindi anche gli spostamenti ddiversi per ogni molla. Di conseguenza, il corpo rigido non si limiterà a traslare, ma ruoterà. Questo avviene nei casi in cui l’asse della forza agente F non corrisponde all’asse dei centri delle rigidezze, ossia l’asse della forza reagente risultante equivalente alle 2 reazioni singole.

Gli spostamenti finali, quindi, risentono della traslazione dlungo al direzione di F e di una rotazione attorno al centro delle rigidezze. In sostanza le due grandezze fondamentali sono la rigidezza traslante K_de la rigidezza rotazionale K_fi. 

Lo scopo dell’esercitazione seguente è quello di analizzare un impalcato strutturale, calcolando la rigidezza traslante, il centro di massa, il centro delle rigidezze, la rigidezza rotazionale e quantificando la ripartizione delle azioni orizzontali (sismiche) sui diversi controventi.

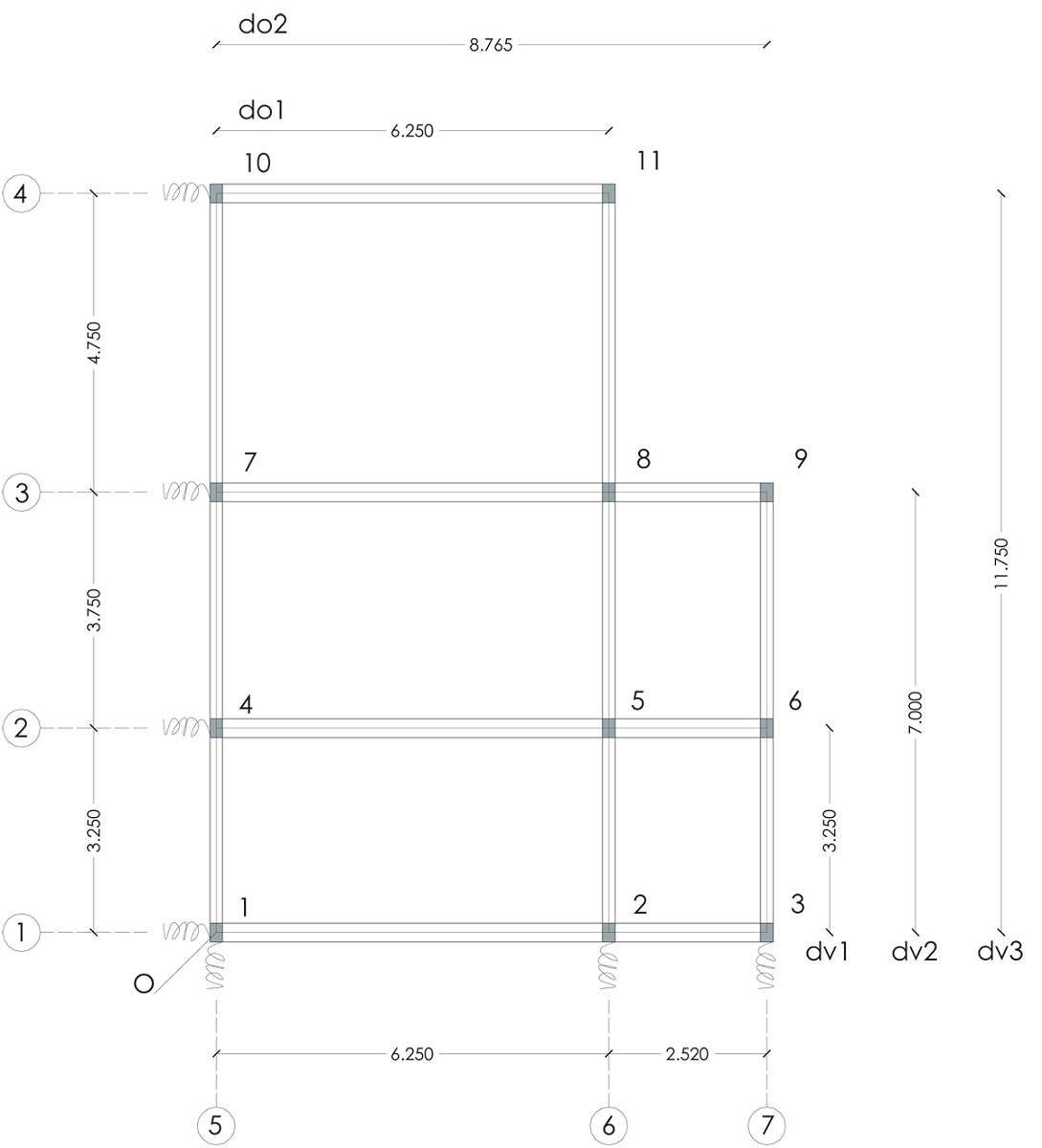
Pianta strutturale e sistema di controventi

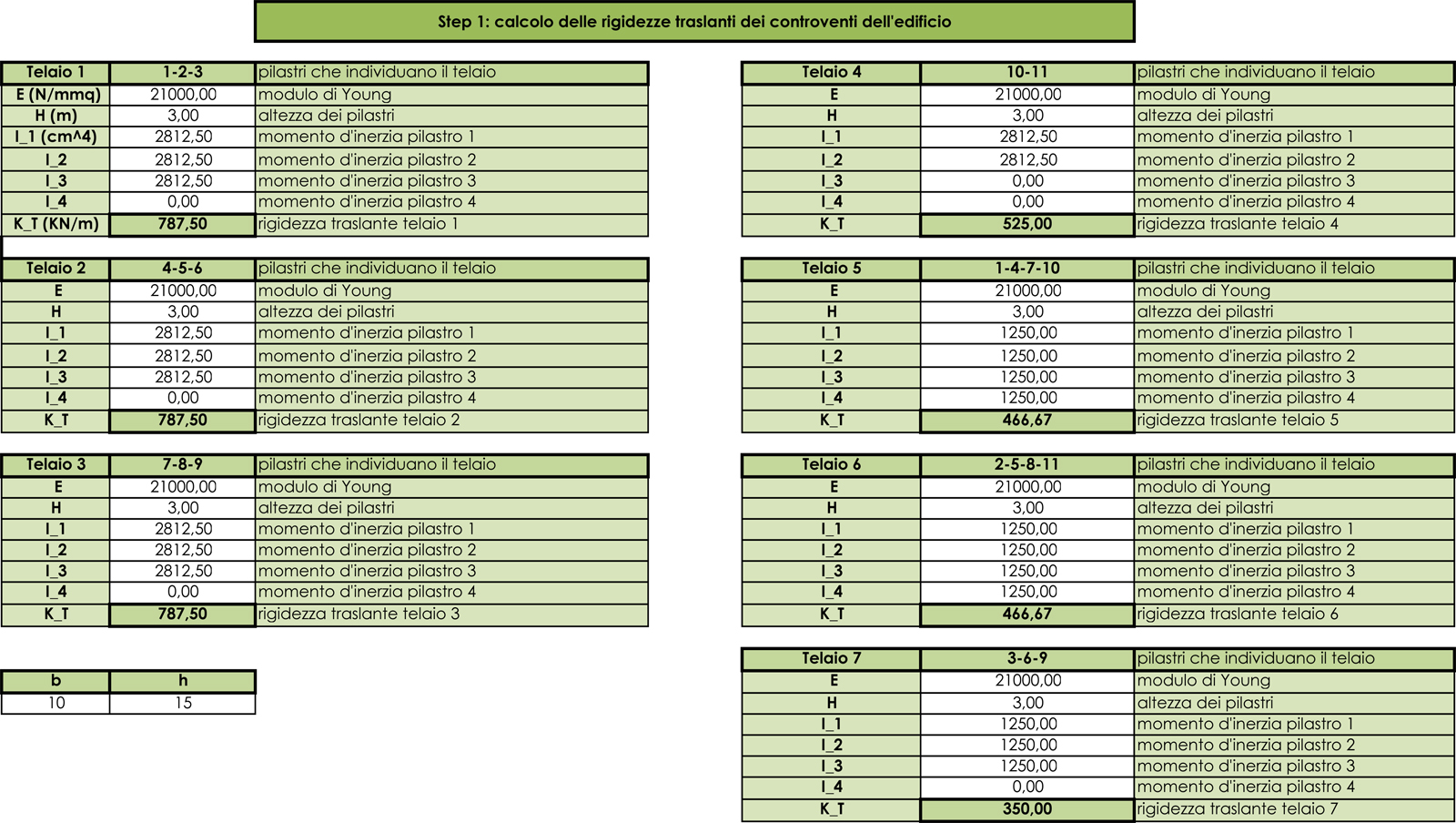
STEP 1

Dopo aver individuato i pilastri che compongono i 7 telai dell’impalcato assegno ad ognuno di loro un materiale (in questo caso ca) e una sezione (b=10 cm; h=15 cm). L’obiettivo è calcolare la rigidezza traslante K_ddi ogni telaio, ovvero la  somma delle rigidezze dei singoli pilastri che lo compongono, la quale come sappiamo dipende dal modulo di Young E, dal Momento d’Inerzia I e dalla luce L (nello specifico l’altezza h).

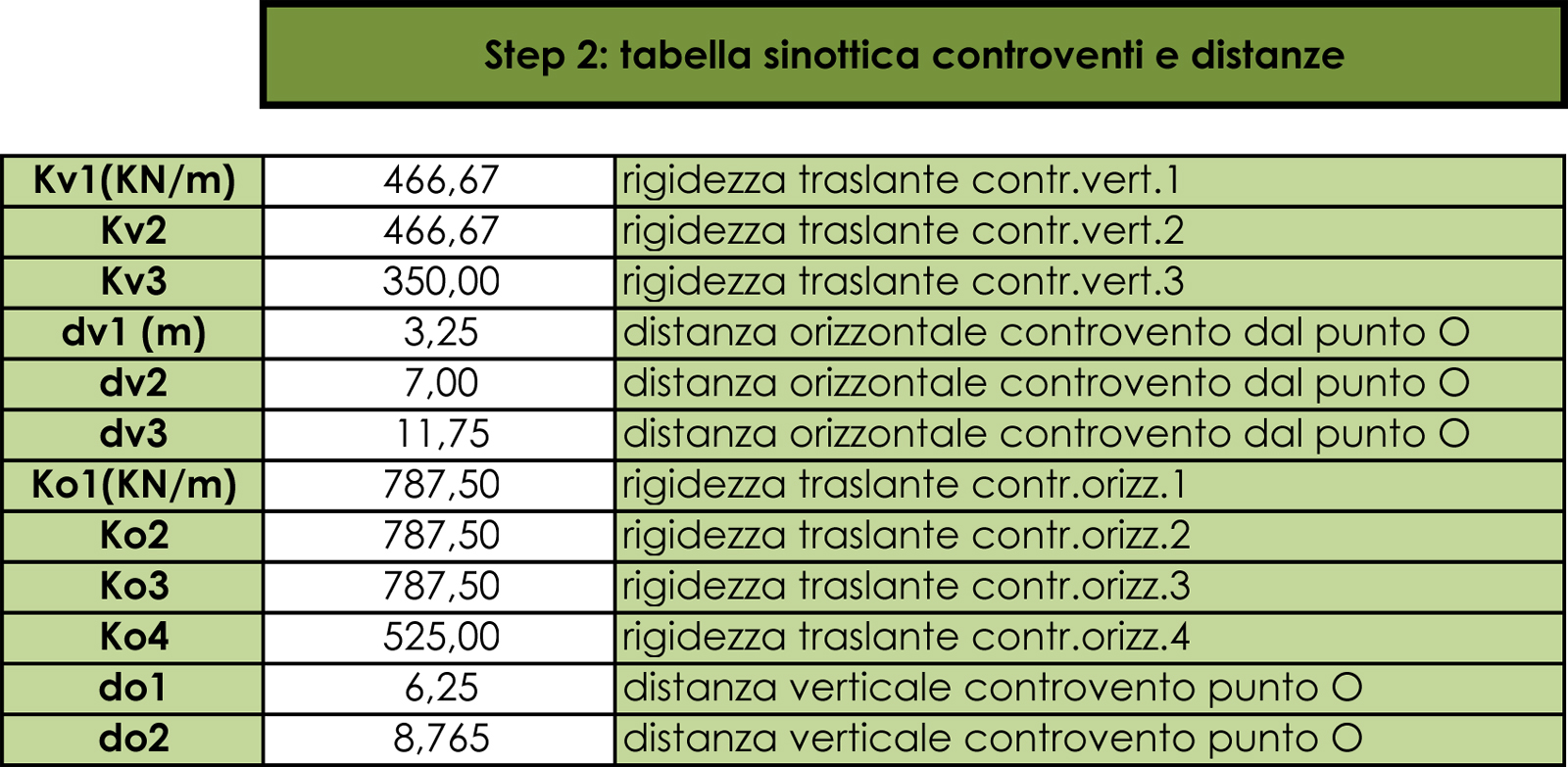
STEP 2

Raccogliamo in una tabella i valori delle rigidezze traslanti dei telai e le distanze degli stessi da un punto O ritenuto origine del sistema di riferimento. Come vedremo queste distanze relative ci serviranno nel calcolo del centro delle rigidezze.

STEP 3

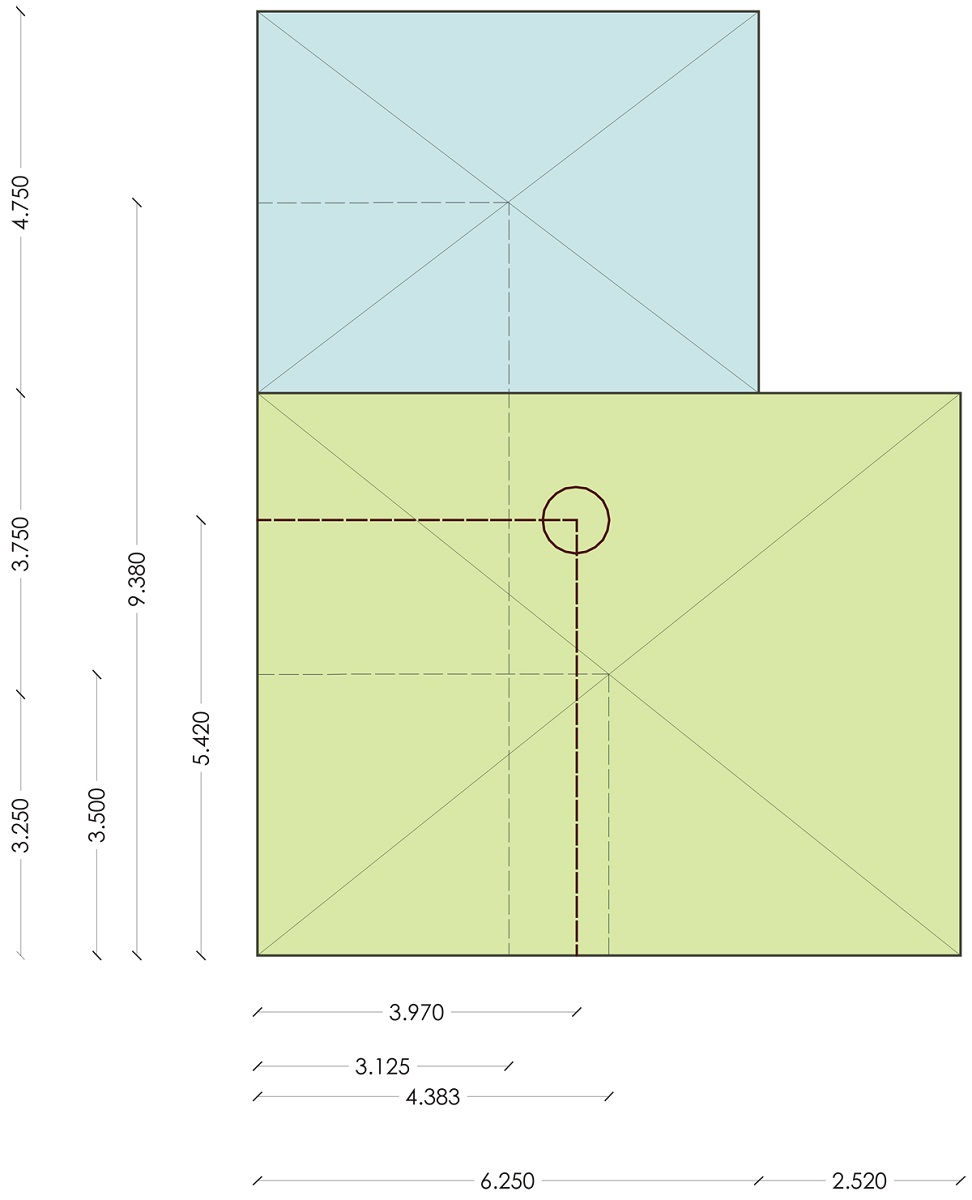
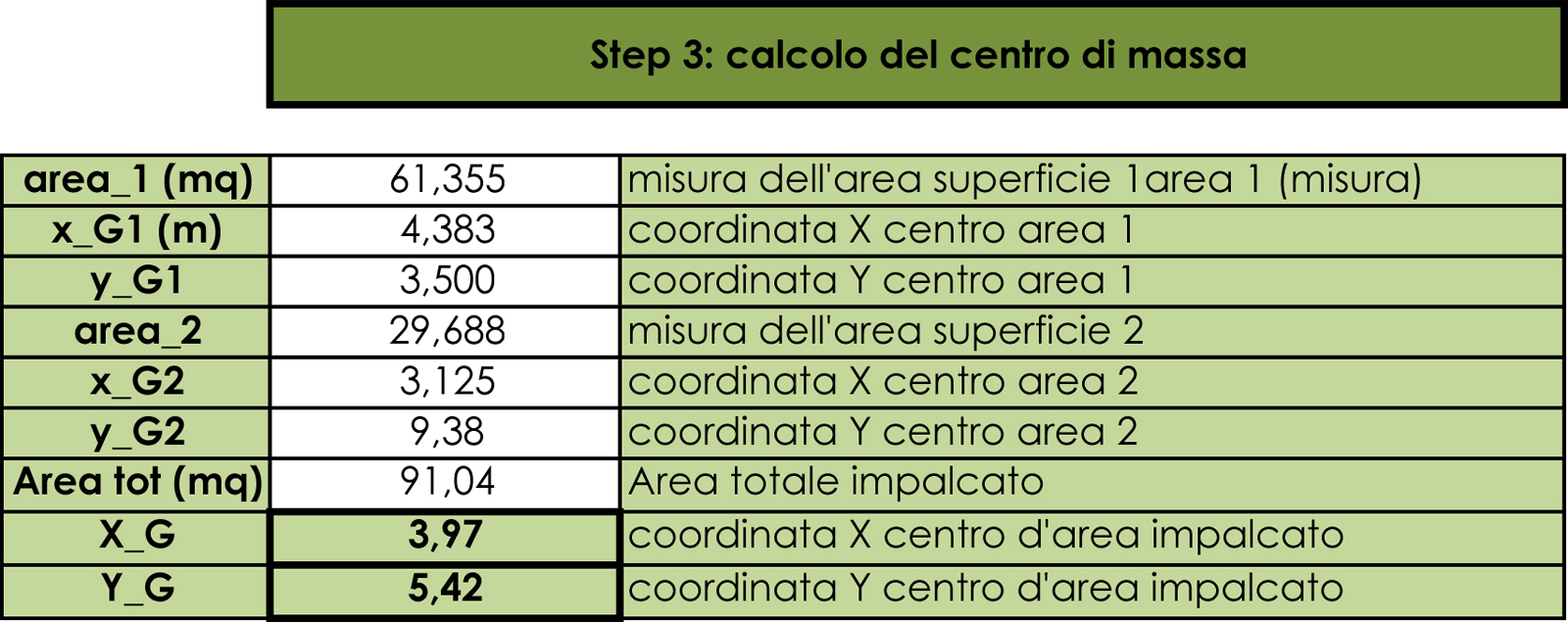
A questo punto calcoliamo il centro di massa del nostro impalcato: il procedimento è puramente i natura geometrica e consiste nel suddividere la pianta in forme semplici (rettangoli) delle quali calcolo il corrispondente centro di massa. Una volta ottenute le coordinate dei 2 centri di massa dei 2 rettangoli, con una semplice media ponderata abbiamo le coordinate del centro di massa dell’impalcato.

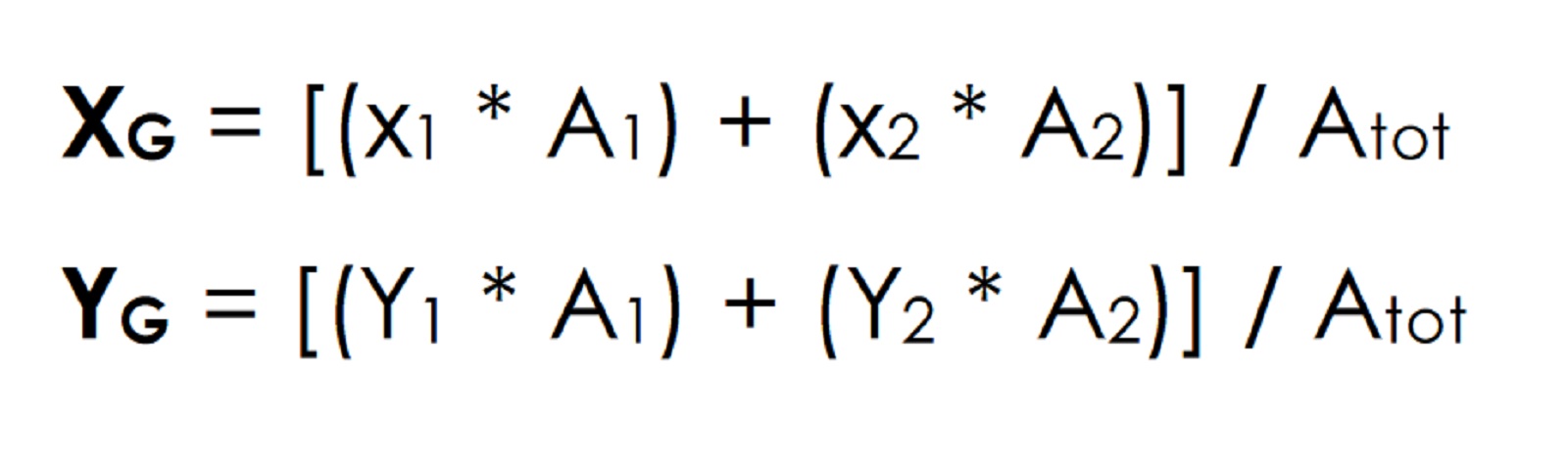
STEP 4

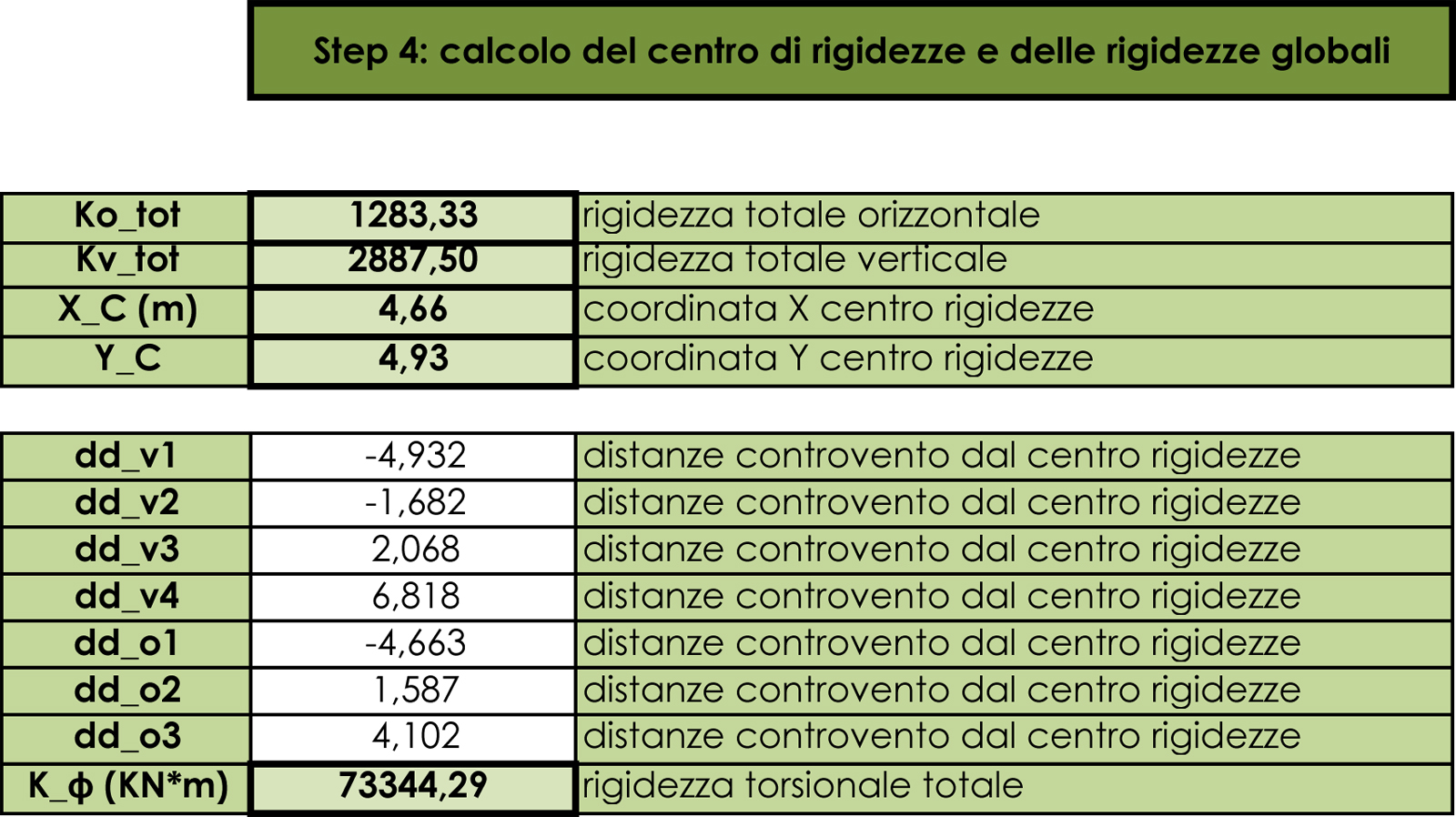
Il quarto step prevede il calcolo del centro delle rigidezze, per il quale necessitiamo delle distanze dall’origine O prima annotate. Infatti, anche in questo caso si tratta di una media ponderata: moltiplichiamo il valore della rigidezza traslante di ogni telaio per la relativa distanza dal punto O e dividiamo la somma ottenuta per la rigidezza traslante totale, sia in orizzontale che in verticale (ossia lungo gli assi x e y del nostro sistema di riferimento perché va ricordato che le forze agenti sono sempre orizzontali e che si sta analizzando il piano dell’impalcato).

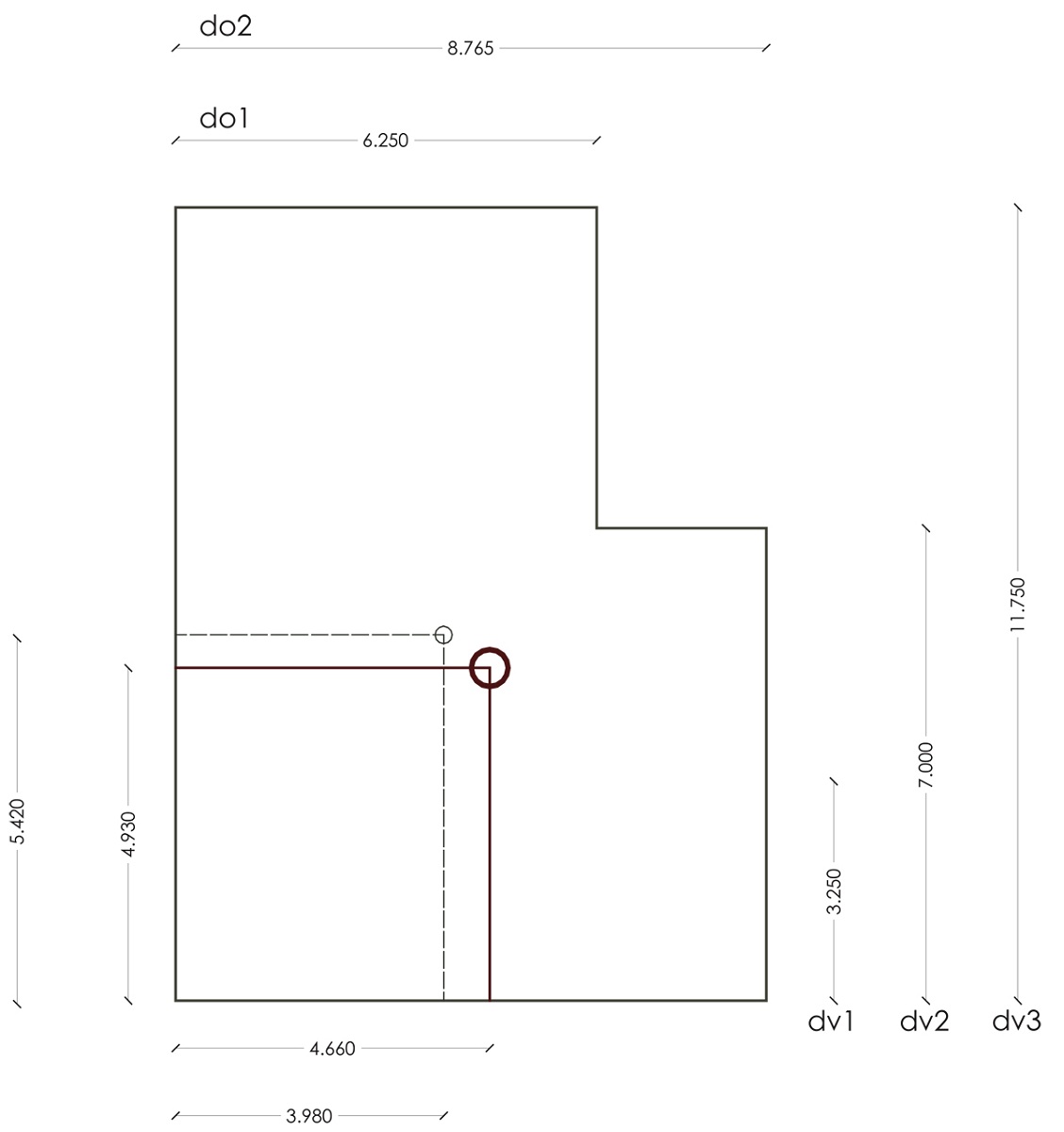
Dopo aver individuato il centro delle rigidezze annotiamo le distanze da esso di ogni controvento poiché sono necessarie ai fini del calcolo della rigidezza rotazionale Kfi: essa è data dalla sommatoria dei prodotti delle rigidezze traslanti di ogni telaio per il quadrato della relativa distanza dal centro delle rigidezze.

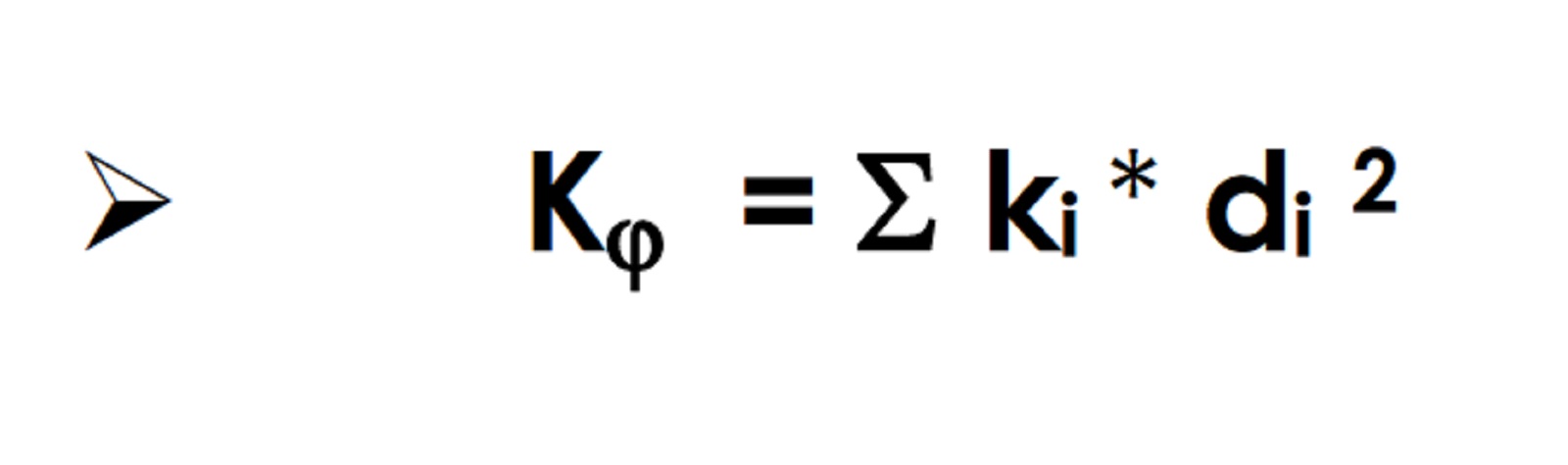
STEP 5

Il quinto passo consiste nell’analisi dei carichi agenti sull’impalcato e sulla loro combinazione (allo SLE dal momento che i valori non vengono amplificati dai coefficienti g). La somma del carico permanente totale e di quello accidentale totale, moltiplicata per il coefficiente di contemporaneità, ci dà il valore dei pesi sismici, i quali, a loro volta, divisi per il coefficiente di intensità sismica, danno il valore della forza sismica orizzontale. 

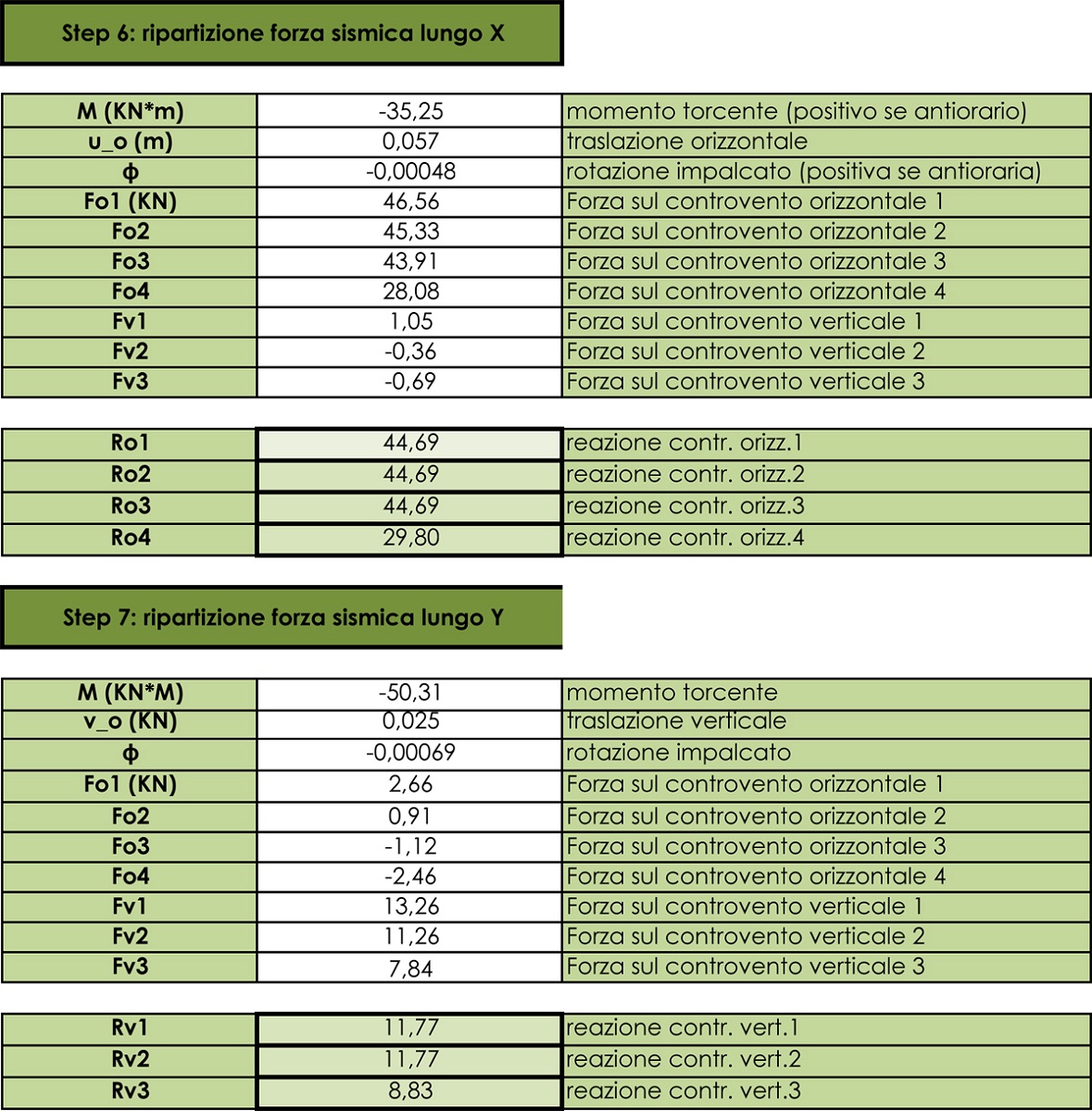
STEP 6-7

Ora non ci resta che quantificare la ripartizione della forza sismica F lungo l’asse x e lungo quello y e, nello specifico, per ognuno dei controventi.

Innanzitutto, ricordiamo che nel momento in cui la forza agente abbia un asse differente da quello del centro delle rigidezze (come nel nostro caso), il corpo non si limita a traslare, ma ruota anche. Per poter conoscere il valore di questa rotazione, calcoliamo il Momento Torcente M per l’asse x, moltiplicando la forza sismica F per il suo braccio, ovvero la differenza tra l’ordinata del centro delle rigidezze e quella del centro di massa, e per l’asse y, utilizzando come braccio la differenza tra le ascisse dei due centri. Poi, calcoliamo la traslazione orizzontale, dividendo F per la rigidezza traslante orizzontale, la traslazione verticale, dividendo F stavolta per la rigidezza traslante verticale, e le rotazioni, dividendo i rispettivi Momenti Torcenti per la rigidezza rotazionale.

A questo punto siamo in grado di conoscere la ripartizione della forza sismica, sia lungo l’asse x che lungo quello y, e il valore delle reazioni dei singoli controventi.