ESERCITAZIONE 3- TRAVE A SBALZO

In questa terza esercitazione ho provato a dimensionare la trave che sostiene uno sbalzo in tre differenti tecnologia costruttive (legno, cls, acciaio). Per fare ciò, seguendo il metodo delle tensioni in cui al  σ max eguaglio l’ Fyd , come per la prima esercitazione, ho dimensionato la trave allo slu per verificarla in campo strutturale, ovvero se le sue dimensioni fossero adeguate a sorreggere i carichi da essa portati. L’unica cosa in cui differisce questa parte del dimensionamento è nel calco del momento max a cui è soggetta la trave che sorregge lo sbalzo in quanto essa non è, come nella prima esercitazione, una trave doppiamente appoggiata, ma una mensola e quindi il suo momento max equivale a ql²/2.

Dopo avere dimensionato la trave, per uno sbalzo, è importantissimo verificarne la deformabilità in rapporto alla sua luce poiché è inammissibile che questa accusi degli spostamenti o abbassamenti che ne impediscano il corretto uso ed un adeguato comfort. Per fare questa verifica si entra nel campo dello stato limite di esercizio (sle) che per tutte e tre le tecnologie si verifica nello stesso modo ovvero:

qe=(G1+G2+ψ11xQ1)x i.                                                

In oltre per calcolare l’abbassamento della trave è importante conoscere il modulo di elasticità del materiale (E) e il suo momento di inerzia (Ix) in quanto lo spostamento max si ricava:

ν max=qel^4/8E

Trovato lo spostamento massimo , secondo normativa, si calcola che il suo rapporto con la luce che deve coprire sia maggiore o uguale a 250. (3.1)

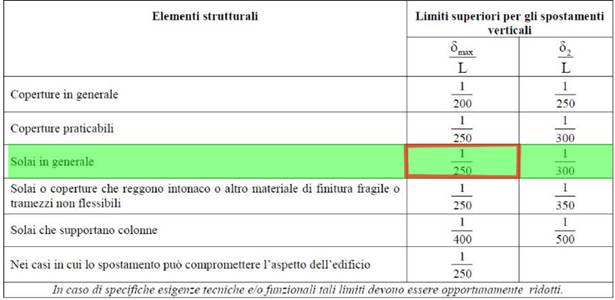
3.1

SBALZO IN LEGNO

3.2

Per prima cosa ho ipotizzato una pianta delle carpenterie della struttura (3.3) e la composizione del solaio della stessa (3.4)

3.3

3.4

A questo punto ho potuto dimensionare la trave per poi andare a verificare allo sle lo sbalzo e capire se la trave da me dimensionata garantisse un abbassamento della stessa entro i limiti di norma. Per fare ciò ho calcolato i carichi allo stato limite di esercizio (qe) e , ricavata la sezione della trave (30X65 cm), ho potuto calcolare il suo momento di inerzia rispetto l’asse sfavorevole ovvero x: Ix=1/12 bh ³; nel  mio caso pari a 686563 cm^4.

Conoscendo il modulo elastico del legno (E),8000 N/mm ², ho ricavato il suo abbassamento max (ν max) pari a 0,52 cm. In questo modo ho verificato il rapporto luce abbassamento e ho osservato che era pari a 416,65 ben superiore a 250.

In questa verifica ho trascurato il peso proprio della trave in quanto il legno è  un materiale relativamente leggero e quindi avrebbe poco influito nel computo totale (3.5).

3.5

Quindi la sezione (30x65 cm) è risultata verificata.

SBALZO IN LEGNO

3.6

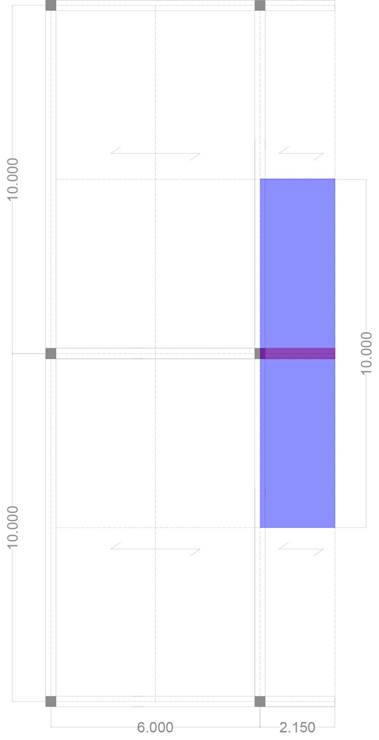
3.7

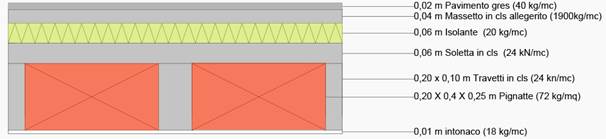
3.8

Al contrario del legno, nel cemento, è molto importante verificare che se aggiungo il peso proprio della trave dimensionata al carico limite ultimo (qu) questa rimanga verificata dato il suo notevole peso strutturale.  Per questo anche quando calcolo il carico allo stato limite d’esercizio (qe) ne devo tenere conto. Come per il legno ho trovato il modulo elastico del cemento (E),21000 N/mm², il suo momeno di inerzia (Ix), 346615 cm^ e quindi ho potuto ricavare il suo ν max= 0,27 cm.

Facendo il rapporto luce abbassamento ho trovato che valeve 798,94>250 (3.9).

3.9

Quindi la sezione (25X55 cm) è risultata verificata.

SBALZO IN ACCIAIO

3.10

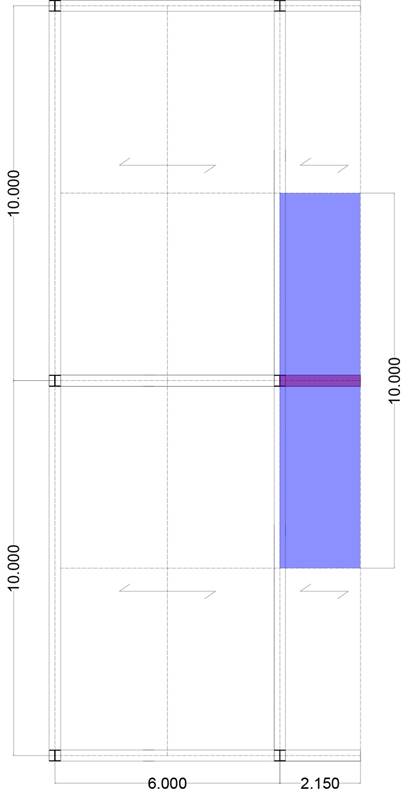
3.11

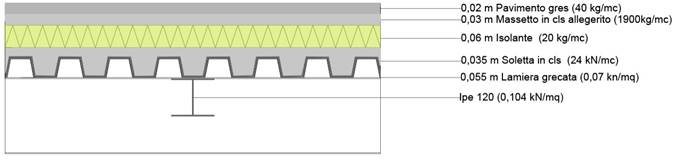
3.12

Ho dimensionato la trave  allo stato limite ultimo ricavandomi il suo (Wx),735,10 cm ³,e quindi scegliendo un profilo che ne soddisfacesse tale valore ovvero una IPE 360 (3.13).

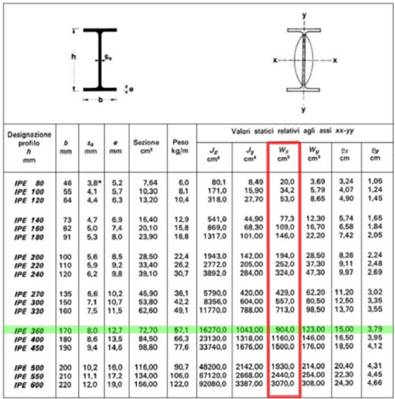
3.13

Come nel cemento anche nell’acciaio il peso della trave è molto influente nel calcolo strutturale e nel caso dell’acciaio è facilmente ricavabile in quanto nei profilari è dichiarato dal costruttore; Quindi sia nel carico allo stato limite ultimo (qu) che in quello allo stato limite d’esercizio(qe) dovrò considerarlo.

Nell’acciaio anche il momento d’inerzia(Ix) è facilmente ricavabile in quanto dichiarato dal costruttore.

Conoscendo questi dati ed il modulo elastico dell’acciaio (E),21o000 N/mm², ho ricavato l’abbassamento  della trave (ν max), 0,373 cm, e quindi ho calcolao il rapporto luce abbassamento uguale a 575,728>250 (3.14).

3.14

Quindi l’IPE 360 è risultata verificata.