blog di Daniele.Tricarico.

In questa esercitazione, con l’ausilio del “metodo delle rigidezze”, ho studiato come si ripartisce una forza orizzontale , come quella che genera un sisma od il carico del vento, sui diversi telai che compongono una struttura. Nel caso preso in esame la struttura è interamente realizzata in cemento armato e composta da telai piani. Tali elementi oltre a trasmettere i carichi verticali alle fondazioni, funzionano da controventi perché sono in grado di sopportare i carichi orizzontali.

Come prima cosa ho individuato i telai che costituiscono la struttura da me progettata (5.1); ovvero 16 telai di cui 8 verticali ed 8 orizzontali,

5.1

In particolare:

-Telaio 1 v  composto da pilastri: 1-4-7-10-13-16-24-32;

- Telaio 2v  composto da pilastri: 2-5-8-11-14-17-25-33;

- Telaio 3v  composto da pilastri: 3-6-9-12-15-18-26-34;

- Telaio 4v  composto da pilastri: 19-27-35;

- Telaio 5v  composto da pilastri: 20-28-36;

- Telaio 6v  composto da pilastri: 21-29-37;

- Telaio 7v  composto da pilastri: 22-30-38;

- Telaio 8v  composto da pilastri: 23-31-39;

- Telaio 1o  composto da pilastri: 1-2-3;

- Telaio 2o  composto da pilastri: 4-5-6;

- Telaio 3o  composto da pilastri: 7-8-9;

- Telaio 4o  composto da pilastri: 10-11-12;

- Telaio 5o  composto da pilastri: 13-14-15;

- Telaio 6o  composto da pilastri: 16-17-18-19-20-21-22-23;

- Telaio 7o  composto da pilastri: 24-25-26-27-28-29-30-31;

- Telaio 8o  composto da pilastri: 32-33-34-35-36-37-38-39.

A questo punto  ho potuto schematizzare i telai con delle molle nel piano, in quanto rappresentano dei vincoli cedevoli elasticamente.(5.2)

5.2

Per calcolare la rigidezza traslante di tutti i controventi, ho dovuto ricavare per  prima cosa il momento d’inerzia di ogni pilastro, stando attento al loro orientamento. Nel ,io caso essendo tutti quadrati hanno tutti uno stesso momento di inerzia  (I=bh^3/12) pari a 213333 cm⁴. Ipotizzando che i talai fossero tutti di tipo shear type ho potuto facilmente ricavare la loro rigidezza. Nel caso fossero telai composti da solo due pilastri la forza aggente su di essi sarebe stata F= (12 EI₁/h³+12 EI₂/h³) δ  la rigidezza sarà pari a

 k=12 EI₁/h³+12 EI₂/h³.

Nel caso esaminato i telai sono composti da più pilastri la rigidezza sarà pari a k=12E/h³(I₁+I₂+…+I_n).

con l’aiuto di un foglio di calcolo excel ho potuto ricavare tutte le rigidezze traslanti.(5.3)

5.3

In una seconda tabella ho potuto riassumere le rigidezze dei singoli telai ed la loro distanza dall’origine degli assi di riferimento. (5.4)

5.4

A questo punto ho ricavato il centro della massa dell’impalcato (G) e poiché è costituito da una forma complessa l’ho sudiviso in modo tale da ottenere forme elementari.(5.5)

5.5

In questo modo ho ottenuto un impalcato composto da due rettangoli di cui ho facilmento individuato il centro di massa G₁ e G₂ e quindi ho ricavato le coordinate del centro di massa dell’intero impalcato:

Gx=A₁^.Gx₁+ A₂^.Gx₂/ A_tot ;      Gy=A₁^.Gy₁+ A₂^.Gy₂/ A_tot .    

In tal modo ho trovato il centro  dell’area dell’impalcato, ma essendo questo di eguale densità in tutti i punti corrisponde al centro di massa dell’impalcato.(5.6)

5.6

Sommando i prodotti delle rigidezze dei telai per le loro distanze dall’origine degli assi di riferimento e dividendo il tutto per la rigidezza totale ho potuto trovare le coordinate del centro di rigidezza (C).(5.7)(5.8)

5.7

5.8

Con questi dati posso sapere se l’impalcato in caso di una forza che agisce sul centro di massa subisce o meno una rotazione. Non si ha rotazione soltanto quando il centro di massa corrisponde con il centro delle rigidezze.

Calcolato il centro di rigidezza ho potuto ricavare la distanza di ogni telaio da questo per potermi ricavare la rigidezza torsionale dell’impalcato(K_φ) sommando i prodotti delle rigidezze dei controventi per il quadrato della lor distanza dal punto di riferimento.(5.9)

5.9

A questo punto ho calcolato i carichi sismici per ricavarmi la forza sismica agente sul centro di massa. Per fare ciò ho ricavato il carico totale permanente G= (q_s+q_p)A_tot ed il tutale dei carichi accidentali Q= q_a^.A_tot..

Seguendo le norme tecniche per le costruzioni (NTC2008) calcolo la combinazione sismica W= G+ψ₂^.Q : in cui ψ₂ è il coefficiente di contemporaneità e vale 0,3 per gli edifici adibiti ad ufficio.

La forza del sisma F=W^.c  quindi un peso per un’ accelerazione.  C è un coefficiente riduttivo che indica l’accelerazione che apporta il sisma che è generalmente inferiore a quella di gravità e dipende dalle zone in cui si costruisce.(5.10)

5.10

Con i dati ricavati fin’ora posso determinare la ripartizione della forza sismica sui controventi e le reazioni cinematiche che ne conseguono. Per fare ciò considero sia che la forza agisca in direzione orizzontale lungo x e sia in direzione verticale y generando in entrambi i casi oltre che una rotazione una traslazione.

Per ricavarmi la traslazione orizzontale e la rotazione ad essa correlata come prima cosa calcolo il momento torcente agente in questa direzione (M) facendo il prodotto tra la forza sismica e la sua distanza dal centro delle rigidezze. Dopo di che posso ricavarmi lo spostamento orizzontale (u) dato dal rapporto tra la forza del sisma e la rigidezza totale in questa direzione. Con il momento torcente posso ricavarmi la rotazione suscitata da tale forza (φ) facendo il rapporto tra il momento torcente e la rigidezza torsionale.

Con i dati ricavati possiamo calcolarci la reazione elastica dei controventi orizzontali ad una forza orizzontale (F_o-n)= k _o-n(u+ φ^.dd_o-n);mentre la reazione elastica dei controventi verticali a tale sforzo è

(F_v-n)= k_v-n^. φ^.dd_o-n. (5.11)(5.12)

5.11

5.12

Considerando una forza agente lungo l’asse verticale oltre a calcolare il momento torcente e la rotazione calcolo la traslazione verticale (v) data dal rapporto tra la forza sismica e la rigidezza totale dei controventi verticali. Invece la reazione elastica dei controventi orizzontali sottoposti a sforzo verticale è (F_o-n)= k_o-n^. φ^.dd_o-n. Mentre quella di quelli verticali è (F_v-n)= k _v-n(u+ φ^.dd_v-n). (5.13)(5.14)

5.13

5.14

Per questa nuova esercitazione, in cui si deve dimensionare un pilastro soggetto a sforzo normale realizzato in legno, cls e d acciaio, ho utilizzato la pianta delle carpenterie della prima esercitazione ripetendola per quattro piani, ottenendo quindi una struttura a più livelli. Per il dimensionamento dei pilastri si è scelto di prendere in esame quello su cui grava un sforzo normale maggiore ovvero quello centrale alla struttura su cui non solo grava il peso portato dalla sua area d’influenza ma anche quello dei 3 pian soprastanti.

PILASTRO IN LEGNO

4.1

4.2

4.3

Nella prima parte dell’esercitazione ho ricavato lo sforzo normale agente sul  pilastro centrale.( 4.4) Come prima cosa ho calcolato l’area d’influenza agente sul pilastro e subito dopo mi sono ricavato il peso strutturale delle travi primari e secondarie moltiplicando l’area della sezione per il suo peso specifico. In particolare la trave principale di sezione (30 x 50 cm) con un peso specifico di 5 kN/mc ha un peso unitario di 0,75 kN/m.  Con questi dati ho potuto ricavare il carico dovuto al peso proprio delle travi sul pilastro (qt)  sommando il prodotto tra il peso unitario e la lunghezza delle travi confluenti sul pilastro e moltiplicandolo per il coefficiente di sicurezza 1.3. Utilizzando il carico strutturale (qu) del solaio, che avevo precedentemente  calcolato nella prima esercitazione,  e moltiplicandolo per il numero di piani della struttura  ho ottenuto lo sforzo normale(N) agente sul pilastro in esame.

4.4

Nella seconda parte dell’esercitazione ho come prima cosa predimensionato il pilastro. (4.5)

Per fare ciò mi è servito conoscere la resistenza a compressione del legno lamellare (fck), il coefficiente di sicurezza (γm), il coefficiente  riduttivo (kmod), il modulo di resistenza elastica (E), (β) il coeficente che rispecchia i gradi di vincolo del pilastro e l’altezza del pilastro (l).

In questo modo ho potuto ricavare la  resistenza di progetto (fcd) facendo il rapporto tra la resistenza compressione e il coefficiente di sicurezza. Cosi ho calcolato la snellezza massima (λmax) data dal  prodotto tra π e la radice del rapporto tra il modulo elastico e la resistenza di progetto. Con la snellezza massima ho potuto ricavare il raggio d’inerzia minimo (ρmin) ottenuto dal rapporto tra la lunghezza del pilastro e la sua snellezza. Dopo essermi calcolato l’area minima che deve avere il pilastro per resistere a compressione (Amin), facendo il rapporto tra lo sforzo normale e la resistenza di progetto, ho potuto ricavarmi la base minima del pilastro (b min) facendo il prodotto 2 e la radice quadrata del prodotto tra tre e il raggio minimo d’inerzia, e poi l’altezza minima (h min) facendo il rapporto tra l’area minima e la base minima.

4.5

Nell’ultima parte dell’esercizio ho dimensionato la sezione in modo tale che rispondesse ai valori trovati ed in particolare la base e l’altezza della sezione scelta fossero maggiori di quelle minime e di conseguenza l’area di questa fosse maggiore di quella minima per resistere a compressione. In questo casa la sezione da me scelta 20x30 cm risulta essere verificata.(4.6)

4.6

PILASTRO IN CLS

4.7

4.8

4.9

Come nel caso del pilastro in legno come prima cosa partendo dalla geometria e dai pesi della struttura ho ricavato lo sforzo normale agente sul pilastro più sollecitato. (4.10)

4.10

Conoscendo il modulo di elasticità (E) del cemento, la sua resistenza a rottura (fck) e ), (β) coefficiente dato dai vincoli agenti sul pilastro ho potuto ricavare: la resistenza di progetto (fcd), l’area minima del pilastro (Amin), la snellezza del pilastro(λmax),il raggio d’inerzia minimo (ρmin), la base minima(b min) e l’altezza minima (h min).( 4.11)

4.11

Con i dati ricavati ho potuto dimensonare il mio pilastro in modo tale che le sue dimensioni fossero maggiori rispetto alle minime ricavate per stare in sicurezza ed in particolare che l’area di desing (A design) fosse maggiore dell’area minima affinche fosse verificata per lo sforzo normale.(4.12)

4.13

Tuttavia il pilastro di cemento necessita di un’ulteriore verifica essendo sottoposto a presso flessione in quanto il nodo con la trave è composto da un incastro e quindi trasmette anche il momento oltre che lo sforzo normale. Per verificarlo a pressoflessione impongo che la tensione massima

(σmax) sia minore della resistenza di progetto.(4.14) La tensione massima la ricavo in funzione dello sforzo normale e del momento, trasmessi dalla trave al pilastro, facendo la somma del rapporto tra lo sforzo normale e l’area del pilastro e il rapporto tra il momento(Mt) e il modulo di resistenza a flessione (W). Il modulo di resistenza a flessione lo calcolo dividendo per sei il prodotto tra la base e l’altezza al quadrato della sezione del pilastro.

Per calcolare il momento invece devo prima calcolarmi alo slu il carico distribuito sulla trava (qt), ovvero facendo la somma del prodotto di uno 1,3 per il carico strutturale con  il prodotto di 1,5 e il carico permanente e con il prodotto di 1,5 ed il carico accidentale.

A questo punto posso calcolarmi il momento agente sul pilastro dividendo per 12 il prodotto tra il carico distribuito sulla trave e l’interasse principale al quadrato.

Ricavati questi dati posso finalmente verificare che la tensione massima è inferiore alla forza di progetto e che quindi la sezione da me scelta di 35x40 cm risulta essere verificata!

4.14

PILATRO IN ACCIAIO

4.15

4.16

4.17

Per la realizzazione del solaio in acciaio, calcolato nella prima esercitazione, mi sono servito di IPE 330 dal peso di 0,49 kN/m, per le travi principali ed IPE 140, dal peso di 0,129 kN/m, per le travi secondarie.

Considerando i diversi pesi degli elementi strutturali, come per le altre esercitazioni mi sono ricavato lo sforzo normale portato dal pilastro maggiormente sollecitato della struttura.(4.18)

4.18

Conoscendo le caratteristiche dell’acciaio ed i tipi di vincolo del pilastro ho potuto calcolare, come nei casi precedenti: l’area minima della sezione(A min), la snellezza (λmax)e il raggio minimo d’inerzia(ρmin).

Ma al contrario dei casi precedenti per scegliere la sezione, non mi sono dovuto ricavare la base e l’altezza minima del pilasto ma mi sono dovuto servire di un ulteriore dato ovvero il momento d’inerzia minimo (I min) che ho ricavato moltiplicato l’area minima per il quadrato del raggio d’inerzia.(4.19)

4.19

A questo punto dal profilario di elementi HEA ho potuto scegliere quello che non solo ha un area superiore a quella minima ma anche un momento di inerzia maggiore a quello minimo in modo tale che garantisca la sua stabilita a sforzo normale. Nel caso da me calcolato ho soddisfato la verifica con un profilo HEA 180. (4.20)

4.20

In questa terza esercitazione ho provato a dimensionare la trave che sostiene uno sbalzo in tre differenti tecnologia costruttive (legno, cls, acciaio). Per fare ciò, seguendo il metodo delle tensioni in cui al  σ max eguaglio l’ Fyd , come per la prima esercitazione, ho dimensionato la trave allo slu per verificarla in campo strutturale, ovvero se le sue dimensioni fossero adeguate a sorreggere i carichi da essa portati. L’unica cosa in cui differisce questa parte del dimensionamento è nel calco del momento max a cui è soggetta la trave che sorregge lo sbalzo in quanto essa non è, come nella prima esercitazione, una trave doppiamente appoggiata, ma una mensola e quindi il suo momento max equivale a ql²/2.

Dopo avere dimensionato la trave, per uno sbalzo, è importantissimo verificarne la deformabilità in rapporto alla sua luce poiché è inammissibile che questa accusi degli spostamenti o abbassamenti che ne impediscano il corretto uso ed un adeguato comfort. Per fare questa verifica si entra nel campo dello stato limite di esercizio (sle) che per tutte e tre le tecnologie si verifica nello stesso modo ovvero:

qe=(G1+G2+ψ11xQ1)x i.                                                

In oltre per calcolare l’abbassamento della trave è importante conoscere il modulo di elasticità del materiale (E) e il suo momento di inerzia (Ix) in quanto lo spostamento max si ricava:

ν max=qel^4/8E

Trovato lo spostamento massimo , secondo normativa, si calcola che il suo rapporto con la luce che deve coprire sia maggiore o uguale a 250. (3.1)

3.1

SBALZO IN LEGNO

3.2

Per prima cosa ho ipotizzato una pianta delle carpenterie della struttura (3.3) e la composizione del solaio della stessa (3.4)

3.3

3.4

A questo punto ho potuto dimensionare la trave per poi andare a verificare allo sle lo sbalzo e capire se la trave da me dimensionata garantisse un abbassamento della stessa entro i limiti di norma. Per fare ciò ho calcolato i carichi allo stato limite di esercizio (qe) e , ricavata la sezione della trave (30X65 cm), ho potuto calcolare il suo momento di inerzia rispetto l’asse sfavorevole ovvero x: Ix=1/12 bh ³; nel  mio caso pari a 686563 cm^4.

Conoscendo il modulo elastico del legno (E),8000 N/mm ², ho ricavato il suo abbassamento max (ν max) pari a 0,52 cm. In questo modo ho verificato il rapporto luce abbassamento e ho osservato che era pari a 416,65 ben superiore a 250.

In questa verifica ho trascurato il peso proprio della trave in quanto il legno è  un materiale relativamente leggero e quindi avrebbe poco influito nel computo totale (3.5).

3.5

Quindi la sezione (30x65 cm) è risultata verificata.

SBALZO IN LEGNO

3.6

3.7

3.8

Al contrario del legno, nel cemento, è molto importante verificare che se aggiungo il peso proprio della trave dimensionata al carico limite ultimo (qu) questa rimanga verificata dato il suo notevole peso strutturale.  Per questo anche quando calcolo il carico allo stato limite d’esercizio (qe) ne devo tenere conto. Come per il legno ho trovato il modulo elastico del cemento (E),21000 N/mm², il suo momeno di inerzia (Ix), 346615 cm^ e quindi ho potuto ricavare il suo ν max= 0,27 cm.

Facendo il rapporto luce abbassamento ho trovato che valeve 798,94>250 (3.9).

3.9

Quindi la sezione (25X55 cm) è risultata verificata.

SBALZO IN ACCIAIO

3.10

3.11

3.12

Ho dimensionato la trave  allo stato limite ultimo ricavandomi il suo (Wx),735,10 cm ³,e quindi scegliendo un profilo che ne soddisfacesse tale valore ovvero una IPE 360 (3.13).

3.13

Come nel cemento anche nell’acciaio il peso della trave è molto influente nel calcolo strutturale e nel caso dell’acciaio è facilmente ricavabile in quanto nei profilari è dichiarato dal costruttore; Quindi sia nel carico allo stato limite ultimo (qu) che in quello allo stato limite d’esercizio(qe) dovrò considerarlo.

Nell’acciaio anche il momento d’inerzia(Ix) è facilmente ricavabile in quanto dichiarato dal costruttore.

Conoscendo questi dati ed il modulo elastico dell’acciaio (E),21o000 N/mm², ho ricavato l’abbassamento  della trave (ν max), 0,373 cm, e quindi ho calcolao il rapporto luce abbassamento uguale a 575,728>250 (3.14).

3.14

Quindi l’IPE 360 è risultata verificata.

Per questa consegna ho deciso di studiare una struttura reticolare che prendesse spunto da quelle usate per fare coperture di grandi luce, come ad esempio quella della stazione Tiburtina(2.1)

2.1

Per prima cosa ho cercato di capire come fossero realizzate queste strutture, ed ho visto che il più delle volte sono realizzate con moduli reticolari tridimensionali piramidali uniti in testa da aste, per costituire una struttura solidale(2.2).

(2.2)

Quindi ho realizzato in SAP 2000 il modello di questa struttura realizzata con moduli piramidali, composti da aste di 2m, ed ho disposto due moduli di questi in larghezza e 5 in lunghezza. Dopo avere vincolato esternamente la struttura con delle cerniere agli spigoli estremi, ho assegnato i vincoli interni alle aste. In fine, dopo aver deciso di realizzare la struttura con dei tubolari in acciaio, ho caricato la struttura nei vertici superiori delle piramidi con un carico di 200 kN (2.3).

2.3

A questo punto con l’ausilio del software ho potuto vedere come la struttura si deformerebbe sotto lo sforzo del carico da me ipotizzato, trascurando il peso proprio della stessa (2.4).

2.4

Con il programma ho anche potuto ricavare il grafico degli sforzi normale a cui è sottoposta la struttura (2.5).

2.5

In questo modo ho potuto osservare quante delle 90 aste componenti la struttura sono soggette a compressione e quante a trazione ovvero 53 a compressione e 37 a trazione.

A  questo potuto ho potuto estrarre il valore esatto dello sforzo a cui è sottoposta ogni singola asta e quindi le ho potute dimensionare tutte con l’ausilio di un foglio di calcolo excel.

ASTE TESE

Come prima cosa scelgo il tipo di acciaio da utilizzare per i profili che comporranno il modulo, nel mio caso un acciaio con una resistenza pari a 235 Mpa. Dopo di che ricavo la resistenza di progetto, fyd, facendo il rapporto tra la resistenza del materiale ed il coefficiente di sicurezza, γ m0 (1,05). A questo punto conoscendo impongo che fyd sia la tensione che deve sopportare la mia asta e quindi facendo il rapporto tra lo sforzo normale a cui è sottoposta l’asta e la resistenza di progetto trovo l’area minima che deve avere l’elemento per resistere a tale sforzo. Amin= N/fyd. In questo modo ho potuto dimensionare tutte le aste.

Ad esempio per la coppia di aste “12-65” sottoposte allo stesso sforzo di  11,592 kN, ho potuto ricavare l’area minima della sezione seguendo i procedimenti sopra elencati (2.6).

2.6

Dopo di che, ho cercato sul profilario un’asta a sezione cilindrica con l’area della sezione uguale o subito superiore  all’area necessaria per sopportare tale sforzo  (2.7).

2.7

2.8

In questo modo ho dimensionato tutte le altre aste sottoposte a tensione (2.9).

2.9

ASTE COMPRESSE

Per dimensionare le aste soggette a compressione ho dovuto considerare più parametri, in quanto, la compressione oltre alla rottura dell’asta porta anche allo sbandamento della stessa, quando va in carico di punta, e ciò è da tenere in considerazione in sede di progetto per cercare di evitarlo. Per questo ai parametri citati prima ho dovuto aggiungere: il modulo di elasticità del materiale (E) pari a 210000 Mpa per l’acciaio; la lunghezza dell’asta considerata (L) , nel mio caso 2 metri; le condizioni di vincolo a bordo dell’asta e quindi il modo in cui essa può sbandare in tale configurazione con in coefficiente (β), nel mio caso pari a 1;la snellezza dell’asta (λ) uguale a π √E/√fyd; il raggio d’inerzia dell’elemento (ρ) , ricavato dal rapporto tra la lunghezza dell’asta e la sua snellezza(λ); il momento d’inerzia(I) pari all’area della sezione per il quadrato del raggio d’inerzia.

Questa volta per la scelta del profilo non pasta vedere l’area della sezione ma bisogna verificare anche se il raggio d’inerzia sia verificato nella sezione scelta. Un  caso esemplare, a tal proposito, mi è venuto nel dimensionamento della coppia di aste “26-60” sottoposte ad uno sforzo di -132 kN. Seguendo i procedimenti sopra elencati, infatti, avevo ricavato che tali aste, per contrastare lo sforzo a cui sono sottoposto, avrebbero dovuto avere un area minima di 6,04 cmq. Quindi ho scelto un profilo rispondente a quell’area. Tuttavia tale profilo non aveva un raggio d’inerzia che eguagliasse quello minimo richiesto per resistere alla compressione a cui era sottoposto e  per questo il profilo non risultava adeguato e quindi troppo snello (2.10),(2.11)

2.10

2.11

Per questo sono stato costretto a prendere la sezione con area immediatamente superiore e con un raggio di ineriza che soddisfacesse quello richiesto dal predimensionamento .(2.12),(2.13)

2.12

2.13

In questo modo ho dimensionato tutte le altre aste compresse (2.14).

2.14

DIMENSIONAMENTO TRAVE IN LEGNO

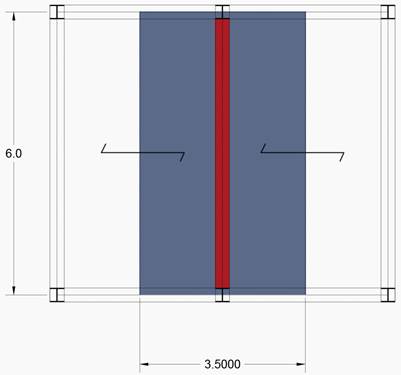
Per dimensionare la trave di un solaio in legno, ho per prima cosa progettato una semplice struttura, di due campate da 3,5 x 6 m, ed ho individuato la trave soggetta a maggiori sollecitazioni.  In questo caso quella centrale su cui grava il peso di un area di influenza di 21 mq dati da una luce di 6 m ed un interasse di 3,4 m.

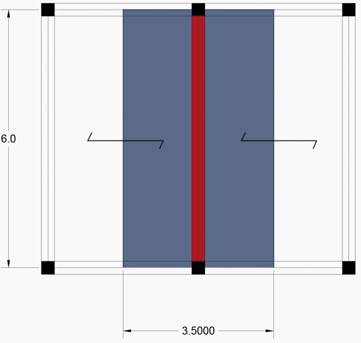
In seguito ho ipotizzato una sezione tipo di un solaio in legno ad orditura  per poter poi calcolare il suo carico complessivo.

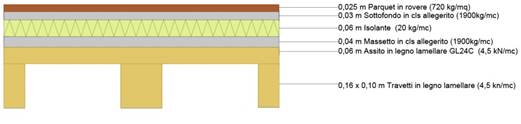
Per calcolare i vari carichi dati dai materiali che compongo la sezione di un metro quadrato di solaio ho moltiplicato il loro volume per il loro peso specifico in kN/mc per ottenere il peso in kN/mq. Qualora i prontuari mi davano il peso specifico di un materiale in kg ho eseguito un’equivalenza per ottenere il valore in kN dividendo il peso in kg per 100.

CARICO STUTTURALE (qs)

Travetti(x2): 0,14 kN/mq

Assito: 0,27 kN/mq

qs= 0,27+0,14= 0,41 kN/mq

CARICO PERMANENTE (qp)

Massetto: 0,76 kN/mq

Isolante: 0,012 kN/mq

Sottofondo: 0,38 kN/mq

Parquet: 0,72 kN/mq

qp= 0,76+0,012+0,38+0,72= 1,88 kN/mq a cui aggiungo un valore forfettario di 1,5 kN/mq per impianti e tramezzi ed ottengo qp= 3,38 kN/mq

CARICO ACCIDENTALE (qa)

SI CONSIDERA QUELLO PER EDIFICI AD USO RESIDENZIALE QUINDI qa= 2 kN/mq

CARICO UNITARIO (qu)

Lo ottengo facendo la somma tra il carico strutturale moltiplicato per il fattore di sicurezza 1,3, il carico permanente moltiplicato per il fattore 1,5 e quello accidentale moltiplicato per il fattore 1,5; la somma la moltiplico poi per l’aria d’influenza del carico ovvero 3,5 metri ed ottenendo qu= 30,29 kN/m.

DIMENSIONAMENTO SEZIONE

Per il dimensionamento della sezione è importante conoscere il momento agente sulla trave che è facilmente ricavabile essendo una trave appoggiata il cui valore sarà dato da rapporto M=ql²/8.

Saputo il momento scelgo il materiale con cui realizzare la trave, nel mio caso legno lamellare Gl24C, il cui fm,k è pari a 24 N/mmq. Con questo trovando dalle tabelle il coefficiente di durata del carico Kmod e il coefficiente di sicurezza  γ m mi ricavo la tensione di progetto fd. In fine con questi dati ed ipotizzando una base della trave mi ricavo l’altezza.

Dalla tabella di calcolo excel ottengo una trave di dimensione 30,00 x 35,38 cm che sovradimensiono a 30x50 cm non avendo ancora considerato il peso della trave nel computo dei carichi. Quindi per verificare se il profilo da me scelto è giusto calcolo il peso specifico della trave e lo aggiungo al carico unitario moltiplicandolo per il coefficiente 1,3.

Trave: 1,35 kN/mq

La sezione ,quindi, risulta essere verificiata!

DIMENSIONAMENTO TRAVE IN CLS

                                          .

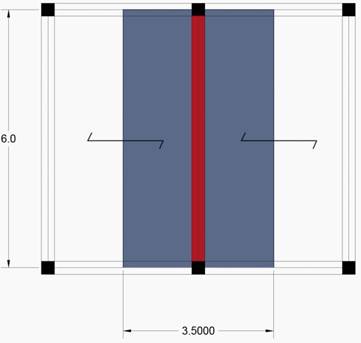
Ho ipotizzato una sezione tipo di un solaio in cemento  per poter poi calcolare il suo carico complessivo. Mediante le tabelle fornite dal produttore delle pignatte ho potuto dimensionare le pignatte stesse e lo spessore della parte strutturale del solaio in base alla sua luce.

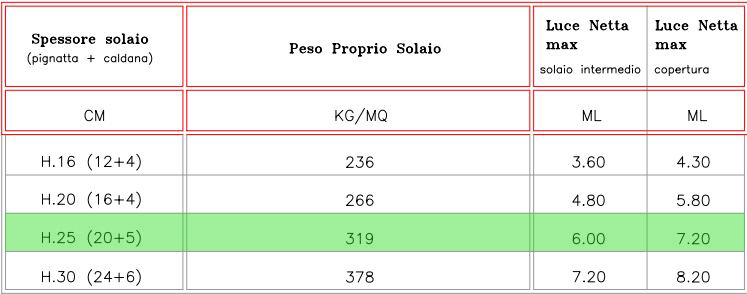
CARICO STRUTTURALE (qs)

Soletta: 1,44 kN/mq

Travetti(x2): 0,96 kN/mq

Pignatte: 0,77 kn/mq

qs= 1,44+0,96+0,77= 3,17 kN/mq

CARICO PERMANENTE (qp)

Intonaco: 0,18 kN/mq

Isolante: 0,012 kN/mq

Massetto: 0,76 kN/mq

Pavimento: 0,40 kN/mq

Tramezzi+impianti: 1,50 kN/mq

qp= 0,18+0,012+0,76+0,40+1,50=  2,85 kN/mq

CARICO ACCIDENTALE (qa)

SI CONSIDERA QUELLO PER EDIFICI AD USO RESIDENZIALE QUINDI qa= 2 kN/mq

CARICO UNITARIO (qu)

Lo ottengo facendo la somma tra il carico strutturale moltiplicato per il fattore di sicurezza 1,3, il carico permanente moltiplicato per il fattore 1,5 e quello accidentale moltiplicato per il fattore 1,5; la somma la moltiplico poi per l’aria d’influenza del carico ovvero 3,5 metri ed ottenendo qu= 39,98 kN/m

DIMENSIONAMENTO SEZIONE

Per il dimensionamento della sezione è importante conoscere il momento agente sulla trave facilmente ricavabile in quanto si tratta di una trave appoggiata. La trave in cemento non è composta di un materiale omogeneo ma è composta da due materiali: cls (reagente a compressione) e l’acciaio (reagente a trazione). Per questo nel progetto devo considerare la resistenza a compressione del cemento(fck) e quella a trazione dell’acciaio(fyk) e poi facendo il rapporto tra le resistenze dei materiali e i loro coefficienti di sicurezza ottengo le rispettive tensioni di progetto fcd per il cemento e fyd per l’acciaio. Nel mio caso ho scelto un cemento con un fck pari a 60N/mmq e un fcd pari a 34,00 N/mmq ed un acciaio con un fyk pari a 450 N/mmq e un fyd  391,30 N/mmq. Con questi dati posso ricavarmi i coefficienti r e β e quindi una volta scelta anche una base ed un coprifero posso ricavarmi l’altezza della sezione.

Dal foglio di calcolo excel ottengo una trave 25 x 40 cm. Come per la trave in legno verifico se la trave ipotizzata è adeguata a sostenere i carichi a cui è sottoposta. Procedo con la verifica aggiungento al carico unitario trovato il carico strutturale della trave moltiplicato per il coefficiente 1.3.

Trave: 2,4 kN/mq

La sezione ,quindi, risulta essere verificiata!

DIMENSIONAMENTO SEZIONE IN ACCIAIO

Ho ipotizzato una sezione tipo di un solaio in cemento  per poter poi calcolare il suo carico complessivo.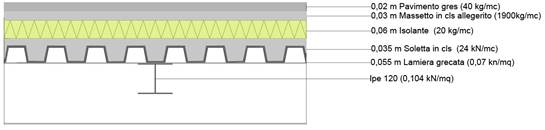

CARICO STRUTTURALE (qs)

Ipe 140: 0,104 kN/mq

Lamiera grecata: 0,07 kN/mq

Soletta: 1,08 Kn/mq

qs= 0,104+0,07+1,08= 1,88 kN/mq

CARICO PERMANENTE (qp)

Isolante: 0,012 kN/mq

Massetto: 0,57 kN/mq

Pavimento: 0,40 kN/mq

Tramezzi+impianti: 1,50 kN/mq

qp= 0,012+0,57+0,40+1,50= 2,47 kN/mq

CARICO ACCIDENTALE (qa)

SI CONSIDERA QUELLO PER EDIFICI AD USO RESIDENZIALE QUINDI qa= 2 kN/mq

CARICO UNITARIO (qu)

Lo ottengo facendo la somma tra il carico strutturale moltiplicato per il fattore di sicurezza 1,3, il carico permanente moltiplicato per il fattore 1,5 e quello accidentale moltiplicato per il fattore 1,5; la somma la moltiplico poi per l’aria d’influenza del carico ovvero 3,5 metri ed ottenendo qu= 32,02 kN/m

DIMENSIONAMENTO SEZIONE

Per il dimensionamento della sezione è importante conoscere il momento agente sulla trave facilmente ricavabile in quanto si tratta di una trave appoggiata. Una volta scelto l’acciaio con il quale realizzare la struttura si ha il suo fyk, nel mio caso pari a 275 N/mmq essendo un acciaio S275. Dal rapporto tra fyk e il coefficiente di sicurezza γ  ottengo fyd ovvero la tensione di progetto. Con questi dati posso ricavarmi il modulo di resistenza Wx con il quale posso scegliere la sezione da utilizzare.

Con il Wx trovato dal profilario degli ipe scelgo quello con il valore più simile a quello trovato e si arrotonda sempre per eccesso.

Come ho fatto per la trave in legno e per quella in cls, verifico se l’ipe trovata è idonea al carico che deve sostenere. Per fare ciò aggiungo al carico unitario il peso della trave moltiplicato per il coefficiente 1.3

Ipe 300: 0,422 kN/mq

La trave non risulta essere verificata perché aggiungendo il peso della trave al carico unitario il Wx che trovo è superiore a quello della ipe 300.

Quindi scelgo l’ipe 330 che è quella successiva alla 330. Calcolo il peso della trave e verifico se questa volta è verificata.

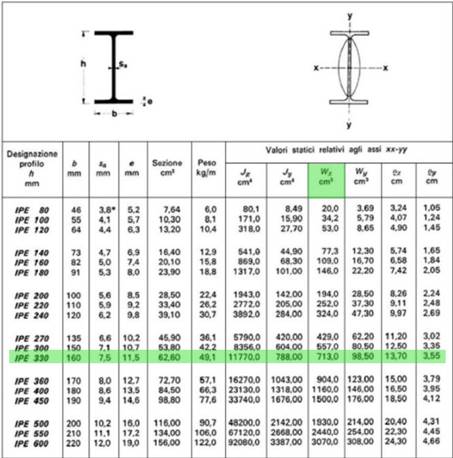
Calcolo il peso dell’ipe 330 e lo aggiungo al carico unitario moltiplicandolo per il coefficiente 1,3

Ipe 330: 0,49 kN/mq

La sezione ,quindi, risulta essere verificiata!