RIPARTIZIONE FORZE SISMICHE

In questa esercitazione, con l’ausilio del “metodo delle rigidezze”, ho studiato come si ripartisce una forza orizzontale , come quella che genera un sisma od il carico del vento, sui diversi telai che compongono una struttura. Nel caso preso in esame la struttura è interamente realizzata in cemento armato e composta da telai piani. Tali elementi oltre a trasmettere i carichi verticali alle fondazioni, funzionano da controventi perché sono in grado di sopportare i carichi orizzontali.

Come prima cosa ho individuato i telai che costituiscono la struttura da me progettata (5.1); ovvero 16 telai di cui 8 verticali ed 8 orizzontali,

5.1

In particolare:

-Telaio 1 v  composto da pilastri: 1-4-7-10-13-16-24-32;

- Telaio 2v  composto da pilastri: 2-5-8-11-14-17-25-33;

- Telaio 3v  composto da pilastri: 3-6-9-12-15-18-26-34;

- Telaio 4v  composto da pilastri: 19-27-35;

- Telaio 5v  composto da pilastri: 20-28-36;

- Telaio 6v  composto da pilastri: 21-29-37;

- Telaio 7v  composto da pilastri: 22-30-38;

- Telaio 8v  composto da pilastri: 23-31-39;

- Telaio 1o  composto da pilastri: 1-2-3;

- Telaio 2o  composto da pilastri: 4-5-6;

- Telaio 3o  composto da pilastri: 7-8-9;

- Telaio 4o  composto da pilastri: 10-11-12;

- Telaio 5o  composto da pilastri: 13-14-15;

- Telaio 6o  composto da pilastri: 16-17-18-19-20-21-22-23;

- Telaio 7o  composto da pilastri: 24-25-26-27-28-29-30-31;

- Telaio 8o  composto da pilastri: 32-33-34-35-36-37-38-39.

A questo punto  ho potuto schematizzare i telai con delle molle nel piano, in quanto rappresentano dei vincoli cedevoli elasticamente.(5.2)

5.2

Per calcolare la rigidezza traslante di tutti i controventi, ho dovuto ricavare per  prima cosa il momento d’inerzia di ogni pilastro, stando attento al loro orientamento. Nel ,io caso essendo tutti quadrati hanno tutti uno stesso momento di inerzia  (I=bh^3/12) pari a 213333 cm⁴. Ipotizzando che i talai fossero tutti di tipo shear type ho potuto facilmente ricavare la loro rigidezza. Nel caso fossero telai composti da solo due pilastri la forza aggente su di essi sarebe stata F= (12 EI₁/h³+12 EI₂/h³) δ  la rigidezza sarà pari a

 k=12 EI₁/h³+12 EI₂/h³.

Nel caso esaminato i telai sono composti da più pilastri la rigidezza sarà pari a k=12E/h³(I₁+I₂+…+I_n).

con l’aiuto di un foglio di calcolo excel ho potuto ricavare tutte le rigidezze traslanti.(5.3)

5.3

In una seconda tabella ho potuto riassumere le rigidezze dei singoli telai ed la loro distanza dall’origine degli assi di riferimento. (5.4)

5.4

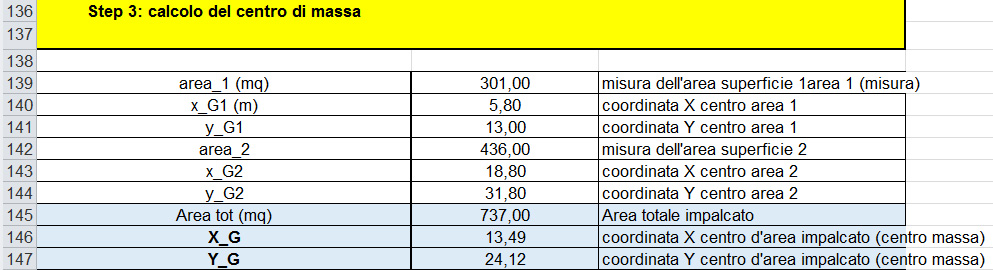
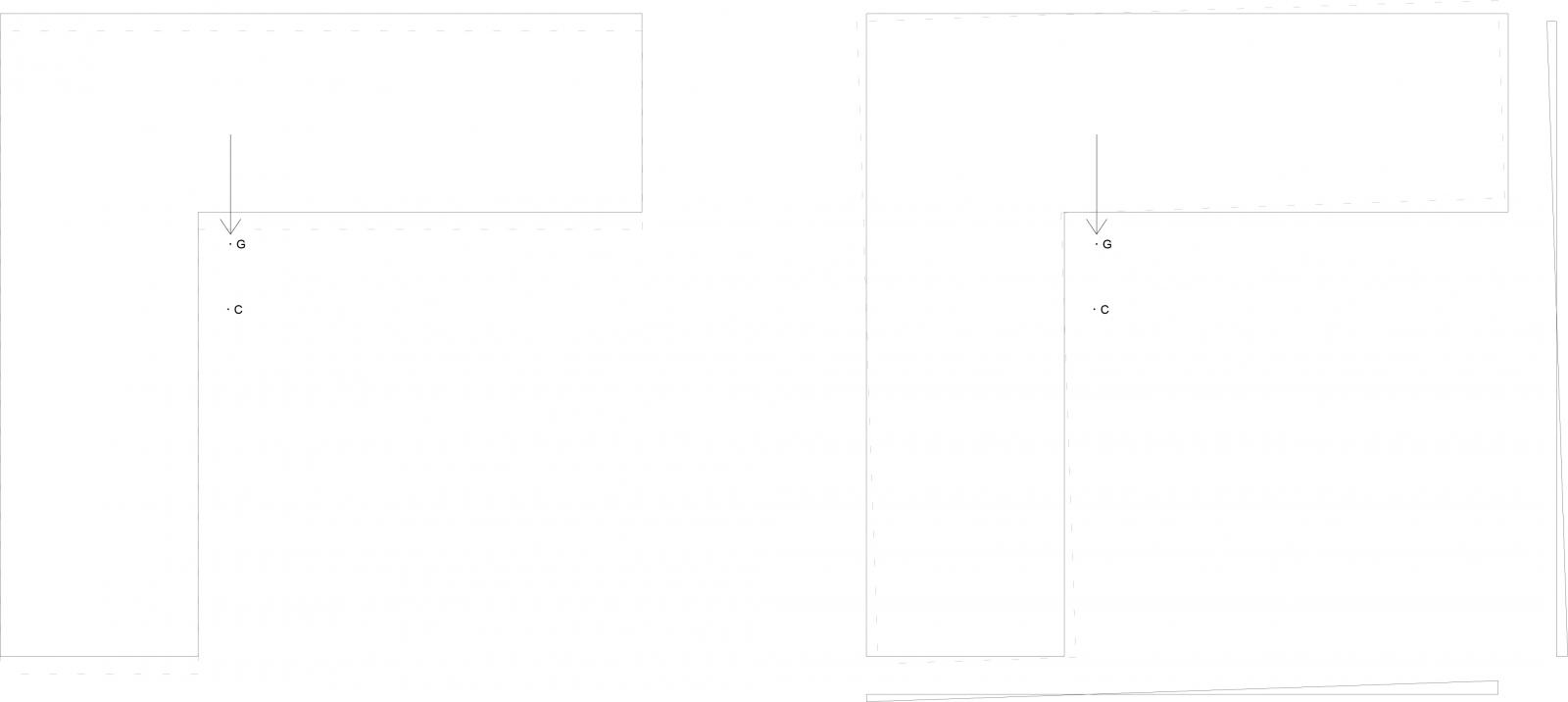
A questo punto ho ricavato il centro della massa dell’impalcato (G) e poiché è costituito da una forma complessa l’ho sudiviso in modo tale da ottenere forme elementari.(5.5)

5.5

In questo modo ho ottenuto un impalcato composto da due rettangoli di cui ho facilmento individuato il centro di massa G₁ e G₂ e quindi ho ricavato le coordinate del centro di massa dell’intero impalcato:

Gx=A₁^.Gx₁+ A₂^.Gx₂/ A_tot ;      Gy=A₁^.Gy₁+ A₂^.Gy₂/ A_tot .    

In tal modo ho trovato il centro  dell’area dell’impalcato, ma essendo questo di eguale densità in tutti i punti corrisponde al centro di massa dell’impalcato.(5.6)

5.6

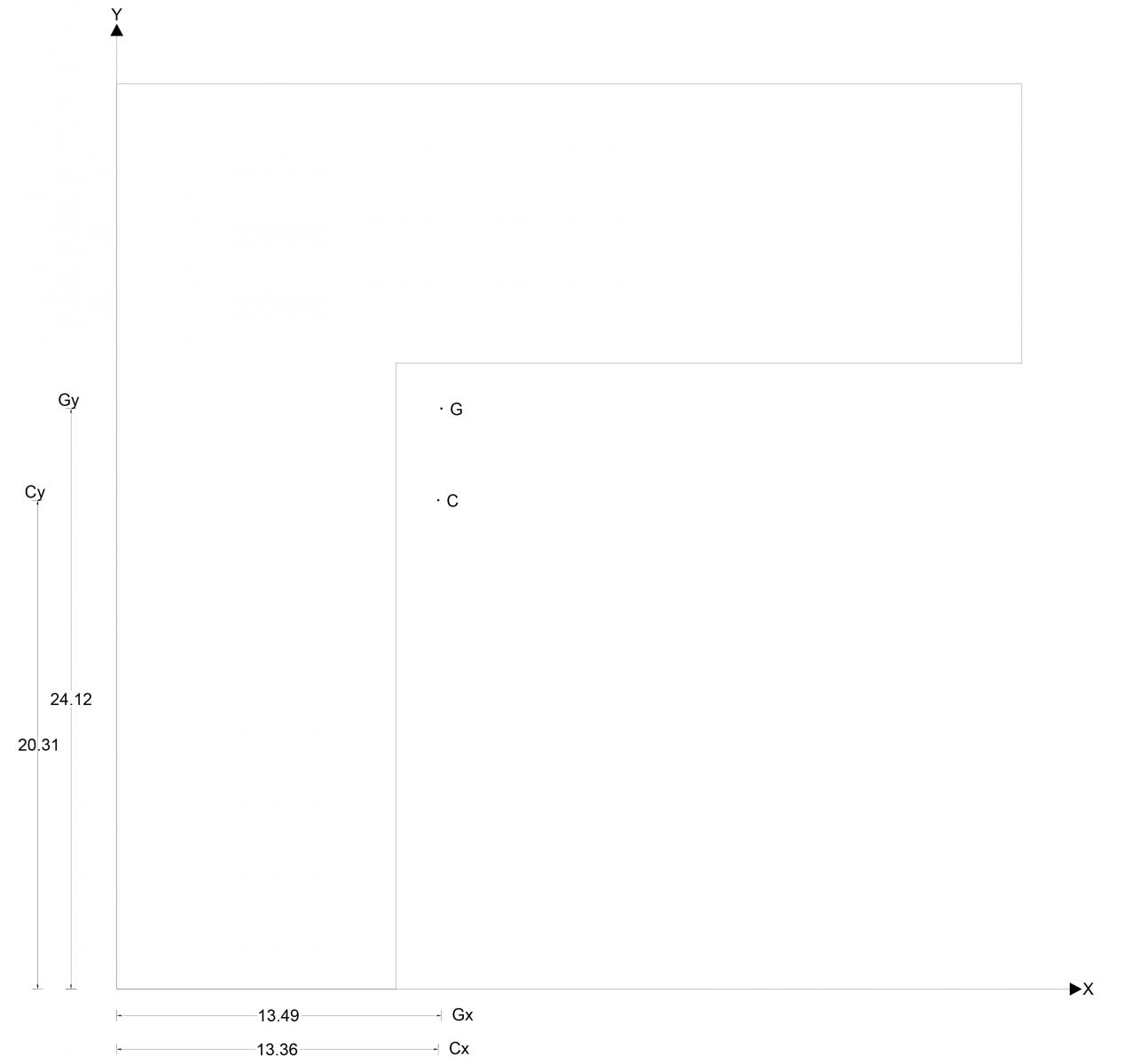
Sommando i prodotti delle rigidezze dei telai per le loro distanze dall’origine degli assi di riferimento e dividendo il tutto per la rigidezza totale ho potuto trovare le coordinate del centro di rigidezza (C).(5.7)(5.8)

5.7

5.8

Con questi dati posso sapere se l’impalcato in caso di una forza che agisce sul centro di massa subisce o meno una rotazione. Non si ha rotazione soltanto quando il centro di massa corrisponde con il centro delle rigidezze.

Calcolato il centro di rigidezza ho potuto ricavare la distanza di ogni telaio da questo per potermi ricavare la rigidezza torsionale dell’impalcato(K_φ) sommando i prodotti delle rigidezze dei controventi per il quadrato della lor distanza dal punto di riferimento.(5.9)

5.9

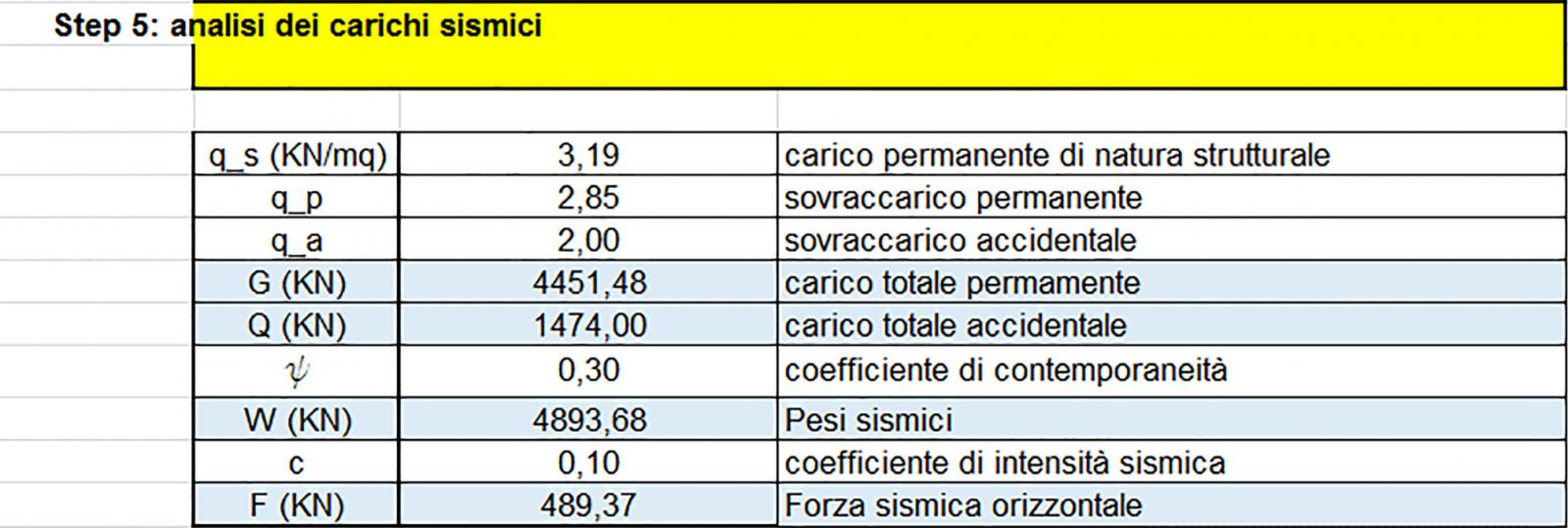
A questo punto ho calcolato i carichi sismici per ricavarmi la forza sismica agente sul centro di massa. Per fare ciò ho ricavato il carico totale permanente G= (q_s+q_p)A_tot ed il tutale dei carichi accidentali Q= q_a^.A_tot..

Seguendo le norme tecniche per le costruzioni (NTC2008) calcolo la combinazione sismica W= G+ψ₂^.Q : in cui ψ₂ è il coefficiente di contemporaneità e vale 0,3 per gli edifici adibiti ad ufficio.

La forza del sisma F=W^.c  quindi un peso per un’ accelerazione.  C è un coefficiente riduttivo che indica l’accelerazione che apporta il sisma che è generalmente inferiore a quella di gravità e dipende dalle zone in cui si costruisce.(5.10)

5.10

Con i dati ricavati fin’ora posso determinare la ripartizione della forza sismica sui controventi e le reazioni cinematiche che ne conseguono. Per fare ciò considero sia che la forza agisca in direzione orizzontale lungo x e sia in direzione verticale y generando in entrambi i casi oltre che una rotazione una traslazione.

Per ricavarmi la traslazione orizzontale e la rotazione ad essa correlata come prima cosa calcolo il momento torcente agente in questa direzione (M) facendo il prodotto tra la forza sismica e la sua distanza dal centro delle rigidezze. Dopo di che posso ricavarmi lo spostamento orizzontale (u) dato dal rapporto tra la forza del sisma e la rigidezza totale in questa direzione. Con il momento torcente posso ricavarmi la rotazione suscitata da tale forza (φ) facendo il rapporto tra il momento torcente e la rigidezza torsionale.

Con i dati ricavati possiamo calcolarci la reazione elastica dei controventi orizzontali ad una forza orizzontale (F_o-n)= k _o-n(u+ φ^.dd_o-n);mentre la reazione elastica dei controventi verticali a tale sforzo è

(F_v-n)= k_v-n^. φ^.dd_o-n. (5.11)(5.12)

5.11

5.12

Considerando una forza agente lungo l’asse verticale oltre a calcolare il momento torcente e la rotazione calcolo la traslazione verticale (v) data dal rapporto tra la forza sismica e la rigidezza totale dei controventi verticali. Invece la reazione elastica dei controventi orizzontali sottoposti a sforzo verticale è (F_o-n)= k_o-n^. φ^.dd_o-n. Mentre quella di quelli verticali è (F_v-n)= k _v-n(u+ φ^.dd_v-n). (5.13)(5.14)

5.13

5.14