ESERCITAZIONE IV DIMENSIONAMENTO DI UN PILASTR

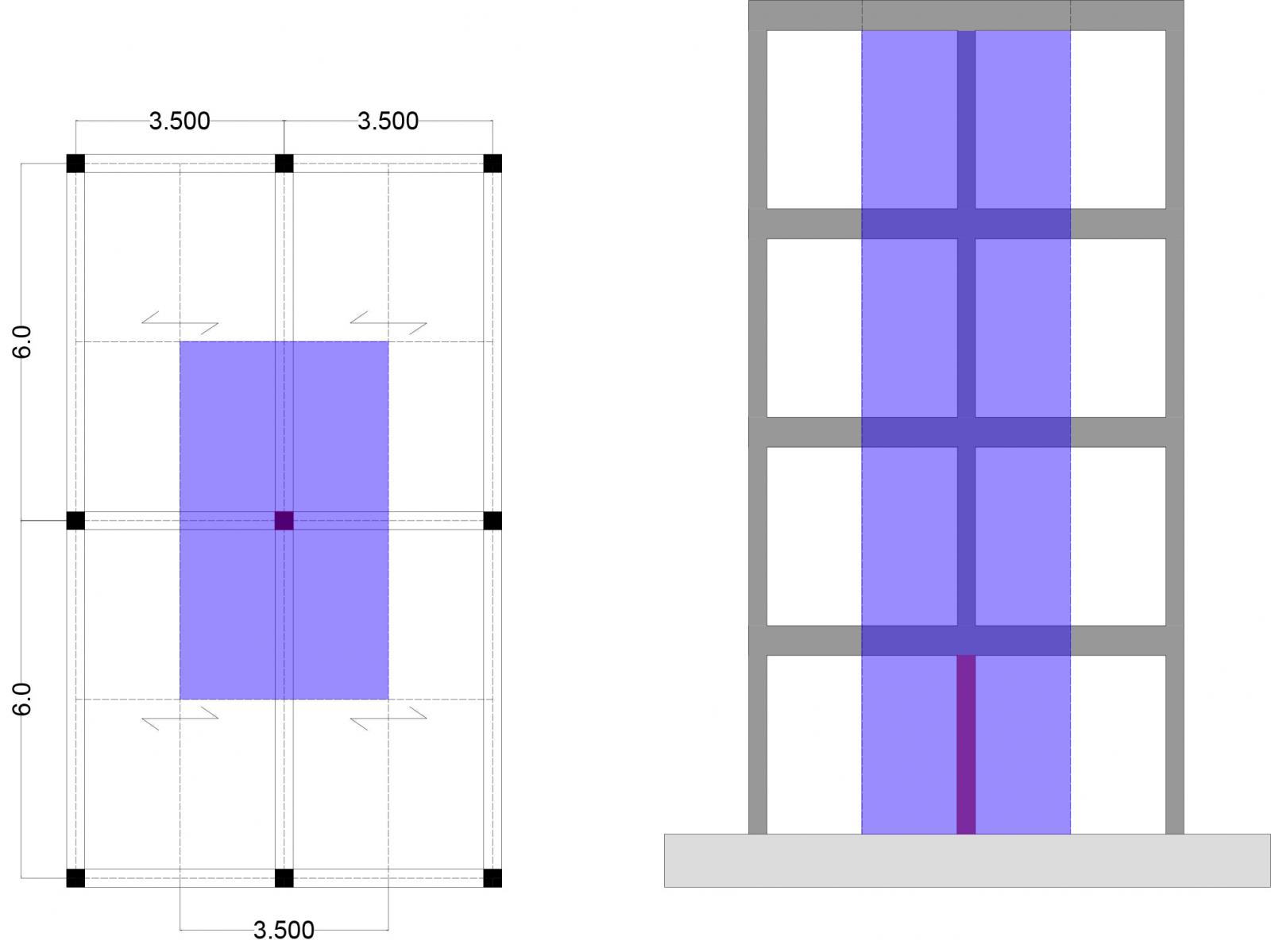
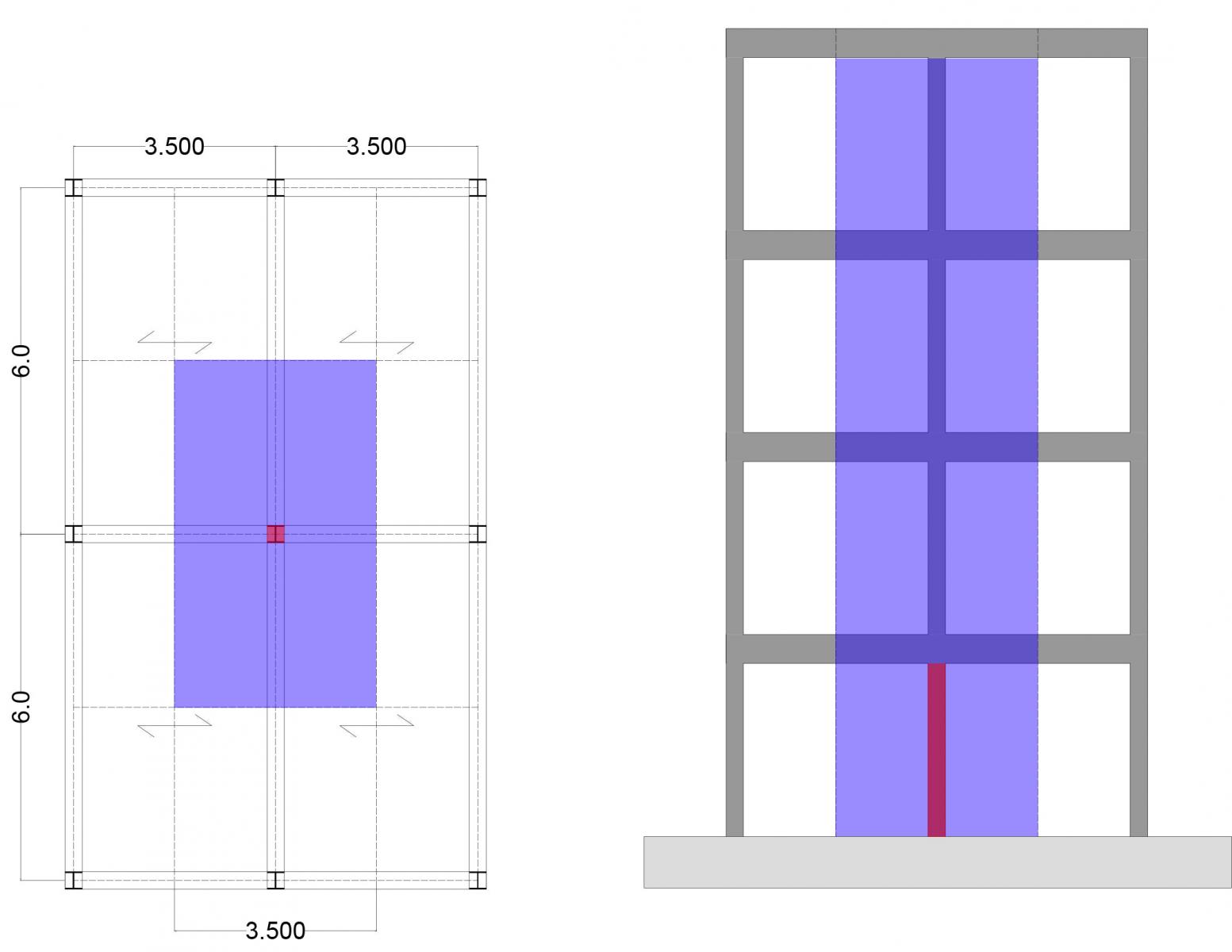
Per questa nuova esercitazione, in cui si deve dimensionare un pilastro soggetto a sforzo normale realizzato in legno, cls e d acciaio, ho utilizzato la pianta delle carpenterie della prima esercitazione ripetendola per quattro piani, ottenendo quindi una struttura a più livelli. Per il dimensionamento dei pilastri si è scelto di prendere in esame quello su cui grava un sforzo normale maggiore ovvero quello centrale alla struttura su cui non solo grava il peso portato dalla sua area d’influenza ma anche quello dei 3 pian soprastanti.

PILASTRO IN LEGNO

4.1

4.2

4.3

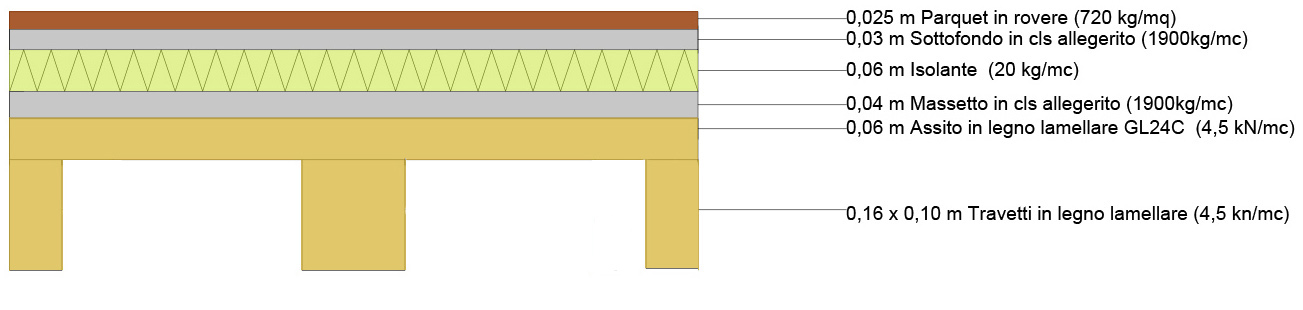
Nella prima parte dell’esercitazione ho ricavato lo sforzo normale agente sul  pilastro centrale.( 4.4) Come prima cosa ho calcolato l’area d’influenza agente sul pilastro e subito dopo mi sono ricavato il peso strutturale delle travi primari e secondarie moltiplicando l’area della sezione per il suo peso specifico. In particolare la trave principale di sezione (30 x 50 cm) con un peso specifico di 5 kN/mc ha un peso unitario di 0,75 kN/m.  Con questi dati ho potuto ricavare il carico dovuto al peso proprio delle travi sul pilastro (qt)  sommando il prodotto tra il peso unitario e la lunghezza delle travi confluenti sul pilastro e moltiplicandolo per il coefficiente di sicurezza 1.3. Utilizzando il carico strutturale (qu) del solaio, che avevo precedentemente  calcolato nella prima esercitazione,  e moltiplicandolo per il numero di piani della struttura  ho ottenuto lo sforzo normale(N) agente sul pilastro in esame.

4.4

Nella seconda parte dell’esercitazione ho come prima cosa predimensionato il pilastro. (4.5)

Per fare ciò mi è servito conoscere la resistenza a compressione del legno lamellare (fck), il coefficiente di sicurezza (γm), il coefficiente  riduttivo (kmod), il modulo di resistenza elastica (E), (β) il coeficente che rispecchia i gradi di vincolo del pilastro e l’altezza del pilastro (l).

In questo modo ho potuto ricavare la  resistenza di progetto (fcd) facendo il rapporto tra la resistenza compressione e il coefficiente di sicurezza. Cosi ho calcolato la snellezza massima (λmax) data dal  prodotto tra π e la radice del rapporto tra il modulo elastico e la resistenza di progetto. Con la snellezza massima ho potuto ricavare il raggio d’inerzia minimo (ρmin) ottenuto dal rapporto tra la lunghezza del pilastro e la sua snellezza. Dopo essermi calcolato l’area minima che deve avere il pilastro per resistere a compressione (Amin), facendo il rapporto tra lo sforzo normale e la resistenza di progetto, ho potuto ricavarmi la base minima del pilastro (b min) facendo il prodotto 2 e la radice quadrata del prodotto tra tre e il raggio minimo d’inerzia, e poi l’altezza minima (h min) facendo il rapporto tra l’area minima e la base minima.

4.5

Nell’ultima parte dell’esercizio ho dimensionato la sezione in modo tale che rispondesse ai valori trovati ed in particolare la base e l’altezza della sezione scelta fossero maggiori di quelle minime e di conseguenza l’area di questa fosse maggiore di quella minima per resistere a compressione. In questo casa la sezione da me scelta 20x30 cm risulta essere verificata.(4.6)

4.6

PILASTRO IN CLS

4.7

4.8

4.9

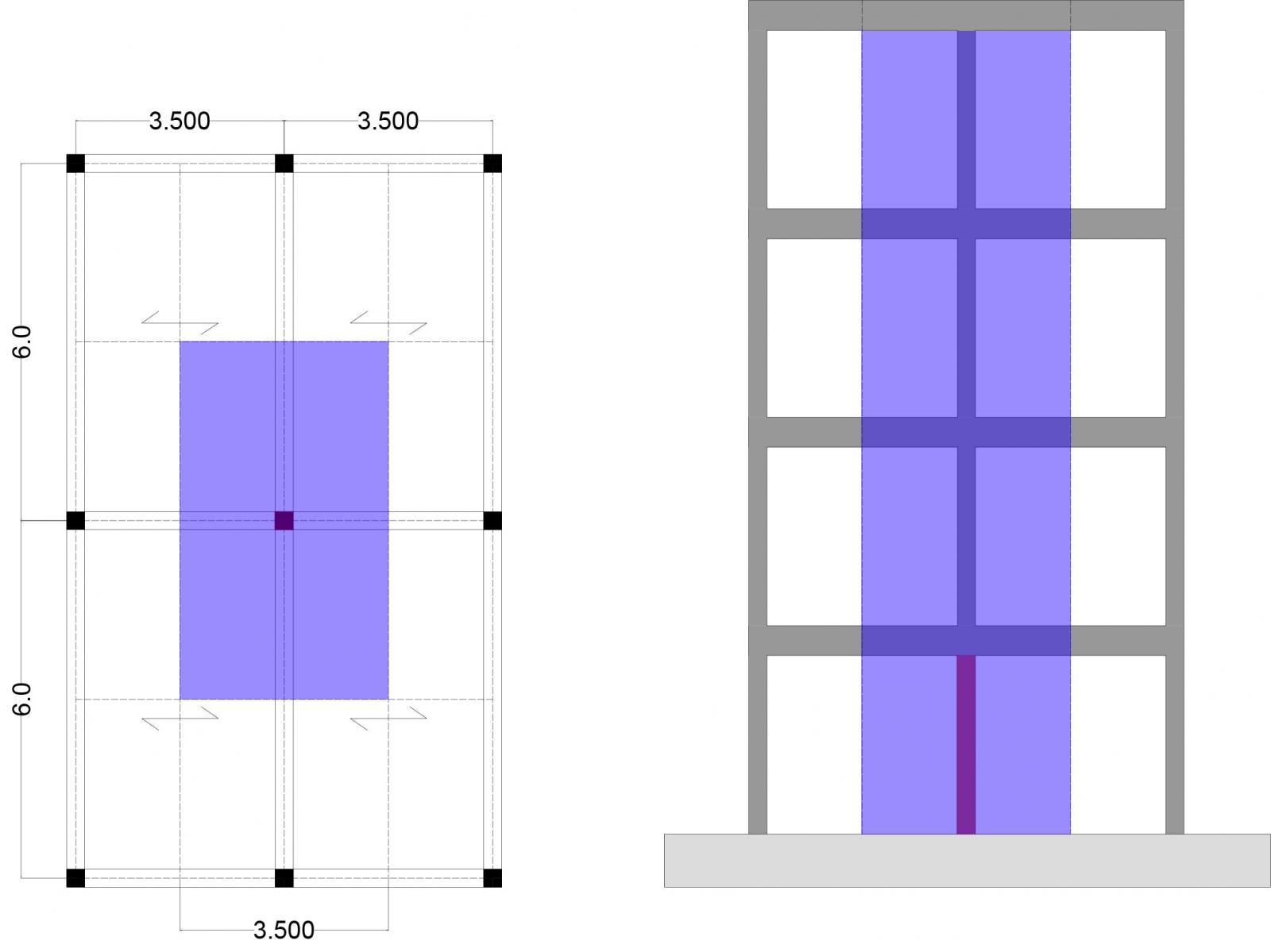
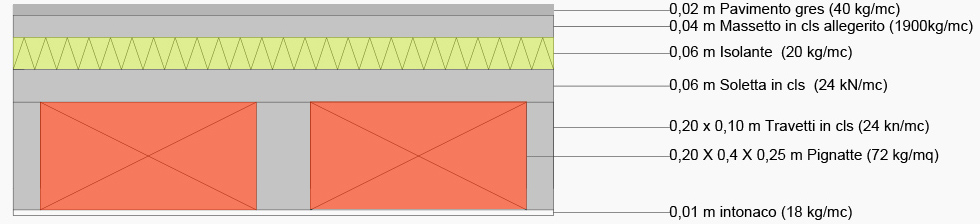
Come nel caso del pilastro in legno come prima cosa partendo dalla geometria e dai pesi della struttura ho ricavato lo sforzo normale agente sul pilastro più sollecitato. (4.10)

4.10

Conoscendo il modulo di elasticità (E) del cemento, la sua resistenza a rottura (fck) e ), (β) coefficiente dato dai vincoli agenti sul pilastro ho potuto ricavare: la resistenza di progetto (fcd), l’area minima del pilastro (Amin), la snellezza del pilastro(λmax),il raggio d’inerzia minimo (ρmin), la base minima(b min) e l’altezza minima (h min).( 4.11)

4.11

Con i dati ricavati ho potuto dimensonare il mio pilastro in modo tale che le sue dimensioni fossero maggiori rispetto alle minime ricavate per stare in sicurezza ed in particolare che l’area di desing (A design) fosse maggiore dell’area minima affinche fosse verificata per lo sforzo normale.(4.12)

4.13

Tuttavia il pilastro di cemento necessita di un’ulteriore verifica essendo sottoposto a presso flessione in quanto il nodo con la trave è composto da un incastro e quindi trasmette anche il momento oltre che lo sforzo normale. Per verificarlo a pressoflessione impongo che la tensione massima

(σmax) sia minore della resistenza di progetto.(4.14) La tensione massima la ricavo in funzione dello sforzo normale e del momento, trasmessi dalla trave al pilastro, facendo la somma del rapporto tra lo sforzo normale e l’area del pilastro e il rapporto tra il momento(Mt) e il modulo di resistenza a flessione (W). Il modulo di resistenza a flessione lo calcolo dividendo per sei il prodotto tra la base e l’altezza al quadrato della sezione del pilastro.

Per calcolare il momento invece devo prima calcolarmi alo slu il carico distribuito sulla trava (qt), ovvero facendo la somma del prodotto di uno 1,3 per il carico strutturale con  il prodotto di 1,5 e il carico permanente e con il prodotto di 1,5 ed il carico accidentale.

A questo punto posso calcolarmi il momento agente sul pilastro dividendo per 12 il prodotto tra il carico distribuito sulla trave e l’interasse principale al quadrato.

Ricavati questi dati posso finalmente verificare che la tensione massima è inferiore alla forza di progetto e che quindi la sezione da me scelta di 35x40 cm risulta essere verificata!

4.14

PILATRO IN ACCIAIO

4.15

4.16

4.17

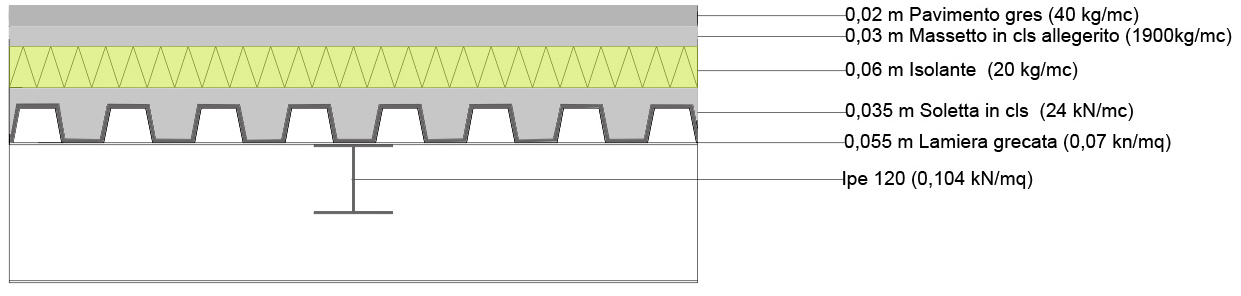
Per la realizzazione del solaio in acciaio, calcolato nella prima esercitazione, mi sono servito di IPE 330 dal peso di 0,49 kN/m, per le travi principali ed IPE 140, dal peso di 0,129 kN/m, per le travi secondarie.

Considerando i diversi pesi degli elementi strutturali, come per le altre esercitazioni mi sono ricavato lo sforzo normale portato dal pilastro maggiormente sollecitato della struttura.(4.18)

4.18

Conoscendo le caratteristiche dell’acciaio ed i tipi di vincolo del pilastro ho potuto calcolare, come nei casi precedenti: l’area minima della sezione(A min), la snellezza (λmax)e il raggio minimo d’inerzia(ρmin).

Ma al contrario dei casi precedenti per scegliere la sezione, non mi sono dovuto ricavare la base e l’altezza minima del pilasto ma mi sono dovuto servire di un ulteriore dato ovvero il momento d’inerzia minimo (I min) che ho ricavato moltiplicato l’area minima per il quadrato del raggio d’inerzia.(4.19)

4.19

A questo punto dal profilario di elementi HEA ho potuto scegliere quello che non solo ha un area superiore a quella minima ma anche un momento di inerzia maggiore a quello minimo in modo tale che garantisca la sua stabilita a sforzo normale. Nel caso da me calcolato ho soddisfato la verifica con un profilo HEA 180. (4.20)

4.20