Quinta Esercitazione _ Ripartizione di una Forza Orizzontale (METODO DELLE RIGIDEZZE)

Ritratto di Lodovica Ana Silva
Inviato da Lodovica Ana Silva il Sab, 23/05/2015 - 08:18

INTRODUZIONE:

In questa quinta esercitazione ci occuperemo di come si distribuisce una forza orizzontale, sia essa di natura sismica e atmosferica (venti), sui diversi telai che compongono la struttura intelaiata piana che, in questo caso, sarà ad un solo piano.

La collaborazione tra travi e pilastri permette, non solo di portare i carichi verticali alle fondazioni, ma anche di sopportare le azioni orizzontali rendendo pilastri-travi dei controventi.

Adotteremo in questo caso una struttura in cemento armato, con una particolare classe tipologica di controventi, ovvero il telaio Shear-type. Questo telaio presenta tutti nodi ad incastro e la trave che viene ipotizzata infinitamente rigida a flessione, rispetto ai pilastri, cui viene attribuita rigidezza k.

NOTA: Ricordo che, affinché un sistema di controventamento sia efficace, gli impalcati vanno considerati corpi rigidi sul proprio piano (al di fuori del quale, invece, si inflettono), per cui i controventi reagiscono alla forza orizzontale, di qualsivoglia natura, che tende a spostarli, attraverso la loro elasticità; il che implica che un controvento, nel piano dell’impalcato, sia un appoggio cedevole elasticamente: hanno comportamento elastico.

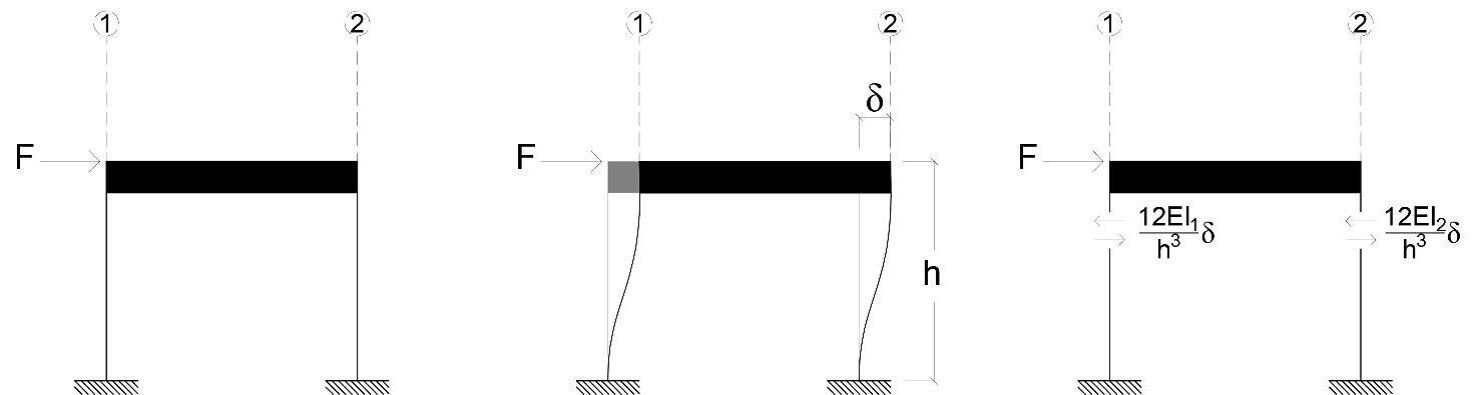
Nella figura precedente è rappresentato un telaio shear-type a due ritti, dove la forza F sposta il traverso, trascinando con sé i due pilastri, che si comportano come una trave doppiamente incastrata. Il legame tra forza F e spostamento δ è esplicitato nella seguente formula F= [(12EI1/h3) + (12EI2/h3)] δ (che vale per un telaio shear-type a due piedritti), dalla quale si ricava che la rigidezza traslante k di ogni pilastro vale 12EI/h3, sapendo che F=kδ.

Ne consegue che, in un caso generico, la rigidezza traslante di un telaio Shear-Type composto da n pilastri è pari a:

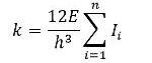
Con questa esercitazione, quindi, saremo in grado di determinare la reazione elastica di ogni controvento che, secondo il principio di azione-reazione sarà uguale ed opposta alla forza orizzontale che ogni singolo controvento è chiamato a ricevere attraverso il solaio.

DISEGNO:

Disegno la pianta strutturale dell’edificio e numero i telai presenti:

Telai // all’asse y                                                                          

Telaio 1v  pilastri 1-5;  Telaio 2v pilastri 2-6-9; Telaio 3v pilastri 3-7-10;  Telaio 4v pilastri 4-8 

Telai // all’asse x

Telaio 1o pilastri 1-2-3-4 ; Telaio 2o pilastri 5-6-7-8;  Telaio 3o pilastri 9-10      

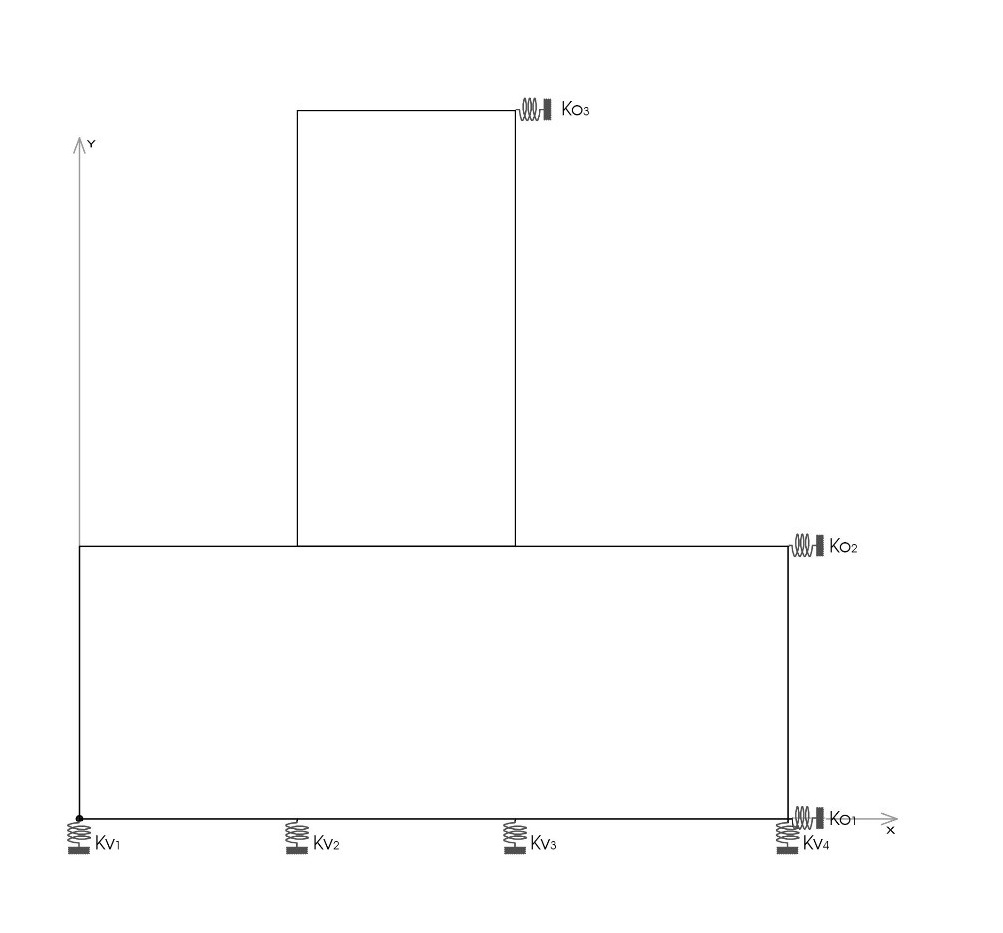
Trattandosi di vincoli cedevoli elasticamente, i controventi vengono assimilati a molle, dotate di una certa rigidezza.

DIMENSIONAMENTO:

Dopo aver aperto il foglio di calcolo excel, inserisco i dati a mia disposizione:

  • E = modulo elastico di Young (espressi in Mpa o N/mm2); per cls con classe di resistenza C20/25
  • H = altezza dei pilastri (nel mio caso valgono m 3.50)
  • I = il momento di inerzia di ciascuno pilastro*1 che collabora alla formazione di ogni telaio

*1 Il momento di Inerzia viene calcolato lungo le due direzioni principali.

  • Momento di inerzia dei pilastri:

            Pilastro m 0.5*0.3

Dove: 

           b= 30 cm;  h= 50 cm

Da cui:

1.     Ix = bh3/12 = 321.500 cm4

2.     Iy = hb3/12 = 112.500 cm4

 

 

Una volta inseriti i risultati dei calcoli, ottengo la rigidezza traslante dei miei 7 telai.

Ora posso passare alla seconda tabella dove, oltre a riassumere la rigidezza di tutti i controventi, inserisco la distanza dei rispettivi controventi dal punto di origine del sistema di riferimento adottato.

Dopodiché, con la terza tabella, passo al calcolo del centro di massa dell’ impalcato, partendo dalla sua suddivisione in forme geometriche semplici e ricavandone i rispettivi centri e aree.

Nel mio caso l’impalcato si compone di due rettangoli perciò, una volta inserite le coordinate dei punti che individuano i due centri, rispetto al punto di origine O, Il file calcola l’area totale ed elabora le coordinate del centro di massa dell’impalcato secondo le formule:

NOTA: Ipotizzo che la densità di massa dell’impalcato sia uniforme su tutto l’impalcato: in questo modo le coordinate ottenute, che individuano il centro d’area dell’impalcato, individueranno anche il centro di massa poiché coincidenti. Qualora la densità dell’impalcato non fosse uniforme, il centro di massa dell’impalcato non coinciderebbe con il centro d’area.

Nella quarta tabella determino:

  • KO =  la rigidezza totale orizzontale (somma delle rigidezze dei singoli controventi orizzontali)
  • KV =  la rigidezza totale verticale (somma delle rigidezze dei singoli controventi verticali)
  • X_c & Y_c= le coordinate del centro delle rigidezze dell’impalcato
  • K_Φ la rigidezza torsionale totale

Il calcolo del centro delle rigidezze avviene attraverso la somma delle combinazioni tra le 

rigidezze e le rispettive distanze dal punto di origine dei controventi; il tutto diviso per la rigidezza totale.

 

NOTA: Ricordo che l’esercitazione richiede che la forza sismica sia applicata nel centro di massa G.

 

Ora, posizionando il centro di massa (G) ed il centro delle rigidezze (C) all’interno dello schema che rappresenta l’impalcato, posso accorgermi qualitativamente se l’impalcato è soggetto a sola traslazione o a traslazione e rotazione. Ciò dipende dal fatto che il centro di massa coincida o meno con quello delle rigidezze.

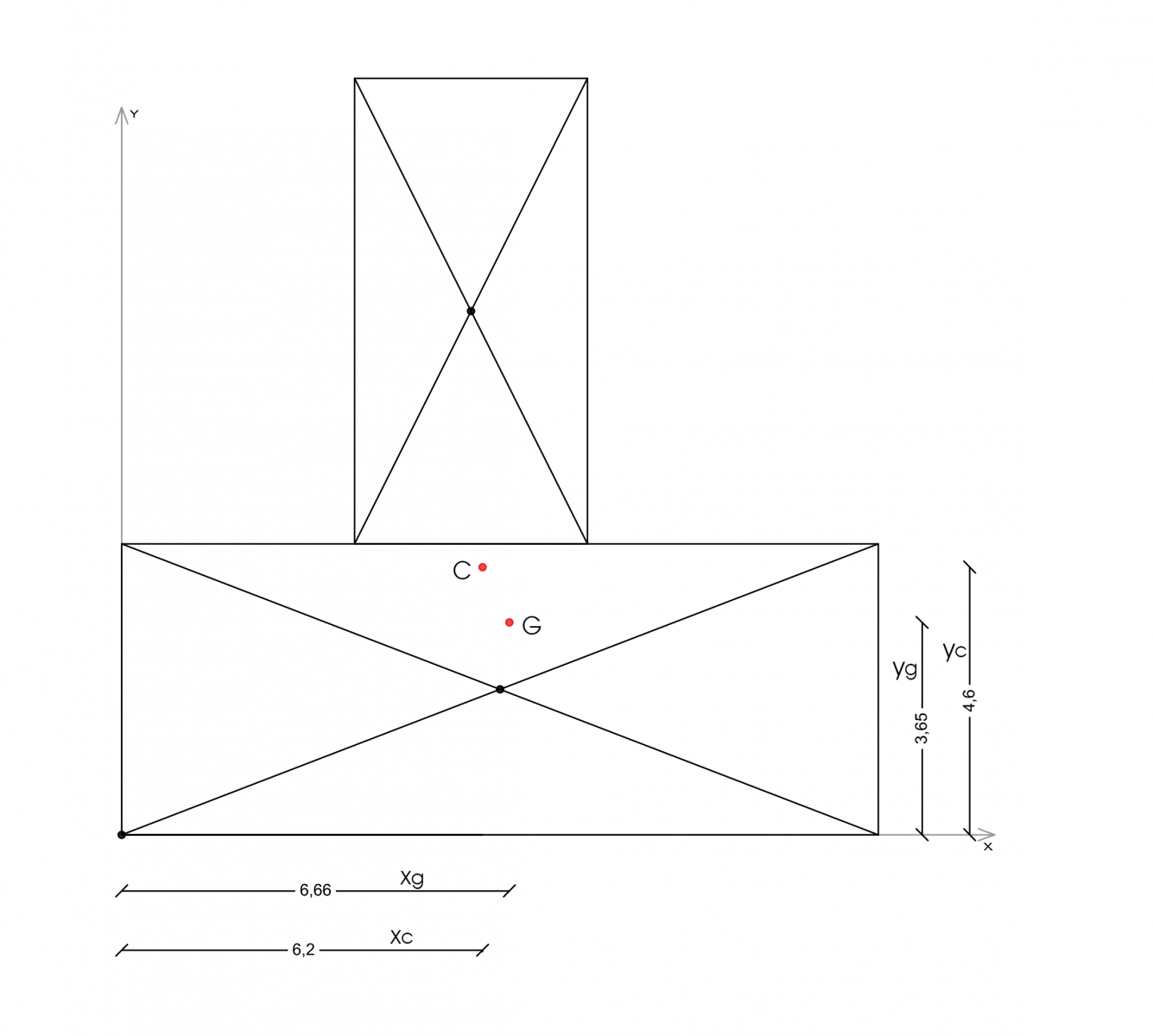Nel mio caso C e G non corrispondono, perciò l’impalcato, in presenza di una forza esterna orizzontale applicata su G, sarà soggetto oltre che alla traslazione anche alla rotazione dovuta al braccio tra forza e centro delle rigidezze (C), che crea un momento.

Dopodiché calcolo la rigidezza torsionale totale K_Φ, il cui valore è ottenuto in funzione delle distanze dei diversi controventi dal centro delle rigidezze.

Con la quinta tabella effettuo l’analisi dei carichi sismici per ricavare la forza sismica che agisce nel centro di massa.

Riprendo i valori dei carichi ricavati nella prima esercitazione http://design.rootiers.it/strutture/node/1713.

A partire da questi valori, il file calcola:

  • G= il carico totale permanente, dato dal prodotto fra l’area totale e la somma dei carichi strutturali e permanenti
  • Q= il carico totale accidentale, dato dal prodotta fra l’area totale e il carico accidentale
  • W= Peso sismico o forza peso, calcolato attraverso la combinazione sismica, che richiede l’uso di ψ*2
  • F= Forza sismica, data dal prodotta fra il peso sismico e c (coefficiente di intensità sismica in base alla localizzazione dell’edificio)

*2 trattasi di un coefficiente di contemporaneità che tiene conto della funzione/categoria dell’impalcato; nel mio caso ho preso il valore riferito agli ambienti ad uso residenziale. 

Le ultime due tabelle indicano come si ripartisce la forza sismica ai vari controventi, a seconda che essa agisca lungo l’asse x o l’asse y, e gli effetti cinematici (traslazione e rotazione rigida) sull’impalcato.

La sesta tabella ricava la forza sismica agente lungo X, la quale causa una traslazione orizzontale u ed una rotazione ϕ.

Il file di calcolo elabora i seguenti dati:

  • M= momento torcente dato dalla formula F . (Yc - Yg)*3
  • U_o= traslazione orizzontale dove u=F/ ko_tot
  • ϕ= rotazione cui è sottoposto l’impalcato; vale f= M/kϕ *4

*3 Nel mio caso è un valore positivo, quindi implica un momento antiorario.

*4 kϕ  è la rigidezza torsionale totale ricavata nella tabella 4.

La settima tabella ricava, invece, la forza sismica agente lungo Y, la quale, a sua volta, causa una traslazione verticale u ed una rotazione ϕ.

Nella tabella successiva, viene ripetuto lo stesso ragionamento, considerando la traslazione verticale:

  • U_v= traslazione verticale dove u=F/ kv_tot

​

Una volta determinati i valori dei gradi di libertà, posso ricavare la forza agente sui singoli controventi nei due casi di carico (verticale e orizzontale).

Noti u_o, v_o, ϕ, posso determinare le reazioni elastiche di ogni controvento attraverso le seguenti formule:

CASO 1 – Forza // all’asse X

  • Fo_n=ko_n(u+ϕ∙ddo_n)       per i controventi orizzontali
  • Fv_n=kv_n∙ϕ∙ddv_n            per i controventi verticali

CASO 2 – Forza // all’asse Y

  • Fv_n=kv_n(v+ϕ∙ddv_n)       per i controventi verticali
  • Fo_n=ko_n∙ϕ∙ddo_n            per i controventi orizzontali

Come già detto, si considera la forza nel piano dell’impalcato prima agente in direzione orizzontale e poi agente in direzione verticale; perciò analizziamo i due casi.

CASO 1 – Forza // all’asse X

CASO 2 – Forza // all’asse Y