blog di Lodovica Ana Silva

INTRODUZIONE:

In questa quinta esercitazione ci occuperemo di come si distribuisce una forza orizzontale, sia essa di natura sismica e atmosferica (venti), sui diversi telai che compongono la struttura intelaiata piana che, in questo caso, sarà ad un solo piano.

La collaborazione tra travi e pilastri permette, non solo di portare i carichi verticali alle fondazioni, ma anche di sopportare le azioni orizzontali rendendo pilastri-travi dei controventi.

Adotteremo in questo caso una struttura in cemento armato, con una particolare classe tipologica di controventi, ovvero il telaio Shear-type. Questo telaio presenta tutti nodi ad incastro e la trave che viene ipotizzata infinitamente rigida a flessione, rispetto ai pilastri, cui viene attribuita rigidezza k.

NOTA: Ricordo che, affinché un sistema di controventamento sia efficace, gli impalcati vanno considerati corpi rigidi sul proprio piano (al di fuori del quale, invece, si inflettono), per cui i controventi reagiscono alla forza orizzontale, di qualsivoglia natura, che tende a spostarli, attraverso la loro elasticità; il che implica che un controvento, nel piano dell’impalcato, sia un appoggio cedevole elasticamente: hanno comportamento elastico.

Nella figura precedente è rappresentato un telaio shear-type a due ritti, dove la forza F sposta il traverso, trascinando con sé i due pilastri, che si comportano come una trave doppiamente incastrata. Il legame tra forza F e spostamento δ è esplicitato nella seguente formula F= [(12EI₁/h³) + (12EI₂/h³)] δ (che vale per un telaio shear-type a due piedritti), dalla quale si ricava che la rigidezza traslante k di ogni pilastro vale 12EI/h³, sapendo che F=kδ.

Ne consegue che, in un caso generico, la rigidezza traslante di un telaio Shear-Type composto da n pilastri è pari a:

Con questa esercitazione, quindi, saremo in grado di determinare la reazione elastica di ogni controvento che, secondo il principio di azione-reazione sarà uguale ed opposta alla forza orizzontale che ogni singolo controvento è chiamato a ricevere attraverso il solaio.

DISEGNO:

Disegno la pianta strutturale dell’edificio e numero i telai presenti:

Telai // all’asse y                                                                          

Telaio 1v  pilastri 1-5;  Telaio 2v pilastri 2-6-9; Telaio 3v pilastri 3-7-10;  Telaio 4v pilastri 4-8 

Telai // all’asse x

Telaio 1o pilastri 1-2-3-4 ; Telaio 2o pilastri 5-6-7-8;  Telaio 3o pilastri 9-10      

Trattandosi di vincoli cedevoli elasticamente, i controventi vengono assimilati a molle, dotate di una certa rigidezza.

DIMENSIONAMENTO:

Dopo aver aperto il foglio di calcolo excel, inserisco i dati a mia disposizione:

• E = modulo elastico di Young (espressi in Mpa o N/mm²); per cls con classe di resistenza C20/25
• H = altezza dei pilastri (nel mio caso valgono m 3.50)
• I = il momento di inerzia di ciascuno pilastro*¹ che collabora alla formazione di ogni telaio

*¹ Il momento di Inerzia viene calcolato lungo le due direzioni principali.

• Momento di inerzia dei pilastri:

            Pilastro m 0.5*0.3

INTRODUZIONE:

L’obiettivo di questa quarta esercitazione è il dimensionamento della sezione del pilastro maggiormente sollecitato, sempre secondo le tre diverse principali tecnologie, ovvero legno, acciaio e calcestruzzo armato.

Trattandosi di un elemento strutturale sottoposto a sforzo normale centrato di compressione, bisogna tener conto, oltre alla rottura per schiacciamento del materiale, di eventuali fenomeni di instabilità euleriana (fenomeno tipico/proprio delle strutture snelle).

Le instabilità sono causate dalla natura fisica delle forze: le forze devono compiere lavoro e quindi spostare il più possibile il loro punto di applicazione nella direzione della forza. Da qui si verifica l’abbassamento del punto di applicazione, con relativo accorciamento delle fibre compresse, e la deformazione assiale dell’elemento strutturale (che noi definiamo contrazione).

L’incognita principale di progetto è l’Area minima (tale da evitare lo schiacciamento) della sezione del pilastro esaminato, che ricaveremo eguagliando la tensione massima sulla sezione alla resistenza di progetto del materiale di cui è composto il nostro pilastro:

σmax= f_cd     e sapendo che N/A_min = f_cd    ricavo    A_min =N/ f_cd 

L’incognita secondaria è il Momento di Inerzia minimo della sezione che ottengo mettendo in relazione la tensione normale massima all’interno dell’elemento strutturale e la tensione critica (con un’uguaglianza), in corrispondenza del carico critico euleriano, del pilastro.

Il carico critico euleriano vale N_critico = π² E I_min /(β l)².

In questa formula viene introdotto un nuovo coefficiente β, che rappresenta l’influenza dei vincoli secondo il seguente schema.

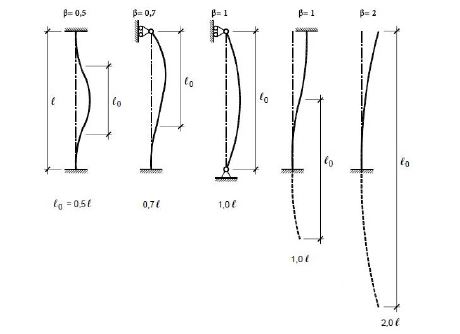
NOTA:

• Ricordando le seguenti relazioni I_min =A ρ_min² e  λ = l₀/ρ_min e sostituendole all’interno della formula del carico critico euleriano ottengo quanto segue: N_critico = π² EA/λ²
• σ_critico ⁼ N_critico /A = π² E/λ²
• Dovremo imporre f_cd<σ_critico ; in questo modo progettiamo in maniera che si inneschi prima il fenomeno di rottura e non dello schiacciamento, poiché quest’ultimo risulta essere un fenomeno di difficile controllo.

­DISEGNO:

Disegno la carpenteria del piano tipo e la sezione del mio edificio:

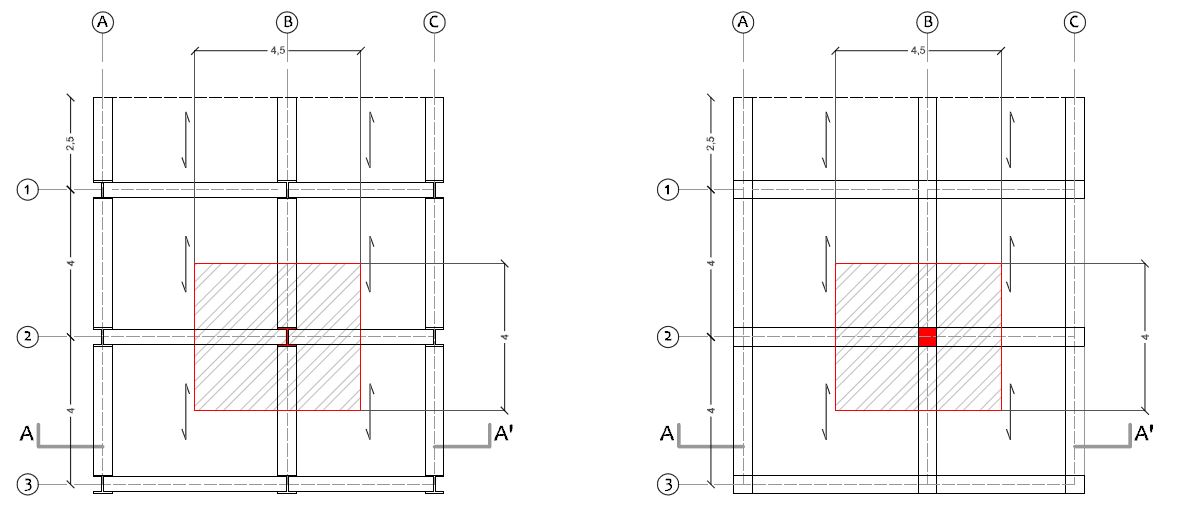
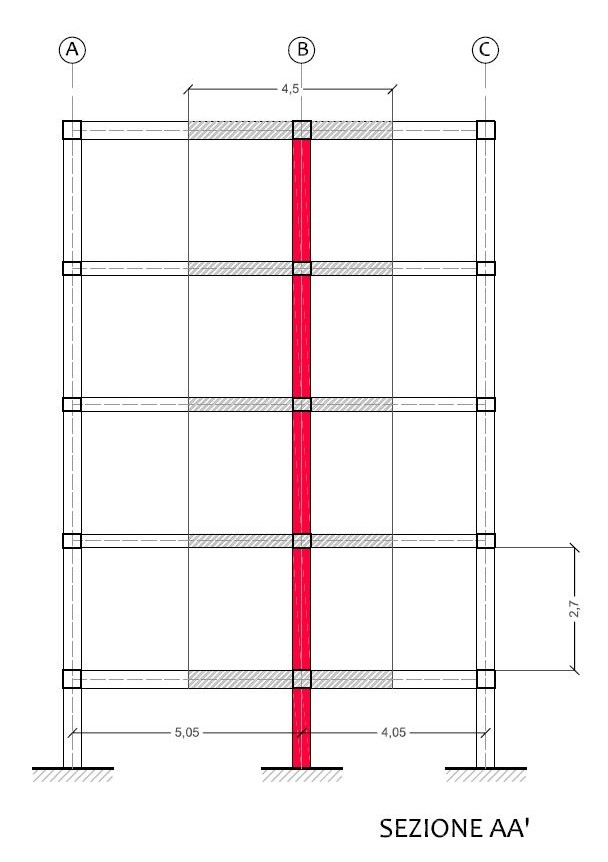
Sto, dunque, considerando un edificio a più piani, con struttura intelaiata piana, ordita da travi che collaborano con i pilastri, secondo il vincolo di appoggio semplice.

Il pilastro più sollecitato è certamente uno di quelli al piano terra, ai quali vengono trasmessi tutti i carichi dei piani superiori. Perciò  individuo il pilastro più sollecitato guardando la pianta di carpenteria del piano terra.

Dopodiché, attraverso il file excel, inserisco i dati per ogni diversa tecnologia.

1_LEGNO

ANALISI:

Riprendo i valori ricavati nella prima esercitazione http://design.rootiers.it/strutture/node/1713 e inserisco i dati a mia disposizione

• L₁ e L₂ = i due lati dell'area di influenza (circondata in pianta con un rettangolo rosso) del pilastro in esame

Ottengo, così, il valore dell’area di influenza (il cui peso è portato dal pilastro). 

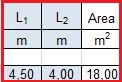
Per il calcolo dello sforzo normale di compressione, devo trovare i valori dei carichi dovuto al peso proprio delle travi che poggiano un’estremità sul pilastro, il carico dovuto al peso del solaio ed il numero dei piani dell’edificio.

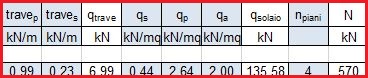
• trave_p = (0,30*0,55)m² x 6KN/m³ = 0,99 KN/m      [trave principale]
• trave_s = (0,25*0,15)m² x 6KN/m³ =  0,225 KN/m    [trave secondaria]

Ottengo q_trave =trave_p*L₁*1,3 + trave_s*L₂*1,3 e lo sforzo normale di compressione agente sul pilastro con la formula N=q_trave+q_solaio*n_piani

Ottengo il valore del carico del solaio dalla combinazione dei tre carichi allo stato limite, il tutto moltiplicato per l’area di influenza.

NOTA: Come già detto, i valori q_s, q_p e q_a  sono stati ripresi dalla prima esercitazione.

PROGETTO:

Procedo ora con il pre-dimensionamento della sezione del pilastro a partire dalla resistenza del materiale e ottenendo quanto vale A_min.

• f_c0,k = resistenza caratteristica a flessione nella direzione delle fibre (dipende dal materiale)
• k_mod = coefficiente di durata del carico (fornito dalla normativa)
•  γ_m = coefficiente di sicurezza

Ottengo così la tensione ammissibile f_c0d = f_c0,k k_mod / γ_m e quindi l'area minima necessaria alla sezione affinché il materiale non giunga a rottura.

• E,005 = modulo elastico in percentile
• β = 1 [caso cerniera-carrello]       (vedere lo schema iniziale)
• l = altezza del pilastro

Ricavo;  

λ_max =  π √(E/f_cd)  [valore massimo di snellezza]

 ρ_{min =} β l/ λ_max 

 Sapendo che nel legno ρ_min= √(1/12) *b ,ricavo attraverso questo formula una delle due dimensioni della sezione, b_min, che ingegnerizzo 

h_min= A_min/b

Devo ingegnerizzare anche l'altezza. Ora ho le due dimensioni che descrivono la sezione del pilastro.

Verifico poi, per sicurezza, che l'Area di design sia maggiore dell'Area minima.

2_ACCIAIO

ANALISI:

Ripeto quanto già fatto nel caso del legno, riprendendo i valori ricavati nella prima esercitazione http://design.rootiers.it/strutture/node/1713 e inserendoli.

• L₁ e L₂ = i due lati dell'area di influenza (descritta in pianta con un rettangolo rosso) del pilastro in esame
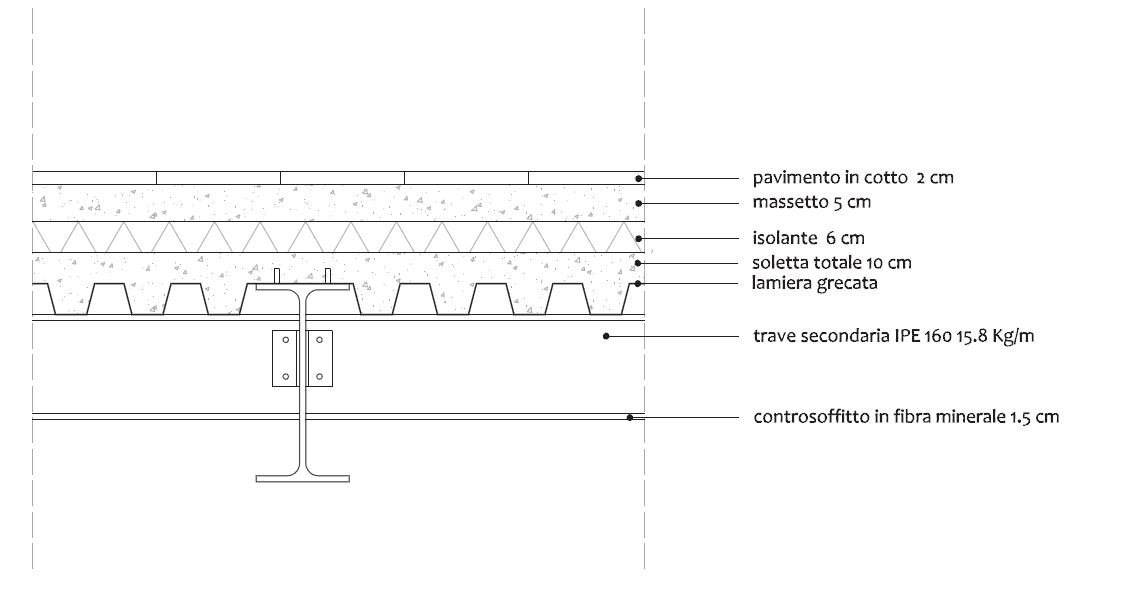
• trave_p = IPE 360 = 57,1 kg/m =0,571 KN/m    [peso trave principale]
• trave_s = IPE 160 = 15,8 kg/m =0,158 KN/m    [peso trave secondaria]

PROGETTO:

• f_yk  = tensione di snervamento caratteristica 
• γ_m = coefficiente di sicurezza
• f_yd = f_yk/ γ_m [resistenza di progetto]

Ottengo l'area minima A_min=N/f_cd

• λ^* = √(E/f_yd)
•  ρ_min = β l/ λ^*
• I_min = Aρ_min² (ricavo dunque il momento di inerzia minimo in funzione del raggio di inerzia minimo)

Attraverso la tabella dei profili HEA ricavo i valori di A_{design ,} I_design e ρ_min maggiori di quelli minimi ottenuti, il cui profilo risulta essere un HEA140.

3_CALCESTRUZZO ARMATO

ANALISI:

Ripeto quanto già fatto nei casi precedenti, riprendendo i valori ricavati nella prima esercitazione http://design.rootiers.it/strutture/node/1713 e inserendoli.

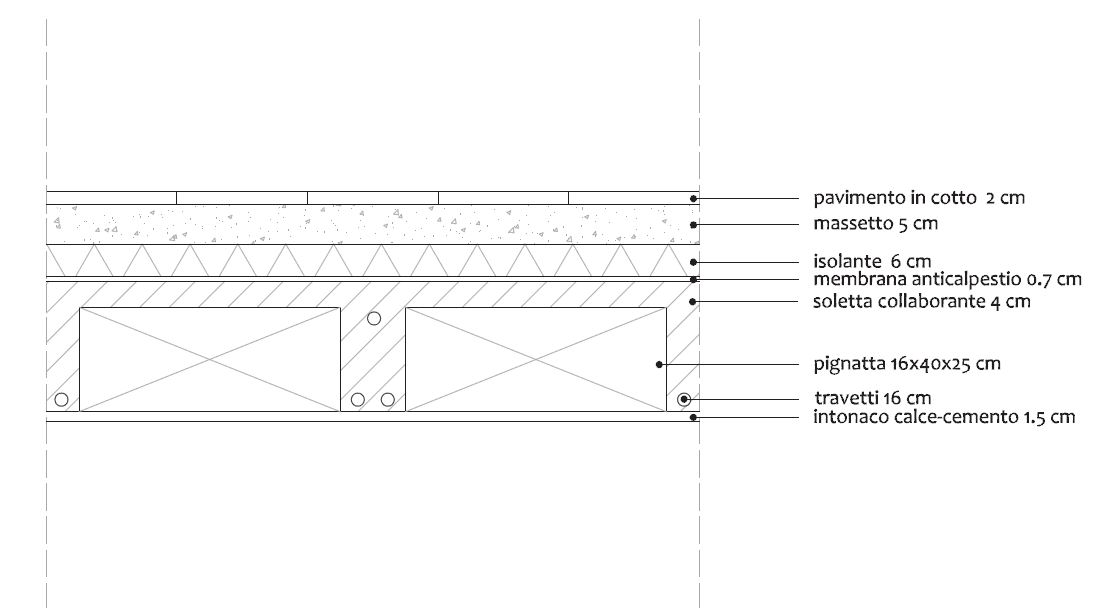
• trave_p = (0,30*0,50)m²*25KN/m2 =3,75 KN     [peso trave principale]
• trave_s = (0,30*0,50)m²*25KN/m2 =3,75 KN     [peso trave secondaria]

​

PROGETTO:

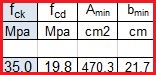
• f_ck =35 (calcestruzzo di classe C35/45)
• f_cd = 0,85*f_ck/1,5

• β =1 [doppio incastro]   (fare riferimento allo schema iniziale)
• l=2,70 m [la luce del pilastro]

Ingegnerizzo i valori minimi ricavati per ottenere le due dimensioni del pilastro = cm 25x45.

Non mi resta che calcolare:

• A_design =b*h
• I_design =(h*b³)/12
• I_max =(b*h³)/12

NOTA: Ricordiamo che, a differenza dei due casi precedenti, il pilastro in cls armato è sottoposto, oltre che a compressione, a presso-flessione, poiché il nodo trave-pilastro è realizzato da un incastro (il che trasmette momento); per evitare fenomeni di instabilità devo verificare che σ_max ​ sia minore o uguale a f_cd.

Per il calcolo della tensione massima devo ricavare i seguenti valori:

• W_max  = bh²/6  [modulo di resistenza a flessione per sezioni rettangolari]
• q_t    [carico sulla trave; combinazione allo SLU dei tre carichi moltiplicati per l’interasse delle travi principali]
• Mt =(q_t* l_p²)/12   [momento nell'estremo della trave, trasmesso da quest’ultima al pilastro]

A questo punto σ_max = N/A + M_t /W_max ≤ f_cd ? Sì, 16,81 ≤ 19,8

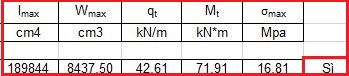
Il pilastro di dimensioni cm 25x45 risulta VERIFICATO!

INTRODUZIONE:

In questa esercitazione, ci occuperemo del dimensionamento di una trave a sbalzo nelle tre diverse tecnologie, ovvero il legno, l'acciaio e il calcestruzzo armato.

• Dopo aver definito la carpenteria di riferimento, individuo la trave maggiormente sollecitata e, nel rettangolo rosso, l'area di influenza di luce l=2,5m e interasse i=4m.

A questo punto posso passare all'analisi di ogni tecnologia.

Prendendo in considerazione la stratigrafia dei solai analizzati nel prima esercitazione, prendo in riferimento i carichi ivi ottenuti. [http://design.rootiers.it/strutture/node/1713]

1_STRUTTURA IN LEGNO

Il procedimento iniziale è lo stesso applicato nella prima esercitazione, quindi i valori delle prime colonne permettono di ricavare h_min, nel caso del legno e del c.a., o W_min, nel caso dell’acciaio.

 NOTA: A differenza della prima esercitazione, dove consideravamo una trave doppiamente appoggiata, in questo caso stiamo prendendo lo schema statico di una mensola, perciò il valore del momento massimo viene ricavato dalla formula: M_max= ql²/2.

ANALISI:

• ​​​q_s = 0.44 KN/m²
• q_p = 2.64 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1.  f_m,k= 24 (legno lamellare GL 24c)                              [resistenza a flessione caratteristica]
2. K_mod = 0.80                                                             [coefficiente di durata del carico]
3. γ _m = 1.50                                                                [coefficiente parziale di sicurezza del materiale]

Con questi valori il file excel è in grado di calcolare la tensione ammissibile f_d c tramite la formula fm,k x kmod / γm.

PROGETTO: 

• Ipotizzo la base della trave pari a 25 cm. Il mio file excel sviluppa un'altezza minima Hmin che richiede di essere ingegnerizzata, data la presenza dei decimali. 
• Dopodichè, assegnando al materiale un modulo elastico E pari a 8000 Mpa, ottengo i seguenti valori:

1.  I_x  (momento di inerzia)  ricavato dalla formula b*h³/12
2. q_e  il carico incidente, dove, a differenza dell'acciaio e del cls armato, non inserisco il peso proprio della trave perché si tratta di un materiale leggero (quindi è trascurabile)

Risulta necessario effettuare la verifica a deformabilità controllando che l’abbassamento massimo del profilo, analizzato in rapporto alla sua luce, non sia tale da deformare la struttura, limitandone l’uso. Per questo la verifica viene fatta facendo riferimento alla stato limite d’esercizio SLE.

v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250 (valore valido per i solai in generale).

_​

 ANALISI:

• ​​​q_s = 2.46 KN/m²
• q_p = 2.97 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1. f_yk= 450 MPa                                   [tensione di snervamento]
2. f_ck = 35 MPa                                    [valore caratteristico di resistenza cilindrica]

Con questi valori il file excel è in grado di calcolare la tensione di progetto del cls f_yd e dell'acciaio f_cd .

PROGETTO: 

• Ipotizzo la base della trave pari a 25 cm e un copriferro δ di 5 cm. Il mio file excel sviluppa un'altezza minima Hmin che, come sopra, ingegnerizzo.
• Dopodichè, assegnando al materiale un modulo elastico E (informazione relativa al materiale)  pari a 8000 Mpa, ottengo i seguenti valori:

1.  I_x (informazione relativa alla geometria) ricavato dalla formula b*h³/12
2. q_e  il carico incidente, dove inserisco il peso proprio della trave
3. v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250

 ANALISI:

• ​​​q_s = 2.46 KN/m²
• q_p = 2.97 KN/m²
• q_a  = 2 KN/m²

^​Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu), e, dopo aver inserito il valore della luce, il momento massimo M_max= ql²/2, trattandosi di una mensola.

• Assumo:

1. f_yk= 235 MPa                                   [tensione di snervamento]

Con questo valore il file excel mi calcola la tensione di progetto f_d dell'acciaio.

PROGETTO: 

• Attrraverso la formula M_max/f_d ottengo il valore W_min ovvero il modulo della resistenza
• Dopodichè, ingegnerizzando il valore del modulo della resistenza, ottengo i seguenti valori dalla tabella dei profili IPE standard:

1.  I_x  corrisponde a J_x nella tabella e si esprime in cm⁴
2. peso, che nella tabella è espresso in Kg/m, devo trasformarla in Kn/m moltiplicando il valore per 10^-2
3. q_e  il carico incidente, dove inserisco il peso proprio della trave
4. v_max l'abbassamento massimo ed il suo rapporto con la luce l/v_max che da normativa deve essere l/ v_max ≥ 250

​

Il profilo IPE scelto è un IPE300.

INTRODUZIONE:

In questa seconda esercitazione abbiamo a che fare con la progettazione e il dimensionamento di una travatura reticolare spaziale, un tipo di struttura che permette di lavorare su grandi luci utilizzando pochi punti di appoggio.

Trattandosi di una struttura complessa, la analizzeremo secondo il modello Eulero-Bernoulli (modello di trave semplificato ad una sola variabile).

DISEGNO:

 Disegno la travatura, nel mio caso cubica, attraverso il programma Sap2000 seguendo questi passaggi:

• File>New Model>Grid Only  facendo attenzione ad inserire le unità di misura con le quali voglio lavorare [KN,m,°C]

• Quick Grid Lines: a questo punto si aprirà questa scheda dove devo inserire il numero delle griglie su cui imposto il mio disegno nelle tre direzioni (Number of Grid Lines), e la spaziatura che voglio fra le linee della griglia (Grid Spacing): in questo modo ottengo le campate strutturali della travatura

​

Mi appaiono due viste; lavoreremo su quella 3D (a destra).

• Selezionando il comando Draw Frame, costruisco la prima campata reticolare cubica; dopodiché, avendo cura di selezionare tutte le facce della campata esclusa quella iniziale, con CTRL+C e CTRL+V la copio e incollo utilizzando l'asse x come riferimento. 

Il 3 indica la distanza del punto di ancoraggio della nuova campata rispetto all'origine degli assi, che corrisponde alla profondità della prima campata.

• Ripeto l'operazione più volte lungo l'asse x, e poi lungo l'asse y.

• Una volta riempita tutta la griglia tridimensionale, e prima di procedere, controllo: 

1. di non aver fatto fatto aste duplicate in qualche punto con il comando Edit>Merge Duplicates 
2. che tutti i nodi siano uniti con il comando Edit>Edit Points>Merge Joints> 0,1 (raggio di vicinanza dei nodi che convergono nello stesso punto al punto stesso)

​​Ora posso vincolare la struttura esternamente ed internamente:

• VINCOLI ESTERNI: seleziono gli spigoli esterni inferiori della mia struttura e gli assegno un cerniera cliccando su Assign>Joint>Restraints>Icona della cerniera 

​

• VINCOLI INTERNI: devo rendere tutti i nodi, delle cerniere interne, perciò selezionare la struttura clicco su Assign>Frame>Releases>Partial Fixity e spunto Moment 2-2 e 3-3 all'inizio (release start) e alla fine (release end) di ogni asta. 

• Definisco il MATERIALE ed il PROFILO delle mie aste in questo modo: Seleziono la struttura>Assign>Frame> Frame Sections>Add New Property>Pipe; in alto su section name lo rinomino come "tubolare" 

​

In questo modo ho assegnato a tutte le aste il profilo in acciaio tubolare cavo.

• Non mi resta che creare ed assegnare i CARICHI CONCENTRATI:

1. Creo il carico puntiforme F con il comando Define>Load Patterns>Load Pattern "F">Self Weight Multiplier "0" (lo privo del peso proprio)>Add New Load Pattern>Seleziono il carico “F”
2. Assegno il carico, selezionando la parte terminale superiore della struttura e cliccando su Assign>Joint Loads>Forces>F>Force Global Z (l'asse lungo la quale si trova F)>inserisco il valore del carico -75kN (negativo perchè è diretto nel verso opposto all'asse z)

​​​​​

ANALISI:

• ANALIZZO la struttura con Run Analysis, facendo attenzione "a far correre" solo il mio carico concentrato e selezionando Run Now.

Da questa analisi posso visualizzare:

• la deformata della mia struttura

• il diagramma degli sforzi normali

• ed il diagramma del momento, che necessariamente deve equivalere a zero in tutti i punti

DIMENSIONAMENTO:

Per il dimensionamento, abbiamo bisogno di conoscere il valore dello sforzo normale in ogni singola asta.

• Perciò da Sap posso creare una tabella che mi mostri tutti questi valori attraverso i seguenti comandi:  Display>Show Tables>Analysis Results>Select Load Patters "F"> Select Load Cases "F"

​

• A questo punto mi si apre una tabella, e dal menù a tendina laterale, seleziono Element Forces–Frames

• Non mi resta che esportare il file in Excel in modo da poterci lavorare: File>Export Current Table>To Excel

La tabella è costituita da una serie di valori, di cui alcuni trascurabili al fine del dimensionamento: quindi ripulisco il file lasciando solo i valori relativi alla numerazione e alla luce delle aste, allo sforzo normale e ai carichi concentrati applicati.

Posso poi procedere ad una ulteriore pulizia, ordinando in modo crescente la luce delle aste per poter conservare solo la lunghezza delle aste diagonali (so già che quelle normali sono pari a 3m) che vale l*radice di 2 ovvero 4,24264 m.

Quindi la lunghezza dei due tipi di aste presenti sono:

• L= 3m
• L= 4,24264 m

Ordino ulteriormente il file:

•  ordinando lo sforzo normale riesco a distinguere le aste tese da quelle compresse.

TRAZIONE:

Inserisco i valori di N superiori allo zero (trazione) nel file excel creato per il dimensionamento.

• Assumo f_yk (coefficiente caratteristico di snervamento) pari a 275 (valore medio) e y_m (coefficiente di sicurezza) pari a 1,05.

Il file individua la tensione di progetto f_d e l'area minima A_{_min} .

Quest'ultimo valore va ingegnerizzato ricorrendo alla tabella che riporta i valori standard dei profili metallici. Qui individuo il valore dell'area immediatamente maggiore rispetto a A_{_min} e ottengo la dimensione del profilato necessario.

Questa operazione andrebbe ripetuta per ogni singola asta.

COMPRESSIONE:

Inserisco i valori di N inferiori allo zero nel file excel creato per il dimensionamento.

• Assumo f_yk (coefficiente caratteristico di snervamento) pari a 275 (valore medio) e y_m (coefficiente di sicurezza) pari a 1,05.

​Il file individua, in questo caso, oltre alla tensione di progetto f_d e l'area minima A_{_min} , anche I_{_min}  e rho_min . Dovrò dunque ingegnerizzare tutti e tre i valori, indiduandolo nella tabella dei profili standard.

INTRODUZIONE:

Lo scopo di questa esercitazione è il dimensionamento di una trave nelle tre diverse tecnologie più comuni, ovvero il legno, l'acciaio e il calcestruzzo armato. 

Il metodo qui utilizzato, mi permette di dimensione l'altezza della sezione della trave maggiormente sollecitata, imponendo che la tensione massima nella trave sia uguale alla tensione di progetto del materiale, definita dalla normativa.

Prenderò in considerazione per tale procedimento, un struttura intelaiata piana, ordito da travi che collaborano con i pilastri, secondo il vincolo di appoggio semplice.

DISEGNO:

Inizio definendo la carpenteria di riferimento per ciascuno solaio. Nella seguente immagine sono rappresentati, da sinistra a destra, l'orditura di un solaio in acciaio (pilastri in profili HE, con travi IPE) e quella di un solaio in cemento armato (pilastri con sezione quadrata).

Procedo con l'individuazione della trave maggiormente sollecitata, dunque esplicito, col rettangolo rosso, la sua area di influenza (il cui peso è portato dalla trave) e misuro la lunghezza dell'interasse; a questo punto posso passare all'analisi di ogni tecnologia.

1_STRUTTURA IN LEGNO

ANALISI:

Con l'aiuto del file excel, posso dimensionare la mia struttura, sulla base di alcuni dati che mi vengono richiesti (quelli nelle caselle azzurre):

• interasse, che nel mio caso è pari a 4m.
• q_s carico strutturale*¹: il carico dovuto al peso proprio degli elementi con funzione portante.
• q_p carico permanente*¹: il carico dovuto al peso proprio degli elementi non portanti durante il suo ciclo di vita utile.
• q_a carico accidentale*¹: il carico che dipende da diversi fattori scatenanti, che possono verificarsi o meno.
• luce, che nel mio caso vale 7m.
• f_m,k resistenza caratteristica a flessione del materiale.
• k_mod coefficiente diminutivo dei valori di resistenza del materiale; dipende dalla durata del carico*²  e la classe di servizio (dipendente dalle condizioni climatiche) del materiale scelto ed è fornito dalla normativa.
• è fornito dalla normativa.
• γ_m coefficiente parziale di sicurezza dipendente dal materiale.
• la base.

*¹Rappresentano i carichi agenti sul solaio e vengono espressi come densità di carico superficiale kN/m².

*² La classe di durata del carico fa riferimento ad un carico costante agente per un certo periodo di tempo nella vita utile della struttura.

Conosco la stratigrafia del solaio, per cui posso calcolarne i diversi carichi, moltiplicando il peso specifico per la quantità di volume di ogni materiale contenuto in un metro quadro (m²) di solaio: 

q_{s travetti} = 6KN/m³ (0.25x1x1)m³/m² = 0.225 KN/m²

q_s tavolato = 6KN/m³ (0.035x1x1)m³/m² = 0.21 KN/m²

• q_s tot = 0.44 KN/m²

q_p caldana = 21KN/m³ (0.04x1x1)m³/m² = 0.84 KN/m²

q_p isolante = 0.2KN/m³ (0.06x1x1)m³/m² = 0.012 KN/m²

q_{p sottofondo} = 0.18KN/m³ (0.03x1x1)m³/m² = 0.0054 KN/m²

q_p pavimento = 28Kg/m² x 10^-2 = 0.28 KN/m²

• q_p tot = 1.14 KN/m² + 1.5 KN/m²(carico forfettario*³ dei tramezzi e degli impianti) = 2.64 KN/m²
• q_a  = 2 KN/m²

*³ viene preso in considerazione un valore forfettario poiché è difficile effettuare precisamente il calcolo, oltre alla variabilità, nella vita di una costruzione, della distribuzione interna e della quantità dei tramezzi.

Il foglio di calcolo mi fornisce il carico totale a metro lineare (qu) ottenuto dalla somma (combinazione di carico) dei carichi considerati con i corrispettivi coefficienti moltiplicativi, forniti dalla normativa in funzione dello stato limite ultimo (SLU), il tutto moltiplicato per l’interasse; e il momento massimo M_max= ql²/8, trattandosi di una trave appoggiata-appoggiata.

PROGETTO:

Ora scelgo la f_m,k= 24 (secondi i dati forniti dalla normativa nel caso di una tecnologia in un legno lamellare con classe di resistenza GL 24c).

Assumo: 

•  K_mod pari a 0.80

•  γ_m pari a 1.45

  Da questi tre valori ricavo la tensione di progetto f_d= (f_m,k . k_mod) / γ_m

  Infine ipotizzo la base della trave pari a 30 cm. Il mio file excel sviluppa un'altezza minima che richiede di essere ingegnerizzata, data la presenza dei decimali, ad un valore che sia compatibile con i profili esistenti sul mercato.

Ciaoo a tutti!! Lodovica