Creazione del modello di una travatura reticolare spaziale con SAP2000

1. Creo un nuovo file, partendo dalla creazione della griglia. Controllo anche che l’unità di misura sia corretta (KN, m, C).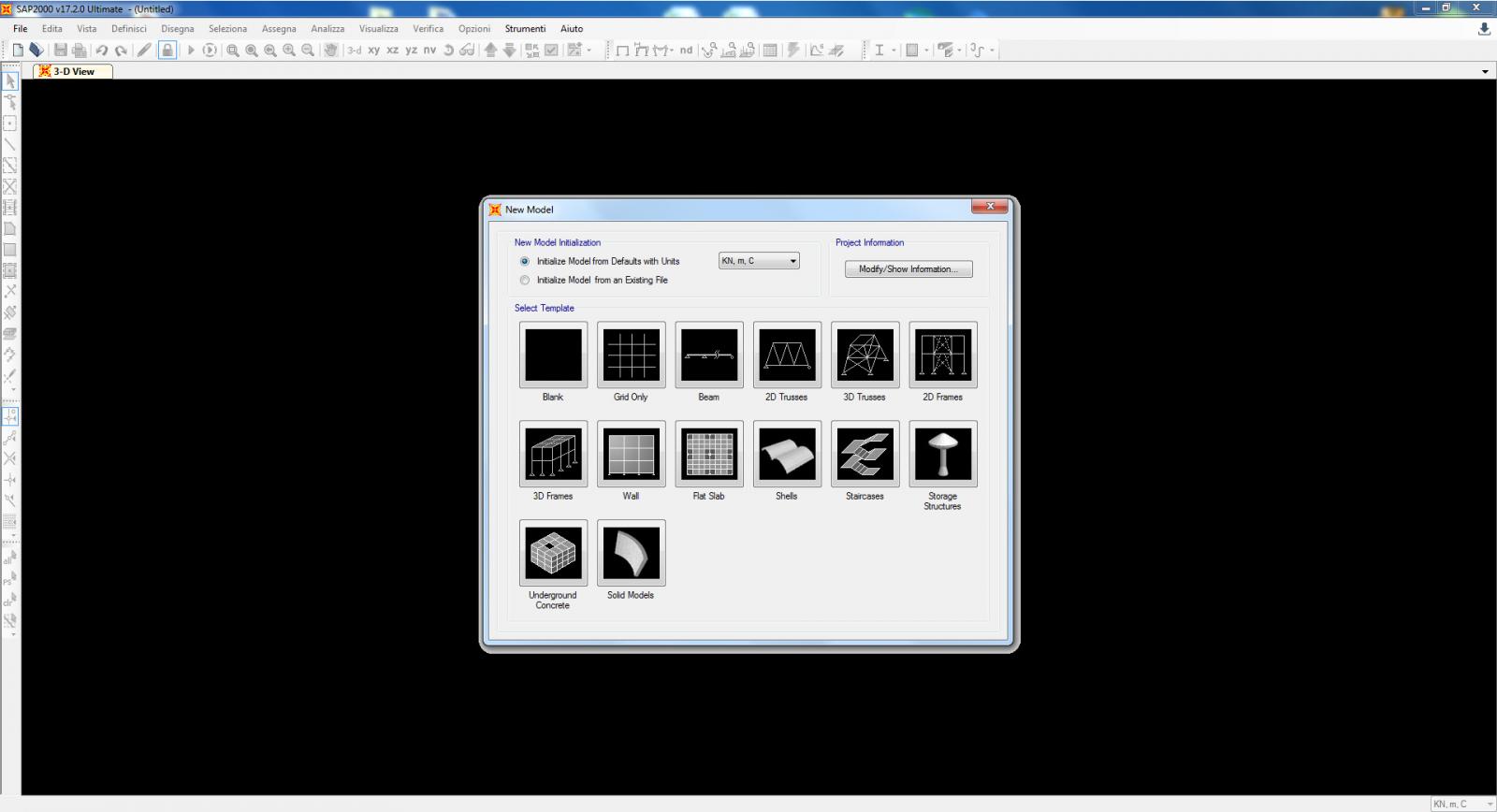

2. Imposto la griglia per il mio modulo iniziale. Assegno come valore nelle direzioni x,y,z 2, ovvero il numero di colonne e righe che userò nel modulo. Decido la lunghezza dei miei frame, aste della travatura reticolare spaziale, di 2m nelle direzioni x e y e 4m nella direzione z.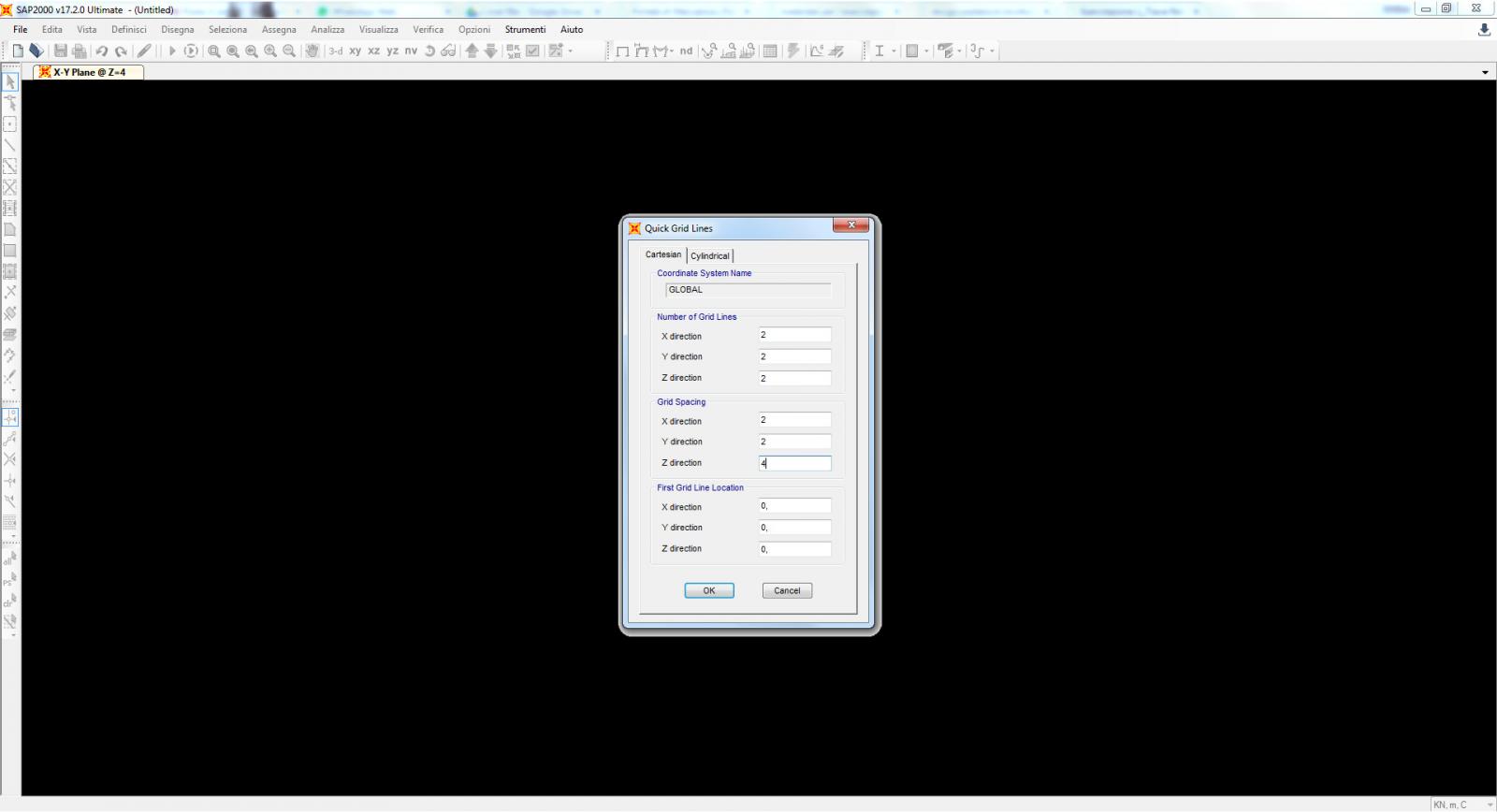

3. Costruisco il modulo della struttura, una piramide con il vertice verso il basso di base 2x2 e altezza 4, successivamente copierò  il modulo fino ad ottenere la struttura complessiva facendo attenzione nella fase di copia a non copiare frame che altrimenti si sovrapporrebbero.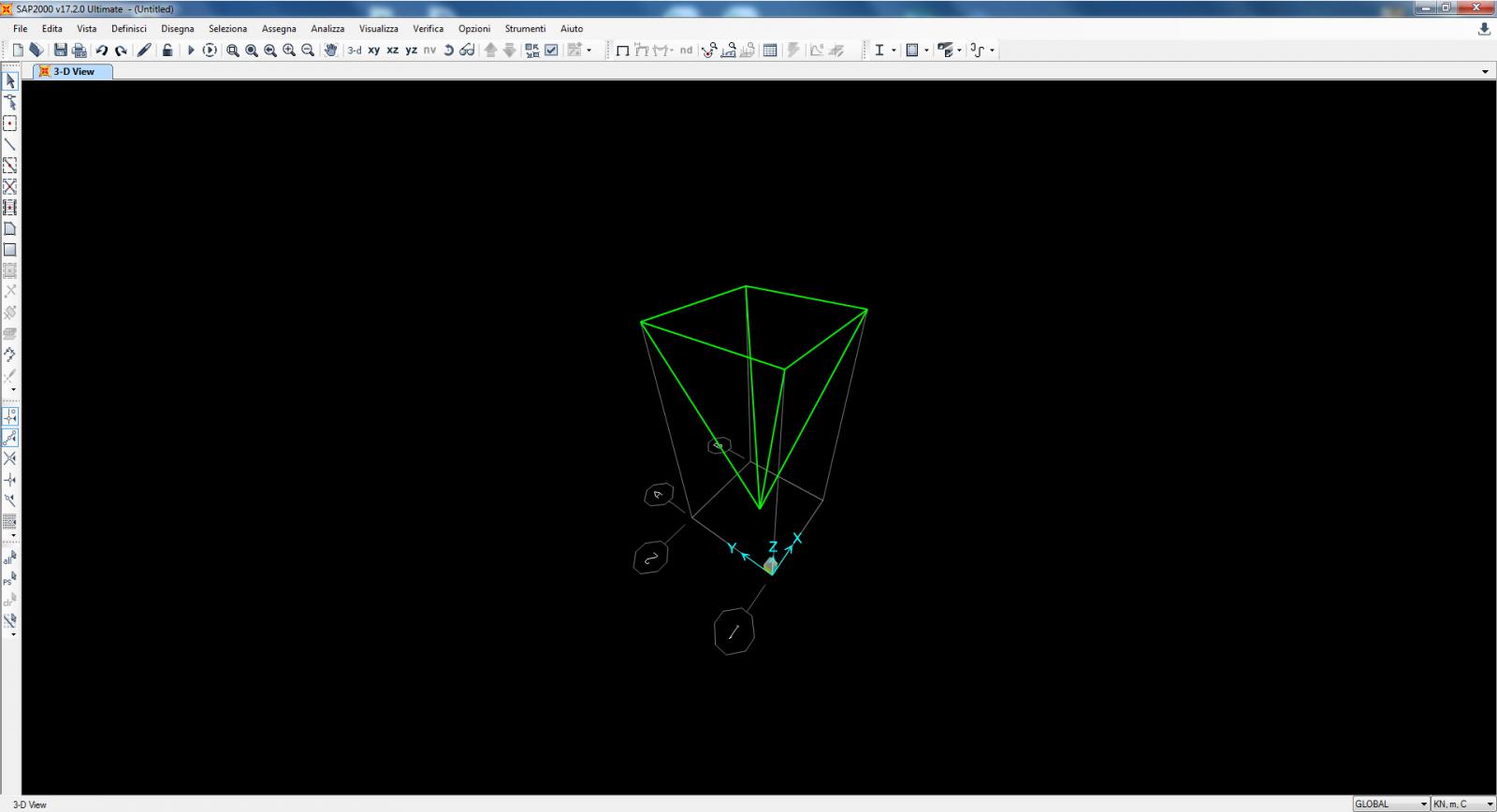

4. Eseguo il rilascio dei momenti nella struttura sicché essendo tutte cerniere interne il momento in esse sarà nullo. [Assign -> Frame -> Releases; spunto il momento di inizio e fine in 22 e 33].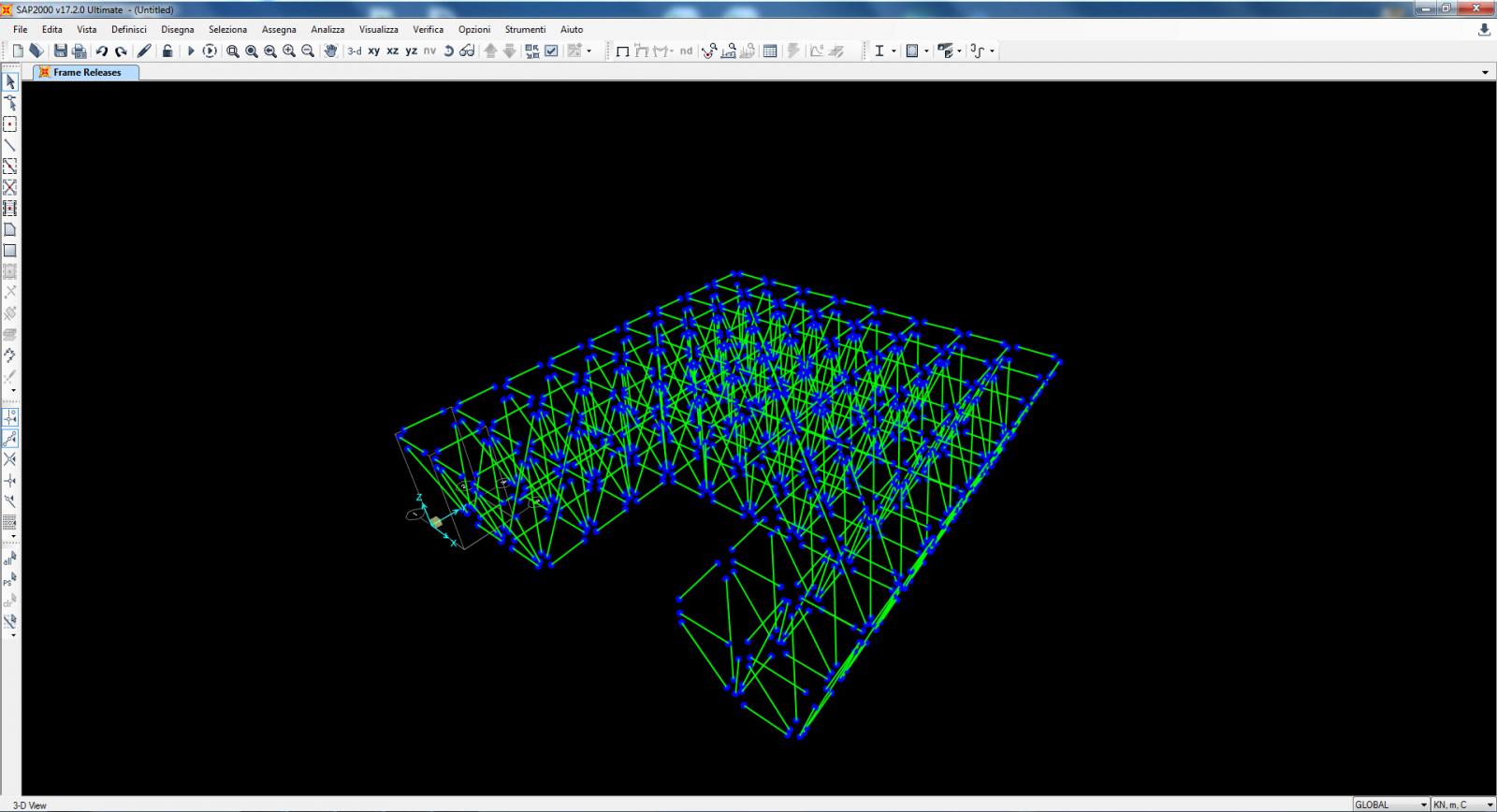

5. Definisco la sezione delle mie aste [Define -> Section Propreties -> Frame Sections; metto “Add new property -> Pipe]. Fatto questo la assegno alla mia struttura.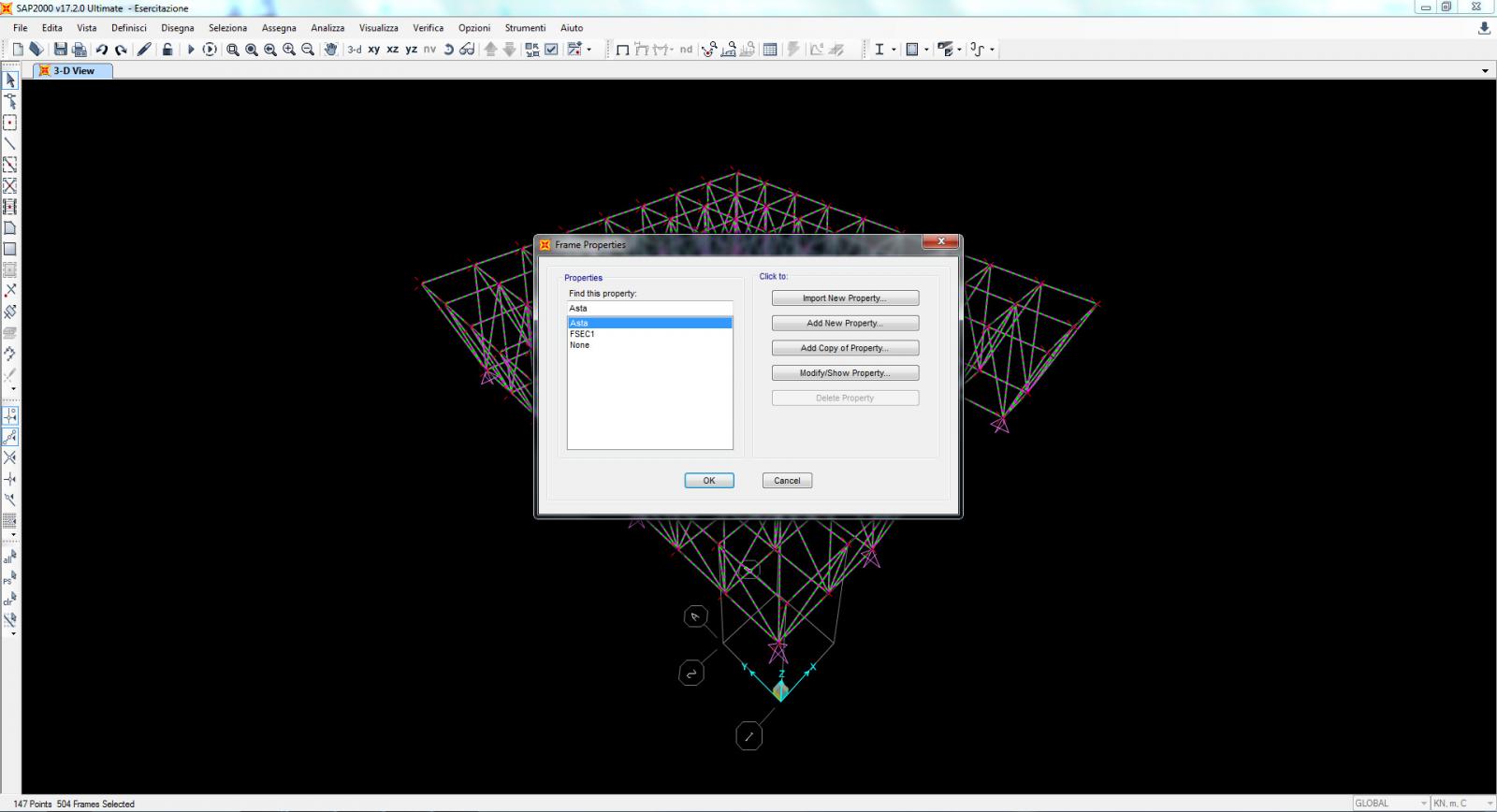

6. Assegno i vincoli alla struttura. Mi sposto sul piano xy al livello z=0. Seleziono i nodi dove applicherò i vincoli e imposto la cerniera come vincolo. [Assign -> Joint -> Restraints].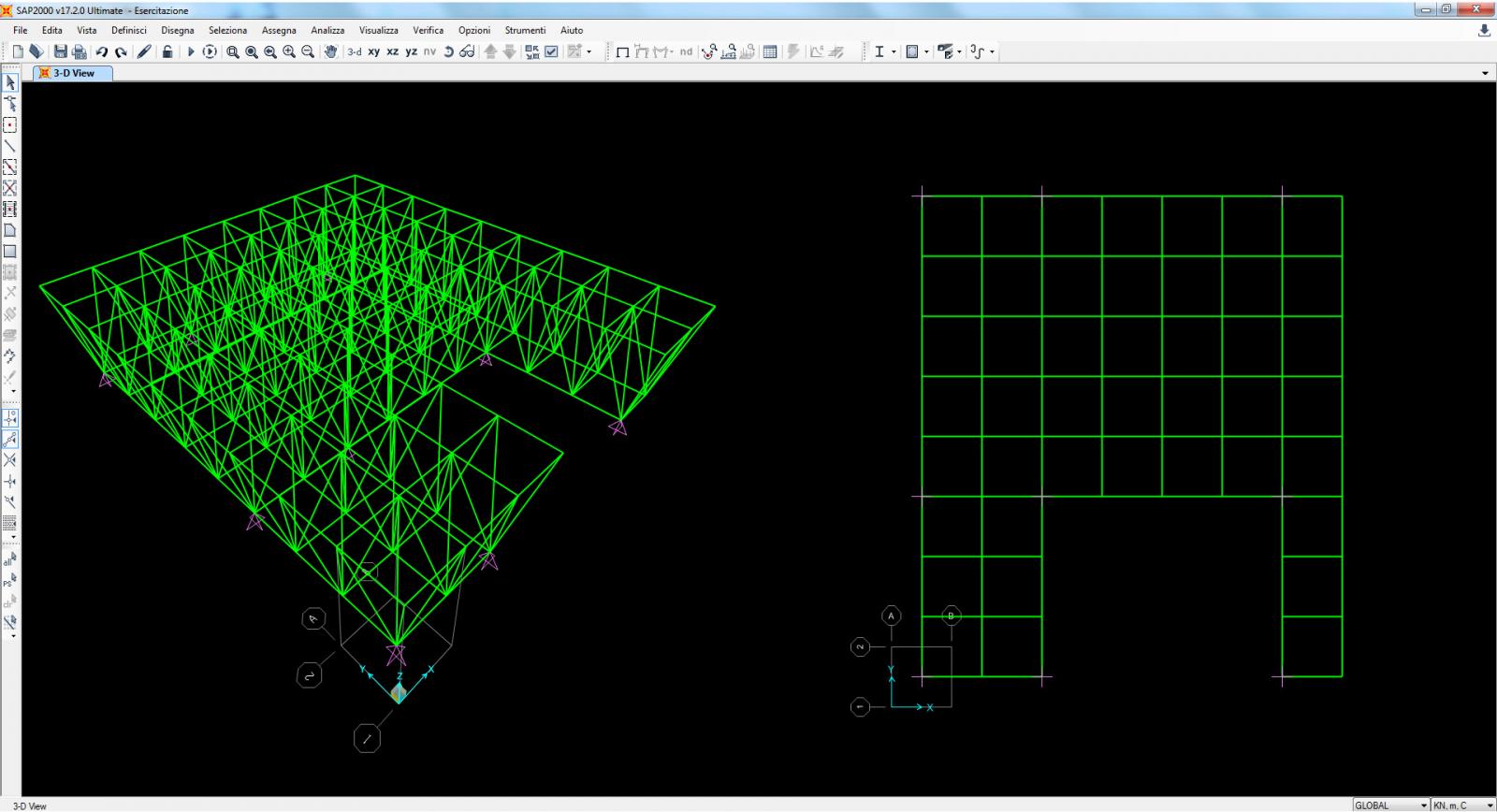

7. Definisco i casi di carico [ Define -> Load patterns] levando il peso proprio e dando un nome alla mia forza (F). Successivamente mi sposto nel piano xy con z=4 e assegno questo carico su ogni nodo della struttura definendo il suo valore con F=-200 rispetto all’asse z, negativo in quanto la sua direzione è verso il basso (nei nodi esterni dimezzo il valore). [Assign -> Joint Loads -> Forces].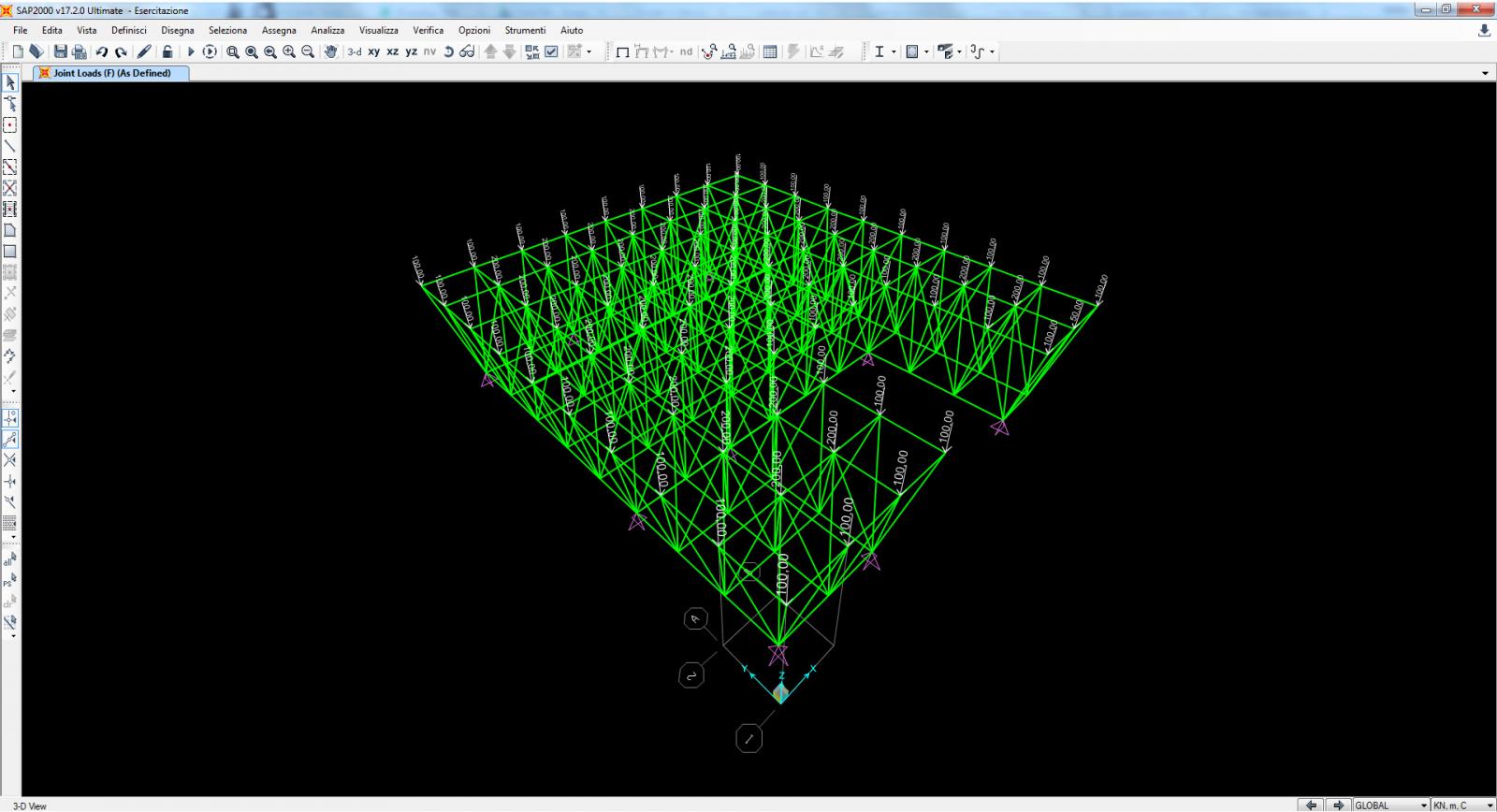

Analisi del Modello

8. Faccio partire l’analisi del modello, facendo attenzione ad eseguire solo l’analisi del caso di carico di cui ho bisogno (F).  8.1. Il programma mi mostra i risultati di deformazione dell’analisi. 8.2. Visualizzo il grafico di sforzo normale di cui successivamente mi ricaverò una tabella, per sicurezza controllo i grafici di taglio e momento, i quali dovranno essere uguali a zero se ho eseguito bene tutti i passaggi.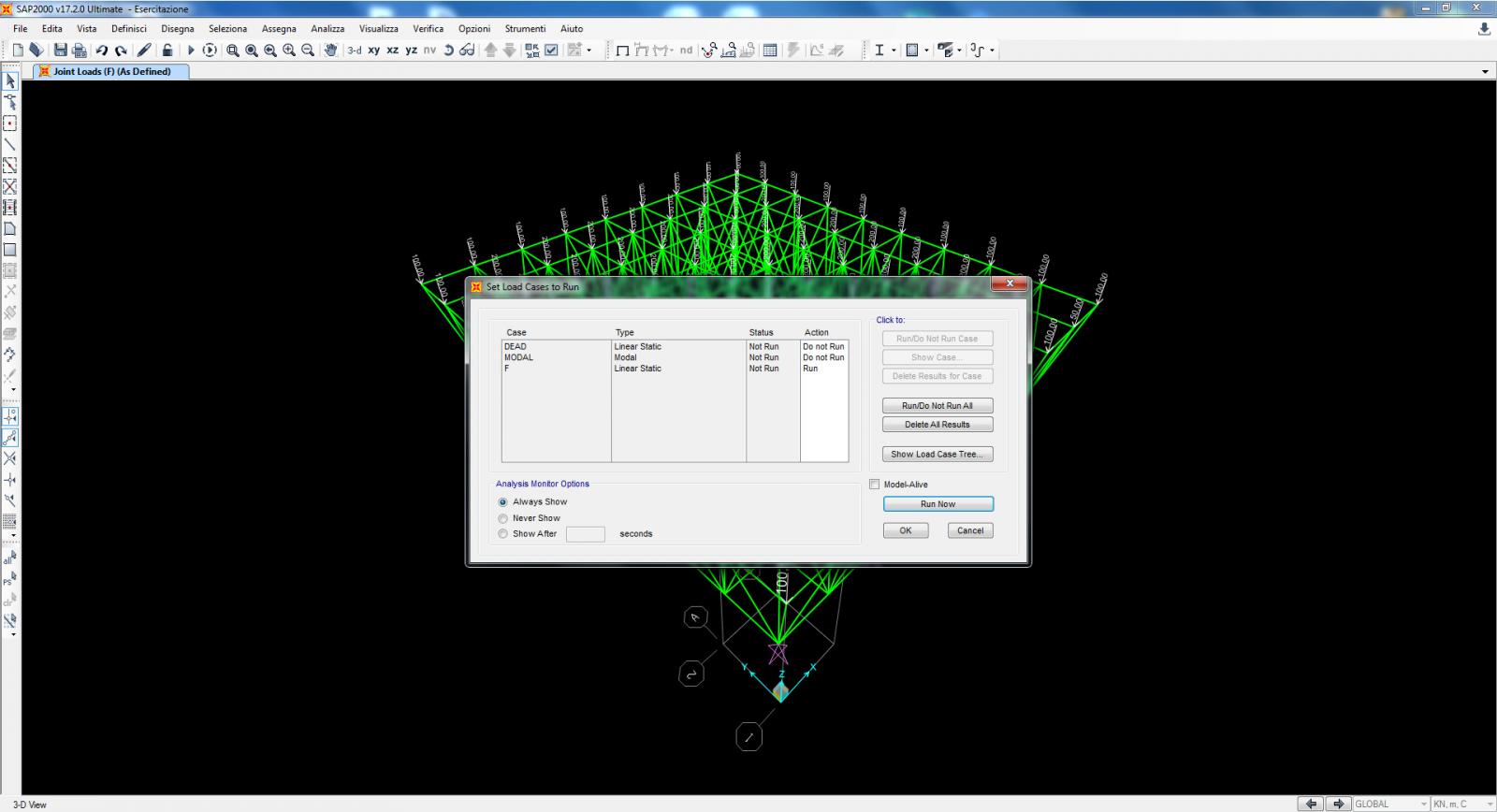

8.1. Il programma mi mostra i risultati di deformazione dell’analisi.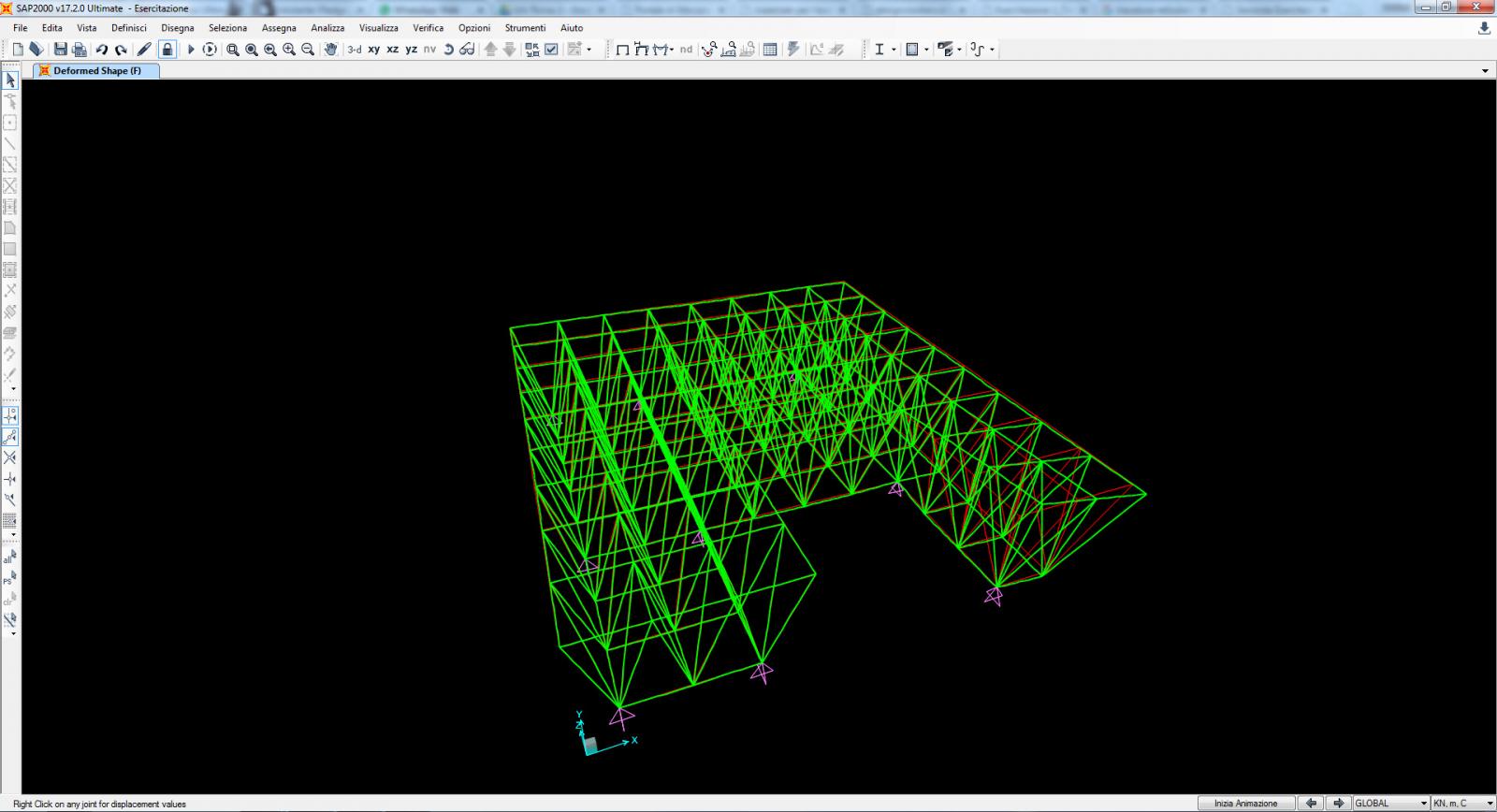 

8.2. Visualizzo il grafico di sforzo normale di cui successivamente mi ricaverò una tabella, per sicurezza controllo i grafici di taglio e momento, i quali dovranno essere uguali a zero se ho eseguito bene tutti i passaggi.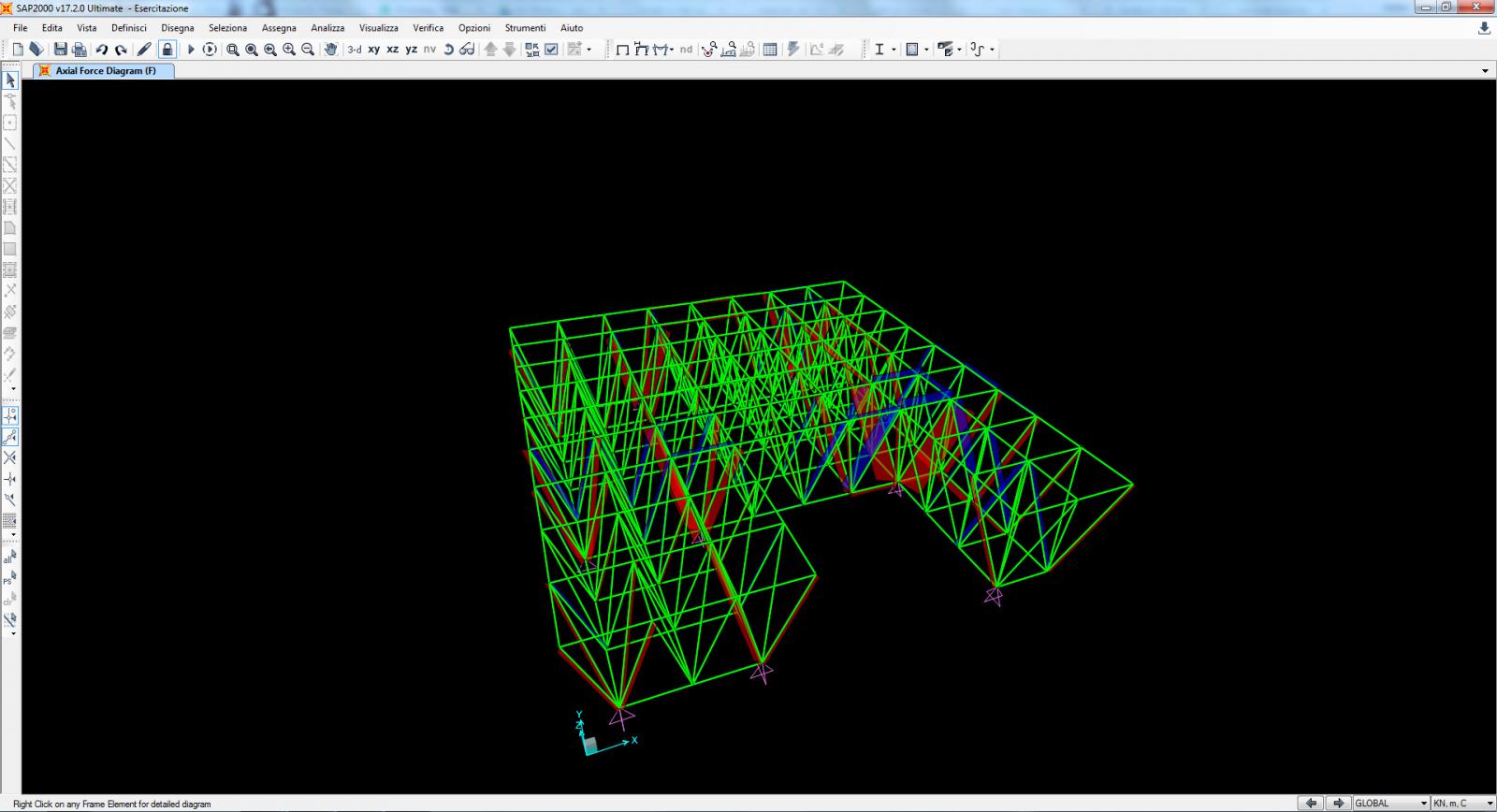

9. Apro le tabelle [Ctrl+T] con i risultati numerici della mia analisi impostando il caso di carico che ho analizzato. Utilizzerò la tabella “Element Forces – Frames”. Seguentemente la esporto in formato .xls per poterla aprire su Excel.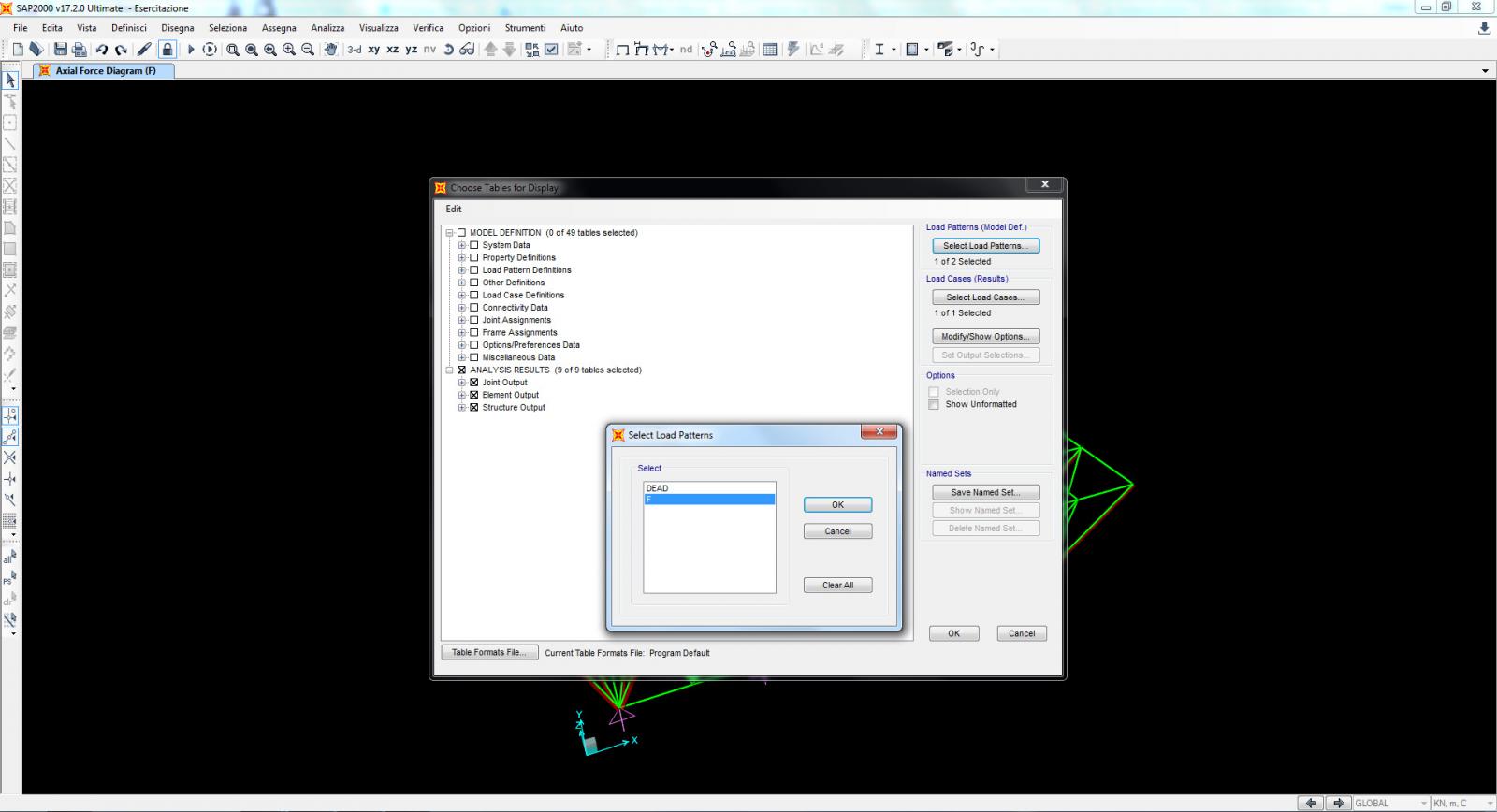

Dimensionamento Struttura

10. Dopo aver ordinato il foglio Excel individuo gli sforzi normali di trazione (+) e di compressione (-). Le lunghezze delle mie aste, essendo il modulo piramidale, sono: orizzontali= 2m, diagonali= 4,243m. Trovo gli ultimi dati che mi mancano: F_yk = 235 Mpa (scelto in base alla classe dell’acciaio), Y_m = 1,05 (coefficiente di sicurezza dell’acciaio), E= 210000 Mpa (Modulo di elasticità), ß = 1 (coefficiente dipendente dai vincoli), Ora ho tutti i dati che mi servono per compilare la tabella.

11. A questo punto devo usare la tabella in due modi diversi:

Per le aste sottoposte a una forza normale di trazione (+) userò la formula: A_min = N • 10 / F_yd .Otterrò una Area minima (A_min) di progetto che dovrò ingegnerizzare, ovvero assegnare all’asta un profilo scelto dal profilario di Area superiore all’A_min. Devo fare attenzione anche a non avere un λ > 200, in quel caso dovrò usare un profilo maggiore, in quanto mi servirà un raggio di inerzia più grande.

Per le aste sottoposte a una forza normale di compressione (-) devo usare un metodo leggermente diverso. Dovrò valutare l’A_min e l’I_min di progetto ed entrambe dovranno essere minori dell’area del profilato, questo perché a compressione c’è rischio che l’asta si curvi. Anche in questo caso λ dovrà essere minore di 200. Per trovare λ*, ρ_min e I_min userò queste formule: λ*= π​ • √(E / F_yd)  ; ρ_min= ß • l • 100 / λ* ; I_min= A_min • ρ_min²