ESERCITAZIONE_2_Valerio Minella

L’analisi descritta dall’esercitazione che segue verte al calcolo del dimensionamento di una trave con tre diversi materiali tecnologici: acciaio, legno e calcestruzzo armato.
L’elemento preso come oggetto di studio è la trave più sollecitata di un impalcato strutturale che rispecchia un livello di un edificio ad uso residenziale meglio descritto dagli elaborati allegati di seguito:
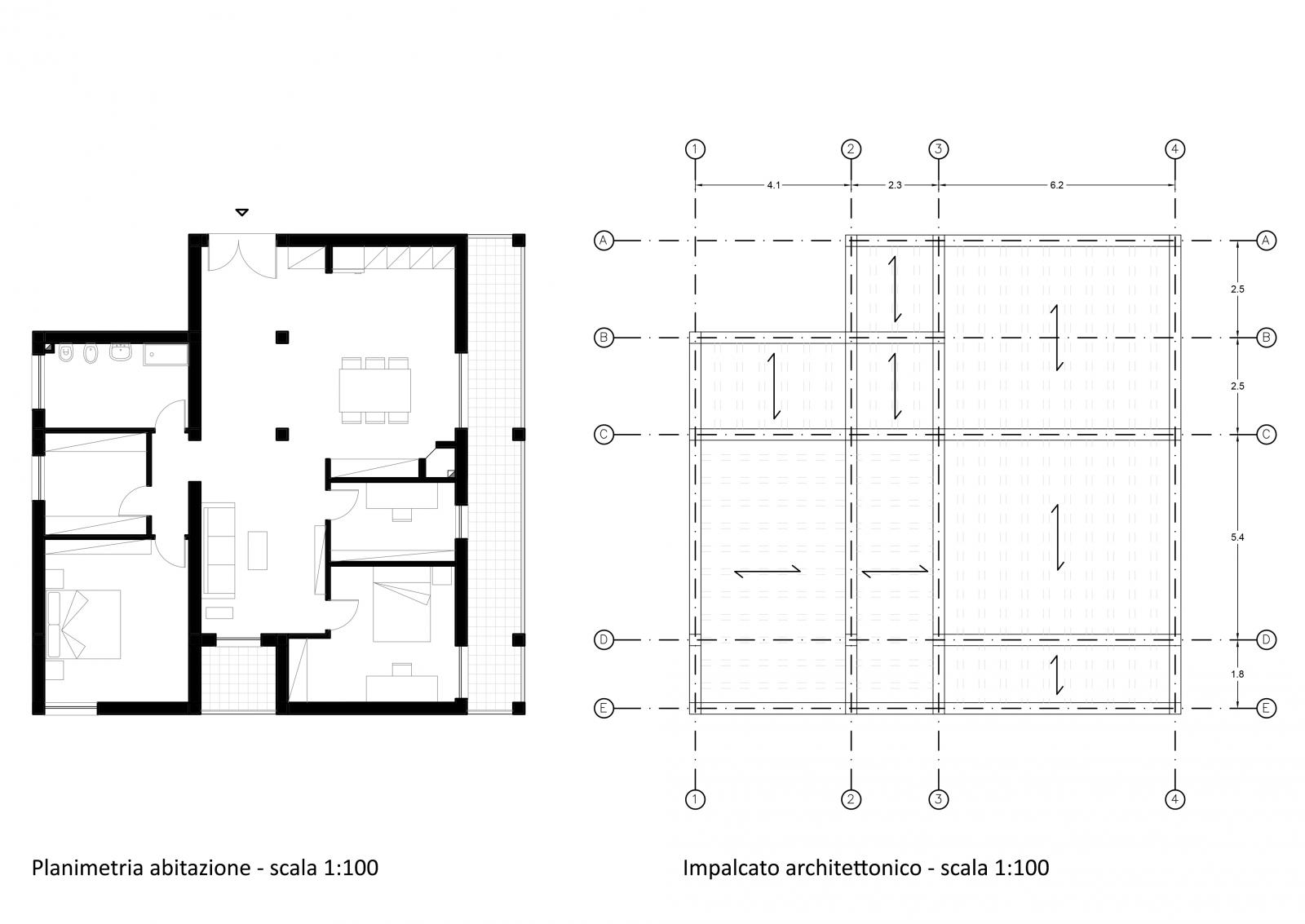
Step-1: Evidenziati gli elementi orizzontali principali, secondo la tessitura del solaio sovrastante, sono state calcolate tutte le aree d’influenza degli stessi con le relative luci e superfici, per permettere la localizzazione del più sollecitato;
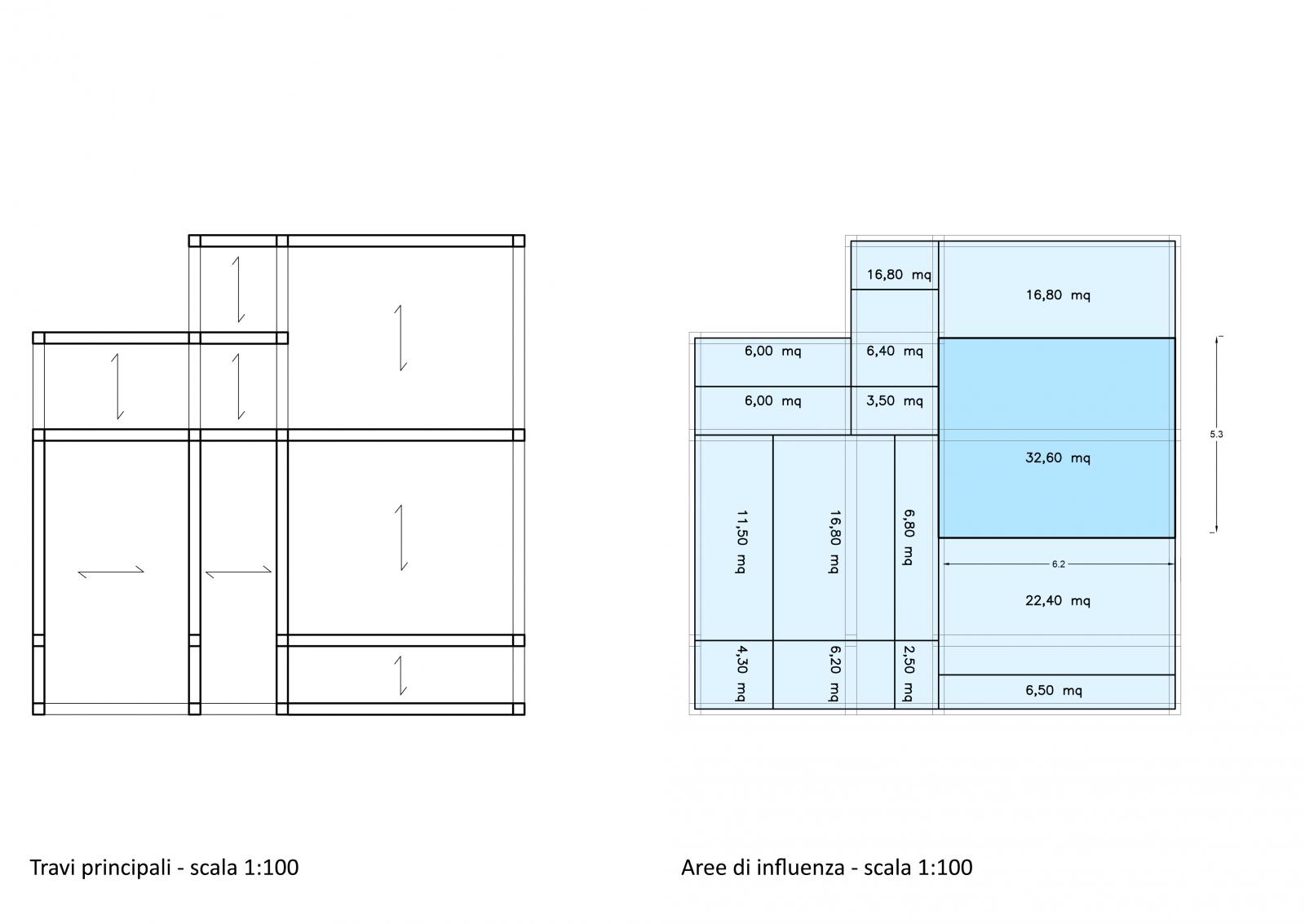
LUCE = 6,20 m
AREA DI INFLUENZA = 32,60 mq
Step-2: Per procedere con i relativi calcoli di dimensionamento dell’elemento evidenziato nell’immagine precedente si analizzano i carichi distribuiti agenti sullo stesso: qs, qp, qa:
Questi carichi, normati dal D.M.14-01-2008, consentono di ricavare il carico totale (qu) calcolato mediante una combinazione dei precedenti impostata secondo la natura dell’analisi che si vuole effettuare, in questo caso allo Stato Limite Ultimo (SLU):
qu = γG1 qs + γG2 qp + γG3 qa
I termini γG1, γG2, γG3 sono coefficienti parziali dei pesi analizzati, imposti dalla normativa e impostati secondo la tabella che segue, prendendo in esame la colonna STR che analizza gli elementi strutturali che si stanno calcolando;
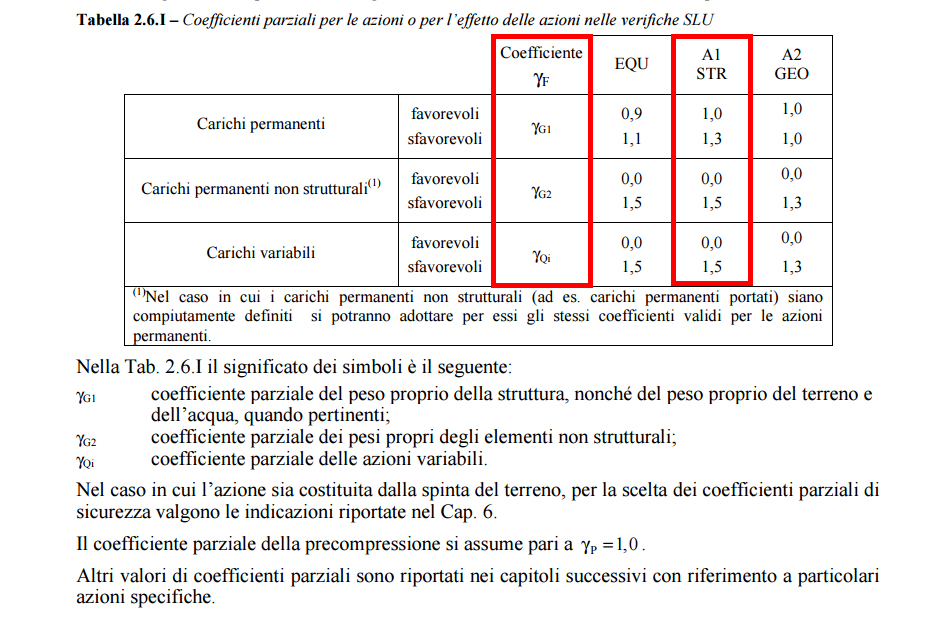
Quindi la combinazione sarà: qu = 1,3 qs + 1,5 qp + 1,5 qa
I carichi qs, qp, qa [KN/mq] rispecchiano rispettivamente:
(qs) carico strutturale ovvero il carico dovuto al peso proprio di tutti gli elementi che svolgono una funzione portante;
(qp) carico permanente ovvero il carico dovuto al peso proprio di tutti gli elementi che gravano sulla struttura portante per il suo intero periodo di vita e che non svolgono alcuna funzione strutturale;
(qa) carico accidentale ovvero i carichi legati alla funzione svolta dall’edificio. Questo carico ha una natura aleatoria, basata su calcoli statistici normati e tabellati che vengono svolti prendendo in considerazione funzione, vita e azioni esterne (quali ad esempio il sisma).
Nel caso dell’elemento analizzato in questa esercitazione, avendo preso un edificio a uso residenziale il carico accidentale sarà:
qa = 2 KN/mq
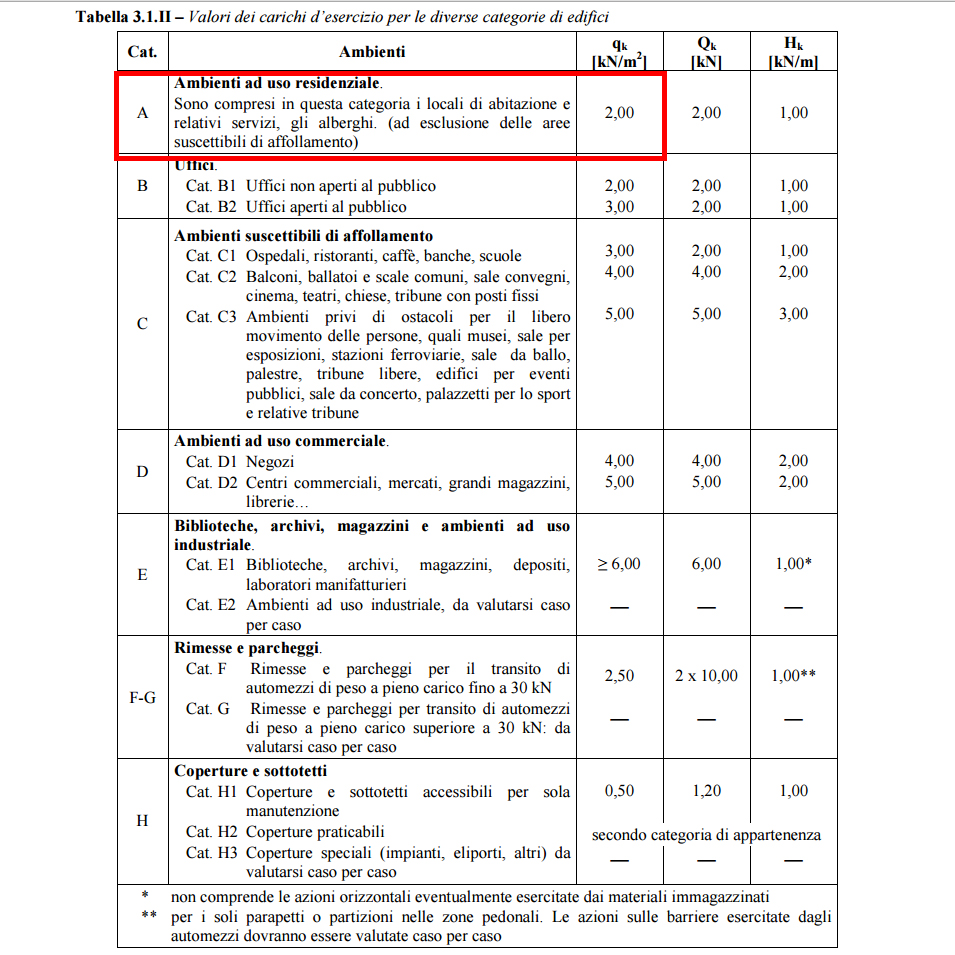
Per il calcolo dei carichi qs e qp, essendo questi legati alla natura degli elementi compresi nel pacchetto tecnologico del solaio si vanno a scegliere tre tipologie differenti dello stesso a seconda del materiale scelto per il dimensionamento della trave.
Le tipologie tecnologiche dei solaio sono stati scelti in base all’abaco dei modelli UNI10355:
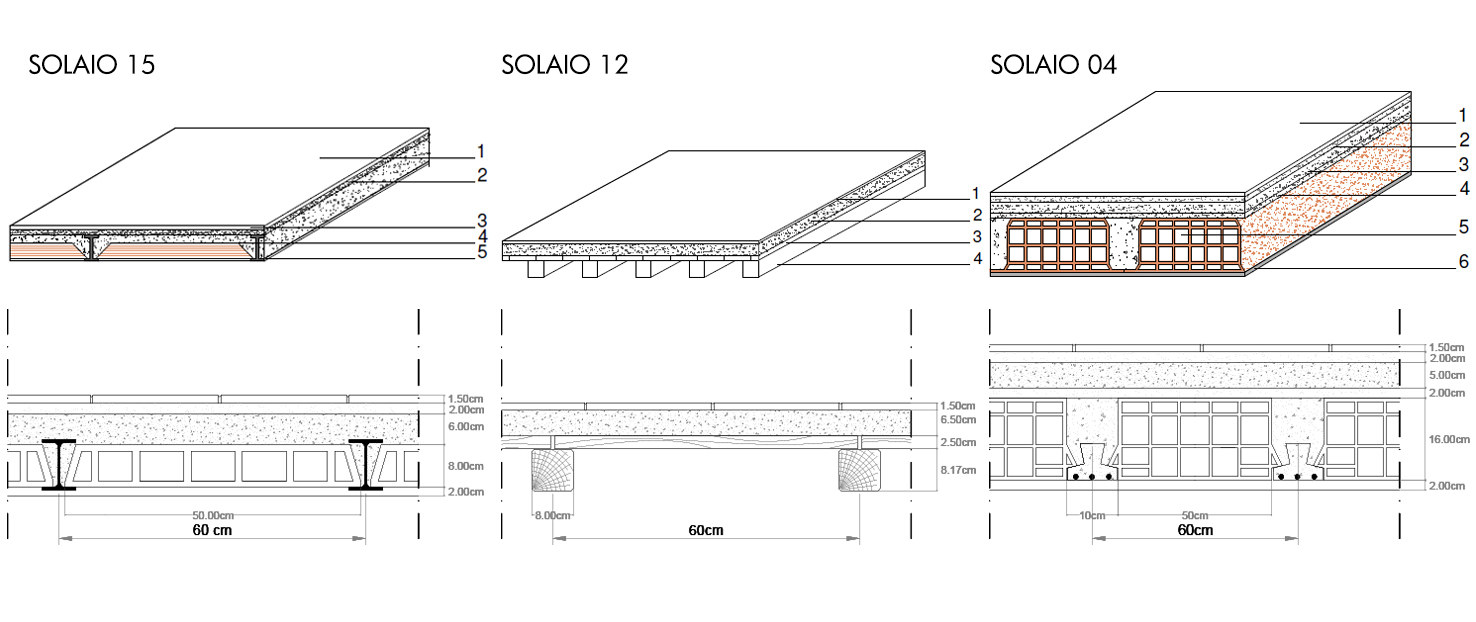
SOLAIO-15 PROFILATI ACCIAIO E TAVELLONI – dimensionamento in acciaio;
SOLAIO-12 SOLAIO IN LEGNO – dimensionamento in legno;
SOLAIO-04 LATERO CEMENTO CON BLOCCHI COLLABORANTI – dimensionamento in calcestruzzo armato.
ACCIAIO

Step-3 acciaio: Ricavati quindi i carichi qs, qp e qa possiamo inserire questi dati all’interno di un foglio excel che permette di effettuare il calcolo di qu, con la formula descritta sopra ed avere quindi il carico complessivo che grava sulla trave da dimensionare.
Essendo i carichi qs, qp e qa espressi in KN/mq, anche qu che si otterrà sarà espresso con la stessa dimensione, bisogna quindi moltiplicare il valore ottenuto di qu per la dimensione perpendicolare alla luce dell’elemento (chiamata nell’immagine come interasse) ottenendo quindi un valore espresso in KN/m ovvero un carico uniformemente distribuito lungo la luce della trave;
 Come riportato nella stringa qui sopra il qu sarà formato dalla seguente operazione:
Come riportato nella stringa qui sopra il qu sarà formato dalla seguente operazione:
qu = (1,3 qs + 1,5 qp + 1,5 qa) x interasse
Step-4 acciaio: Si può ricavare ora il momento massimo (MMAX) dell’elemento sostenendo che si tratti di una trave appoggiata-appoggiata il cui momento massimo si trova alla mezzeria della luce e equivale a ql2/8, dove “l” viene sostituito dalla luce dell’elemento e “q” dal carico qu ricavato nello Step-3 acciaio;

Step-5 acciaio: Sapendo il valore del momento massimo che agisce sulla trave, per il dimensionamento si utilizza la formula di Navier:
σmax = (Mmax/Ix) ymax
dove Ix è il momento d’inerzia della sezione secondo l’asse x e ymax è la distanza delle fibre che si considerano rispetto all’asse y.
Essendo i profilati in acciaio tutti ingegnerizzati e tabellati, servirà un parametro minimo su cui basare la scelta della sezione più opportuna, quindi, una volta scelto il tipo di materiale (quindi una resistenza caratteristica fyk ) si avrà bisogno del modulo di resistenza (Wx) che è:
Wx = Ix/ ymax
Che dipende dalle caratteristiche geometriche della sezione, opportunamente tabellato e calcolato per ogni profilo ingegnerizzato.
Si può quindi sintetizzare il tutto con la formula:
Wmin = Mmax/fd
dove fd è la resistenza di progetto del materiale acciaio scelto, ricavata da fd = fyk / γm (con γm = 1.05 coefficiente di sicurezza normato), e σmax = fd e Wmin il parametro utile per la scelta del Wdesign;
Wmin < Wdesign
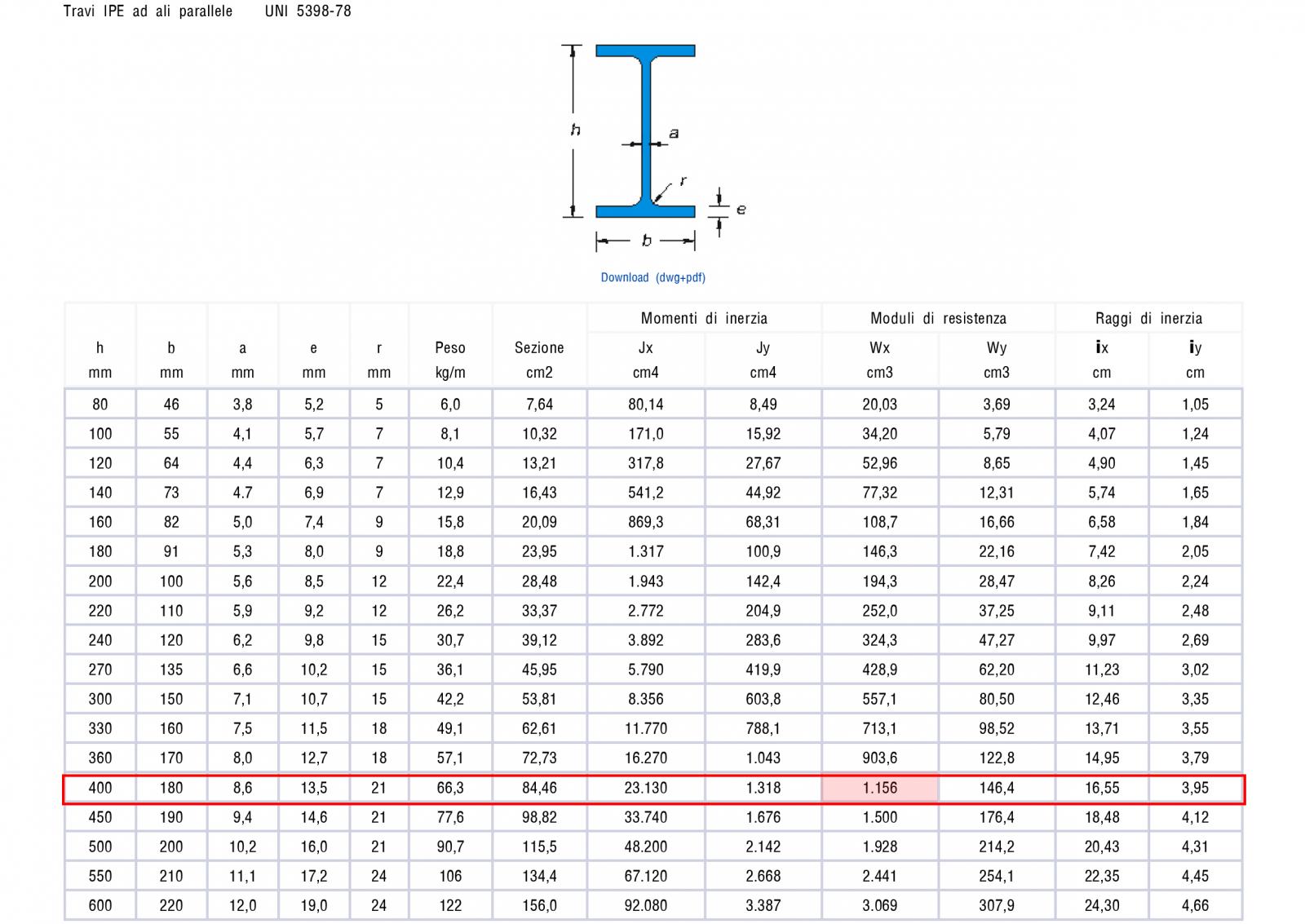
Step-6 acciaio: Da profilario (in questo caso si è scelto il catalogo dei profilati IPE dell’azienda Oppo) si può ricavare la sezione che meglio risponde alle esigenze strutturali, economiche e di progetto.

LEGNO
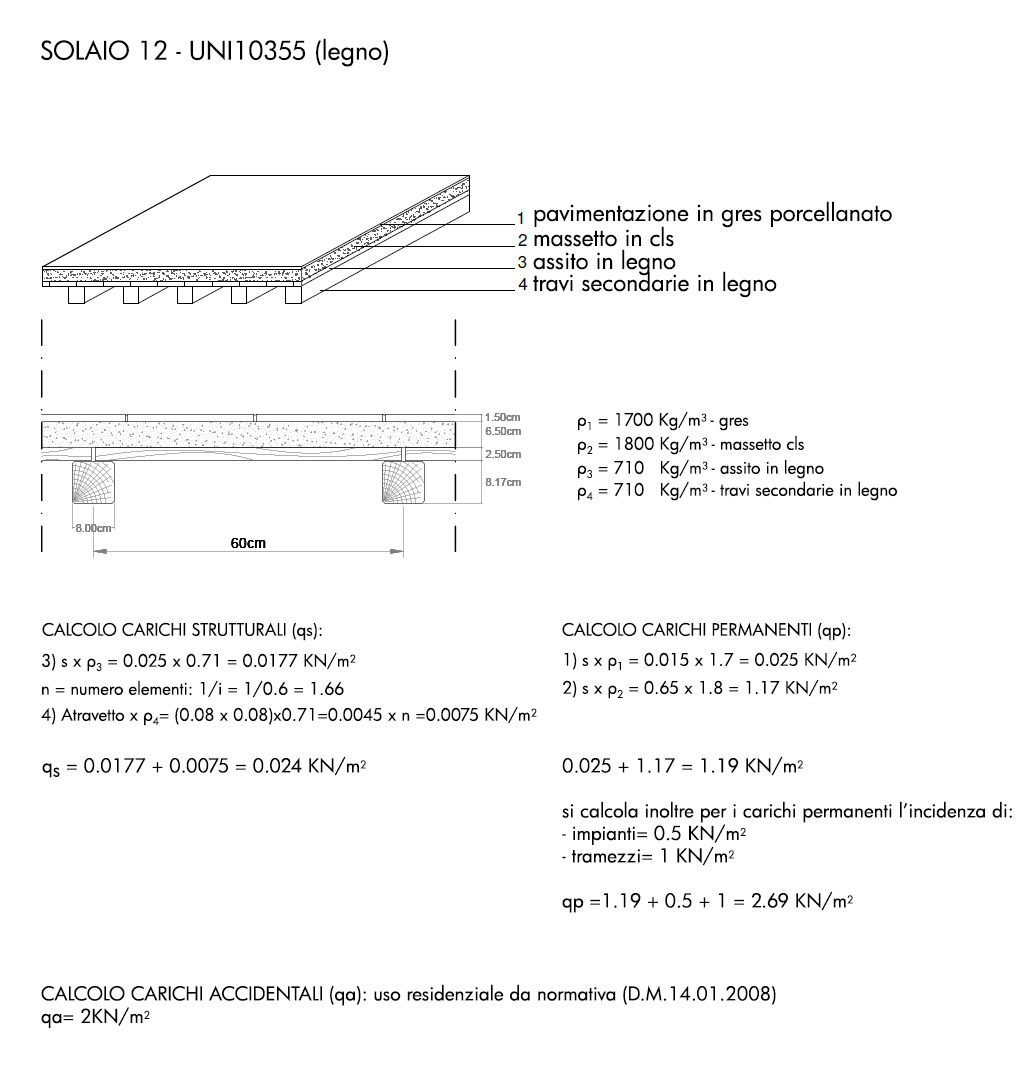
Step-3/4 legno: Come per il dimensionamento in acciaio anche per il legno si segue il metodo utilizzato nello Step-3 acciaio per il calcolo di qu e nello Step-4 acciaio per ricavare il momento massimo;
qu = (1,3 qs + 1,5 qp + 1,5 qa) x interasse
Mmax = ql2/8

Step-5 legno: Ricavato il momento massimo “Mmax” si procede con il determinare la resistenza di progetto del legno scelto per il dimensionamento:
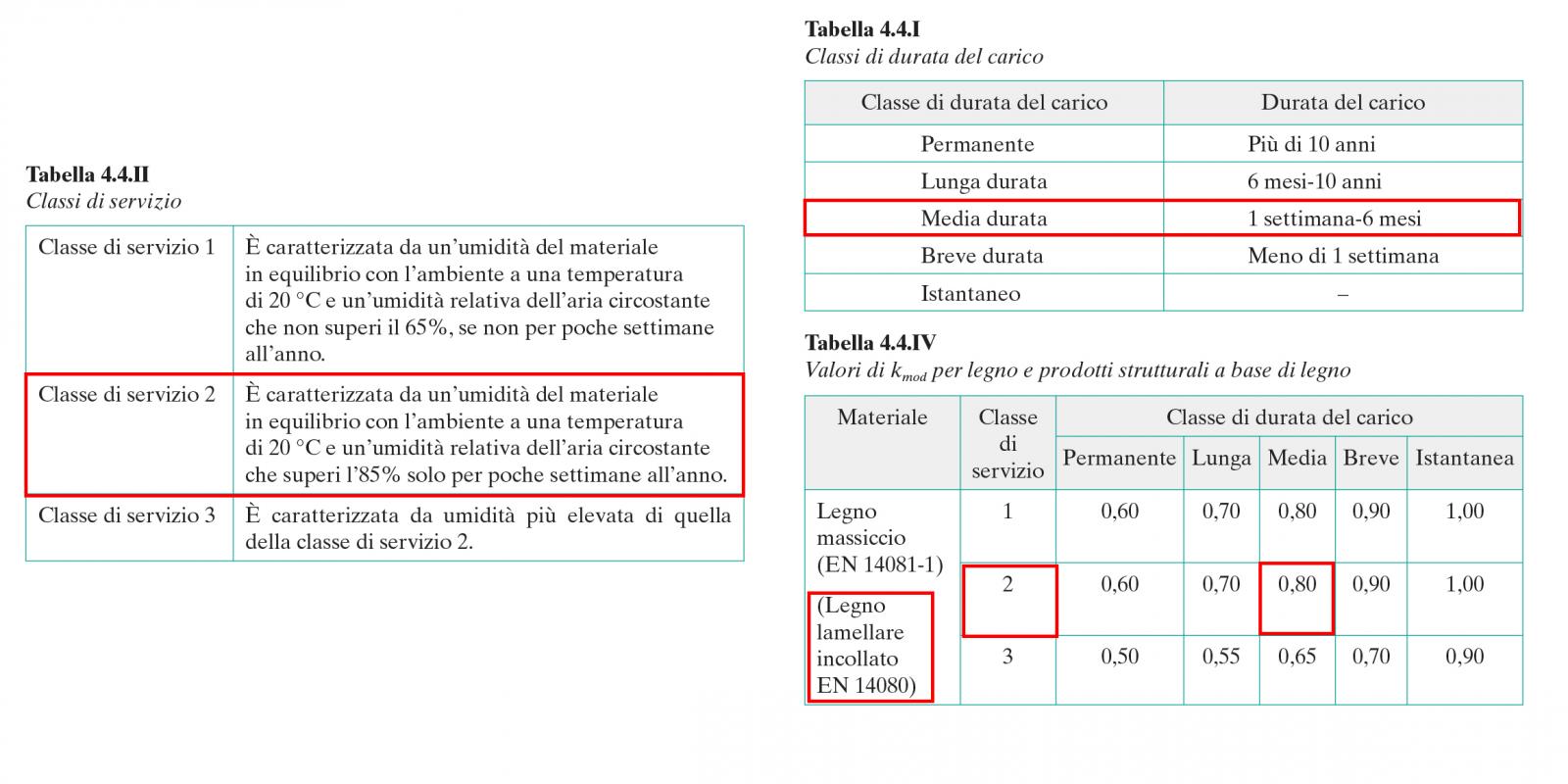
fd = Kmod fmk / γm
la resistenza di progetto del materiale legno viene calcolata in parte come quella dell’acciaio (fmk / γm), con γm = 1.50 (per cautela verso un materiale che viene ingegnerizzato ancora da poco tempo nel paese) e fmk = resistenza caratteristica a flessione, il quale si differenzia dalla resistenza a trazione e compressione del legno poiché questo essendo un materiale ortotropo non ha resistenze uguali per ogni direzione, ed in maniera differente data la presenza di Kmod quale coefficiente diminutivo della resistenza del materiale che considera sia la permanenza del carico sull’elemento che si analizza sia le condizioni di umidità dell’ambiente su cui questo viene realizzato;
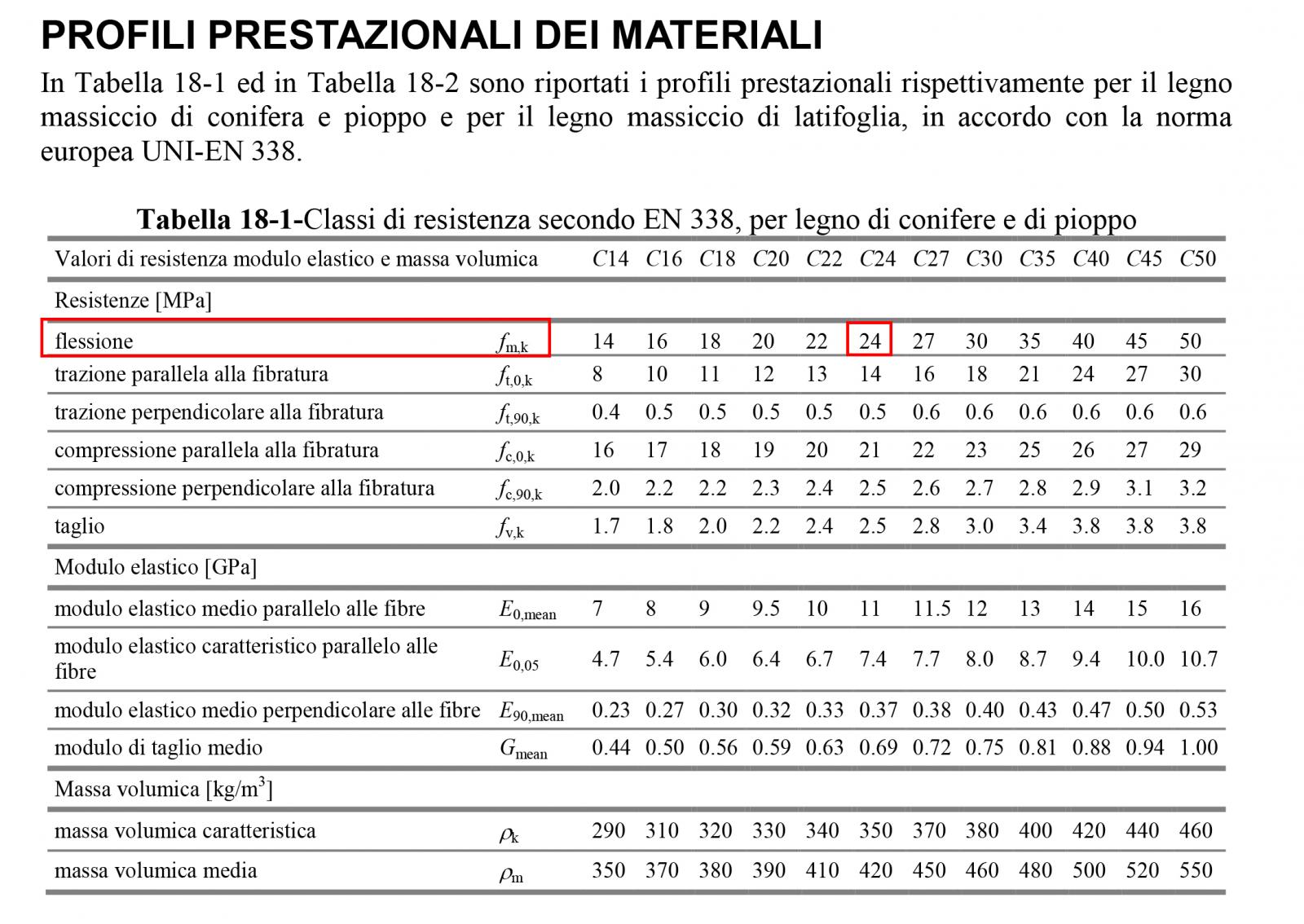

Step-6 legno: Scelto il materiale e ricavata la tensione di progetto si procede determinando una dimensione della base (b) della sezione rettangolare che si vuole dimensionare, lasciando come unica incognita da ricavare l’altezza (h). Come detto prima, poiché il legno è un materiale ingegnerizzato le sue sezioni sono tabellate (in maniera diversa tra le aziende) quindi si può scegliere la base da profilari o ipotizzarla;
b = 35 cm
Riprendendo i concetti espressi per il dimensionamento della sezione in acciaio:
σmax = (Mmax/Ix) ymax
σmax =fd
quindi:
fd = Mmax / Wmin
Ix per sezioni rettangolari è Ix = bh3/12 ovvero Wmin = Ix / ymax quindi Wmin = bh2/6 per ymax = h/2, posso ricavare ora il valore dell’altezza con la formula:
Mmax / fd = Wmin
Mmax / fd = bh2/6
h2 = 6 Mmax / bfd
h2 = RAD2 (Mmax/b) x RAD2 (6/fd)
poiché si è scelto σmax = fd il valore che si otterrà di “h” sarà il valore minimo dell’altezza che di dovrà scegliere per il dimensionamento;
hmin < H

CALCESTRUZZO ARMATO

Step-3/4 c.a.: Come per il dimensionamento in acciaio e legno, si ricava il qu con lo stesso metodo descritto nello Step-3 acciaio/legno e il momento massimo con lo Step-4 acciaio/legno;
qu = (1,3 qs + 1,5 qp + 1,5 qa) x interasse
Mmax = ql2/8

Step-5 c.a.: Per il calcolo della trave in c.a., essendo questa composta da due diversi materiale, si deve scegliere sia un acciaio per l’armatura a trazione sia il calcestruzzo per la sezione rettangolare da dimensionare:
per l’acciaio (B450C)
fd = fyk /γm
dove γm =1,15
per il calcestruzzo, una volta scelta la classe (C25/30)
fcd = αcc x fck/ γc
dove γc = 1,50 , αcc = 0,85 coefficiente riduttivo per le resistenze a lunga durata e fcd resistenza a compressione del calcestruzzo scelto;

Step-6 c.a.: Poiché la sezione che si va a dimensionare è rettangolare, come che per il legno, fissiamo il valore della base b = 35 cm, per poter ricavare il valore dell’altezza Hmin.
L’incognita da ricavare è quindi hu ovvero l’altezza UTILE della sezione, attraverso l’uguaglianza tra triangoli simili nel diagramma delle tensioni, come nella figura, tenendo conto dell’omogenizzazione del materiale acciaio in calcestruzzo, essendo questo dimensionamento composto da due materiali tra loro differenti:

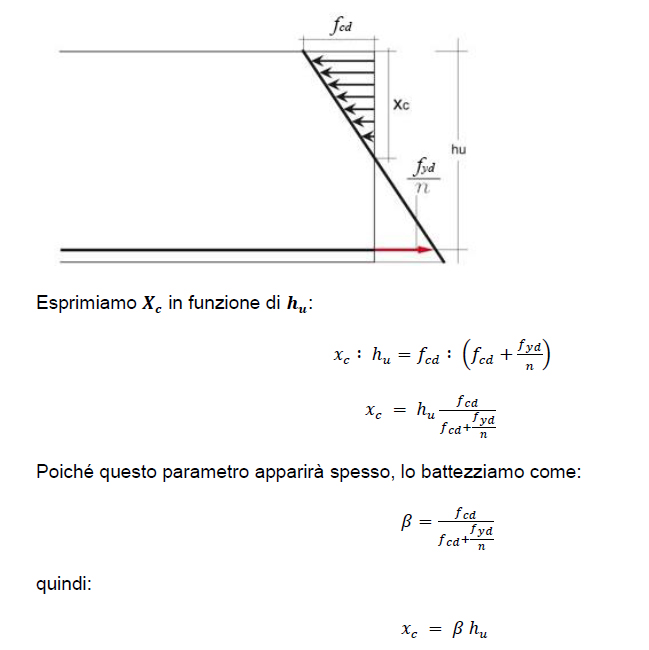
(nella stringa excel il parametro α=β)
Step-7 c.a.: Ottenuto il parametro hu = altezza utile, si fissa δ come distanza tra interasse dell’armatura in acciaio e la sezione “inferiore” del calcestruzzo:
Hmin = hu + δ

Step-8 c.a.: Ricavato Hmin, si va a dimensionare la sezione scegliendo, con b = 35 cm, il valore dell’altezza:
Hdesign > Hmin
(le dimensioni devono essere adattate a misure idonee per la cantierizzazione, poiché il calcestruzzo armato non è ingegnerizzato come il legno e il ferro)
Step-9 c.a.: La sezione in calcestruzzo, a differenza di quella in legno che ha un peso limitato dato il basso peso specifico del materiale stesso (γ=710 Kg/mc) e quella in acciaio molto snella data la grande resistenza del materiale (fyk = 235 MPa), deve essere analizzata anche in base al peso proprio dell’elemento dimensionato, poiché non trascurabile dato l’elevato peso specifico di questo materiale (γ=2500 Kg/mc).
Infatti la seconda riga della stringa qui in basso riporta gli stessi calcoli effettuati per il dimensionamento, calcolando all’interno del qs anche il valore del peso proprio dell’elemento appena dimensionato e serve come verifica al calcolo precedente.




