DIMENSIONAMENTO E VERIFICA DI UN TELAIO IN CLS ARMATO _ Lozonschi_Miloro

• MODELLAZIONE DEL TELAIO

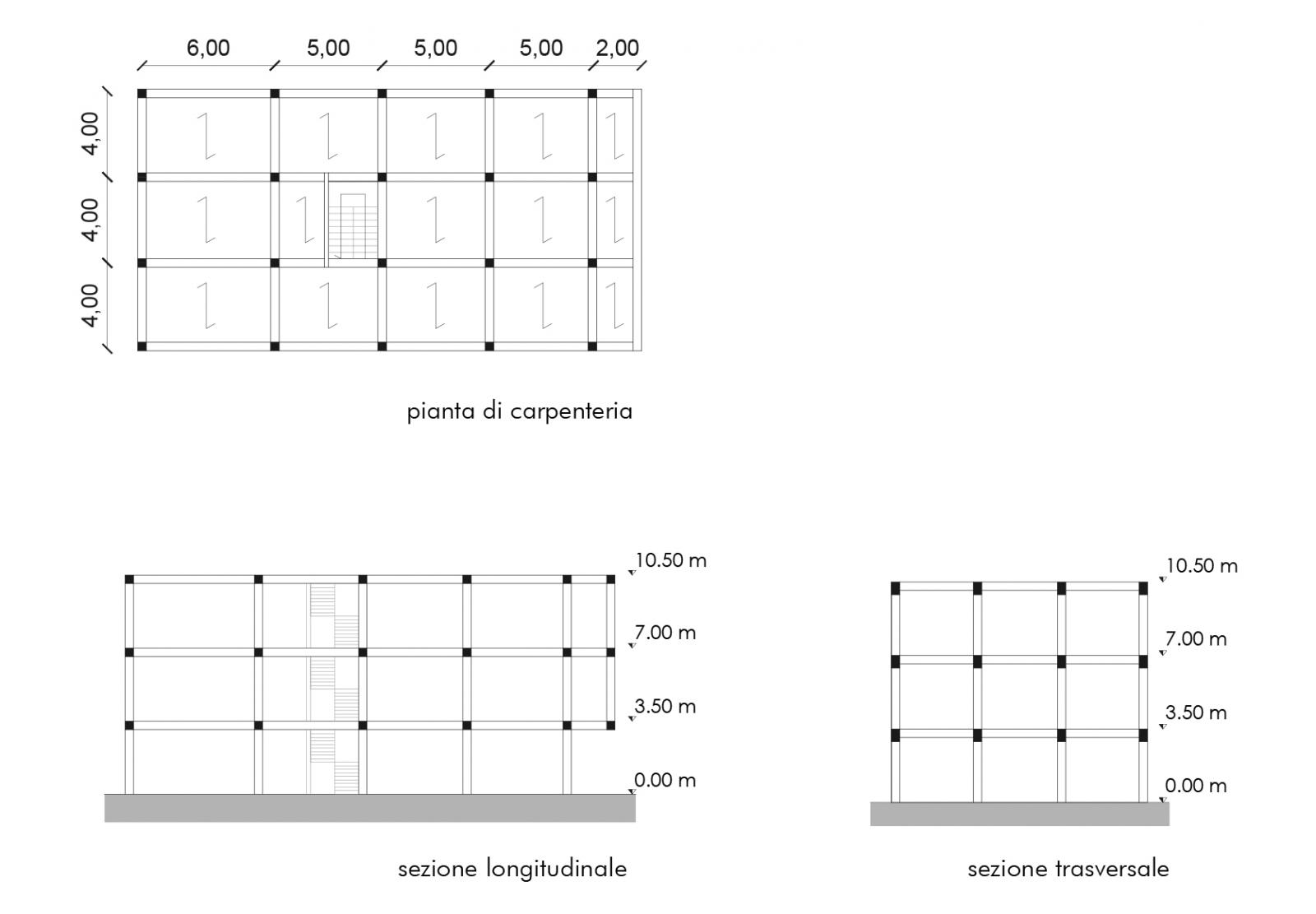
Per la modellazione dell’edificio è stato utilizzato direttamente il software di SAP2000 andando, in seguito al predimensionamento delle sezioni, ad assegnare le informazioni relative al materiale, alle sezioni degli elementi e ai carichi verticali ed orizzontali. Innanzitutto è stata disegnata la struttura del primo livello e poi replicata in altezza fino ad ottenere l’altezza prestabilita dell’edificio. Essendo un telaio di elementi verticali e orizzontali tra loro collegati da nodi rigidi, assegno un vincolo interno (Assign/Joint/Constraint/Diaphragm) e ai pilastri del piano terra il vincolo di incastro esterno al terreno. Assengnando il diaphragm, si impone a tutti i punti un’unica rotazione attorno all’asse z, in modo da ottenere un impalcato rigido.

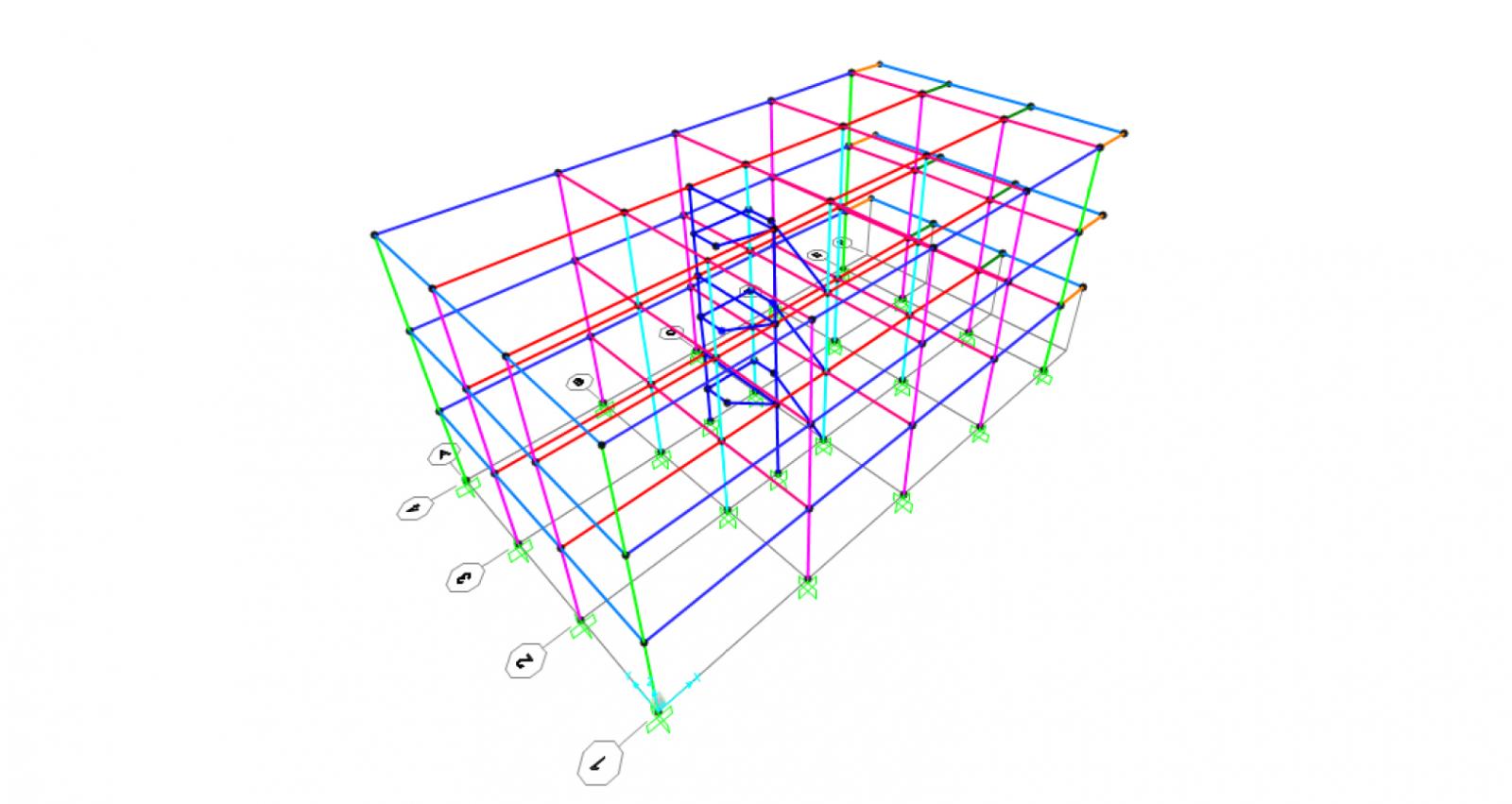
Per facilitare l’assegnazione delle sezioni ottenute dal predimensionamento degli elementi verticali e orizzontali, si creano dei gruppi di selezione per le travi e i pilastri.

• PREDIMESIONAMENTO DELLE TRAVI 

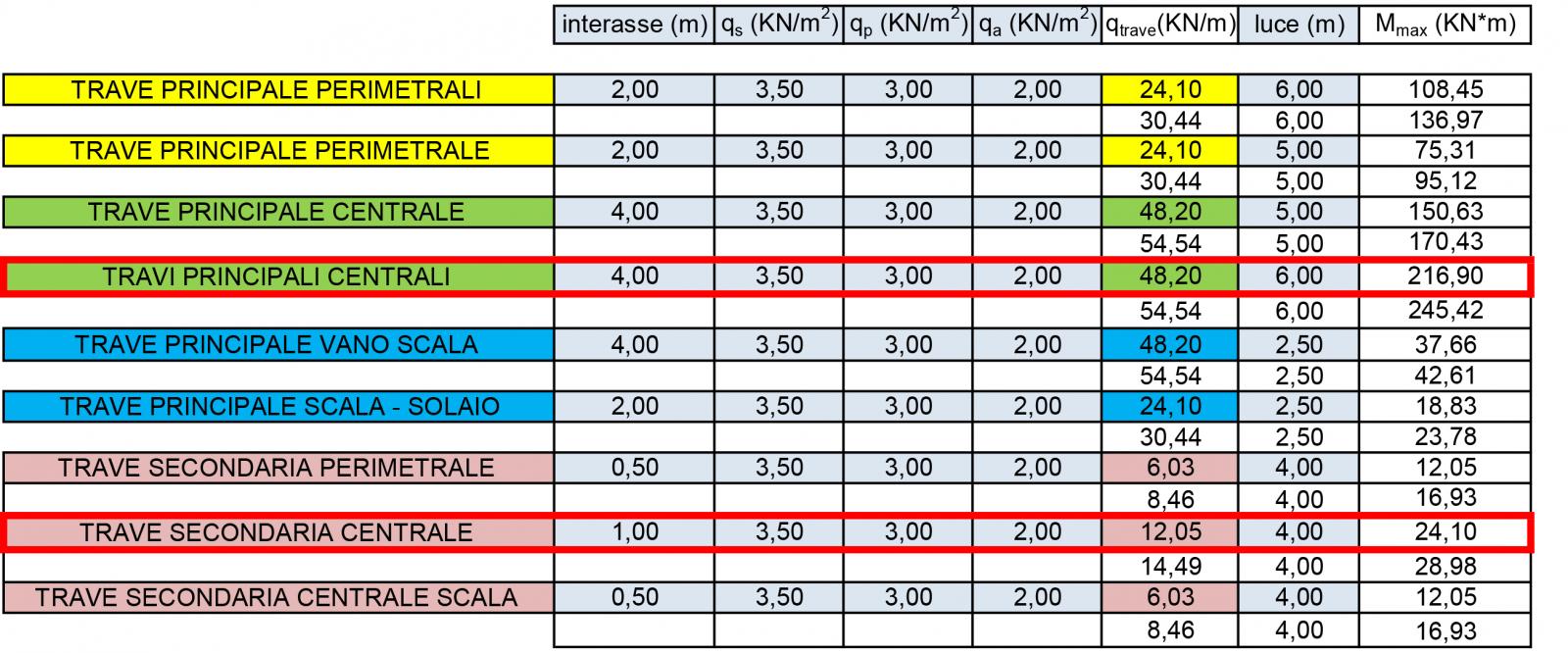
Procedo con individuare le aree di influenza delle travi e misurarne l’interasse.

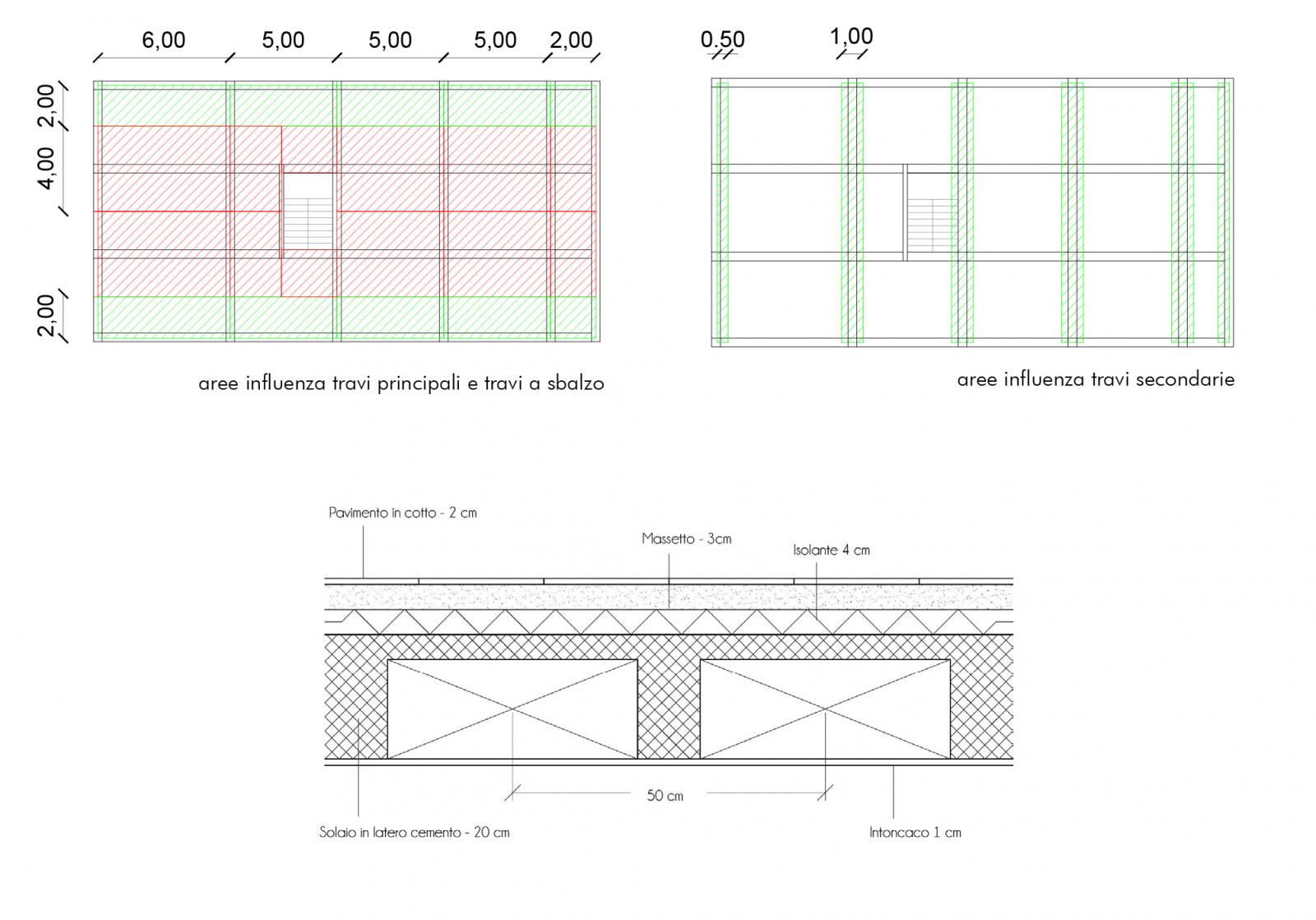
Scelto il solaio in laterocemento dell’impalcato ne considero un metro quadro di normativa per calcolarne il peso. Per definire la combinazione di carico allo stato limite ultimo SLU devo tener conto dei coefficienti di sicurezza.

• q_s = 3,50 KN/m²

• q_p = 3,00 KN/m²

• q_a = 2,00 KN/m²

• q_u = q_s x 1,3 + q_p x 1,5+ q_a x 1,5 = 12,05 KN/m²

Calcolato il carico del solaio, espresso come densità di carico superficiale in [KN/m² ], lo moltiplico per l’interasse trovando il carico lineare incidente sulle travi q_trave [KN/m].

q _trave = q_solaio x l

Per vedere quali siano le travi più sollecitate, considero il valore più grande del momento M_max sulle travi soggette a flessione  . Il momento massimo si calcola con il carico q_trave per la luce della trave. Per una trave doppiamente appoggiata il M_max è ql²/ 8 .

Per determinare l’altezza utile h_u , ovvero la distanza tra il lembo superiore del cls compresso e il baricentro delle armature tese, ho bisogno di alcuni dati e di fissare la misura della base. La formula di progetto è h_{u =} r x √ (M_max/ b ). I dati di cui ho bisogno sono le resistenze caratteristiche dell’acciaio e del cls per ricavare le tensioni di progetto relative al materiale e i moduli elastici da cui ricavo il coefficiente di omogenizzazione. Impongo che la tensione di progetto del cls sia uguale alla tensione massima nella trave, per poterla dimensionare e trovare l’altezza ingegnerizzata H_ing .

Scelgo un acciao di armatura S450C e un cls C28/35.

• f_yd = f _yk / 1,15

• f_cd = ( f_ck / 1,5 ) x 0,85

• r = √( 2 / ( f_cd ( 1 - beta / 3 ) beta ) ) 

• beta = f_cd / ( f_cd  + (  f_yd / n ) )

• n = Ef / Ec =  15       Coefficiente di omogenizzazione 

Trovate le tensioni di progetto posso determinare l’altezza utile h_u e, sommandola al copriferro, calcolare l’altezza minima che deve avere la sezione per non inflettersi.

• Hmin = h_u + delta

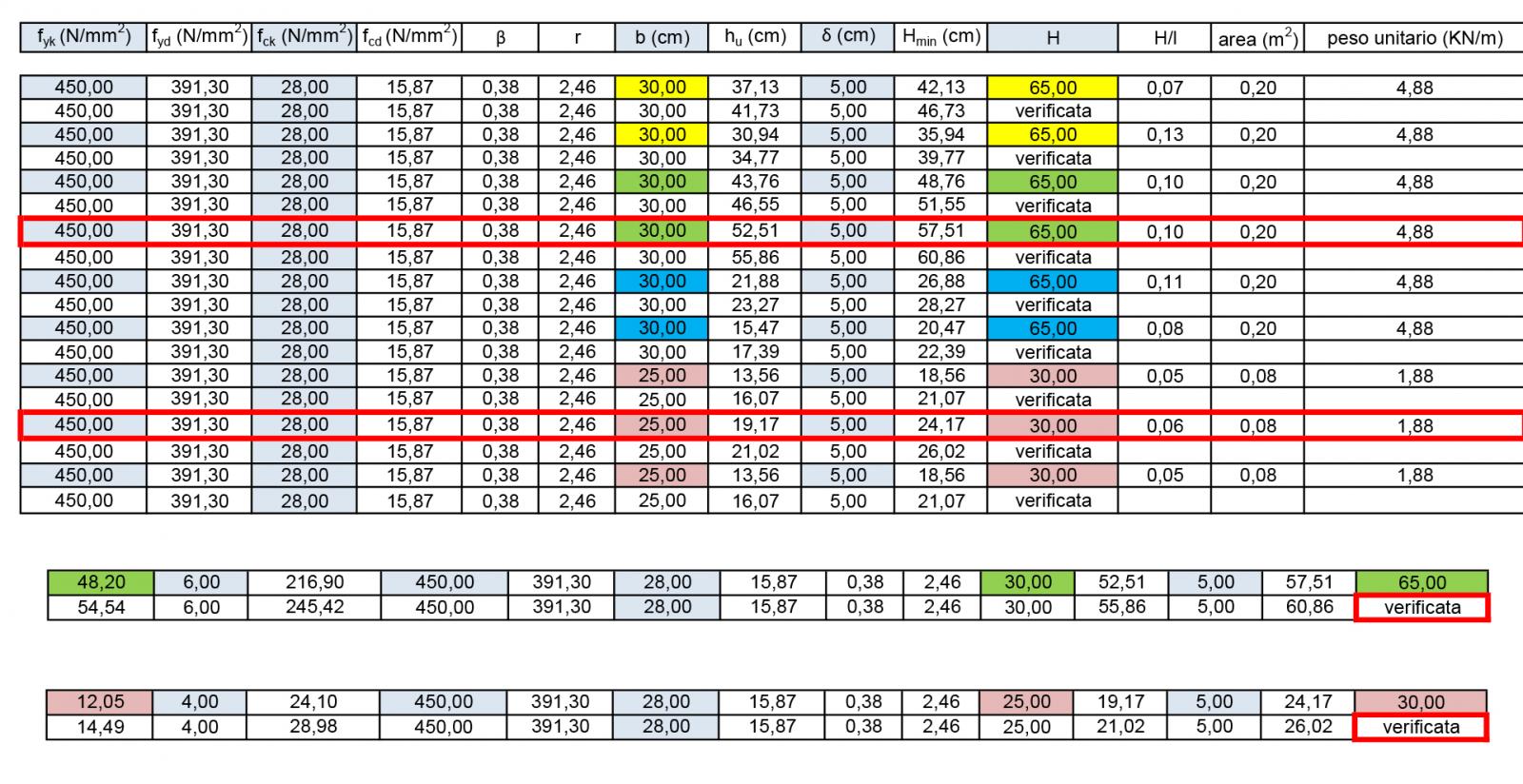
Per verificare se la sezione ingegnerizzata sia in grado di tenere il peso proprio e i carichi, aggiungo al carico totale del solaio il peso unitario della trave ( Peso specifico del cls moltiplicato all’area della sezione ) e lo motiplico per il 1,3. Considerando il peso proprio della trave, la sezione H_ing risulta comunque maggiore dell’altezza minima e la verifica è soddisfatta.

• PREDIMESIONAMENTO DELLE TRAVI A SBALZO

Il procedimento di progetto è uguale al precedente, calcolato il carico lineare posso determinare il momento massimo flettente per la formula dell’altezza utile h_u .

Una volta verificata la sezione ingegnerizzata, che deve essere maggiore della h_u, devo verificare che la trave non si abbassi troppo. La verifica degli abbassamenti si effettua allo stato limite d’esercizio e bisogna verificare che l’abbassamento massimo v_max sia maggiore di un certo limite di deformabilità di 1/250 della luce della mensola. Il valore dell’abbassamento si può calcolare con l’equazione della linea elastica che tiene in considerazione il momento flettente della mensola M_max = ql²/ 2, il modulo elastico della trave E_cls e momento d’inerzia I_x = b x h³ / 12 per sezioni rettangolari.  

• PREDIMESIONAMENTO DEI PILASTRI

Si è proceduto individuando l’area di influenza di ciascun pilastro. Il pilastri maggiormente sollecitati sicuramente saranno quelli al piano terra, poiché su questi verrano trasmessi tutti i carichi dei piani superiori.

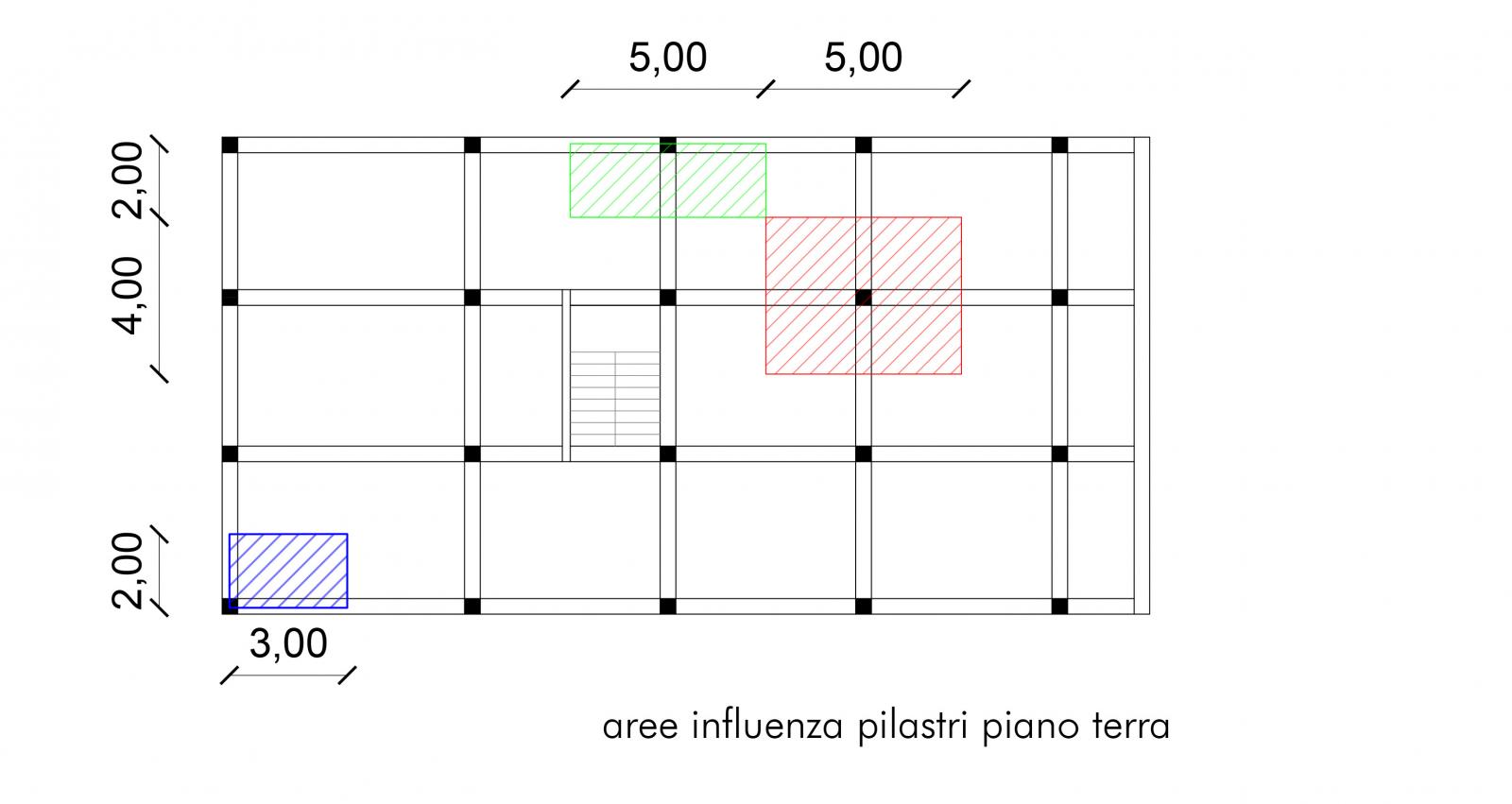
L’area di influenza ha come dimensioni L_p e L_s e varia in base alla posizione dei pilastri se posti centralmente, perimetralmente o angolarmente. Calcolata l’area osservo che quelli più sollecitati saranno i pilastri centrali, quelli con l’area di influenza maggiore e quindi con sforzo normale maggiore. Per determinare lo sforzo normale di compressione N, vado a considerare sia il peso delle travi sia il peso del solaio relativo all’area di influenza. Il peso delle travi, gravante nell’area di influenza dei pilastri, si ricava sommando i contributi di ogni trave e moltiplicando per 1,3.

• q_trave = ( trave_p + trave_s ) x 1,3                                               [ KN/m ]

Il carico dovuto al solaio si ricava dalla combinazione allo stato limite ultimo del carico strutturale, di quello permanente e di quello accidentale, il tutto moltiplicato per l’area di influenza per ottenere una forza concentrata.

• q_solaio = ( q_s x 1,3 + q_p x 1,5+ q_a x 1,5 ) x A                            [ KN/m₂] x [ m₂ ] = [ KN ]​

A questo punto posso calcolare la forza di compressione sommando il q_trave e il q_solaio e moltiplicando per il numero dei piani. Una volta ricavato lo sforzo di compressione sui pilastri posso dimensionare la sezione uguagliando la tensione massima nella trave alla resistenza di progetto del materiale e ottenere l’area minima che deve avere la sezione per evitare la rottura.

• f_cd = sigma _max                      sigma _max = N / A

• f_cd = N / A

• A _min = N / f_cd​

Per elementi strutturali in cls armato le sezioni dei pilastri sono rettangolari e la formula della base minima è 2√3 x p_min ovvero in funzione della snellezza del pilastro. Per trovare il raggio minimo di inerzia devo prima deteminare la snellezza e la luce libera di inflessione che tiene conto dei vincoli a cui è soggetto il pilastro .

• lamba = π √ (E / f _cd )                     l₀ = l x beta

• p_min = √ (l₀ / lamba )

Trovato il raggio di inerzia calcolo la base minima b_min e la sovradimensiono nell’ingegnerizzazione. Per dimensionare l'altezza minima della sezione h_min ,divido la base ingegnerizzata per l’area precedentemente calcolata nel dimensionamento a resistenza. L'altezza ingegnerizzata descrive la sezione rettangolare del pilastro in cls armato, da cui si ricava l’area di progetto Adesign.

• h_min= b / A _min

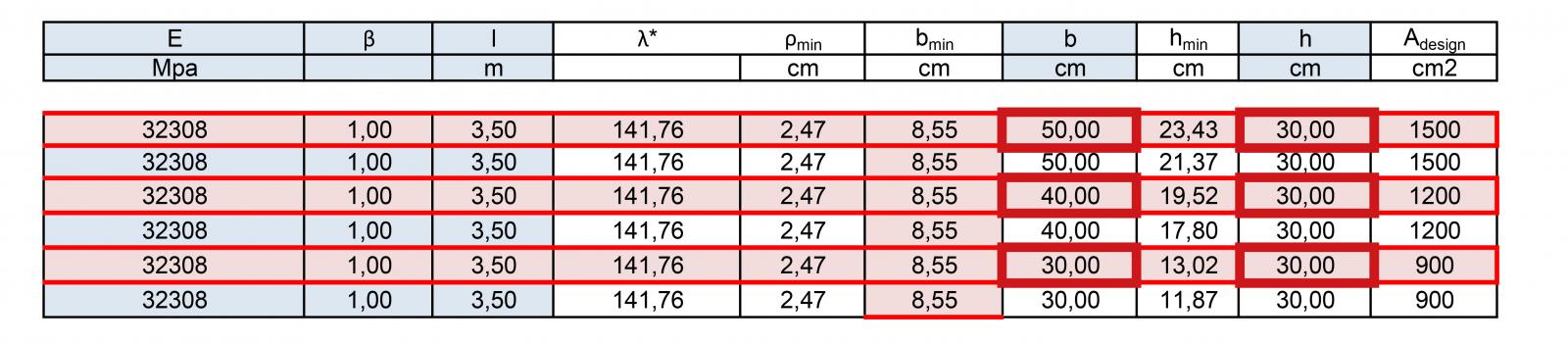
Si è scelto di adottare sezioni di lato non inferiore a 30 cm e dunque di area non inferiore a 900 cm² . Le sezioni dimensionate sono 50 x 30 cm, 40 x 30 cm e 30 x 30 cm rispettivamente per i pilastri del piano terra, primo piano e piano secondo. Per la verifica della sezione poiché nel cemento armato il nodo rigido tra trave e pilastro trasmette momento, il pilastro deve resistere a pressoflessione.

•ANALISI DEL TELAIO DIMESIONATO IN SAP

Per la verifica a pressoflessione dei pilastri è stato necessario introdurre il telaio su SAP per ricalcolare correttamente le sollecitazioni della struttura. Dopo aver effettuato il predimesionamento degli elementi strutturali sui fogli di calcolo di excel, ne è stata effettuata l'assegnazione delle sezioni sul modello di SAP precedentemente creato.

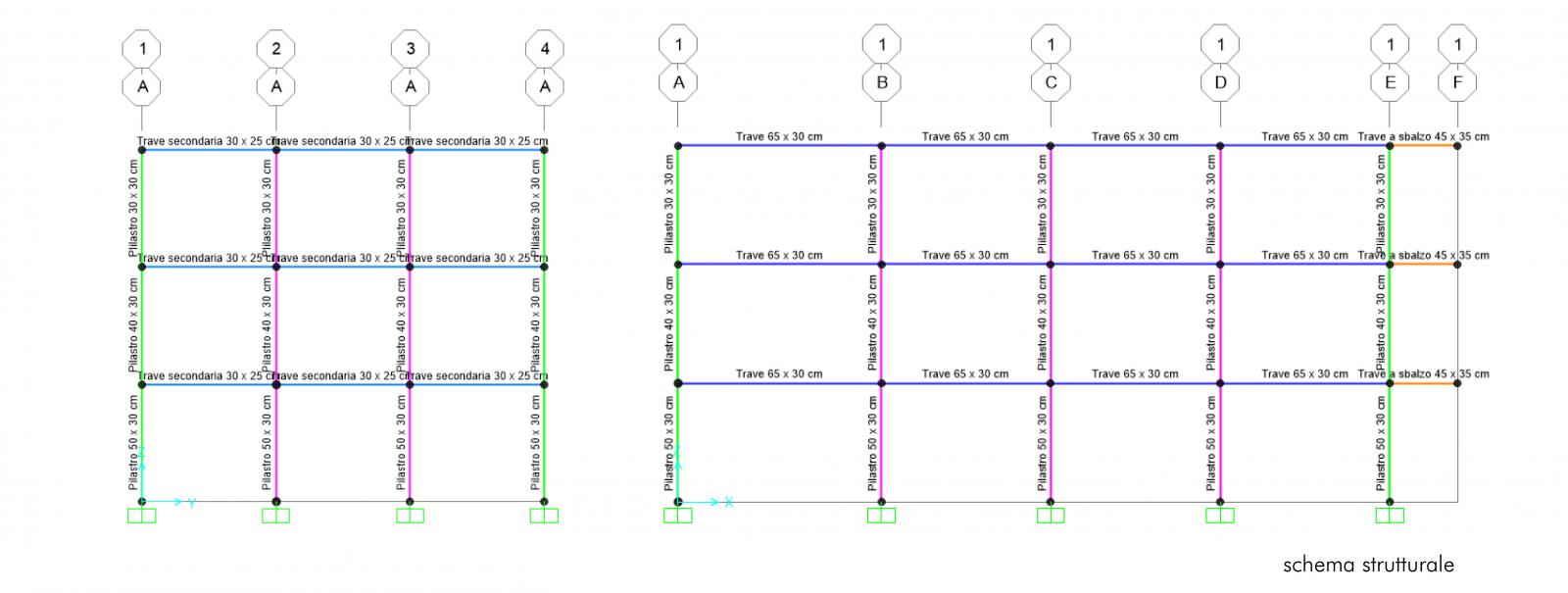
Come prima cosa, avendo dimensionato sezioni rettangolari, per i pilastri si dovrà tener conto dell'orientamentamento e quindi del valore del momento di inerzia che inciderà sulla rigidezza traslante del telaio. Si è provveduto a ruotare i pilastri perimetrali posti lungo l'asse Y ( sistema globale ) andando a ruotare di 90° gli assi locali degli elementi. In questo modo il momento d’inerzia aumenta in quanto la base e l'altezza sono invertite e di conseguenza maggiore sarà la rigidezza.

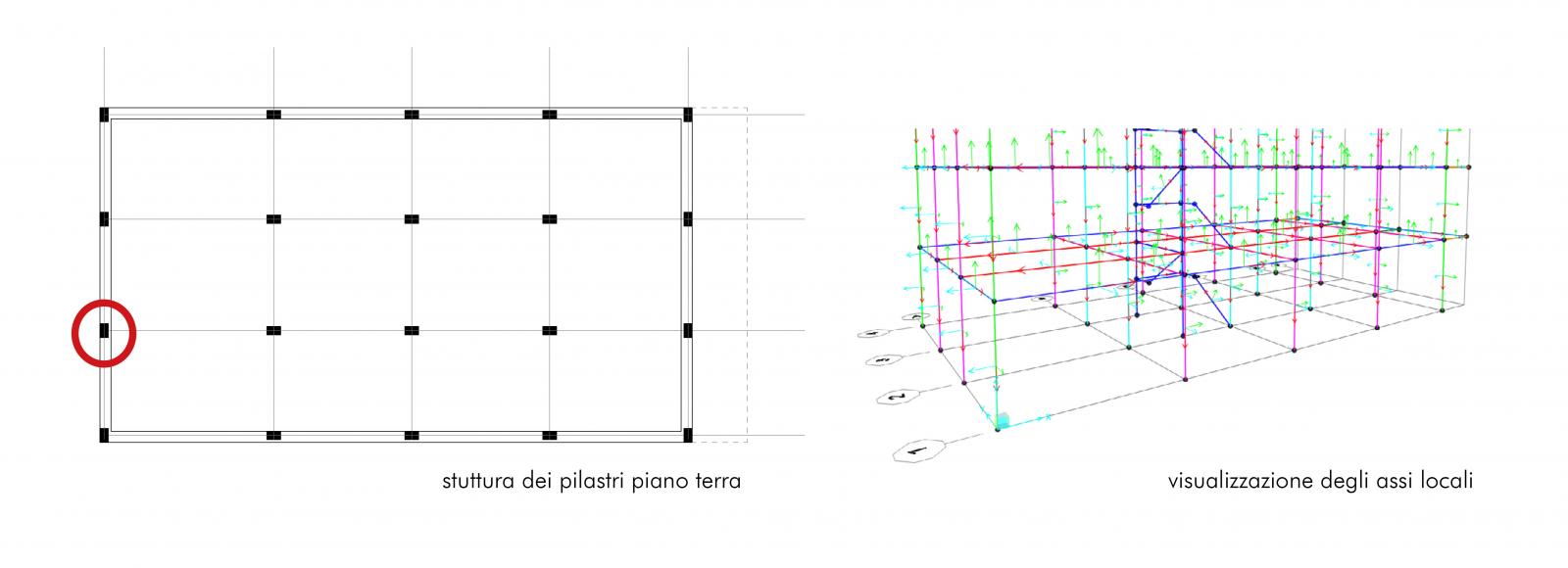
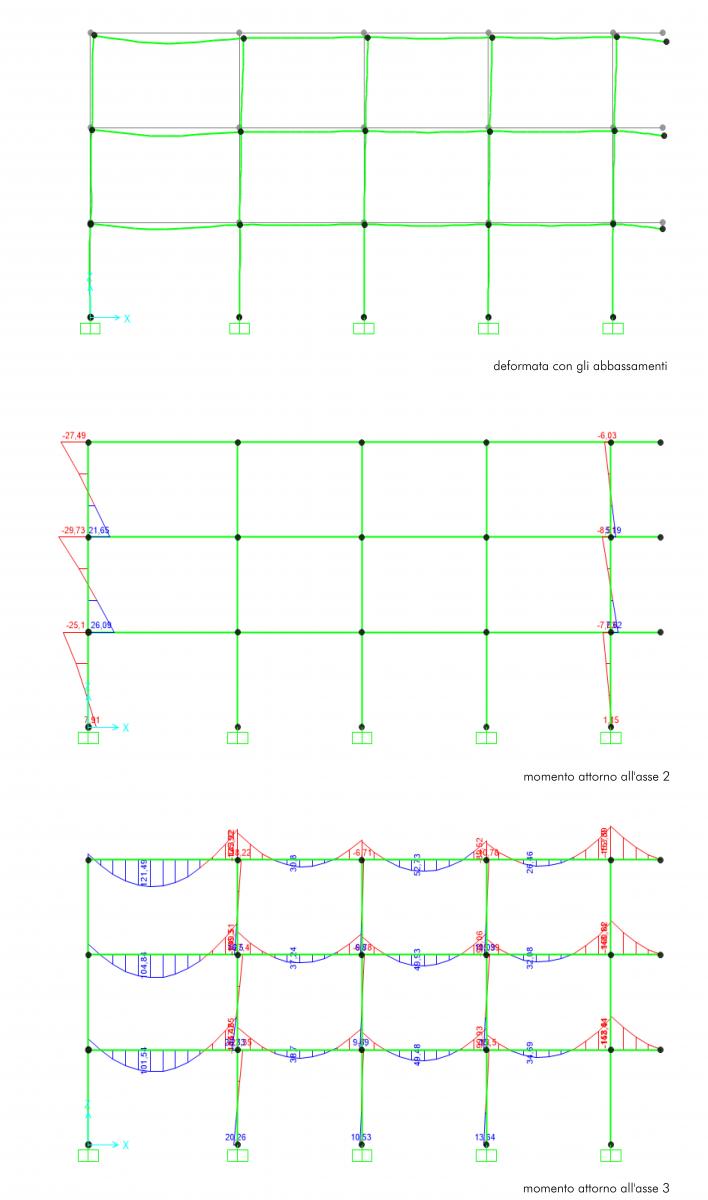
• SOLLECITAZIONI MASSIME

Definisco il valore dei carichi lineari, ottenuti dai fogli excel, e li assegno alle travi che trasmetteranno momento ai pilastri. Alle perimetrali è stato aggiunto il contributo del tompagno. Il carico della tamponatura esterna in laterizio forato è stato calcolato prima al metro quadro e moltiplcato poi per l'interpiano netto ovvero l'altezza del pilastro. Nell'analisi delle sollecitazioni considero anche le forze orizzontali del vento lungo la direzione X e Y . L'azione del vento agisce sulle tamponature dei piani e da queste viene trasmesso ai pilastri sottoforma di carico distribuito linearmente lungo l'altezza.

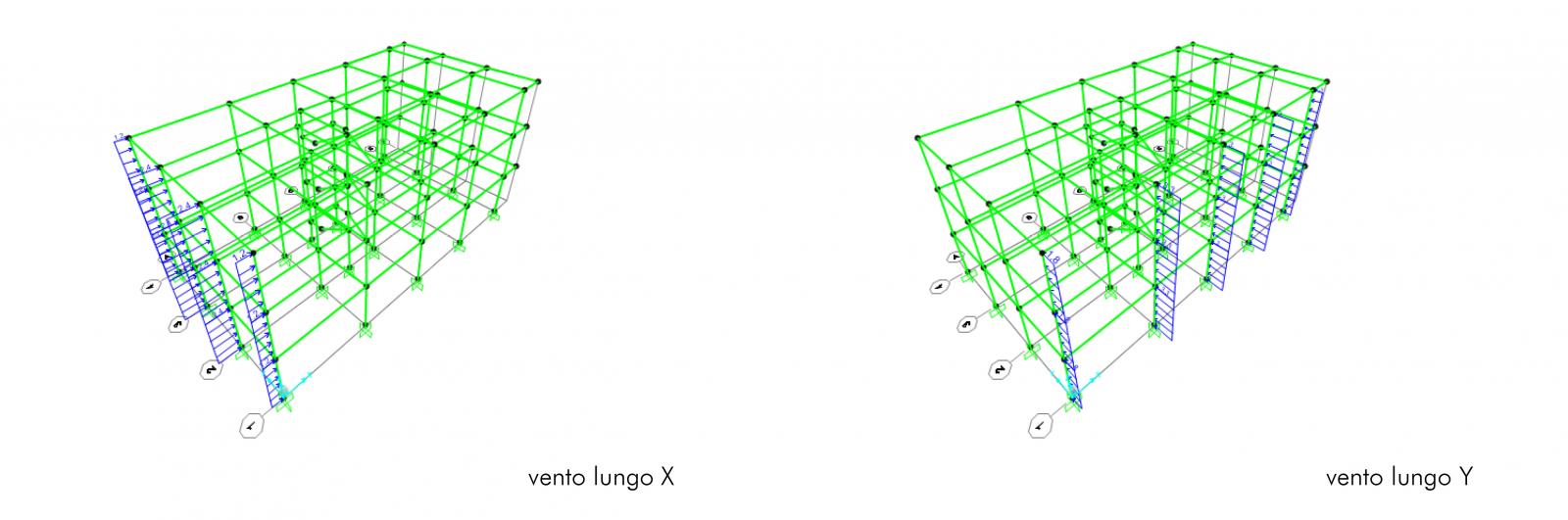
Per ricavare le sollecitazioni massime e verificare le sezioni dimensionate, seleziono i pilastri in base ai gruppi mandando l'analisi con COMBO_Y e COMBO_X per valutare quale sia la condizione più gravosa. Dall'analisi i valori di COMBO_X risultano simili alla combinazione SLU per questo si è scelto di considerare solo l'azione del vento agente sul sopravento maggiore.

• VERIFICA DEI PILASTRI A PRESSOFLESSIONE

Dopo aver mandato l'analisi con i carichi verticali e orizzontali, ricavo le nuove sollecitazioni di progetto che andrò ad inserire nella tabella excel ai fini dell'assegnazione dei pilastri nelle tabelle della piccola, moderata e grande eccentricità. Per suddividere i pilastri nelle tre eccentricità è stata fatta una tassonomia in base al piano e sono stati individuati i pilastri in pianta per distiguerli in base all'orientamento ( per i pilastri ruotati è stato condiserato M attorno all'asse locale 2). Sono stati quindi inseriti i pilastri nel file excel di verifica della pressoflessione. In base al rapporto tra N e M si ricava il valore dell'eccentricità e si confronta il valore ottenuto con h/6 e h/2 .

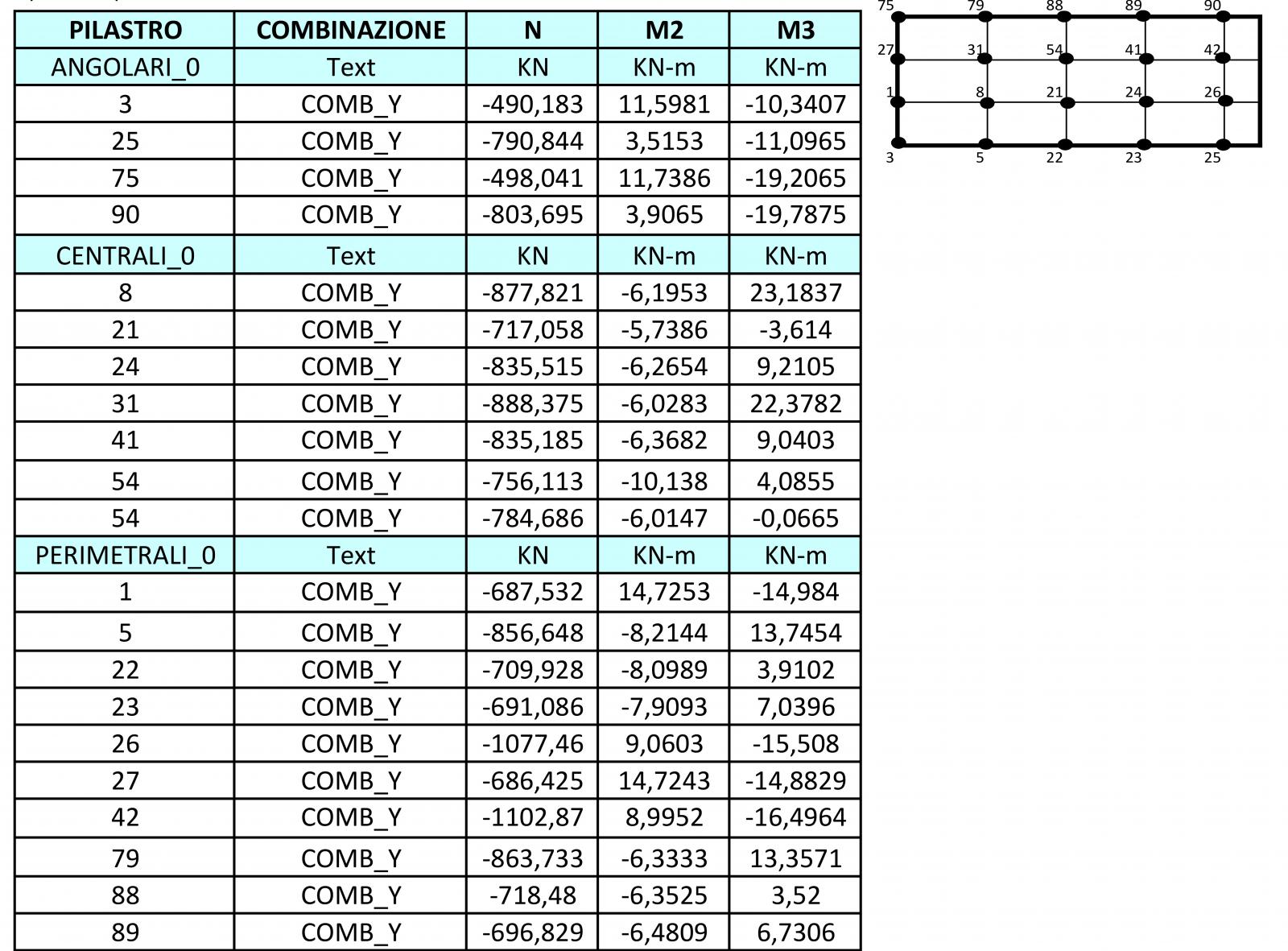
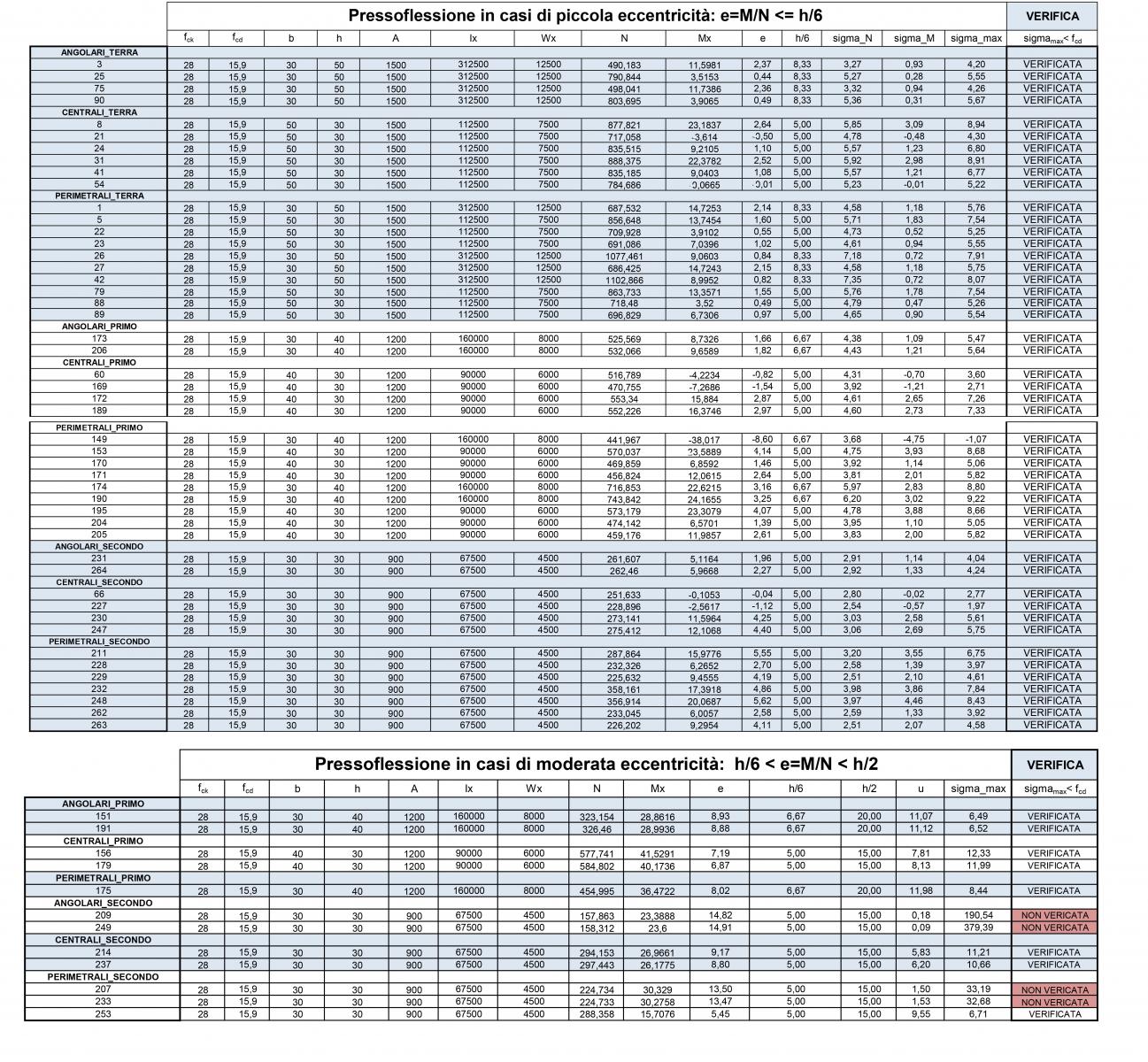
I pilastri del piano terra risultano tutti in piccola eccentricità, quelli del primo piano rientrano sia nella moderata che nella piccola mentre quelli dell'ultimo piano ricevendo una sforzo di compressione minore avranno l'eccentricità più grande. Una volta classificati in base all'eccentricità, per verificare il pilastro a pressoflessione si deve imporre che la tensione massima sia minore della resistenza di progetto.

• sigma_max ≤ f_cd

La tensione massima può essere calcolata in funzione dello sforzo normale di compressione e il momento.

• sigma_max = N / A + M / W_max

Dalla verifica risultano non verificate le sezioni 30 x 30 cm di quattro pilastri dell'ultimo piano. Cambiando le dimensioni della sezione con 40 x 40 cm la verifica risulta soddisfatta.