Esercitazione 3_Verifica telaio in calcestruzzo armato in zona sismica.

Studentesse: Santacesaria Elena, Schettini Benedetta.

Sulla base dell’edificio precedentemente analizzato nella prima parte della consegna, abbiamo questa volta studiato il comportamento della struttura in zona sismica.

Abbiamo analizzato la pianta strutturale e abbiamo individuato i telai che la compongono, dividendoli in verticali e orizzontali.

I controventi possono essere schematizzati come molle, ognuno con la sua rigidezza, in quanto si comportano in modo elastico.

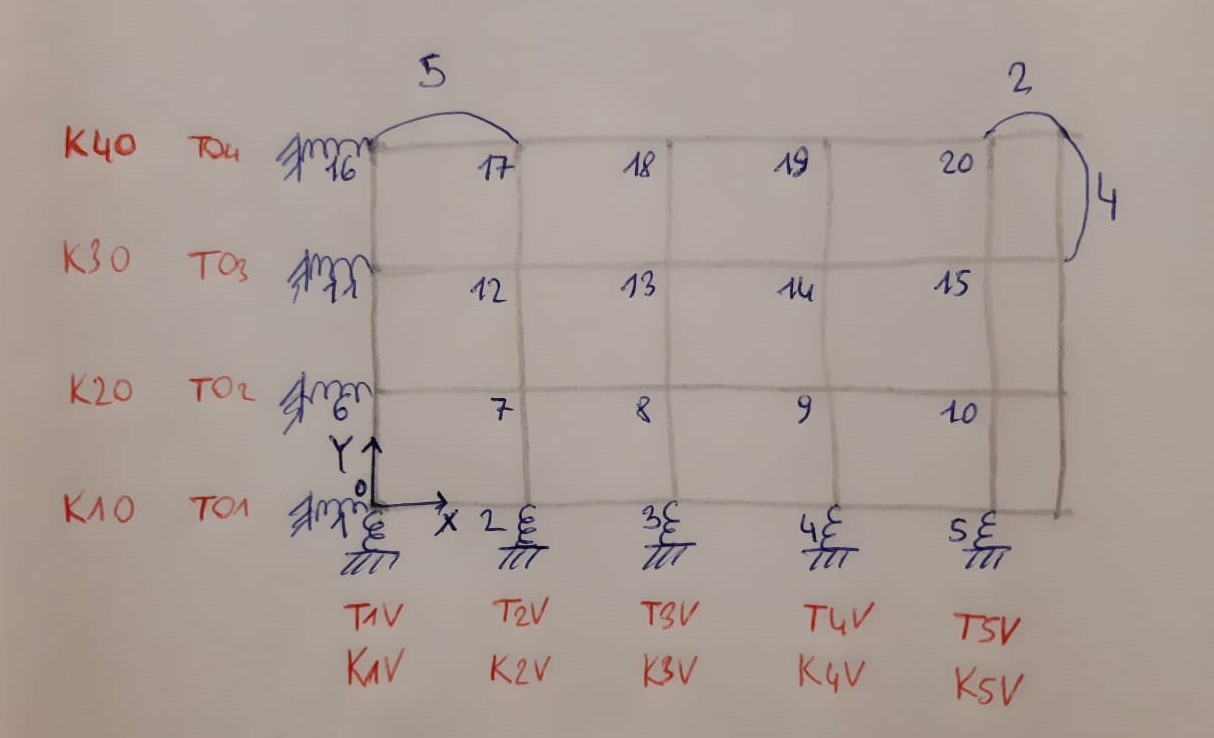
Calcolo delle rigidezze traslanti dei controventi dell’edificio

Abbiamo calcolato la rigidezza di ogni controvento tramite la formula K = (12EI)/H^3

Tabella sinottica controventi e distanze

La tabella mostra le rigidezze di tutti i telai e le rispettive distanze dal punto di origine O del sistema di riferimento scelto.

Calcolo del centro di massa dell’impalcato

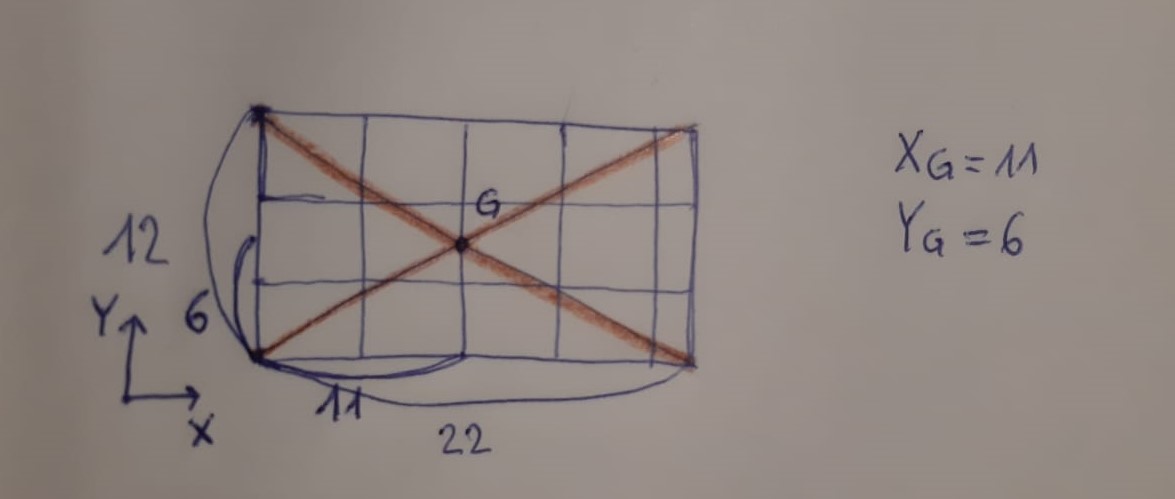
Il nostro impalcato ha una forma rettangolare e una densità di massa uniforme, quindi per individuare il centro di massa G è bastato tracciare le diagonali della figura e trovarne il centro geometrico.

Calcolo del centro delle rigidezze e delle rigidezze globali

Abbiamo calcolato le rigidezze totali (verticali e orizzontali) sommando le singole rigidezze dei controventi.

Tramite queste abbiamo ricavato le coordinate del centro delle rigidezze (Xc;Yc).

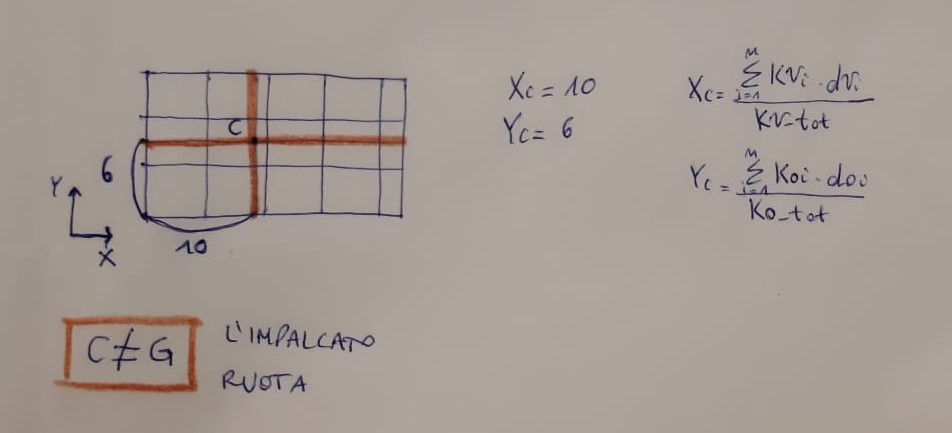
Abbiamo verificato che il centro delle rigidezze non coincide con il centro di massa.

Abbiamo ricalcolato le distanze dei controventi questa volta ponendo l’origine del nostro sistema di riferimento sul centro delle rigidezze.

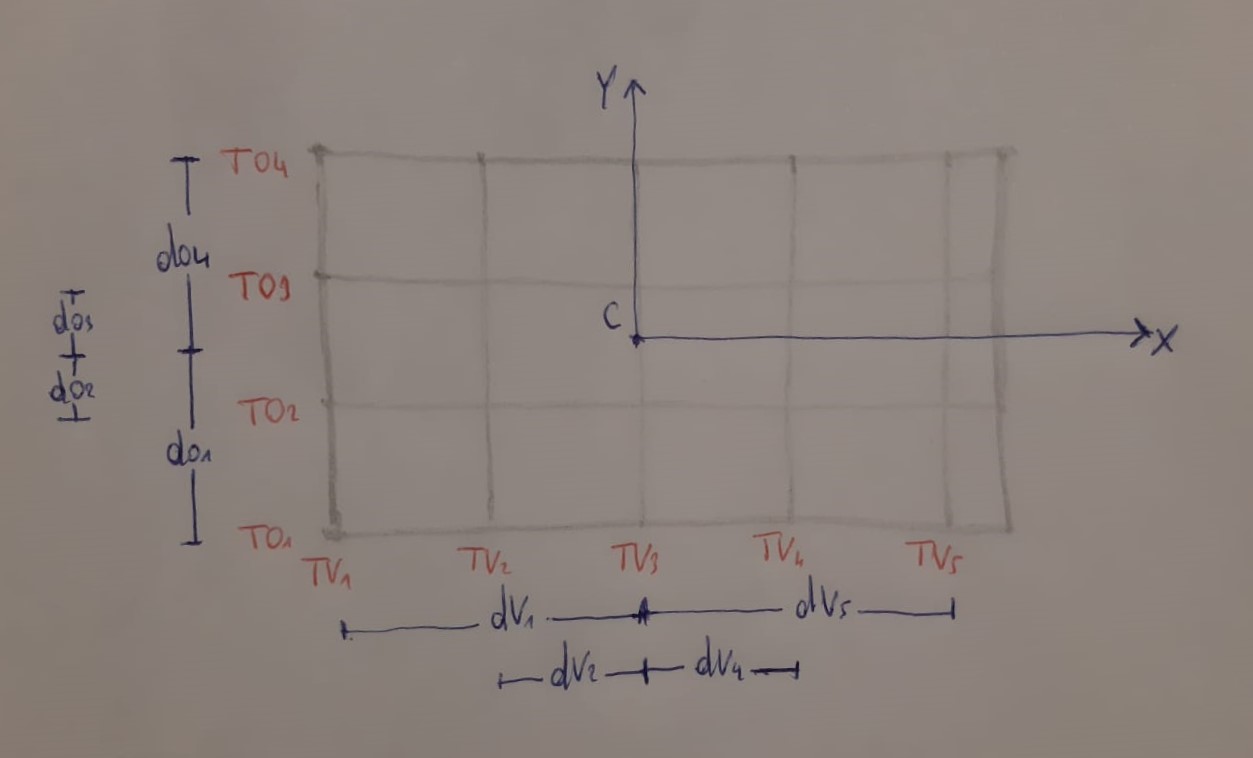
Potendo così calcolare il valore della rigidezza torsionale totale Kφ.

Essendo il nostro impalcato nella casistica in cui il centro delle rigidezze non coincide con il centro di massa, andremo incontro ad una traslazione e ad una rotazione indotta dal momento prodotto dalla forza esterna rispetto al centro delle rigidezze (c’è quindi un braccio).

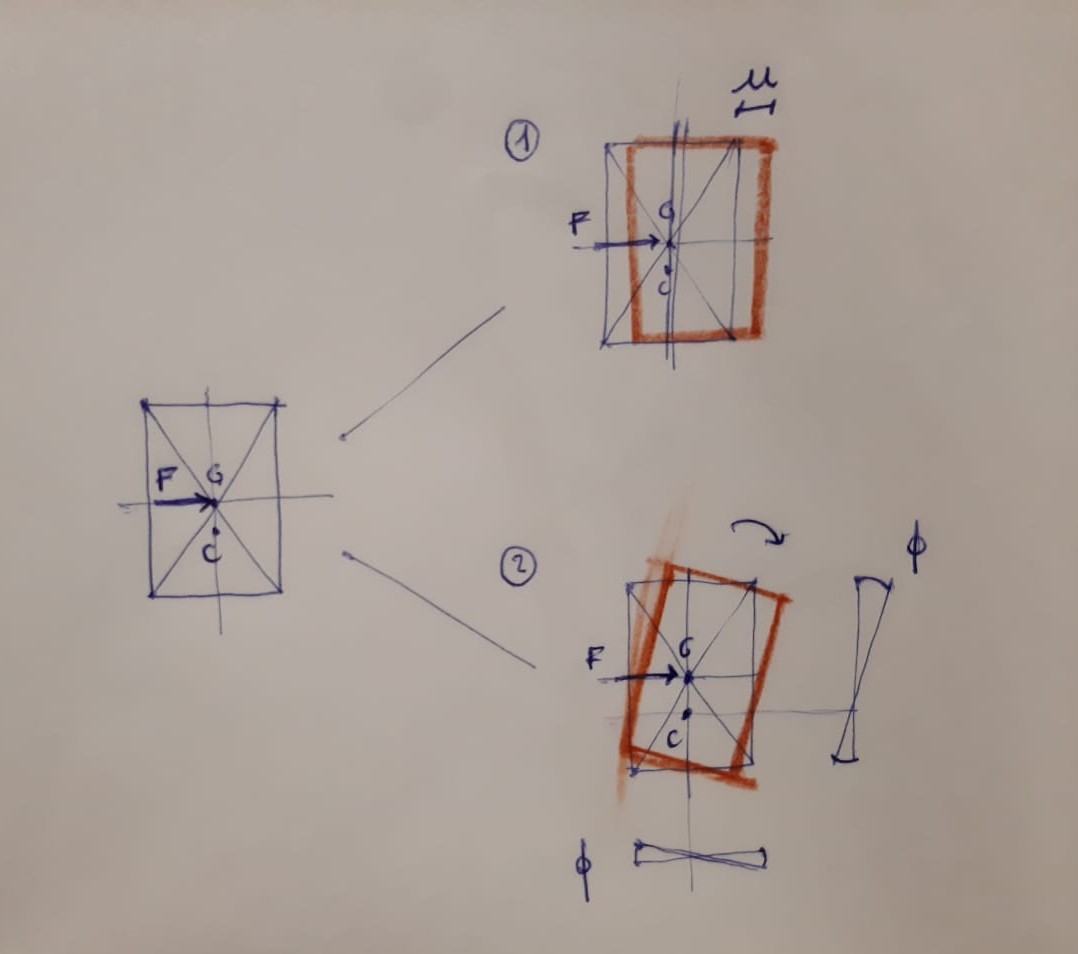
Analisi dei carichi sismici

Abbiamo calcolato il valore del carico totale permanente G e del carico totale accidentale Q tramite il valore dei carichi per unità di superficie (qp,qs,qa).

Abbiamo poi calcolato il peso sismico W tramite la formula W=G+Q*Ψ

Ψ rappresenta il coeff. Di contemporaneità.

Quindi abbiamo calcolato la forza sismica agente sul centro di massa dell’edificio tramite la formula F=W*c

C rappresenta il coeff. d’intensità sismica che varia in base alla localizzazione dell’edificio, nel nostro caso assume il valore 0,15.

Adesso che abbiamo calcolato la forza sismica, possiamo sapere in che modo essa si ripartisce sui vari piani del nostro edificio.

Fi=hi/(Σihi) *Fs

Verifichiamo che la forza sismica non si ripartisce equamente sui vari piani, ma che essa cresce in funzione dell’altezza.

Ripartizione della forza sismica lungo X e lungo Y

Lungo X

Nel nostro edificio, il centro di massa e il centro delle rigidezze hanno la stessa ordinata, dunque non si sviluppa un momento e quindi una rotazione, ma solo una leggera traslazione orizzontale.

Lungo Y

Diversamente, C e G, hanno diversa ascissa, dunque la forza agisce nel centro di massa G e si sviluppa un momento torcente in quanto c’è un braccio rappresentato dalla distanza tra i due centri (C e G) e una traslazione verticale.

Abbiamo calcolato le rotazioni e le traslazioni con le seguenti formule.

u= F/Ko_tot

v=F/Kv_tot

φ= M/Kφ

Quindi abbiamo ricavato le forze sui singoli controventi  nei 2 casi di carico tramite le formule.

Fo_n=Ko_n (u+ φ*ddo_n)

Fv_n=Kv_n* φ*ddv_n

Modello

Prima di procedere abbiamo assegnato un diafram diverso per ogni piano rendendo così ogni impalcato un corpo rigido.

Abbiamo quindi applicato su SAP2000 le forze sismiche agenti su ogni piano, lungo X e lungo Y.

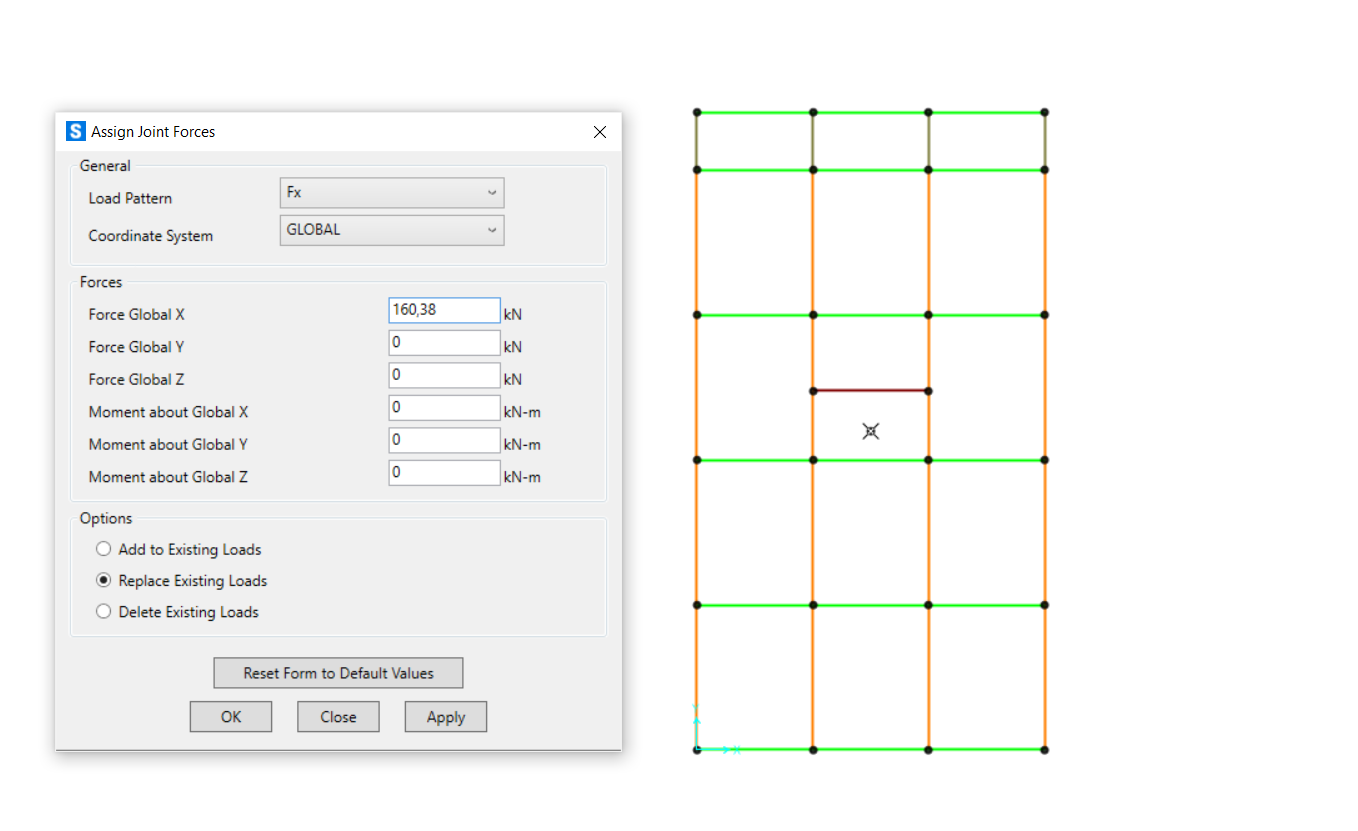
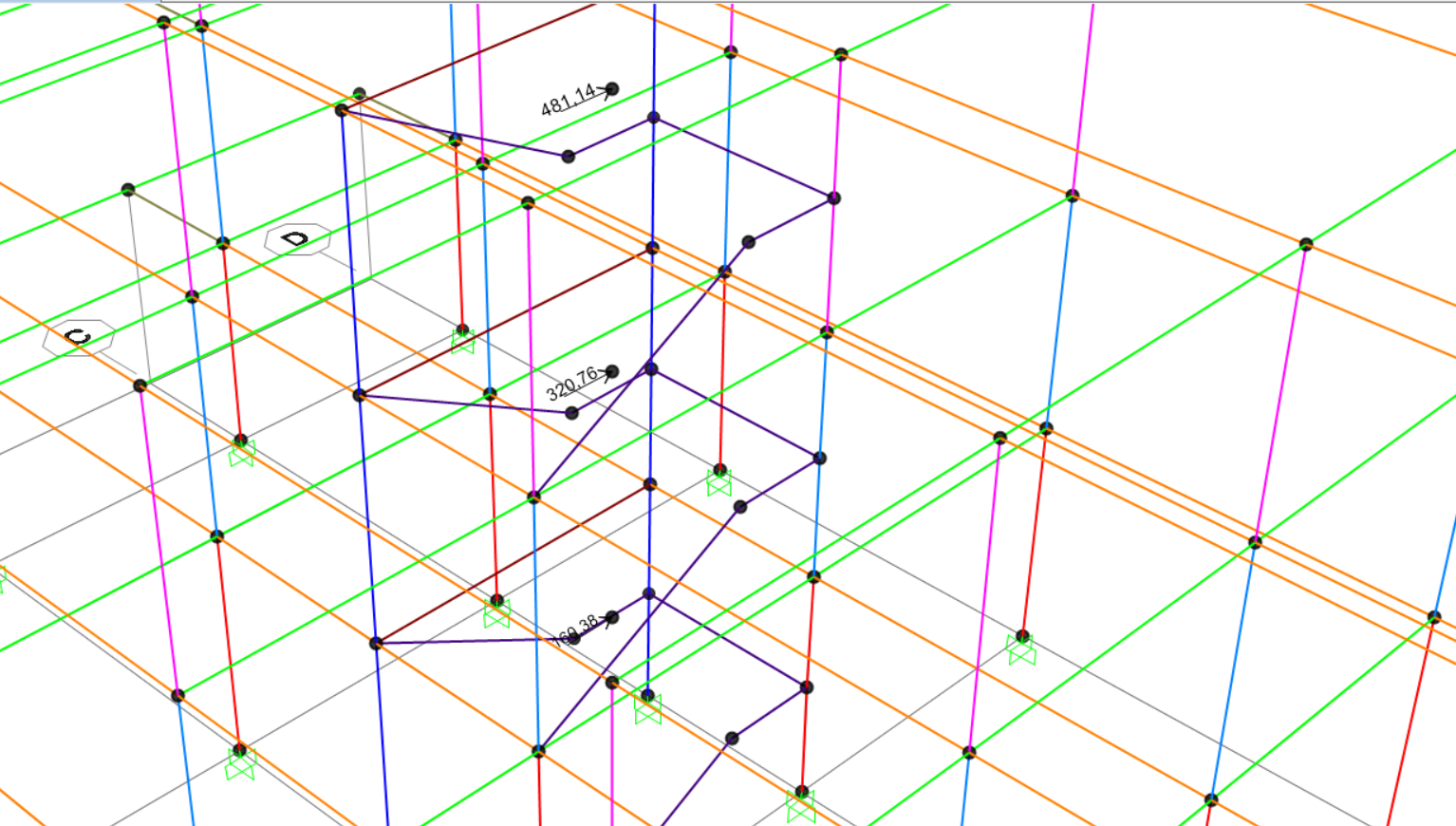
Abbiamo creato una nuova combinazione considerando i carichi verticali precedentemente assegnati e l’azione delle forze sismiche.

Quindi abbiamo mandato l’analisi solamente con la combinazione SLU+FY in quanto lungo X non si sviluppa momento torcente.

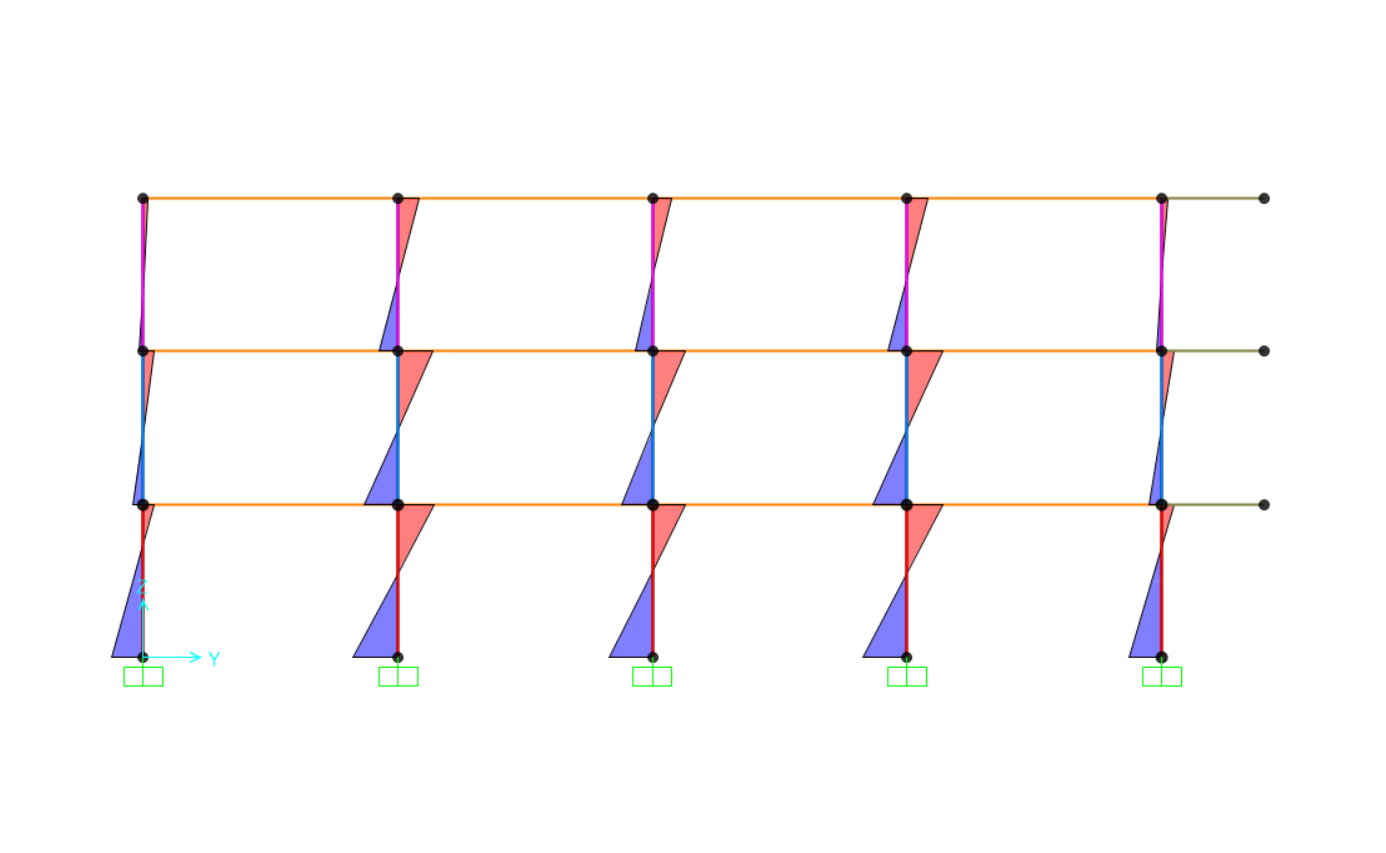
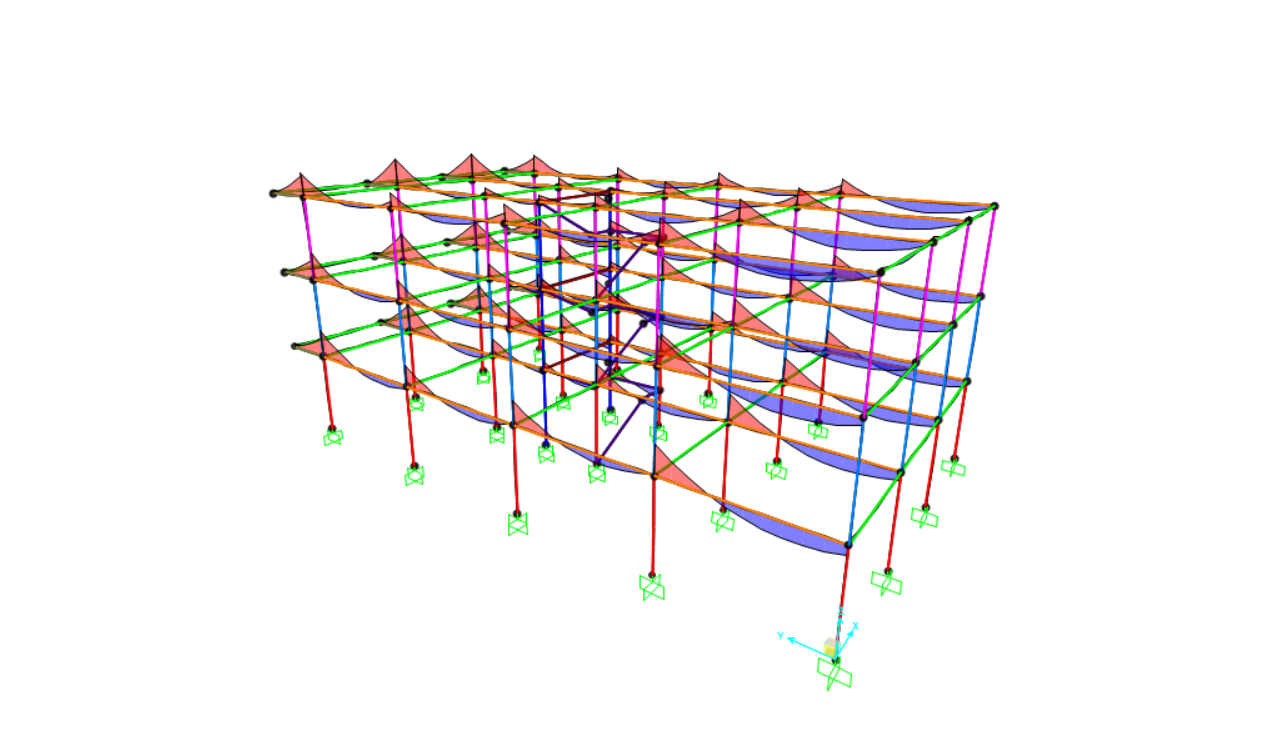
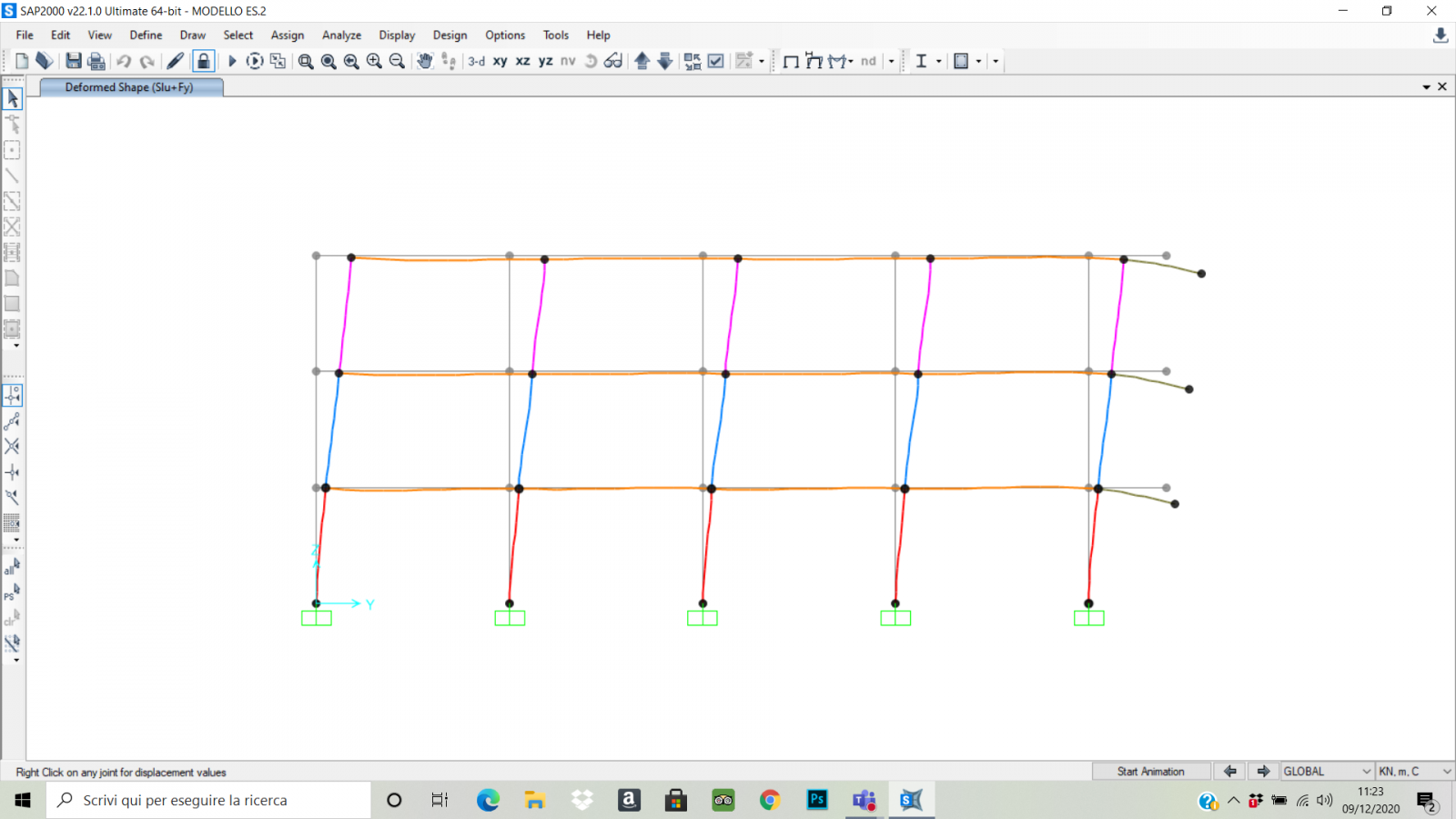
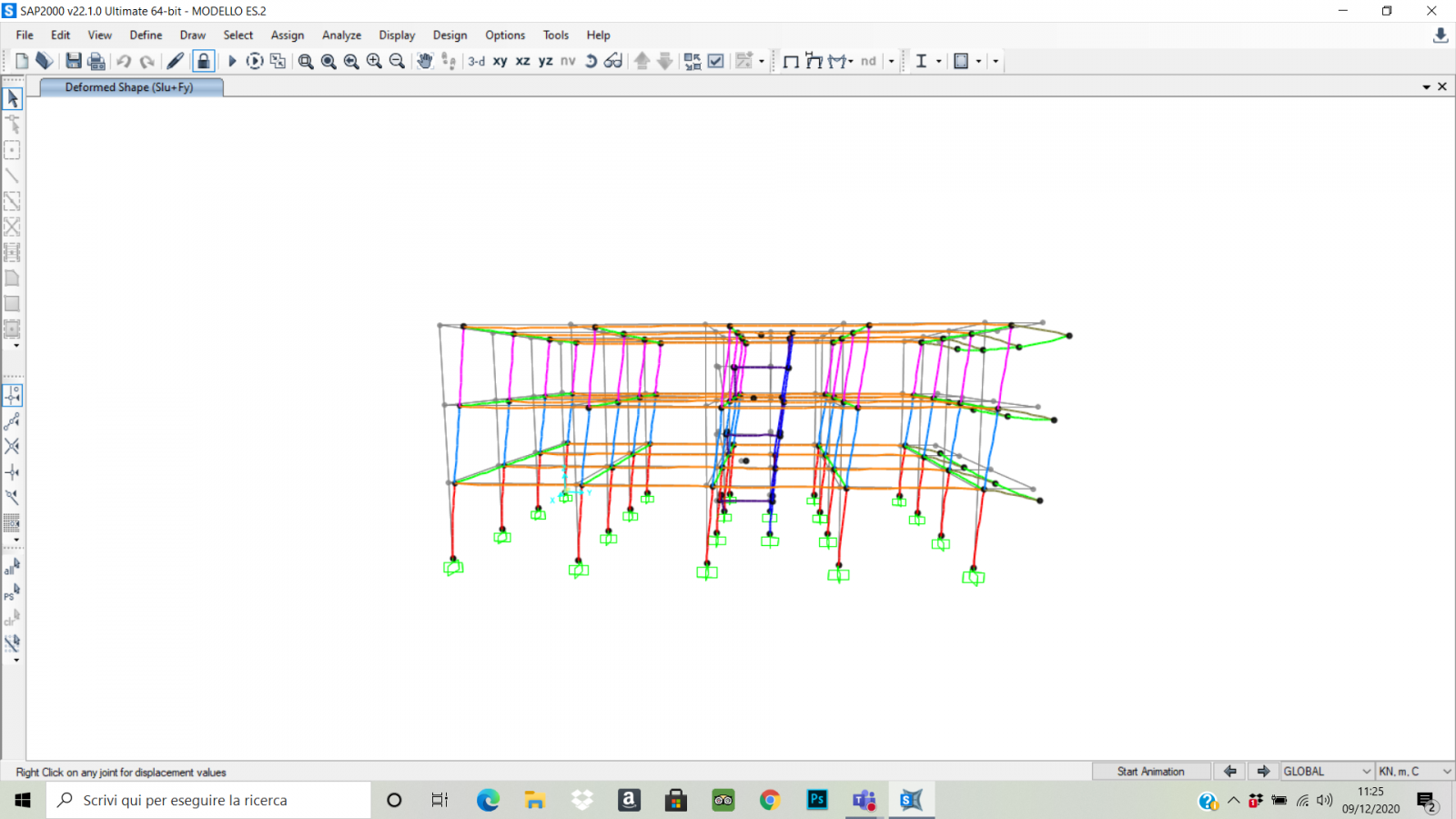
Abbiamo estrapolato i nuovi valori delle sollecitazioni (N,M) agenti sui pilastri per poterli verificare nuovamente a pressoflessione e dividerli in base alla loro eccentricità.

I nostri pilastri risultano verificati in piccola e moderata eccentricità.