RIPARTIZIONE DI FORZE ORIZZONTALI AGENTI SU UNA STRUTTURA IN CLS_Lozonschi_Miloro

RIPARTIZIONE DI FORZE ORIZZONTALI AGENTI SU UNA STRUTTURA IN CLS

Per questa esercitazione è stato considerato un edificio in cls armato, precedentemente dimensionato e modellato su SAP, come un insieme di telai ''shear type'' con le relative rigidezze traslanti. Essendo un telaio di elementi verticali e orizzontali tra loro collegati da nodi rigidi, questi potranno avere doppia funzione se disposti adeguatamente; resistere al peso della costruzione e di resistere alle forze orizzontali, in questo caso si è considerata l'azione sismica. Per la ripartizione delle forze orizzontali è stato necessario applicare un diaphragm ad ogni piano, cioè un vincolo interno, che colleghi le teste dei pilastri ad un unico corpo rigido piano, l'impalcato. In questo modo si impone a tutti i punti del piano di ruotare attorno all’asse Z nel centro delle rigidezze C, e di non inflettersi fuori dal piano.

L'edificio è definito dal seguente impalcato:

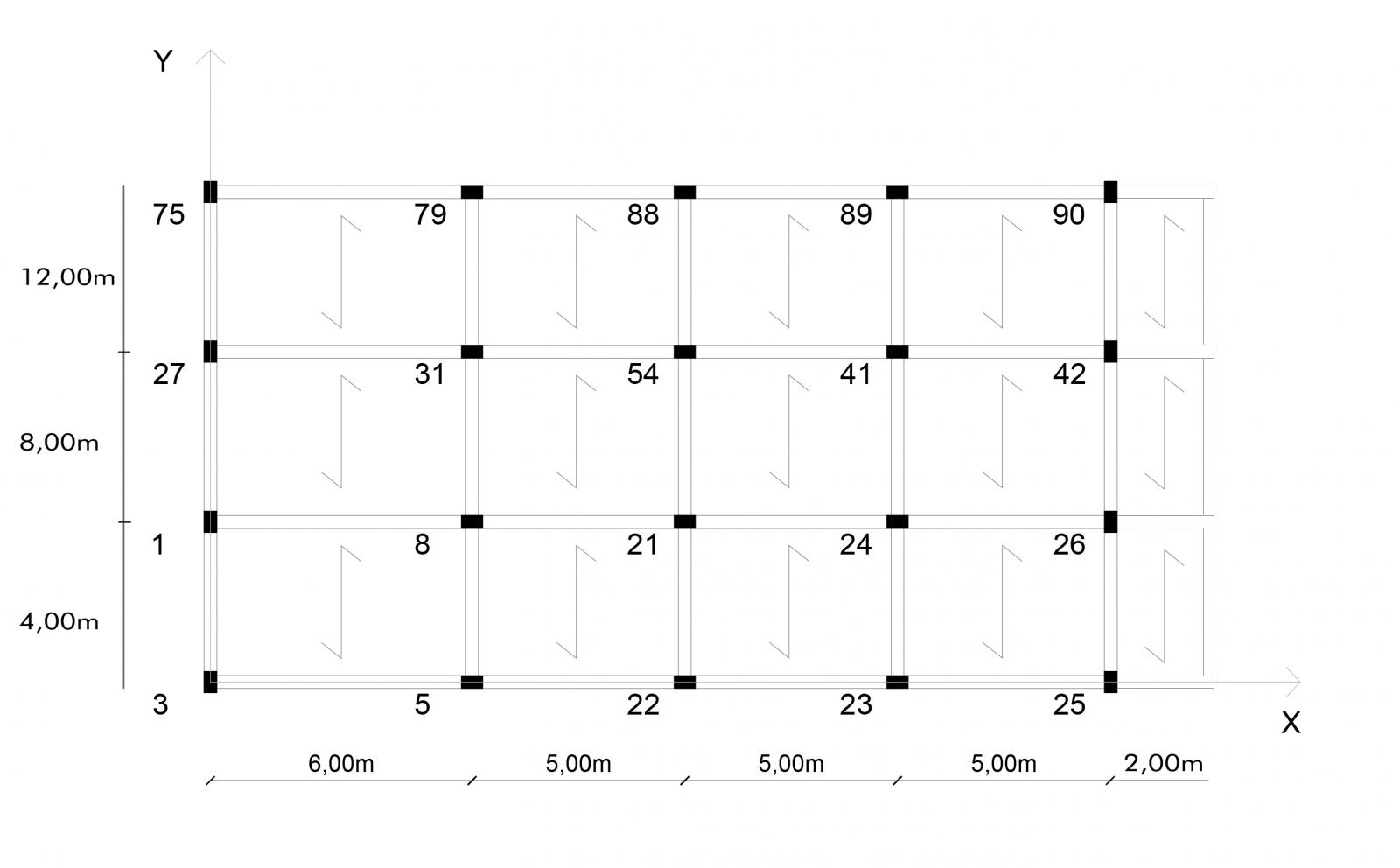
I solai sono orditi come indicato in figura ed i pilastri hanno le seguenti sezioni con diversi momenti d'inerzia e conseguenti rigidezze:

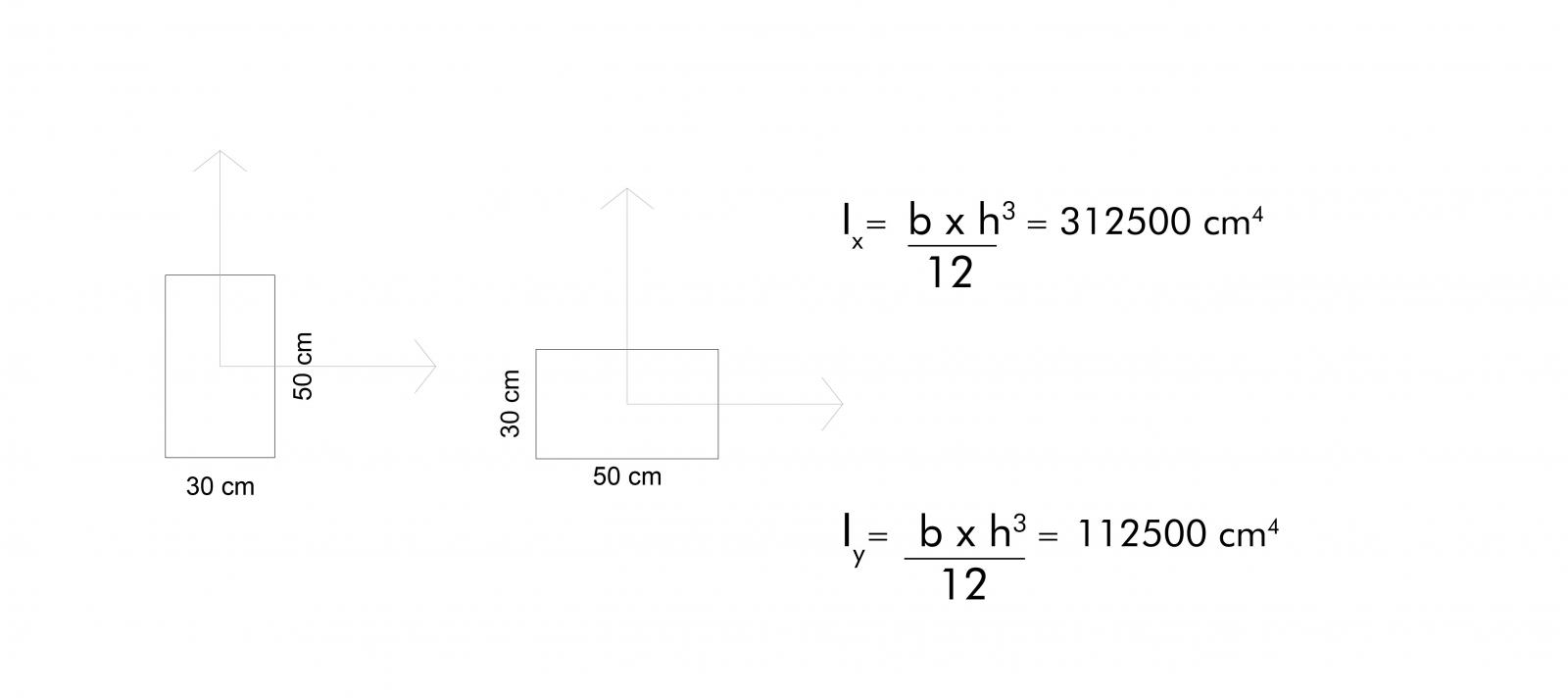
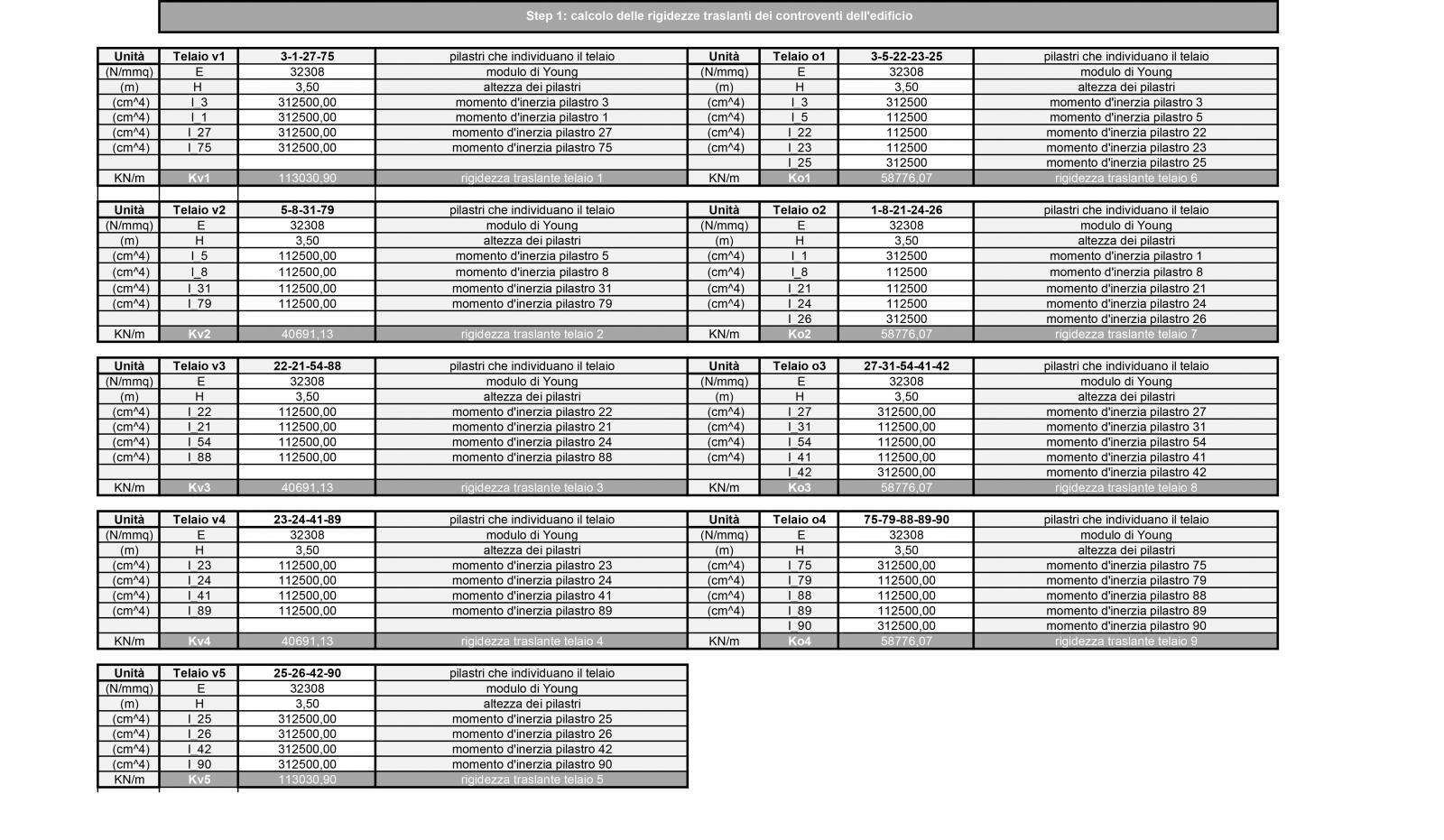
• CALCOLO DELLE RIGIDEZZE DEI CONTROVENTI

Nella figura si possono individuare nove telai, cinque paralleli all’asse Y e quattro paralleli all’asse X :

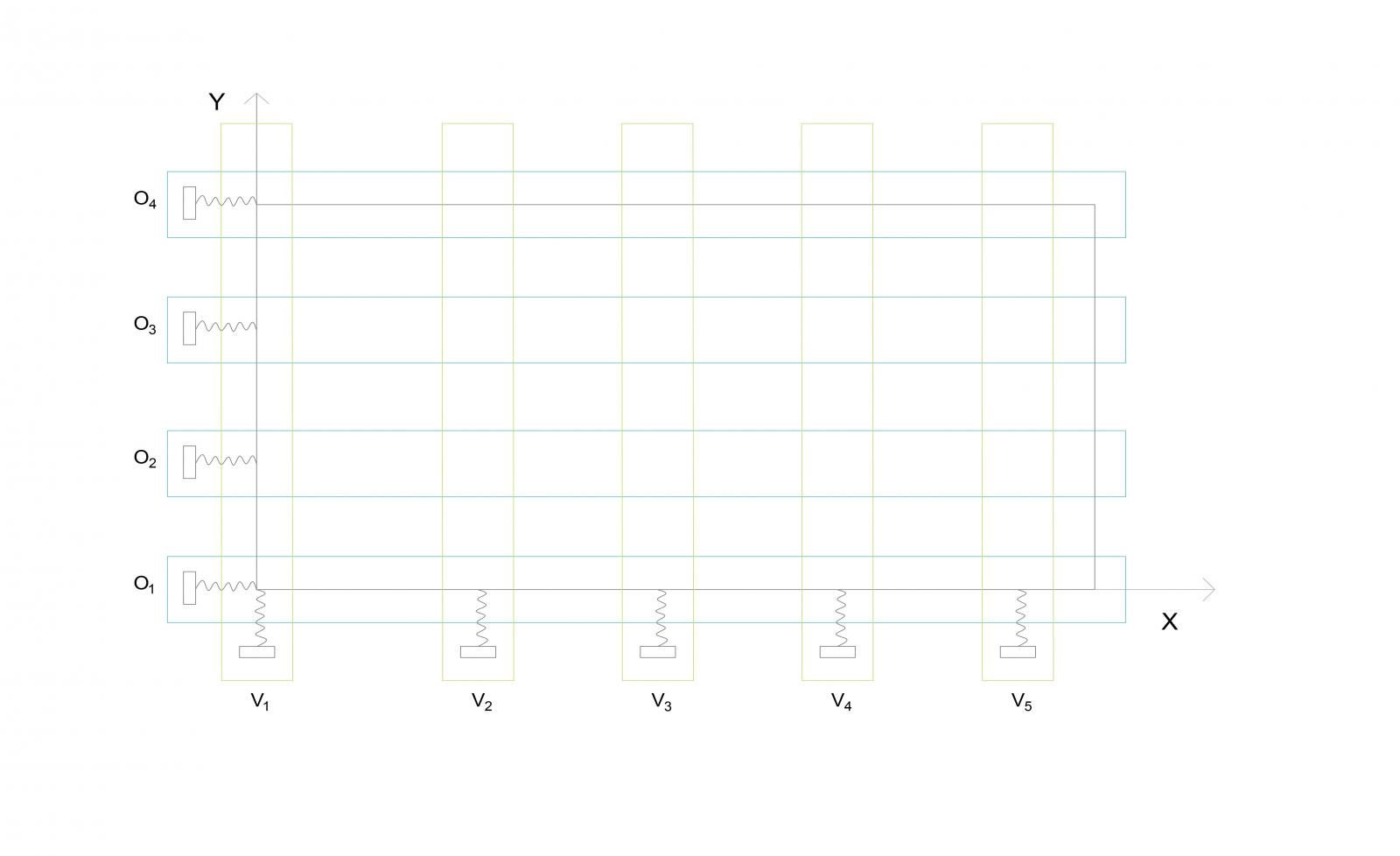
Il solaio è ipotizzabile rigido nel suo piano, mentre i controventi sono cedevoli elasticamente e rappresentabili come molle. Nelle tabelle del foglio excel inseriamo il valore dei momenti d’inerzia per calcolare la rigidezza traslante con cui ogni telaio si oppone alle forze orizzontali.

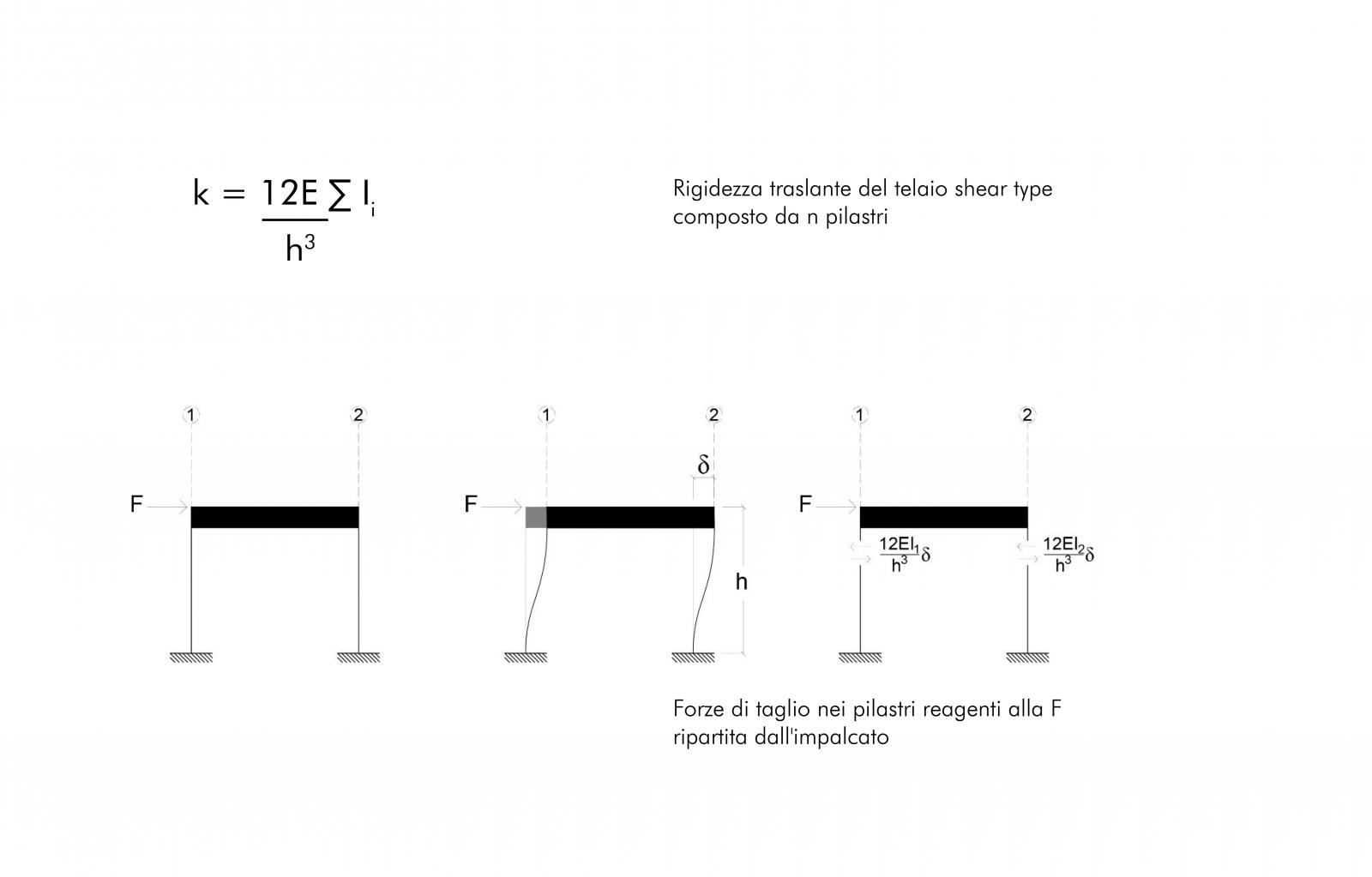
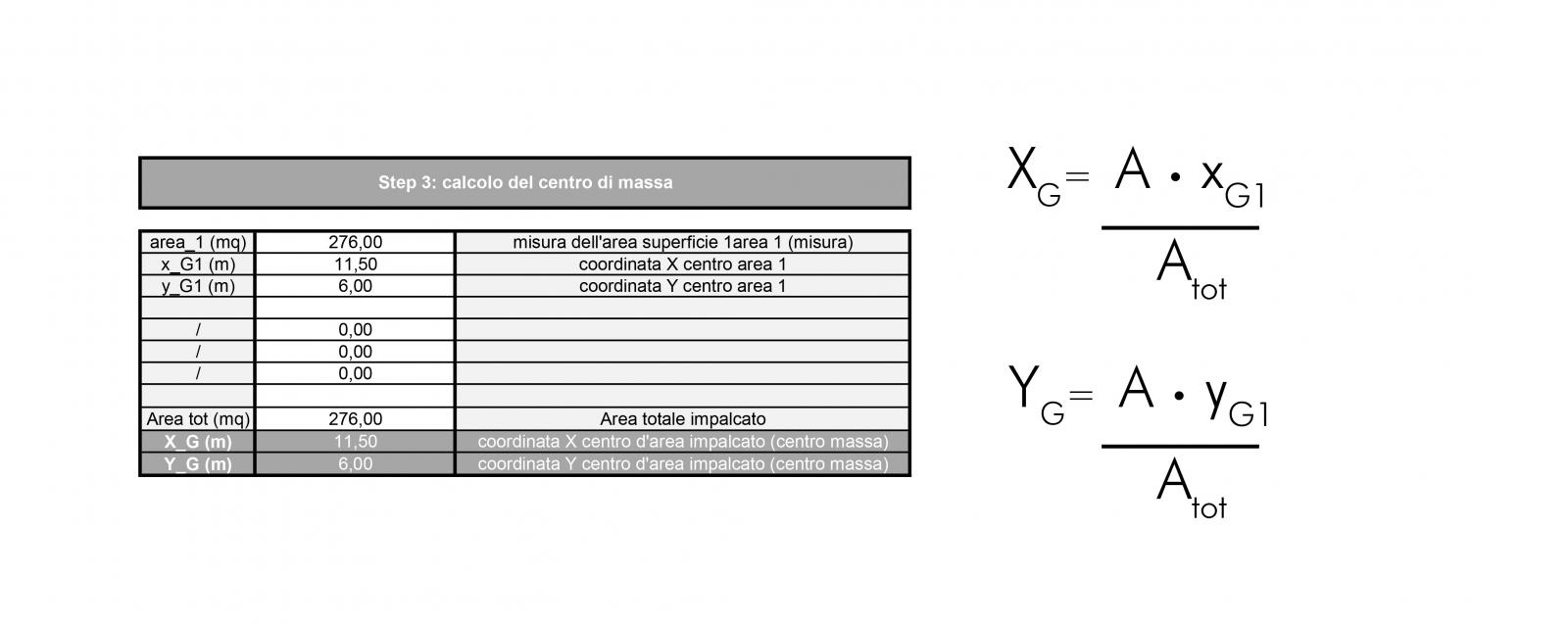
• CALCOLO DEL CENTRO DI MASSA

Nel caso di un impalcato rigido con densità di massa uniforme su tutto l'impalcato il centro di massa coincide con il centro d'area. Calcoliamo il centro di massa dell'impalcato in quanto sarà il punto di applicazione della forza sismica.

• CALCOLO DEL CENTRO DELLE RIGIDEZZE

Trovate le rigidezze traslanti dei controventi verticali e orizzontali, si inseriscono nella tabella sinottica con le relative distanze dal centro di rotazione O. Il calcolo del centro delle rigidezze dipende dalle rigidezze globali dei controventi verticali Kv, tot e orizzontali Ko, tot tote dalle distanze rispetto ad O.

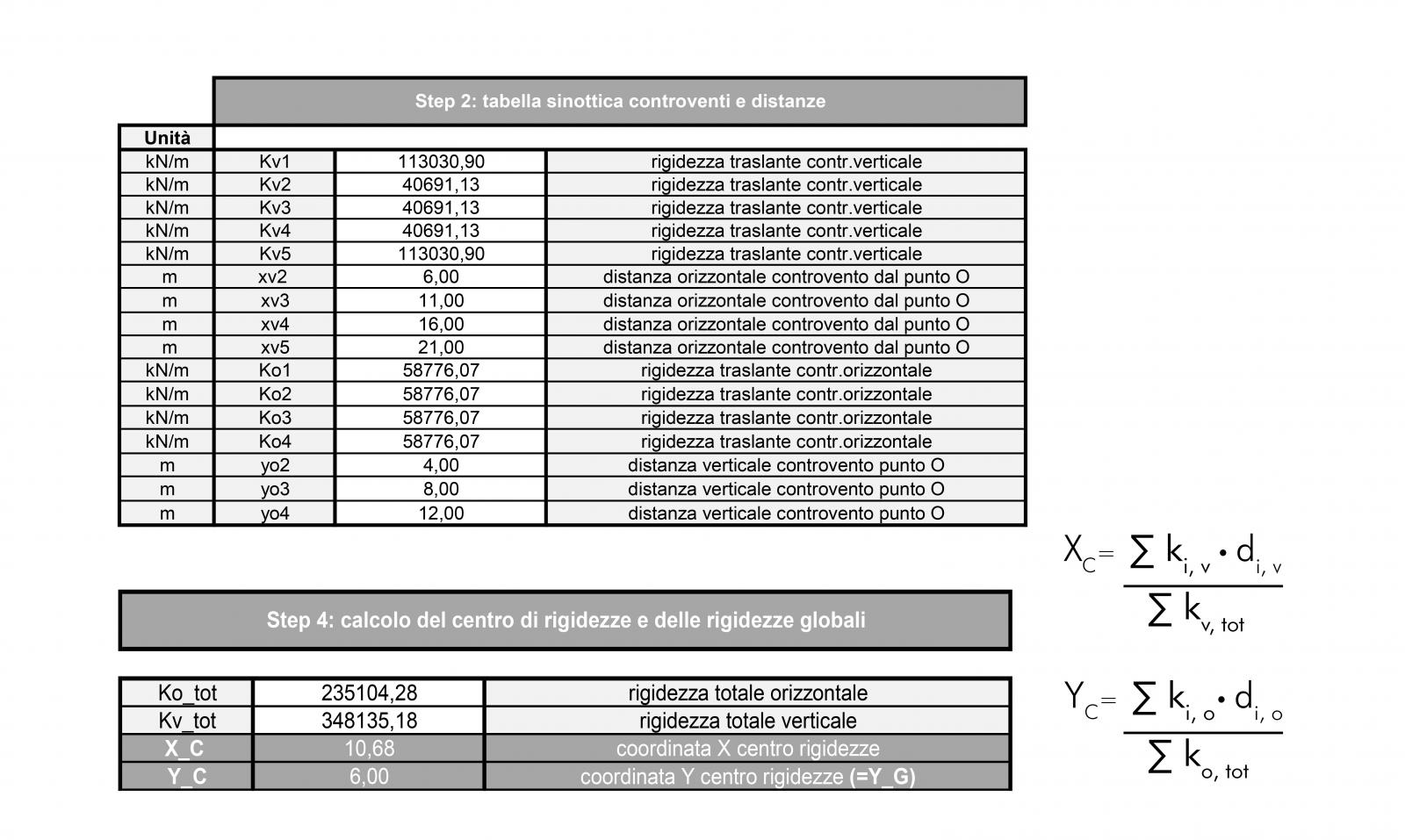
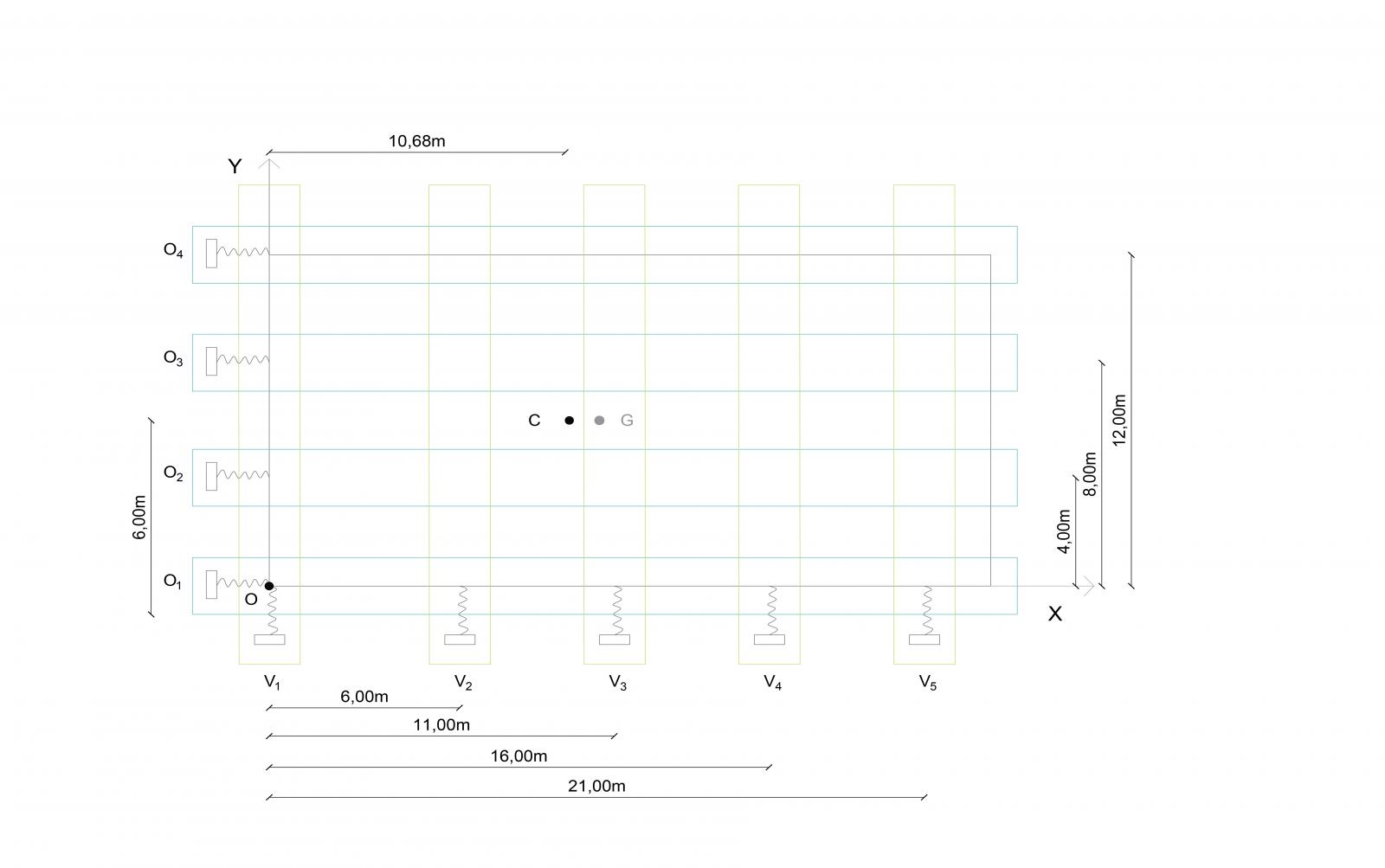
Il centro delle rigidezze C non coincide con il centro di massa G ma risultano avere stessa ordinata Y; quest’operazione ci consente di verificare se l’impalcato subisce una rotazione o sola traslazione. Considerando C come il centro di rotazione di tutti i punti dell'impalcato rigido attorno all'asse Z, la forza sismica Fs esterna applicata a G lungo Y, NON passa per il centro delle rigidezze e quindi avrà luogo una rotazione e una traslazione verticale. La forza sismica Fs applicata lungo X, PASSA per il centro e quindi ci sarà sola traslazione orizzontale.

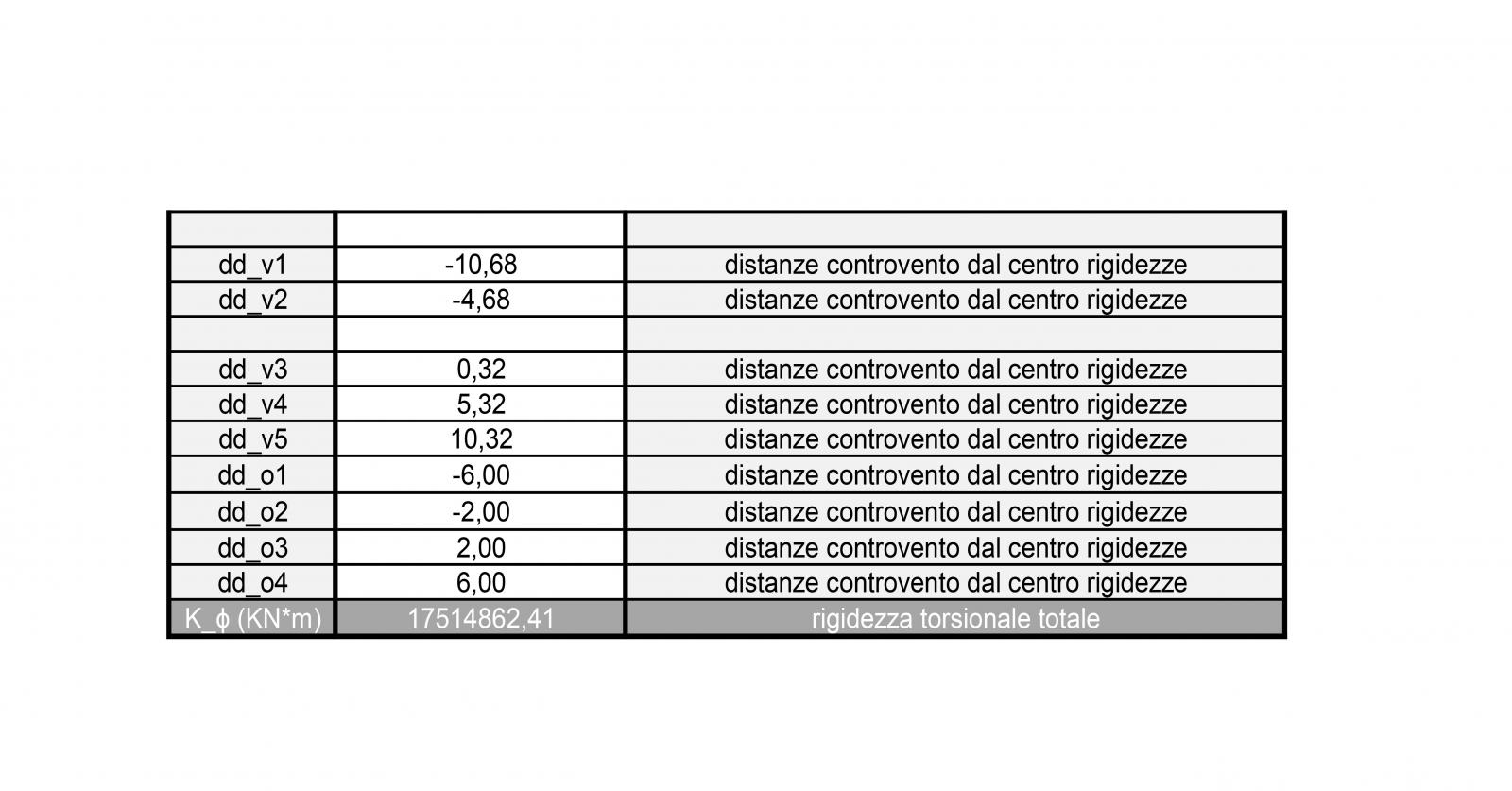
• CALCOLO DELLA RIGIDEZZA TORSIONALE

Oltre a calcolare le coordinate del centro di rigidezza, ricaviamo anche il valore della rigidezza torsionale, calcolando tutte le distanze dei diversi controventi dal nuovo centro di rotazione C per trovare la rigidezza torsionale e in seguito calcolare la rotazione dell'impalcato.

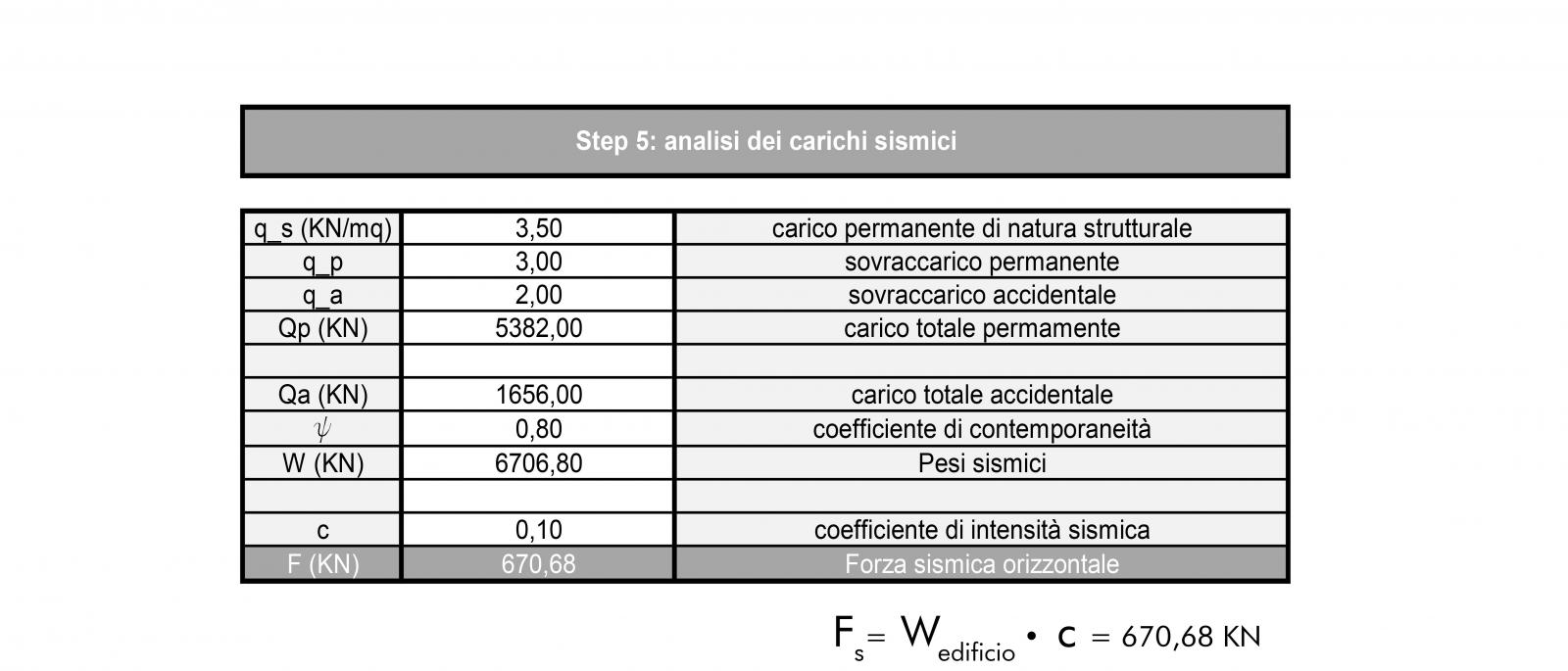
• CALCOLO DEI CARICHI ORIZZONTALI

Per la ripartizione delle forze orizzontali, manca ora solo il carico orizzontale, essendo questo ipotizzabile come una forza sismica, si ricava tale carico dalla formula:

F s = W edificio • c

Vengono inseriti nella tabella i valori dei carichi che definiscono il tipo di solaio e calcoliamo la forza peso dell'edificio, uguale alla massa dell'edificio per l'accelerazione.

Insieme all’utilizzo dei coefficienti di contemporaneità e di intensità sisimica si ricava la forza sismica orizzontale da applicare sul centro di massa.

W edificio = P = Mg ( Forza Peso dell'edificio in KN )

P = QS + QP + 0,8 • QA ( 0,8 corrisponde al valore del coefficiente di contemporaneità)

QS = npiani • A tot • qs

Qp = npiani • A tot • qp

Qa= npiani • A tot • qa

Introduciamo un coefficiente di intesità sismica c per tenere conto della sismicità del luogo di progettazione dell’edificio.

• RIPARTIZIONE DELLE FORZE ORIZZONTALI

Si dovrà ora quantificare la ripartizione della forza sismica FS sui controventi con le relative reazioni elastiche, e gli effetti cinematici sull’impalcato in termini di traslazione e di rotazione rigida:

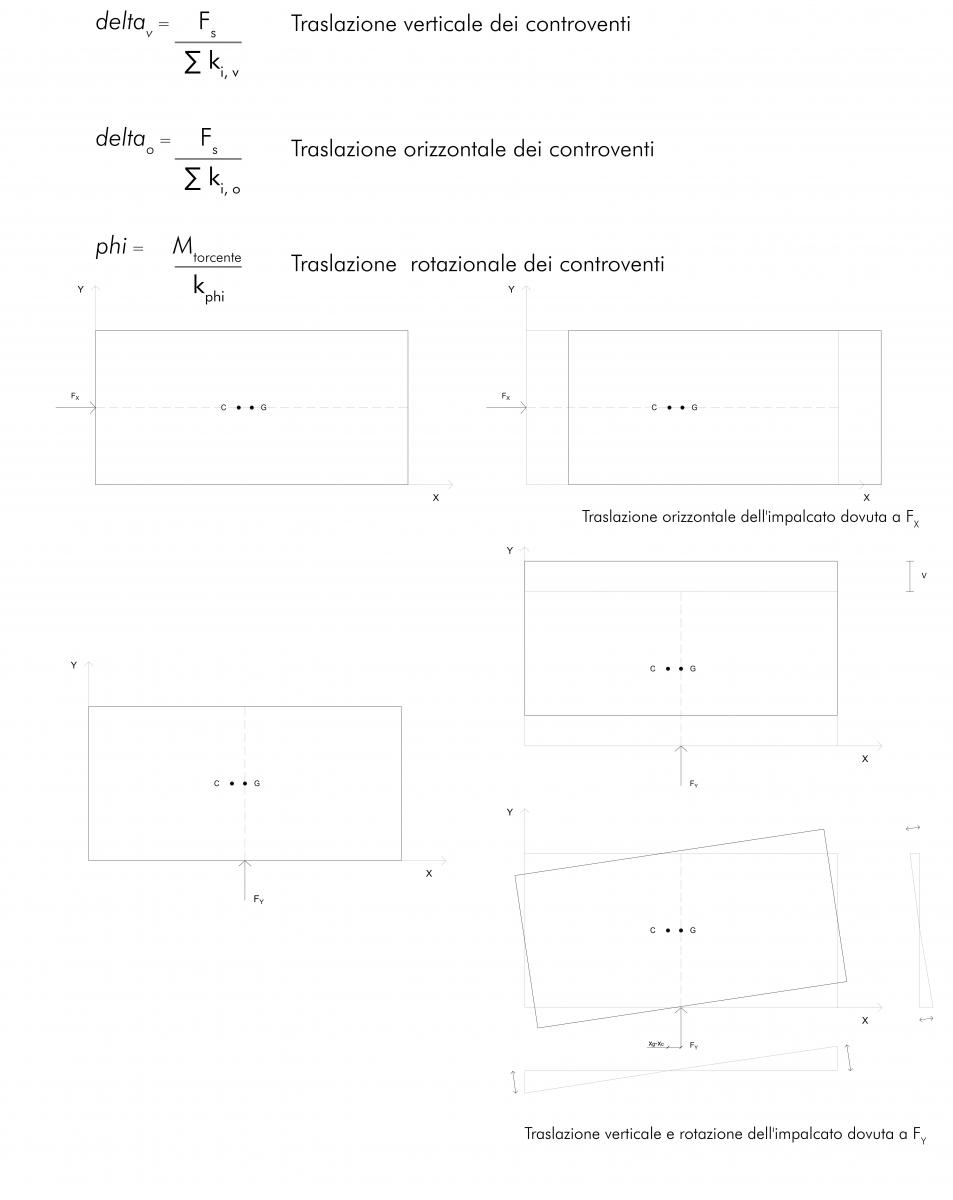
Quando la forza è parallela all’asse X, le reazioni elastiche dei controventi verticali e orizzontali sono uguali a:

Ri, v = ki, v ( delta,v • ddi, v ) = ki, v ( delta,v • 0 ) = 0

Ri, o = ki, o ( delta,o + phi • ddi, o ) = ki, o • delta,o

Quando la forza è parallela all’asse Y, le reazioni elastiche dei controventi verticali e orizzontali sono uguali a:

Ri, v = ki, v ( delta,v + phi • ddi, v )

Ri, o = ki, o ( phi • ddi, v )

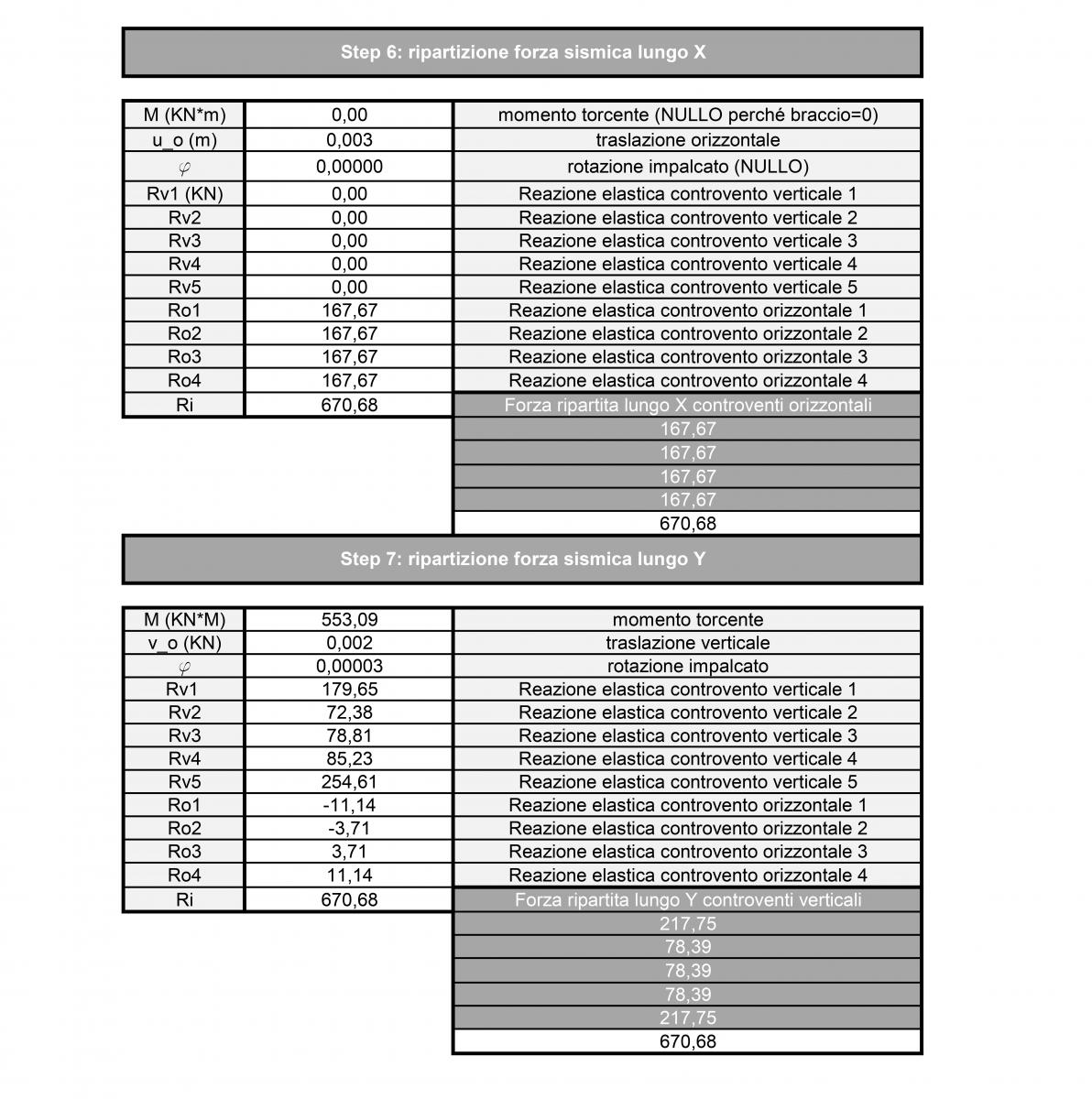
La forza ripartita lungo X, controbilanciata dalle reazioni dei controventi orizzontali, è uguale alla traslazione orizzontale per la rigidezza traslante del controvento e non genera rotazione perché l'asse passa per il centro delle rigidezze dove si annulla il Momento Torcente avendo braccio nullo.

La forza ripartita lungo Y, controbilanciata dalle reazioni dei controventi verticali, genera una traslazione verticale e una rotazione attorno al centro delle rigidezza.

Fx = k,o • delta,o

Fy = k,v • delta,v

• ASSEGNAZIONE CARICHI ORIZZONTALI

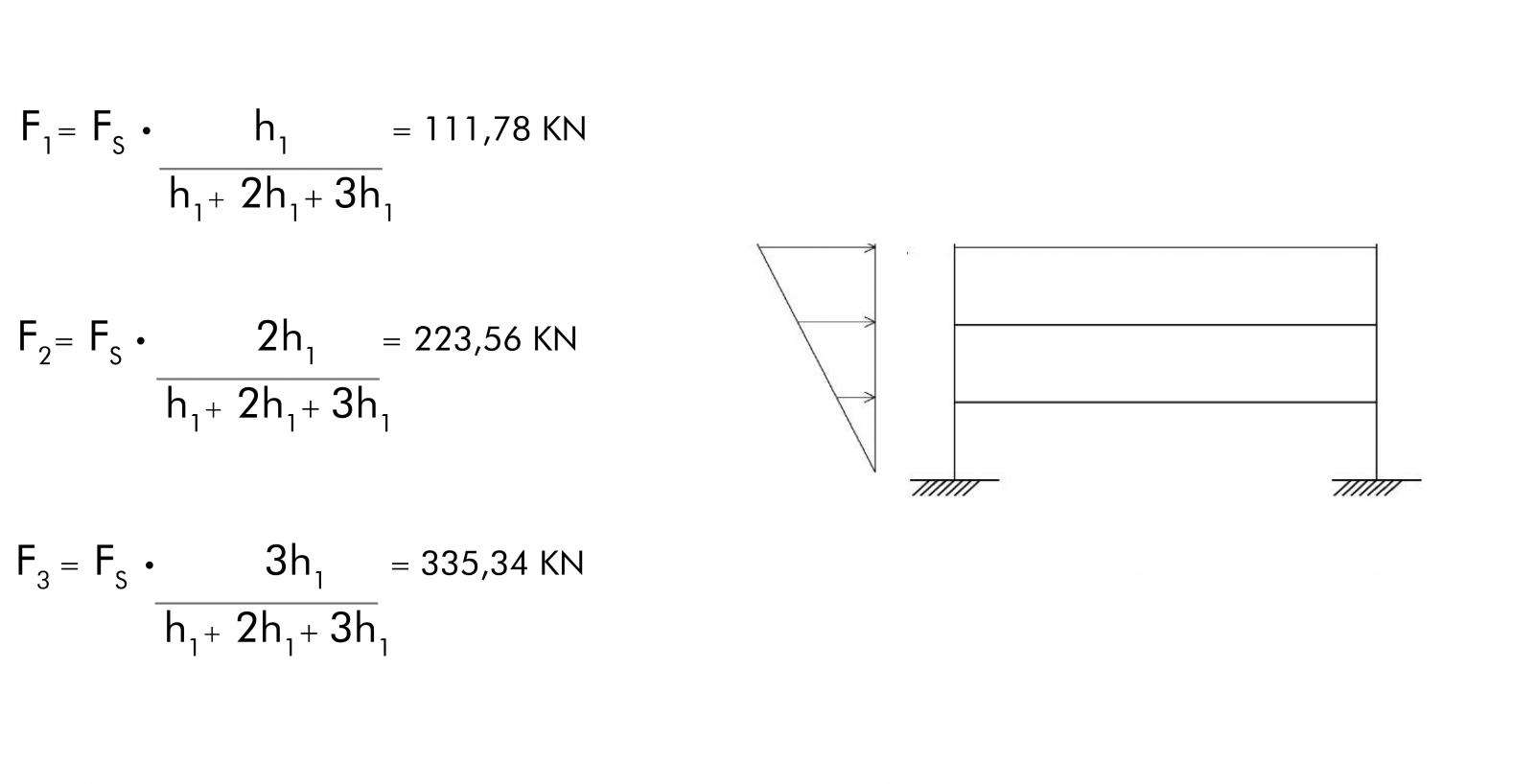
Fi = FS • hi / ∑ hi

Fi corrisponde al valore della forza sismica da applicare nel centro di massa di ciascun piano. Fi risulta direttamente proporzionale alla quota, gli ultimi piani subiscnono maggiormente l’azione sismica, ed è per questo che la distribuzione della forza sismica ha un andamento triangolare.

• VERIFICA A PRESSOFLESSIONE DEI PILASTRI

Dopo aver mandato l'analisi con il carico SLU e la forza sismica F lungo Y, ricaviamo le nuove sollecitazioni di progetto che verranno inserite nella tabella excel ai fini della verifica a pressoflessione dei pilastri.

Dalla verifica risultano non verificate le sezioni 30 x 30 cm di due pilastri angolari dell'ultimo piano che ricevono maggiore flessione. Andando a cambiare le dimensioni della sezione con 40 x 40 cm la verifica risulta soddisfatta.

Sovrapposizione degli effetti: Traslazione orizzotale e rotazione, Piano XY

Sovrapposizione degli effetti: Traslazione orizzontale e rotazione, Piano ZY