Dimensionamento di massima di un aggetto risolto con una trave Vierendeel

Studentesse: Mariani Lucia, Maurelli Ilaria

INTRODUZIONE

Una trave Vierendeel è una tipologia di travatura reticolare costituita da due correnti, uno superiore e uno inferiore, collegati da montanti irrigiditi che non hanno quindi bisogno di essere controventati con aste diagonali.

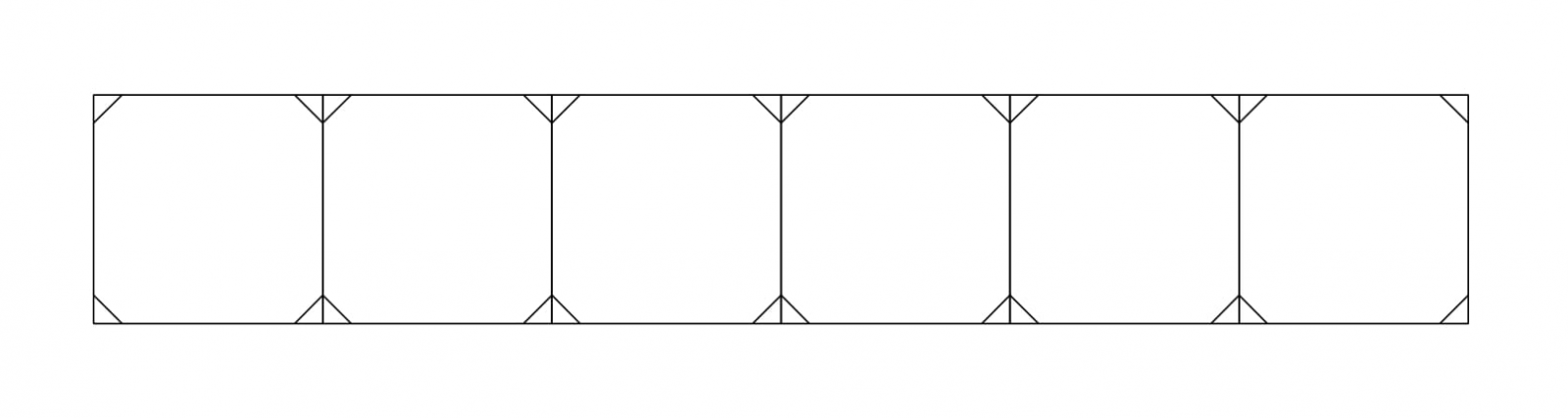
A differenza di una travatura reticolare, dove tutte le aste risultano collegate tramite cerniere e soggette unicamente a sforzo normale, la trave Vierendeel presenta dei collegamenti rigidi tra gli elementi e sviluppa sollecitazioni di taglio e momento flettente sia negli elementi orizzontali che in quelli verticali.

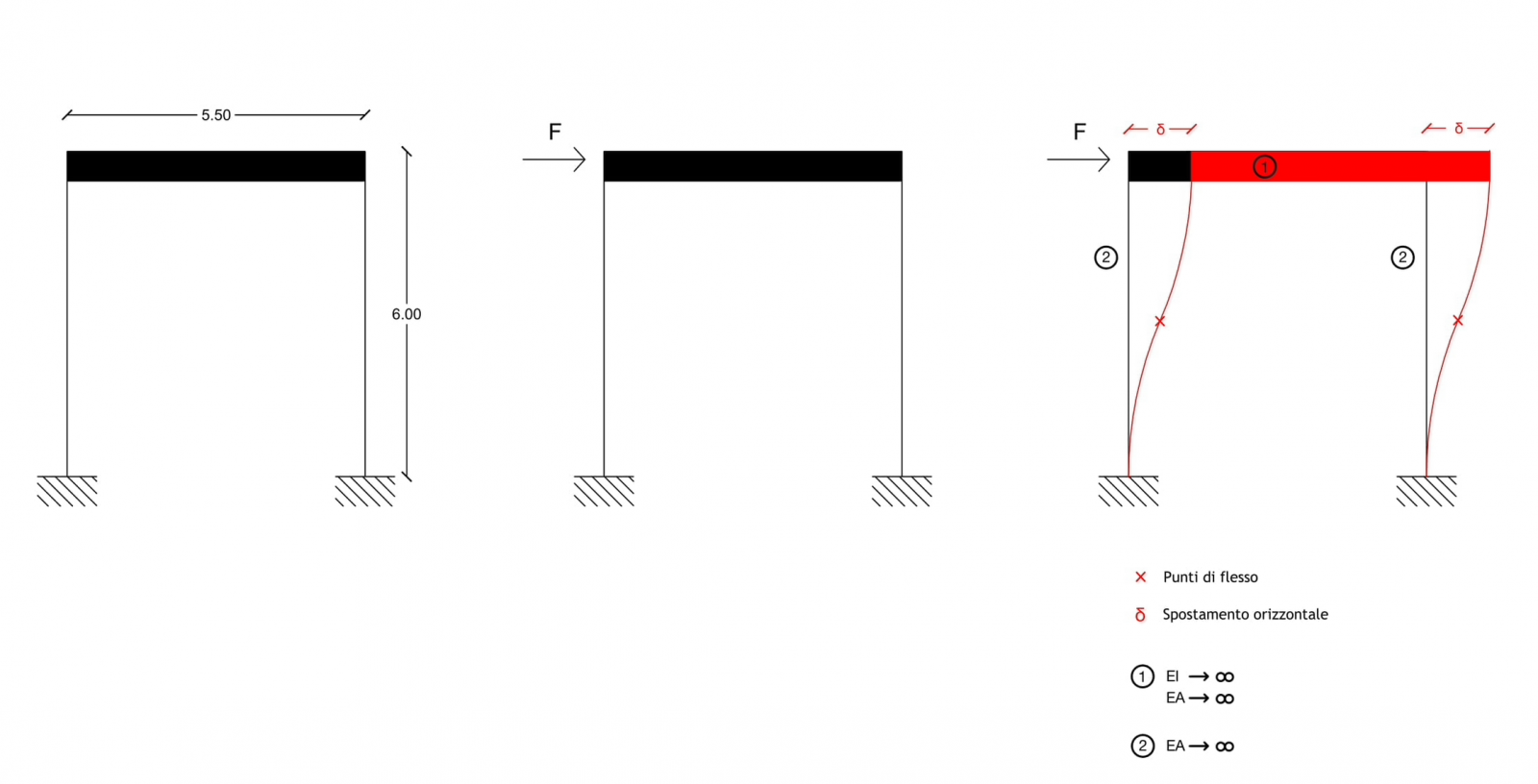
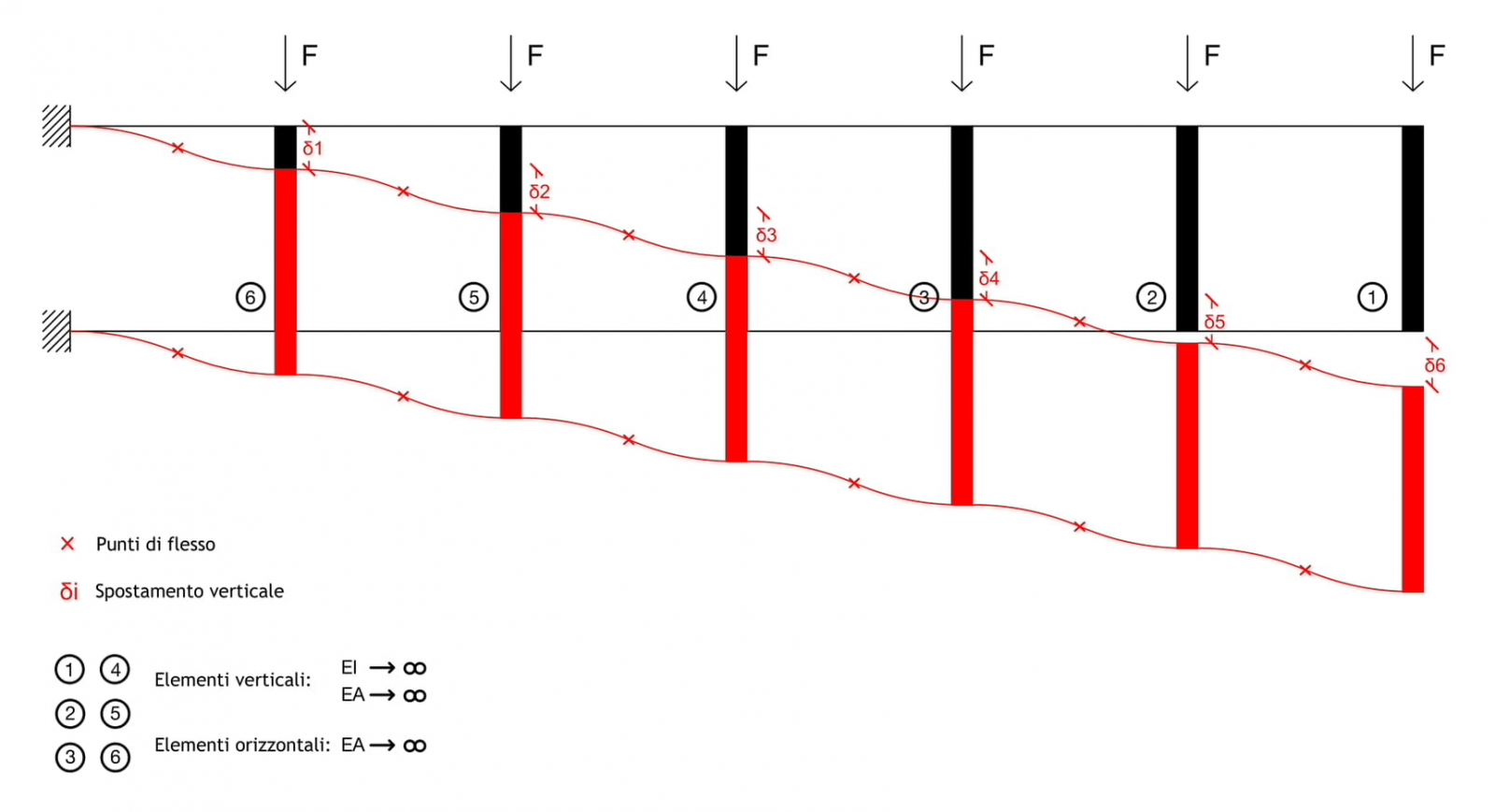
Una modello di trave Vierendeel può essere studiato come un modello di Telaio Shear-Type semplicemente ruotato rigidamente di 90 gradi.
Un telaio Shear-Type è un modello che presenta un elemento orizzontale (trave) infinitamente rigido, sia assialmente che flessionalmente, e due elementi verticali (pilastri) infinitamente rigidi assialmente.
I tre elementi che compongono il telaio Shear-Type sono collegati tra loro tramite nodi rigidi che non permettono quindi la rotazione, e i due pilastri sono vincolati a terra da un incastro.

Una trave Vierendeel è quindi composta da due correnti che hanno le stesse caratteristiche dei pilastri del telaio Shear-Type (infinitamente rigidi assialmente) e una serie di montanti che hanno invece le stesse caratteristiche del traverso del telaio Shear-Type (infinitamente rigido assialmente e flessionalmente).

GEOMETRIA

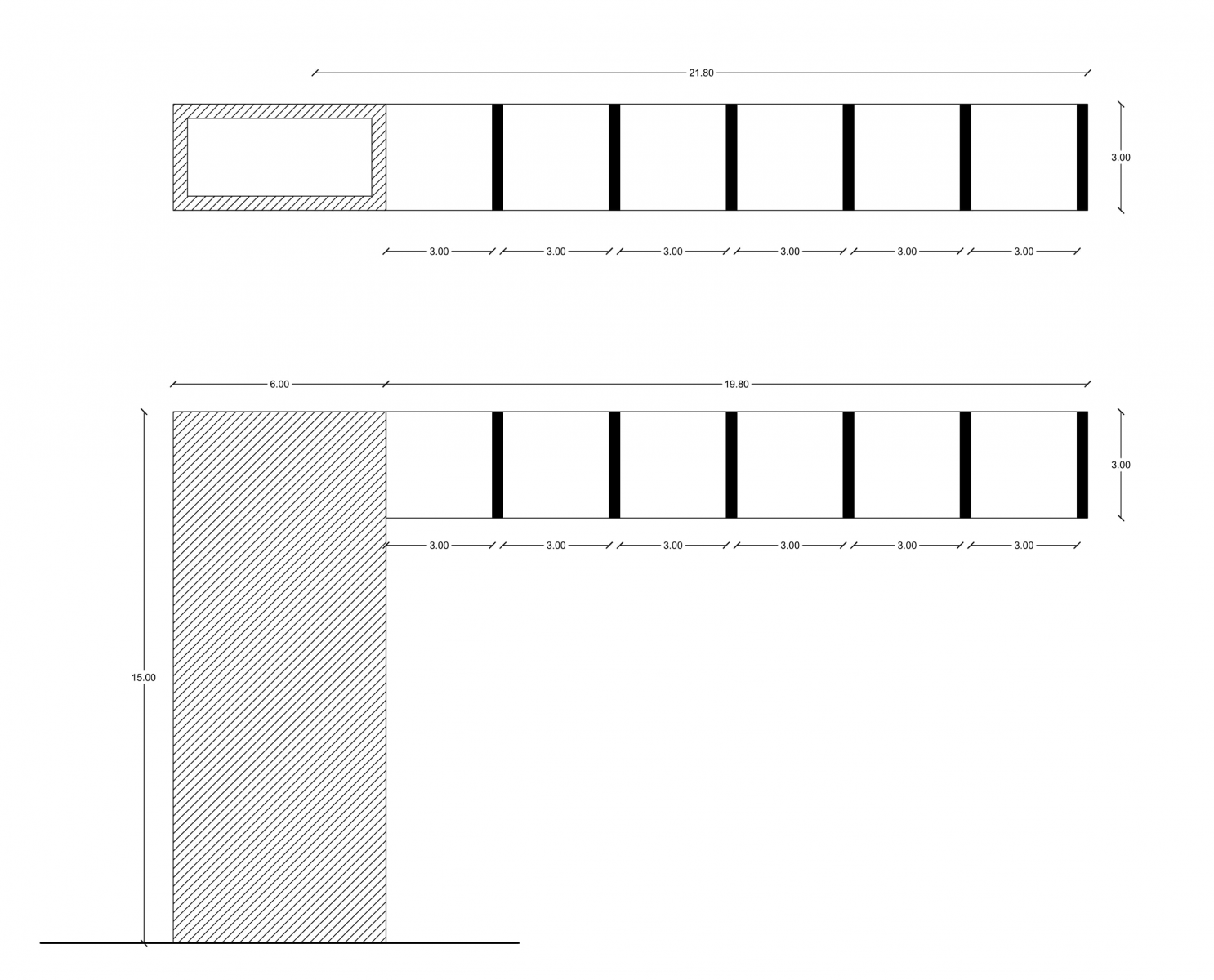
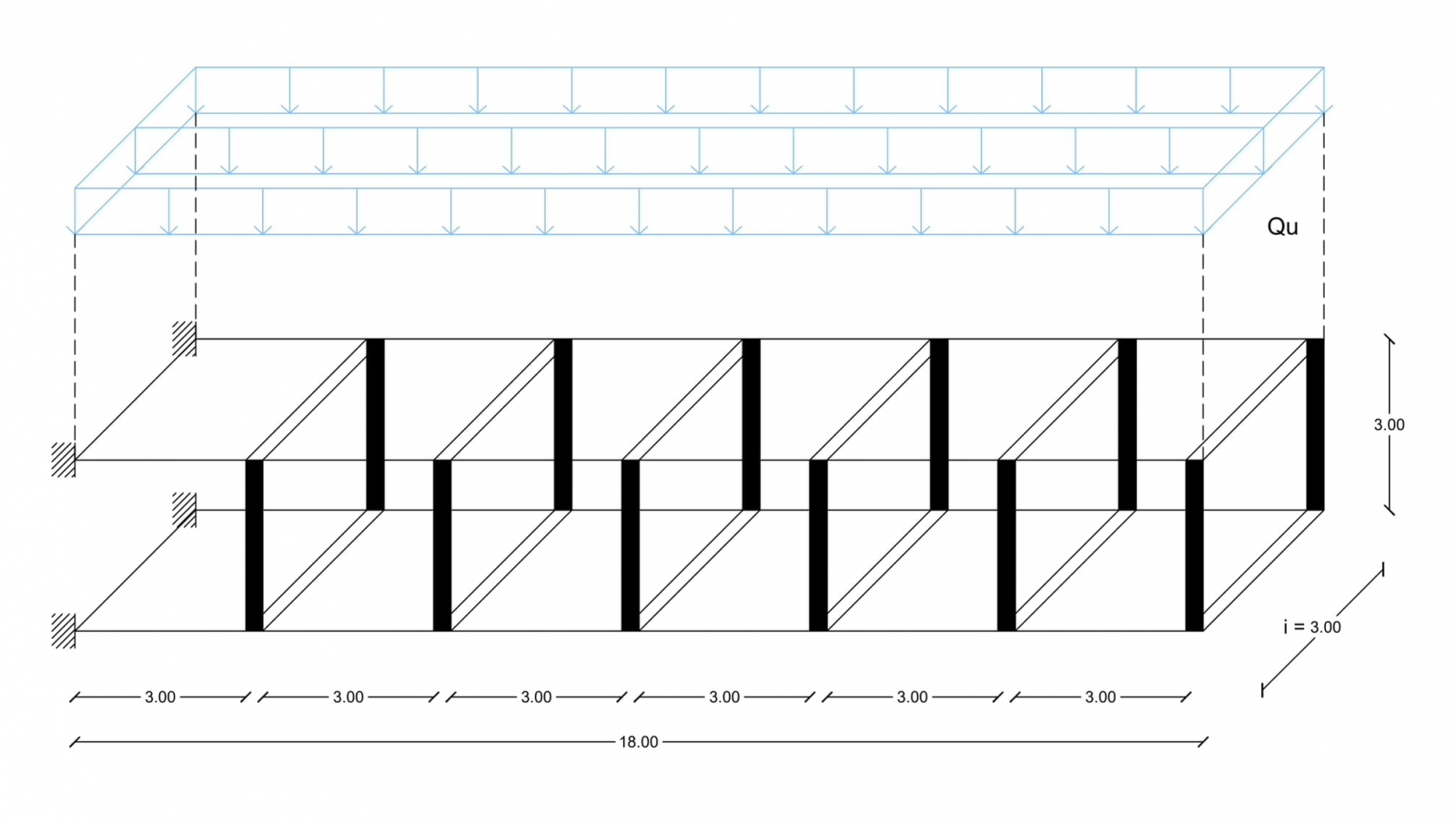
Abbiamo immaginato di effettuare un dimensionamento di massima di una trave Vierendeel aggettante, vincolata a una sola estremità da un setto.

Una trave Vierendeel è immediatamente riconoscibile dalla sua geometria.
Nel nostro caso è infatti caratterizzata da un ritmo di sei campate quadrate da 3,00 metri di luce in entrambe le direzioni (x e y) per 3,00 metri di altezza; una grande luce aggettante di 18,00 metri, la presenza di pilastri infinitamente rigidi e un supporto molto robusto.
Come supporto abbiamo ipotizzato una gabbia ascensore di 3,00 x 6,00 metri con uno spessore murario dei setti di 0,40 metri.

ANALISI DEI CARICHI

Per prima cosa abbiamo effettuato un analisi dei carichi per ricavare il valore delle forze concentrate che agiscono su ogni pilastro della trave Vierendeel.
Abbiamo quindi calcolato i carichi agenti su un metro quadrato di solaio suddividendoli nelle tre categorie
Carichi permanenti strutturali
Sovraccarichi permanenti non strutturale
Carichi accidentali

Analisi dei carichi di un solaio in laterocemento

1. Pavimentazione in parquet = 2 cm = 0,02 m
2. Massetto = 3 cm = 0,03 m
3. Isolante = 4 cm = 0,04 m
4. Soletta collaborante = 5 cm = 0,05 m
5. Pignatte = 20 cm = 0,20 m
6. Travetti = 20 cm = 0,20 m
7. Intonaco = 1,5 cm = 0,015 m

Spessore totale solaio = 35,5 cm = 0,355 m

Carico distribuito superficiale

1. 0,02 m x 7,2 KN/m³ = 0,144 KN/mq
2. 0,03 m x 20 KN/m³ = 0,60 KN/mq
3. 0,04 m x 0,2 KN/m³ = 0,008 KN/mq
4. 0,05 m x 25 KN/m³ = 1,25 KN/mq
5. 2 (0,2 x 0,12 x 1) m³/m² x 25 KN/m³ = 1,20 KN/m²
6. 2 (0,38 x 0,20 x 1) m³/m² x 15 KN/m³ = 2,28 KN/m²
7. 0,015 m x 18 KN/m³ = 0,27 KN/m²

Carico strutturale q_S
Soletta + travetti + pignatte
1,25 KN/m² + 1,2 KN/m² + 2,28 KN/m² = 4,73 KN/m²
Sovraccarico permanente q_P
Parquet + massetto + isolante + intonaco + incidenza impianti + incidenza tramezzi
0,144 KN/m² + 0,6KN/m² + 0,008 KN/m² + 0,27 KN/m² + 0,5 KN/m² + 1 KN/m² = 2,52 KN/m² = 2,52 KN/m²
Carico accidentale q_a
Dato fornito dalla normativa in base alla destinazione d’uso = 2,00 KN/m²

Abbiamo successivamente considerato le combinazioni di carico fornite dalla normativa per le verifiche agli stati limite utilizzando coefficienti parziali di sicurezza sfavorevoli

Combinazione di carico allo stato limite d’esercizio SLE
γ̃s qs + γ̃p qp + γ̃a qa = 1 x 4,73 KN/m² + 0,7 x 2,52 KN/m² + 0,7 x 2 KN/m² = 7,88 KN = 7,9 KN/m²
qe = 7,90 KN/m²
Combinazione di carico allo stato limite ultimo SLU
γs qs + γp qp + γa qa = 1,3 x 4,73 KN/m² + 1,5 x 2,52 KN/m² + 1,5 x 2 KN/m² = 12,89 KN/m² = 12,9 KN/m²
qu = 12,90 KN/m²

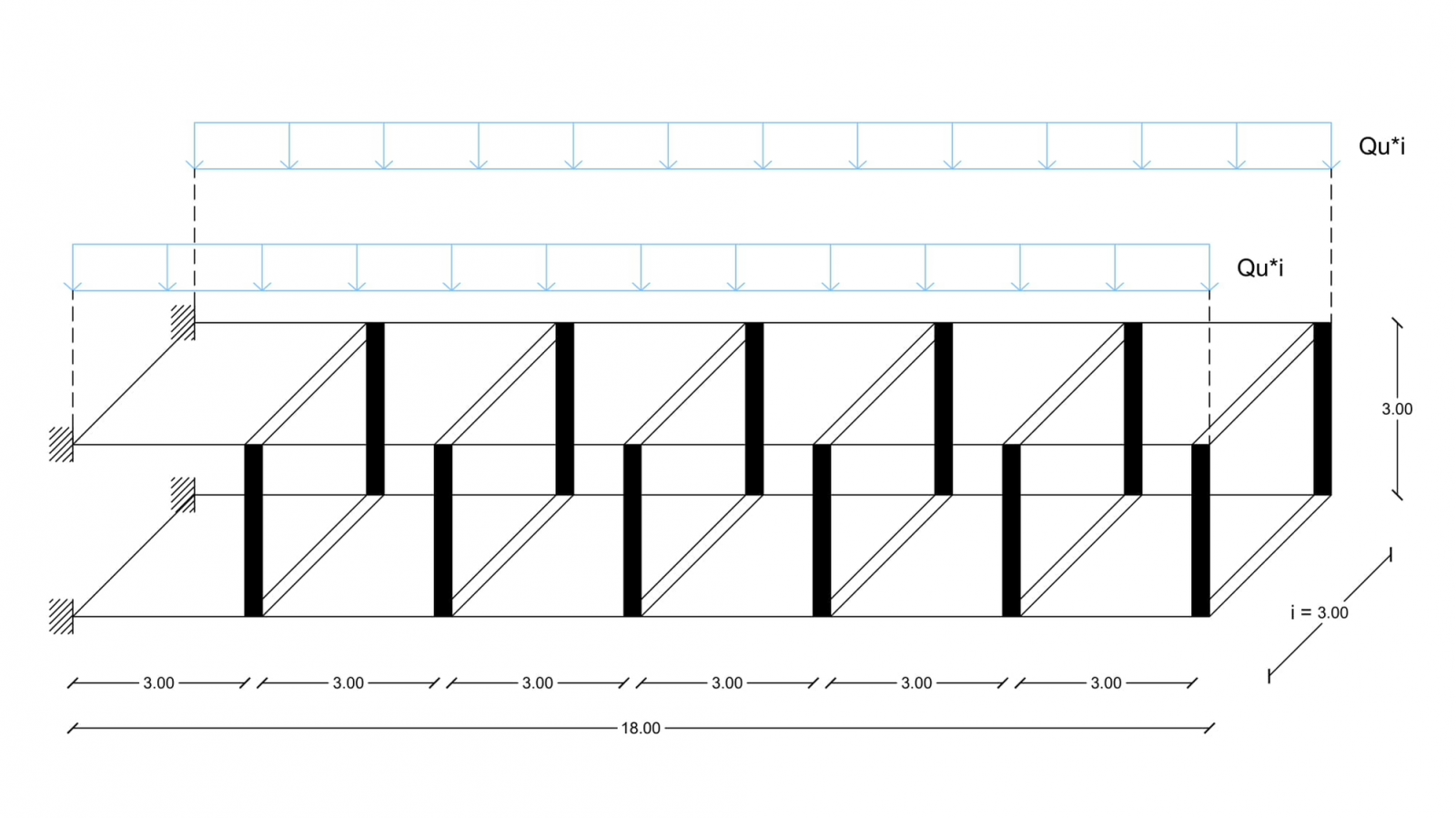
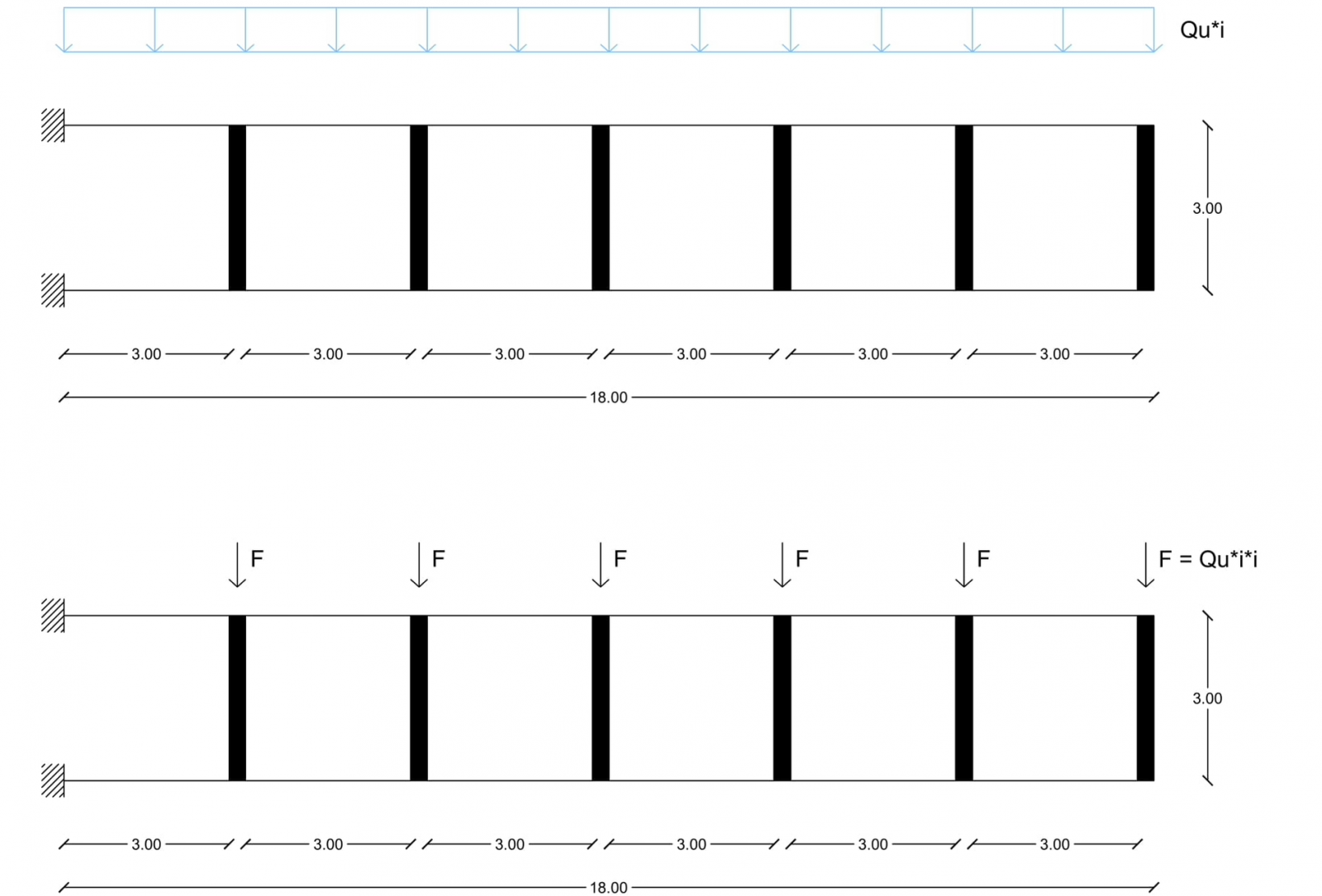
Una volta ottenuto il valore della combinazione di carico allo stato limite ultimo, essendo un valore distribuito sulla superficie, abbiamo moltiplicato il valore per l’interasse lungo l’asse y (3,00 m), e successivamente per l’interasse lungo l’asse x (3,00 m), ottenendo i singoli valori delle forze concentrate agenti sui pilastri.

Qu * i = 12,90 KN/m² * 3,00 m = 38,70 KN/m
F = Qu * i * i = 38,70 KN/m * 3,00 m = 116,10 KN
F = 116,10 KN

SOLLECITAZIONI

Deformata
Il diagramma della deformata equivale al diagramma di un telaio Shear-Type deformato ruotato di 90 gradi.
La deformazione dei correnti ha due diverse curvature, il punto in cui avviene il cambiamento di curvatura è esattamente pari a L/2 cioè al punto di flesso dove la tangente taglia la curva.
In quel punto il momento flettente risulterà pari a zero perchè momento flettente e curvatura sono strettamente legati dalla relazione
M = (EI) X

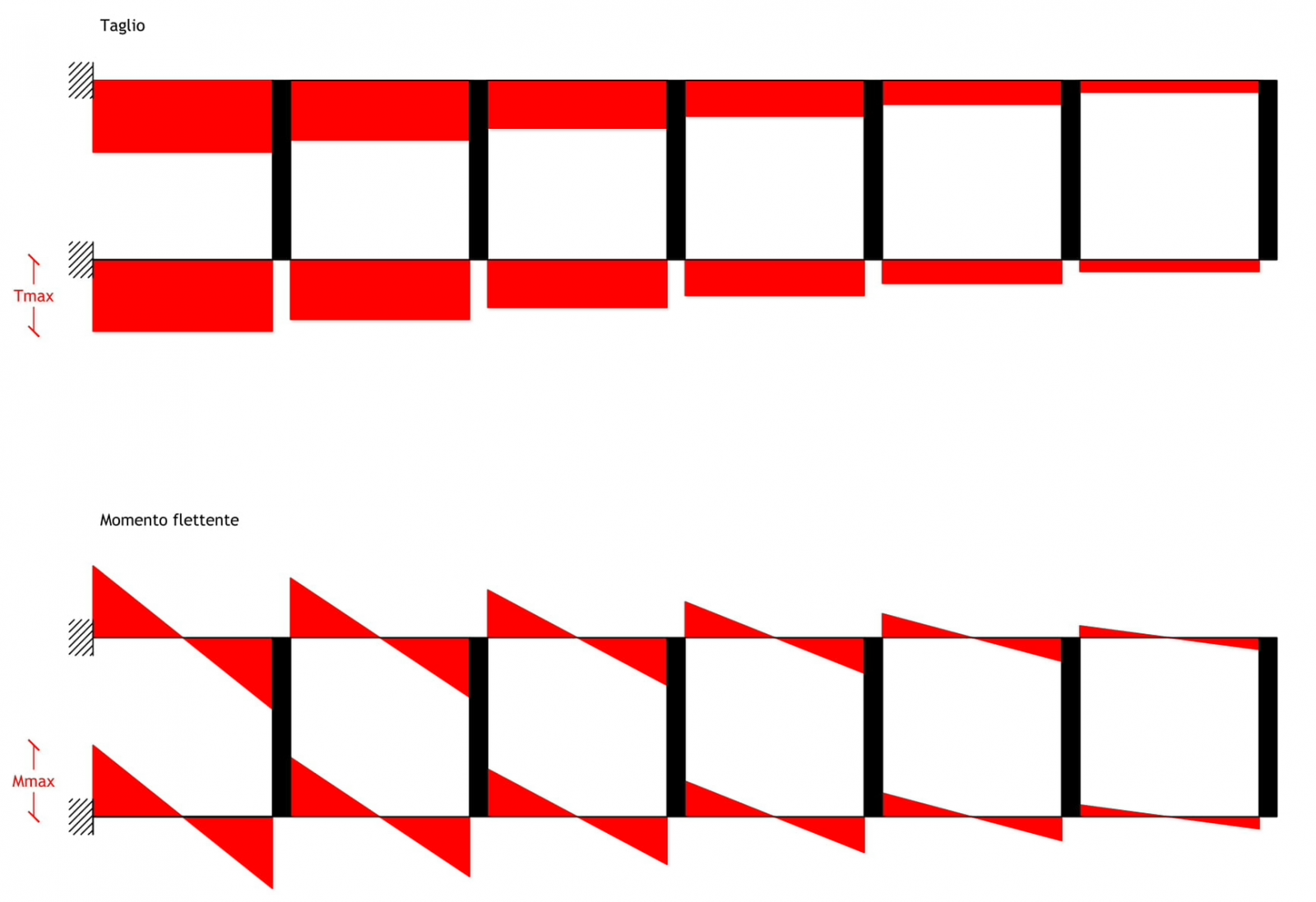
Taglio
Il diagramma del taglio è costante ma il valore aumenta di asta in asta mano a mano che ci avviciniamo al vincolo di incastro esterno, dove avremo il valore massimo.

Momento flettente
Il diagramma del momento è lineare perché non c’è carico ripartito sulla trave.
La pendenza della retta che individua l’andamento del momento flettente è il valore del taglio e quindi anche il valore del momento massimo si trova in corrispondenza del vincolo esterno.
Il diagramma del momento flettente si annulla nel punto di flesso della deformata, cioè in mezzeria.

EQUILIBRIO

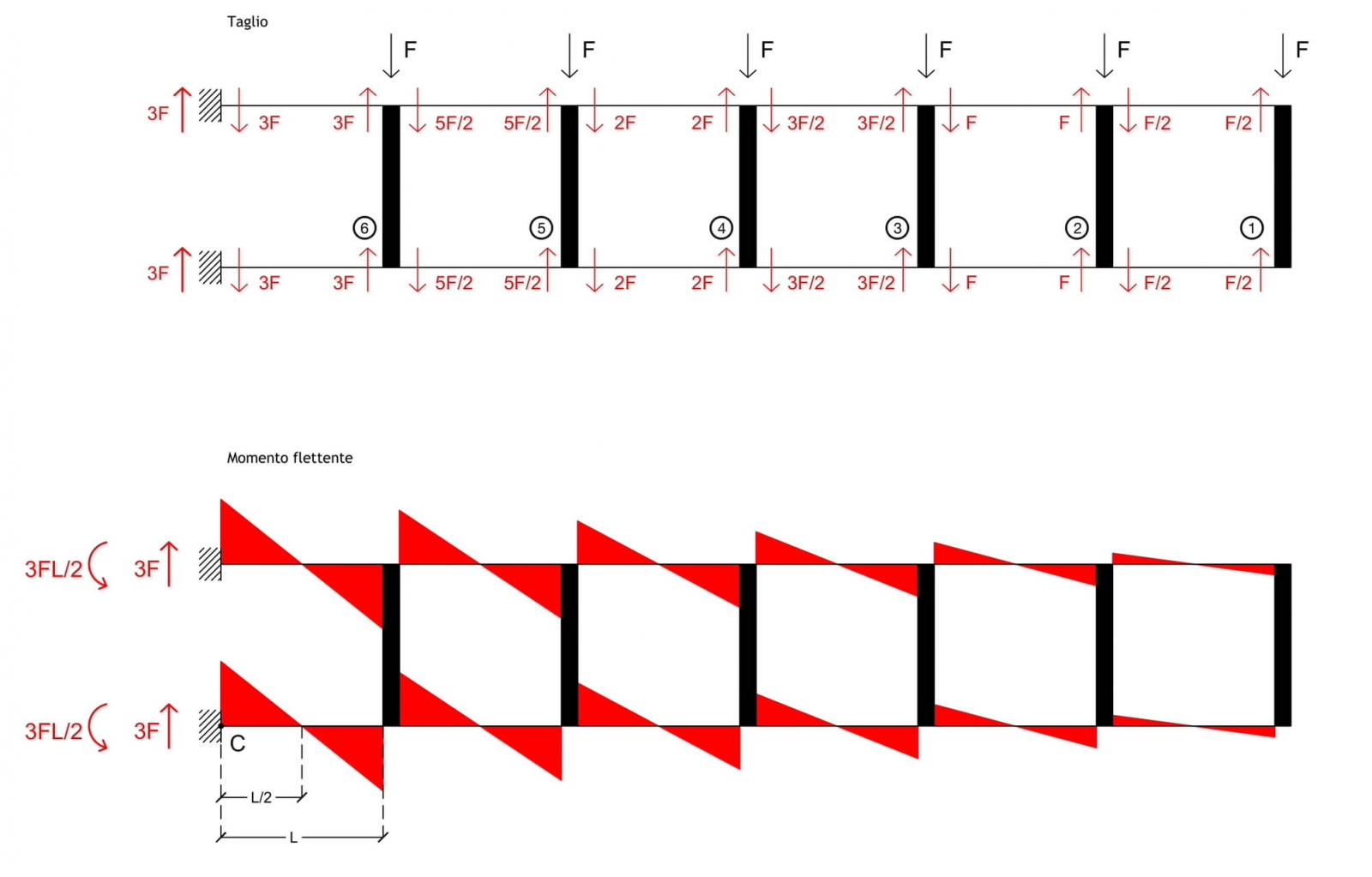
Per verificare che la morfologia scelta, trave Vierendeel e setto, siano effettivamente equilibrati a traslazione e a rotazione, calcoliamo le sollecitazioni presenti in corrispondenza dei vincoli e verifichiamo che soddisfino le equazioni di equilibrio.

Assumendo che in ogni singolo tratto della trave (immaginando di effettuare dei tagli) deve essere verificato l’equilibrio delle forze interne, possiamo dedurre che in corrispondenza del vincolo di incastro (con il quale approssimiamo il setto) si svilupperà una forza verticale uguale e opposta a quella che si sviluppa all’interno del corrente 6, con valore 3F.

In corrispondenza del vincolo si svilupperà inoltre un momento antiorario che dovrà bilanciare la rotazione oraria generata dalle forze verticali.
Tale valore del momento è ottenuto come

Momento = Taglio x Braccio
M = 3F x L/2 = 3FL/2

Dove il braccio è la distanza tra il centro di rotazione e il punto di flesso della deformata, cioè dove il momento si annulla.

A questo punto verifichiamo l’equilibrio a traslazione e a rotazione

L’equilibrio alla traslazione verticale è verificato in quanto la somma delle forze concentrate è equilibrata dalle due forze che si sviluppano in corrispondenza dei vincoli.
F - F - F - F - F - F + 3F + 3F = 0
- 6F + 6F = 0

L’equilibrio alla rotazione risulta
3FL/2 + 3FL/2 - FL - 2FL - 3FL - 4FL - 5FL - 6FL ≠ 0
3FL/2 + 3FL/2 - FL - 2FL - 3FL - 4FL - 5FL - 6FL = -18FL

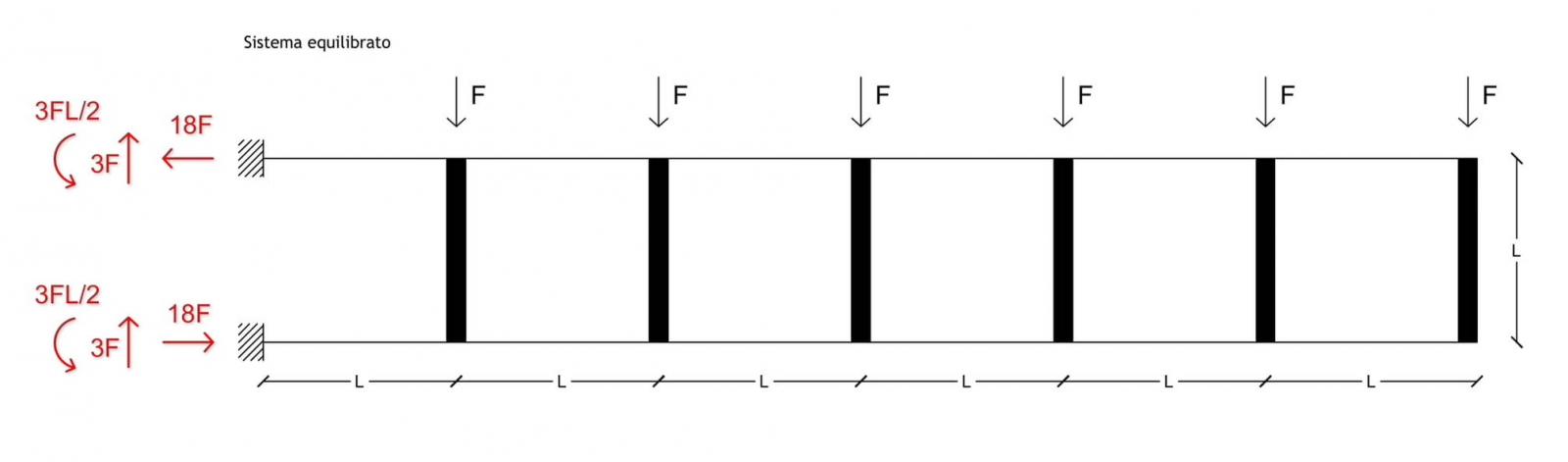
Notiamo che l’equilibrio alla rotazione non è verificato e risulta un momento orario non equilibrato pari a 18FL
Non essendoci altre forze che possono generare una rotazione, il momento risultante sarà equilibrato da una coppia di forze orizzontali uguali e opposte con braccio della coppia pari all’altezza della trave Vierendeel, quindi L.
Tali forze avranno un valore pari a

Momento = Forza x Braccio
Forza = Momento / Braccio 
Fo = 18FL / L = 18 F

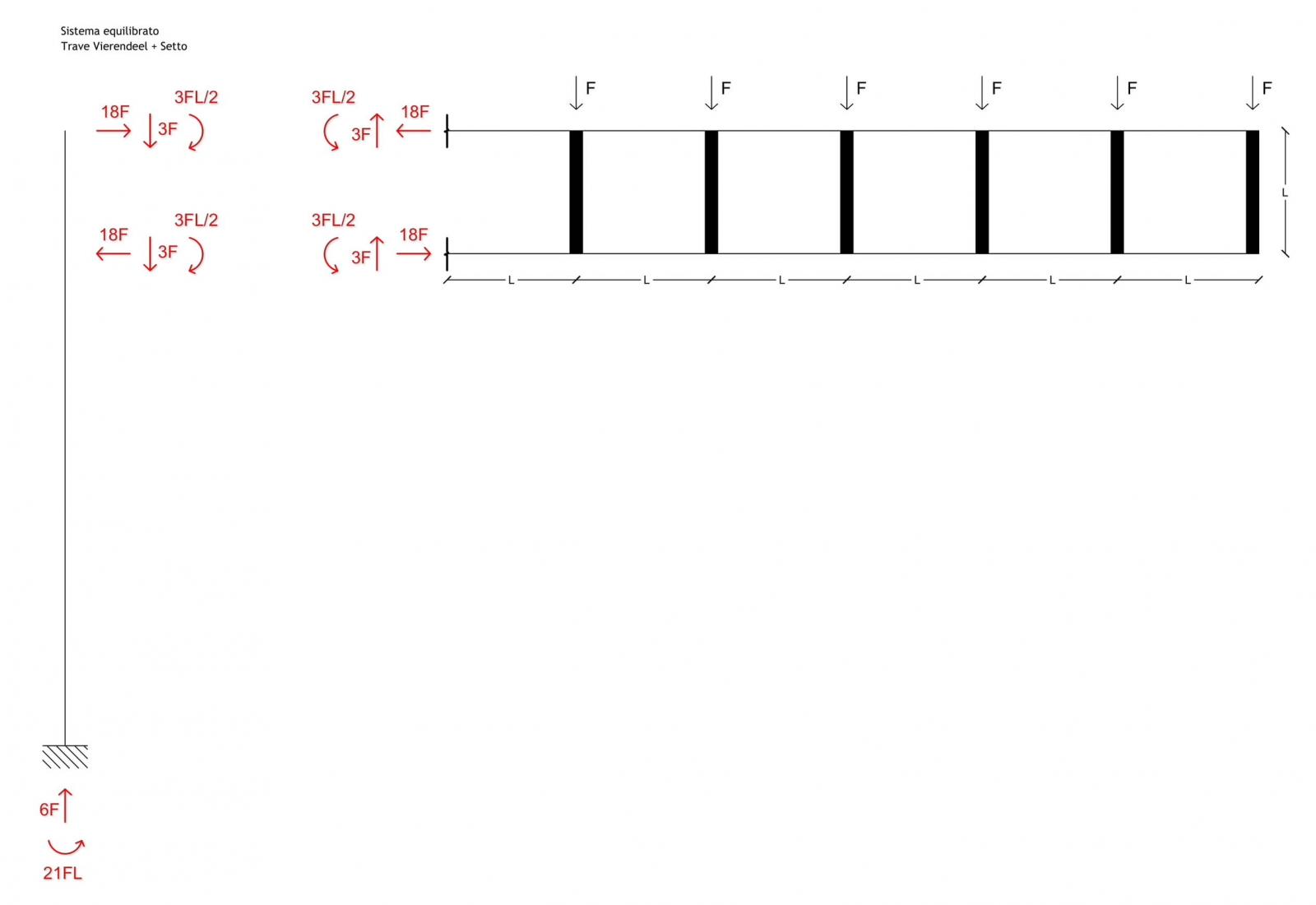
A questo punto verifichiamo che tutto il sistema, compreso il setto, modellato come una mensola incastrata nell’estremità inferiore, sia in equilibrio.
Calcoliamo quindi le sollecitazioni che raggiungono l’incastro a terra affinché il sistema sia equilibrato

Forze verticali
Forze concentrate verticali
F + F + F + F + F + F = 6F
Forze verticali equilibranti
3F + 3F = 6F

Momento
Momenti generati dalle forze concentrate verticali
FL + 2FL + 3FL + 4FL + 5FL + 6FL = 21FL
Momenti equilibranti e momento generato dalla coppia di forze
3FL + 3FL + 18 FL = 21 FL

MODELLAZIONE IN SAP2000

Per la modellazione del sistema strutturale su SAP abbiamo effettuato i seguenti passaggi

1. Per prima cosa abbiamo modellato la geometria della trave Vierendeel grazie alla griglia e gli strumenti di disegno “Frame” e “Special Joint” 
2. Successivamente siamo passate alla modellazione del setto grazie allo strumento “Poly Area”, provvedendo a discretizzare le superfici definite in porzioni più piccole.
   In questo modo il programma sarà facilitato nel calcolo strutturale e il setto risulterà modellato in maniera più accurata e verosimile
3. Abbiamo poi assegnato i vincoli esterni di tipo incastro alla base del setto
   

   

   

4. Per simulare un nodo rigido interno, abbiamo definito i rilasci agli estremi degli elementi strutturali, in particolare nel punto di collegamento tra la trave Vierendeel e il setto (non abbiamo assegnato alcun rilascio alle estremità, in questo modo la rotazione intorno a tutti gli assi nel punto di collegamento tra gli elementi è pari a zero)
5. A questo punto abbiamo definito le sezioni di prova dei correnti (30x50 cm) e dei montanti (40x80 cm) e abbiamo scelto come materiale un calcestruzzo ordinario C28/35.
   

   

   Tali sezioni sono state scelte per simulare una situazione reale di trave Vierendeel: se avessimo voluto simulare un modello di trave Vierendeel, avremmo potuto aumentare significativamente il valore del modulo di elasticità (E) del materiale scelto, in questo modo la rigidezza assiale e quella flessionale sarebbero state approssimativamente tendenti a infinito.
   Nel nostro caso, scegliendo di riprodurre una condizione realistica, abbiamo semplicemente aumentato la dimensione della sezione dei montanti rispetto a quella dei correnti, in questo modo l’inerzia dei montanti risulta significativamente maggiore rispetto a quella dei traversi e, di conseguenza, anche la rigidezza

6. Abbiamo poi definito la sezione del setto grazie allo strumento “Area Section” scegliendo la tipologia “SHELL”, e selezionando la voce “Shell Thick” che tiene conto anche dell’azione del taglio, assegnando uno spessore di 40 centimetri e un calcestruzzo ordinario C28/35.
   Un setto modellato con la tipologia “SHELL” è un modello di guscio con comportamento a membrana, un comportamento che comprende sia gli spostamenti nel piano (modello LASTRA) che gli spostamenti fuori dal piano (modello PIASTRA)
7. In fine abbiamo assegnato agli elementi strutturali le sezioni precedentemente definite
8. Successivamente abbiamo definito il carico agente sulla trave Vierendeel fissando il relativo fattore moltiplicatore del peso proprio dalla voce “Load Patterns” : F (0)
9. A questo punto abbiamo assegnato il valore della forza concentrata (F = 116,10 KN), calcolato precedentemente grazie all’analisi dei carichi, in corrispondenza del baricentro di ogni montante
   

   

10. A questo punto abbiamo avviato l’analisi del modello “Run Analysis”;
11. Abbiamo visualizzato la configurazione deformata della struttura e i diagrammi delle sollecitazioni agenti (N, T, M);
12. In fine abbiamo esportato le tabelle Excel relative ai valori delle sollecitazioni nei montanti e nei correnti della trave Vierendeel
    

    

    

    

    

VERIFICHE

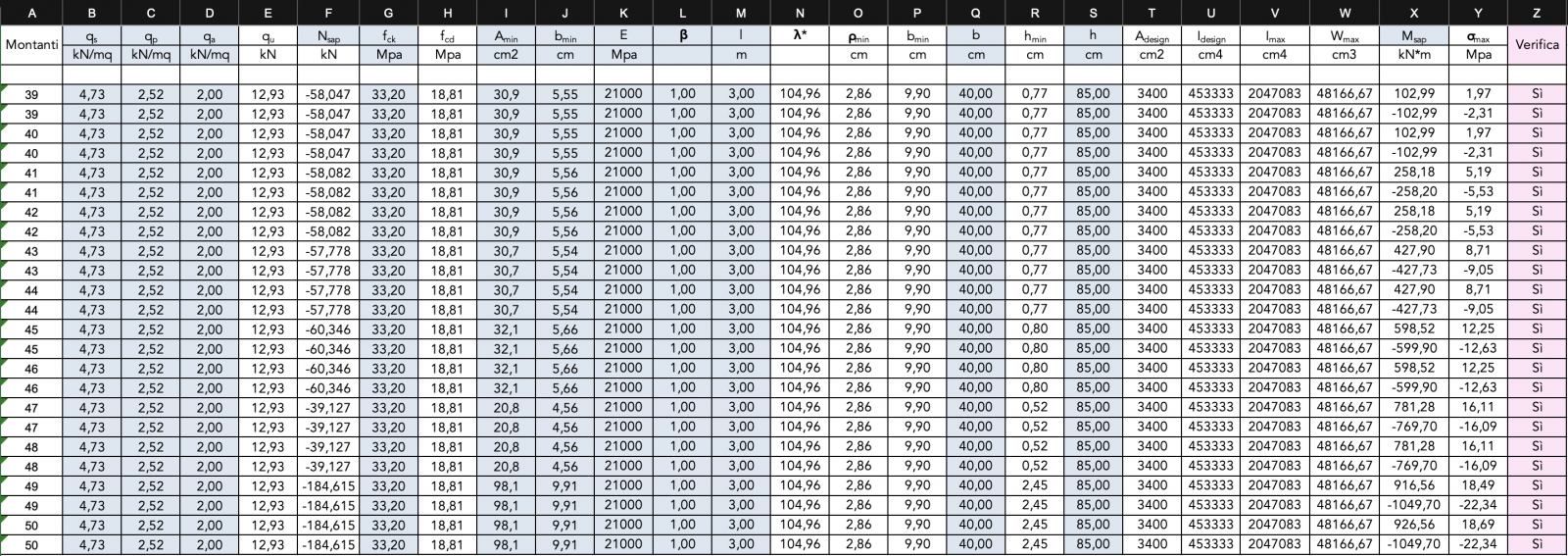
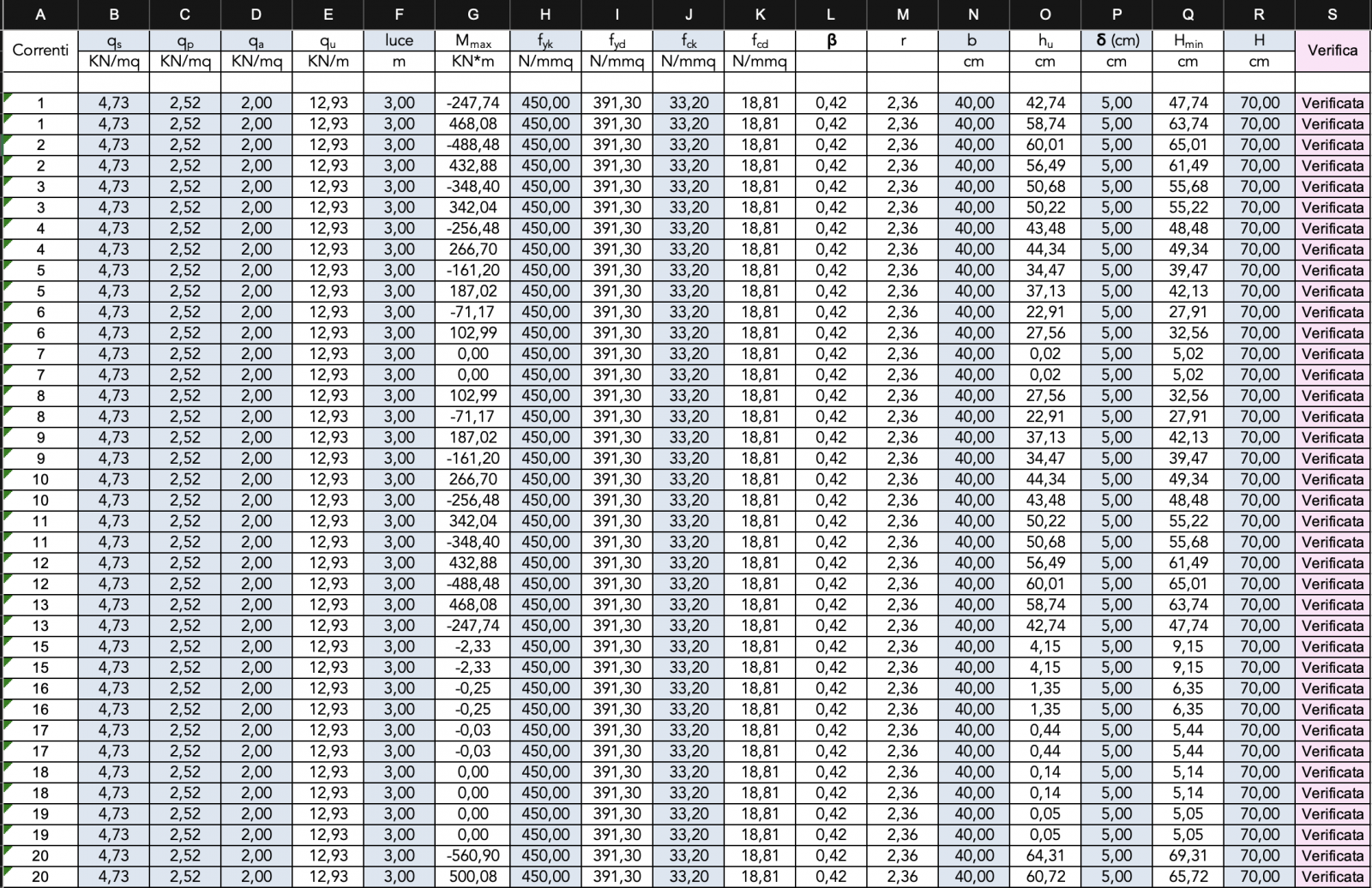
Verifica degli elementi strutturali
Le verifiche sono state effettuate grazie alle tabelle Excel relative alla verifica degli elementi in calcestruzzo: per i pilastri abbiamo effettuato la verifica a pressoflessione mentre per i correnti abbiamo effettuato la verifica a flessione.
Inizialmente la verifica delle sezioni di prova risultava non soddisfatta: abbiamo aumentato quindi la classe di resistenza del calcestruzzo da un C28/35 a un C3240 e incrementato la dimensione delle sezioni.
Le dimensioni minime affinché la verifica fosse soddisfatta sono risultate per i correnti 40x70 cm e per i montanti 40x85.
La sezione dei montanti risulta dimensionata in maniera ragionevole, per quanto riguarda i correnti invece, conoscendo la geometria e le caratteristiche della trave Vierendeel, ci saremmo aspettate una dimensione minore della sezione.
La dimensione ottenuta potrebbe però essere spiegata dal passaggio da un modello ideale di trave Vierendeel (ottenuto come rotazione del modello Shear-Type) a un modello più realistico.

Verifica delle sollecitazioni
Avendo effettuato inizialmente l'analisi del modello statico da cui, grazie alle equazioni di equilibrio, sono risultati i valori degli sforzi di taglio e di momento flettente, abbiamo deciso di verificare se i valori risultanti dal modello in SAP corrispondessero effettivamente ai valori ottenuti dall'analisi statica.

Sappiamo che i valori dello sforzo di taglio variano per ognuno dei sei correnti della trave Vierendeel e conoscendo il valore della forza concentrata F che abbiamo applicato, possiamo calcolarli

1. T=F/2 = 58,05 KN
2. T=F = 116,10 KN
3. T=3F/2 = 174,15 KN
4. T=2F = 232,20 KN
5. T=5F/2 = 290,25 KN
6. T=3F = 348,30 KN

Dall'analisi del modello abbiamo estrapolato i valori del taglio e li abbiamo confrontati

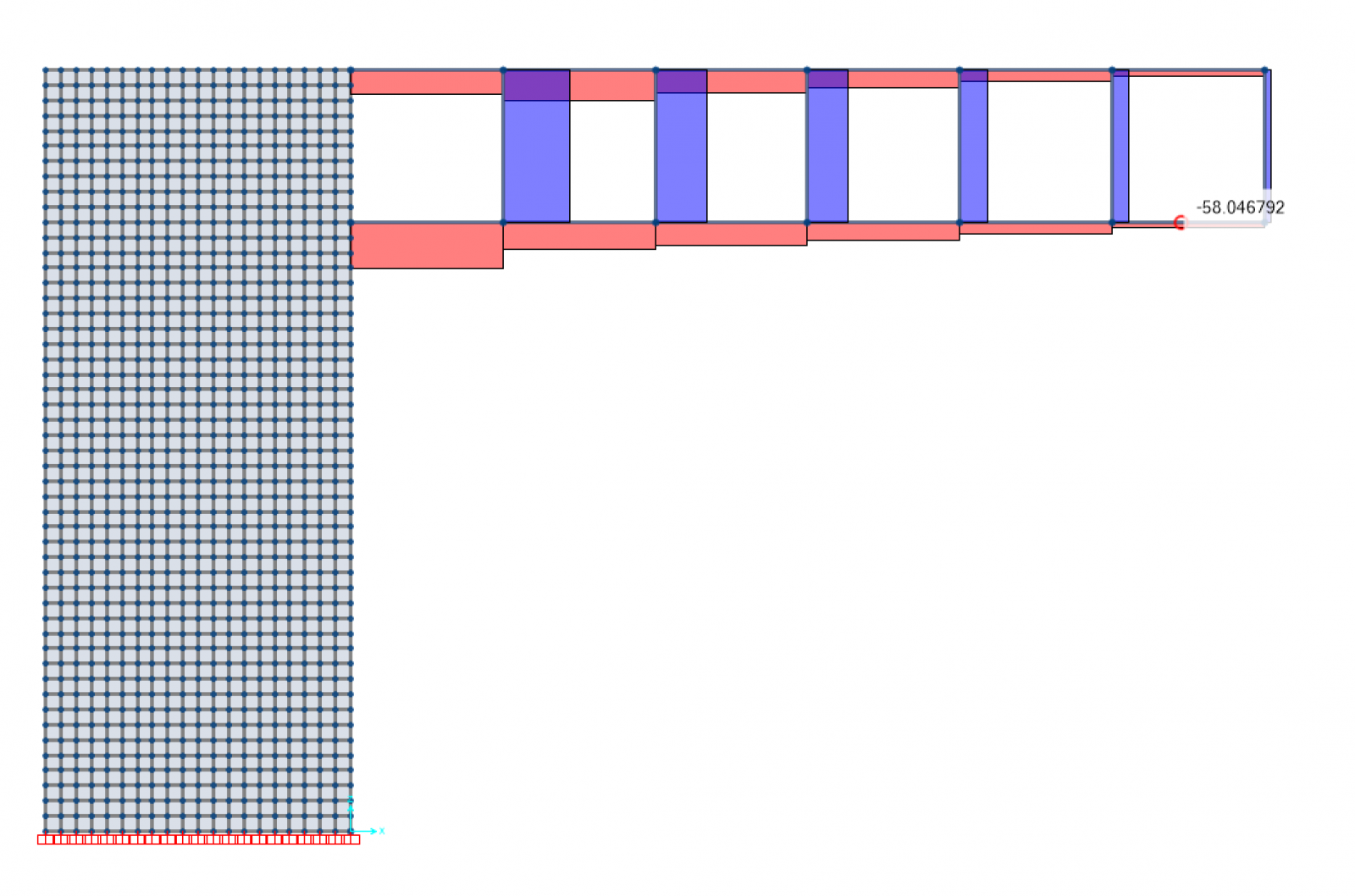
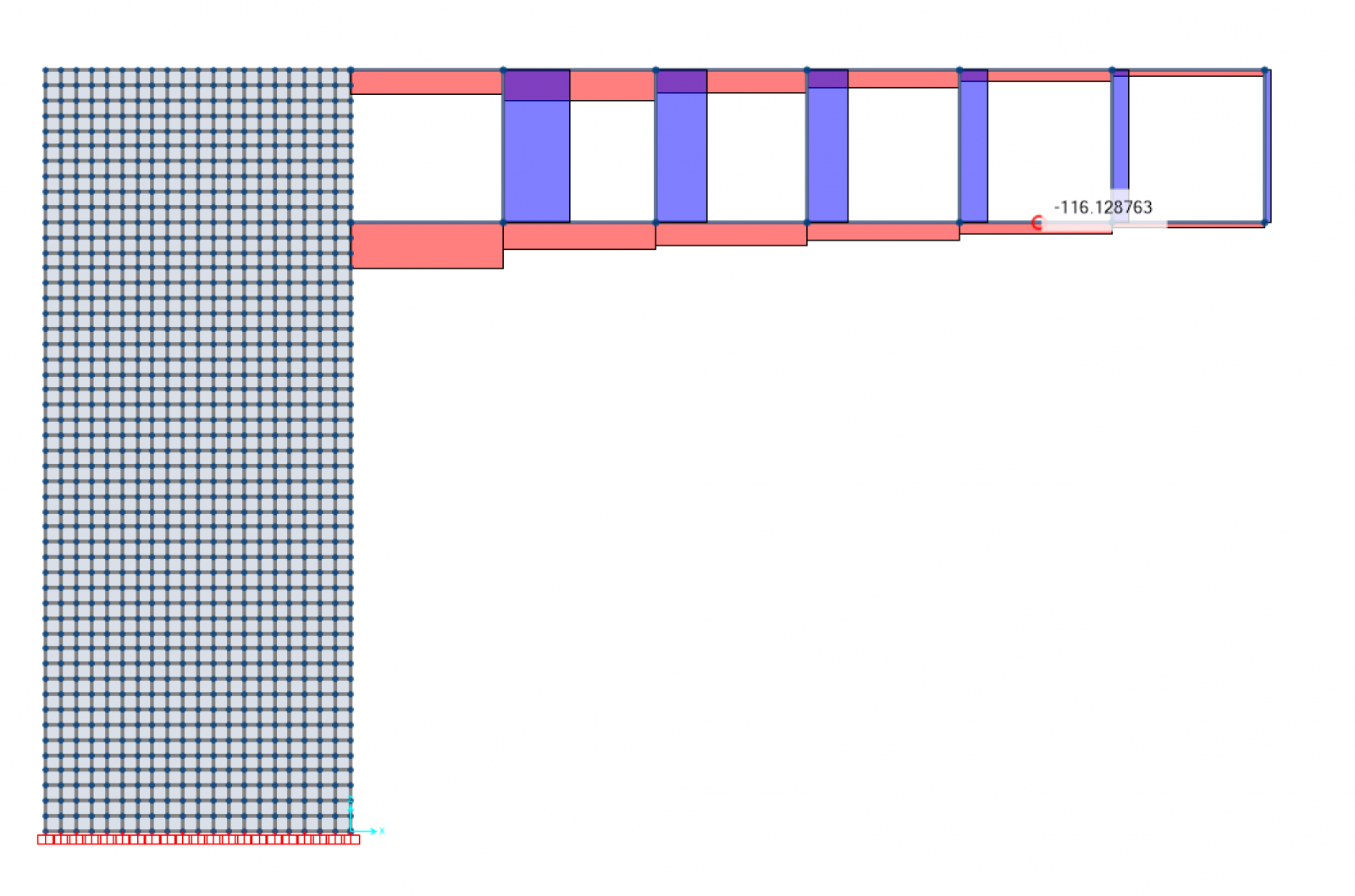
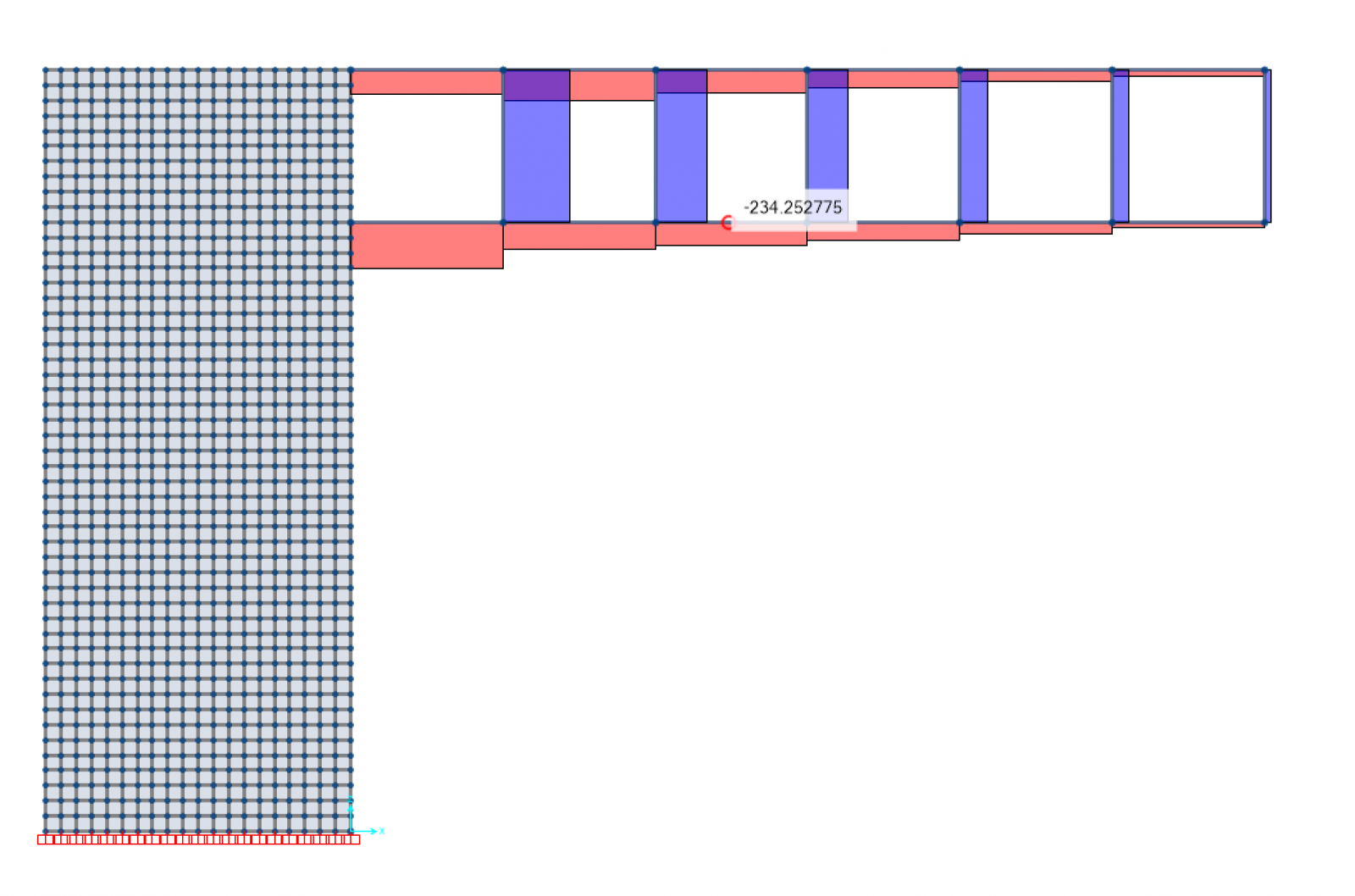
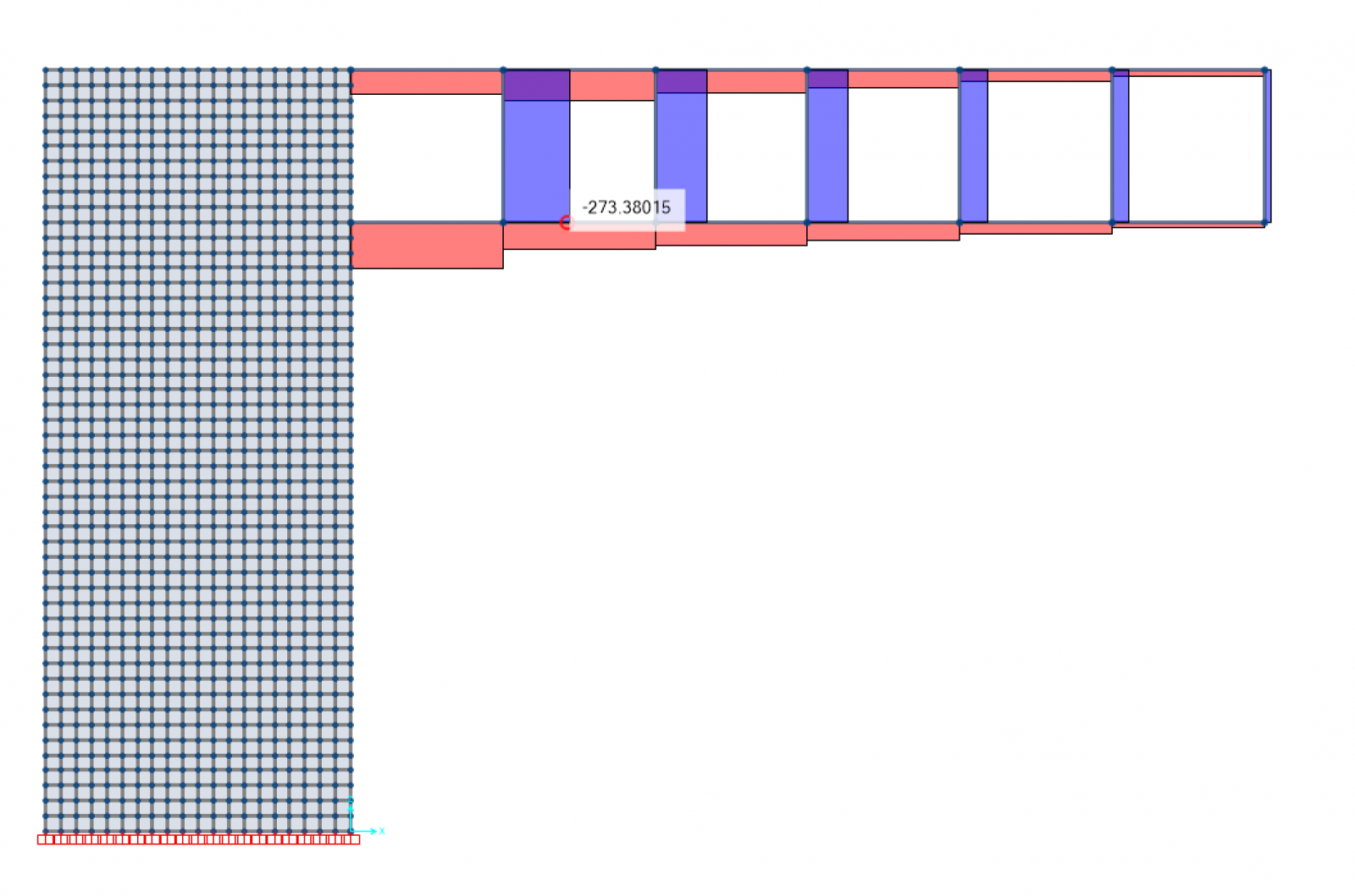
Considerando che i valori che escono dal modello sono approssimati più precisamente rispetto ai calcoli semplificati che abbiamo effettuato, possiamo riscontrare che i valori dello sforzo di taglio sono verificati.

Sapendo che il momento equivale al valore del taglio moltiplicato per il braccio (L/2 = 1,5m) possiamo dedurre che anche i valori del momento flettente siano verificati, essendo dipendenti dallo sforzo di taglio e da un valore della luce che rimane costante.

Verifica agli abbassamenti
Abbiamo infine effettuato la verifica agli abbassamenti.
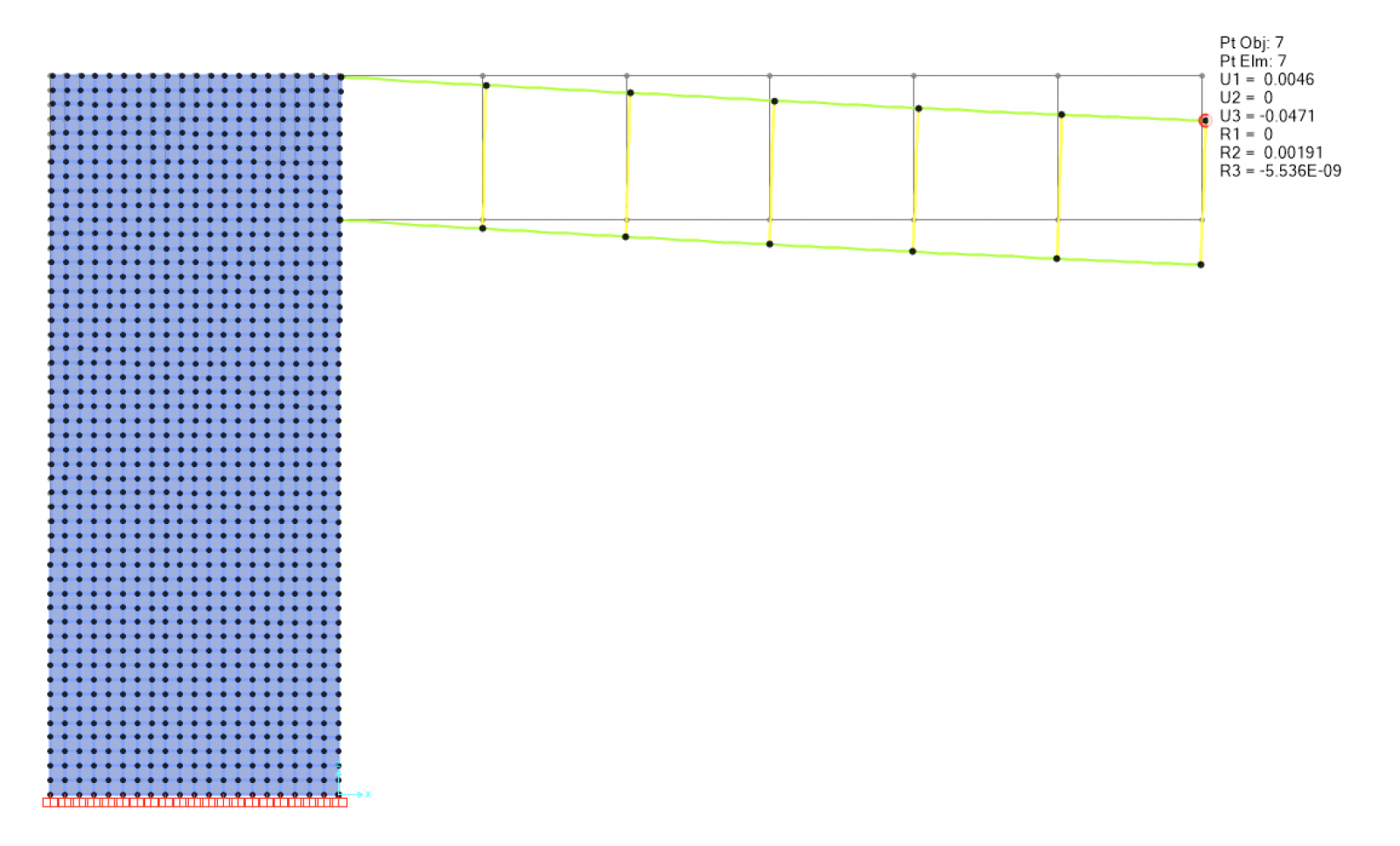
Il valore assoluto dell’abbassamento che risulta dal modello in SAP è 
U3 = 0,0471 m

Affinché l’abbassamento sia verificato deve risultare
U3 < Ltot/200
Dove Ltot è la distanza maggiore dall’estremo libero all’incastro
Ltot = 18 m

Ltot/200 = 0,09 m
0,0471 m < 0,09 m

La verifica agli abbassamenti è soddisfatta.