blog di Lucia.Mariani

Studentesse: Lucia Mariani, Ilaria Maurelli

 

INTRODUZIONE
Un graticcio è una morfologia strutturale che ha un comportamento meccanico assimilabile a quello di una piastra.
Una piastra è un modello meccanico bidimensionale di un corpo reale (tridimensionale) con le seguenti caratteristiche geometriche:

• Due dimensioni (lungo le direzioni x e y) sono paragonabili tra loro, cioè hanno lo stesso ordine di grandezza
• Le due dimensioni paragonabili sono molto superiori rispetto alla terza dimensione (spessore lungo la direzione z)
• I carichi che agiscono sulla piastra sono perpendicolari al piano medio

Il modello di piastra è caratterizzato da diversi comportamenti cinematici

• Spostamenti
  • Spostamento verticale
• Deformazioni
  • Curvatura torsionale
  • Curvatura flessionale
  • Rotazione

GEOMETRIA

Abbiamo immaginato di progettare un graticcio di travi inflesse di dimensioni 50,00 x 50,00 metri posto alla base di un edificio composto da tre piani sorretti dal graticcio stesso.

Per ottimizzare la modellazione del graticcio possiamo utilizzare un modello di piastra: il modello di piastra è un modello semplificato per poter dimensionare un sistema molto più complesso come il graticcio di travi inflesse.

Il modello del continuo equivalente è in grado di darci informazioni attendibili sul comportamento effettivo del graticcio: come si deforma, come si inflette, quali sono i punti critici della morfologia strutturale.

Dopo aver definito le dimensioni principali, abbiamo ipotizzato di posizionare degli elementi verticali di appoggio (pilastri) ogni 10 metri in modo tale che per ogni lato ci siano cinque appoggi.

Abbiamo differenziato le dimensioni delle sezioni dei pilastri distinguendo tra pilastri angolari e pilastri perimetrali: questo perchè i pilastri angolari hanno un comportamento rispetto a quelli perimetrali che invece vengono sollecitati maggiormente.

Pilastri angolari: 1,50 x 1,50 metri

Pilastri perimetrali: 2,0 x 1,2 metri

Essendo i pilastri perimetrali a sezione rettangolare, per assicurare la stessa inerzia in entrambe le direzioni del graticcio, abbiamo ipotizzato di orientare otto pilastri con il momento di inerzia maggiore lungo x e i restanti otto pilastri con il momento di inerzia maggiore lungo y.

ANALISI DEI CARICHI

Abbiamo effettuato un analisi dei carichi del solaio in laterocemento dell'edificio sorretto dal graticcio.
Abbiamo quindi inizialmente calcolato i carichi agenti su un metro quadrato di solaio suddividendoli nelle tre categorie

• Carichi permanenti strutturali
• Sovraccarichi permanenti non strutturale
• Carichi accidentali

Analisi dei carichi di un solaio in laterocemento

• Pavimentazione in parquet = 2 cm = 0,02 m
• Massetto = 3 cm = 0,03 m
• Isolante = 4 cm = 0,04 m
• Soletta collaborante = 5 cm = 0,05 m
• Pignatte = 20 cm = 0,20 m
• Travetti = 20 cm = 0,20 m
• Intonaco = 1,5 cm = 0,015 m

Spessore totale del solaio = 35,50 cm = 0,355 m

Carico distribuito superficiale

• 0,02 m x 7,2 KN/m³ = 0,144 KN/m²
• 0,03 m x 20 KN/m³  = 0,60 KN/m²
• 0,04 m x 0,2 KN/m³  = 0,008 KN/m²
• 0,05 m x 25 KN/m³ = 1,25 KN/m²
• 2 (0,2 x 0,12 x 1) m³/m x 25 KN/m³  = 1,20 KN/m²
• 2 (0,38 x 0,20 x 1) m³/m² x 15 KN/m³  = 2,28 KN/m²
• 0,015 m x 18 KN/m³  = 0,27 KN/m²

Carico strutturale q_s
Soletta + travetti + pignatte
1,25 KN/m² + 1,2 KN/m² + 2,28 KN/m² = 4,73 KN/m²

Sovraccarico permanente q_p
Parquet + massetto + isolante + intonaco + incidenza impianti + incidenza tramezzi
0,144 KN/m² + 0,6 KN/m² + 0,008 KN/m² + 0,27 KN/m² + 0,5 KN/m² + 1 KN/m² = 2,52 KN/m² = 2,52 KN/m²

Carico accidentale q_a
Dato fornito dalla normativa in base alla destinazione d’uso (residenziale) = 2,00 KN/m²

Abbiamo successivamente considerato le combinazioni di carico fornite dalla normativa per le verifiche agli stati limite utilizzando coefficienti parziali di sicurezza sfavorevoli

Combinazione di carico allo stato limite d’esercizio SLE
Questo valore di carico allo stato limite di esercizio ci servirà per le verifiche agli abbassamenti.
γ̃s qs + γ̃p qp + γ̃a qa = 1 x 4,73 KN/m² + 0,7 x 2,52 KN/m² + 0,7 x 2 KN/m² = 7,88 KN/m² = 7,9 KN/m²
q_e = 7,90 KN/m²

Combinazione di carico allo stato limite ultimo SLU
Questo valore di carico allo stato limite ultimo ci servirà per le verifiche di resistenza degli elementi inflessi e presso inflessi (travi del graticcio, pilastri di appoggio)
γs qs + γp qp + γa qa = 1,3 x 4,73 KN/m² + 1,5 x 2,52 KN/m² + 1,5 x 2 KN/m² = 12,89 KN/m² = 12,9 KN/m²
q_u = 12,90 KN/m²

Una volta ottenuto il valore della combinazione di carico agli stati limite, essendo un valore distribuito sulla superficie, abbiamo moltiplicato il valore per le dimensioni della piastra e moltiplicando per il numero di piani, ottenendo così il valore della forza concentrata equivalente al carico dovuto ai tre piani.

Forza concenrata SLE
50,00 m x 50,00 m x 7,90 KN/m² x 3 piani = 59250 KN

Forza concenrata SLU
50,00 m x 50,00 m x 12,90 KN/m² ​x 3 piani = 96750 KN

 

MODELLAZIONE SU SAP2000

Una volta definita la geometria principale, abbiamo cominciato a modellare la piastra su SAP.

Per prima cosa abbiamo definito il materiale, abbiamo scelto un calcestruzzo ad alte prestazioni (C50/60) essendo il graticcio una morfologia molto complessa e impegnativa dal punto di vista strutturale.

Il passo successivo è stato quello di modellare la piastra con lo strumentoo "Poly area" e assegnarle una sezione "Shell" e selezionando la voce “Shell Thick” che tiene conto anche dell’azione del taglio, assegnando uno spessore di 1,50.

Successivamente abbiamo discretizzato la piastra in porzioni di 0,50 m x 0,50 metri; questa discretizzazione aiuta il programma di calcolo ad eseguire un'analisi più accurata in modo che il modello potesse essere più assimilabile a un modello realistico.

Dal momento che stiamo utilizzando un modello di piastra per simulare il comportamento di un graticcio di travi inflesse, dobbiamo tenere conto del fatto che le deformazioni secondarie presenti in un continuo dovute all'effetto Poisson, in questo caso, saranno trascurabili.

Questo avviene perchè il graticcio composto da travi è assimilabile al modello di piastra dal punto di vista del comportamento meccanico ma la geometria del graticcio non è assimilabile a quella di un continuo.

Per trascurare questo comportamento, abbiamo creato un materiale fittizio a partire da un calcestruzzo ad alte prestazioni (C50/60) ponendo il coefficiente di Poisson pari a zero: in questo modo simuliamo in un oggetto continuo (shell) il comportamento di un oggetto discreto.

Abbiamo attribuito alla piastra discretizzata il materiale precedentemente definito.

Per quanto riguarda la modellazione dei pilastri, abbiamo scelto un altezza di 4 metri e abbiamo attribuito ad ognuno di essi le sezioni precedentemente definite differenziando in pilastri angolari e pilastri perimetrali.

A questo punto abbiamo assicurato la stessa inerzia lungo le due direzioni x e y ruotando di 90 gradi gli assi locali dei pilastri appartenenti a due dei quattro lati della piastra.

Per completare la modellazione della geometria del modello abbiamo assegnato i vincoli esterni di tipo incastro alla base di ogni pilastro.

A questo punto abbiamo definito il carico F considerando un fattore moltiplicatore di peso proprio pari a 1: questo passaggio è necessario affinche nel calcolo del modello venga considerato anche il peso proprio della struttura che, nel caso del calcestruzzo, non può essere trascurato.

Una volta trovati i valori della forza concentrata equivalente, dobbiamo distribuirli nei nodi a seconda dell'area di influenza di carico che inciderà in ogni nodo.

Da SAP troviamo che il numero totale dei nodi è 10201.

Di questi, in base alle aree di influenza, sappiamo che quelli centrali prenderanno una forza concentrata pari al 100%, i nodi che si trovano sul perimetro prenderanno una forza concentrata parti al 50%, quelli angolari prenderanno invece una forza concentrata pari al 25% del totale.

Per trovare la forza totale che agisce su di un singolo nodo facciamo la somma di tutti i nodi centrali (che prendono il 100%) ai quali aggiungiamo la metà dei nodi perimetrali (che prendono il 50% della forza totale e perciò possiamo immaginarli come la metà dei nodi che prendono il 100% della forza) ai quali aggiungiamo infine uno solo dei quattro nodi angolari (che prende il 25% della forza totale quindi possiamo immaginare di considerare un solo nodo che prende il 100% della forza)

9801 (nodi centrali) + 198 (nodi perimetrali) + 1 (nodo angolare) = 10 000 nodi

A questo punto dividiamo il valore delle forze precedentemente calcolate per il numero di nodi e troviamo il valore della forza applicata ad un singolo nodo.

SLE
F_TOT = 59250 KN / 10 000 = 5,925 KN

• Nodi centrali
  F = 5,925 KN
• _{Nodi perimetrali}
  F = 2,9625 KN
• Nodi angolari
  F = 1,481 KN

SLU
F_TOT = 96750 KN / 10 000 = 9,675 KN

• Nodi centrali
  F = 9,675 KN
• _{Nodi perimetrali}
  F = 4,8375 KN
• Nodi angolari
  F = 2,41875 KN

 

Definiamo a questo punto due diversi carichi con fattore moltiplicatore di peso proprio pari a 1

• F_SLE
• F_SLU

E applichiamo ai nodi centrali, perimetrali e angolari i valori precedentemente calcolati.

Ora possiamo avviare l'analisi del modello di piastra equivalente, prima con la combinazione di carico allo stato limite di esercizio e successivamente con la combinazione di carico allo stato limite ultimo.

 

VERIFICHE

Verifica agli abbassamenti

L'analisi con il carico allo SLE ci serve per la verifica degli abbassamenti

U₃ = -0,0853 m

Lo spostamento verticale deve essere inferiore a 1/200 della luce.
Essendo la nostra luce di 50 metri, l'abbassamento risulta verificato:

50 m / 200 = 0,25 m > 0,0853 m

 

Verifiche di resistenza

L'analisi con il carico allo SLU ci serve per la verifica di resistenza degli elementi inflessi e pressoinflessi.

Dai diagrammi del momento flettente intorno agli assi locali 1 e 2 (M11, M22), notiamo che otteniamo gli stessi valori, questo perchè il sistema è perfettamente simmetrico, sia nella geometria, sia nei carichi applicati.

Verifichiamo il valore massimo del momento, in corrispondenza di un pilastro, che equivale a 22157,31 KNm

A questo punto, per verificare il dimensionamento della piastra abbiamo utilizzato la tabella Excel ti verifica a flessione delle travi, ponendo come base uno spessore di 1,50 metri.

Avendo ottenuto un valore dell'altezza utile maggiore rispetto a quella di progetto (2,09 metri) abbiamo verificato che l'incremento in percentuale non fosse superiore al 40%.

Abbiamo deciso quindi di passare al dimensionamento del graticcio poichè abbiamo sfruttato il modello di piastra per creare un equivalenza in rigidezza in base al momento di inerzia della sezione.

L'equivalenza in rigidezza non implica però una equivalenza del peso della piastra rispetto a quello del graticcio, questo perchè il momento di inerzia è proporzionale alla terza potenza dell'altezza della sezione mentre il peso è proporzionale alla prima potenza dell'altezza della sezione.

Questo è dovuto al fatto che il graticcio di travi inflesse, rispetto al modello di piastra, ha un peso notevolmente inferiore dovuto al fatto che non è un continuo pieno ma è formato da travi che si alternano a vuoti.

 

DIMENSIONAMENTO

Dimensionamento graticcio

Per dimensionare le travi del graticcio abbiamo calcolato il momento di inerzia di una porzione di piastra di dimensioni 1,00 m x 1,00 m

I_x =  (bh³ / 12)
I_x = 1,00 m x (1,50 m)³ / 12 = 0,28125 m⁴

Da questo risultato sappiamo che in una porzione di graticcio di un metro quadrato non posso dare un valore di inerzia inferiore a quello ottenuto.

A questo punto abbiamo scelto un interasse per le travi del graticcio, i = 2,50 m
In una porzione di interasse di 2,50 m avremo quindi una inerzia di:
I_x =  (bh³ / 12)
Dove la base è 2,50 m
I_x = 2,50 m x (1,50 m)³ / 12 = 0,703125 m⁴

Ipotizziamo un valore della base delle travi del graticcio pari a 0,60 m e calcoliamo l'altezza della sezione sapendo che il momento di inerzia deve essere circa 0,70 m⁴

h =  (12 I_x / b) ^1/3

h =  (12 x 0,703125 m⁴/ 0,80 m) ^1/3 = 2,20 m (circa)

La sezione della trave del graticcio ottenuta è 0,80 m x 2,20 m

 

MODELLAZIONE GRATICCIO SU SAP2000

Nel modello precedentemente sviluppato, elimino la piastra discretizzata per sostituirla con le travi del graticcio appena dimensionate.

Per simulare un nodo rigido interno ad ogni incrocio tra le travi e tra travi e pilastri, separo le travi modellate ad ogni intersezione, in modo che non siano continue.

A questo punto assegnamo nuovamente i carichi precedentemente calcolati su ogni nodo del graticcio.

Per fare  questo, dividiamo il valore delle forze per il numero di nodi e troviamo il valore della forza applicata ad un singolo nodo.

361 (nodi centrali) + 38 (nodi perimetrali) + 1 (nodo angolare) = 400 nodi

SLE
F_TOT = 59250 KN / 400 = 148,125 KN

• Nodi centrali
  F = 148,125 KN
• _{Nodi perimetrali}
  F = 74,0625 KN
• Nodi angolari
  F = 37,03125 KN

SLU
F_TOT = 96750 KN / 400 = 241,875 KN

• Nodi centrali
  F = 241,875 KN
• _{Nodi perimetrali}
  F = 120,9375 KN
• Nodi angolari
  F = 60,46875 KN

Assegnamo a questo punto ai nodi centrali, perimetrali e angolari i valori precedentemente calcolati, distinguendo sempre secondo le due combinazioni di carico.

• F_SLE
• F_SLU

Ora possiamo avviare l'analisi del modello del graticcio, prima con la combinazione di carico allo stato limite di esercizio e successivamente con la combinazione di carico allo stato limite ultimo.

 

VERIFICHE

Verifica agli abbassamenti

L'analisi con il carico allo SLE ci serve per la verifica degli abbassamenti

U₃ = -0,1166 m

Lo spostamento verticale deve essere inferiore a 1/200 della luce.
Essendo la nostra luce di 50 metri, l'abbassamento risulta verificato:

50 m / 200 = 0,25 m > 0,1166 m

 

Verifiche di resistenza

L'analisi con il carico allo SLU ci serve per la verifica di resistenza degli elementi inflessi e pressoinflessi.

Diagramma dello sforzo normale

Notiamo dal diagramma dello sforzo normale che il graticcio si comporta come una  serie di portali formati da due pilastri sullo stesso asse e le travi che li congiungono.

Diagramma del momento flettente

Se ci concentriamo su un pilastro perimetrale, notiamo che il valore del momento flettente è molto elevato in corrispondenza del nodo rigido tra trave e pilastro, questo comporterà una deformazione eccessiva del pilastro, che tenderà quindi ad instabilizzarsi.

Per evitare che questo accada, possiamo aumentare la rigidezza torsionale della trave di bordo, in questo modo, parte del momento flettente che arriva al nodo sarà assorbito dalla trave di bordo irrigidita e il pilastro subirà di meno la deformazione.

A questo punto torniamo sul modello SAP, selezioniamo le travi di bordo e assegnamo  una sezione con rigidezza torsionale maggiore.

Essendo il pilastro molto sollecitato, scegliamo di utilizzare una sezione rettangolare cava che ci consente di aumentare la larghezza senza andare a gravare ulteriormente sul peso proprio dell'intero sistema.

La trave di bordo avrà quindi una sezione cava di 2,20 m x 1,50 m x 0,08 m x 0,08 m

 

 

 

 

 

 

  

 

 

A questo punto abbiamo verificato la sezione dei pilastri soggetti a pressoflessione con il valore del momento ottenuto dopo aver ri assegnato la sezione della trave di bordo.

Sforzo normale di compressione

Momento flettente

Verifica sul file Excel dei pilastri soggetti a presso flessione

Dalla verifica a pressoflessione abbiamo infine notato che i pilastri necessitano di un incremento della sezione per poter soddisfare la verifica.

Per questa ragione abbiamo aumentato la base da 1,20 m a 1,80 m.
Avendo dimensioni molto grandi, i pilastri sono assimilabili a dei piccoli setti.
Questo è giustificato dal fatto che il graticcio è una struttura molto impegnativa che serve a coprire luci molto ampie e di conseguenza necessita di appoggi altrettanto imponenti.

Abbiamo infine verificato l'eccentricità dei pilastri

 

VERIFICA FINALE

Dopo aver ri assegnato le sezioni dei pilastri su SAP e la trave di bordo, abbiamo effettuato la verifica finale agli abbassamenti e a resistenza di tutte le sezioni.

Deformata

Sforzo normale

Momento flettente

 

MODELLO 3D

 

Studentesse: Mariani Lucia, Maurelli Ilaria

INTRODUZIONE

Una trave Vierendeel è una tipologia di travatura reticolare costituita da due correnti, uno superiore e uno inferiore, collegati da montanti irrigiditi che non hanno quindi bisogno di essere controventati con aste diagonali.

A differenza di una travatura reticolare, dove tutte le aste risultano collegate tramite cerniere e soggette unicamente a sforzo normale, la trave Vierendeel presenta dei collegamenti rigidi tra gli elementi e sviluppa sollecitazioni di taglio e momento flettente sia negli elementi orizzontali che in quelli verticali.

Una modello di trave Vierendeel può essere studiato come un modello di Telaio Shear-Type semplicemente ruotato rigidamente di 90 gradi.
Un telaio Shear-Type è un modello che presenta un elemento orizzontale (trave) infinitamente rigido, sia assialmente che flessionalmente, e due elementi verticali (pilastri) infinitamente rigidi assialmente.
I tre elementi che compongono il telaio Shear-Type sono collegati tra loro tramite nodi rigidi che non permettono quindi la rotazione, e i due pilastri sono vincolati a terra da un incastro.

Una trave Vierendeel è quindi composta da due correnti che hanno le stesse caratteristiche dei pilastri del telaio Shear-Type (infinitamente rigidi assialmente) e una serie di montanti che hanno invece le stesse caratteristiche del traverso del telaio Shear-Type (infinitamente rigido assialmente e flessionalmente).

GEOMETRIA

Abbiamo immaginato di effettuare un dimensionamento di massima di una trave Vierendeel aggettante, vincolata a una sola estremità da un setto.

Una trave Vierendeel è immediatamente riconoscibile dalla sua geometria.
Nel nostro caso è infatti caratterizzata da un ritmo di sei campate quadrate da 3,00 metri di luce in entrambe le direzioni (x e y) per 3,00 metri di altezza; una grande luce aggettante di 18,00 metri, la presenza di pilastri infinitamente rigidi e un supporto molto robusto.
Come supporto abbiamo ipotizzato una gabbia ascensore di 3,00 x 6,00 metri con uno spessore murario dei setti di 0,40 metri.

ANALISI DEI CARICHI

Per prima cosa abbiamo effettuato un analisi dei carichi per ricavare il valore delle forze concentrate che agiscono su ogni pilastro della trave Vierendeel.
Abbiamo quindi calcolato i carichi agenti su un metro quadrato di solaio suddividendoli nelle tre categorie
Carichi permanenti strutturali
Sovraccarichi permanenti non strutturale
Carichi accidentali

Analisi dei carichi di un solaio in laterocemento

1. Pavimentazione in parquet = 2 cm = 0,02 m
2. Massetto = 3 cm = 0,03 m
3. Isolante = 4 cm = 0,04 m
4. Soletta collaborante = 5 cm = 0,05 m
5. Pignatte = 20 cm = 0,20 m
6. Travetti = 20 cm = 0,20 m
7. Intonaco = 1,5 cm = 0,015 m

Spessore totale solaio = 35,5 cm = 0,355 m

Carico distribuito superficiale

1. 0,02 m x 7,2 KN/m³ = 0,144 KN/mq
2. 0,03 m x 20 KN/m³ = 0,60 KN/mq
3. 0,04 m x 0,2 KN/m³ = 0,008 KN/mq
4. 0,05 m x 25 KN/m³ = 1,25 KN/mq
5. 2 (0,2 x 0,12 x 1) m³/m² x 25 KN/m³ = 1,20 KN/m²
6. 2 (0,38 x 0,20 x 1) m³/m² x 15 KN/m³ = 2,28 KN/m²
7. 0,015 m x 18 KN/m³ = 0,27 KN/m²

Carico strutturale q_S
Soletta + travetti + pignatte
1,25 KN/m² + 1,2 KN/m² + 2,28 KN/m² = 4,73 KN/m²
Sovraccarico permanente q_P
Parquet + massetto + isolante + intonaco + incidenza impianti + incidenza tramezzi
0,144 KN/m² + 0,6KN/m² + 0,008 KN/m² + 0,27 KN/m² + 0,5 KN/m² + 1 KN/m² = 2,52 KN/m² = 2,52 KN/m²
Carico accidentale q_a
Dato fornito dalla normativa in base alla destinazione d’uso = 2,00 KN/m²

Abbiamo successivamente considerato le combinazioni di carico fornite dalla normativa per le verifiche agli stati limite utilizzando coefficienti parziali di sicurezza sfavorevoli

Combinazione di carico allo stato limite d’esercizio SLE
γ̃s qs + γ̃p qp + γ̃a qa = 1 x 4,73 KN/m² + 0,7 x 2,52 KN/m² + 0,7 x 2 KN/m² = 7,88 KN = 7,9 KN/m²
qe = 7,90 KN/m²
Combinazione di carico allo stato limite ultimo SLU
γs qs + γp qp + γa qa = 1,3 x 4,73 KN/m² + 1,5 x 2,52 KN/m² + 1,5 x 2 KN/m² = 12,89 KN/m² = 12,9 KN/m²
qu = 12,90 KN/m²

Una volta ottenuto il valore della combinazione di carico allo stato limite ultimo, essendo un valore distribuito sulla superficie, abbiamo moltiplicato il valore per l’interasse lungo l’asse y (3,00 m), e successivamente per l’interasse lungo l’asse x (3,00 m), ottenendo i singoli valori delle forze concentrate agenti sui pilastri.

Qu * i = 12,90 KN/m² * 3,00 m = 38,70 KN/m
F = Qu * i * i = 38,70 KN/m * 3,00 m = 116,10 KN
F = 116,10 KN

SOLLECITAZIONI

Deformata
Il diagramma della deformata equivale al diagramma di un telaio Shear-Type deformato ruotato di 90 gradi.
La deformazione dei correnti ha due diverse curvature, il punto in cui avviene il cambiamento di curvatura è esattamente pari a L/2 cioè al punto di flesso dove la tangente taglia la curva.
In quel punto il momento flettente risulterà pari a zero perchè momento flettente e curvatura sono strettamente legati dalla relazione
M = (EI) X

Taglio
Il diagramma del taglio è costante ma il valore aumenta di asta in asta mano a mano che ci avviciniamo al vincolo di incastro esterno, dove avremo il valore massimo.

Momento flettente
Il diagramma del momento è lineare perché non c’è carico ripartito sulla trave.
La pendenza della retta che individua l’andamento del momento flettente è il valore del taglio e quindi anche il valore del momento massimo si trova in corrispondenza del vincolo esterno.
Il diagramma del momento flettente si annulla nel punto di flesso della deformata, cioè in mezzeria.

 

EQUILIBRIO

Per verificare che la morfologia scelta, trave Vierendeel e setto, siano effettivamente equilibrati a traslazione e a rotazione, calcoliamo le sollecitazioni presenti in corrispondenza dei vincoli e verifichiamo che soddisfino le equazioni di equilibrio.

Assumendo che in ogni singolo tratto della trave (immaginando di effettuare dei tagli) deve essere verificato l’equilibrio delle forze interne, possiamo dedurre che in corrispondenza del vincolo di incastro (con il quale approssimiamo il setto) si svilupperà una forza verticale uguale e opposta a quella che si sviluppa all’interno del corrente 6, con valore 3F.

In corrispondenza del vincolo si svilupperà inoltre un momento antiorario che dovrà bilanciare la rotazione oraria generata dalle forze verticali.
Tale valore del momento è ottenuto come

Momento = Taglio x Braccio
M = 3F x L/2 = 3FL/2

Dove il braccio è la distanza tra il centro di rotazione e il punto di flesso della deformata, cioè dove il momento si annulla.

A questo punto verifichiamo l’equilibrio a traslazione e a rotazione

L’equilibrio alla traslazione verticale è verificato in quanto la somma delle forze concentrate è equilibrata dalle due forze che si sviluppano in corrispondenza dei vincoli.
F - F - F - F - F - F + 3F + 3F = 0
- 6F + 6F = 0

L’equilibrio alla rotazione risulta
3FL/2 + 3FL/2 - FL - 2FL - 3FL - 4FL - 5FL - 6FL ≠ 0
3FL/2 + 3FL/2 - FL - 2FL - 3FL - 4FL - 5FL - 6FL = -18FL

Notiamo che l’equilibrio alla rotazione non è verificato e risulta un momento orario non equilibrato pari a 18FL
Non essendoci altre forze che possono generare una rotazione, il momento risultante sarà equilibrato da una coppia di forze orizzontali uguali e opposte con braccio della coppia pari all’altezza della trave Vierendeel, quindi L.
Tali forze avranno un valore pari a

Momento = Forza x Braccio
Forza = Momento / Braccio 
Fo = 18FL / L = 18 F

A questo punto verifichiamo che tutto il sistema, compreso il setto, modellato come una mensola incastrata nell’estremità inferiore, sia in equilibrio.
Calcoliamo quindi le sollecitazioni che raggiungono l’incastro a terra affinché il sistema sia equilibrato

Forze verticali
Forze concentrate verticali
F + F + F + F + F + F = 6F
Forze verticali equilibranti
3F + 3F = 6F

Momento
Momenti generati dalle forze concentrate verticali
FL + 2FL + 3FL + 4FL + 5FL + 6FL = 21FL
Momenti equilibranti e momento generato dalla coppia di forze
3FL + 3FL + 18 FL = 21 FL

MODELLAZIONE IN SAP2000

Per la modellazione del sistema strutturale su SAP abbiamo effettuato i seguenti passaggi

1. Per prima cosa abbiamo modellato la geometria della trave Vierendeel grazie alla griglia e gli strumenti di disegno “Frame” e “Special Joint” 
2. Successivamente siamo passate alla modellazione del setto grazie allo strumento “Poly Area”, provvedendo a discretizzare le superfici definite in porzioni più piccole.
   In questo modo il programma sarà facilitato nel calcolo strutturale e il setto risulterà modellato in maniera più accurata e verosimile
3. Abbiamo poi assegnato i vincoli esterni di tipo incastro alla base del setto
   

   

   

4. Per simulare un nodo rigido interno, abbiamo definito i rilasci agli estremi degli elementi strutturali, in particolare nel punto di collegamento tra la trave Vierendeel e il setto (non abbiamo assegnato alcun rilascio alle estremità, in questo modo la rotazione intorno a tutti gli assi nel punto di collegamento tra gli elementi è pari a zero)
5. A questo punto abbiamo definito le sezioni di prova dei correnti (30x50 cm) e dei montanti (40x80 cm) e abbiamo scelto come materiale un calcestruzzo ordinario C28/35.
   

   

   Tali sezioni sono state scelte per simulare una situazione reale di trave Vierendeel: se avessimo voluto simulare un modello di trave Vierendeel, avremmo potuto aumentare significativamente il valore del modulo di elasticità (E) del materiale scelto, in questo modo la rigidezza assiale e quella flessionale sarebbero state approssimativamente tendenti a infinito.
   Nel nostro caso, scegliendo di riprodurre una condizione realistica, abbiamo semplicemente aumentato la dimensione della sezione dei montanti rispetto a quella dei correnti, in questo modo l’inerzia dei montanti risulta significativamente maggiore rispetto a quella dei traversi e, di conseguenza, anche la rigidezza

6. Abbiamo poi definito la sezione del setto grazie allo strumento “Area Section” scegliendo la tipologia “SHELL”, e selezionando la voce “Shell Thick” che tiene conto anche dell’azione del taglio, assegnando uno spessore di 40 centimetri e un calcestruzzo ordinario C28/35.
   Un setto modellato con la tipologia “SHELL” è un modello di guscio con comportamento a membrana, un comportamento che comprende sia gli spostamenti nel piano (modello LASTRA) che gli spostamenti fuori dal piano (modello PIASTRA)
7. In fine abbiamo assegnato agli elementi strutturali le sezioni precedentemente definite
8. Successivamente abbiamo definito il carico agente sulla trave Vierendeel fissando il relativo fattore moltiplicatore del peso proprio dalla voce “Load Patterns” : F (0)
9. A questo punto abbiamo assegnato il valore della forza concentrata (F = 116,10 KN), calcolato precedentemente grazie all’analisi dei carichi, in corrispondenza del baricentro di ogni montante
   

   

10. A questo punto abbiamo avviato l’analisi del modello “Run Analysis”;
11. Abbiamo visualizzato la configurazione deformata della struttura e i diagrammi delle sollecitazioni agenti (N, T, M);
12. In fine abbiamo esportato le tabelle Excel relative ai valori delle sollecitazioni nei montanti e nei correnti della trave Vierendeel
    

    

    

    

    

VERIFICHE

Verifica degli elementi strutturali
Le verifiche sono state effettuate grazie alle tabelle Excel relative alla verifica degli elementi in calcestruzzo: per i pilastri abbiamo effettuato la verifica a pressoflessione mentre per i correnti abbiamo effettuato la verifica a flessione.
Inizialmente la verifica delle sezioni di prova risultava non soddisfatta: abbiamo aumentato quindi la classe di resistenza del calcestruzzo da un C28/35 a un C3240 e incrementato la dimensione delle sezioni.
Le dimensioni minime affinché la verifica fosse soddisfatta sono risultate per i correnti 40x70 cm e per i montanti 40x85.
La sezione dei montanti risulta dimensionata in maniera ragionevole, per quanto riguarda i correnti invece, conoscendo la geometria e le caratteristiche della trave Vierendeel, ci saremmo aspettate una dimensione minore della sezione.
La dimensione ottenuta potrebbe però essere spiegata dal passaggio da un modello ideale di trave Vierendeel (ottenuto come rotazione del modello Shear-Type) a un modello più realistico.

Verifica delle sollecitazioni
Avendo effettuato inizialmente l'analisi del modello statico da cui, grazie alle equazioni di equilibrio, sono risultati i valori degli sforzi di taglio e di momento flettente, abbiamo deciso di verificare se i valori risultanti dal modello in SAP corrispondessero effettivamente ai valori ottenuti dall'analisi statica.

Sappiamo che i valori dello sforzo di taglio variano per ognuno dei sei correnti della trave Vierendeel e conoscendo il valore della forza concentrata F che abbiamo applicato, possiamo calcolarli

1. T=F/2 = 58,05 KN
2. T=F = 116,10 KN
3. T=3F/2 = 174,15 KN
4. T=2F = 232,20 KN
5. T=5F/2 = 290,25 KN
6. T=3F = 348,30 KN

Dall'analisi del modello abbiamo estrapolato i valori del taglio e li abbiamo confrontati

Considerando che i valori che escono dal modello sono approssimati più precisamente rispetto ai calcoli semplificati che abbiamo effettuato, possiamo riscontrare che i valori dello sforzo di taglio sono verificati.

Sapendo che il momento equivale al valore del taglio moltiplicato per il braccio (L/2 = 1,5m) possiamo dedurre che anche i valori del momento flettente siano verificati, essendo dipendenti dallo sforzo di taglio e da un valore della luce che rimane costante.

Verifica agli abbassamenti
Abbiamo infine effettuato la verifica agli abbassamenti.
Il valore assoluto dell’abbassamento che risulta dal modello in SAP è 
U3 = 0,0471 m

Affinché l’abbassamento sia verificato deve risultare
U3 < Ltot/200
Dove Ltot è la distanza maggiore dall’estremo libero all’incastro
Ltot = 18 m

Ltot/200 = 0,09 m
0,0471 m < 0,09 m

La verifica agli abbassamenti è soddisfatta.

Studentesse: Mariani Lucia, Maurelli Ilaria

Dopo aver precedentemente effettuato la progettazione di massima dell’edificio sottoposto alla combinazione di carico allo stato limite ultimo e all'azione del vento, ci siamo concentrate sull’analisi del comportamento del fabbricato sottoposto ad azione sismica orizzontale.

Definizione dei controventi e delle rigidezze

Come prima cosa, definita la geometria dell'impalcato, abbiamo numerato i pilastri e successivamente individuato i controventi orizzontali e verticali in corrispondenza dei telai.

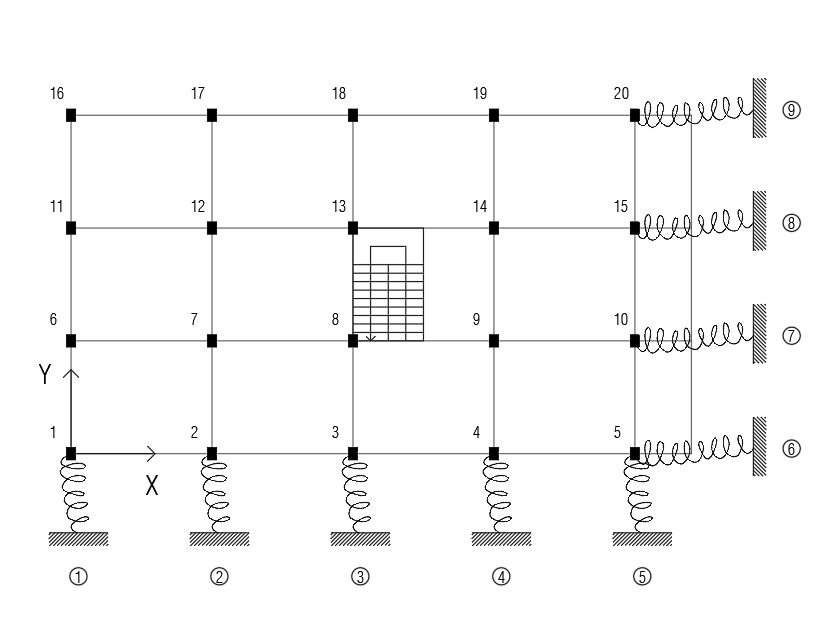
Successivamente abbiamo svolto una breve analisi per capire quale fosse l'orientamento ottimale dei pilastri in presenza dell'azione sismica.

Nell'esercitazione precedente, i nostri pilastri erano stati orientati in base allo studio dell'azione del vento, con la dimensione maggiore lungo l'asse orizzontale.

I pilastri del piano terra (32x44) cm, possono essere orientati in due diverse direzioni.
In base all'orientamento del pilastro ciò che influisce sul calcolo delle rigidezze è il momento di inerzia I, che dipende dalla sezione e dal suo orientamento in pianta.

Abbiamo calcolato il momento di inerzia della sezione rettangolare in entrambi i casi di orientamento: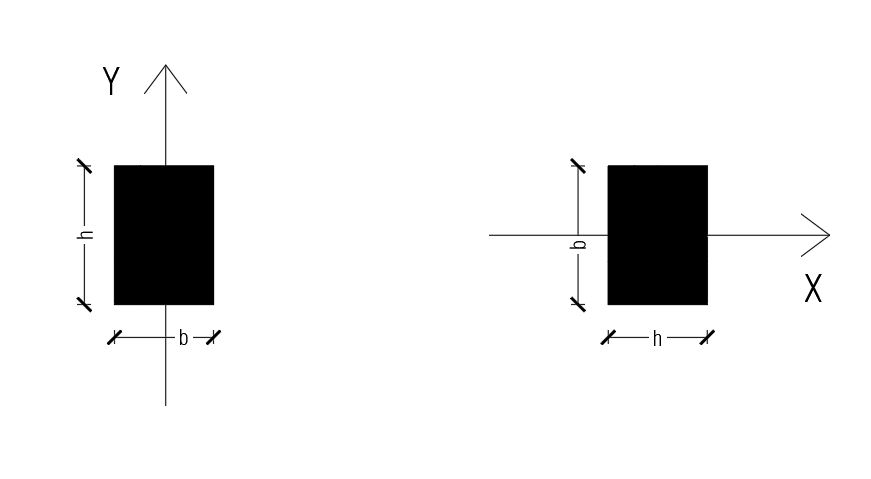

I₁ = bh³ / 12 = 32 cm x 44³ cm³ / 12 = 227157 cm⁴
I₂ = hb³ / 12 = 44 cm x 32³ cm³ / 12 = 120149 cm⁴

Abbiamo poi calcolato il rapporto tra i due momenti
di inerzia

I₁ / I₂  = 227157 cm⁴ / 120149 cm⁴ = 1,9 = 2 (circa)

Dal calcolo del rapporto vediamo come orientando il pilastro con la dimensione maggiore l'ungo l'asse orizzontale, otteniamo un momento di inerzia che è pari a circa il doppio rispetto all'orientamento con la dimensione maggiore lungo l'asse verticale.

Per quanto riguarda il nostro impalcato rigido, essendo i telai orizzontali individuati da 5 pilastri e i telai verticali individuati da 4 pilastri, e sapendo che la rigidezza totale è la somma delle rigidezze traslanti dei controventi lungo una direzione, abbiamo scelto di orientare il pilastro in modo tale da ottenere un maggiore momento di inerzia lungo la direzione verticale, cioè quella individuata da un minor numero di controventi.

In questo modo, otteniamo due valori di rigidezza traslante non troppo distanti tra loro, questo ci assicura una discreta rigidezza dell'impalcato in entrambe le direzioni, non potendo prevedere da quale delle due inciderà la forza del sisma.

Dopo aver definito l'orientamento e successivamente le rigidezze dei telai, abbiamo scelto di considerare un  punto O come centro provvisorio, in corrispondenza del pilastro 1.

In base al nostro centro abbiamo potuto così definire le diverse distanze dal punto O, sia per i controventi orizzontali che per i controventi verticali.

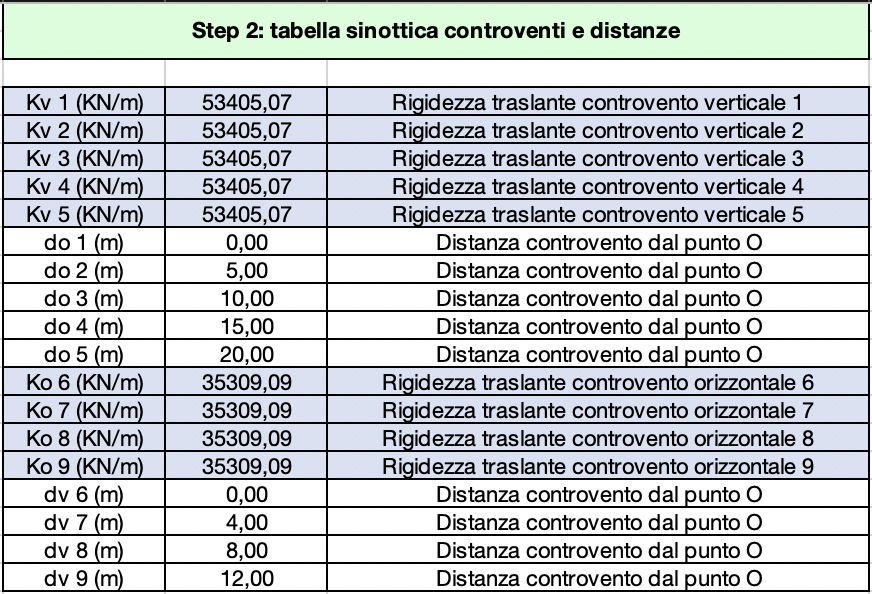
In fine abbiamo potuto completare la tabella sinottica dei controventi con le relative rigidezze traslanti nelle due direzioni, orizzontale e verticale e le distanze ottenute.

 

Calcolo del centro d’area e centro di massa

Successivamente abbiamo definito il centro d'area (centro di massa) del nostro impalcato.
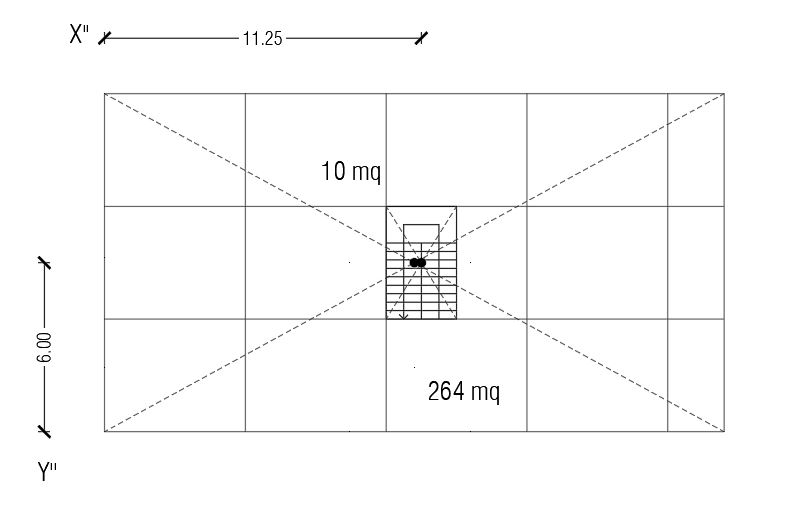
Come prima cosa abbiamo calcolato le aree che caratterizzano la nostra pianta, l’area totale dell'impalcato (Area 1 = 264 m²) e l’area del blocco scale (Area 2 = 10 m²).
Per trovare l'area effettiva, abbiamo quindi sottratto l'area del blocco scale al valore dell'area totale, trovando il valore di 254 m².

Dopo aver ottenuto i valori delle due aree, abbiamo calcolato i rispettivi centri d'area C₁ (x₁;y₁) e C₂ (x₂;y₂).

A questo punto siamo state in grado di calcolare i valori effettivi delle coordinate del centro d'area G (X_G e Y_G) relativo all'area totale cioè la differenza delle due aree (Atot = A₁ - A₂ = 254 m²). 

A₁ = B x H 
A₂ = b x h 
C₁ = (x₁;y₁)
C₂ = (x₂;y₂) 

x_G =  (A₁ x₁ - A₂ x₂)  / (A₁ - A₂)
y_G =  (A₁ y₁ - A₂ y₂)  / (A₁ - A₂)

A₁ = 254,00 m²
A₂ = 10,00 m²
C₁ = (11,00 m ; 6,00 m)
C₂ = (11,25 m ; 6,00 m) 

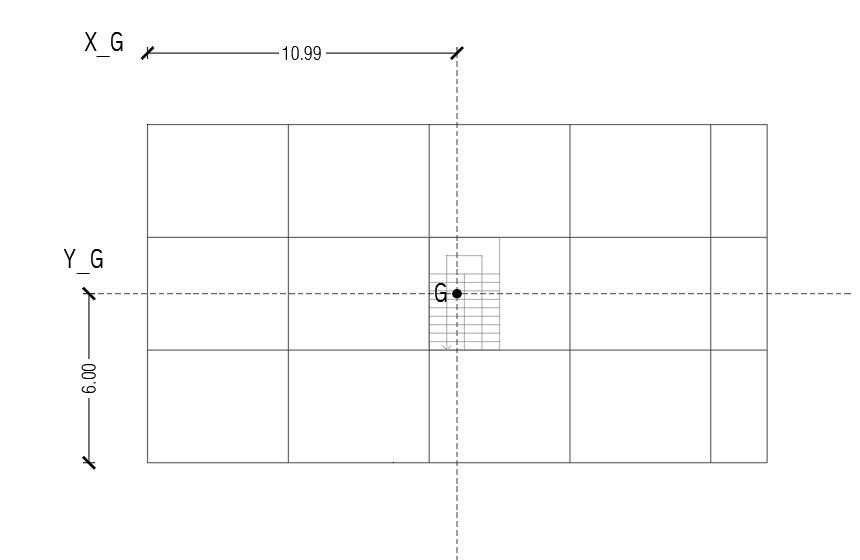
x_G = (254,00 m² x 11,00 m) - (10,00 m² x 11,25 m) / (254,00 - 10,00) m² = 10,99 m 
y_G = (254,00 m² x 6,00 m) - (10,00 m² x 6,00 m) / (254,00 - 10,00) m² = 6,00 m 

Calcolare il centro di un sistema di forze significa poter controllare e saper individuare il punto geometrico attorno al quale la risultante dei momenti statici è uguale a zero.
Questo concetto di centro è fondamentale ai fini dell’analisi che stiamo effettuando perché ci permetterà di individuare il centro delle rigidezze.
Questo punto ci consente di avere coscienza di dove la forza sismica verrà applicata producendo così una traslazione e una rotazione rigida dell'impalcato.

 

Calcolo del centro delle rigidezze

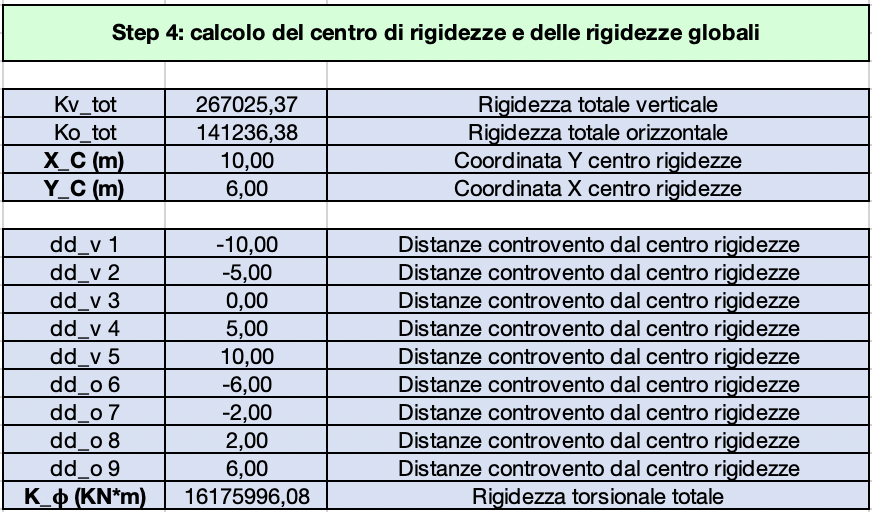
Per il calcolo del centro delle rigidezze, abbiamo definito prima di tutto la rigidezza totale dei controventi in direzione orizzontale e quella dei controventi in direzione verticale
K_{o_tot}​ = 141236,38 KN/m
K_{v_tot} = 267025,37 KN/m

Successivamente abbiamo trovato i valori delle coordinate del centro delle rigidezze C (X_c ; Yc)

X_c = (Sommatoria delle rigidezze dei controventi verticali per le relative distanze y) / (Sommatoria delle rigidezze dei controventi verticali K_{v_tot})
X_c = (K_{v_1} x y₁ + K_{v_2} x y₂  + K_{v_3} x y₃  + K_{v_4} x y₄  + K_{v_5} x y₅) / K_{v_tot} 
X_c = 10,00 m

Y_c = (Sommatoria delle rigidezze dei controventi orizzontali per le relative distanze x) / (Sommatoria delle rigidezze dei controventi orizzontali K_{o_tot})
Y_c = (K_{o_6} x x₆ + K_{o_7} x x₇  + K_{o_8} x x₈  + K_{o_9} x x₉) / K_{o_tot} 
Y_c = 6,00 m

 

Considerazioni:

Abbiamo a questo punto ottenuto i valori delle coordinate del centro d'area (centro di massa) e del centro delle rigidezze.

Centro di massa
X_G = 10,99 m
Y_G = 6,00 m

Centro delle rigidezze
X_C = 10,00 m
Y_C = 6,00 m

Affinché l'edificio possa rispondere adeguatamente alla forza sismica agente, il centro di massa dell'impalcato e il centro delle rigidezze non devono essere troppo distanti tra loro.
In caso contrario, si verificherebbe la formazione di un braccio troppo grande tra i gli assi dei due centri che comporterebbe una rotazione eccessiva dell'impalcato rigido con conseguente collasso.

Calcolo della forza sismica 

Per prima cosa abbiamo definito la forza sismica come il prodotto della massa investita dal sisma per il valore dell'accelerazione sismica di trascinamento (F = m x a).

Queste accelerazioni sismiche sono indotte dal movimento del terreno che le trasferisce all’edificio: qui, incontrando le masse orizzontali (solai), si tramutano in forze.

Per questa ragione, nella formula stessa che descrive il valore della forza F_s, possiamo constatare come la forza sismica non è altro che una frazione della forza peso.
Più una struttura è pesante, e quindi più massa ha, più sarà sensibile all’azione del sisma.

F_s = m x a
F_s =​ m x g x C
F_s = P x C

C= 0,2 è il coefficiente di intensità sismica ricavato dalla normativa in base alla localizzazione dell’edificio che stiamo analizzando: tale coefficiente, sempre minore di 1, ci da un'idea di quanto la nostra struttura è vulnerabile al sisma.

P è la forza peso, descritta come prodotto tra il valore della massa m per l'accelerazione gravitazionale g.
 
P = Q_s + Q_p + 0,8 Q_a 

Q = (Numero di piani dell'edificio) x (Area di un piano al netto del vano scale) x (Valore del carico superficiale distribuito al metro quadrato)

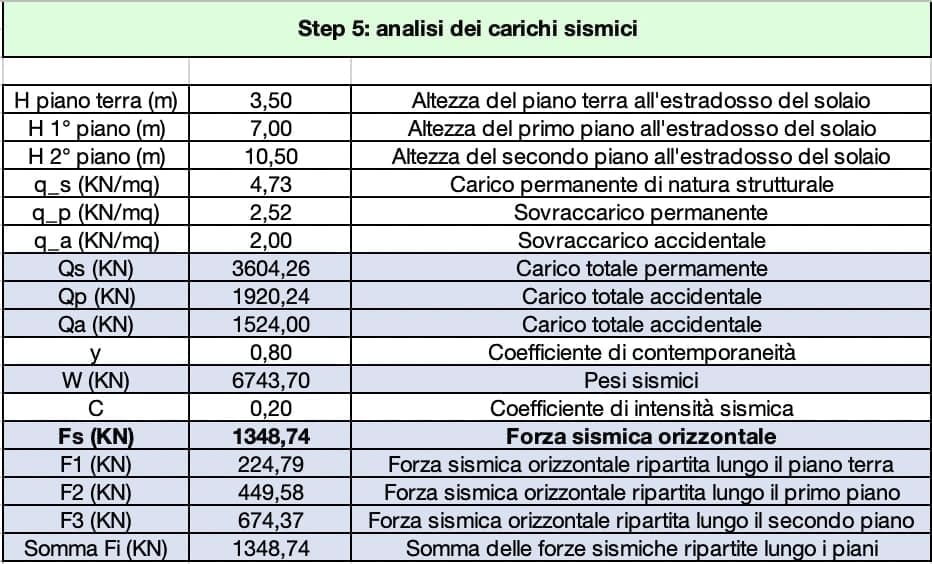
Q_s = 3 x 254,00 m² x 4,73 KN/m² = 3604,26 KN 
Q_p = 3 x 254,00 m² x 2,52 KN/m² = 1920,24 KN 
Q_a = 3 x 254,00 m² x 2,00 KN/m² = 1524,00 KN 

P = 3604,26 KN + 1920,24 KN + 0,8 x 1524,00 KN = 6743,70 KN 

F_s = 6743,70 KN x 0,2 = 1348,74 KN

Osservando le precedenti formule possiamo notare come l’analisi del carico Q dipenda non soltanto dai carichi strutturali, dai sovraccarichi permanenti e da quelli accidentali, bensì anche dal numero dei piani che compongono l’edificio e dall’area della superficie di un piano al netto della scala.
Questo deriva dal fatto che la forza sismica dipende non solo dalla localizzazione geografica e topografica dell’edificio (coefficiente d’intensità sismica C) ma, come abbiamo già detto, dalla massa che essa investe e quindi, dal valore dei pesi sismici che compongono l’intero edificio.
 

 

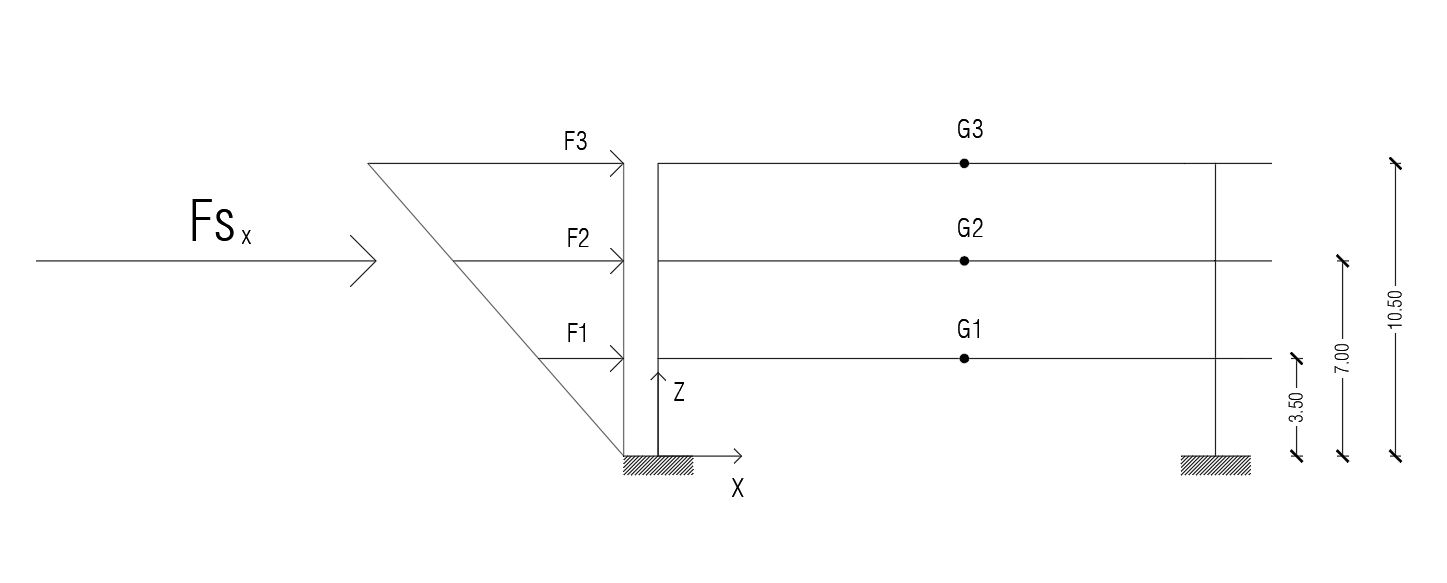
Calcolo della ripartizione della forza sismica per piano

La forza sismica, approssimata come forza orizzontale concentrata, è in realtà descritta da un andamento lineare crescente in proporzione all'altezza dell edificio.
Per questa ragione il valore della forza sismica che colpisce ogni piano è differente.

Per calcolarla abbiamo utilizzato la seguente formula:
F_i = (Altezza interpiano considerato) / (Somma delle altezze relative ai piani) x (Forza sismica)

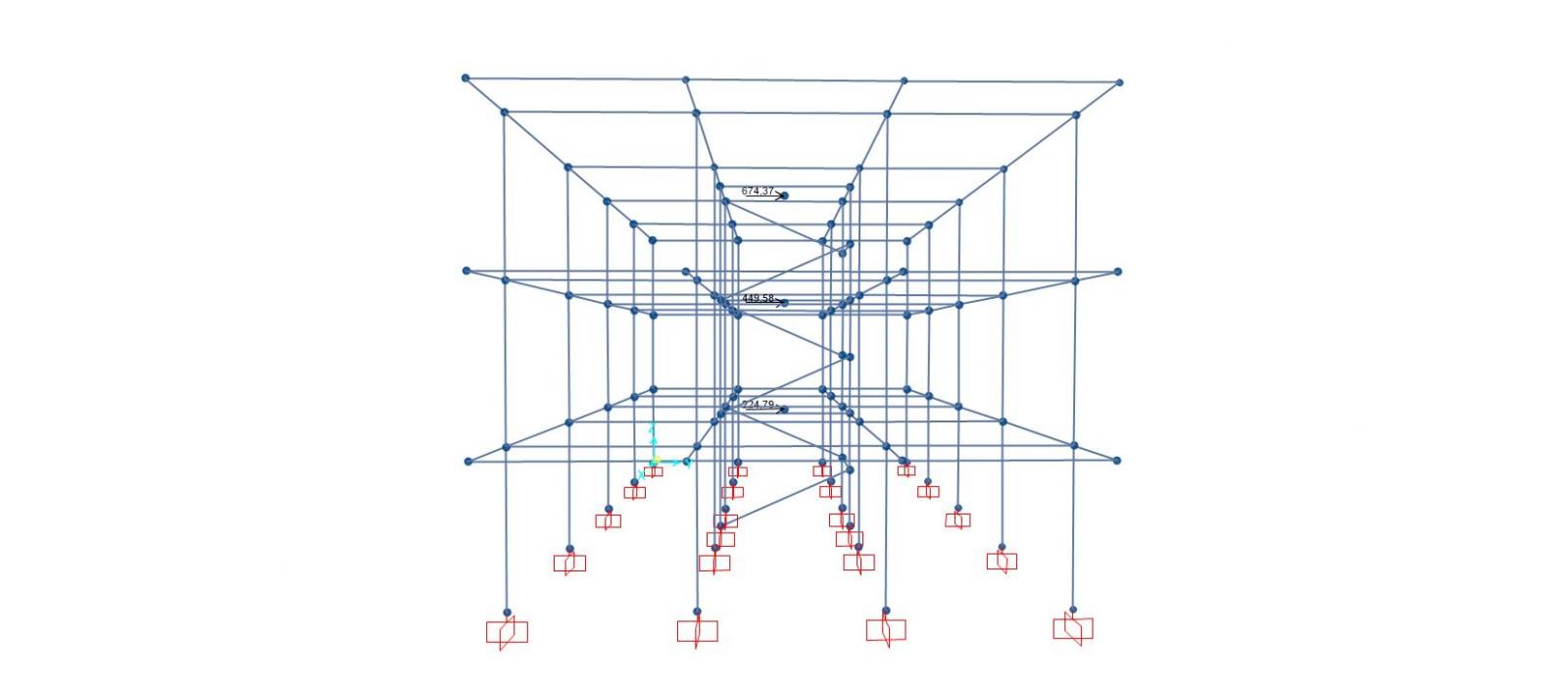
F₁ = (3,50 m / (3,50+7,00+10,50) m x 1348,74 KN = 224,79 KN 
F₂ = (7,00 m / (3,50+7,00+10,50) m x 1348,74 KN = 449,58 KN
F₃ = (10,50 m / (3,50+7,00+10,50) m x 1348,74 KN = 674,37 KN

Per verificare i valori ottenuti della forza sismica nei vari piani abbiamo usato un metodo proporzionale. Quando un edificio è regolare in pianta e in alzato la forza sismica si ripartisce secondo l'andamento lineare crescente precedentemente descritto.
Di conseguenza abbiamo considerato che la forza sismica totale F_s = 1348,74 KN si ripartisce di piano in piano secondo un unità crescente: il primo piano sarà investito da una forza sismica pari ad un unità di F_s, il secondo da una forza pari a due unità, il terzo piano da una forza pari a tre unità.

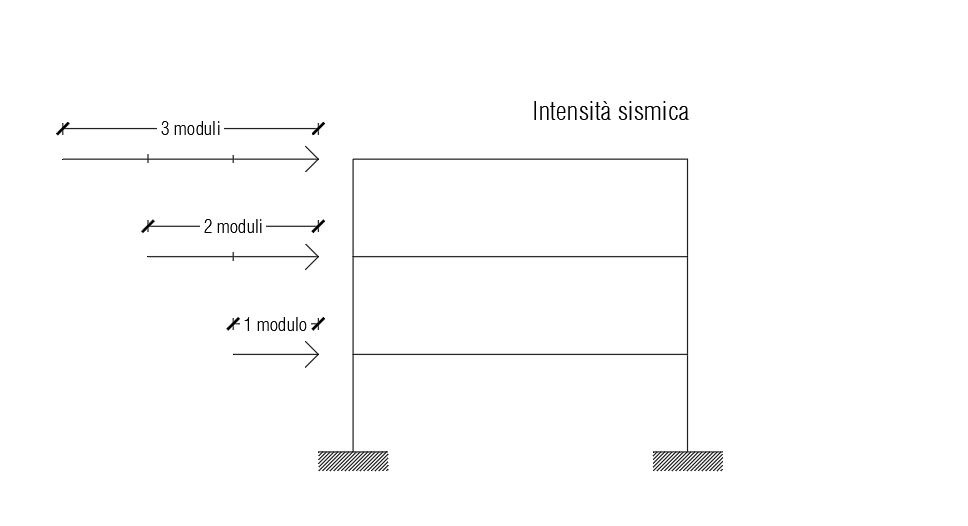
Abbiamo quindi suddiviso il valore totale di F_s in 6 unità ottenendo così il valore unitario di forza
U_F = 1348,74 KN / 6 = 224,79 KN

Questo valore equivale perciò al valore della forza agente sul primo piano:
F₁ = 224,79 x 1 = 224,79 KN
Per trovare il valore della forza agente sul secondo piano abbiamo moltiplicato questo valore per 2 unità:
F₂ = 224,79 x 2 = 449,58 KN
Abbiamo ripetuto lo stesso procedimento per il terzo piano moltiplicando per 3 unità ottenendo la forza agente su quel piano:
F₂ = 224,79 x 3 = 674,37 KN.

Abbiamo così constatato che i valori precedentemente ottenuti sono verificati.

 

Calcolo della ripartizione della forza sismica lungo le due direzioni X e Y

Per il calcolo della ripartizione della forza sismica, abbiamo innanzitutto calcolato il valore del momento torcente dell'impalcato nelle due direzioni come forza per braccio:

M_x = F_s x (X_C - X_G)
M_x = 1348,74 KN x (10,00 m - 10,99 m)
M_x = 1335,47 KNm

M_y = F_s x (Y_C - Y_G)
M_y = 1348,74 KN x (6,00 m - 6,00 m)
M_y = 0 KNm

Sapendo che la forza sismica è definita in funzione della rigidezza dalla seguente equazione lineare:
Forza sismica = Rigidezza x Spostamento
Spostamento = Forza sismica / Rigidezza

Abbiamo calcolato il valore della traslazione orizzontale e di quella verticale relative all'impalcato
u_orizzontale = F_s / K_{o_tot}​ 
u_orizzontale = 0,010 m

v_verticale = F_s /  K_{v_tot} 
v_verticale = 0,005 m

Successivamente abbiamo calcolato i valori di rotazione, sempre differenziando le due direzioni x e y su cui agisce il sisma, come rapporto tra il momento torcente e il valore della rigidezza torsionale totale trovato precedentemente:

ϕ_x = M_x / K_ϕ
ϕ_x = 1335,47 KNm / 16175996,08 KNm
ϕ_x = 0,00008

ϕ_y = M_y / K_ϕ
ϕ_y = 0 KNm / 16175996,08 KNm
ϕ_y = 0

Dopo aver calcolato questi valori siamo stati in grado di calcolare le singole forze agenti sui controventi orizzontali e verticali nel caso della forza sismica agente lungo la direzione X e nel caso della forza sismica agente lungo la direzione Y

F_{i_x} = K_i x (u_orizzontale + d_i x ϕ_x)

F_{i_y} = K_i x (v_verticale + d_i x ϕ_y)

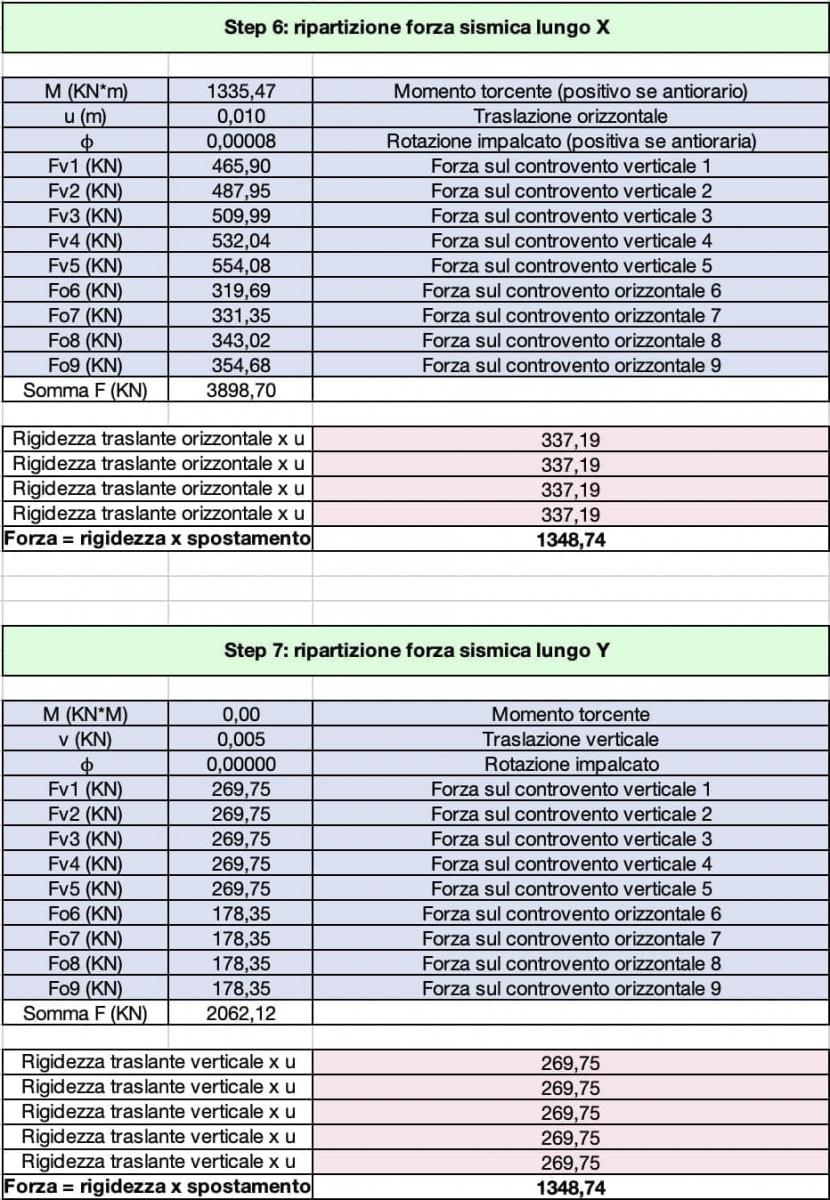
Infine, per verificare i calcoli effettuati, abbiamo calcolato la forza sismica totale incidente su ogni controvento sia in direzione orizzontale che in direzione verticale e abbiamo verificato che la somma di tutte le forze relative ai controventi in una stessa direzione equivalesse al valore della forza sismica.

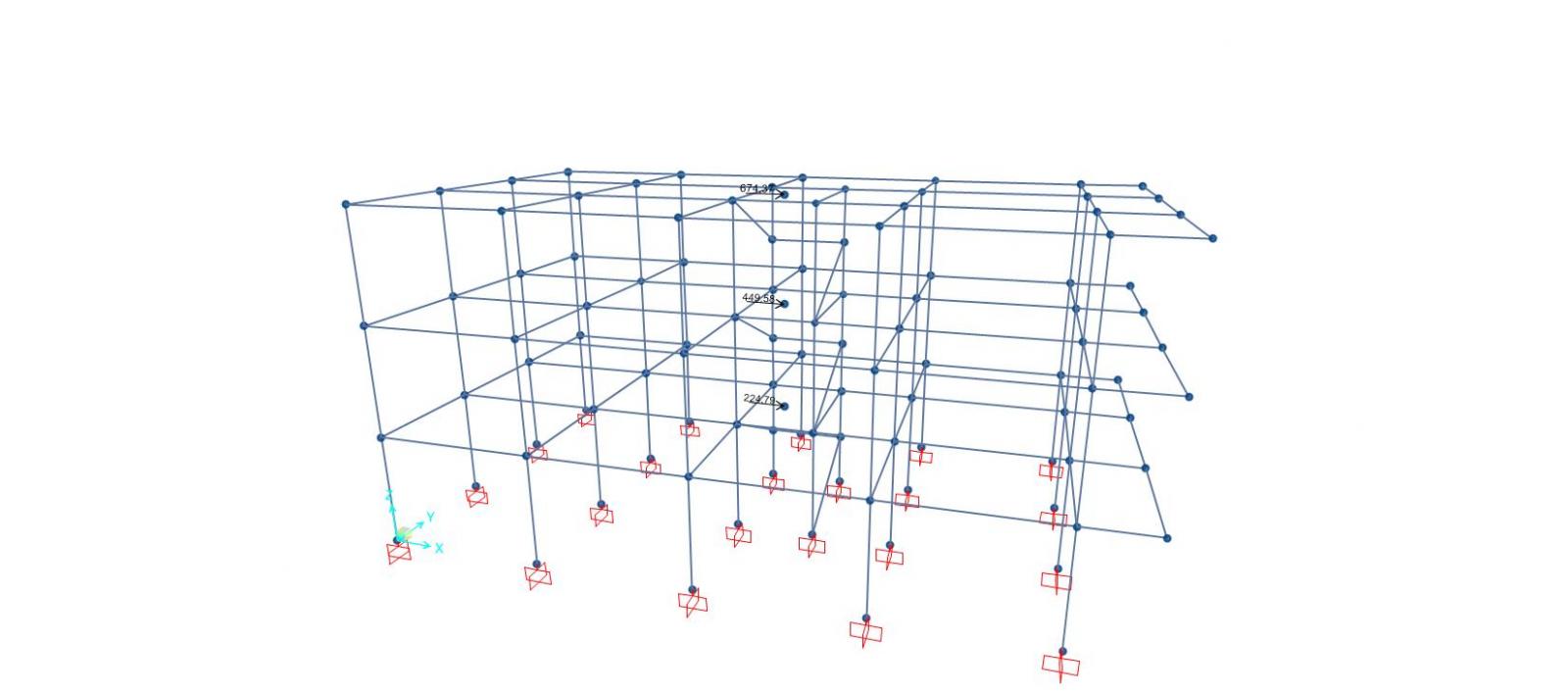
Modellazione su SAP2000

- ASSEGNAZIONE DEL CENTRO DI MASSA E DEL DIAPHRAM

Abbiamo iniziato la modellazione assegnando ad ogni impalcato il centro di massa calcolato precedentemente tramite lo strumento "Special Joint".
Successivamente abbiamo attribuito a tutti i punti appartenenti al piano orizzontale dell’edificio il vincolo "Diaphram", simulando così il comportamento di corpo rigido. 
Questo comportamento impone ad ogni punto appartenente al piano dell’impalcato di ruotare o traslare in maniera omogenea e non indipendente.
Prima dell’assegnazione abbiamo creato tre differenti "Constrains", uno per ogni quota z dell'edificio (z = 3,50 m; z = 7,00 m; z = 10,50 m), questo perché è necessario definire un impalcato rigido differente a seconda del piano orizzontale su cui i punti giacciono.
 

- DEFINIZIONE DEI LOAD PATTERNS

Dopodiché siamo andate a definire due load pattern differenti, "Sisma X" e "Sisma Y", assegnando come moltiplicatore di peso proprio un valore pari a zero in modo da non considerare il peso proprio dell'edificio, già presente nella combinazione lineare SLU.
Queste due forze rappresentano due azioni orizzontali che potrebbero verificarsi in un caso reale, lungo un’asse piuttosto che un altro: le nostra analisi, infatti, è orientata a metterci nella condizione di poter assicurare una risposta dei controventi adeguata in entrambe le direzioni.
 

- APPLICAZIONE DELLA FORZA SISMICA

Secondo piano
Abbiamo inserito il valore della forza F3 = 674,37 KN nelle due direzioni "Sisma X" e "Sisma Y"
Primo piano
Abbiamo inserito il valore della forza F2 = 449,58 KN nelle due direzioni "Sisma X" e "Sisma Y"
Piano terra
Abbiamo inserito il valore della forza F1 = 224,79 KN nelle due direzioni "Sisma X" e "Sisma Y"

- DEFINIZIONE DELLE COMBINAZIONI DI CARICO

Dopo aver assegnato il valore delle forze nei vari centri di massa abbiamo definito due combinazioni di carico “Load Combination” per il sisma lungo X e per il sisma lungo Y (oltre alla combinazione SLU già definita per la scorsa esercitazione), moltiplicando ogni singolo carico per il relativo coefficiente parziale di sicurezza:

- Combinazione allo stato limite ultimo: SLU

Qs (1,3)
Qp (1,5)
Qa (1,5)
PP (1,3)

- Combinazione: Sisma lungo la direzione X

SLU (1)
Sisma X (1)

- Combinazione: Sisma lungo la direzione Y

SLU (1)
Sisma Y (1)
 

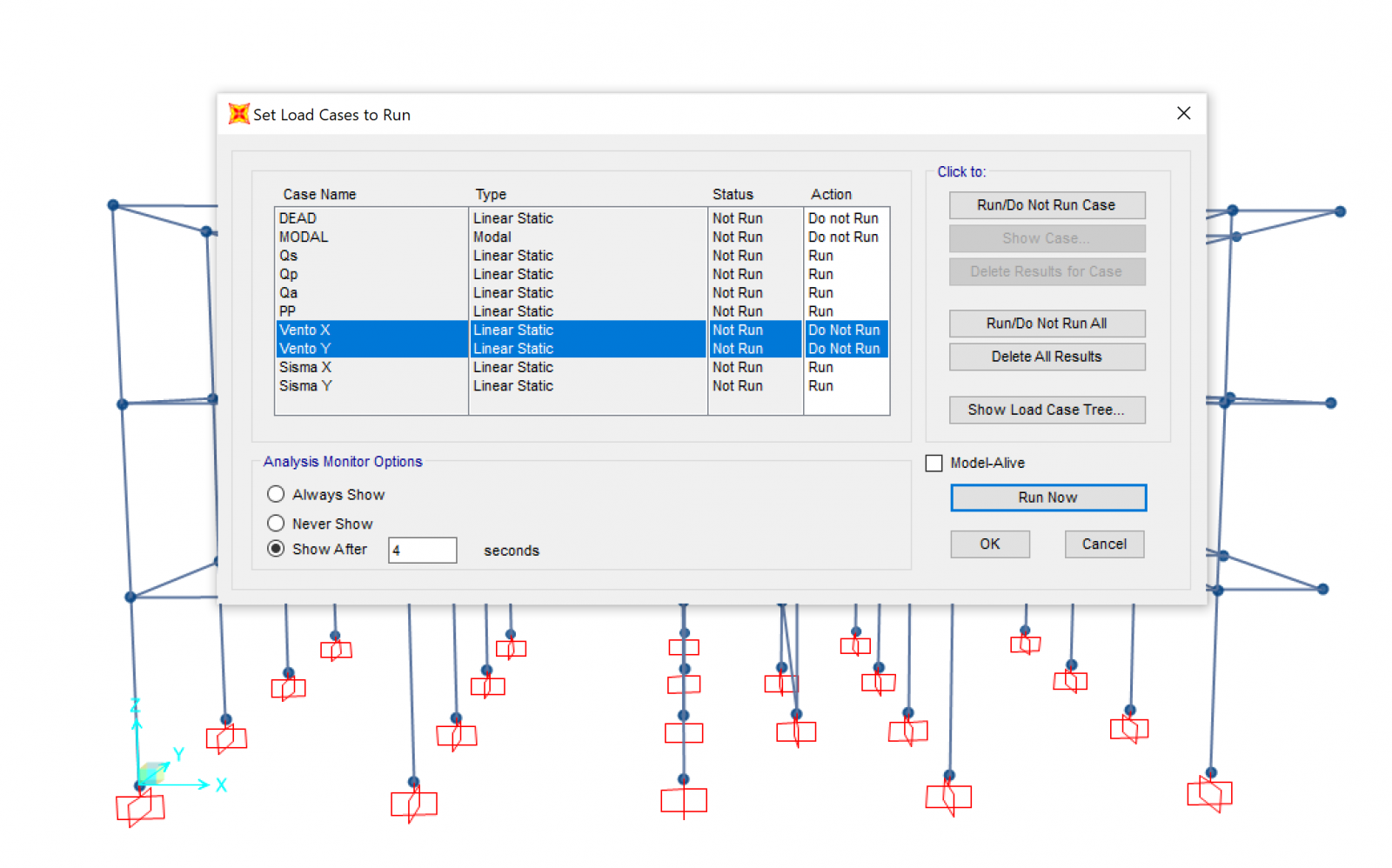
- AVVIO DELL'ANALISI

A questo punto, dopo aver simulato la condizione di impalcato rigido per ogni piano, aver applicato le forze sismiche nel centro di massa differenziandole al crescere dei piani e aver definito le combinazioni di carico che ci interessa analizzare, abbiamo avviato l'analisi del modello "Run Analysis"

Considerando che difficilmente la forza sismica e l'azione del vento agiscono entrambe contemporaneamente con massima intensità, abbiamo deciso di considerare tutti i carichi definiti (Q_s, Q_P, Q_A, PP, Sisma X, Sisma Y) tranne i carichi relativi al vento.

A questo punto abbiamo osservato i diagrammi delle deformate e delle sollecitazioni agenti (N, T, M) nei due casi di combinazione lineare di carico e successivamente abbiamo estratto i valori delle forze nella tabella Excel per andare a verificare le dimensioni delle sezioni dei pilastri soggetti a presso flessione.

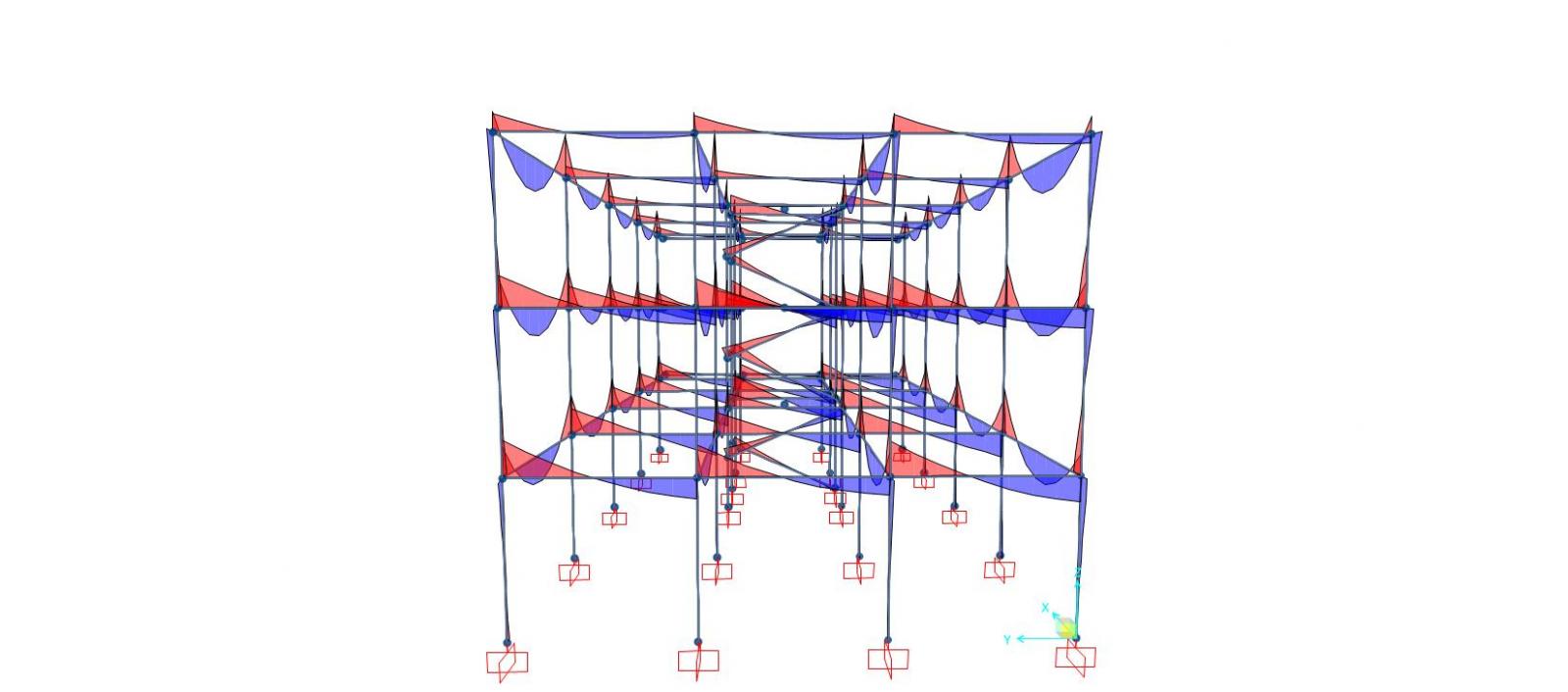
Combinazione Sisma Y
Deformata

Diagramma del momento flettente (intorno all'asse 3)

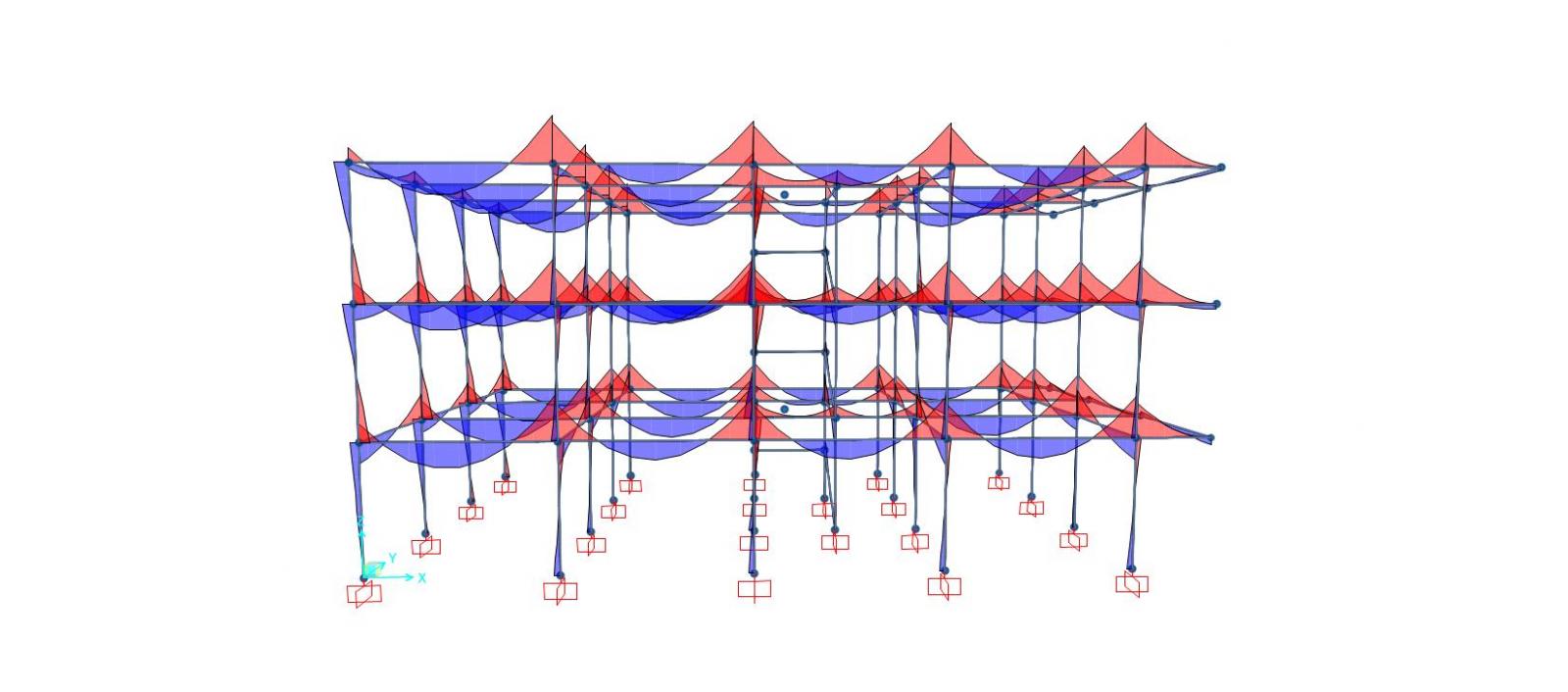
Combinazione Sisma X
Deformata

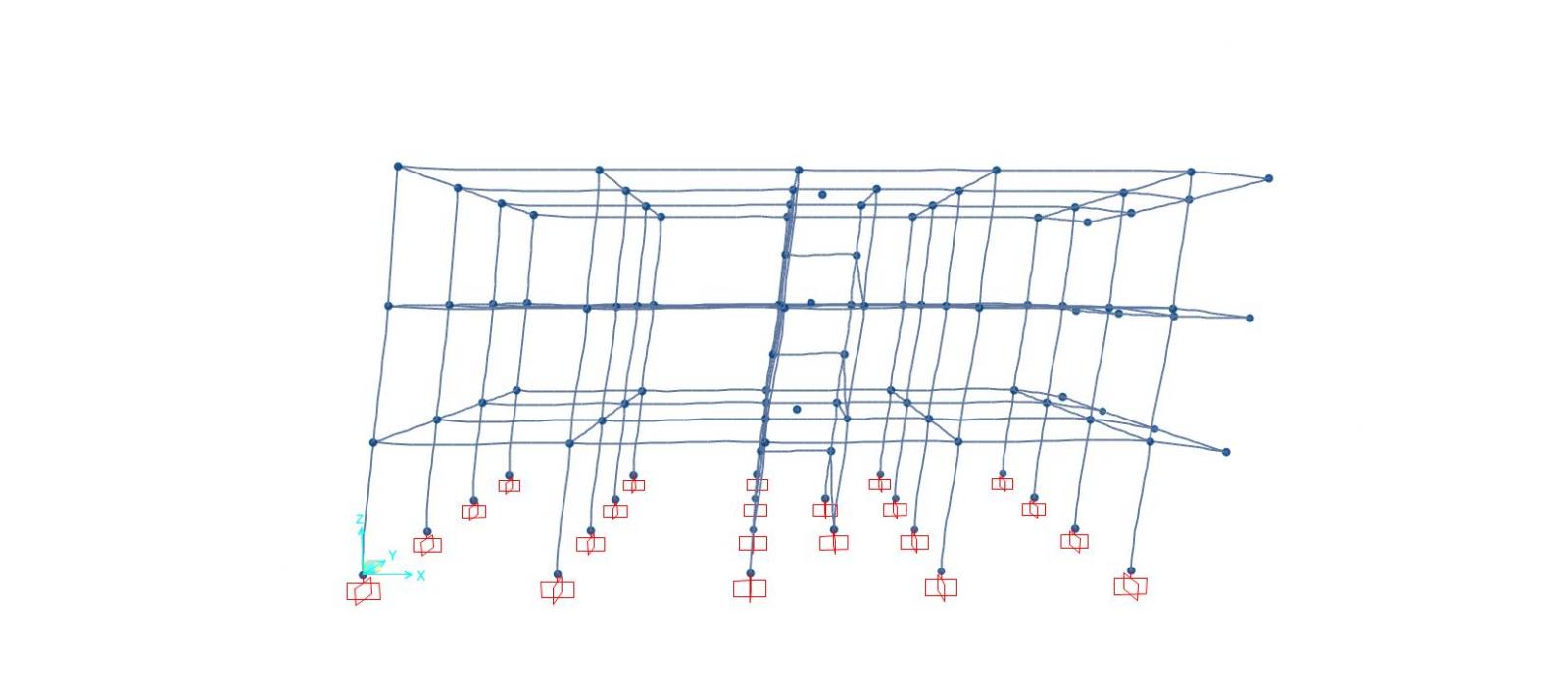
Diagramma del momento flettente (intorno all'asse 3)

Modello tridimensionale
L'orientamento del pilastri è stato invertito in base alle considerazioni riguardanti le rigidezze traslanti dei controventi lungo le due direzioni precedentemente illustrate.

Verifica a pressoflessione dei pilastri

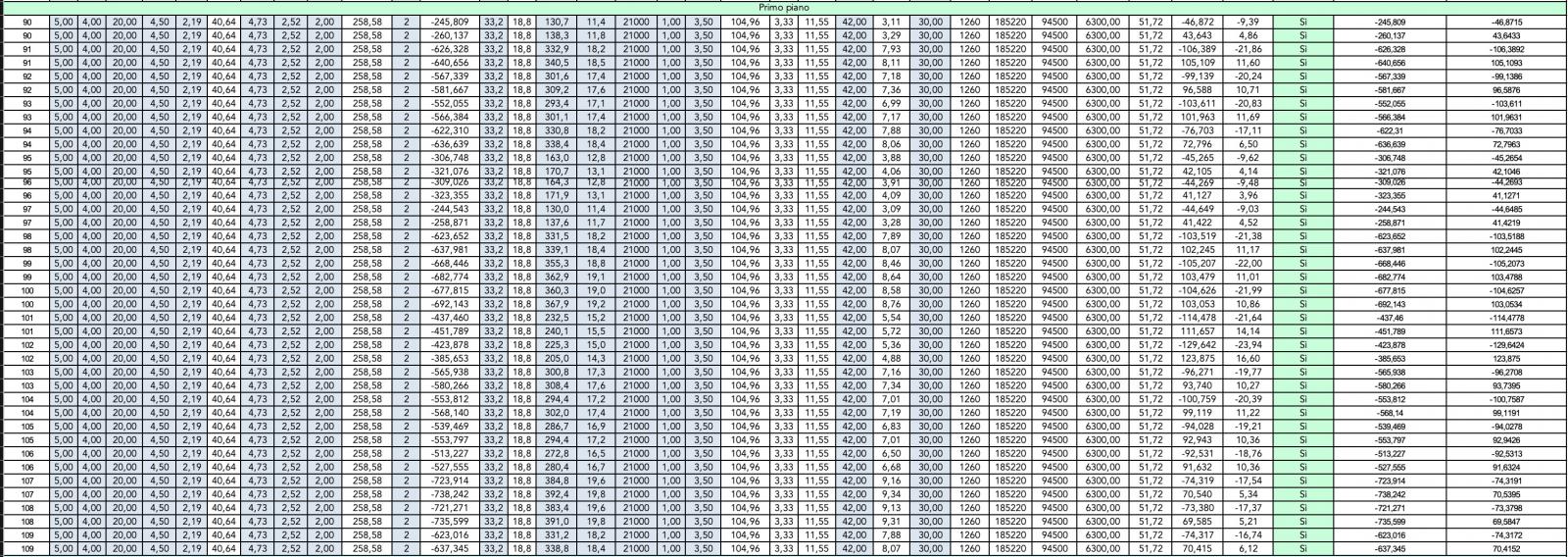
Dopo aver estratto i valori delle sollecitazioni da SAP, le abbiamo suddivise secondo le due combinazioni di carico "Sisma X" e "Sisma Y" .
A questo punto abbiamo importato i valori nel file Excel relativo alla verifica dei pilastri a pressoflessione differenziando le tabelle relative all'azione del sisma lungo l'asse X e all'azione del sisma lungo l'asse Y.

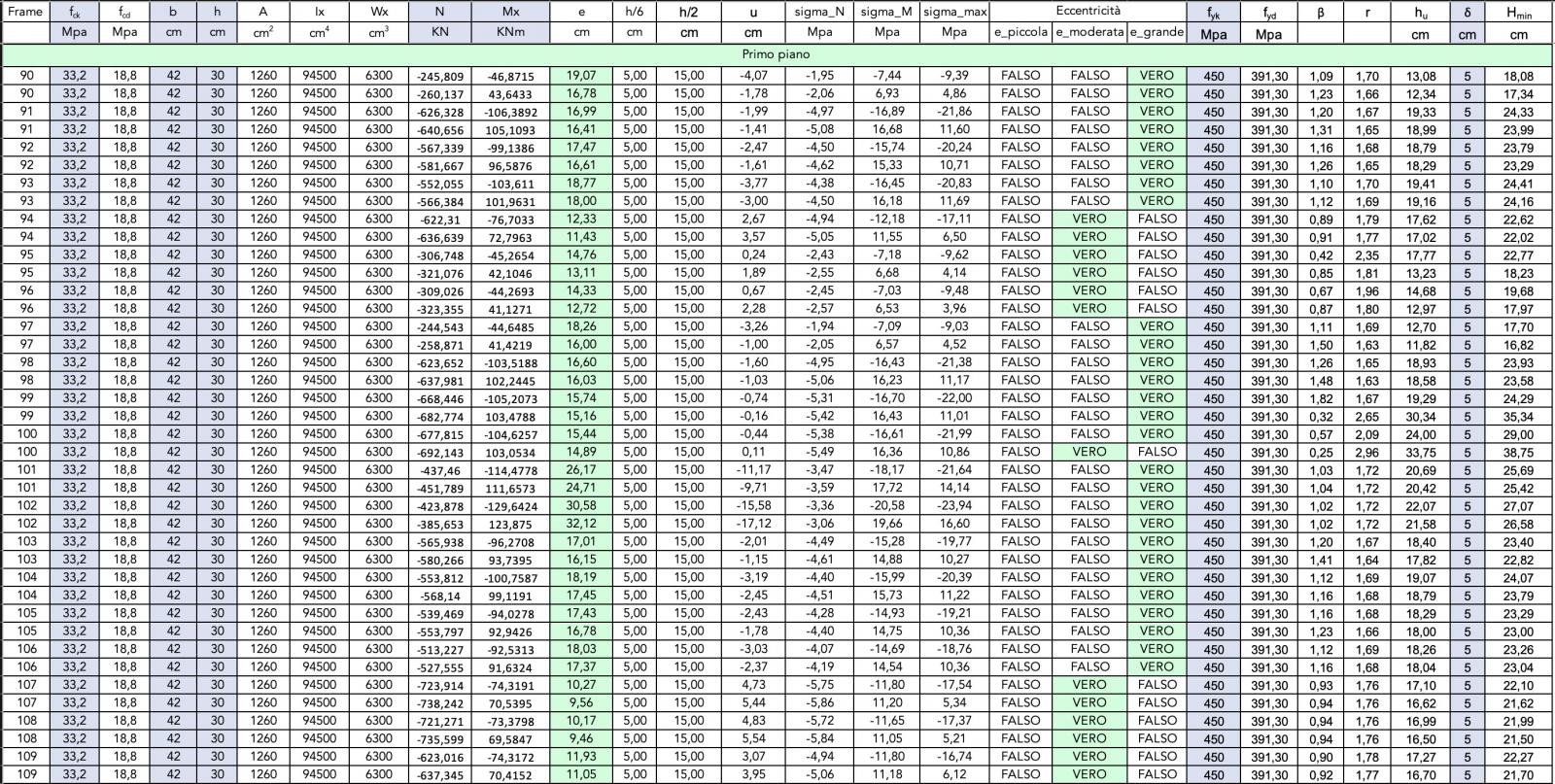
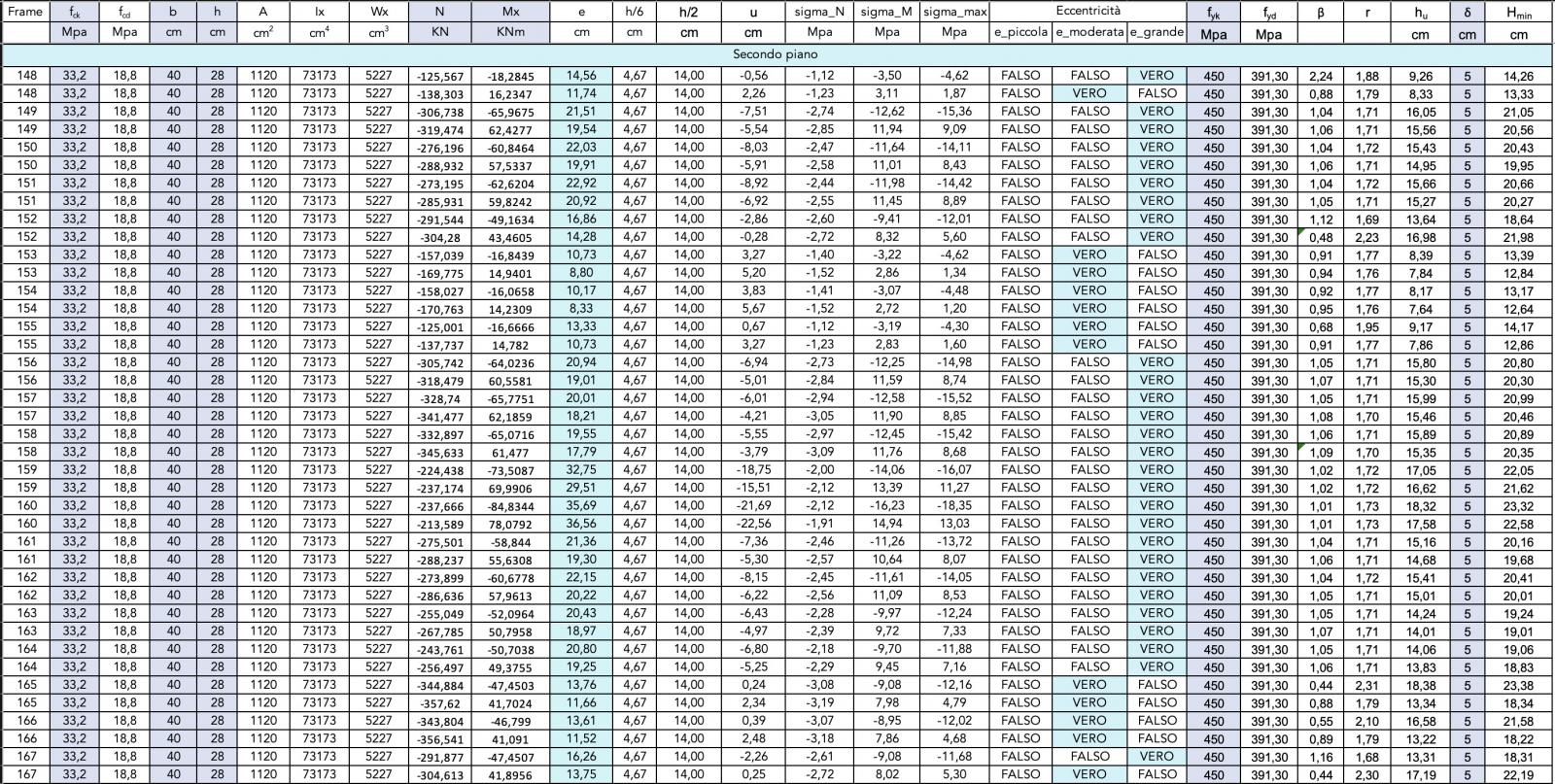
Sisma lungo la direzione X - Verifica pilastri a pressoflessione

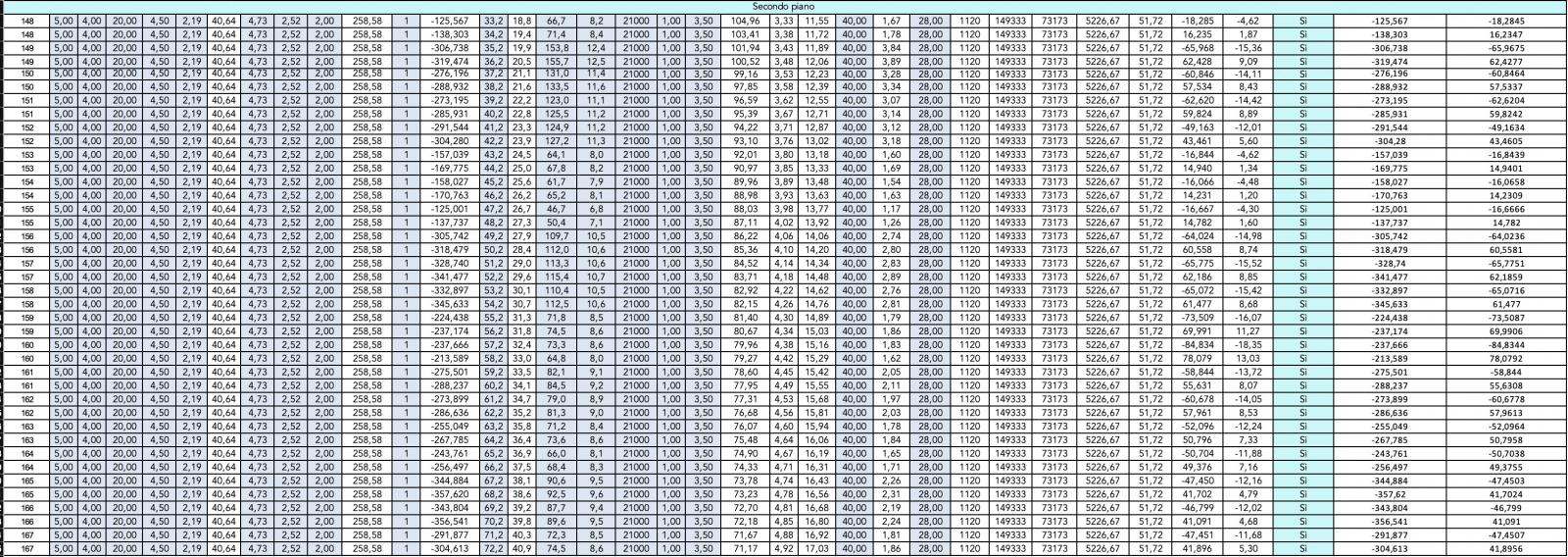
Sisma lungo la direzione Y - Verifica pilastri a pressoflessione

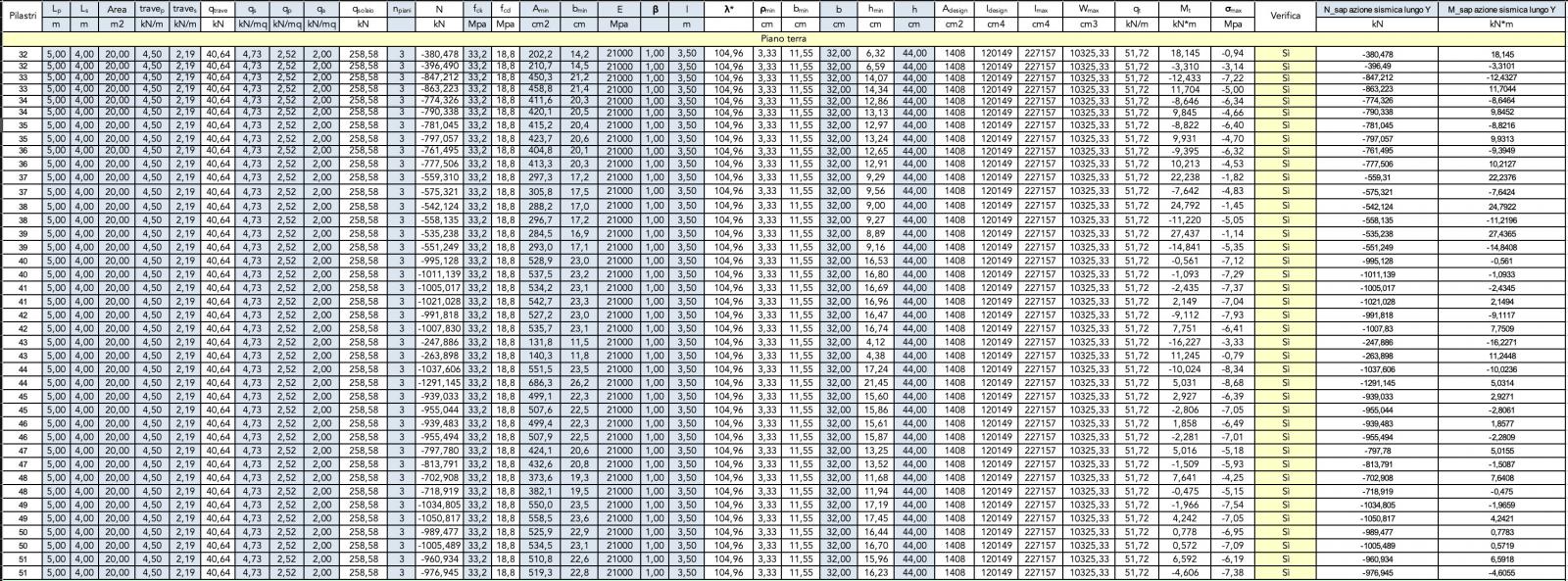
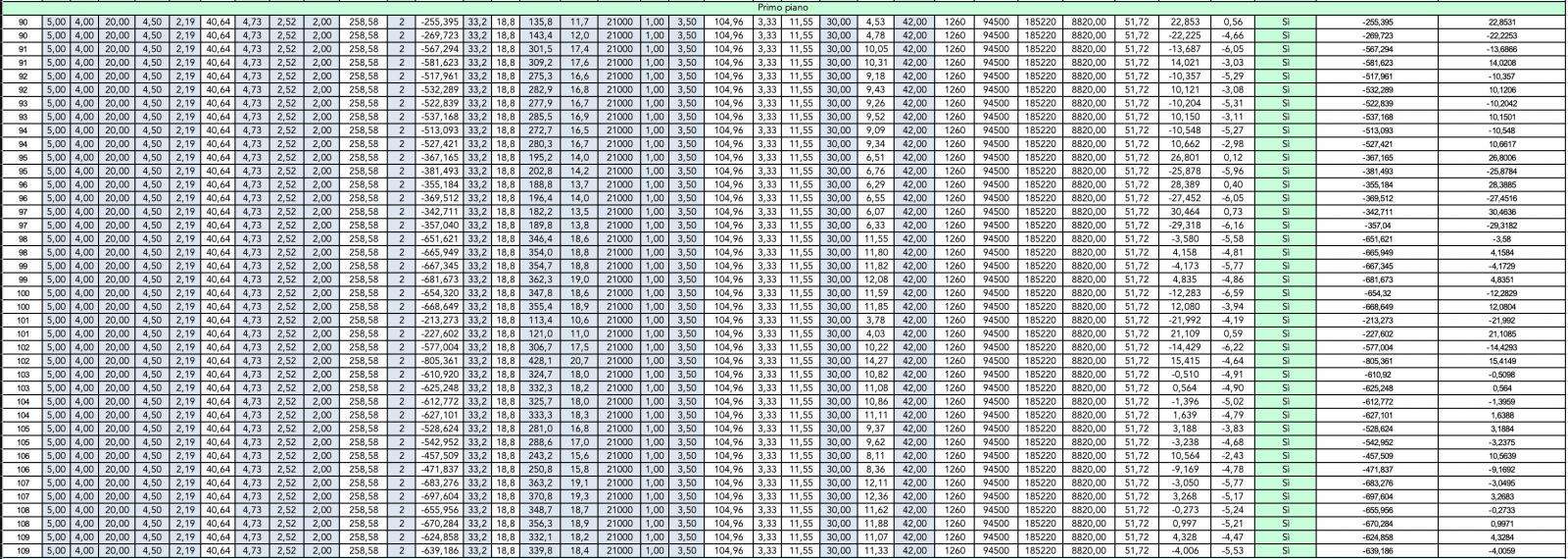
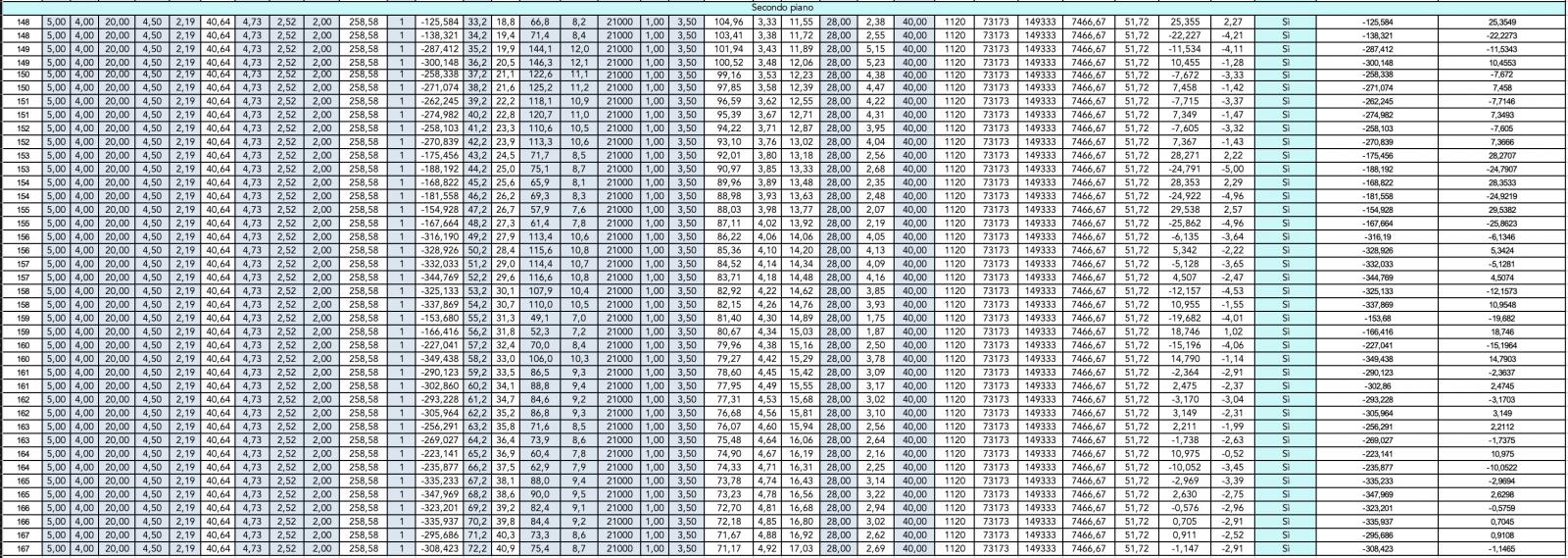
Le tabelle Excel evidenziano che il dimensionamento di massima delle sezioni di pilastri che era stato effettuato per l'esercitazione precedente è sufficiente a rispondere adeguatamente all'azione orizzontale della forza sismica in entrambe le direzioni.

 

Eccentricità

Sisma lungo la direzione X - Eccentricità dello sforzo normale

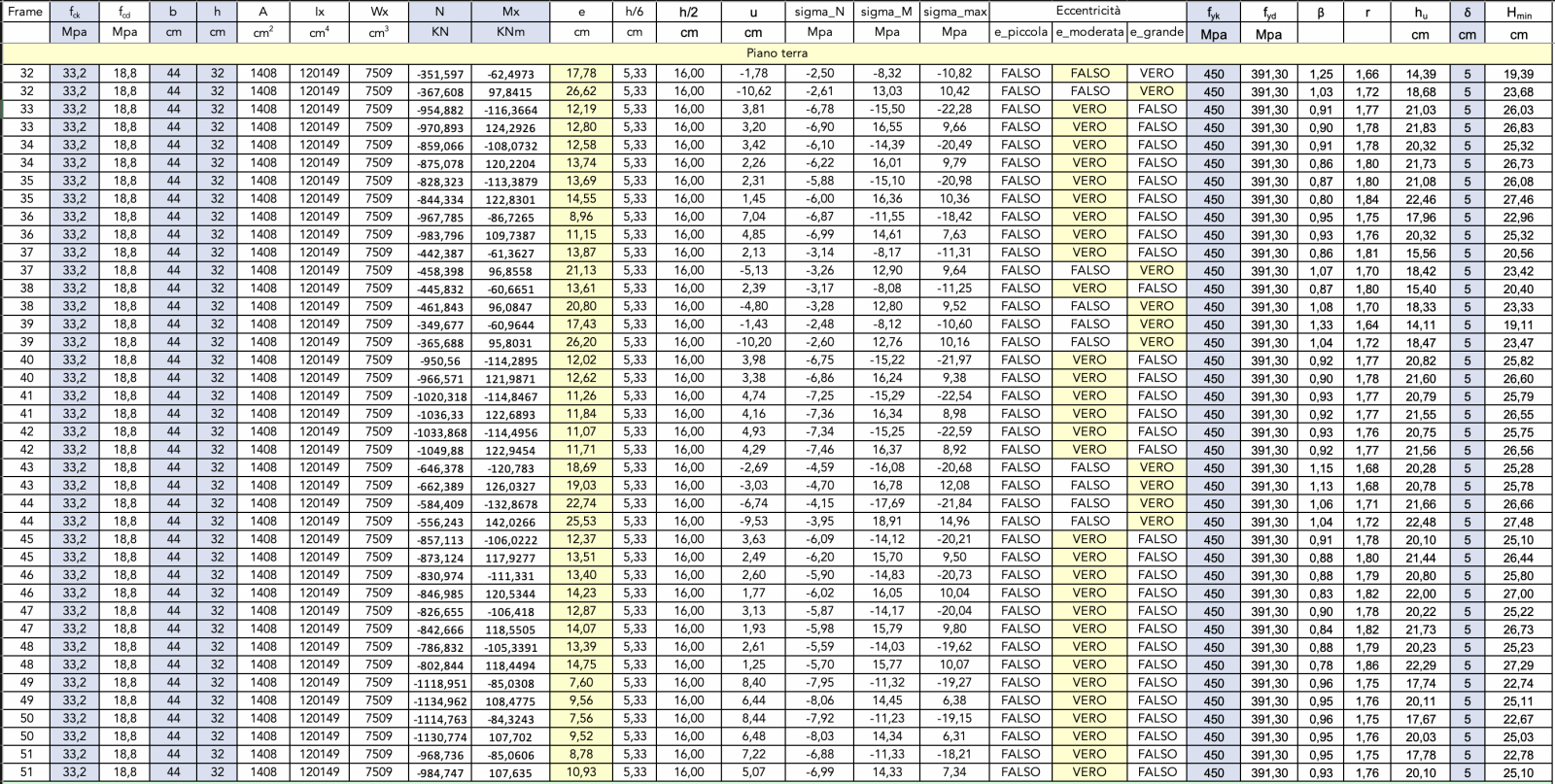
Sisma lungo la direzione Y - Eccentricità dello sforzo normale

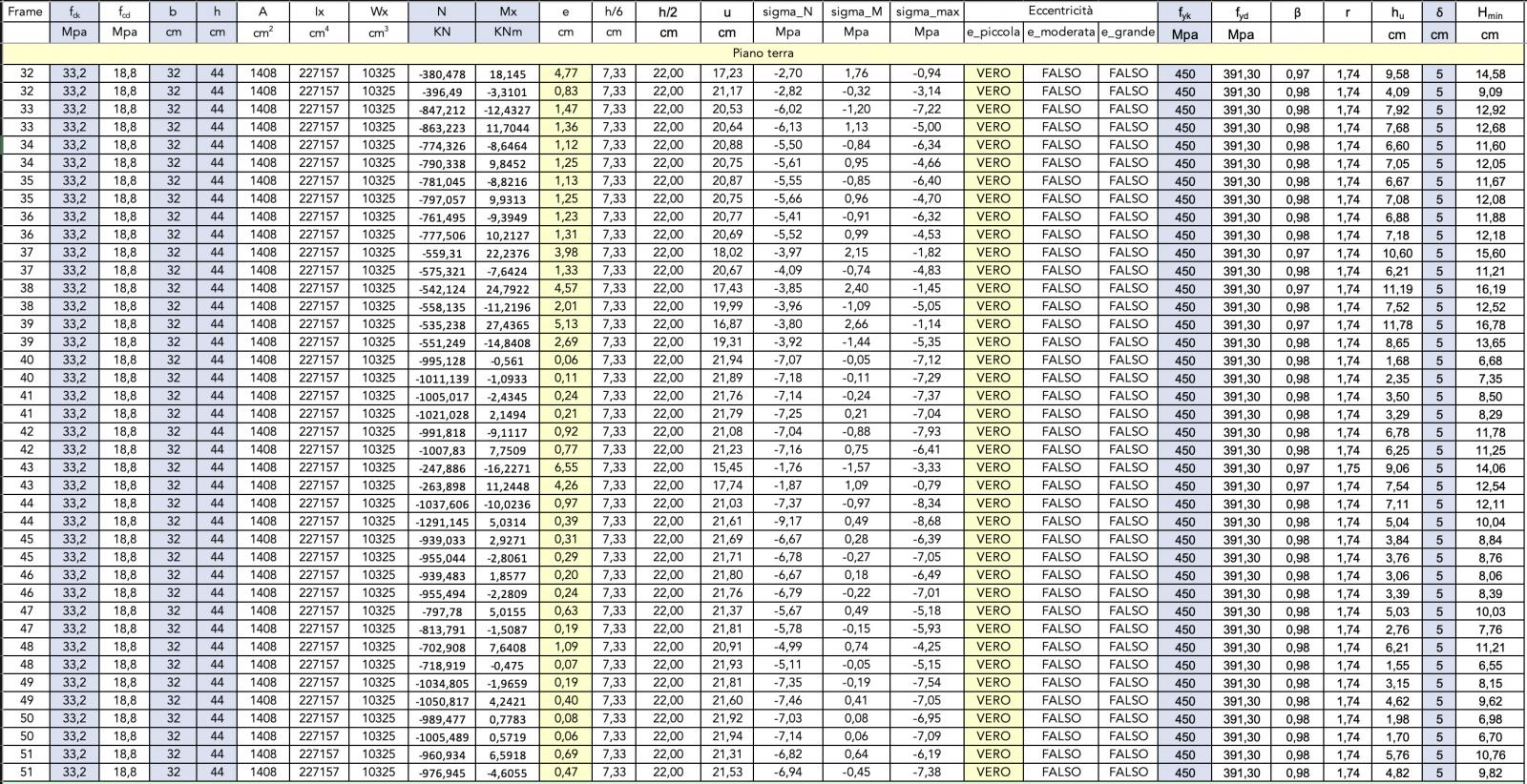
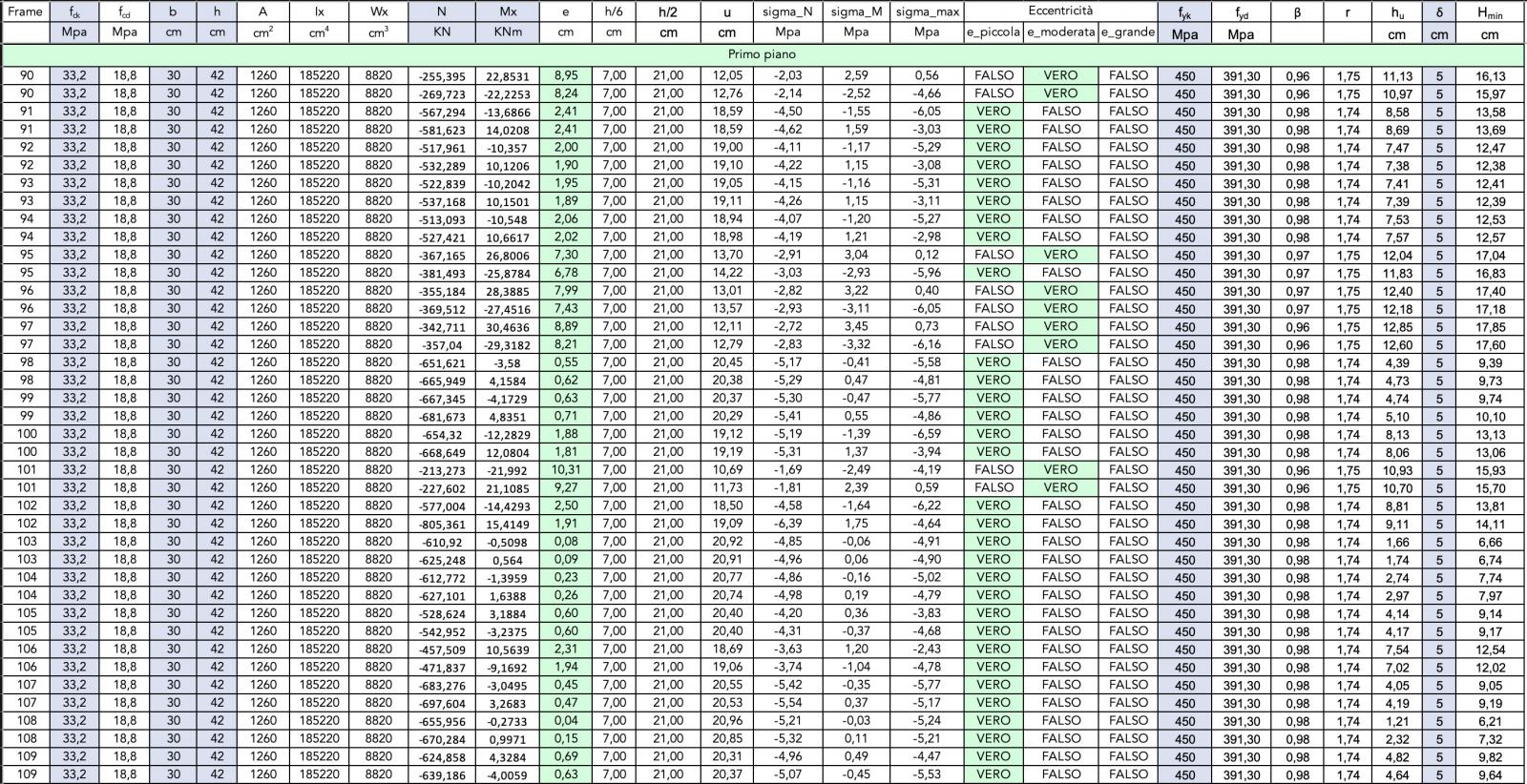
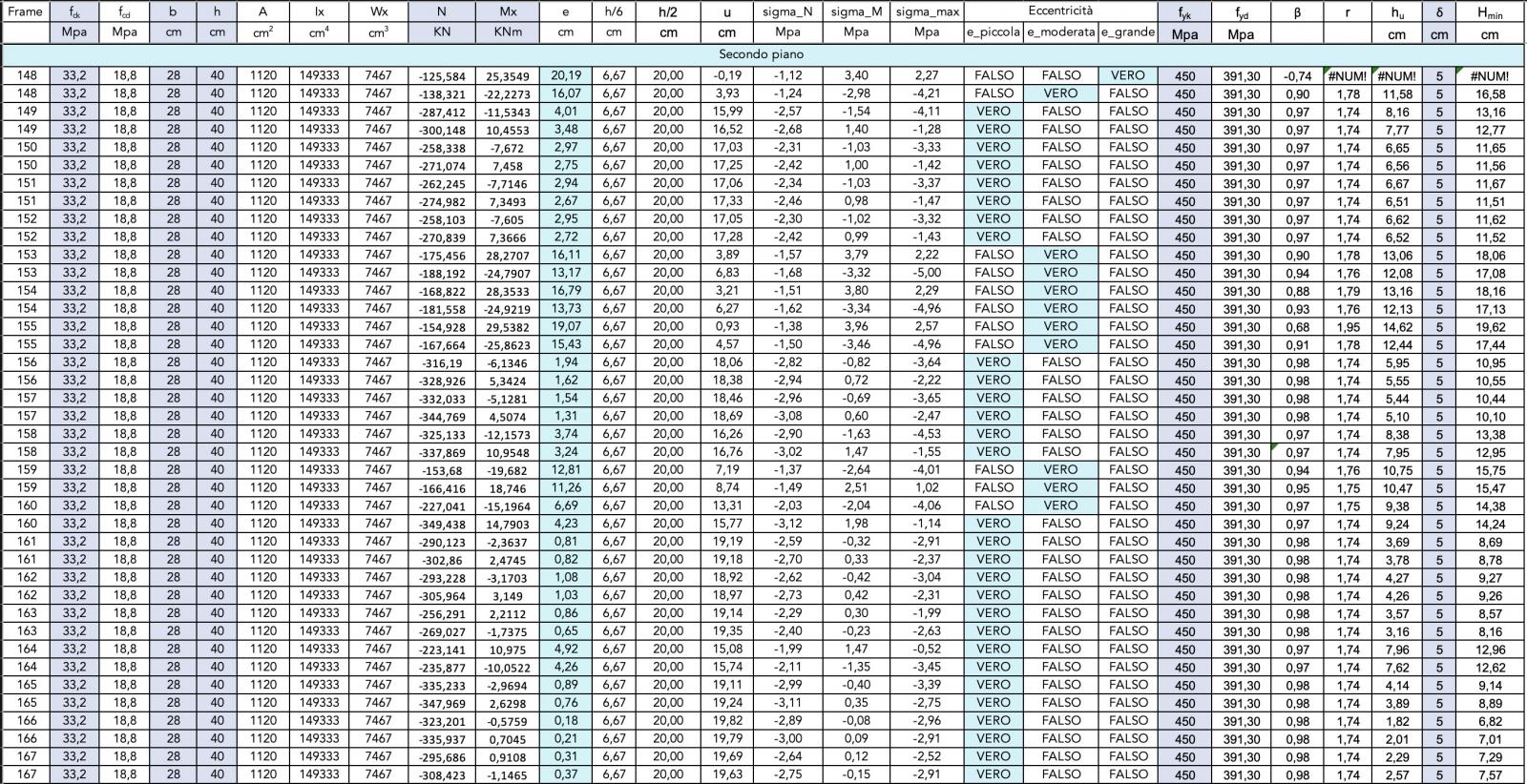
In fine abbiamo verificato, con i nuovi valori dello sforzo normale e del momento flettente, i valori dell'eccentricità relativa allo sforzo assiale N di compressione sui pilastri.
Tale eccentricità di N è dovuta alla compresenza dello sforzo di compressione e della flessione.

Dal confronto con i precedenti calcoli risulta che alcuni pilastri, evidentemente soggetti ad una flessione più elevata, sono passati da un valore di piccola eccentricità ad un valore di eccentricità moderata; altri pilastri che risultavano invece in condizione di eccentricità moderata sono passati ad avere un valore di eccentricità grande.

 

 

Studentesse: Mariani Lucia, Maurelli Ilaria

Progetto della geometria
Abbiamo progettato un edificio regolare in calcestruzzo armato con le seguenti caratteristiche:
Dimensioni della pianta: 22,00x12,00 metri
- Altezza totale: 10,50 metri
- Altezza interpiano: 3,50 metri
- Numero di piani: 3
- Lievi aggetti: mensole di 2,00 metri
- Gabbia scala con travi a ginocchio di dimensioni  2,50x4,00 metri
- Comportamento a telaio

 

 

Analisi dei carichi
Dopo aver definito la geometria, abbiamo definito i carichi superficiali distribuiti su un metro quadrato di solaio che, dopo essere stati convertiti in carichi linearmente distribuiti, dovranno essere assegnati alle aste orizzontali.
Queste ultime sono state differenziate, dopo aver definito l'orditura del solaio, in travi principali e travi secondarie e, successivamente, sono state suddivise anche in base al carico agente su di esse.

Tassonomie delle travi
- Travi principali perimetrali
   Interasse 2,00 metri
   (Portano il peso proprio, il peso del solaio e il peso del tompagno)
- Travi principali centrali
   Interasse 4,00 metri
   (Portano il peso proprio e il peso del solaio) 
- Travi secondarie perimetrali
   Interasse 0,50 metri
   (Portano il peso proprio e il peso del tompagno)
- Travi secondarie centrali
   Interasse 1,00 metri
   (Portano il peso proprio)

Abbiamo quindi calcolato i carichi agenti su un metro quadrato di solaio suddividendoli nelle tre categorie
- Carico permanenti strutturali
- Sovraccarico permanente non strutturale
- Carico accidentali

Analisi dei carichi di un solaio in laterocemento

1. Pavimentazione in parquet
   2 cm = 0,02 m
2. Massetto
   3,00 cm = 0,03 m
3. Isolante
   4,00 cm = 0,04 m
4. Soletta collaborante
   5,00 cm = 0,05 m 
5. Pignatte
   20,00 cm = 0,20 m
6. Travetti
   20,00 cm = 0,20 m
7. Intonaco
   1,50 cm = 0,015 m

​Spessore totale solaio = 35,50 cm = 0,355 m

Calcolo del carico distribuito superficiale

1. 0,02 m x 7,20 KN/m³ = 0,144 KN/m²
2. 0,03 m x 20,00 KN/m³ = 0,60 KN/m²
3. 0,04 m x 0,20 KN/m³ = 0,008 KN/m²
4. 0,05 m x 25,00 KN/m³ = 1,25 KN/m²
5. 2 (0,20 x 0,12 x 1,00) KN/m³ x 25 KN/mc = 1,20 KN/m²
6. 2 (0,38 x 0,20 x 1,00) m³/m² x 15 KN/mc = 2,28 KN/m²
7. 0,015 m x 18,00 KN/m³ = 0,27 KN/m²

- Carico strutturale q_s
   Soletta + Travetti + Pignatte
   1,25 KN/m² + 1,20 KN/m² + 2,28 KN/m² = 4,73 KN/m²
- Sovraccarico permanente q_p
   Parquet + Massetto + Isolante + Intonaco + Incidenza impianti + Incidenza tramezzi
   0,144 KN/m² + 0,60 KN/m² + 0,008 KN/m² + 0,27 KN/m² + 0,50 KN/m² + 1,00 KN/m² = 2,52 KN/m² = 2,52 KN/m²
- Carico accidentale q_a
   Dato fornito dalla normativa in base alla destinazione d’uso = 2,00 KN/m²

A questo punto abbiamo considerato le combinazioni di carico fornite dalla normativa per le verifiche agli stati limite, utilizzando coefficienti parziali di sicurezza sfavorevoli.

Combinazione di carico allo stato limite ultimo SLU
γs qs + γp qp + γa qa = 1,30 x 4,73 KN/m² + 1,50 x 2,52 KN/m² + 1,50 x 2,00 KN/m² = 12,89 KN/m² = 12,90 KN/m²
q_u = 12,90 KN/m²
Combinazione di carico allo stato limite d’esercizio SLE
γ̃s qs + γ̃p qp + γ̃a qa = 1,00 x 4,73 KN/m² + 0,70 x 2,52 KN/m² + 0,70 x 2,00 KN/m² = 7,88 KN = 7,90 KN/m²
qe = 7,90 KN/m²

Successivamente abbiamo calcolato il carico linearmente distribuito del tompagno che andrà a gravare sul perimetro dell’edificio (travi principali perimetrali, travi secondarie perimetrali)

Analisi dei carichi del tompagno 

1. Intonaco esterno
   2,00 cm = 0,02 m
2. Isolante
   5,00 cm = 0,05 m
3. Rasante
   1,00 cm = 0,01 m
4. Blocchi in laterizio forati
   20,00 cm = 0,20 m
5. Intonaco interno
   2,00 cm = 0,02 m

Spessore totale tompagno = 30,00 cm = 0,30 m
Altezza totale tompagno =
(altezza interpiano) - (spessore del solaio) =
350,00 cm - 35,50 cm = 314,50 cm = 3,145 m

Calcolo del carico distribuito lineare
0,02 m x 3,145 m x 18,00 KN/m³ = 1,13 KN/m
0,05 m x 3,145 m x 0,20 KN/m³ = 0,03 KN/m
0,01 m x 3,145 m x 0,30 KN/m³ = 0,009 KN/m
0,20 m x 3,145 m x 8,00 KN/m³ = 5,00 KN/m
0,02 m x 3,145 m x 18,00 KN/m³ = 1,13 KN/m
Peso totale tompagno = 7,299 KN/m = 7,30 KN/m

Infine, grazie moltiplicando i carichi superficiali ottenuti rispettivamente per gli interassi delle membrature su cui agiscono, abbiamo ottenuto i carichi linearmente distribuiti da assegnare su SAP.

Carico dovuto al vento

Per quanto riguarda gli elementi strutturali verticali, abbiamo considerato un contributo del vento pari a 0,50 KN/m² e, dopo aver suddiviso i pilastri in base al loro interasse, abbiamo calcolato il carico distribuito verticale agente su ogni pilastro nelle due direzioni x e y.

Tassonomie dei pilastri
- Pilastri perimetrali
   Interasse 5,00 metri
   (Subiscono il carico trasmesso dal solaio alle travi principali e l’azione orizzontale del vento lungo le due direzioni x e y)
- Pilastri angolari
   Interasse 2,50 metri
   (Subiscono il carico trasmesso dal solaio alle travi principali e l’azione orizzontale del vento lungo le due direzioni x e y)
- Pilastri centrali
   (Subiscono il carico trasmesso dal solaio alle travi principali per tutti i piani sovrastanti)

Pre dimensionamento
Per il pre dimensionamento delle membrature ci siamo basate su tre modelli fondamentali di aste:
- Mensola verticale
- Trave doppiamente appoggiata
- Mensola orizzontale

Pilastri
Modello: mensola verticale
Per pre dimensionare gli elementi strutturali verticali che compongono il nostro edificio, abbiamo per prima cosa effettuato il calcolo per la base minima di un pilastro in calcestruzzo di altezza 3,50 m
b_min = 2√3ρ_min = 2√3 x 3,33 cm = 11,55 cm
Dividendo il valore dell'area minima ottenuta per questo valore della base, abbiamo trovato la dimensione minima dell'altezza del pilastro
h_min = 159,00 cm² / 11,55 cm = 13,77 cm
Il pre dimensionamento è stato effettuato considerando una dimensione della base e dell'altezza dell'elemento maggiore rispetto alle dimensioni minime trovate in quanto, data l’entità della struttura e sulla base delle precedenti esercitazioni effettuate su SAP, il valore minimo risultava troppo piccolo per poter costituire la base di un pilastro in grado di resistere alle sollecitazioni agenti.
Lo sforzo di compressione utilizzato per il pre dimensionamento è stato calcolato considerando il carico allo stato limite ultimo moltiplicato per l’area di influenza del pilastro, a questo è stato aggiunto il peso proprio delle travi in calcestruzzo, il tutto moltiplicato per il numero di piani.
Dopo aver calcolato la tensione massima dovuta allo sforzo di compressione, abbiamo verificato che essa non superasse il valore della resistenza di calcolo a compressione del calcestruzzo scelto (C40/32)
N/A + M_t/W_max < di f_cd

Travi
Modello: trave doppiamente appoggiata
Per il pre dimensionamento degli elementi strutturali orizzontali abbiamo ipotizzato, sulla base delle precedenti esercitazioni effettuate su SAP, in aula e in autonomia, una dimensione delle travi compatibile con i carichi agenti sull’edificio, differenziando secondo le diverse tassonomie precedentemente elencate.
Il valore del momento flessionale considerato per il pre dimensionamento equivale al valore del momento massimo in campata per un modello di trave doppiamente appoggiata sottoposta a carico orizzontale linearmente distribuito, tale valore equivale a ql²/8.
Abbiamo poi definito le resistenze dei materiali: C32/40 per il calcestruzzo e acciaio S450 per le armature.
A questo punto, grazie alla teoria della flessione della trave, abbiamo potuto determinare i valori di β ed r.
Una volta determinati questi valori, abbiamo stabilito arbitrariamente una dimensione della base in modo tale da poter determinare l’altezza utile h_u e di conseguenza l’altezza totale H minima della trave in calcestruzzo.
Aggiungendo poi, oltre ai carichi precedentemente considerati, anche il peso proprio della trave stessa, e ripetendo i calcoli, abbiamo potuto ottenere il valore reale dell’altezza minima H: questo valore ci è servito per verificare le dimensioni delle sezioni da noi precedentemente ipotizzate.

Mensole
Modello: mensola orizzontale
Per il pre dimensionamento delle mensole abbiamo effettuato lo stesso procedimento precedentemente utilizzato per il pre dimensionamento delle travi.
La sola differenza sta nella scelta del valore di calcolo del momento flessionale che, in questo caso, equivale al valore del momento massimo (in corrispondenza del vincolo di incastro) di una trave che presenta una estremità incastrata a un’altra estremità libera, sottoposta al medesimo carico orizzontale linearmente distribuito. Tale valore equivale a ql²/2.

Una volta verificate tutte le sezioni ipotizzate abbiamo quindi definito su SAP le dimensioni delle sezioni per ogni tipologia di elemento strutturale:

Dimensioni degli elementi che compongono il telaio
Pilastro piano terra = 32x44 cm 
Pilastro primo piano = 30x42 cm 
Pilastro secondo piano = 28x40 cm 
Travi principali = 60x30 cm 
Travi secondarie = 35x25 cm 
Mensole = 50x30 cm 

Dimensioni degli elementi che compongono la scala
Trave a ginocchio = 30x20 cm 
Cordolo = 45x30 cm 
Montanti = 30x30 cm 

 

Modellazione in SAP2000
Per la modellazione dell’edificio su SAP abbiamo seguito le seguenti fasi:

- Per prima cosa abbiamo modellato la geometria dell’edificio su SAP grazie alla griglia e gli strumenti di disegno “Frame” e “Special Joint” ;

- Abbiamo poi assegnato i vincoli esterni di tipo incastro alla base dei pilastri del piano terra;

- Per simulare un nodo rigido interno, abbiamo definito i rilasci agli estremi delle aste (non abbiamo assegnato nessun rilascio alle estremità, in questo modo la rotazione intorno a tutti gli assi nel punto di collegamento tra gli elementi è pari a zero);

- Per facilitare la successiva assegnazione dei carichi, abbiamo suddiviso i vari elementi del modello in diversi gruppi:

Pilastri 0 _ Angolari
Pilastri 0 _ Perimetrali
Pilastri 0 _ Centrali
Pilastri 1 _ Angolari
Pilastri 1 _ Perimetrali
Pilastri 1 _ Centrali
Pilastri 2 _ Angolari
Pilastri 2 _ Perimetrali
Pilastri 2 _ Centrali
Travi principali _ Perimetrali
Travi principali _ Centrali
Travi secondarie _ Perimetrali
Travi secondarie _ Centrali
Corpo scala

 

- Grazie a tale suddivisione abbiamo assegnato agli elementi strutturali le sezioni precedentemente definite;

- Successivamente abbiamo definito i carichi fissando il relativo fattore moltiplicatore del peso proprio “Load Patterns”, in questo modo abbiamo potuto considerare il peso proprio di ogni singolo elemento che compone il modello grazie al carico PP:

Qs (0)
Qp (0)
Qa (0)
PP (1)
Vento X (0)
Vento Y (0)

- Abbiamo poi definito le diverse combinazioni di carico “Load Combination” moltiplicando ogni singolo carico per il relativo coefficiente parziale di sicurezza:

- Combinazione allo stato limite ultimo: SLU
   Qs (1,3)
   Qp (1,5)
   Qa (1,5)
   PP (1,3)
- Combinazione: Vento lungo la direzione X
   SLU (1)
   Vento X (1)
- Combinazione: Vento lungo la direzione Y
   SLU (1)
   Vento Y (1)

- Dopo aver definito i carichi, abbiamo assegnato a ogni elemento strutturale i rispettivi valori del carico distribuito ottenuti dall’analisi dei carichi precedentemente svolta;

- Per simulare una struttura a telaio con impalcato rigido, abbiamo assegnato il vincolo “Diaphram” dalla voce “Costrains” per tutti gli elementi orizzontali presenti per ogni piano.
In questo modo, sotto l'effetto delle forze agenti, l'impalcato si comporterà come un corpo rigido;

- Avendo scelto delle sezioni rettangolari per gli elementi verticali, abbiamo orientato i singoli pilastri con l'asse d'inerzia maggiore lungo la direzione di maggiore sollecitazione per garantire una deformazione contenuta;

 

 

 

 

- A questo punto abbiamo avviato l’analisi del modello “Run Analysis”;

- Abbiamo visualizzato la configurazione deformata della struttura, in particolare gli spostamenti verticali in corrispondenza degli aggetti, e i diagrammi delle sollecitazioni agenti (N, T, M);

- In fine abbiamo esportato le tabelle Excel relative ai valori delle sollecitazioni nella combinazione di carico allo stato limite ultimo per la verifica degli elementi inflessi e pressoinflessi.

Verifica

Verifica delle aste orizzontali
Abbiamo sostituito i valori esportati dal modello nella tabella Excel relativa alla verifica delle travi principali, secondarie e delle mensole orizzontali e abbiamo controllato che la verifica fosse soddisfatta per ogni elemento.

Travi principali

Travi secondarie

Mensole

Verifica delle aste verticali

Abbiamo creato un altro file Excel in cui abbiamo calcolato l'eccentricità dello sforzo assiale agente sui pilastri, abbiamo suddiviso questi ultimi nei vari piani inserendo le tre categorie di eccentricità, piccola moderata e grande.
Abbiamo poi verificato di quanto lo sforzo assiale fosse decentrato rispetto all'asse baricentrico dell'asta, ripetendo questa considerazione per ogni piano.
Al piano terra l'eccentricità risulta piccola in quanto i pilastri sono maggiormente soggetti a sforzo normale di compressione; al primo piano si presentano i primi pilastri con eccentricità moderata mentre all'ultimo piano i  pilastri presentano anche valori di grande eccentricità.

L'aumento della dimensione dell'eccentricità, che è definita come rapporto tra il momento intorno all'asse x e lo sforzo normale, spiega la morfologia degli elementi verticali, data l'entità degli sforzi a cui essi sono sottoposti.

Pilastri

Eccentricità

Modello 3D