2_ESERCITAZIONE SULLA LINEA ELASTICA_26-03-2013

ESERCITAZIONE SULLA LINEA ELASTICA_26-03-2013

Dal momento che il sistema è iperstatico per poterlo risolvere ricorriamo al metodo d’integrazione della linea elastica, il quale ci permette di individuare quella che è la nostra incognita principale, ovvero lo spostamento verticale massimo (v_s) della deformata (meglio sottolineare che per la trave si adotta il modello di Eulero-Bernoulli).

• Avendo chiaro l’obiettivo, possiamo analizzare le 8 equazioni fondamentali (3 di EQUILIBRIO, 3 della DEFORMAZIONE e 2 COSTITUTIVE): queste non vengono usate tutte contemporaneamente, ma solitamente sono divise in 2 gruppi a seconda del fatto che si stia investigando su uno spostamento assiale (e quindi sullo sforzo normale) o su uno spostamento trasversale (e di conseguenza sugli sforzi di taglio e momento flettente).

• Per questo motivo possiamo concentrarci solo sul secondo e su “sole” 5 equazioni, ossia quelle dello spostamento verticale v, della rotazione della sezione di trave j, del momento flettente M, del taglio T e della curvatura c.

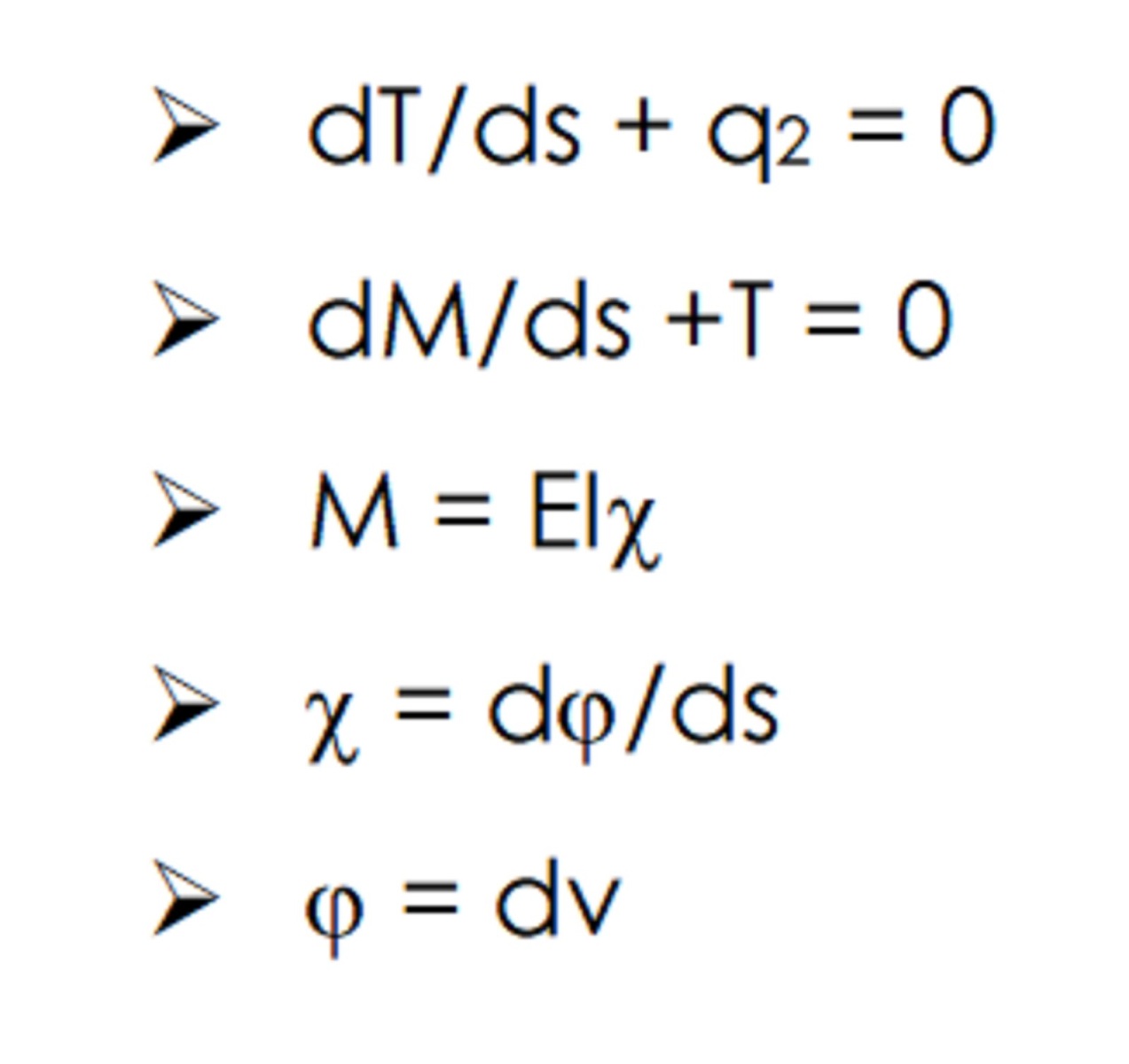
• Il  metodo analitico della linea elastica non può prescindere dall’analisi delle condizioni al bordo: per poter risolvere l’equazione dello spostamento verticale v_s necessitiamo di 4 equazioni con risultato noto poiché l’equazione suddetta presenta 4 incognite, ovvero le costanti di integrazione C₁, C₂, C₃ e C₄ (“accumulate” durante le diverse integrazioni che ci hanno condotto alla determinazione dell’equazione stessa).

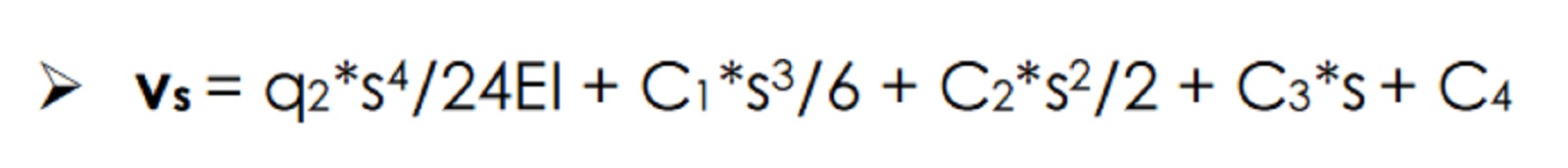
• Nel nostro caso specifico abbiamo per s=0 (nell’estremo sinistro, in prossimità dell’incastro) spostamento verticale e rotazione della sezione della trave nulle (v₍₀₎ = 0 e j₍₀₎= 0). Sostituendo sia v che jcon le rispettive equazioni, derivate sempre dall’integrazione dell’equazione della linea elastica per lo spostamento verticale a cui facciamo riferimento (q₂ = d⁴v/ds⁴) si constata che c₃ e c₄ hanno valore nullo.

• Per s=l (estremo destro, coincidente col carrello) abbiamo, invece, che lo spostamento verticale è sempre nullo, mentre stavolta la rotazione della sezione è diversa da 0, ma ignota. Necessitiamo, quindi, di un’ulteriore equazione nota e prendiamo in considerazione quella del momento che in prossimità della cerniera del carrello deve essere uguale a 0.

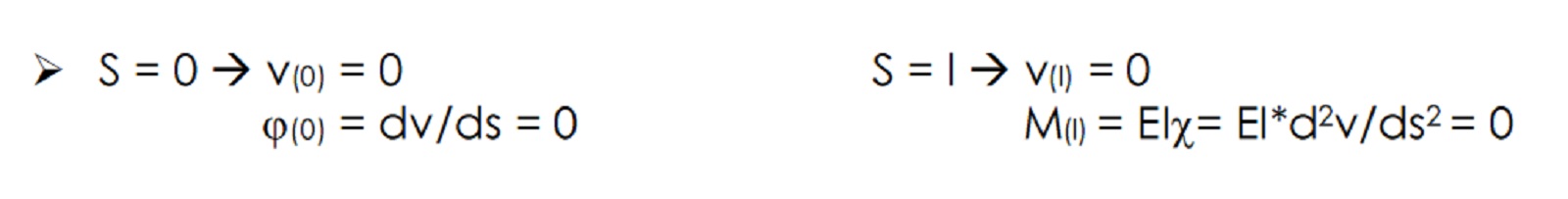
• Le due equazioni relative al bordo l, messe a sistema, ci permettono di calcolare le costanti c1 e c2 che al momento sono le ultime due incognite rimaste.

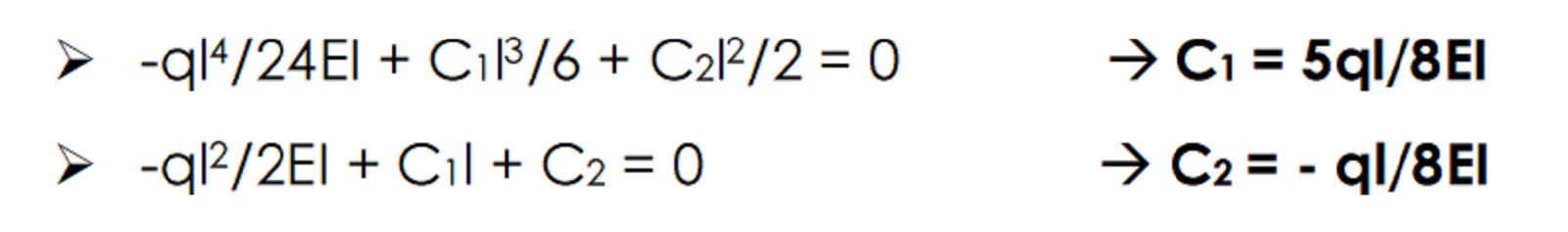
• In realtà, oltre alle 4 costanti C che abbiamo calcolato, c’è un ulteriore dato incognito, senza il quale non è possibile calcolare l’abbassamento verticale: si tratta del valore da assegnare alla variabile s all’interno dell’equazione dello spostamento verticale. Sappiamo che all’abbassamento verticale massimo corrisponde un valore nullo della derivata della funzione che approssima la deformata della trave. È sufficiente, quindi, derivare la funzione v_(s) e trovare i valori di s per i quali la derivata si annulla.

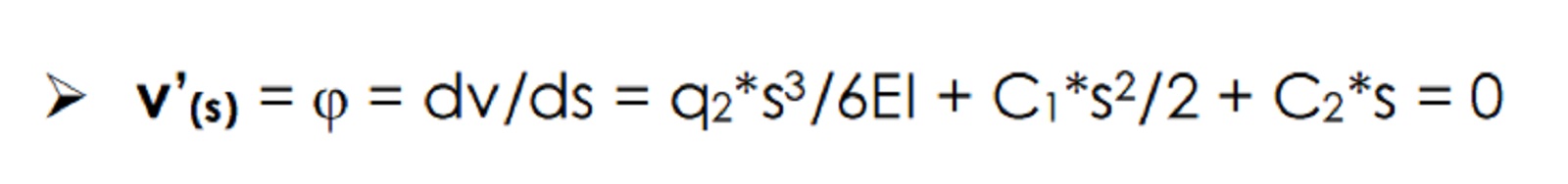
• Risolvendo questa equazione di terzo grado (ricordarsi di mettere in evidenza la s per trovare la prima soluzione e avere un’equazione di secondo grado) otteniamo 3 valori di s per i quali la derivata è nulla, ma solo 2 sono da prendere in considerazione (in quanto uno si riferisce ad un valore di s maggiore di l): s = 0, relativo all’incastro, e s =(15 - (33)^1/2)/16=0,578.

(NB: per semplificare il calcolo l è stato posto =1)

• Finalmente siamo in grado di calcolare lo spostamento verticale. Sostituiamo il valore di s = 0,578 e delle costanti C all’interno dell’equazione di v_(s):

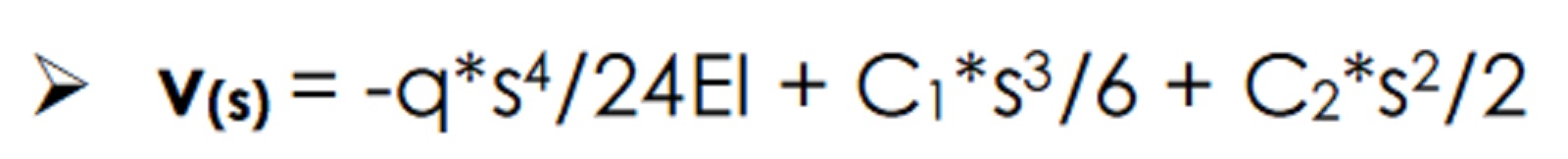
• Il risultato è in funzione di q/EI. Per avere un risultato esclusivamente numerico basta assegnare un valore al carico q, scegliere il materiale per avere un modulo elastico E e la sezione della trave per avere il momento d’inerzia I.

• L’ultimo passo consistenel diagrammare il Taglio e il Momento. Per il primo possiamo dire che l’andamento è lineare e abbiamo un taglio negativo massimo in prossimità dell’incastro e uno positivo massimo nel vincolo destro; l’intersezione con l’asse della trave corrisponde a s=5/8 L. Il momento, di conseguenza, avrà andamento parabolico, con un massimo positivo nell’incastro, curvatura verso il basso e valore zero nel carrello; ad s=5/8 L corrisponde un momento negativo massimo.