ESERCITAZIONE II_Dimensionamento di una trave in legno

Considero un solaio in legno di 6x8m.

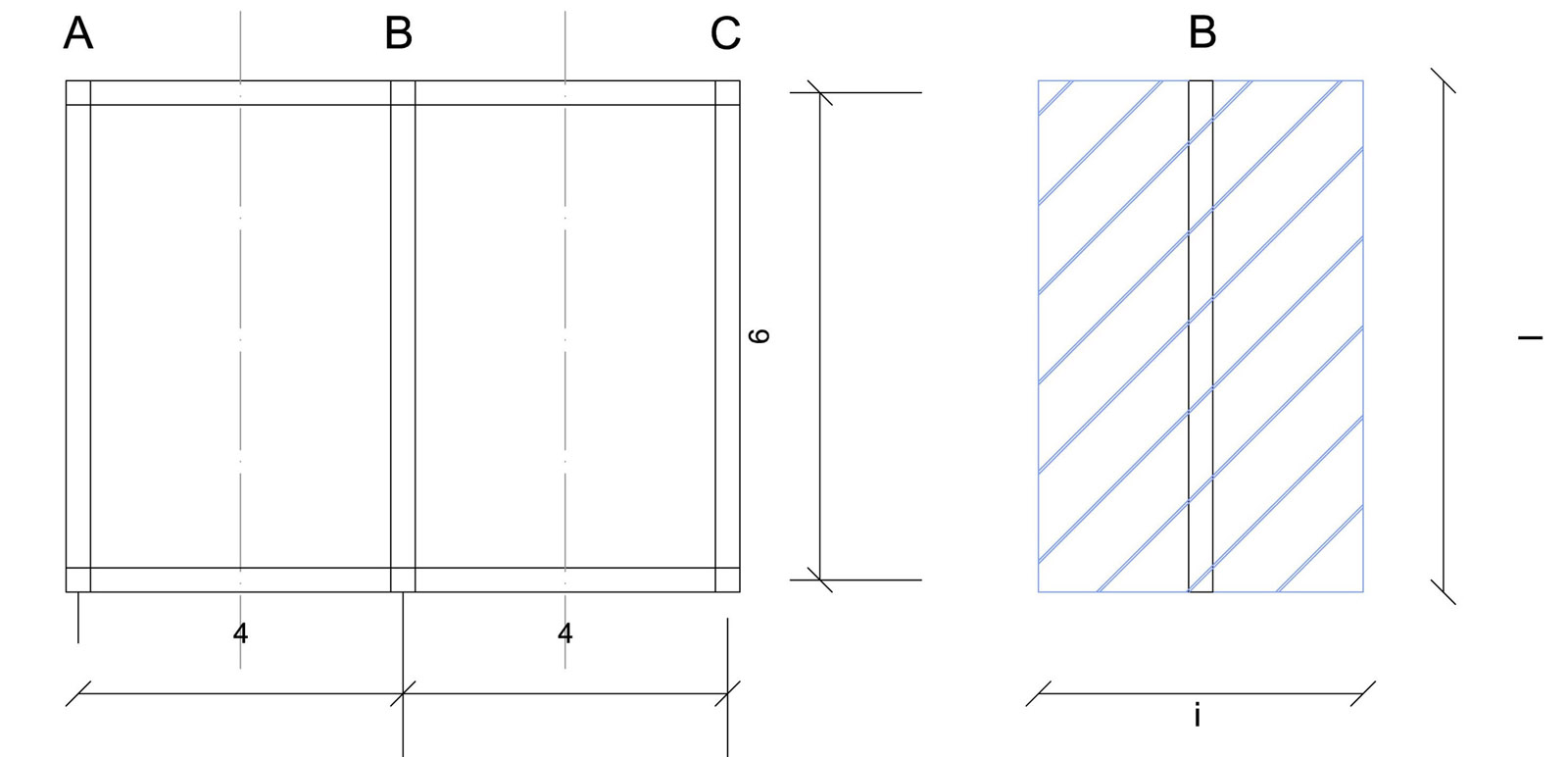
La trave più sollecitata risulta la B, con area d'influenza più ampia (le luci in tal caso sono tutte uguali)

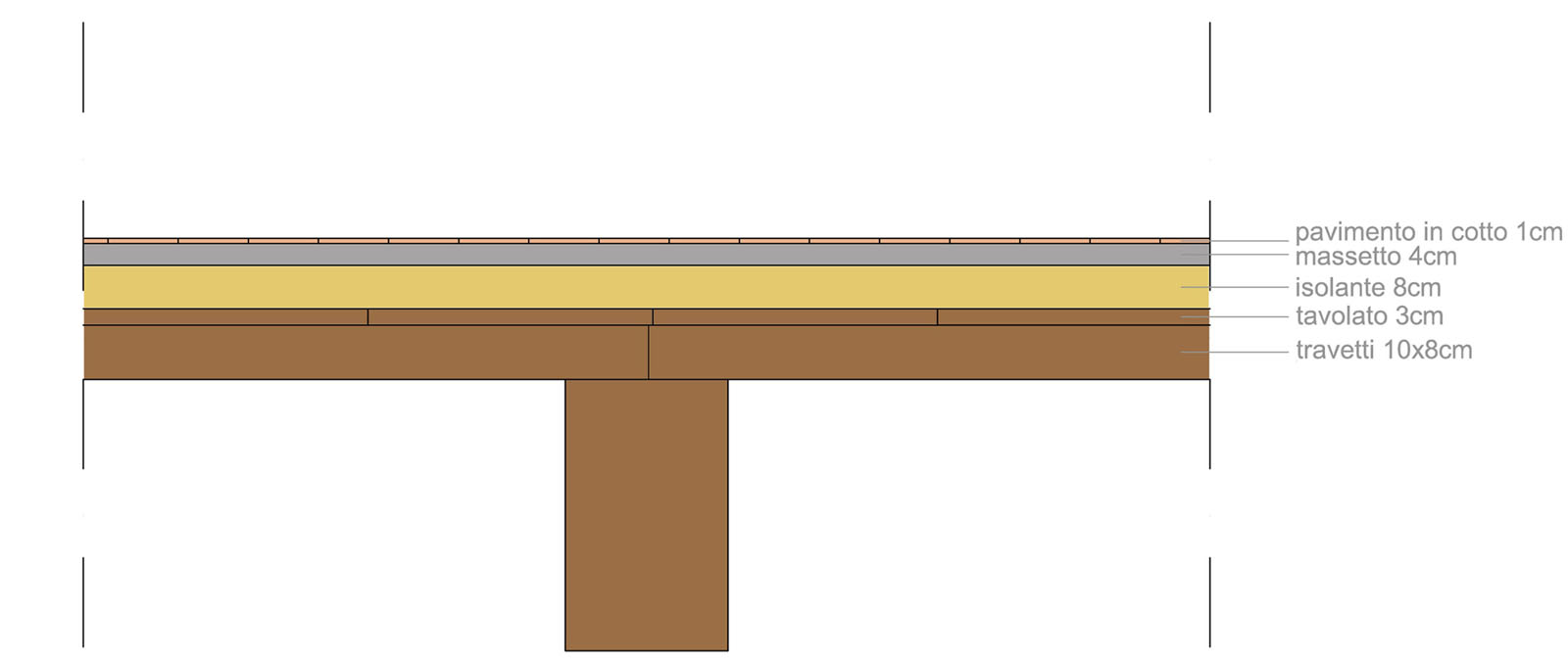
Il solaio è costituito dal seguente pacchetto:

Calcolo carichi strutturali q(s):

• travetti in legno lamellare di conifere (8x10cm) con P= 6KN/m^3

  6*1*2(0.08*0.1)=0.096 KN/m^2

• tavolato in legno lamellare di conifere (3cm) P= 6KN/m^3

6*1*1*0.3=0.18 KN/m^2

q(s) tot=0,276KN/m^2*γs=0,36KN/m^2

Calcolo carichi permanenti non strutturali q(p):

• isolante (8cm)_ lana di roccia P= 1.3KN/m^3

  1.3*1*1*0.08=0.104KN/m^2

• massetto (4cm)_malta di calce P= 18KN/m^3

  18*1*1*0.04=0.72KN/m^2

• pavimento (1cm) in cotto P= 28KN/m^3

  28*1*1*0.08=0.104KN/m^2

• incidenza impianti: 0.05KN/m^2

q(p) tot= 1,604KN/m^2*γp=2,406KN/m^2

Calcolo carichi accidentali q(a)

ambiente ad uso abitativo: 2.00 KN/m^2 da normativa

q(a)=2.00 KN/m^2*γp=3KN/m^2

Calcolati i valori dei differenti carichi, ho inserito nel foglio Excel, li stessi, la luce della trave e il suo interasse. Avendo deciso di utilizzare un legno di classe GL24c, inserisco il suo valore caratteristico a flessione fmk=24 N/mm^2.

Dati i risultati ottenuti, verifico che la resistenza di progetto, sia maggiore o uguale alla σamm:

fd = kmod* fmk/γm ⇒ fd=(0,6*24)/1,45=9.93N/mm^2

fd = resistenza caratteristica di progetto

kmod = coefficiente di degrado nel tempo

γm = coefficiente di sicurezza

σamm = M/Wx ⇒ Wx = 1/6 bh^3 =⇒ σamm=(0,6*24)/1,45=9.93N/mm^2

Quindi σamm = fd

Per sicurezza, aumento il valore dell'altezza da 45.72cm a 50cm.