blog di riccardo.prosperini

INTRODUZIONE:

In questa esercitazione vedremo come si ripartisce una forza orizzontale (di natura sismica o atmosferica) sui telai che compongono la struttura intelaiata, che in questa esercitazione sarà di un solo piano.

Il sistema trave-pilastro permette, oltre che trasmettere i carichi verticali alle fondazioni, di sopportare le forze orizzontali rendendo i sistemi pilastro-trave dei controventi. La struttura esaminata sarà in cemento armato, e la tipologia dei controventi è chiamata telaio SHEAR-TYPE, che presenta tutti nodi all'incastro e la trave è ipotizzata infinitamente rigida a flessione rispetto ai pilastri, che vengono dotati di rigidezza k.

N.B.: Affinchè un sistema di controventamento sia efficace, gli impalcati vengono considerati corpi rigidi sul proprio piano (mentre al di fuori si inflettono) perciò i controventi reagiscono alla forza orizzontale che tende a spostarli, con la loro elasticità, ciò impone che un controvento, nel piano impalcato, sia un appoggio cedevole elasticamente.

Nella figura sopra è rappresentato un telaio shear-type a due ritti, dove la forza F sposta il traverso, che di conseguenza trascina con se i pilastri (si comportano come una trave doppiamente appoggiata). Il legame tra F e sigma (spostamento) è esplicitato nella formula F= [(12EI₁/h³) + (12EI₂/h³)]sigma (valevole per un telaio shear-type a due piedritti), dalla quale si ricava che k (rigidezza traslante di ogni pilastro)=12EI/h³,poichè F=k*sigma. Nel caso generale:

Grazie a questa esercitazione saremo in grado di determinare la reazione elastica di ogni controvento che sarà uguale ed opposta alla forza orizzontale che ogni singolo controvento è chiamato a ricevere attraverso il solaio (secondo il principio di azione-reazione).

DISEGNO:

Telai // all'asse y

Telaio 1v pilastri 1-5-9 ; Telaio 2v pilastri 2-6-10 ; Telaio 3v pilastri 3-7 ; Telaio 4v pilastri 4-8

Telai // all'asse x

Telaio 1o pilastri 1-2-3-4 ; Telaio 2o pilastri 5-6-7-8 ; Telaio 3o pilastri 9-10

Trattandosi di vincoli cedevoli elasticamente, i controventi vengono assimilati a molle.

DIMENSIONAMENTO:

Apro il file Excel, inserisco i dati di cui dispongo:

E=Modulo Elastico di Young (in Mpa o N/mm²); per cls con classe di resistenza C20/25

H=altezza dei pilastri (nel mio caso 3,5 m)

I=momento di inerzia di ciascun pilastro (calcolato lungo le due direzioni principali) che collabora alla formazione di ogni telaio.

Momento d'inerzia dei pilastri:

Pilastro m 0,5*0,3                     b=30 cm      h=50 cm       I_x= bh³/12 = 312500 cm4            I_y= hb³/12 = 112500 cm⁴                                                      

Inserisco i risultati nei calcoli e ottengo la rigidezza traslante dei miei 7 telai.

Nella seconda tabella riassumo le rigidezze dei controventi e inseriamo la distanza  dei rispettivi controventi dal punto di origine del sistema di riferimento da me adottato.

Nella terza tabella calcolo il centro di massa dell'impalcato, suddividendo l'area in forme geometriche  semplice delle quali mi ricaverò i singoli centri d'area.

Una volta trovate le coordinate rispetto a O dei singoli centri di massa, il file Excell mi calcola l'area totale dell'impalcato e il centro di massa totale grazie alle formule:

N.B. Le formule adottate si riferiscono ad un impalcato la quale densità sia omogenea su tutta l'area, trovandomi così sia il centro d'area che quello di massa, poichè coincidenti. Se la densità non fosse omogenea le formule adottate non sarebbero più valide.

Nella quarta tabella troviamo:

K_o=rigidezza totale orizzontale (somma delle rigidezze dei singoli controventi orizzontali)

K_v=rigidezza totale verticale (somma delle rigidezze dei singoli controventi verticali)

X_c e Y_c=coordinate dei centri di rigidezze dell'impalcato

K_phi=rigidezza torsionale totale.

Il centro delle rigidezze viene calcolato con la somma delle combinazioni tra le rigidezze e le rispettive distanze dal punto di origine. il tutto diviso per la rigidezza totale.

N.B.: La forza sismica deve essere applicata nel centro di massa G.

Dopodichè, posiziono i punti G e C (centro delle rigidezze) nello schema del mio impalcato, potendo così intuire se esso sarà soggetto solo a traslazione o anche a rotazione, ciò dipenderà dalla coincidenza o meno dei due punti.

In questo caso C e G non coincidono, anche se per poco, perciò in presenza di una forza orizzontale l'impalcato sarà soggetto sia a traslazione che a una rotzione, quest'ultima dovuta al braccio tra forza e centro delle rigidezze, creando un momento.

Con la quinta tabella effettuo l’analisi dei carichi sismici per ricavare la forza sismica che agisce nel centro di massa.

Riprendo i valori ottenuti nell'esercitazione per il dimensionamento della trave.

A partire da questi valori, il file calcola:

• G= il carico totale permanente, dato dal prodotto fra l’area totale e la somma dei carichi strutturali e permanenti
• Q= il carico totale accidentale, dato dal prodotta fra l’area totale e il carico accidentale
• W= Peso sismico o forza peso, calcolato attraverso la combinazione sismica, che richiede l’uso di ψ*²
• F= Forza sismica, data dal prodotta fra il peso sismico e c (coefficiente di intensità sismica in base alla localizzazione dell’edificio)

*² trattasi di un coefficiente di contemporaneità che tiene conto della funzione/categoria dell’impalcato; nel mio caso ho preso il valore riferito agli ambienti ad uso residenziale.

Le ultime due tabelle indicano come si ripartisce la forza sismica ai vari controventi, a seconda che essa agisca lungo l’asse x o l’asse y, e gli effetti cinematici (traslazione e rotazione rigida) sull’impalcato.

La sesta tabella ricava la forza sismica agente lungo X, la quale causa una traslazione orizzontale u ed una rotazione ϕ.

Il file di calcolo elabora i seguenti dati:

• M= momento torcente dato dalla formula F ^. (Y_c - Y_g)*³
• U_o= traslazione orizzontale dove u=F/ k_{o_tot}
• ϕ= rotazione cui è sottoposto l’impalcato; vale f= M/k_ϕ *⁴

*³ Nel mio caso è un valore positivo, quindi implica un momento antiorario.

*⁴ k_ϕ  è la rigidezza torsionale totale ricavata nella tabella 4.

La settima tabella ricava, invece, la forza sismica agente lungo Y, la quale, a sua volta, causa una traslazione verticale u ed una rotazione ϕ.

Nella tabella successiva, viene ripetuto lo stesso ragionamento, considerando la traslazione verticale:

• U_v= traslazione verticale dove u=F/ k_{v_tot}

Una volta determinati i valori dei gradi di libertà, posso ricavare la forza agente sui singoli controventi nei due casi di carico (verticale e orizzontale).

Noti u_{_o}, v_{_o}, ϕ, posso determinare le reazioni elastiche di ogni controvento attraverso le seguenti formule:

CASO 1 – Forza // all’asse X

• Fo_n=ko_n(u+ϕ∙ddo_n)       per i controventi orizzontali
• Fv_n=kv_n∙ϕ∙ddv_n            per i controventi verticali

CASO 2 – Forza // all’asse Y

• Fv_n=kv_n(v+ϕ∙ddv_n)       per i controventi verticali
• Fo_n=ko_n∙ϕ∙ddo_n            per i controventi orizzontali

Come già detto, si considera la forza nel piano dell’impalcato prima agente in direzione orizzontale e poi agente in direzione verticale; perciò analizziamo i due casi.

INTRODUZIONE: In questa esercitazione dimensioneremo una trave a sbalzo nelle tre principali tecnologie: legcemento armato e acciaio.

Definita la carpenteria di riferimento, individuo la trave maggiormente sollecitata e l'area di influenza di luce L=2,5 m e interasse I=4,55 m (nel rettangolo rosso).

Prendo in considerazione la stratigrafia dei solai utilizzati per il dimensionamento della trave e i carichi trovati.

1_STRUTTURA IN LEGNO

La parte iniziale del procedimento è la stessa applicata nella seconda esercitazione, quindi i risultati di h min,per il legno e il c.a., e di W min,per l'acciaio, saranno gli stessi.

N.B. Differentemente dalla seconda esercitazione, dove prendavamo in considerazione una trave doppiamente appoggiata, ora consideriamo lo schema statico di una mensola, quindi il valore del momento massimo sarà M=ql^2/2.

ANALISI:

qs:  0,51 KN/m^2

qp:  2,54 KN/m^2

qa:  2 KN/m^2

Il foglio Excell mi fornisce il carico totale a metro lineare (qu) e, inserita la luce, il momento massimo Mmax: ql^2/2.

Assumo:

f m.k.=24               (legno lamellare GL 24c)           [resistenza a flessione caratteristica]

k mod=0,80                                                             [coefficiente di durata del carico]

ym=1,50                                                                  [coefficiente parziale di sicurezza del materiale]

Con questi valori il file Excell può calcolarmi la tensione ammissibile fd=(fmk * k mod)/ym.

PROGETTO:

Ipotizzo la base della trave di 25 cm. Il foglio elettronico svilupperà un valore di H min (altezza minima) che richiederà di essere ingegnerizzata a causa della presenza dei decimali.

Assegno al materiale un modulo elastico E=8000 Mpa.

Ottengo:

1. Ix (momento di inerzia) = (b*h^3)/12

2. qe (carico incidente) dove non vi è inserito il peso proprio della trave poichè si tratta di un materiale leggero, a differenza dell'acciao e del cls armato.

Occore fare la verifica a deformabilità controllando che l'abbassamento massimo del profilo, studiato in rapporto con la luce, non sia tale da deformare la struttura, ostacolandone l'uso. Perciò la verifica viene fatta riferendosi allo stato limite di esercizio (SLE).

v max (abbassamento massimo); L (luce)/v max > 250 (valore valido per i solai in generale)

2_STRUTTURA IN CALCESTRUZZO ARMATO

ANALISI:

qs: 2,12 KN/m^2

qp: 1,9 KN/m^2

qa: 2 KN/m^2

Il file Excell mi da qu (carico totale a metro lineare) e M max (momento massimo)=ql^2/2, inserendo prima la luce.

Assumo:

fyk [tensione di snervamento]= 450 Mpa

fck [valore caratteristico di resistenza cilindrica] = 35 Mpa

Con questi valori posso calcolarmi le tensioni di progetto fyd (acciaio) e fcd (cls).

PROGETTO:

Ipotizzo la base della trave uguale a 25 cm e un copriferro sigma = 5 cm. Il foglio elettronico mi da un'altezza minima (hmin) che poi ingegnerizzerò.

Assumo un modulo elastico del materiale E = 8000 Mpa.

Mi trovo:

Ix = (b*h^3)/12

qe = carico incidente, dove inserisco il peso della trave.

v max = abbassamento massimo

L (luce)/ v max > 250

3_STRUTTURA IN ACCIAIO

ANALISI:

qs: 1,78 KN/m^2

qp: 1,81 KN/m^2

qa: 2 KN/m^2

Il file Excell mi da qu (carico totale a metro lineare) e M max (momento massimo)=ql^2/2, inserendo prima la luce.

Assumo:

fyk = 235  ( tensione di snervamento)

Il foglio elettronico mi calcola fd (tensione di progetto) dell'acciao.

PROGETTO:

W min (modulo di resistenza) = M max/fd

Ingegnerizzo il valore di W min.

Ottengo i seguenti valori dalla tabella dei profili IPE standard:

Ix (Jx nella tabella)  [cm^4]

peso [in Kg/m nella tabella, per convertire il valore in KN/m moltiplico per 10^-2]

qe (carico incidente) dove aggiungo il peso della trave

v max = abbassamento massimo

L (luce)/ v max > 250

INTRODUZIONE:

In questa esercitazione dimensioneremo una trave in tre diverse tecnologie: legno, calcestruzzo e acciaio.

Attraverso questo metodo, potrò dimensionare l'altezza della sezione della trave più sollecitata; imporro l'uguaglianza della tensione masima della trave con la tensione di progetto del materiale, data dalla normativa.

Assumeremo una struttura intelaiata piana (travi che collaborano con i pilastri, secondo il vincolo di appoggio semplice).

DISEGNO:

Definisco la carpenteria di riferimento. Nell'immagine è mostrata l'orditura di un solaio in cemento armato e in acciaio.

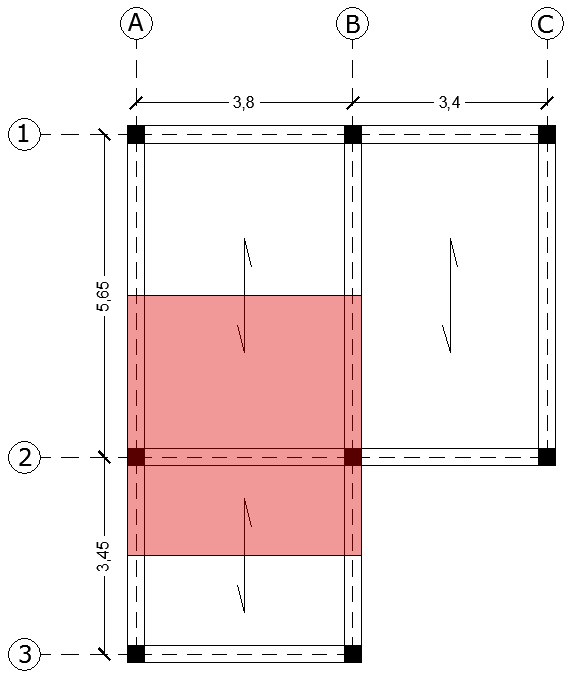
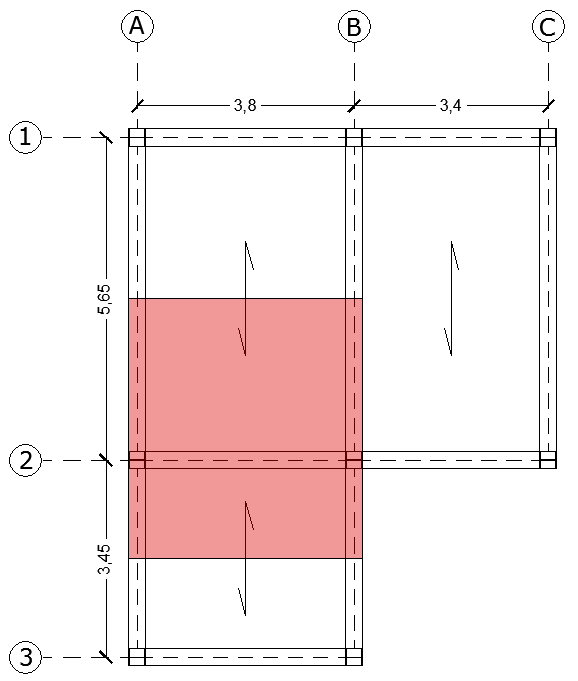
Individuata la trave maggiormente sollecitata esplicito la sua area di influenza (di cui la trave ne porta il peso)  e misuro la lunghezza dell'interasse.

A (area) = I (interasse) x L (luce) = 4,55 m x 4,1 m = 18,66 m^2

Procedo poi con l'analisi delle tre tecnologie.

1_STRUTTURA IN LEGNO

ANALISI:

Con l'ausilio del foglio Excel, sono in grado di dimensionare la struttura, utilizzando alcuni dati richiesti (nelle caselle grigie):

- Interasse: 4,55 m

- qs (carico strutturale): dovuto al peso proprio degli elementi strutturali.                                                                      

- qp (carico permanente): dovuto al peso proprio degli elementi non portanti durante il suo ciclo di vita.

- qa (carico accidentale): dovuto a diversi fattori scatenanti, che possono accadere o meno.

- luce: 4,1 m

- f m,k: resistenza caratteristica a flessione del materiale.

- k mod: coefficiente diminutivo dei valori di resistenza del materiale, dovuto alla durata del carico e la classe di servizio ( dipende dalle condizioni climatiche ) del materiale scelto ed è fornito dalla normativa.

- ym: coefficiente parziale di sicurezza del materiale.

- base.

N.B. i carichi agenti sul solaio sono espressi in KN/m^2. La classe di durata del carico fa riferimento ad un carico costante agente per un certo periodo di tempo nella vita della struttura.

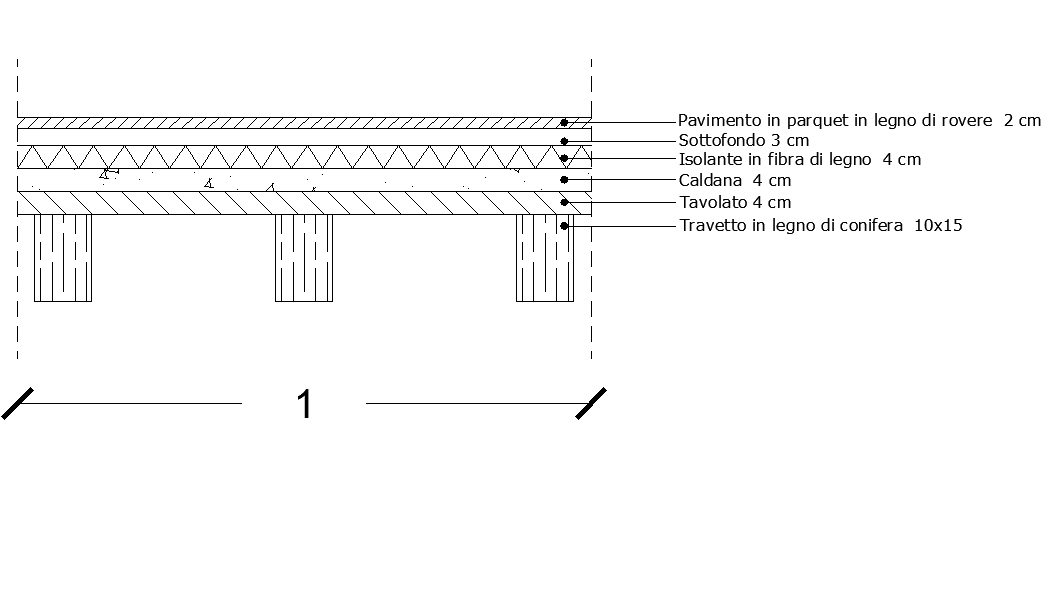
Posso calcolarmi i carichi, poichè conosco la stratigrafia del solaio, moltiplicando il peso specifico per la quantità di volume di ogni metro quadro di solaio:

qs travetti: 6 KN/m^3 (0,15x0,1x1) m^3/m^2 = 0,27 KN/m^2

qs tavolato: 6 KN/m^3 (0,04x1x1) m^3/m^2 = 0,24 KN/m^2

- qs totale: 0,51 KN/m^2

qp caldana: 20 KN/m^3 (0,04x1x1) m^3/m^2 = 0,8 KN/m^2

qp isolante: 2,3 KN/m^3 (0,04x1x1) m^3/m^2 = 0,092 KN/m^2

qp sottofondo: 0,18 KN/m^3 (0,03x1x1) m^3/m^2 = 0,0054 KN/m^2

qp pavimento: 7,2 KN/m^3 (0,02x1x1) m^3/m^2 = 0,144 KN/m^2

- qp totale: 1,0414 KN/m^2 + 1,5 KN/m^2 (carico forfettario di tramezzi e impianti) = 2,54 KN/m^2

qa: 2 KN/m^2

N.B. nel qp totale il carico di tramezzi e impianti è forfettario poichè é difficile effettuare precisamente il calcolo a causa delle molte variabili.

Il file Excel mi fornisce il carico totale a metro lineare ( qu ) che si ottiene sommando ( combinazione di carico ) i carichi considerati con i rispettivi coefficienti moltiplicativi , forniti dalla normativa in funzione dello stato limite ultimo ( SLU ) tutto moltiplicato per l'interasse ; e il momento massimo M max: (qu l^2)/8, poichè stiamo parlando di una trave doppiamente appoggiata.

PROGETTO:

Scelgo f m,k = 24 (dai dati forniti dalla normativa nel caso di una tecnologia in un legno lamellare con classe di resistenza GL 24c ).

Assumo k mod = 0,80 e ym = 1,45.

Da questi dati ricavo la tensione di progetto fd = ( f m,k x k mod) / ym.

Infine ipotizzo la base della trave uguale a 30 cm. Il foglio elettronico sviluppa però un' altezza minima che ha bisogno di essere ingegnerizzata ad un valore corrispondenteai valori esistenti sul mercato.

2_STRUTTURA IN CEMENTO ARMATO

ANALISI:

Mi trovo il carico ultimo ( qu ) utilizzando lo stesso procedimento utilizzato per il solaio in legno:

- qs totale: 2,12 KN/m^2

- qp totale: 0,4 KN/m^2 + 1,5 KN/m^2 = 1,9 KN/m^2

- qa: 2 KN/m^2

N.B. le pignatte non dovrebbero essere considerate elemento strutturale bensì elemento di alleggeriemento, da cassaforma a perdere per la gettata di cls, ma tradizionalmente si include nel carico strutturale.

PROGETTO:

Stimato il carico ultimo, inserita la luce e il momento massimo introduco le tensioni caratteristiche del cls e dell'acciao f ck e f yk in base alla tecnologia scelta. Scelgo un acciaio da armatura B450 A con f yk = 450 e il calcestruzzo di classe C35/45 con Rck ( valore caratteristico di resistenza cubica ) = 45

Da ciò ottengo i valori di resistenza di progetto del calcestruzzo f cd.

Ipotizzo una base b = 30 cm e mi ricavo  l'altezza utile Hu, aggiungendo però il copriferro ( indicato nella tabella con la lettera sigma ), ovvero la distanza tra il baricentro dell'armatura e il filo del calcestruzzo teso.

Ingegnerizzo l'altezza della trave ( decina subito superiore a H min ) e controllo che la mia sezione sia "verificata".

N.B. il foglio Excel per il cemento armato a bisogno di più dati  poichè si tratta di un materiale disomogeneo, composto da cls e acciaio.

3_ACCIAIO

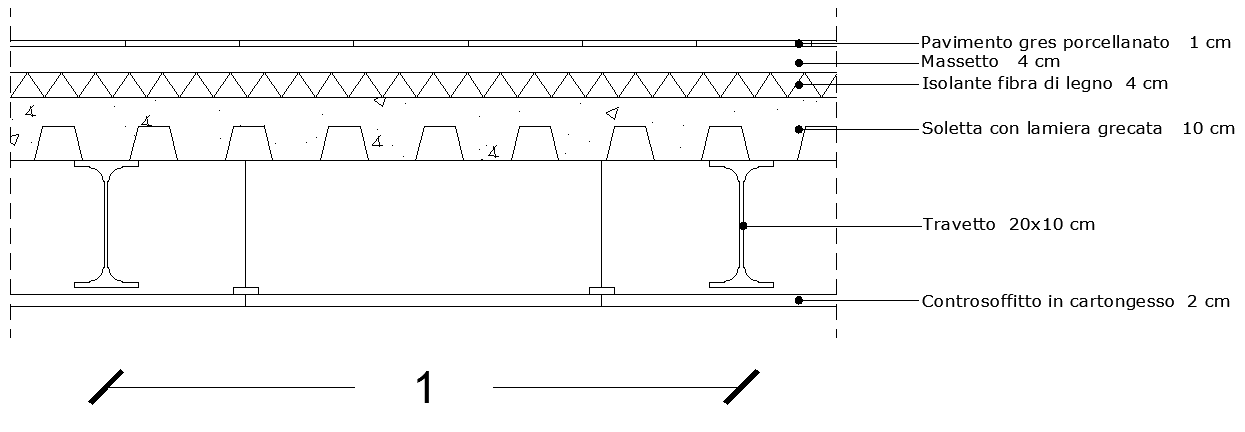
ANALISI:

qs totale: 1,78 KN/m^2

qp totale: 0,314 KN/m^2 + 1,5 KN/m^2 = 1,81 KN/m^2

qa: 2 KN/m^2

PROGETTO:

Inserisco la luce e il peso massimo (ql^2/8) e procedo scegliendo la classe di resistenza del materiale (classe media: S275 , f y,k (resistenza caratteristica) = 275 ).

Posso ora calcolare nel foglio elettronico la tensione di progetto fd e il modulo di resistenza a flessione minimo Wx min, che verrà poi ingegnerizzato.

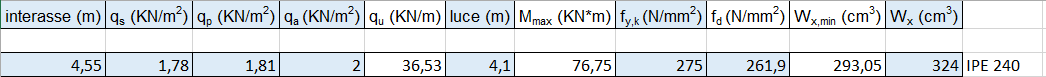
N.B. fd si calcola a partire dalla tensione di snervamento dell'acciaio scelto, con ym ( coefficiente parziale di sicurezza) = 1,05.

Per il dimensionamenrto della sezione di trave in acciao, ho determinato il modulo di resistenza a flessione minimo da utilizzare affinchè la tensione massima di ogni fibra del materiale non superi la tensione di progetto.

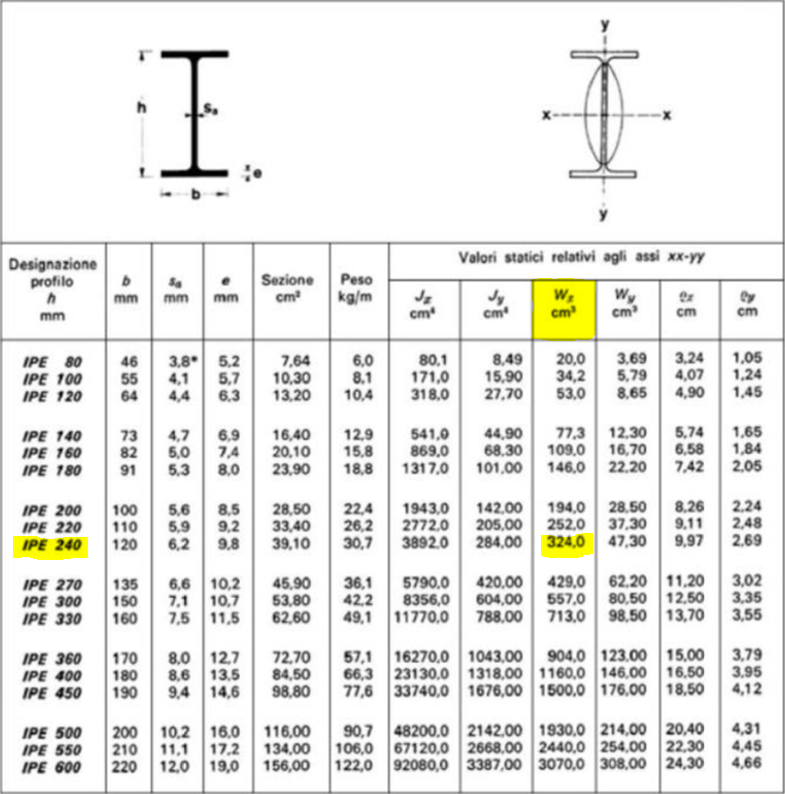
Nella tabella qui sotto individuo la trave che più si avvicina alla resistenza a flessione richiesta dalla mia tecnologia, selezionando il profilo IPE presente sul mercato, con resitenza a flessione subito maggiore a quella trovata da me.

Modellazione con SAP 2000: File-New Model-Grid Only,inserendo le unità di misura con cui voglio lavorare[KN,m,C°]
Nella finestra Quick Grid Lines inserisco il numero delle griglie su cui imposto il mio disegno nelle tre direzioni (Number of Grid Lines), e la spaziatura che voglio fra le linee della griglia (Grid Spacing) creando una sola campata:

Con Draw Frame costruisco la prima campata reticolare cubica. Dopodichè me la copio e incollo con Ctrl+C e Ctrl+V lungo gli assi x e y finchè non realizzo la struttura reticolare desiderata:

Il 6 indica la distanza del punto di ancoraggio della nuova campata rispetto all'origine degli assi, che è uguale alla profondità della prima campata.

VINCOLI ESTERNI:seleziono quattro nodi a caso della struttura (ma che non siano allineati) e gli assegno una cerniera: Assign-Joint-Restraints-Icona della cerniera:

VINCOLI INTERNI:rendo tutti i nodi cerniere interne, quindi seleziono tutta la struttura e poi Assign-Frame-Releases-Partial Fixity e spunto Moment 2-2 e 3-3 sia su Start che su End:

MATERIALE E PROFILO:Seleziono la struttura, poi Assign-Frame-Frame Sections-Add New Property-Pipe e la nomino "asta":

CARICO CONCENTRATO:creo il carico puntiforme " f " (Define-Load Patterns-Load Pattern " f "-Self Weight Multiplier " 0 " (lo privo di peso proprio)-Add New Load Pattern-Seleziono " f ". Assegno il carico selezionando la parte terminale superiore della struttura e procedendo poi con Assign-Joint-Joint Loads-Forces- "f"-Force Global z (asse lungo la quale si troverà "f" )- Inserisco il valore del carico " - 150 KN " (negativo perchè è diretto nel verso opposto all'asse z):

N.B.: Ai nodi perimetrali della struttura verrà assegnato un carico che corrisponde alla metà del carico assegnato ai nodi centrali della struttura,poichè i carichi agiscono su una superficie intorno al nodo che corrisponde alla metà della superficie nella quale i carichi agiscono sui nodi centrali.

Analisi: analizzo la struttura (Run Analysis), facendo "correre" (Run) solo i miei carichi concentrati:

DEFORMATA                                                                          DIAGRAMMA SFORZO  NORMALE

N.B.: I diagrammi del Taglio e del Momento devono equivalere a zero.

Dimensionamento: Abbiamo bisogno di conoscere il valore dello sforzo normale di ogni singola asta:

- Creo da SAP una tabella che mi mostri questi valori ( Display-Show Tables-Analysis Results-Select Load Patterns " f "-Select Load Cases " f ").

- Seleziono dal menù a tendina laterale Element Forces-Frames.

- Lo esporto in Excel ( File-Export Current Table-to Excel).

Ripulisco il file dai valori che non mi servono, lasciando i valori relativi alle numerazioni e alle luci delle aste, allo sforzo normale e ai carichi concentrati applicati, e ordino in modo crescente la luce delle aste per conservare solo la lunghezza delle aste normali L (che è uguale a 6 m ) e la lunghezza delle aste diagonali (che è uguale a L moltiplicato per la radice di 2 = 6* radice di 2 = 8,49 m ).

Se ordino anche lo sforzo normale distinguo tra aste compresse e aste tese.

Trazione: Inserisco i valori di N superiori allo zero (trazione) nel file Excel creato per il dimensionamento:

- Scelgo un acciaio (S235, acciao molto duttile, buono per prestazioni antisismiche) dalla quale dovrò prendere il coefficiente di snervamento fgk (= 275 Mpa) e il coefficiente di sicurezza ym (= 1,05) e da questi dati dovrò trovare la tensione di progetto fd attraverso la formula fd=fgk/ym e poi l'Area minima di progetto A_min con la formula A_min= N/fd

Il valora A_min va ingegnerizzato,cioè va preso il profilo standard disponibile immediatamente superiore al valore da me trovato.

Compressione: Inserisco i valori di N inferiori allo zero (compressione) nel file Excel omettendo il segno " meno" ai fini del calcolo strutturale:

- Assumo i valori di fyk e ym uguali a quelli utilizzati per la trazione.

- Oltre ai valori di fd e A_min dovrò ricavarmi anche i valori dell' Inerzia minima I_min, il raggio di inerzia minimo della sezione rho_min e la snellezza massima dell'asta lambda*, assumendo come dati anche il Modulo di Elasticità E (=210000 Mpa) e un coefficiente beta che dipende dalle condizioni di vincolo (nel nostro caso=1). Dovrò dunque ingegnerizzare i risultati trovati, individuandoli nella tabella dei profili standard: