3 ESERCITAZIONE _ VERIFICA A DEFORMABILITA’ DI UNA TRAVE
La terza esercitazione prevede di eseguire la verifica a deformabilità di una trave all’interno di un solaio tipo dotato di uno sbalzo. Tale operazione di calcolo verrà svolta sia per una trave in legno, per una in cemento armato ed infine per una in acciaio, tramite l’impiego di un foglio Excel preimpostato.
Si è ipotizzata una carpenteria-tipo di un solaio con sbalzo posto all’interno di un edificio che ospita uffici privati, quindi non aperti al pubblico; per tale ragione si è considerato un sovraccarico accidentale pari a 2 kN/mq, come riportato nella normativa tecnica.
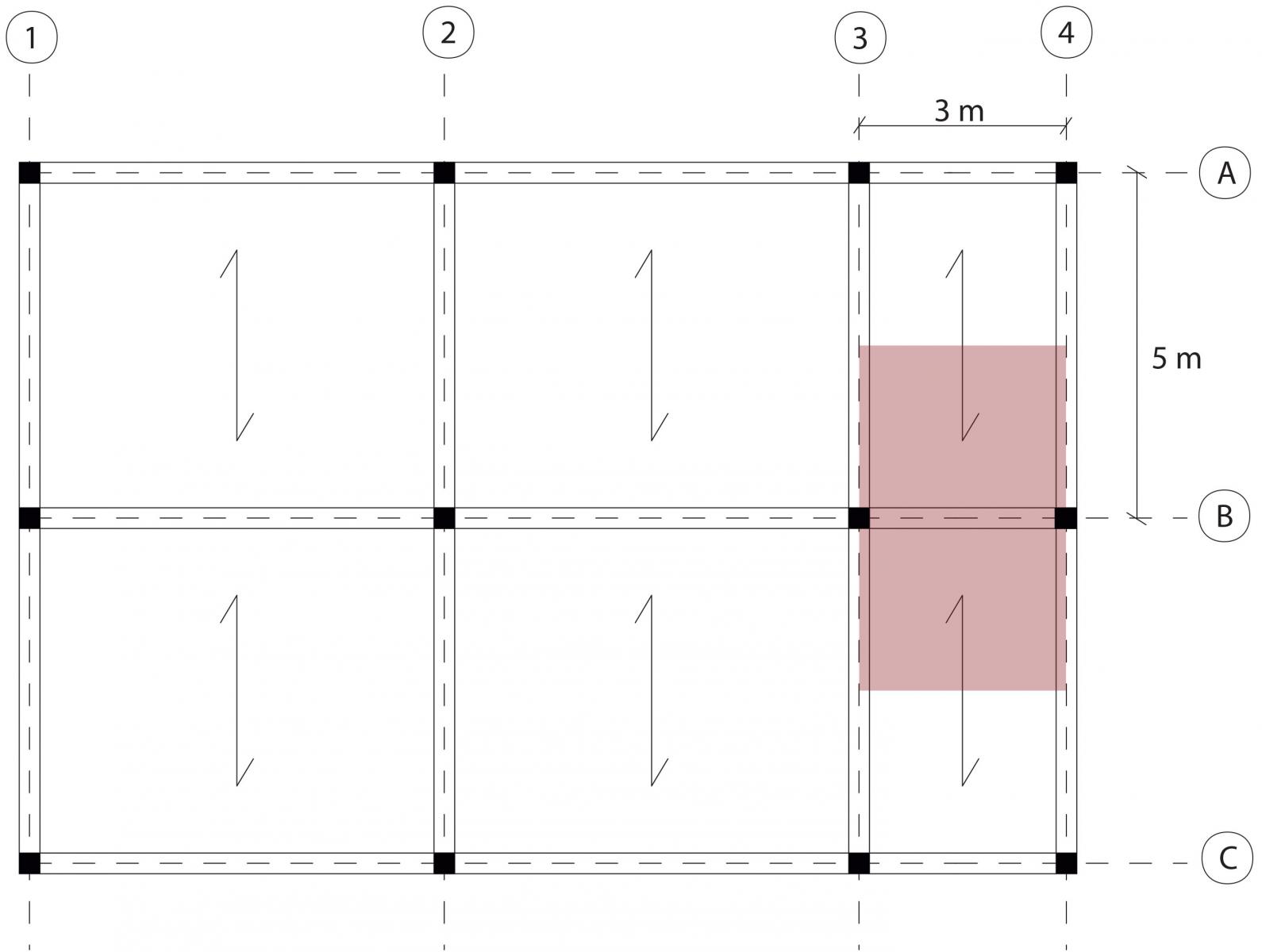
Il solaio che si è ipotizzato prevede un interasse pari a 5m e una luce, cioè lo sbalzo nel caso specifico, pari a 3m. (Fig. 01)
TRAVE IN LEGNO
Si parte dall’analisi dei carichi di un solaio in legno, la cui stratigrafia è rappresentata dai seguenti componenti (Fig. 02)
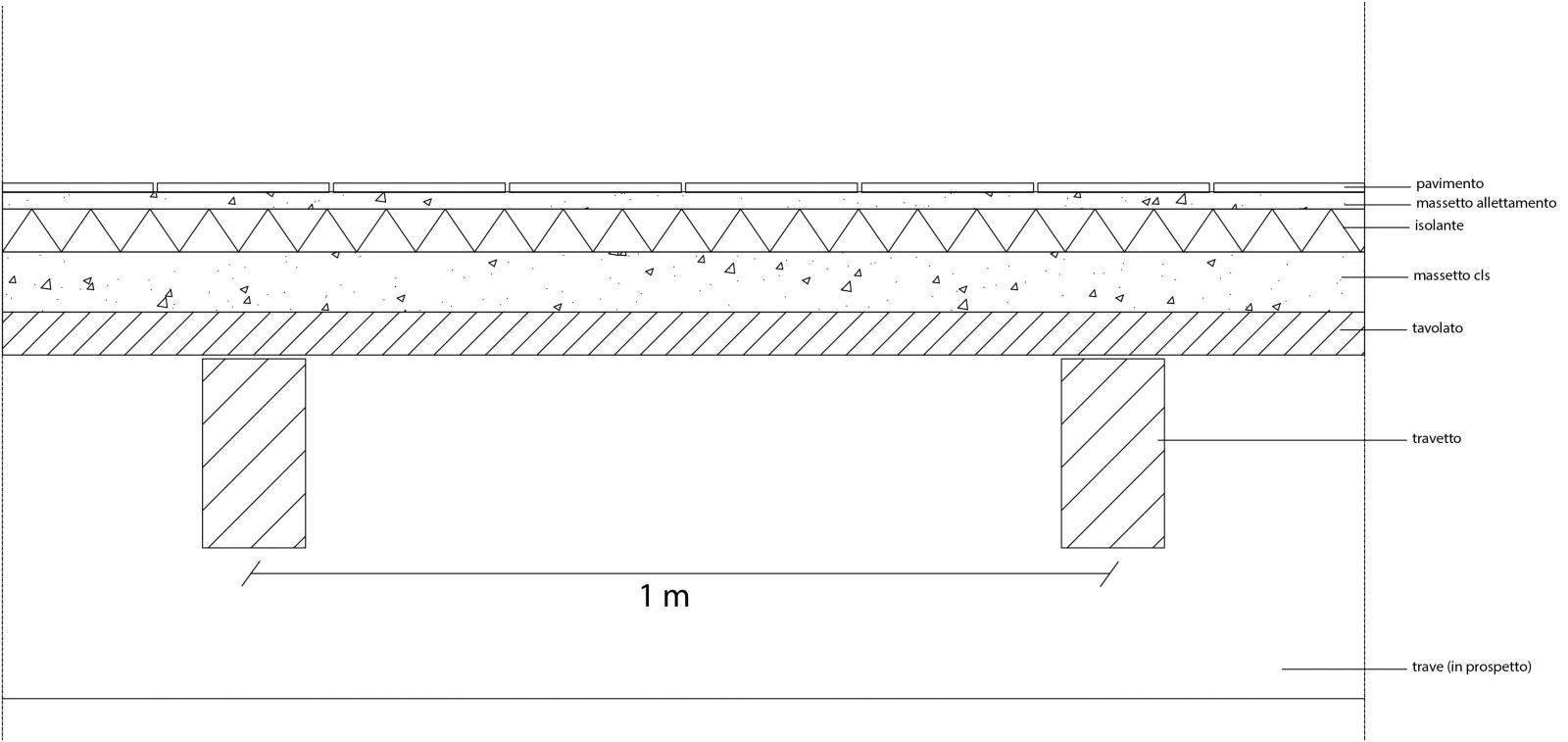
travetti in legno lamellare di conifera: sezione 0,12m x 0,22m, peso specifico 6kN/mc
tavolato di legno: spessore 0,05 m, peso specifico 6kN/mc
massetto di cls: spessore 0,07m, peso specifico 24 kN/mc
isolante in fibra di legno : spessore 0,05m, peso specifico 0,6 kN/mc
massetto di allettamento per il pavimento (malta di cemento): spessore 0,02m, peso specifico 21 kN/mc
pavimento in gres porcellanato: spessore 0,01m, peso specifico 8kN/mc
impianti: peso specifico da normativa 0,5 kN/mq
tramezzi: peso specifico da normativa 1 kN/mq
_ Carichi permanenti strutturali (peso proprio degli elementi strutturali del solaio, quindi i travetti, escludendo il peso della trave)
Qs : 1 x 0,12m x 0,22m x 6kN/mc = 0,156 kN/mq
_ Carichi permanenti non strutturali (peso proprio degli elementi non strutturali che compongono il pacchetto del solaio)
Qp: tramezzi: 1kN/mq
impianti: 0,5kN/mq
pavimento: 0,01m x 8kN/mc = 0,08 kN/mc
massetto di allettamento: 0,02m x 21kN/mc = 0,42 kN/mq
isolante: 0,05m x 0,6kN/mc = 0,03 kN/mq
massetto cls: 0,07m x 24 kN/mc = 1,68 kN/mq
tavolato: 0,05m x 6kN/mc = 0,3 kN/mq
Qp Tot: 4,01 kN/mq
_ Carichi accidentali (destinazione d’uso dell’edificio, fornito dalla normativa)
Qa: 2 kN/mq
I valori dei carichi trovati si possono, quindi, inserire nel foglio di calcolo Excel al fine di vedere se l’abbassamento della trave sia accettabile o meno e per fare ciò basta verificare che il rapporto tra la luce e l’abbassamento massimo sia maggiore di 250 -> l/vmax > 250
Per la verifica a deformabilità della trave posta in corrispondenza dello sbalzo si deve scegliere il tipo di legno che si vuole utilizzare per la trave stessa, ad esempio un legno lamellare di conifera GL24h, con resistenza caratteristica fm,k pari a 24 MPa e con un modulo elastico (E) pari a 11600 MPa. (Fig. 03)

Si devono ipotizzare, inoltre, le dimensioni geometriche della sezione della trave, per cui si è pensato di fissare una base pari a 35 cm e un’altezza pari a 50 cm.
Dopo aver inserito tutti i dati nel foglio Excel preimpostato si ottiene il suddetto abbassamento: 1,01 cm con un rapporto tra luce e abbassamento massimo pari a 297,79 che è maggiore di 250, quindi la verifica a deformabilità è stata soddisfatta. (Fig. 04)

Se nei carichi si considera anche il peso proprio della trave ipotizzando una sezione pari a 35cm x 50 cm, si devono ricalcolare i carichi e bisogna inserire nuovamente il valore così trovato nella tabella Excel. (Fig. 05)

Qs = 0,156 kN/mq + (1 x 0,3m x 0,5m x 6kN/mc) = 1, 146 kN/mq
Dai calcoli eseguiti grazie al foglio Excel si ottiene, così, un abbassamento massimo della trave pari a 0,87 cm, con un rapporto tra l/vmax pari a 343,79, quindi sempre verificato. L’unica variazione ottenuta sta nella l’altezza della trave aumentata di 5 cm. La sezione della trave, quindi, ha dimensioni pari a 35 cm x 55 cm. Ciò vuol dire che per sopportare un tale carico la trave ha bisogno di un’altezza maggiore.
TRAVE IN CEMENTO ARMATO
Si parte, anche nel caso di una struttura in cemento armato, dall’analisi dei carichi del solaio, la cui stratigrafia è rappresentata dai seguenti componenti (Fig. 06)
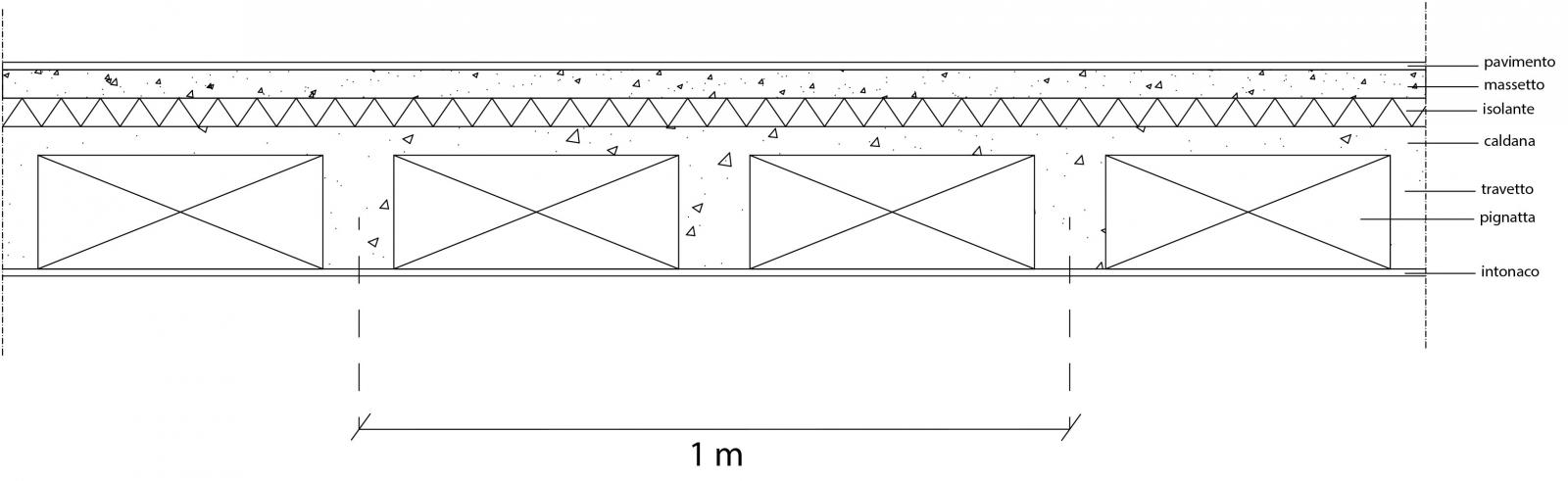
travetti: sezione 0,10m x 0,16m, peso specifico 25kN/mc
pignatte: sezione 0,16m x 0,4m, peso specifico 5,5kN/mc
caldana: spessore 0,04m, peso specifico 25 kN/mc
isolante in fibra di legno : spessore 0,04m, peso specifico 0,6 kN/mc
massetto di allettamento per il pavimento (malta di cemento): spessore 0,04m, peso specifico 21 kN/mc
pavimento in gres porcellanato: spessore 0,01m, peso specifico 8kN/mc
intonaco: spessore 0,015m, peso specifico 2kN/mc
impianti: peso specifico da normativa 0,5 kN/mq
tramezzi: peso specifico da normativa 1 kN/mq
_ Carichi permanenti strutturali (peso proprio degli elementi strutturali del solaio, quindi le pignatte, i travetti e la caldana)
Qs : (2 x 0,16m x 0,4m x 5,5kN/mc) + (2 x 0,1m x 0,16m x 25kN/mc) + (1m x 0,04m x 25kN/mc) = 0,704 kN/mq + 0,8 kN/mq + 1 kN/mq = 2,504 kN/mq
_ Carichi permanenti non strutturali (peso proprio dei gli elementi non strutturali che compongono il pacchetto del solaio)
Qp: tramezzi: 1kN/mq
impianti: 0,5kN/mq
pavimento: 0,01m x 8kN/mc = 0,08 kN/mq
massetto di allettamento: 0,04m x 21kN/mc = 0,84 kN/mq
isolante: 0,04m x 0,6kN/mc = 0,024 kN/mq
intonaco: 0,015m x 2kN/mc = 0,03 kN/mq
Qp Tot: 2,47 kN/mq
_ Carichi accidentali (destinazione d’uso dell’edificio, fornito dalla normativa)
Qa: 2 kN/mq
Dopo aver calcolato i carichi, che gravano sul solaio, si deve scegliere la classe di resistenza dell’acciaio di armatura; nella relativa tabella contenuta nella normativa tecnica ci sono due valori: B450A e B450C, l’unica differenza che intercorre tra i due valori sta nell’allungamento totale al carico massimo (Agt), considerando una struttura con prestazioni massime, si sceglie l’acciaio di classe B450C che è più duttile ed ha un limite di incrudimento maggiore.
Inoltre, bisogna calcolare anche la classe di resistenza del calcestruzzo, si sceglie un valore intermedio tra quelli riportati nella normativa tecnica, in particolare si è deciso di utilizzare un cls di classe C50/60, un cls di alte prestazioni.
Tutti i valori sopra riportati vanno, ora, riportati nel foglio di calcolo Excel al fine di verificare che l’abbassamento massimo della trave rientri nei limiti ammissibili per cui possa valere la seguente relazione l/vmax >250. Prima si deve fissare arbitrariamente la base della sezione della trave, che si è ipotizzata pari a 20 cm ed un copriferro pari a 4 cm. (Fig. 07)

Dai calcoli ottenuti tramite il foglio Excel si può vedere che l’abbassamento massimo è pari a 1,18 cm con rapporto tra la luce ed il suddetto abbassamento massimo di 254,58, per cui la mensola è verificata a deformabilità.
Se nei carichi si considera anche il peso proprio della trave che ha una sezione pari a 20cm x 45 cm, si devono ricalcolare i carichi e bisogna inserire nuovamente il valore così trovato nella tabella Excel. (Fig. 08)

Qs = 2,504 kN/mq + (1 x 0,2m x 0,45m x 25kN/mc) = 4,754 kN/mq
Anche in questo caso, nonostante l’aumento del carico strutturale, il rapporto tra la luce e l’abbassamento massimo ottenuto, pari a 1,13 cm, è uguale a 266,62, per cui esso risulta essere ancora una volta maggiore di 250 per cui la verifica a deformabilità è soddisfatta.
TRAVE IN ACCIAIO
Si considera, infine, un solaio in acciaio, la cui stratigrafia è rappresentata di seguito (Fig. 09)
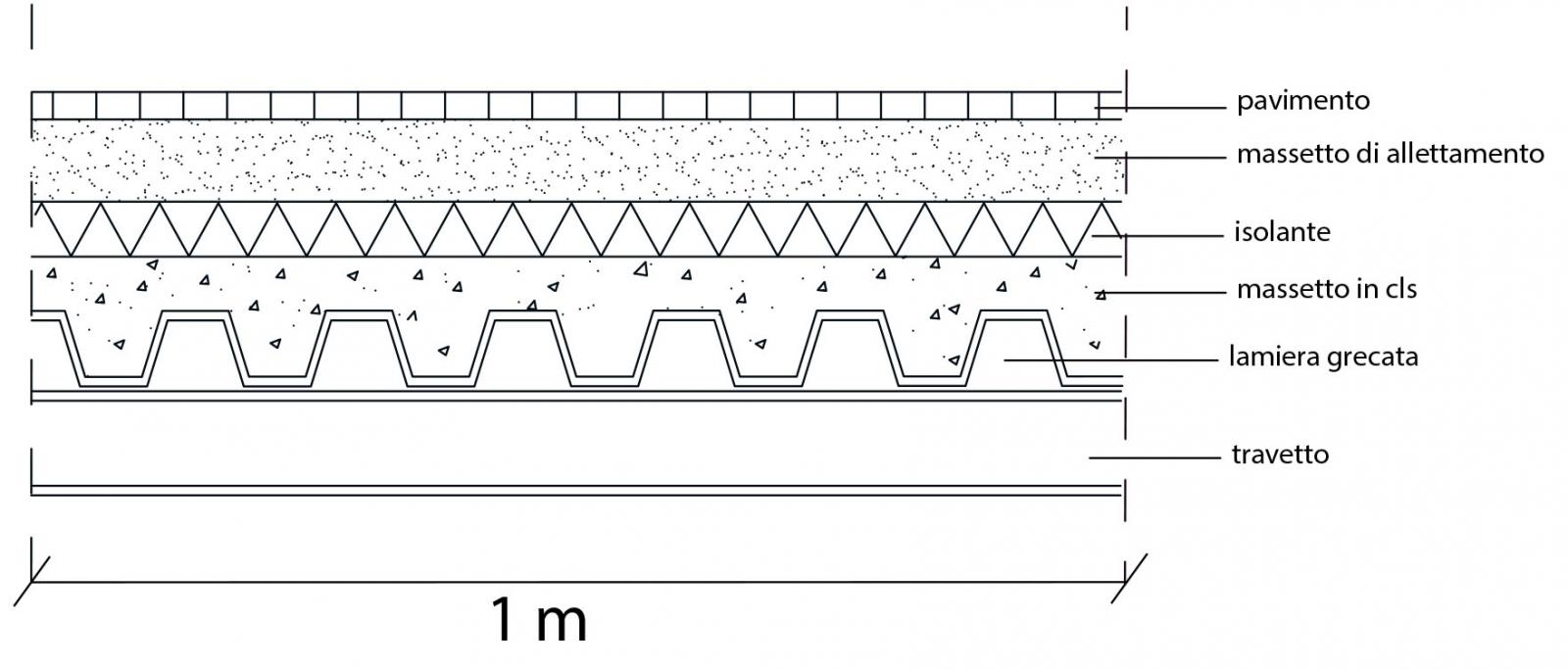
lamiera grecata HI BOND A55/P600 - spessore 7mm+ massetto in cls: spessore 0,011m, sovraccarico totale della soletta 2,30 kN/mq
isolante: spessore 0,04m, peso specifico 0,6 kN/mc
massetto di allettamento per il pavimento (malta di cemento): spessore 0,06m, peso specifico 21 kN/mc
pavimento in gres porcellanato: spessore 0,01m, peso specifico 8kN/mc
impianti: peso specifico da normativa 0,5 kN/mq
tramezzi: peso specifico da normativa 1 kN/mq
_ Prima di tutto si dimensiona il travetto:
_ Carichi permanenti strutturali (peso proprio degli elementi strutturali del solaio: il travetto, il massetto in cls e la lamiera grecata)
Qs : 2,30 kN/mq
_ Carichi permanenti non strutturali (peso proprio dei gli elementi non strutturali che compongono il pacchetto del solaio)
Qp: tramezzi: 1kN/mq
impianti: 0,5kN/mq
pavimento: 0,01m x 8kN/mc = 0,08 kN/mq
massetto di allettamento: 0,06m x 21kN/mc = 1,26 kN/mq
isolante: 0,04m x 0,6kN/mc = 0,024 kN/mq
Qp Tot: 2,864 kN/mq
_ Carichi accidentali (destinazione d’uso dell’edificio, fornito dalla normativa)
Qa: 2 kN/mq
Si sceglie la classe di resistenza dell’acciaio S235 con una tensione di snervamento caratteristica pari a 235 MPa.
Si inseriscono i valori ricavati dai calcoli nel foglio Excel. (Fig. 10)

Nel caso del dimensionamento degli elementi strutturali in acciaio non si ottiene il valore dell’altezza della trave, come avviene per il c.a. e per il legno, ma il modulo di resistenza minimo Wx. Grazie a tale valore è possibile ricavare il profilato con Wx maggiore riportato nelle tabelle dei profilati in acciaio. Dato che il Wx ottenuto è pari 788,80 cm3, si può scegliere un profilato IPE 360 con Wx pari a 904,0 cm3 . (Fig. 11)

Per precisione va specificato che, una volta trovato il profilato della trave, sono stati inseriti precedentemente nel foglio Excel sia il peso che il momento d’inerzia relativi all’IPE 360.
Dai calcoli eseguiti grazie al foglio di calcolo si può vedere che l’abbassamento massimo della trave è pari a 1,23 cm con un rapporto l/vmax pari a 243,76 < 250, per cui la verifica a deformabilità non è soddisfatta.
Per ovviare a tale problema si può, ad esempio, ridurre l’interasse portandolo da 5m a 4m. (Fig. 12)

Cambiando l’interasse, infatti si ottiene un’IPE 300 (Fig. 13) producendo un abbassamento della trave pari a 0,91cm con un rapporto l/vmax = 273,28 > 250 per cui la verifica a deformabilità della mensola è soddisfatta.

Considerando nei calcoli dei carichi anche il peso proprio della trave scelta, si ricalcola la somma dei carichi strutturali:
Qs = (2,3kN/mq + 0,42kN/m) = 2,72 kN/mq
Si ottiene così un abbassamento massimo di 0,96 cm con un rapporto l/vmax = 259,99 > 250, quindi la verifica è soddisfatta. (Fig. 14)

Dall’analisi effettuata per solai caratterizzati dalla presenza di uno sbalzo ipotizzato pari a 3m per le tre tecnologie costruttive (legno, cemento armato, acciaio) si può notare che i diversi materiali, che hanno diversi moduli di resistenza, presentano anche diversi valori per ciò che riguarda l’abbassamento relativo della trave a sbalzo. In modo particolare, il legno che è dotato di una resistenza inferiore presenta, invece, un abbassamento della trave inferiore, quindi è meno deformabile rispetto alle altre due tecnologie. Tra queste ultime è l’acciaio, più resistente, ad essere più deformabile, tanto da dovere necessitare una riduzione, ad esempio, dell’interasse affinché si potessero ottenere una deformabilità e un abbassamento accettabili.
Commenti recenti