blog di lorenzo.prn

Con la quinta esercitazione vado a calcolare come diversi telai, assunti shear type, si ripartiscano la forza orizzontale, che può essere quella sismica o del vento, attraverso il metodo delle rigidezze. La tecnologia adottata per l'impalcato è quella del cemento armato, con pilastri 30x40 cm, orientati in maniera diversa.

In totale l'impalcato dell'edificio presenta 8 telai, 4 verticali e 4 orizzontali, costituiti dai pilastri:

1-V : 1-2

2-V : 3-4

3-V : 5-6-7-8

4-V : 9-10-11-12

1-O : 5-9

2-O : 1-3-6-10

3-O : 2-4-7-11

4-O : 8-12

Usando i simboli dei controventi, vincoli cedevoli elasticamente, vado a indicarli in pianta:

L'altezza dei pilastri segue inoltre quella dell'esercitazione precedente, cioè 3 metri, dato utile, insieme al modulo di Young e del Momento d'Inerzia di ogni singolo pilastro, calcolato in base al loro orientamento.

Nel secondo step si riassumono le distanze di ciascun controvento dall'origine:

Calcolo ora il centro di massa, attraverso la grandezza delle aree semplici che si ricavano dall'impalcato, due rettangoli, e le coordinate dei loro centri d'area, che vengono inseriti nella formula:

X_G= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_tot

Y_G= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

Con il totale delle rigidezze orizzontali e verticali, e le rigidezze di ogni singolo controvento insieme al loro braccio rispetto all'origine, calcolo il centro delle rigidezze, con le formule:

X_C= K_V-2*d_V-2 + K_V-3*d_V-3 + K_V-4*d_V-4 / K_Vtot

Y_C= K_O-2*d_O-2 + K_O-3*d_O-3 + K_O-4*d_O-4 / K_Otot

_{E ricavo la distanza di ogni singolo controvento dal centro delle rigidezze:}

I due centri, quello di massa e quello delle rigidezze, si trovano a non coincidere, creando eventualmente un braccio che va a provocare nella struttura, con una forza applicata, un momento oltre che una traslazione semplice.

Ora è il momento di calcolare la forza sismica: prima di tutto riporto i carichi del solaio in cemento armato delle esercitazioni precedenti, poi moltiplico i carichi strutturali e accidentali con l'area del solaio. Introduco il coefficiente di contemporaneità ψ, che risulta dalle norme tecniche essere 0,30 per edifici residenziali, e calcolo il peso sismico.

Con l'ultimo coefficiente c di riduzione della forza sismica calcolo quest'ultima; c è un dato legato alla sismicità della zona presa in esame, ad esempio Roma, e quindi risulta essere 0,10 secondo le norme.

Infine si calcola come la forza sismica agisce sui controventi, provocando traslazioni orizzontali e verticali, insieme alla rotazione, prima lungo X e poi lungo Y:

Di seguito rappresento le traslazioni e le rotazioni, fortemente sovradimensionate per rendere l'idea dello spostamento e della direzione:

Con questa esercitazione si procede a dimensionare un pilastro nei tre sistemi costruttivi quali il legno, l'acciaio e il calcestruzzo. Nell'ultimo caso terremo conto, oltre allo sforzo normale, anche della pressoflessione dato che gli agganci nel calcestruzzo sono incastri.

L'orditura segue quella delle esercitazioni precedenti e, considerando l'area di influenza, andiamo a trovare il pilastro più sollecitato, su cui graveranno il peso di più solai e pilastri superiori ad esso corrispondenti.

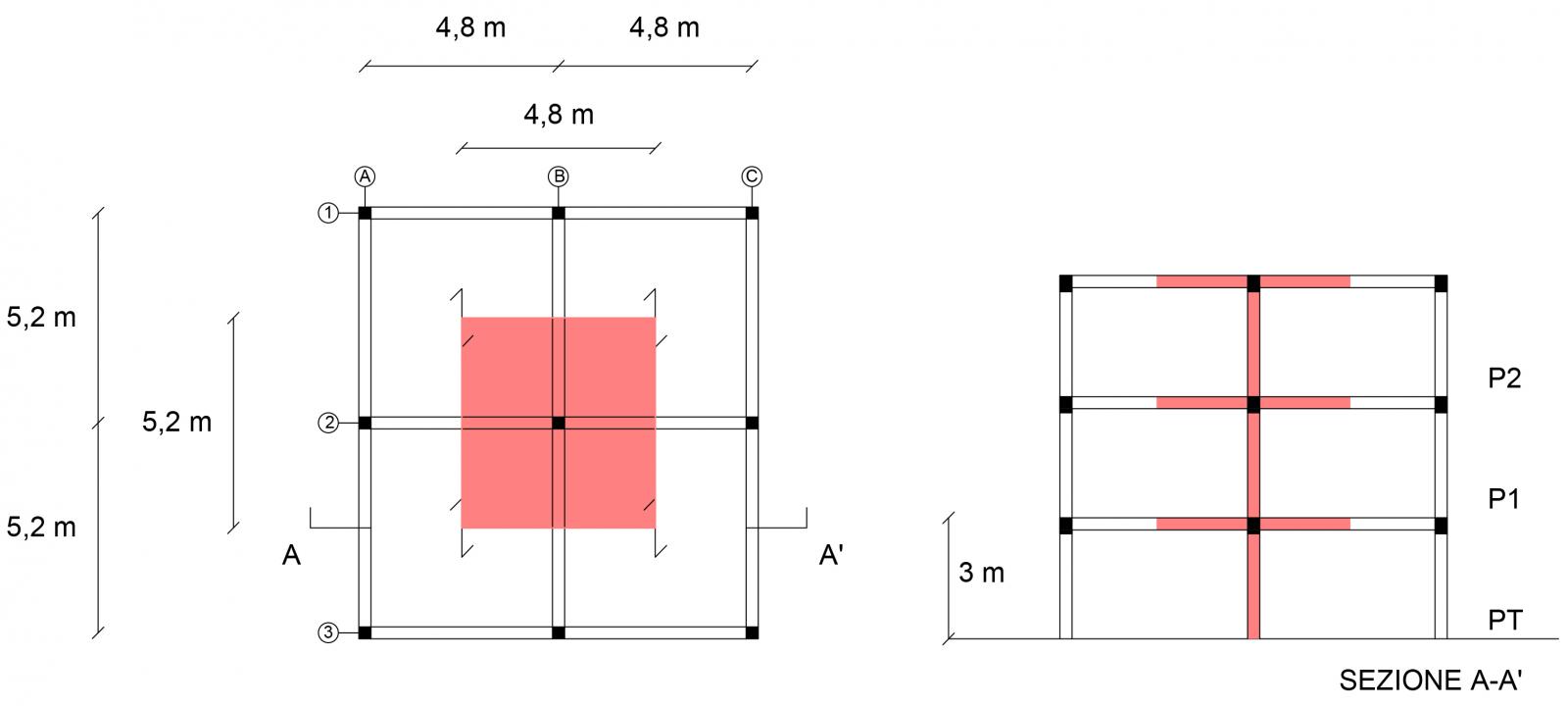
LEGNO

Considerando il solaio delle precedenti esercitazioni, inizio col dimensionare il pilastro in legno.

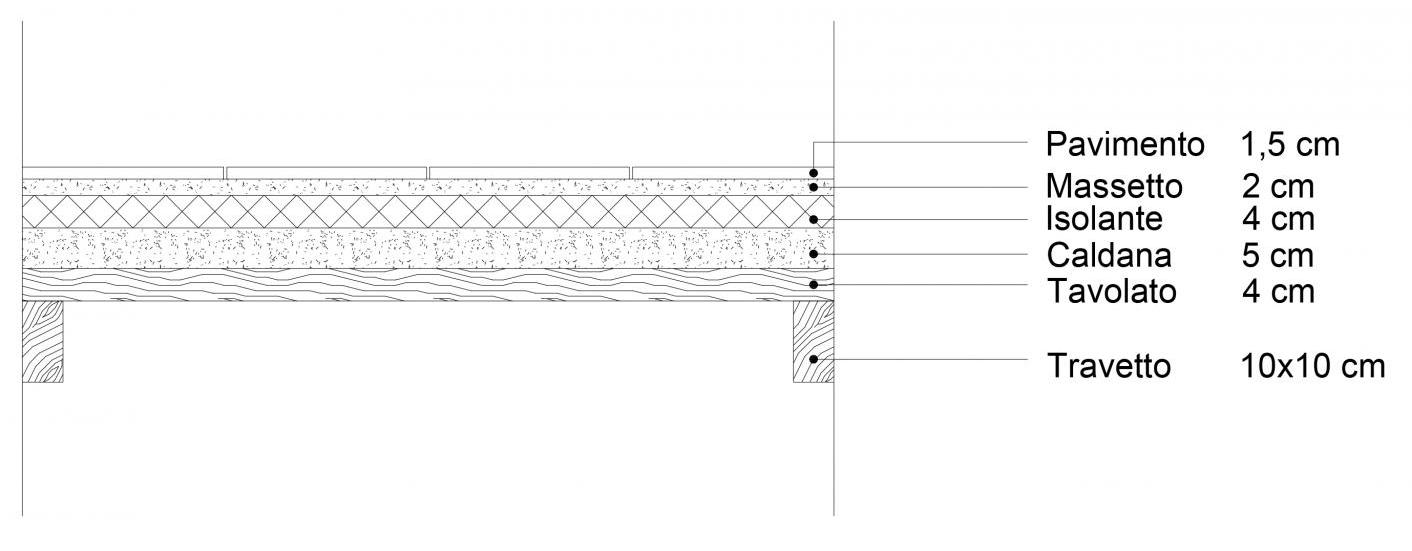
Inserisco i dati dell'area di influenza:

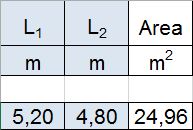
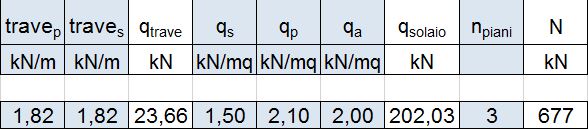
Ricavo quindi il peso della trave primaria e secondaria moltiplicando l'area delle sezioni delle travi per il peso specifico del legno 

trave_p=(0,65x0,40) m² x 7 kN/m³ =1,82 kN/m

trave_s=(0,65x0,40) m² x 7 kN/m³ =1,82 kN/m

Ottengo così il carico totale delle travi; compilando poi i carichi del solaio con i dati precedenti ottengo anche il carico totale del solaio. Lo sforzo Normale sarà quindi calcolato, tendendo conto anche del numero di piani.

Calcolo la resitenza a compressione di progetto del pilastro attraverso i dati del materiale ligneo scelto precedentemente, il legno lamellare incollato omogeneo GL 28h, con f_c,0,k = 26,5 MPa, coefficente correttivo k_mod = 0,7 e coefficente di sicurezza y_m = 1,45; infine si calcola l'area minima della sezione del pilastro.

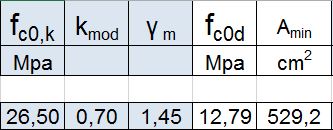
Considerando β = 1, quindi l = h (caso appoggiato/appoggiato), vado a ricavare la base e l'altezza minima del pilastro, inserisco i dati di ingegnerizzazione e ottengo l'area di progetto e il momento di inerzia di progetto.

Infine deve risultare verificato che l'area di progetto sia maggiore dell'area minima, come in questo caso.

Si può procedere quindi a dimensionare i pilastri superiori, cambiando i dati relativi ai piani.

ACCIAIO

Per l'acciaio prendo in considerazione la stessa sezione della precedente esercitazione, con travi primarie IPE 500 e secondarie IPE 240, di acciaio S275.

trave_p = 90,7 kg/m = 0,90 kN/m

trave_s = 30,7 kg/m = 0,30 kn/m

Dopo aver trovato il carico delle travi, immetto i dati dei carichi per il solaio in acciaio e ottengo il carico totale di questo. Inserendo infine il numero dei piani ho il mio sforzo Normale.

Ora uso i dati dell'acciaio scelto: la tensione di snervamento e il coefficente di sicurezza del materiale, ricavando la tensione ammissibile e l'area minima.

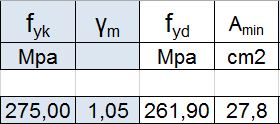
Sempre considerando β = 1 e l = h, vado a ricavare tramite l'inerzia minima il profilo HEA da scegliere, facendo attenzione all'area della sezione con quella minima di progetto e al raggio minimo d'inerzia.

Ora calcolo il resto dei pilastri superiori:

Chiaramente i pilastri superiori mantengono la stessa sezione, in quanto pur cambiando dimensione dell'area minima e l'inerzia minima, il raggio d'inerzia minima non cambia.

CEMENTO ARMATO

Uso sempre la stessa sezione dell'esercitazione precedente con un calcestruzzo di classe C45/55 e acciaio B450A.

Calcolo i pesi delle travi, sapendo che il peso specifico del calcestruzzo è 24 kN/m³:

trave_p = (0,55 x 0,40) m x 24 kN/m³ = 5,28 kN/m

trave_s = (0,55 x 0,40) m x 24 kN/m³ = 5,28 kN/m

Quindi con il carico totale delle travi e quello del solaio, inserendo il numero di piani ottengo lo sforzo Normale.

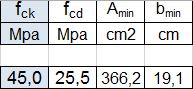
Con i dati riferiti al calcestruzzo scelto inserisco la resistenza caratteristica di 45 MPa, ottenendo l'area e la base minima.

Sapendo che nel caso del calcestruzzo gli agganci sono realizzati come incastri, quindi trasmettono momento, sottoponendo il pilastro a presso-flessione, vado a considerare la luce minima di inflessione uguale a l/2 e β = 0,5 (caso incastro/incastro).

Ingegnerizzo quindi base e altezza in modo tale da garantire che la tensione massima di progetto sia minore o uguale alla tensione di resistenza e che l'area di progetto sia maggiore dell'area minima.

Calcolo poi gli altri pilastri superiori:

Con la terza esercitazione vado a dimensionare una trave a sbalzo costituita da tre materiali, il legno, l'acciaio e il calcestruzzo armato. Ne verifico poi la deformabilità, calcolando l'abbassamento massimo della mensola attraverso il rapporto tra la luce della trave e il suo spostamento, sempre maggiore di 250.

La pianta della carpenteria segue alcune decisioni progettuali del Laboratorio di Progettazione 3 del Prof. Desideri e vuole indagare una delle possibilità di aggetto del nostro edificio.

SOLAIO IN LEGNO

Per il solaio prendo i carichi che ho ottenuto nella prima esercitazione per inserirli nel file excel.

In questo nuovo foglio di calcolo il momento massimo che risulta essere ql²/2 trattandosi di una mensola. Inoltre assumo la base della trave di 30 cm secondo un principio di continuità con i pilastri.

Dopo aver ingegnerizzato l'altezza, verifico la sezione allo Stato Limite di Esercizio. Nella verifica non si tiene conto del peso proprio della trave in legno.

La trave è verificata poichè il rapporto tra luce e spostamento (680) è maggiore di 250, secondo normativa.

SOLAIO IN ACCIAIO

Per l'acciaio, dopo aver trovato il modulo di resistenza a flessione minimo W_x per ingegnerizzare la sezione si inserisce nella colonna successiva il valore del momento di inerzia I_x del profilo, che ha come modulo di resistenza a flessione W_x un valore maggiore rispetto a quello trovato.

Come trave ho un IPE 360 di base 170 mm, con un momento di inerzia di 16270 cm⁴ e un peso di 57,1 kg/m, incluso quest'ultimo nei calcoli per il carico di esercizio q_e.

La trave è verificata poichè il rapporto tra luce e spostamento (340) è maggiore di 250, secondo normativa.

SOLAIO IN LATEROCEMENTO

Anche qui per la base della trave utilizzo i 30 cm del lato del pilastro, arrivando ad avere una trave alta 45 cm.

Per la deformabilità calcolo sempre il carico di esercizio q_e includendo il peso della trave.

La trave è verificata poichè il rapporto tra luce e spostamento (421) è maggiore di 250, secondo normativa.

Con la seconda esercitazione si inizia a usare il programma SAP2000 costruendo una travatura reticolare tridimensionale, nel mio caso cubica, in acciaio a sezione quadrata. 

Le aste risultano sollecitate a sforzo normale, sia di trazione che di compressione, mentre sono assenti sollecitazioni di taglio, flessione e torsione. 

Dal programma quindi apro un New model, imposto l'unità di misura KN, m, C e scelgo come spazio di lavoro Grid Only.

Ho impostato la maglia strutturale cubica di lato 4,00 m; volendo avere 4 cubi lungo l'asse Y e 2 cubi lungo l'asse X, e un'altezza 1 lungo Z devo impostare una griglia X=3 Y=5 Z=2.

Con il comando Frame draw disegno il modulo base e controvento l'intera struttura. Per controllare se ci siano duplicati o se qualche linea non sia stata collegata in modo corretto a un nodo vado su Edit>Edit points>Merge duplicate e su Edit>Edit points>Merge joints.

Selezione i quattro appoggi laterali della struttura e gli assegno il vincolo cerniera andando su Assign>Joint>Restraints e selezionando il carrello.

Ora sblocco i vari nodi da sforzo flessionale selezionando tutta la struttura e andando su Assign>Frame>Release partial fixity.

Per questa struttura ho deciso di utilizzare dei profilati a sezione quadrata di acciaio quindi devo assegnarli alla struttura selezionandola e andando su Assign>Frame>Frame sections>Add new property>Tube. Imposto i dati in modo che i lati siano uguali.

Imposto un nuovo schema dei carichi andando su Define>Load pattern e inserisco un nuovo parametro F con un Self Weight Multiplier uguale a 0.

Seleziono adesso i nodi superiori dove vado ad aggiungere i carichi che gravano sulla struttura, poi vado su Assign>Joint Loads>Forces e aggiungo una forza lungo l'asse Z di -150 KN poichè diretta verso il basso.

Faccio partire l'analisi lineare statica cliccando su Run analysis e lasciando solamente la forza F come oggetto di indagine (gli altri dati devono essere impostati su Do not run), e ottengo infine la mia struttura deformata e il diagramma dei carichi normali, tutto attivabile tramite i tasti con il disegno dei telai in alto nella barra degli strumenti.

Cliccando su Display>Show tables posso controllare i vari dati dell'analisi spuntando Analysis Results e selezionando come dati a destra nella finestra il valore F. Andiamo sulla tabella Element Forces - Frames ed esportiamola in un file Excel per ottenere i dati utile per il dimensionamento delle aste.

Provvedo ad eliminare i dati ripetuti andando nel menù Dati>Rimuovi duplicati, ordino i miei sforzi dal più piccolo al più grande e li sposto conseguentemente nelle tabelle excel preimpostate per trazione e compressione.

TRAZIONE

Per prima cosa incollo gli sforzi nella prima colonna.

Come acciaio scelgo un S 235 JR H della ditta SICAM con un valore di tensione di snervamento di 235 MPa.

Ottenute le aree minime attraverso il valore dello sforzo e della tensione di progetto, provvedo a ingegnerizzarle attraverso il controllo della tabella dei profilati.

Ottengo 5 profili diversi che non differiscono talvolta in dimensione quanto nello spessore, poichè la ditta presenta una moltitudine di soluzioni diverse per una stessa grandezza di sezione.

COMPRESSIONE

Incolliamo ancora una volta i valori di compressione negativi.

Per la luce sono andato sul modello di SAP e cliccando su View>Set Display Options e spuntando in Frames/Cables/Tendons Labels ho potuto vedere i numeri delle aste così da poter distinguare tra aste dritte (4,00 m) e aste diagonali (5,65 m). Come acciaio ho sempre lo stesso.

Ottengo ora una serie di parametri minimi del profilo ossia l'area minima, il momento di inerzia minimo e il raggio di inerzia minimo. Sempre attraverso il profilario faccio in modo di ingegnerizzare tutte le aste in modo tale che tutti questi tre dati siano sempre superiori a quelli minimi.

Alla fine ho solamente tre profilati diversi. L'attenzione cade sui primi 2 carichi in cui l'area minima ha svolto un ruolo fondamentale nella decisione del profilo mentre per gli altri due il ruolo fondamentale è stato quello del raggio di inerzia.

Con questa esercitazione si procede al dimensionamento di una trave sollecitata a flessione di un solaio prima ligneo, poi in acciaio e infine in calcestruzzo armato.

Di seguito la pianta di carpenteria

La trave più sollecitata ha luce di 6 m e interasse di 8 m.

SOLAIO IN LEGNO

I travetti hanno un interasse di 1 m, quindi nell'analisi viene considerato il peso di un singolo travetto.

L'analisi dei carichi è stata svolta usando una tabella excel, calcolando carichi strutturali, permanenti (a cui si è sempre aggiunta l'influenza di possibili impianti e tramezzi) e accidentali (calcolati ogni volta per la destinazione residenziale).

Inserendo l'interasse della trave con i diversi carichi combinati con i coefficenti di sicurezza ottengo il carico ultimo lineare; quest'ultimo insieme alla luce ci fornisce il Momento ultimo della trave.

Si sceglie quindi come tecnologia il legno lamellare incollato omogeneo di classe di resistenza GL 28h, con f_m,k pari a 28 N/mm^2.

Definisco inoltre la classe di durata del carico, di lunga durata (6 mesi – 10 anni), e la classe di servizio, la 2.

Come valore k_mod ho quindi 0,70. Invece come coefficiente parziale di sicurezza relativo al materiale y_m ho quello relativo al legno lamellare incollato, cioè 1,45.

Non rimane che impostare la base della trave, che seguirà per comodità la larghezza dei pilastri fissata a 40 cm, avendo come risultato un altezza approssimata a 65 cm.

SOLAIO IN ACCIAIO

Come parte strutturale è stata usata una lamiera grecata completa di un getto di completamento il cui spessore è stato calcolato secondo il prontuario della ditta Hi-Bond che forniva conseguentemente il peso al metro quadro del carico.

Attraverso la tabella excel sono stati calcolati i carichi strutturali, permanenti e accidentali.

Avendo precedentemente inserito i calcoli per ottenere il Momento massimo attraverso l’analisi dei carichi, scelgo il tipo di acciaio con cui intendo realizzare la trave, cioè Fe 430/S275.

Sapendo infine lo sforzo di progetto e il Momento di resistenza a flessione minimo posso scegliere la mia IPE che sarà un IPE 500 con W_x uguale a 1930 cm³, con base di 20 cm.

SOLAIO IN LATEROCEMENTO

Le pignatte sono state calcolate secondo il loro peso al metro quadro, moltiplicandole per 8, poichè lunghe 25 cm, aggiungendo gli elementi in calcestruzzo per i carichi strutturali, per poi calcolare i carichi permanenti e accidentali.

Inseriti questi dati nel file excel otteniamo il carico ultimo lineare e Momento massimo; scegliamo quindi che tipo di calcestruzzo vogliamo usare secondo le classi di resistenza del materiale, in questo caso C45/55, e la resistenza caratteristica dell'acciaio, il B450A.

Ottengo automaticamente le tensioni di progetto e da queste si determina l'altezza utile della sezione che, con l'aggiunta del copriferro, darà l'altezza minima.

Ingegnerizzo infine portando l'altezza della sezione a un valore immediatamente superiore al valore minimo.

Gli ultimi dati forniscono il peso proprio della trave conoscendo il peso del calcestruzzo armato, con ciò si procede alla verifica della sezione che dovrà avere un'altezza ingegnerizzata superiore a quella minima indicata dal foglio excel nella seconda riga, come in questo caso in cui risulta verificata.