La quarta esercitazione prevede il dimensionamento a sforzo normale del pilastro più sollecitato in un generico edificio di più piani (nel mio caso 4) nelle tre diverse tecnologie: legno, acciaio e cemento armato.
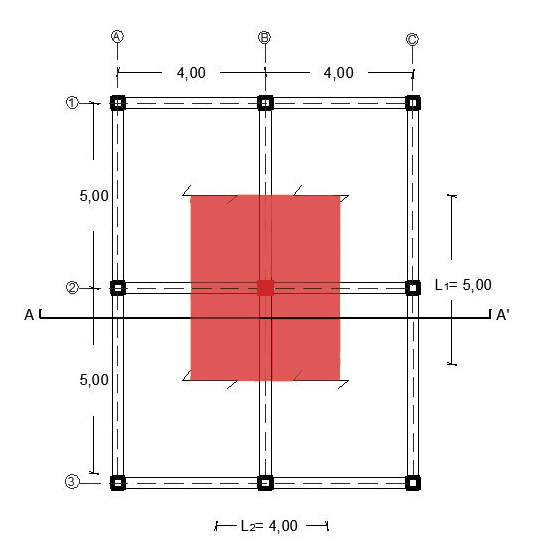
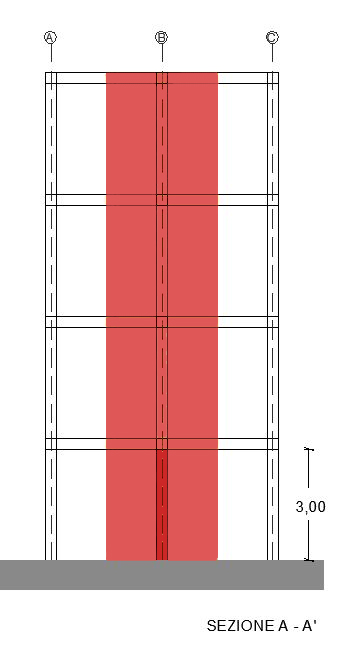
Dunque individuiamo il pilastro in questione evidenziandolo in rosso, su di esso grava il carico di travi e solaio dei piani superiori.
Individuo l’area d’influenza maggiore che sarà:
Ai = L1xL2 = 5x4 = 20mq
LEGNO
Utilizzo il solaio e i carichi delle esercitazioni precedenti.
Innanzitutto calcolo il peso unitario della trave:
Trave= area della sezione x peso specifico del materiale = (0,45x0,3)mq x 5 KN/mc= 0,675 KN/m
Inserendo i dati in tabella ottengo il carico totale della trave, che si ricava dal calcolo:
qtrave= (trave p x L1 x 1,3) + (trave s x L2 x 1,3)= 125,16 KN
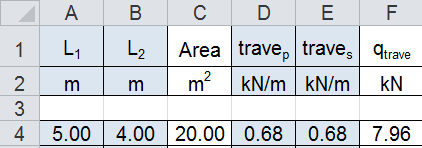
Per calcolare il valore complessivo del carico agente, inserisco i valori dei carichi agenti sul solaio: carichi strutturali (qs), carichi permanenti (qp) e carichi accidentali (qa). Quindi:
qsolaio= (qs x 1,3 + qp x 1,5 + qa x 1,5) x Ai= (0,36 KN/mq x 1,3 + 1,86 KN/mq x 1,5 + 2 KN/mq x 1,5) x 20 mq = 125,16 KN
A questo punto tramite il foglio excel calcolo lo sforzo di compressione N:
N = (qtrave x qsolaio) x npiani= 532 KN
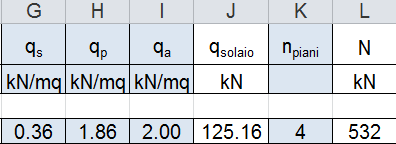
Posso calcolare, così, l’area minima necessaria affinché il materiale non entri in crisi. Inserisco, dunque, i dati relativi al materiale nel foglio excel, che sono:
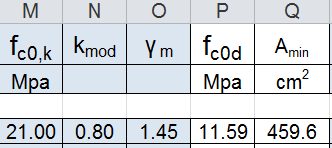
- la resistenza a compressione (fc0,k) 21MPa
- il coefficiente della durata di carico kmod 0,8
- il coefficiente parziale di sicurezza γm 1,45
Attraverso questi valori il foglio mi ricava il valore della tensione ammissibile e dell’area minima:
fc0d = fc0,k x kmod / γm =11,59 MPa
Amin = 459,6 cm2
Sapendo che il modulo di elasticità E = 8800MPa, β = 1 e l’altezza del pilastro è di 3 m, mi calcolo tramite il foglio excel:
- il valore massimo di snellezza λmax= 86,54
- valore minimo del raggio d’inerzia ρmin= 3,47 cm
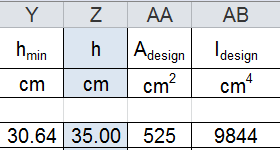
- la base minima bmin= 12,01 cm , la quale va ingegnerizzata, dunque b= 15 cm
- l’altezza minima hmin= 30,64 cm,la quale va ingegnerizzata, dunque h= 35 cm

Calcolo l’area di progetto della sezione :
Adesign= b x h= 525 cm2
Infine verifico che Adesign>Amin dunque il dimensionamento è verificato
ACCIAIO
Per l’acciaio procedo analogamente, utilizzo per i carichi del solaio i valori usati nella prima esercitazione, e per il peso unitario della trave quello fornito dalla tabella dei profilati per la IPE che avevo scelto.
IPE 400= 66,3 Kg/m= 0,66 KN/m
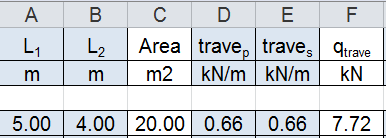
Inserisco (come ho fatto il per il legno) i valori in tabella arrivando al calcolo di N.

Posso ora calcolare l’area minima affinché il materiale non entri in crisi, quindi inserisco i dati relativi al materiale:
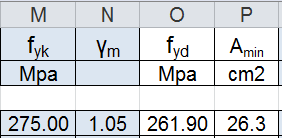
- tensione di snervamento (f,yk) 275MPa
- il coefficiente parziale di sicurezza (γm) 1,05
Ho ricavato così il valore della tensione ammissibile e dell’area minima
fyd= fyk / γm =261,90 MPa
Amin= 26,3 cm2
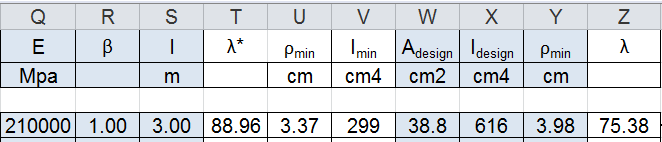
Sapendo che il modulo di elasticità E= 210000 MPa, β= 1 e l’altezza del pilastro è di 3m, mi calcolo tramite il foglio excel:
- valore massimo di snellezza λmax= 88,96
- valore minimo del raggio d’inerzia ρmin= 3,37 cm
- calcolo il momento d’inerzia minimo Imin= 299 cm4
Rispetto ai valori ricavati, ingegnerizzo la sezione, scegliendo un profilo HEA con valori maggiori rispetto a quelli minimi trovati. Scelgo un profilo HEA160
Verifico che Adesign>Amin, che è verificato
Infine verifico che λ< λ*, ed è verificato.
CEMENTO ARMATO
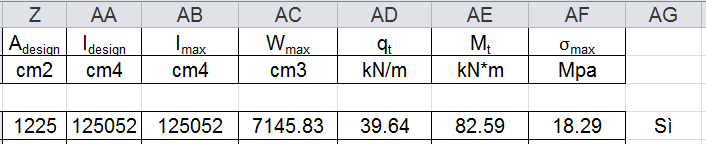
Per il cemento armato procedo analogamente al dimensionamento del pilastro in legno, inserisco i dati relativi alla prima esercitazione e calcolo l’altezza minima.
Per il calcestruzzo devo inoltre verificare che la tensione massima sia minore della resistenza di progetto: σmax < fcd, ed è verificato.


Commenti recenti