ESERCITAZIONE VI: Ripartizione delle forze sismiche

ABSTRACT: La seguente esercitazione prenderà in analisi una pianta strutturale di un edificio a un piano. Attraverso la modellizzazione del solaio come impalcato infinitamente rigido orizzontalmente (una modellazione analoga è già stata incontrata per i telai shear-type della trave Vieerendel http://design.rootiers.it/strutture/node/954) si analizzeranno gli effetti di una forza orizzontale valutando le rigidezze dei suoi controventi, necessari a impedire la rotazione lungo l'asse z.

Il controvento è un vincolo cedevole con rigidezza K (kN/m) visualizzabile come una molla elastica poichè capace di reagire a trazione e compressione solamente lungo il proprio proprio asse.
L'impalcato ha rigidezza proporzionale alla distanza dal centro delle rigidezze. Se gli assi (x e y) del centro delle rigidezze e del centro delle masse coincidono allora il solaio non sarà in grado di ruotare.

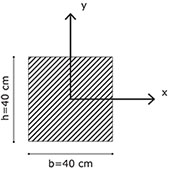
Considerato il telaio in figura si assegnano pilastri con la seguente sezione.

il momento di inerzia del pilastro è dunque dato da I=bh³/12 ⇒

I=40 cm^.40³/12=213333 cm⁴

Il telaio dunque assume in pianta, secondo il modello adottato, la seguente configurazione:

Dove la rigidezza di ogni controvento (modellato come un telaio shear-type) viene calcolata come segue (in modo analogo al post http://design.rootiers.it/strutture/node/151):

F= (12EI_1B/h³ + 12EI_2B/h³ + 12EI_3B/h³ + 12EI_4B/h³ + 12EI_5B/h³ ) δ⇒

⇒ F= k δ  ⇒ k= 12E/h³ (I_1B+I_2B+I_3B+I_4B+I_5B)

NB come esemplificazione è stata presa la sezione lungo B

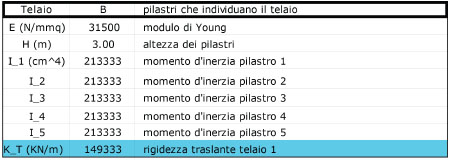
Esempio di tabella per il calcolo delle rigidezza dei telai (per visualizzare tutti i calcoli scaricare il file .xls allegato)

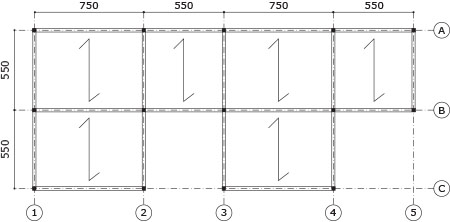
I telai per i quali calcolare k dunque saranno A,B, 1C-2C e 3C-4C orizzontalmente e 1,2,3,4 e 5 verticalmente.

Individuiamo quindi il centro di massa cdm dividendo la struttura nelle seguenti porzioni di area e sfruttiamo il foglio excel per il calcolo delle sue coordinate.

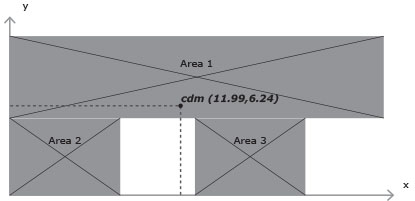
Attraverso il foglio di calcolo (sempre opportunamente adattato al telaio in questione) si trova il centro delle rigidezze CK

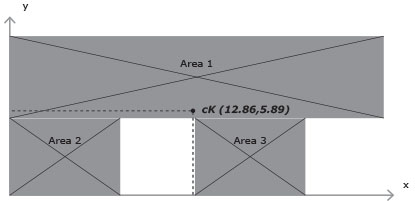
I due centri sono traslati l'uno rispetto l'altro ci si aspetta dunque che su ogni "molla" agisca una forza diversa da 0 in grado di contrastare l'effetto della rotazione.

I valori di tale forze sono opportunamente evidenziati sul foglio Excel.