Esercitazione

Disegno le 3 possibili deformate dei piani dovute all’azione delle 3 forze e considero le sollecitazioni di taglio che agiscono sui pilastri e sui traversi.

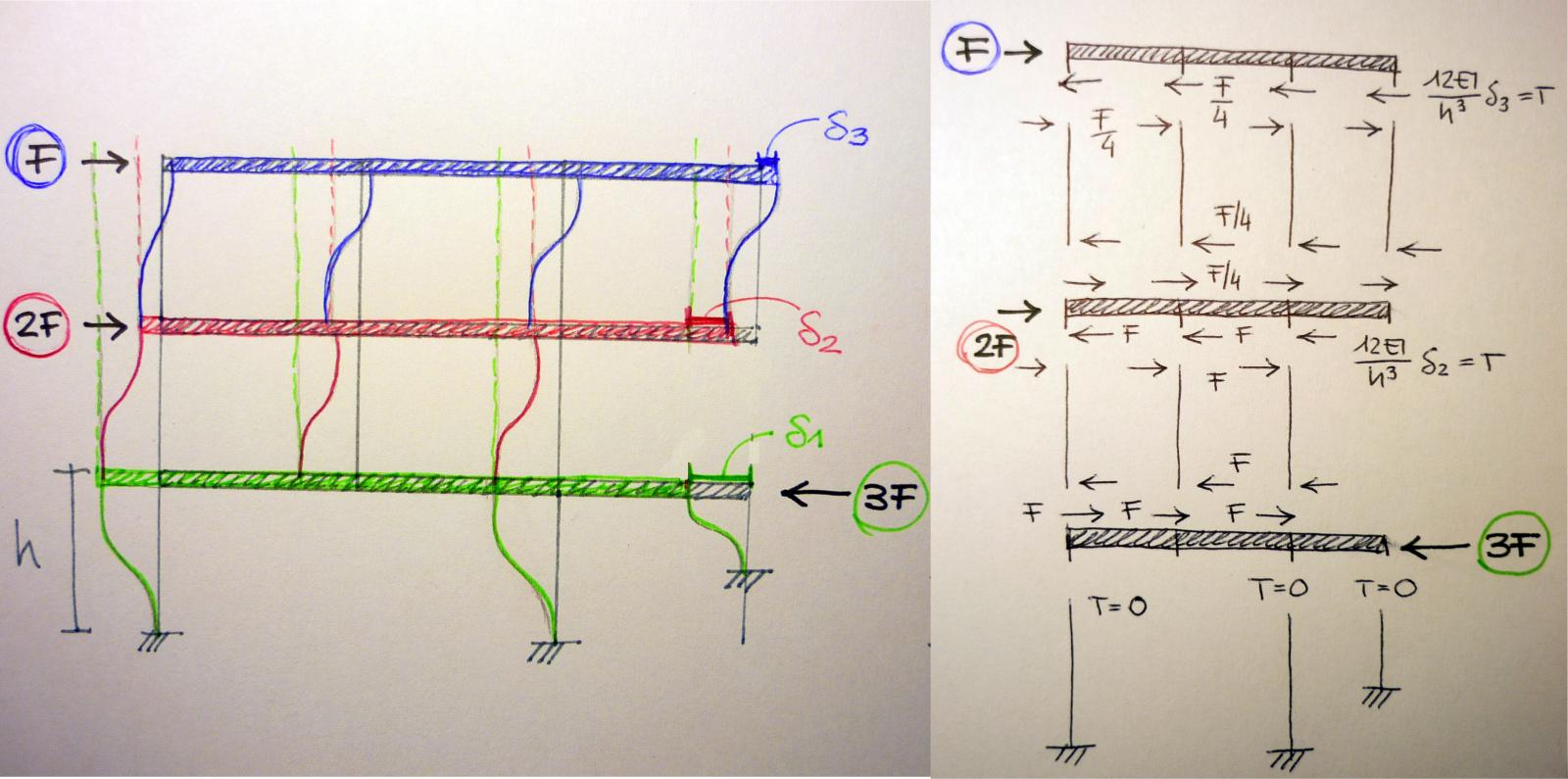
Bilanciando le forze sul traverso del terzo piano la forza che agisce è pari alla somma dei tagli moltiplicata per lo spostamento.

F= 4 (12EI/h³) δ3 = (48EI/h³)δ3

δ3= Fh³/48EI --> T = (12EI/h³)*( Fh³/48EI) = F/4

M= (6EI/h²)*( Fh³/48EI) = Fh/8

 Sul traverso del secondo piano agisce sempre una forza verso destra però di intensità doppia, quindi lo spostamento δ2 sarà maggiore e pari a:

δ2= Fh³/12EI --> T = (12EI/h³)*( Fh³/12EI) = F

M= (6EI/h²)*( Fh³/12EI) = Fh/2

Sul traverso al piano terra agisce le sollecitazioni di taglio T=F dei tre pilastri superiori che bilanciano la forza applicata a destra --> 3T = 3F --> δ2 = 0

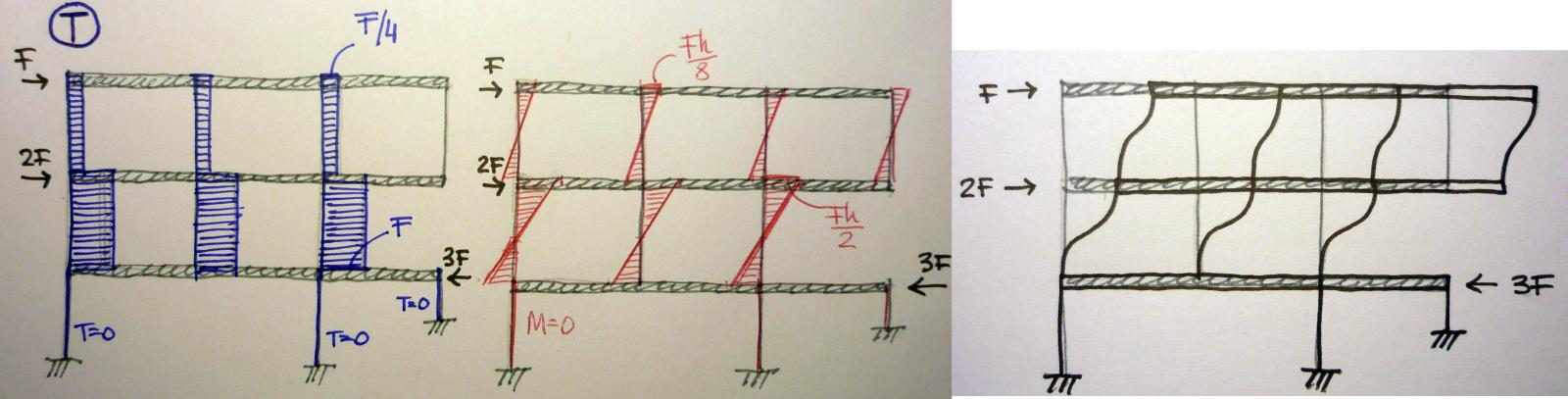
Quindi i pilastri a terra non presentano taglio: l’altezza del terzo pilastro è ininfluente rispetto al calcolo della sollecitazione e del momento visto che il taglio sul traverso e la forza applicata sono uguali.

VERIFICA SAP

COME DISEGNATO NEL GRAFICO DEI MOMENTI , CON LE TRAVI SHEAR TYPE IL MOMENTO VIENE SMORZATO IN H/2.

NEL PRIMO LIVELLO  LO SPOSTAMENTO E' NULLO , NON C'E' TAGLIO,MOMENTO E QUNDI NON C'E' DEFORMAZIONE. LA DEFORMAZIONE TOTALE E' DATA DA d2 d3.

Dopo aver trovato i valori di δ1, δ2 e δ3 posso calcolare i momenti dei pilastri con la formula

M = (6EI/l²)*δ

δ1= Fl³/12EI --> M = (6EI/l²)*( Fl³/12EI) = Fl/2

δ2= 0 --> M = 0

δ3= Fl³/36EI --> M = (6EI/l²)*( Fl³/36EI) = Fl/6

 Il momento massimo è sui pilastri al primo piano, il secondo livello non si sposta (δ2= 0) quindi ha momento nullo, all’ultimo piano arriva un terzo del momento massimo.

MI SCUSI PER IL RITARDO

Per prima cosa mi determino la deformata ipotizzata in base alle forze in gioco, scegliendomi gli spostamentin relativi delta. Il secondo passo consiste nel fare un esploso della struttura che mi consideri tutte le reazioni agenti sui pilastri e sui traversi. di questi ultimi andremo a imporre l'equlilibrio ricordandoci che queste forze sono pari a 12EI/l³ x delta

In tal caso partendo dall'ultimo livello via via scendendo sino all'ultimo mi scrivo le equazioni di equilibrio tra le forze esterne e quelle di risposta agenti sui traversi in funzione dei rispettivi spostamenti delta che chiameremo d₁ d₂ e d₃

equazione 1: F - 12EI/h³ x d₃ x 4 = 0   F=48EI/h³ xd₃    d₃ = Fh³ /48EI

equazione 2: 2F+(48EI/h³ xd₃ = F) -12EI/h³ xd₂ x3 =0    2F+F -36EI/h³ xd₂ =0  3F=36EI/h³ xd₂  d₂ = Fh³ /12EI

equazione 3: -3F +36EI/h³ xd₂ +12EI/h³ xd₁ x2 +12EI/(h/2)³ xd₁ =0  -3F + 36EI/h³ xFh³ /12EI +24EI/h³ xd₁ +96EI/h³ xd₁    =0    -3F+3F +d₁x(120/h³ )=0   d₁ = 0

una volta ottenuti i valori di delta possiamo ridisegnare la deformata e sostituiti questi nei valori delle forze di taglio e momento determinare questi ultimi e tracciarne il grafico

M₃ = 6EI/h² x d₃ = Fh/8

M₂ = 6EI/h² x d₂ = Fh/2

T₃ = 12Ei/h³ x d₃ = F/4

T₂ = 12EI/h³ x d₂ = F

in allegato le immagini che graficizzano deformata, momentoe taglio

Esercizio del 17/05/2011