Esercizio 2
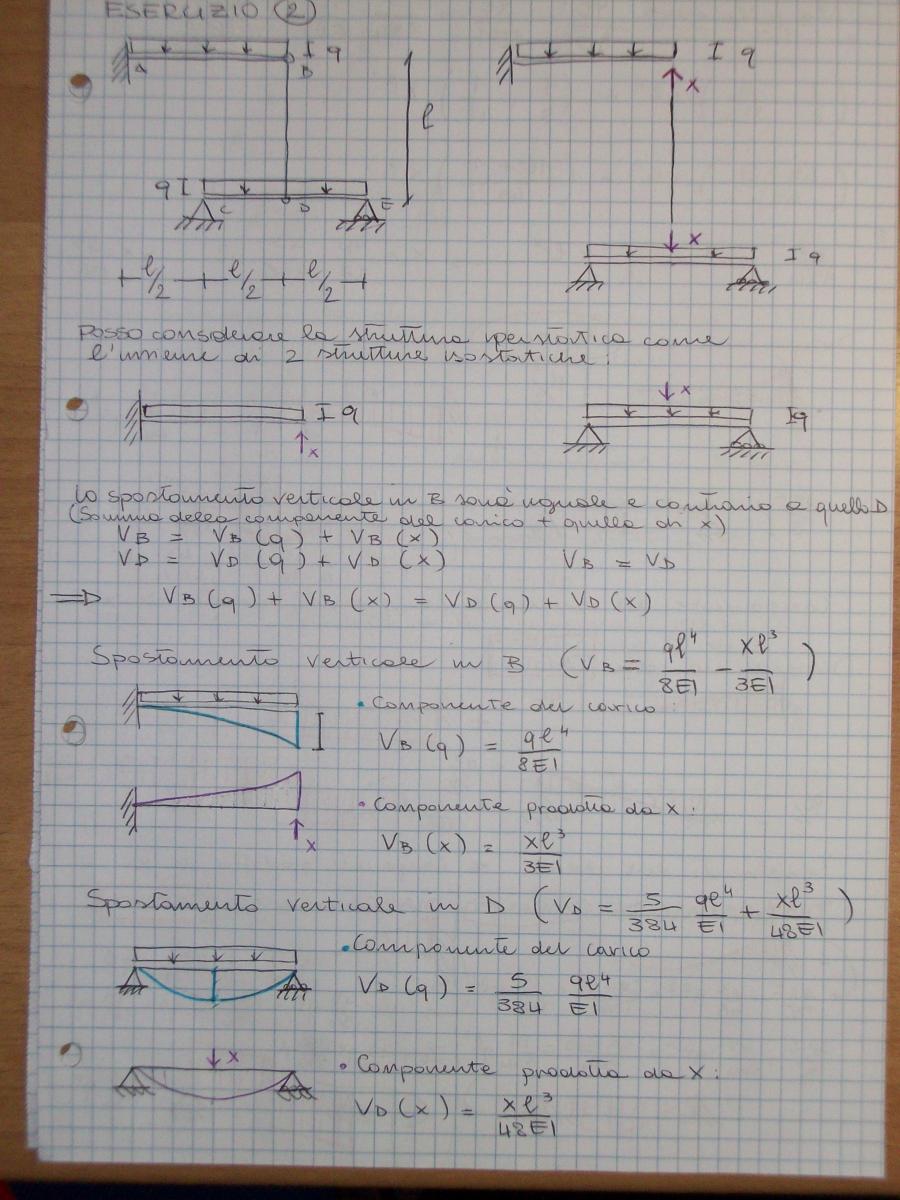
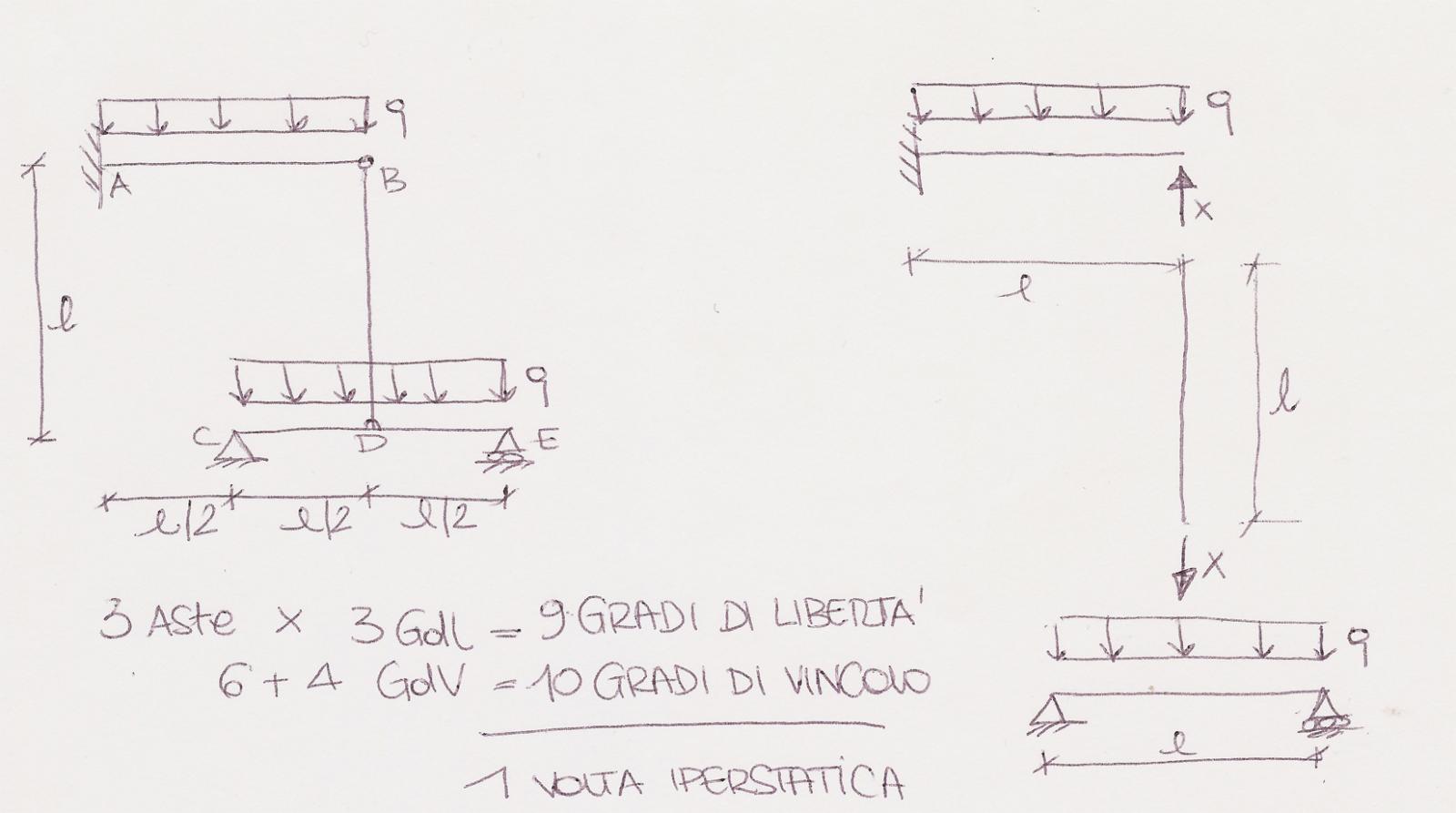
1) Mi trovo una struttura isostatica assimilabile a quella iperstatica data
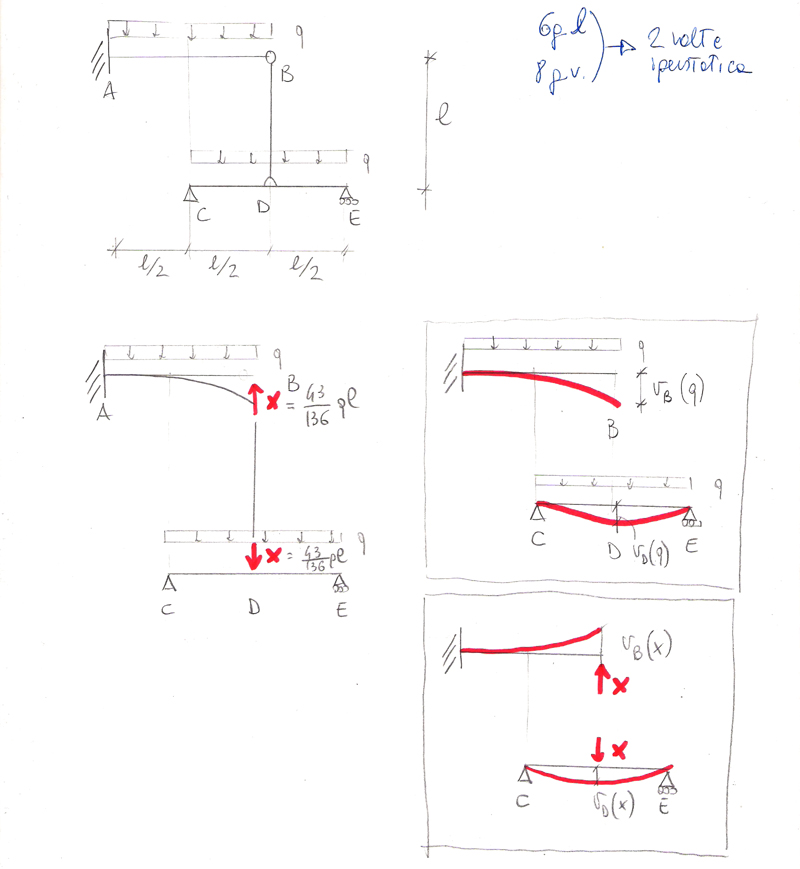
2) Individuo l’ incognita iperstatica (x) e calcolo lo spostamento verticale nei punti in cui insiste (B e D)
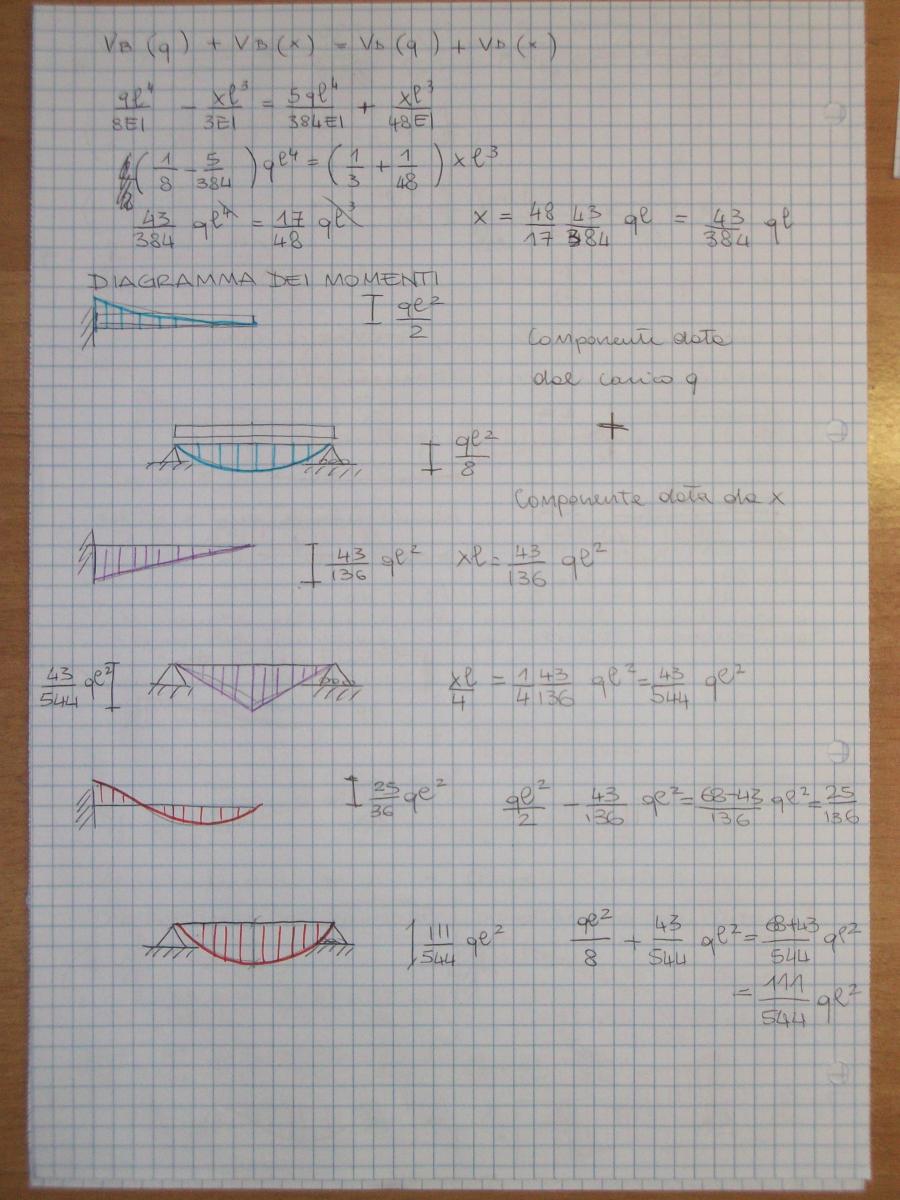
3) Risolvo l’equazione trovata (vB=vD) e trovo il valore di x
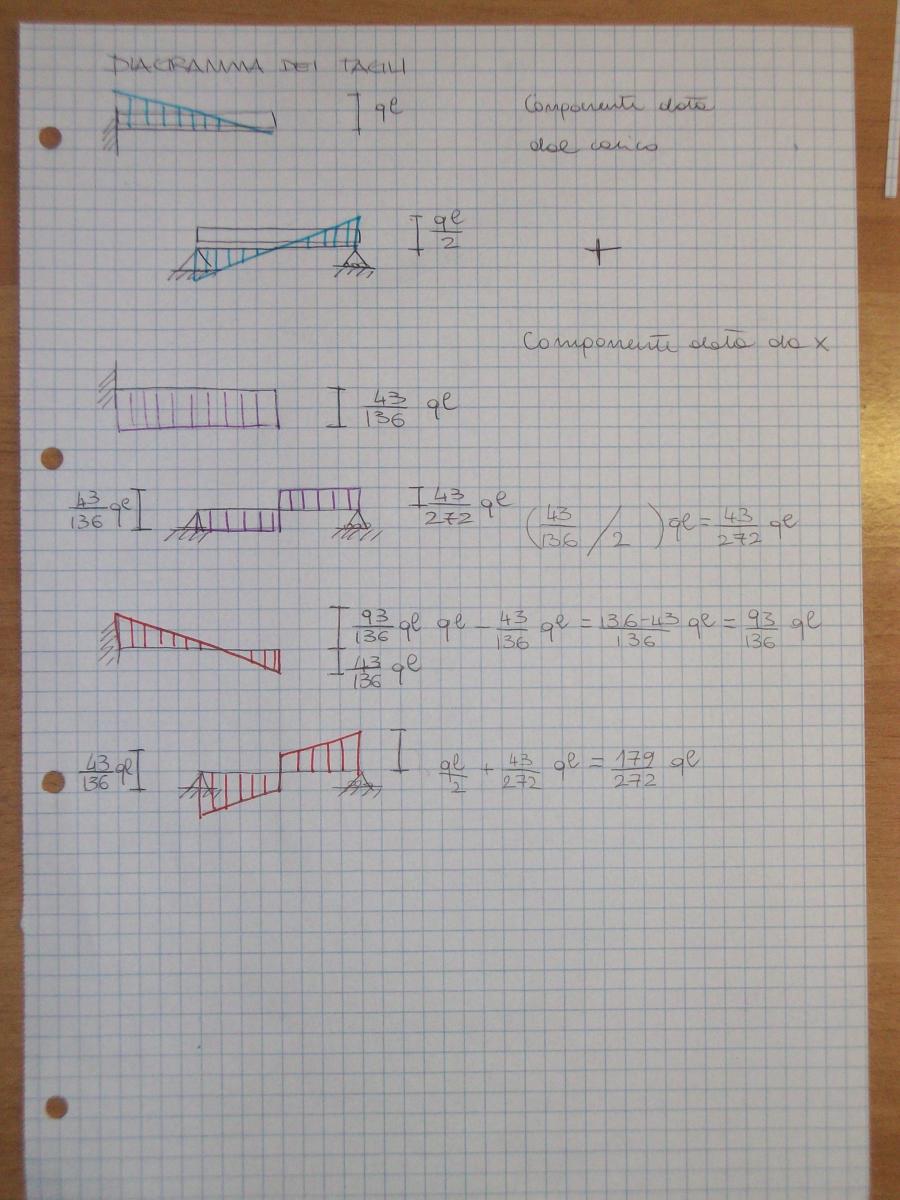
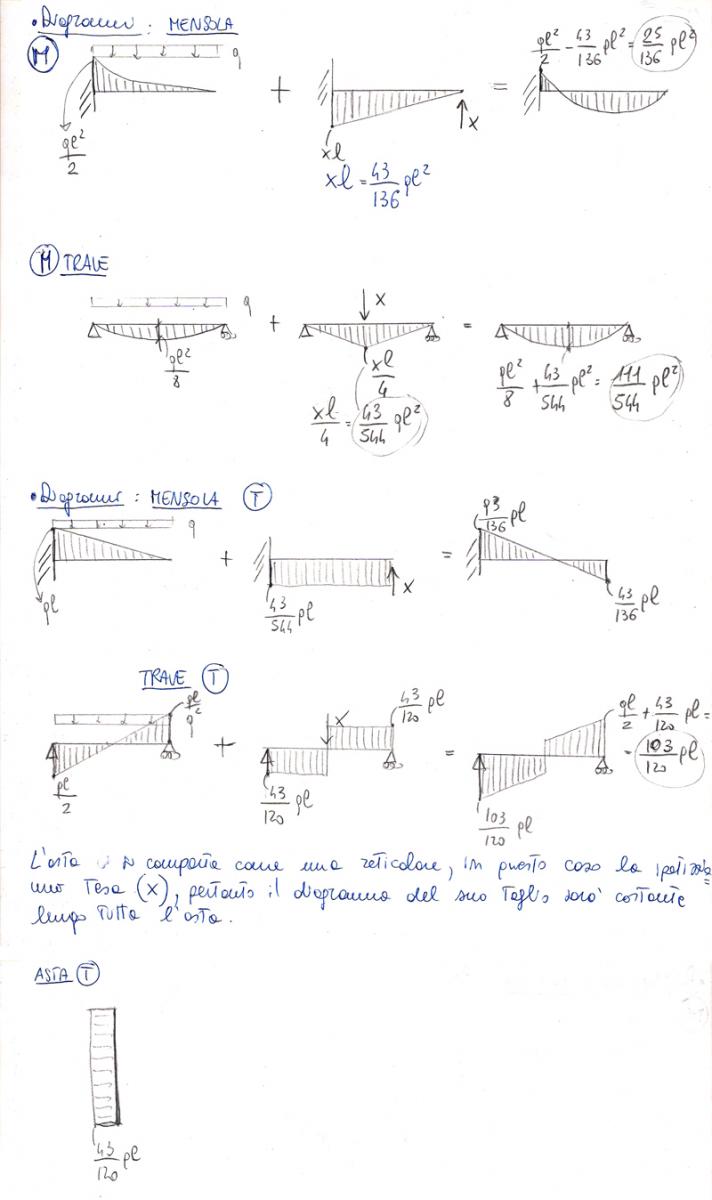
4) Studio il grafico del momento e del taglio
Esercizio 1
1) Mi trovo una struttura isostatica assimilabile a quella iperstatica data
2) Individuo le incognite iperstatiche (x1 e x2) e calcolo la rotazione relativa nei punti in cui insistono (B e C)
3) Metto a sistema le due equazioni trovate, al fine di ricavare il valore di x1 e x2
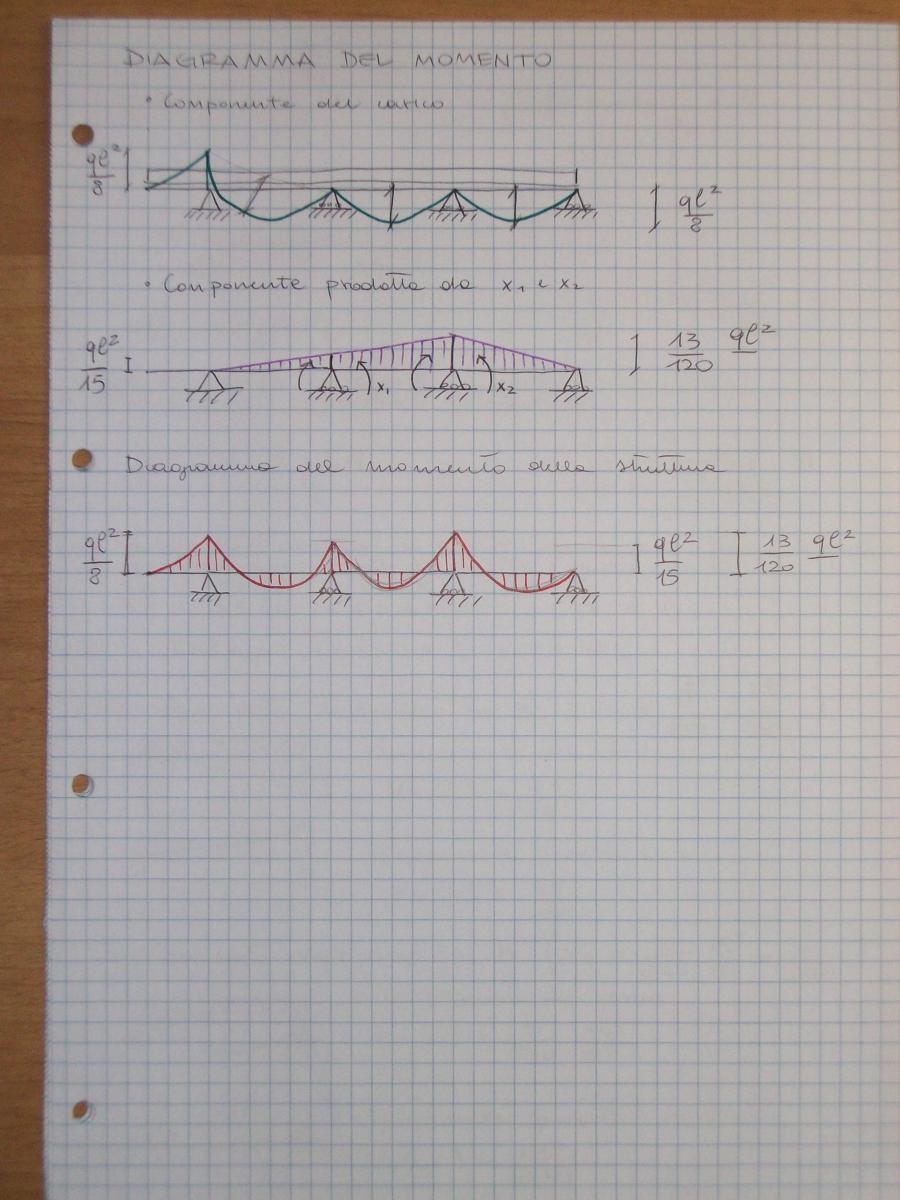
4) Studio il grafico del momento (dato dalla somma di due componenti: quella generata dal carico distribuito e quella dovuta alle incognite iperstatiche)


Metodo delle forze
Esercizio 1

Esercizio 2

Inviato da Anonimo (non verificato) il Mer, 27/04/2011 - 13:13
Metodo delle forze
Esercizio 1


Esercizio 2



ESERCIZIO 2 - METODO DELLE FORZE
Considero il pendolo (asta BD) indeformabile assialmente, quindi lo spostamento di B sarà uguale a quello di D
Asta A-B
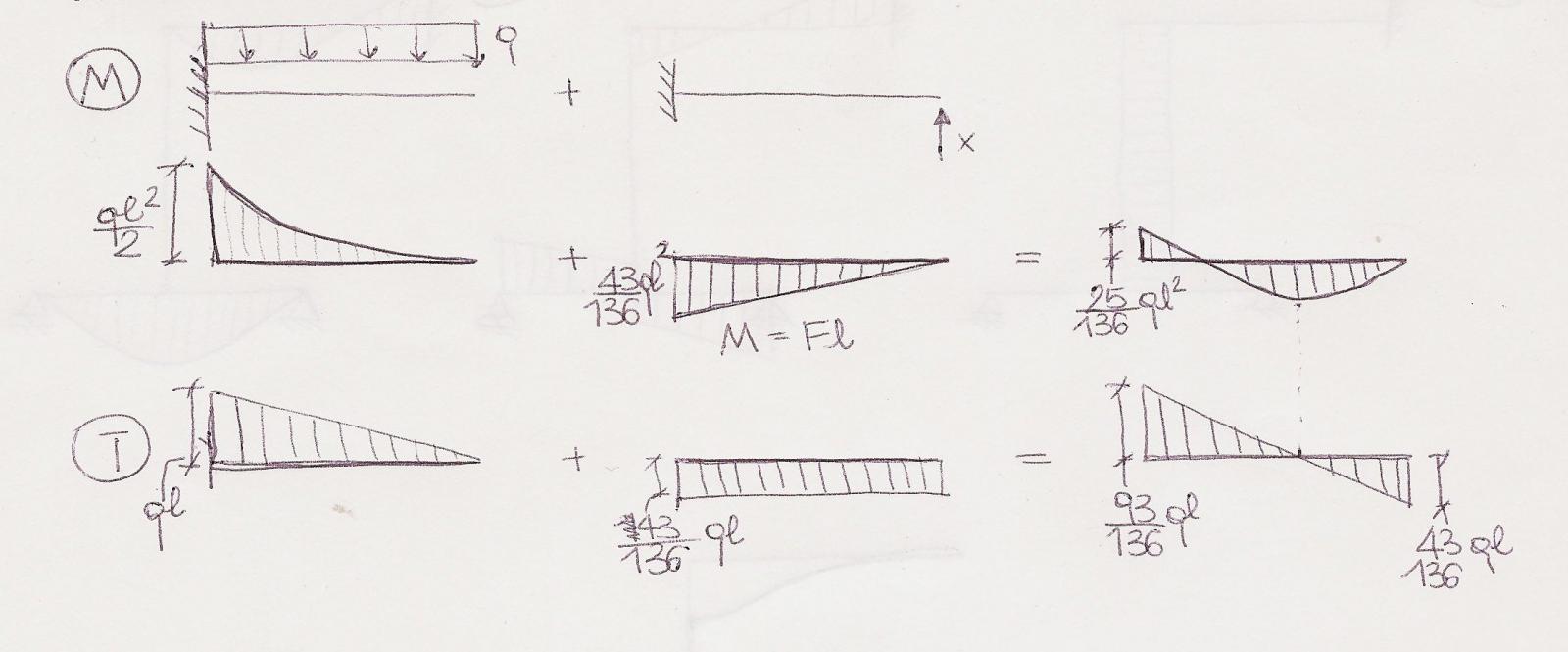
Asta C-E
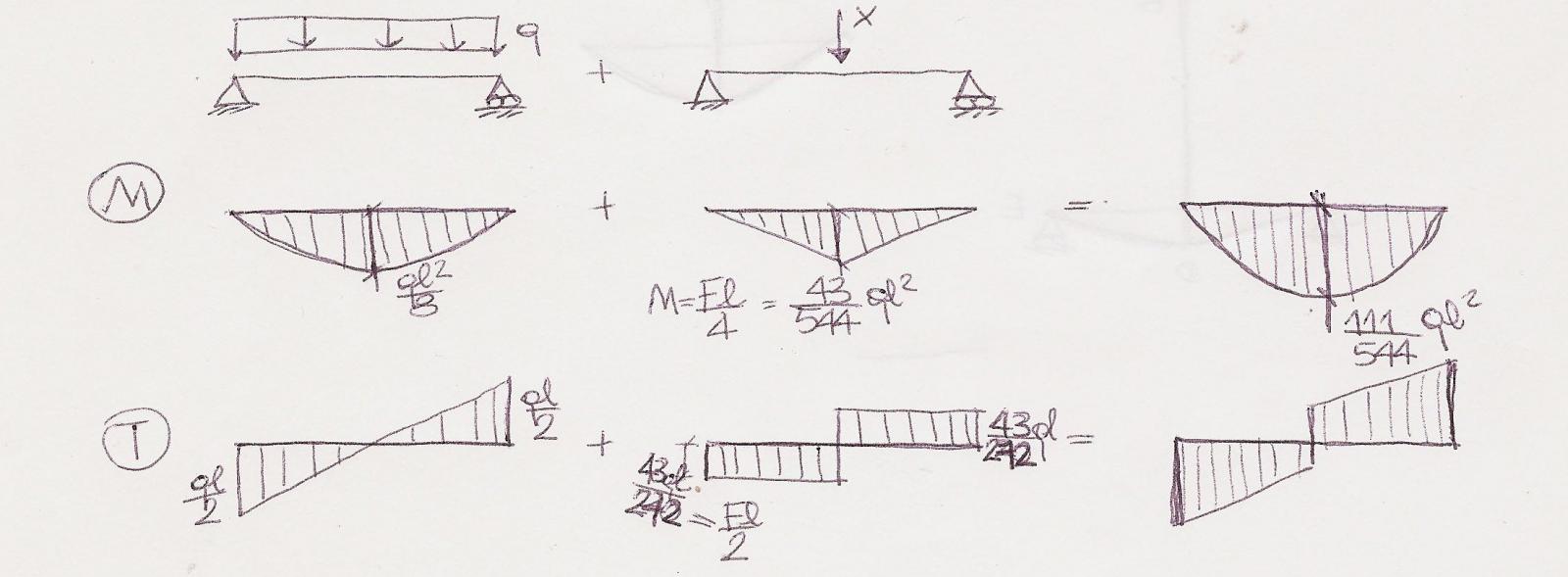
ESERCIZIO 1 - METODO DELLE FORZE
Impongo l'uguaglianza tra la rotazione di destra e di sinistra nei punti B e C
Trovo x1 e x2 impostando un sistema tra le due equazioni trovate
Diagrammi delle sollecitazioni (sovrapposizioni degli effetti)
La prima esercitazione l'ho erroneamente aggiunta il 04/04 come commento al primo intervento.
ESERCITAZIONE 2
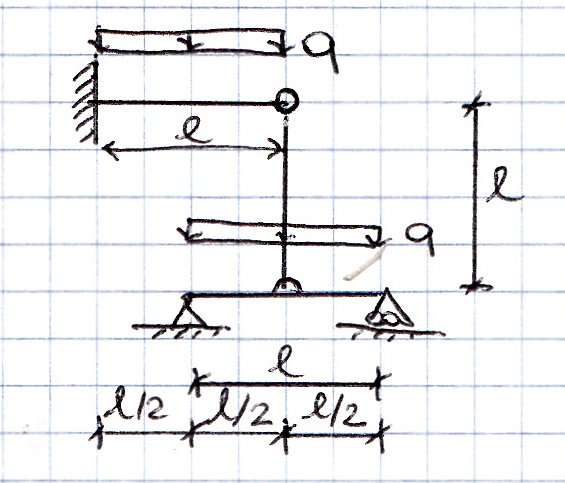
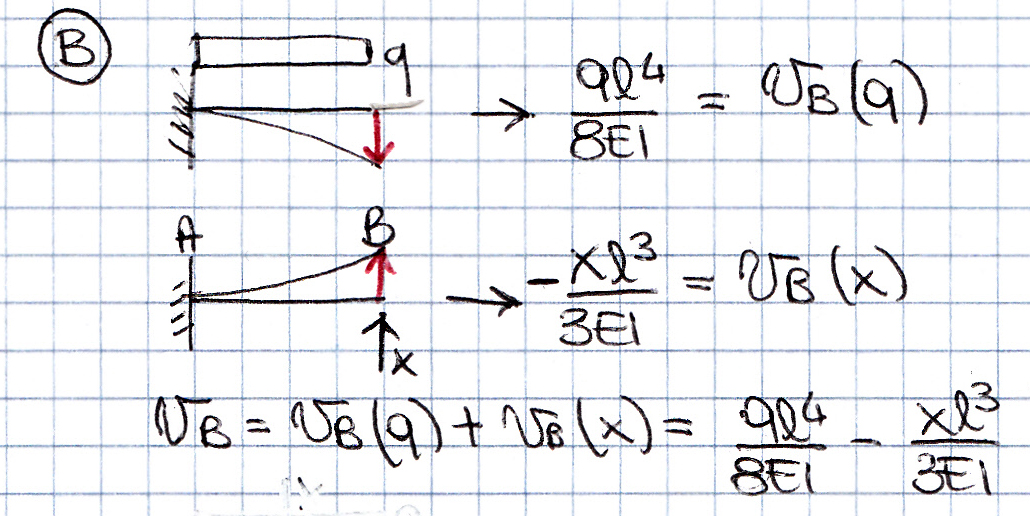
La struttura presa in esame è 1 volta iperstatica quindi per poterne studiare la deformazione le conferisco 1 GdL sostituendo l’asta BD con x, supponendo l’asta tesa. In questo modo ottengo due strutture isostatiche: la mensola con carico distribuito q e forza concentrata all’estremo B, x, e la trave appoggiata con carico distribuito q e forza concentrata in mezzeria x.
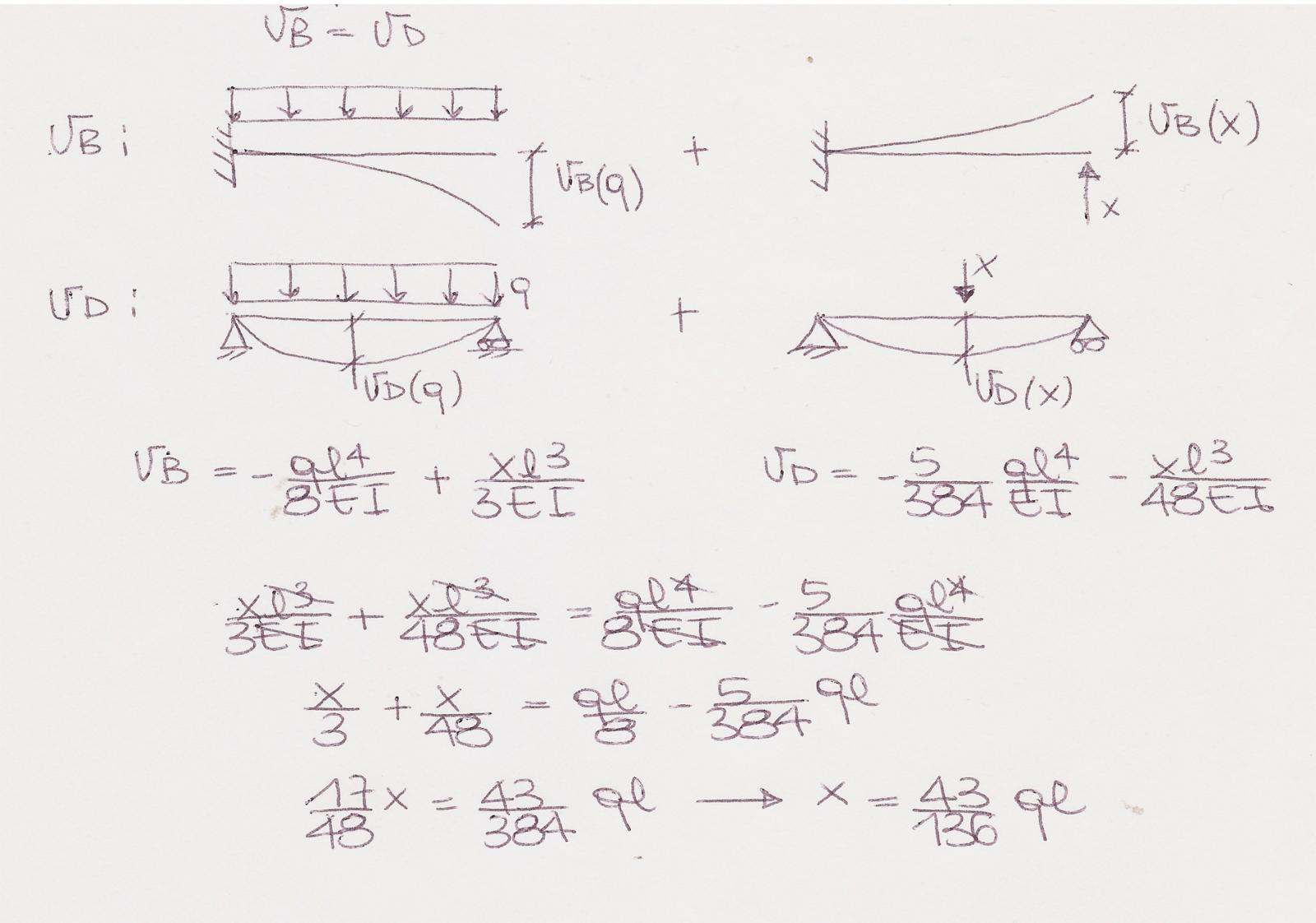
Dobbiamo porre come condizione vB = vC poiché abbiamo eliminato l’asta ma teniamo in considerazione la sua azione: impedisce l’allontanamento e l’avvicinamento dei punti B e D.
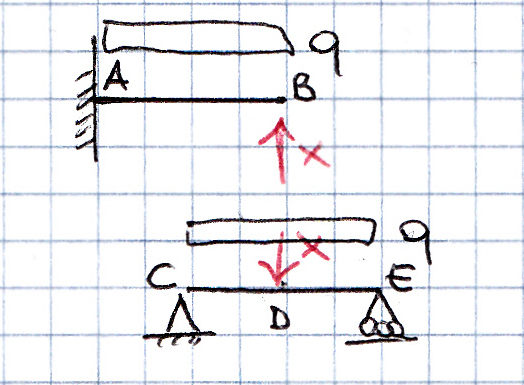
Punto B: lo spostamento relativo vB = vB(q) + vB(x) Risulta quindi: vB = ql4/8EI – xl3/3EI
Punto D: l lo spostamento relativo vD = vD(q) + vD(x) Risulta quindi: vD = 5ql4/384EI + xl3/48EI
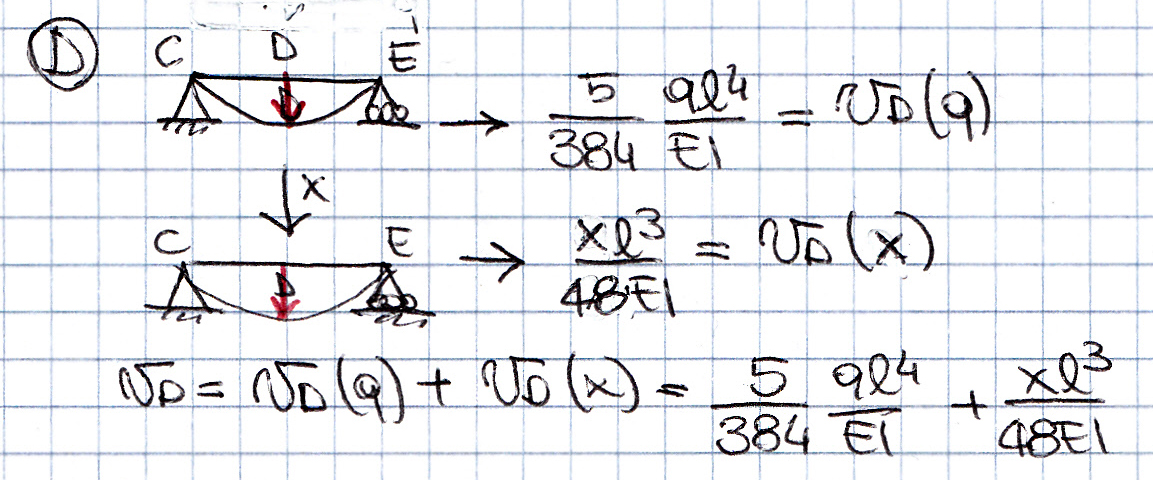
Posto vB = vD ottengo: x = 43ql2/136

DIAGRAMMA DEL MOMENTO
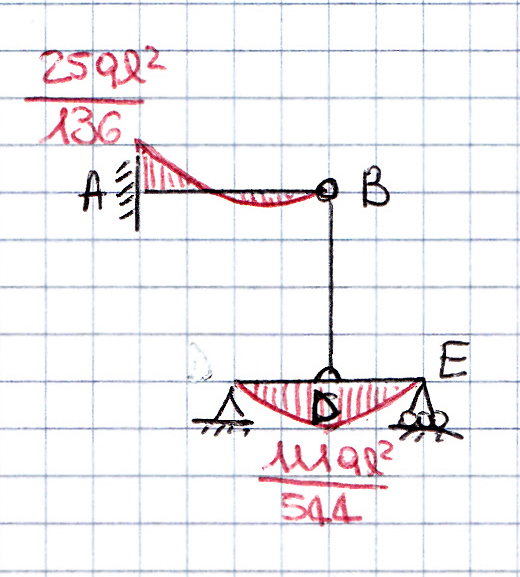
Verifica con SAP 2000
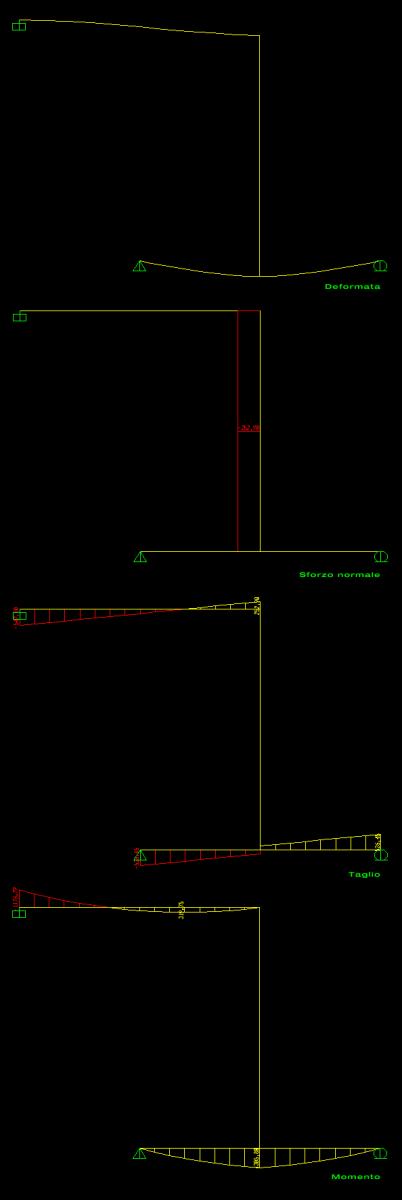
Inviato da silvia saggese il Mar, 26/04/2011 - 18:06
Pagine
Commenti recenti