SdC(b) (LM PA)

Tre ipotesi di trave doppiamente appoggiata (cerniera + carrello) con luce di 20 metri e carico distribuito di 20KN/m:

PRIMO CASO

Considero una semplice trave IPE. Il momento massimo si trova in mezzeria ed è pari a

(q*l^2)/8 = (20KN/m * 20^2m^2)/8 = 1000KN * m

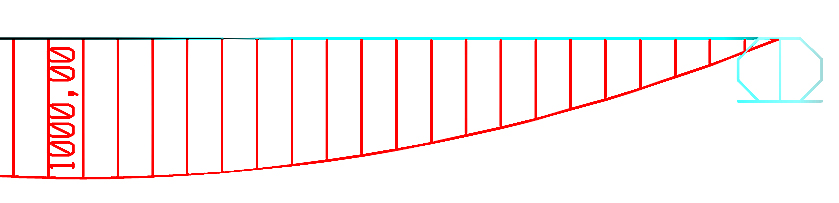
Sapendo che la sigma dell’acciaio è pari a 235 KN/n e ponendo n=1.2 posso applicare la formula

Mmax = sigma * Wmin      cioè       1000KN * m = 195.84 N/mm^2 * Wmin

Posso quindi calcolare Wmin = (10^7 N*cm)/(19584 N / cm^2) = 5106.2 cm^3

Sulle tabelle di dimensionamento la IPE più grande è la IPE 600 con una Wx = 3069 cm^3 inferiore al valore trovato.

SECONDO CASO

Prendo in considerazione una trave reticolare con passo di 2m e altezza di 2m. In questo caso ci sono sia aste tese che aste compresse quindi ai fini del calcolo del dimensionamento differenzio lo sforzo normale massimo a compressione da quello a trazione (poiché per il dimensionamento a compressione devo considerare l’instabilità euleriana).

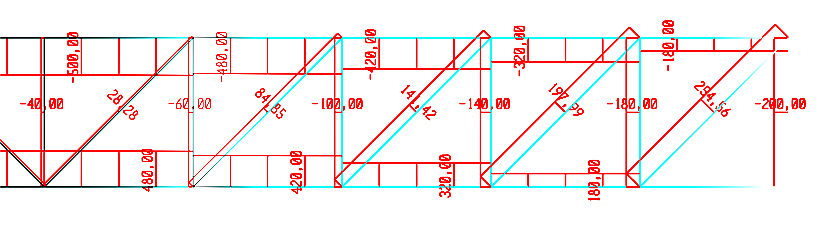
Considero prima le aste tese:

Nmax = 480 KN

Aammissibile = N / sigma = 480000N * n /  fyk = 480000 N * 1.2 / (235 N / mm^2) = 2451.06 mm^2

Scelgo quindi il profilato con sezione circolare cava con d x s = 76.1mm x 3.6 mm, area metallica = 8.2 cm^2, W = 14.2 cm^3

Considero ora le aste compresse:

Nmax = (q*l^2)/(8*h) = 500 KN

Aammissibile = N / sigma = 500000N * n /  fyk = 500000 N * 1.2 / (235 N / mm^2) = 2553.19 mm^2

Ora applico la formula per l’instabilità euleriana

Ncrit = (p^2 * E * Jmin) / Lo^2

N = 500000 N = Ncrit/n= [p^2 * (210000 N/mm^2) * Jmin] / 4800000 mm^2

Posso quindi calcolare Jmin = (4800000 mm^2 * 500000 N) / [p^2 * (210000 N/mm^2)] = 3639672 mm^4

Scelgo dalla tabella dei profilati la sezione con Jmin uguale o immediatamente superiore:

d x s = 139.7 x 4.0, area metallica = 17.10 cm^2, W = 56.20 cm^3, J = 393.0 cm^4

TERZO CASO

Considero una trave vierendeel con passo di 2m e altezza di 2m

Mmax = 96.37 KN * m

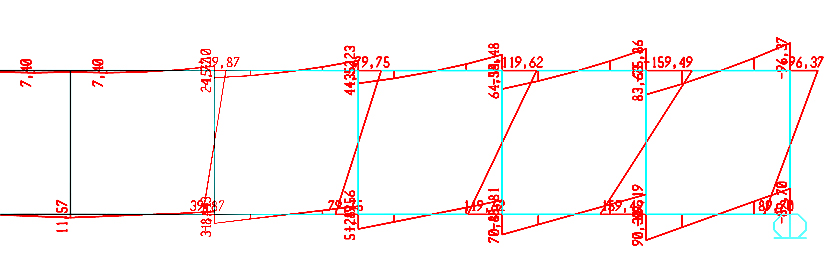
Nmax = 110 KN

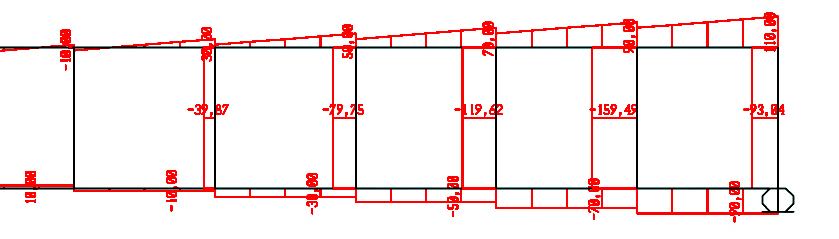
W = Mmax /sigma  cioè       96.37KN * m /(195.84/mm^2) = 492.09 cm^3

Scelgo dalla tabella dei profilati scatolari quadri a x s = 250mm x 8mm con W = 605,00 cm^3 e sezione metallica = 77.4 cm^2

Verifico che la sezione sia sufficiente affinchè [(N/A) + (M/W)] < s

(110 KN / 7740 mm^2) + [(96370 KN*mm)/605000 mm^3] = 173,49 N/mm^2 < 195.84 N/mm^2

La sezione è verificata.

DIMENSIONAMENTO TRAVE SEMPLICE

DIMENSIONAMENTO TRAVE RETICOLARE

DIMENSIONAMENTO TRAVE VIERENDEEL

L'esercizio prevedeva il dimensionamento delle travi in acciaio con 3 strutture diverse:

1)una trave appoggiata - appoggiata

2)una trave reticolare

3)una trave vierendel

L'acciaio scelto è di classe Fe360/235     (con un coefficiente di sicurezza=1,2)

Qui di seguito sono svolti gli esercizi relativamente il dimensionamento di tre tipologie diverse di travi in acciaio:

1. profilo IPE;
2. profilo tubolare cavo circolare;
3. profilo tubolare cavo quadrato.

DIMENSIONAMENTO trave semplice, doppiamente appoggiata:

DIMENSIONAMENTO trave reticolare:

DIMENSIONAMENTO trave Vierendeel: