News

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Esercitazione 1

Un accenno sulle Travature Reticolari

Le travature reticolari sono strutture composte da un insieme di aste appartenenti allo stesso piano che generano un forma in grado di coprire ampie luci. La generica travatura reticolare è caratterizzata da correnti superiori e correnti inferiori, montanti e diagonali. Inoltre la struttura reticolare prevede nel suo sistema un insieme di cerniere, “nodi”, che sono gli unici punti che ricevono le forze e le ridistribuiscono sulle aste attraverso le azioni di contatto, in questo caso solo attraverso gli sforzi assiali N perché sono gli unici ad agire su questo tipo di strutture. Altra peculiarità è che le aste possono essere tese o compresse a seconda del tipo di forze che agiscono sulla struttura o scariche se queste hanno solamente la funzione di completamento geometrico della struttura.

Travatura reticolare simmetrica

Questo tipo di travatura reticolare presenta un struttura regolare con dei carichi concentrati nei nodi e la sua geometria presenta una simmetria rispetto all’asse centrale, quello passante per il nodo D. Per questo motivo, prima di eseguire l’esercizio, si deduce che al fine di calcolare le azioni di contatto sulla trave, sarà necessario sezionare solamente metà struttura perché questa è simmetrica.                                                                               

Prima di procedere con il calcolo delle reazioni vincolari, verifico che la struttura sia isostatica attraverso la formula: V = L (gradi di vincolo = gradi di libertà)                                                                                                                          

I gradi di vincolo a loro volta sono: V = Ve + Vi   (Gradi di vincolo  = vincoli esterni + vincoli interni)              

I vincoli esterni sono 3, 2 per la cerniera (traslazione orizzontale e verticale) e 1 per il carrello (traslazione verticale); quelli interni invece si calcolano con la formula: 2 (n-1)(n numero di aste che la cerniera collega).                                                                                                                                                                          

Nodi A-H: 2 (2-1)= 2 x 2= 4                                                                                                                                         

Nodi B-G: 2 (3-1)= 4 x 2= 8                                                                                                                                         

Nodi C-D-E: 2 (4-1)= 6 x 3= 18; quindi i gradi di vincolo interni sono: 30 Vi + 3 Ve = V.                                       

Essendo V = L (struttura isostatica); allora L = 33.                                                                 

Un’ altra formula ancora più rapida per verificare l’isostaticità è: Ve + a = 2n(vincoli esterni + numero di aste = 2 numero dei nodi). In questo caso abbiamo 3+11=2 (7).                              

A questo punto possiamo calcolare le reazioni vincolari attraverso gli equilibri alle traslazioni orizzontale e verticale. Da questi otteniamo che Ru1= 0 perché non deve equilibrare alcuna forza orizzontale; mentre le reazioni Rv1 e Rv2 equilibrano le tre forze concentrate F quindi saranno pari a: Rv1=Rv2=3/2F.                                                    

Ottenuti i valori delle reazioni vincolari si può procedere al calcolo delle azioni di contatto sulla travatura reticolare attraverso due metodi:                                                                                                                                              

1)METODO DELLE SEZIONI DI RITTER                                                                                                                    

2) METODO DEI NODI                                                                                                                                          

1)con questo metodo si opera una sezione che tagli 3 aste NON CONVERGENTI SULLO STESSO NODO e si determinano le azioni di contatto su ogni asta attraverso gli equilibri alle traslazioni verticali e orizzontali, e l’equilibrio dei momenti rispetto ad un polo scelto;                                                                                              

2)con questo metodo invece si isolano i nodi della struttura e si calcolano le azioni di contatto solo attraverso gli equilibri alle traslazioni verticali e orizzontali.                                                                                                             

In entrambi i casi le azioni di contatto, di compressione o di trazione, sono raffigurate con semplici frecce la cui punta può essere uscente dall’asta/nodo o entrante nell’asta/nodo; la differenza tra i due metodi è che nel primo, quello delle sezioni, la freccia uscente dall’asta indica per convenzione la trazione quindi uno sforzo positivo, nel caso opposto indica compressione quindi sforzo negativo; nel metodo dei nodi il ragionamento è lo stesso in quanto le frecce uscenti dai nodi indicano la trazione e quelle entranti la compressione.                                                        Scegliendo il metodo delle sezioni di Ritter, analizzo il nodo B e attraverso l’equilibrio dei momenti rispetto al nodo C ricavo lo sforzo assiale

N1= -2F (il meno indica che il verso della freccia precedentemente ipotizzato di trazione, è di compressione quindi lo cambio). Eseguendo invece l’equilibrio dei momenti rispetto al nodo B ottengo lo sforzo assiale N3= 3/2 F (essendo positiva la forza, il verso della freccia ipotizzato è corretto, quindi di trazione). Infine eseguendo l’equilibrio alla traslazione verticale ottengo il valore dello sforzo assiale N2= F/2dato dalla scomposizione dello sforzo N2 nelle sue due componenti orizzontale e verticale.

Avendo già determinato lo sforzo assiale N3, analizzo il nodo A eseguendo l’equilibrio alla traslazione orizzontale. Da questo ricavo il valore dello sforzo assiale N4= -3/2 F, dato dalla scomposizione nelle sue due componenti orizzontale e verticale.

Infine studio l’ultima sezione di Ritter, quella che fa riferimento al nodo D e determino attraverso il momento rispetto al polo D e l’equilibrio alla traslazione verticale, gli ultimi due sforzi assiali N5= 5/2 F e N6= -F/2.

Attraverso il grafico elaborato dal software SAP, è possibile ottenere una conferma su quali siano i carichi conferiti a ciascuna asta e quali di queste siano compresse o tese. Ciò è possibile perché questo software ci permette di disegnare interamente la struttura assegnando alle singole aste i vincoli predisposti (cerniere, carrelli o incastri) nonché i carichi (distribuiti o concentrati) su qualsiasi trave o nodo. 

Il compito più grande svolto da SAP è di determinare la deformata qualitativa della struttura in esame che per strutture così semplici è abbastanza palese mentre per altre più complesse no.

Travatura reticolare asimmetrica                                                                    

Lo scopo di questo esercizio è quello di risolvere una struttura reticolare asimmetrica attraverso il METODO DEI NODI, precedentemente enunciato.

Come per quella simmetrica, anche qui dobbiamo preventivamente verificare l’isostaticità della struttura.   

V = L(gradi di vincolo = gradi di libertà)                                                                                     

V = Ve + Vi   (Gradi di vincolo  = vincoli esterni + vincoli interni)                                                   

2 (n-1) (n numero di aste che la cerniera collega)                                                                      

Nodi A-G: 2 (2-1)= 2 x 2= 4                                                                                                 

Nodi B-D-F: 2 (3-1)= 4 x 3= 12                                                                                            

Nodo E: 2 (4-1)= 6 x 1= 6                                                                                                         

Nodo C: 2 (5-1)= 8 x 1= 8 quindi i gradi di vincolo interni sono: 30 Vi + 3 Ve = V     V=L=33

Ora possiamo procedere al calcolo delle reazioni vincolari attraverso gli equilibri alle traslazioni orizzontale e verticale e all’equilibrio dei momenti rispetto ad un polo prefissato. Dall’equilibrio alla traslazione orizzontale otteniamo che Rub=Rug quindi sappiamo che le due reazioni sono uguali e opposte; dalla traslazione verticale invece troviamo il valore di Rvb= 2F verso l’alto, quindi a bilanciare le due forze concentrate F, infine attraverso l’equilibrio dei momenti rispetto al polo in A stabiliamo il valore di Rub e Rug= 3F.                                                     

A questo punto, avendo calcolato tutte le reazioni vincolari, procediamo al calcolo delle azioni di contatto attraverso il METODO DEI NODI. Assegniamo a F il valore di 10KN e a L il valore di 1m.  Ricordo che essendo una travatura reticolare, le azioni di contatto che andremo a calcolare saranno tutti sforzi normali N.    

Partiamo dal nodo B perché sono note le reazioni vincolari Rub (30KN) e Rvb (20KN) e facciamo gli equilibri alle traslazioni orizzontale e verticale per determinare gli sforzi N1, N2 e N3. Eseguendo i calcoli ci rendiamo subito conto che non è possibile ottenere dei risultati perchè i due equilibri (traslazione orizzontale e verticale) prevedono due sistemi ognuno in due incognite quindi irrisolvibile.                                                                                                                   

Proviamo quindi con il nodo G, altro nodo dove insiste la reazione vincolare Rug (30KN) e qui notiamo che per l’equilibrio alla traslazione verticale abbiamo solo la componente verticale dello sforzo assiale N10 che non è bilanciata da alcuna forza quindi il suo contributo è 0 sia in direzione orizzontale che verticale, ovvero l’asta è SCARICA (N10= 0). A questo punto possiamo facilmente calcolare lo sforzo N11= 30KN.

Procedendo verso sinistra vi è il nodo F dove abbiamo le due traslazioni, verticale e orizzontale, espresse ognuna con un sistema ad una incognita quindi banalmente risolvibile. Da questo infatti ricaviamo N8= 30KN e N9= 10KN.

Nel nodo E invece, scompongo lo sforzo assiale N7 nelle sue due componenti (orizzontale e verticale) ottenendo il valore di N7= 10KN e di conseguenza sfrutto la sua componente orizzontale pari a 10KN per calcolare lo sforzo assiale N6= -10KN (il meno, come al solito, indica che bisogna cambiare il verso della freccia).                                                                                       

Il nodo D invece presenta nel suo equilibrio un’altra asta scarica, eseguendo infatti gli equilibri alle due traslazioni orizzontale e verticale, si ottengono N1= -10KN e N5= 0.                                                                                                                        

Infine dal nodo B otteniamo altri due sforzi assiali N2= -20KN e N3= 0 mentre dal nodo C, ultima cerniera rimasta, deduciamo dai calcoli che N4= 0.               

Una volta determinati i valori di N su ogni singola asta, ridisegno la struttura su SAP facendo uso della griglia alla quale abbiamo precedentemente assegnato le campate lungo l’asse x (ascissa) e lungo l’asse z (ordinata) e i loro valori in metri. Impongo, fissati gli appoggi della travatura (cerniera e carrello), che ogni asta sia incernierata all’altra ma che venga impedita la trasmissione del momento da un’ asta all’altra. Infine assegno i carichi concentrati sui nodi C ed F e faccio partire l’analisi della deformazione.      

Esercizi sugli archi a tre cerniere e vari

Esercizio n°1

In questo esercizio, è stata analizzata una “mensola” alla quale sono sovrapposti due carichi assiali: ql (carico concentrato all’estremo libero) e q (carico distribuito lungo la trave ma solo nel tratto che va dall’incastro fino a l). Come sappiamo i carichi concentrati e distribuiti danno risultati ben diversi che ora vedremo.                                                                                                                        

Per prima cosa notiamo che i gradi di vincolo e di libertà coincidono: v= l (3=3). Determiniamo quindi le reazioni vincolari che in questo caso sono molto semplici da calcolare in quanto, avendo solo forze assiali, non sono previsti l’equilibrio alla traslazione verticale e ai momenti perchè non gravano forze verticali o momenti concentrati sulla struttura.

 

Dalle reazioni vincolari infatti otteniamo che dall’equilibrio alla traslazione orizzontale (ΣFx = 0) Rua= 2ql reazione derivante dall’incastro e atta ad equilibrare le due forze mentre dall’equilibrio alla traslazione verticale (ΣFy = 0) Rva= 0 perché non deve equilibrare alcuna forza verticale e così anche (ΣMa = 0) Ma=0.

Analizzando le azioni di contatto sulla trave possiamo quindi dire che l’unica tensione che si sviluppa all’interno della trave è quella Normale ed è N=2ql.

Analizzando la struttura ai “bordi”, notiamo che all’incastro la N= 2ql data dalla sovrapposizione del carico concentrato ql, che dà un grafico di N costante, e del carico distribuito q, che invece dà un grafico di N lineare in quanto varia dalla mezzeria all’incastro. All’estremo libero invece, lo sforzo normale è equilibrato da una sola forza di trazione, il carico concentrato ql, che determina di conseguenza un grafico costante di N su tutta la lunghezza della trave.

Esercizio n°2

L’argomento di questo esercizio è una trave su 3 appoggi con due momenti concentrati sull’appoggio centrale che tuttavia funge da cerniera quindi non permette il passaggio del momento flettente (o “di continuità”) e di conseguenza nemmeno la rotazione relativa, rotazioni uguali a sinistra e a destra della cerniera (φs=φd). Anche per questa struttura, essendo isostatica, v= l.

Dagli equilibri alle traslazioni orizzontali, verticali e di momento, otteniamo che Rua= 0 in quanto non insistono forze assiali sulla struttura; Rva= Rvb e Rvb= Rvd in quanto coppie di forze che controbilanciano i due momenti esterni c. La coppia Rva-Rvb è antioraria per controbilanciare c orario mentre la coppia Rvb-Rvd è oraria perché deve controbilanciare l’altro momento antiorario c. In valore assoluto Rva, Rvb e Rvd hanno tutte lo stesso valore c/l.

Dal grafico del taglio si può notare come vi sia un salto nel punto in cui sono concentrati i due momenti pari proprio a c, il valore del momento. Questo comporta nel grafico del momento un punto angoloso (di spigolo o “cuspide”) che corrisponde ad un cambio di pendenza in quanto punto di incrocio dei due momenti lineari negativi perché tendono le fibre superiori della trave.

Esercizio n°3

Analizziamo ora un arco a 3 cerniere con una forza concentrata F in mezzeria, ovvero sulla cerniera. Prima di svolgere l’esercizio però è necessario fare alcuni ragionamenti di carattere qualitativo che permettono di risolvere più facilmente e velocemente l’equilibrio della struttura.

Come sappiamo, l’arco a tre cerniere è chiamato così perché presenta, oltre quelle alla base, anche una terza cerniera collocata sul tratto orizzontale che ci da 2 reazioni vincolari verticali e 2 orizzontali, tutte uguali e opposte. In questo caso però, essendo il portale simmetrico sia per geometria che per carico, la forza verticale F è equilibrata dalle sole 2 reazioni verticali date dalle 2 cerniere agli appoggi perché le reazioni della cerniera centrale essendo opposte causerebbero solo antisimmetria.

Spesso per le strutture come i portali, può risultare utile analizzare la struttura per porzioni più ridotte come in questo caso dove il portale, essendo simmetrico, è stato diviso a metà rendendo più semplice e rapido il calcolo delle reazioni vincolari. Dal primo corpo infatti troviamo che Rva= F/2, il risultato è giusto in quanto è l’unica reazione verticale che deve equilibrare la forza F/2 mentre dall’equilibrio dei momenti rispetto al polo A ricaviamo che Rub=Rua= Fl/2h. Questo ci fa capire che le reazioni orizzontali non sono nulle come invece si potrebbe pensare non essendoci carichi orizzontali; esse infatti servono ad equilibrare il momento orario generato dalla forza F per il braccio l/2. Allo stesso modo nel secondo corpo troviamo che Rub=Ruc= Fl/2h eRvc= F/2. Trovate le reazioni vincolari, analizziamo le azioni di contatto sul portale. Per fare ciò utilizziamo il metodo qualitativo dei “bordi”. Partendo infatti dalla cerniera in A troviamo che lo sforzo N è costante e di compressione in tutti i tratti ma assume il valore N= F/2 sui tratti verticali e N= Fl/2h sul tratto orizzontale. Anche il taglio presenta un grafico costante nei due tratti verticali pari a T=Fl/2h, positivo nel primo tratto verticale e negativo nel secondo; nel tratto orizzontale invece, vi è un grafico costante del taglio T=F/2, negativo nel primo tratto e positivo nel secondo mentre sulla cerniera, essendoci la forza concentrata F, vi sarà un salto pari alla forza F.

Infine nel grafico dei momenti vi sono andamenti lineari, dovuti ai grafici costanti del taglio, pari a M=Fl/2. I momenti sono tutti negativi in quanto tendono le fibre superiori e vi è un punto angoloso che coincide con la  cerniera orizzontale che è dovuto al salto del taglio.

Attraverso il software di calcolo SAP è stato possibile riscontrare gli stessi risultati  per le azioni di contatto e la deformata qualitativa. Questo infatti, essendo uno strumento immediato e semplice da utilizzare, spesso è stato utile anche come punto di partenza per risolvere strutture complesse che a mano avrebbero richiesto parecchio tempo. Non è il caso dei portali.

DEFORMATA QUALITATIVA                                                                               GRAFICO DEL TAGLIO

                            

GRAFICO DELLA NORMALE                                                                         GRAFICO DEL MOMENTO

                                             

 

Esercizio n°4

Svolto il portale con il carico concentrato in mezzeria, possiamo passare ad un portale più complesso per il quale assegneremo anche dei valori numerici al carico q e alle luci l e h.

q=100KN/m  h=10m  l=5m

In questo caso può essere utile analizzare il portale in due parti separate e farne l’equilibrio dei momenti rispetto ai poli A e B. Dai due equilibri ricaviamo che Ruc= 250KN e Rvc= 500KN.

A questo punto, una volte determinate Ruc e Rvc, con le equazioni di equilibrio alle traslazioni verticali e orizzontali dei due corpi, posso ricavare velocemente Rva, Rua, Rvb e Ruc.

Dall’equilibrio alla traslazione orizzontale del primo corpo ottengo infatti che:                                

Rua= 1000-Ruc (250KN)= 750KN mentre dall’equilibrio alla traslazione verticale ottengo che       

-Rva= Rvc (500KN) quindi anche Rva=500KN.

Dall’equilibrio alla traslazione orizzontale del secondo corpo ottengo che:                                   

Ruc (250KN)= -Rub quindi Rub= 250KN mentre dall’equilibrio alla traslazione verticale ottengo che –Rvc (500KN)= Rvb quindi anche Rvb= 500KN.                                                                  

Ultimo step sono le azioni di contatto dalle N,T e M. Dallo sforzo normale otteniamo un valore costante per i tratti ascendenti pari a N= 500KN positivo nel primo tratto e negativo nel secondo, mentre in quello orizzontale lo sforzo normale è costantemente positivo e pari a N= 250KN. Dal grafico del taglio invece otteniamo dei grafici più particolari, nel primo tratto verticale infatti il grafico ha un andamento lineare o “a farfalla”, effetto del carico distribuito che assume in A il valore T= 750KN e al nodo T= 250KN. Sul tratto orizzontale invece l’andamento è costante ed è pari a T=500KN mentre sul secondo tratto verticale il taglio assume un valore negativo pari a T=250KN.

Il momento invece presenta un andamento parabolico positivo (fibre tese sotto) nel primo tratto verticale e il valore massimo lo assume dove il taglio è nullo (perché il momento è la derivata del taglio) mentre al nodo termina con un valore di M= 2500KN che viene ribaltato sul tratto orizzontale dove invece l’andamento è a farfalla. Infine sul secondo tratto verticale vi è un andamento lineare negativo (fibre tese sopra) che mantiene al nodo il valore di M= 2500KN e che rappresenta la continuità tra tratto orizzontale e verticale.

DEFORMATA QUALITATIVA                                                                         GRAFICO DELLA NORMALE

     

GRAFICO DEL TAGLIO                                                                             GRAFICO DEL MOMENTO

 

Esercizio n°5

Come per il portale con un carico distribuito, analizziamo adesso il portale con due forze concentrate F.

       

Anche per questa struttura è vantaggioso analizzare le due parti che la compongono separatamente ma solo per le reazioni orizzontali Rua, Rub e Ruc. Infatti per le reazioni verticali Rva e Rvb, non dovendo controbilanciare alcuna forza, è possibile fare il solo equilibrio dei momenti rispetto ad un polo scelto (A in questo caso) e determinare i valori delle singole reazioni. Rva=Rvb= Fh/2l.

Dalla prima parte otteniamo che Rvc (reazione della cerniera interna)= Fh/2l ad equilibrare la reazione Rva. Invece dalla sommatoria dei momenti rispetto al polo C ricaviamo la reazione    Rua= -F quindi cambio il verso che è giustamente opposto a quello della forza F. Per il secondo tratto della struttura andrà fatto lo stesso ragionamento della prima parte ricavando l’ultima reazione incognita che è Rub= F.

Dai grafici delle azioni di contatto notiamo che i due tratti verticali sono sollecitati da uno sforzo N= Fh/2l pari alle reazioni vincolari Rva e Rvb. Il primo positivo perché di trazione, il secondo negativo di compressione. Sul tratto orizzontale non vi sono sforzi normali in quanto non vi sono forze che agiscono sull’asse della trave e le due forze F concentrate sono applicate ad h/2 creando così un salto nel grafico del taglio. Rua e Rub generano un grafico di T costante e negativo ma fino ad h/2 dove le forze concentrate F generano il salto. Sul tratto orizzontale invece il taglio è costantemente T= Fl/2h ed è generato dalla coppia Rva e Rvb.

Analizzando invece il grafico dei momenti riscontriamo sui tratti verticali un andamento lineare da 0 ad h/2 che corrisponde ad un grafico costante del taglio, ad h/2 avviene il salto nel taglio quindi un punto di spigolo nel grafico dei momenti che implica un cambio di pendenza della retta che diventa verticale assumendo un valore di M= Fh. Sul tratto orizzontale invece il momento si annulla nella cerniere interna e assume un andamento a farfalla del valore di M=Fh e tendendo le fibre inferiori nel primo tratto e superiori nel secondo.

DEFORMATA QUALITATIVA                                                                              GRAFICO DEL TAGLIO

GRAFICO DELLA NORMALE                                                                           GRAFICO DEL MOMENTO

                                                 

Esercizio n°6

Per terminare lo studio sui portali analizziamo invece un particolare arco a 3 cerniere chiamato “portale zoppo” (ovvero le cui altezze variano nei due tratti verticali).

             

Per determinare le reazioni vincolari sono stati eseguiti due equilibri ai momenti rispetto ai poli A e C che messi a sistema hanno reso più semplice il calcolo delle reazioni vincolari della cerniera centrale, Rub e Rvb. Una volte determinata Rvb, i corpi sono stati analizzati separatamente e quindi attraverso l’equilibrio alla traslazione verticale è stato possibile determinare i valori delle altre due reazioni Rva e Rvc entrambe di valore Fh/2l. Anche per le reazioni orizzontali i corpi sono stati studiati separatamente infatti dall’equilibrio alla traslazione orizzontale del primo corpo abbiamo ottenuto Rua= 2/3F; mentre dall’equilibrio alla traslazione orizzontale del secondo corpo la reazione Ruc è proprio uguale a Rub, Rub=Ruc= F/3.

Come si nota dal grafico delle azioni di contatto, nella struttura in esame si genera un sforzo Normale costante pari Fh/6l di trazione nel primo tratto e di compressione nel secondo. Sul tratto orizzontale invece il valore di N è negativo perché di compressione e pari a F/3.                                       

Nel grafico del Taglio invece è facilmente distinguibile il salto dovuto alla forza concentrata F applicata ad h/2 che da un T=  -2/3F e un T= F/3 mentre sul tratto orizzontale il grafico è costantemente positivo e pari a T= Fh/6l mentre sul secondo tratto verticale è pari a T= F/3.         

Nei portali in ultima analisi possiamo quindi dire che gli sforzi Normali verticali diventano di Taglio sui tratti orizzontali e viceversa per la continuità del nodo. Allo stesso modo i momenti assumono gli stessi valori nei nodi perché sono proprio questi i punti dove il momento flettente viene trasferito da un tratto orizzontale ad uno verticale.                                                

Il punto più interessante nel grafico dei Momenti coincide con il punto in cui avviene il salto nel Taglio che causa nel grafico dei momenti un punto angoloso o di cuspide e quindi un cambio di pendenza della retta o meglio di derivata nulla.

DEFORMATA QUALITATIVA                                                                            GRAFICO DEL TAGLIO

                         

          GRAFICO DELLA NORMALE                                                          GRAFICO DEL MOMENTO

              

 

                                       

Esercitazione 2

L’argomento di questa esercitazione è il progetto di una trave dimensionata con il sussidio del foglio elettronico excel da cui ho potuto ricavarne un dimensionamento adeguato. L’edificio scelto è il progetto di Laboratorio 1 di una casa unifamiliare a Fiumicino e ho stabilito di progettare la trave del solaio maggiormente sollecitata nei tre materiali: legno, acciaio e cls.    

SOLAIO IN LEGNO

Per questo tipo di solaio i passi da eseguire sono i seguenti:

1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)

2)calcolo delle dimensioni del travetto in legno a partire da un dato ipotizzato, la base e relativa verifica.

3)calcolo delle dimensioni della trave in legno a partire da un dato ipotizzato, la base e relativa verifica.

Progetto della Trave sull’allineamento B2-B3

Progetto dei travetti di interasse 1m e luce 2.2m

Calcolo dei carichi per i travetti

Qs = 0,21 KN/mq Carico Strutturale

Assito in legno (s = 0.035) P = V x g = Volume x Peso specifico = (1m x 1m x 0,035m) calcolato per un’area di 1m x 1m) x 6KN/mc

Qa = 2KN/mq Sovraccarico accidentale per una civile abitazione

Qp = 1,73KN/mq Carico permanente non strutturale

Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq

Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq

Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq

Caldana (s= 0,04) = 10KN/mc = 0,4KN/mc

Impianti 0,5KN/mq

Q tot= 0,21+2+1,73= 3,94KN/mq Carico totale al mq

A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:

3,94KN/mq x 1m = 3,94KN/m

Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8; impostate poi la resistenza a snervamento fmk e il suo coefficiente moltiplicativo kmod, ottengo la tensione di progetto fd.

Adotto una base ragionevole pari a 8cm e ottengo l’altezza attraverso la formula:             

h = (6 x M x 1000/(bfd ))^0,5

Verifica del travetto

Ottenute le dimensioni del travetto, aggiungo al carico strutturale quello dei travetti

(0,08m x 0,15m x 6KN/mc)/1m = 0,072KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.

Q’s = 0,21+0,072= 0,282KN/mq

Momento = ql^2/8= (4,012 x 2,2 x 2,2)/8= 2,427KNm

h’= (6M/bfd )^0,5 = (6 x 2,43 x 1000/8 x 9,66)^0,5= 13.7cm il dimensionamento precedentemente eseguito è corretto Trave GH28 8x15

Progetto della trave di interasse 2,2m e luce 4,075m

Calcolo dei carichi per la trave

Qs = 0,282KN/mq Carico Strutturale

Assito in legno (s = 0.035) P = V x g = Volume x Peso specifico = (1m x 1m x 0,035 m) calcolato per un’area di 1m x 1m) x 6KN/mc -> 0,21 KN/mq

Travetti in legno (0,08m x 0,15m x 6KN/mc)/ 1m = 0,072KN/mq

Qa = 2KN/mq Sovraccarico accidentale per una civile abitazione

Qp = 1,73KN/mq Carico permanente non strutturale

Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq

Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq

Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq

Caldana (s= 0,04) = 10KN/mc = 0,4KN/mc

Impianti 0,5KN/mq

Q tot= 0,282+2+1,73= 4.012KN/mq

Come per i travetti, inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:

3,94KN/mq x 2,2m = 8,826KN/m

Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8; impostate poi la resistenza a snervamento fmk e il suo coefficiente moltiplicativo kmod, ottengo la tensione di progetto fd.

Adotto una base ragionevole pari a 15cm e ottengo l’altezza attraverso la formula:                            

h = (6 x M x 1000/(bfd ))^0,5

Verifica della trave

Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave        

(0,15m x 0,30m x 6KN/mc)/2,2m = 0,123KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.

Q’s = 0,282+0,123= 0,405KN/mq

Momento = ql^2/8= (9,097 x 4,075 x 4,075)/8= 18,88KNm

h’= (6M/bfd )^0,5 = (6 x 18,88 x 1000/15 x 9,66)^0,5= 27,97cm il dimensionamento precedentemente eseguito è corretto Trave GH28 15x30cm

SOLAIO IN ACCIAIO

Anche per questo tipo di solaio i passi da eseguire sono i seguenti:

1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)

2)calcolo delle dimensioni del travetto in acciaio a partire da un dato ipotizzato, la base e relativa verifica.

3)calcolo delle dimensioni della trave in acciaio a partire da un dato ipotizzato, la base e relativa verifica.

Progetto della Trave sull’allineamento B2-B3

Progetto dei travetti di interasse 1m e luce 2.2m

Qs = 1,65KN/mqCarico Strutturale

Lamiera grecata in acciaio A55/P600 h = 0,055m e s = 0,02 cm

Getto di completamento in cls armato h = 0,045 m

Qa = 2KN/mqSovraccarico accidentale per una civile abitazione

Qp = 1,43KN/m Carico permanente non strutturale

Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq

Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq

Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq

Pannello in cartongesso (s= 0,12) = 0,1KN/mq

Impianti 0,5KN/mq

Q tot= 1,65+2+0,2+0,6+0,03+0,1+0,5= 5,08KN/mq

A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:

3,94KN/mq x 1m = 3,94KN/m

Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.

Impostata la resistenza a snervamento fyk = 235N/mmq, ottengo la tensione di progetto

fd = 204,35N/mmqe il modulo di resistenza a flessione Wx = 15,04cm^3.

Scelgo un Wx = 20,03cm^3 a cui corrisponde una profilato

IPE80 b = 4,6cm h = 8cm P = 0,06KN/m.

Verifica del travetto

Ottenute le dimensioni del travetto, aggiungo al carico strutturale quello del travetto 0,06KN/m/1m = 0,06KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.

Q’s = 0,06+1,65=1,71KN/mq

Momento = ql^2/8= (5,14 x 2,2 x 2,2)/8= 3,109KNm

Con il nuovo valore di momento ottengo un modulo di resistenza a flessione

Wx = 15,22cm^3 che è minore del modulo di resistenza scelto Wx = 20,03cm^3 quindi la sezione è verificata.

Progetto della trave di interasse 2,2m e luce 4,075m

Q’s = 1,71KN/mqCarico Strutturale

Lamiera grecata in acciaio A55/P600 h = 0,055m e s = 0,02 cm

Getto di completamento in cls armato h = 0,045 m

Trave IPE80 0,06KN/m2

Qa = 2KN/mqSovraccarico accidentale per una civile abitazione

Qp = 1,43KN/mCarico permanente non strutturale

Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq

Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq

Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq

Pannello in cartongesso (s= 0,12) = 0,1KN/mq

Impianti 0,5KN/mq

Q tot= 1,71+2+0,2+0,6+0,03+0,1+0,5= 5,14KN/mq

A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:

5,14KN/mq x 2,2m = 11,308KN/m.

Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.

Impostata la resistenza a snervamento fyk = 235N/mmq, ottengo la tensione di progetto

fd = 204,35N/mmqe il modulo di resistenza a flessione Wx = 114,86cm^3. Scelgo un

Wx = 146,3cm^3 a cui corrisponde una profilato

IPE180 b = 9,1cm h = 18cm P = 0,188KN/m.

Verifica della trave

Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave 0,188KN/m/2,2m = 0,085KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.

Q’s = 0,085+1,71=1,795KN/mq

Momento = ql^2/8= (11,495 x 4,075 x 4,075)/8= 23,86KNm

Con il nuovo valore di momento ottengo un modulo di resistenza a flessione Wx = 116,76cm^3 che è minore del modulo di resistenza scelto

Wx = 146,3cm^3 quindi la sezione è verificata.

SOLAIO IN CLS

Per questo tipo di solaio i passi da eseguire sono i seguenti:

1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)

2)calcolo delle dimensioni della trave in cls armato a partire dal solaio e relativa verifica.

Progetto della Trave sull’allineamento B2-B3

Imges impalcato e particolare

Progetto della trave di interasse 2,2m e luce 4,075m

Qs = 2,66KN/mq

Getto di completamento in cls armato h = 0,04 m

Pignatta h = 0,2 m l = 0.4 m

Travetti in acciaio l = 0.1 m

Qp = 1,43KN/mCarico permanente non strutturale

Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq

Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq

Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq

Pannello in cartongesso (s= 0,12) = 0,1KN/mq

Impianti 0,5KN/mq

Q tot= 2,66+2+0,2+0,6+0,03+0,1+0,5= 6,09KN/mq

A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:

6,09KN/mq x 2,2m = 13,398KN/m.

Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.

Impostata la resistenza a snervamento fyk = 235N/mmq e la classe del cls C40/50, ottengo la tensione di progetto dell’acciaio fyd = 391,3N/mmq e del cls fcd = 22,86N/mmq.

Ipotizzata una base ragionevole b = 15cm, ottengo un h utile = 20,28cm dalla formula

h = r(Mx1000/(fcd xb))^0,5. Dall’altezza che mi occorre non è quella utile ma quella della trave che è la somma dell’altezza utile più il copriferro (non resiste alla flessione ma è importantissimo perché ci “avverte” attraverso la fessurazione, del raggiungimento da parte della trave del collasso): 

H = h utile + delta. Essendo il copriferro pari a 5cm e avendo ottenuto un H = 25,28cm, adotto un H = 30cm perché comunemente le altezze delle travi hanno valori interi che possono incrementare solo di un valore di 5 in 5cm.

Verifica della trave

Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave (0,15m x 0,30m x 25KN/mc)/2,2m = 0,51KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.

Q’s = 2,66+0,51= 3,17KN/mq

Momento = ql^2/8= (30,14 x 4,075 x 4,075)/8= 62,56KNm

h’ utile = r(Mx1000/(fcd xb))^0,5 = 2,25 (62,56 x 1000/(22,86 x15) = 21,12cm.

H’ = h utile + delta = 21,12 + 5= 26,12 cm quindi il dimensionamento precedentemente eseguito è corretto. Trave  in cls  C40/50 15x30cm

 

Esercitazione 3

Travatura reticolare spaziale

Disegno e analisi su SAP

L’argomento di questa esercitazione è il progetto di una travatura reticolare spaziale, di 4 moduli ripetuti per 6 file adottando un modulo di base di 2x2x2m, disegnata prima su Autocad e poi importata su SAP 2000. Prima di eseguire il disegno della struttura sono state impostate l’unità di misura in metri e le coordinate x,y,z nell’origine, per esportare con più facilità il file su SAP.

Con il comando polilinea disegniamo una trave a C con un’asta diagonale al suo interno, che rappresenta il modulo base da dover replicare per ottenere quello più complesso della travatura reticolare spaziale.

Tenendo premuti shift e la rotella del mouse passiamo alla vista 3D che ci mostra il nostro disegno “schiacciato” lungo la pianta, il piano xy. Volendo riprodurre la struttura in 3D, quindi disporre in verticale il nostro modulo, usiamo il comando ruota 3D e digitiamo l’asse x che corrisponde all’asse di rotazione e poi clicchiamo sull’asse y che corrisponde all’asse da ruotare.

Una volta ruotato il disegno, lo selezioniamo e adottando il comando serie lo riproduciamo 4 volte (righe = 1, colonne = 4, distanza 2m) lungo l’asse x che è l’asse lungo il quale ci interessa eseguire la serie. Quadruplicato il modulo, chiudiamo con una linea l’ultimo perché come detto prima, il modulo base è una C con un linea diagonale.

Adesso disegniamo la stessa struttura in direzione y ricordandoci di non duplicare le aste verticali già disegnate per la prima serie. Con il comando serie quadruplichiamo anche queste aste ottenendo una “parvenza” di travatura reticolare spaziale. Completiamo questa prima fila inserendo anche le diagonali per i correnti superiori e inferiori aiutandoci con il comando orbita (shift e tasto sinistro del mouse).

Ora che la prima fila è completata possiamo replicarla in serie ma dobbiamo ricordarci di cambiare l’UCS collocando l’asse x al posto dell’asse y così da facilitare il lavoro (UCS -> 3p e selezioniamo le direzioni che vogliamo assegnare agli assi x,y,z). Riproduciamo 7 volte la riga dei 4 moduli precedentemente creati con il comando serie (righe = 1, colonne = 7, distanza 2m) perché anche se la nostra struttura è composta da 4 moduli x 6 file è più semplice una volta eseguita la serie rimuovere linee aggiuntive piuttosto che aggiungerle.  

Disegnata la struttura, il modello è stato esportato nel formato .dxf  per poter esser letto dal software di calcolo SAP.

Una volta importato il modello, sono stati assegnati i vincoli agli estremi della struttura, 4 cerniere che costituiscono gli appoggi (seleziono il nodo -> assign -> joint -> restraints -> translation 1 e 2 che indicano l’impedimento delle traslazioni verticale e orizzontale), mentre per tutti gli altri nodi sono state selezionate le aste e sono state spuntate le caselle che indicano il rilascio dei momenti flettente e torcente quindi sono state inserite cerniere sferiche, perché operiamo in 3D (assign -> frame -> releases/partial fixity -> moment 22, moment 33 start e end che indicano l’inizio e la fine dell’asta).

A questo punto abbiamo definito il materiale di cui sono composte le aste, l’acciaio (define -> materials -> add new material ->acciaio) e dopo averle selezionate lo abbiamo assegnato (assign -> frame -> frame sections -> add new property -> pipe (profilo cavo circolare) -> materiale acciaio).

Infine attraverso la vista 2D dall’alto, piano xy, abbiamo selezionato i nodi ma solo dopo aver scrupolosamente spuntato la casella che rende invisibili le aste per poter assegnare facilmente i carichi che gravano sulla struttura (set display options -> frame/cables/tendons -> frames not in view).      

                                                                 

N.B.Non basta semplicemente selezionare i nodi dalla vista xy ma bisognare imporre a SAP che i carichi vengano assegnati sui nodi superiori quindi sempre con i nodi selezionati (view -> set 2D view -> plane xy -> z=2 perché 2 è l’altezza della travatura reticolare spaziale).

Definiamo quindi il carico con il nome di forza concentrata (define -> load patterns -> add new load pattern -> forza concentrata -> dead -> self weight multiplie = 0 perché non vogliamo che nell’analisi venga considerato il peso proprio).

Selezionati i nodi, assegniamo il carico F = -40KN sull’asse z, asse ortogonale alla travatura e negativo perché rivolto verso il basso come una forza gravitazionale (assign -> joint loads -> forces -> load pattern name = forza concentrata -> force global z = -40KN).

Ora che sono stati assegnati anche i carichi possiamo lanciare l’analisi ricordandoci però di limitarla alle sole forze concentrate che abbiamo collocato sulla struttura e non agli altri carichi che compaiono nella tabella (run analysis -> modal e dead -> do not run case -> forza concentrata -> run case -> run now).    

                                                         

Sempre su SAP è possibile ricavare la tabella formato Excel che raffigura gli sforzi assiali che gravano su ogni singola asta (display -> show tables -> analysis results -> element output -> file -> export current table -> to excel).

N.B.= questo è possibile farlo solo dopo aver lanciato l’analisi e aver spuntato il comando che permette di visualizzare gli sforzi assiali sulle aste.

Di questi sforzi prenderemo in considerazione solamente i due valori massimi di trazione e compressione per eseguire il dimensionamento delle aste e farne le opportune verifiche a resistenza, snellezza e stabilità.

Per dimensionare l’asta di una struttura reticolare, si adotta la formula σ= N/A perché si considera semplicemente la tensione derivante dallo sforzo normale N che agisce su un’area A.

Dimensionamento dell’asta tesa e relativa verifica a resistenza.

In questo caso, per dimensionare l’asta tesa, è necessario prima calcolare l’area minima, A min e poi farne la verifica a resistenza. Adottando infatti un acciaio da carpenteria S275 quindi con un fyk = 275MPa (N/mmq), un gm₁=1,05 e tenendo in considerazione lo sforzo normale massimo di trazione ricavato dalla tabella excel di SAP, N = 258,93KN, otteniamo che A min = 258,93KN x 1000 x 1,05/275 N/mmq = 988 mmq = 9,9 cm².

Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è di poco maggiore al valore ottenuto dal calcolo per stare in sicurezza. Adotto un profilo con un dxs (diametro x spessore)= 88,9 x 4,0 mm   A = 10,7 cm²     Jx (momento d’inerzia) = 96,3 cm⁴    Wx (modulo di resistenza) = 21,7cm³    ρ (rho, raggio d’inerzia) = 3,0 cm.

A questo punto, dopo aver dimensionato l’asta tesa, ne eseguo la verifica a resistenza perché per l’acciaio teso l’unica verifica veramente significativa è quella a resistenza. Molto semplicemente si calcola la tensione di progetto fd e si verifica che questa sia minore/uguale alla tensione a snervamento dell’acciaio fyk. -> fd ≤fyk

fd = 258,93KN x 1000/10,7cm²x 100 = 241,99 MPa (N/mm²) -> 241,99MPa ≤ 275MPa -> asta verificata a resistenza.

Dimensionamento dell’asta compressa e relative verifiche a resistenza, snellezza e stabilità.

Per dimensionare correttamente l’asta compressa invece, non basta eseguire la verifica a resistenza perché essendo compressa è soggetta al carico di punta o meglio conosciuto come carico critico euleriano che provoca lo sbandamento dell’asta. Per ovviare allo sbandamento dovuto ad un valore elevato del rapporto h/l della trave, si stabilisce come è vincolata la trave e in base a quello si trova il P critico (carico critico).

Quindi oltre alla verifica a resistenza, vanno eseguite altre due verifiche, quella a snellezza e quella a stabilità. Per dimensionare l’asta compressa svolgiamo gli stessi passaggi di quella tesa perché se pur compressa, sempre di acciaio parliamo.

Adottiamo l’acciaio S275 quindi con un fyk = 275MPa (N/mmq), un gm₁=1,05 e teniamo in considerazione lo sforzo normale massimo di compressione ricavato dalla tabella excel di SAP, N = 307,25KN.

Dalla formula σ= N/A otteniamo che A min = 307,25KN x 1000 x 1,05/275 N/mmq = 1117 mmq = 11,17 cm².

Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è di poco maggiore al valore ottenuto dal calcolo per stare in sicurezza. Adotto un profilo con un dxs (diametro x spessore)= 114,3 x 3,6 mm   A = 12,5 cm²     Jx (momento d’inerzia) = 192 cm⁴    Wx (modulo di resistenza) = 33,6cm³     ρ (rho, raggio d’inerzia) = 3,92 cm.

Verifica  a resistenza

fd ≤fyk

fd = 307,25KN x 1000/12,5cm²x 100 = 245,8 MPa (N/mm²) -> 245,8MPa ≤ 275MPa -> asta verificata a resistenza.

Verifica  a snellezza

λ<200

λ= l₀/ρconl₀= βx l e ρ= raggio d’inerzia della sezione in esame

β= numero di semionde visibili per il tipo di vincolo in esame

Nel nostro caso, l’asta della travatura reticolare, va considerata come una trave doppiamente incernierata quindi la β = 1 e di conseguenza l₀= l. Il raggio d’inerzia lo desumiamo dalle tabelle ed è ρ= 3,92 cm. λ = 283 cm x 1 /3,92 cm = 72,2<200 -> asta verificata a snellezza.

Verifica  a stabilità

Nd ≤Nbrd    dove Nd  è lo sforzo assiale che agisce sull’asta in esame mentre Nbrd   è la resistenza all’instabilità per l’asta compressa ed è pari a Nbrd = χA fyk/gm₁. A loro volta χ = 1/Φ+(Φ²-⁻λ²)^0,5≤1 ;

⁻λ= (Afyk / Pcritico)^0,5 ;

 Φ= 0,5[1+α (⁻λ– 0,2)+ ⁻λ²] e α è un coefficiente chiamato fattore di imperfezione ed è α=0,21

A sua volta, perché l’asta sia verificata,Nbrd<P critico  dove P critico = p² E Jmin/l₀².

Eseguendo i calcoli ottengo che:

P critico = (3,14²x 210000N/mm²x 192 cm⁴ x 10000 / 283²cm x 10)/1000 = 496,4KN

⁻λ² = 12,5cm²x 100 x 275MPa/496,4 x 1000 = 0,69

Φ = 0,5[1+0,21(√0,69-0,2)+0,69] = 0,9

χ = 1/ 0,9+(0,9²-0,69²)^0,5 =0,68≤1

Nbrd  = (0,68 x 12,5cm²x 100 x 275MPa/1,05)/1000 = 222,62KN

N.B. = il risultato ottenuto non è accettabile perchè Nd deve essere ≤Nbrd mentre invece in questo caso Nd = 307,25KN ≥222,62KN = Nbrd. Quindi bisogna adottare un’area maggiore, quindi un profilo più grande per garantire la verifica a stabilità.

Eseguiamo nuovamente i calcoli:

Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è superiore al valore adottato precedentemente. Prendiamo quindi un profilo con un dxs (diametro x spessore)= 114,3 x 4,5 mm   A = 15,5 cm²     Jx (momento d’inerzia) = 234 cm⁴    Wx (modulo di resistenza) = 41cm³  ρ (rho, raggio d’inerzia) = 3,89 cm.

Verifica  a resistenza

fd ≤fyk

fd = 307,25KN x 1000/15,5cm²x 100 = 198,225 MPa (N/mm²) -> 198,225MPa ≤ 275MPa -> asta verificata a resistenza.

Verifica  a snellezza

λ<200

 λ= l₀/ρ con l₀= βxl e ρ= raggio d’inerzia della sezione in esame

β= numero di semionde visibili per il tipo di vincolo in esame

quindi la β = 1 e di conseguenza l₀= l. Il raggio d’inerzia lo desumiamo dalle tabelle ed è

ρ= 3,89 cm. λ = 283 cm x 1 /3,89 cm = 72,75<200 -> asta verificata a snellezza.

Verifica  a stabilità

Nd ≤Nbrd   

P critico = (3,14²x 210000N/mm²x 234 cm⁴ x 10000 / 283²cm x 10)/1000 = 606,24KN

⁻λ² = 15,5cm²x 100 x 275MPa/604,95 x 1000 = 0,703

Φ = 0,5[1+0,21(√0,7-0,2)+0,7] = 0,9186

χ = 1/ 0,9168+(0,9168²-0,69²)^0,5 =0,769≤1

Nbrd  = (0,769x 15,5cm²x 100 x 275MPa/1,05)/1000 = 312,2KN

Adesso anche la verifica a stabilità risulta corretta infatti Nd≤Nbrd ovvero 307,25KN≤312,2KN -> asta verificata a stabilità.

Esercitazione 4

Ripartizione delle forze sismiche (in collaborazione con Beatrice Nanni, Flavia Valdarnini, Sabrina Zhu)

(le travi in grigio corrispondono alle travi portanti, ovvero quelle che portano tutti i carichi gravanti sul solaio)

L'impalcato in esame è una struttura a forma di T composta da 5 telai shear type in direzione verticale e 3 telai shear type in direzione orizzontale. Di questi telai, 5 sono i controventi determinati in base all’orditura del solaio.

La struttura è 2 volte iperstatica quindi per risolvere il sistema è stato necessario definire il solaio come un corpo rigido piano (per il quale vale traslazione orizzontale, verticale e rotazione rigida attorno ad un punto) e introdurre vincoli elastici (molle) che si comportano secondo la legge di Hooke F= K δ. I pilastri sono stati posizionati in modo tale da avere il momento d’inerzia massimo nella direzione del momento flettente derivante dal carico del solaio.

Con il sussidio del foglio di calcolo excel, che permette un riscontro in termini numerici rapido e completo, è stato possibile analizzare lerigidezze dei controventi, il centro di massa, il centro delle rigidezze, l’analisi dei carichi sismici e la ripartizione del sisma lungo l’asse X e Y.

Rigidezze dei controventi

Primo Step                                                                                                                             

In questa tabella è stata calcolata la rigidezza di ogni singolo controvento attraverso la formula:

K = 12 EJ/H³dove E (modulo di Young, per l’acciaio 210000 MPa; per il cls  21000 MPa), J (momento d’inerzia, in direzione X = bh³/12 ; in direzione Y = hb³/12) e H (altezza del solaio interpiano pari a 4m).

Secondo Step                                                                                                                                    

Stabilite le rigidezze dei controventi sono state calcolate le distanze di questi da un punto fisso chiamato O (origine). Per il telaio verticale 4-9 e il telaio orizzontale 1-2-3 le distanze dall’origine sono pari a 0 in quanto i telai sono collocati sulla retta che congiunge con l’origine O.

Centro di massa

Terzo Step                                                                                                                               

Una volta stabilite le rigidezze dei telai e le loro distanze dall’origine O, l’impalcato è stato suddiviso in due aree A1= 36,6m² e A2 = 28,38m² delle quali sono stati calcolati i centri di massa. Per determinare i centri di massa è stato preso come punto di riferimento l’origine O e sono state determinate le distanze (x_G1,y_ G1) e le distanze (x_ G2,y_ G2). Infine è stato calcolato il centro di massa dell’intera struttura secondo le sue coordinate

X_G: (A1x_G1)+(A2x_G2)/A1+A2= 6,60m

Y_G: (A1y_G1)+(A2y_G2)/A1+A2= 4,28m

Calcolo del centro di rigidezze e delle rigidezze globali

Quarto Step                                                                                                                            

Determinate tutte le rigidezze dei controventi (vedi Step 1) orizzontali e verticali, è stata calcolata la rigidezza totale traslante verticale e quella totale traslante orizzontale : Kvtot e Kotot. Dalle due rigidezze totali si è ottenuto il centro delle rigidezze in base alla formula:

X_C=(kv1 dv1)+(kv2 dv2)+(kv3 dv3)+(kv4 dv4)+(kv5 dv5)/kvtot = 6,52m

Y_C=(ko1 do1)+(ko2 do2)+(ko3 do3)/kotot = 5,45m

Una volta determinata la posizione del centro delle rigidezze, sono state invece determinate le distanze dei controventi verticali (ddv) e quelli orizzontali (ddo) dal centro delle rigidezze.

Analisi dei carichi sismici

Quinto Step                                                                                                                             Attraverso questa tabella è stata determinata la forza sismica che corrisponde al prodotto tra la massa dell’edificio per l’accelerazione che il corpo subisce per effetto del trascinamento (dato dalla Normativa in riferimento alla tipologia strutturale): F= ma dove a= cg, c <1 (coeff. di intensità sismica, più è alto maggiore è il sisma) e g (accelerazione gravitazionale).

F= mcg= c(mg)= cPdove P o W (forza peso) = G (sovraccarico tot. permanente (qs+qp)Atot) x Ψ (coefficiente di contemporaneità = 0.80) x Q (sovraccarico accidentale dato dalla destinazioned’uso dell’edificio).

Ripartizione forza sismica lungo X e Y

Sesto e Settimo Step                                                                                                                       

Con questo step è stata studiata la ridistribuzione della forza sismica sui controventi orizzontali. Prima di stabilire la distribuzione della forza sui controventi, è stato necessario determinare il valore del momento torcente (rotazione dell’impalcato dovuta alla mancata coincidenza tra centro delle masse e centro delle rigidezze): Mt= Fxb dove F (Forza sismica) e b (distanza dal punto C (centro delle rigidezze) al punto G (centro delle masse)). Bisogna fare attenzione però perché essendo la forza sismica ripartita lungo X e Y, il braccio b cambia se si considera il Momento torcente lungo X o lungo Y. Infatti nel caso di X: b= (Y_C - Y_G); nel caso di Y: b= (X_C – X_G). Per determinare invece la traslazione orizzontale dell’impalcato la formula è: Uo= F/kotot mentre per quella verticale si ha: Vo= F/kvtot.

ex_1) CALCOLO DI UNA STRUTTURA RETICOLARE SIMMETRICA CON IL METODO DELLE SEZIONI DI RITTER

Ciao Ragazzi!

Oggi impareremo a verificare se una struttura è ISOSTATICA e a calcolarla con il metodo delle SEZIONI DI RITTER!

VERIFICA DELLA STRUTTURA ISOSTATICA

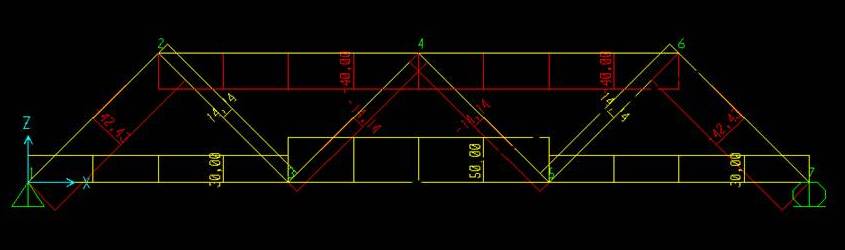
Considero la seguente struttura:

 

Per verificare che la struttura sia isostatica devo avere la seguente condizione:  V= l

 Il numero dei vincoli deve essere uguale al numero dei gradi di libertà della struttura.

Il numero di gradi di vincolo è dato dal numero di aste presenti nella struttura moltiplicato per il numero di gradi di libertà di ogni elemento.

l = 11 (aste)  x3 (gradi di libertà) =33

La struttura ha anche dei vincoli esterni che in questo caso sono 3: due sono i gradi di libertà che blocca la cerniera  a sinistra e uno è il grado di libertà che blocca il carrello a destra.

Per calcolare il numero di vincoli interni:    V_i = 2*(n -1)     n= numero di aste che arrivano alla cerniera interna.

La cerniera interna in A toglie 2 gradi di libertà : 2(2-1)=2

La cerniera interna in B e G toglie 4 gradi di libertà : 2(3-1)=4

La cerniera interna in C – D e E toglie 6 gradi di libertà : 2(4-1)=6

Quindi: V_i= 2+2+4+4+6+6+6=30

V=V_e+V_i

V= 3 V_e + 30 V_i = 33

V 33 = l 33

La struttura è ISOSTATICA!  

CALCOLO DELLE REAZIONI VINCOLARI

Adesso calcoliamo le reazioni vincolari esterne della struttura. Abbiamo una cerniera che porta una reazione verticale (R_va) e una orizzontale (R_ua) e un carrello che porta una reazione verticale (R_vb). Poi abbiamo 3 carichi puntuali da 20KN sui nodi B - D e G.

Possiamo notare che la struttura è simmetrica perché rispetto all’asse di simmetria:

• le reazioni vincolari a destra e sinistra sono simmetriche
• il diagramma del momento flettente M e dello sforzo normale N sono simmetrici
• il diagramma del taglio T è emisimmetrico
• le deformazioni sono simmetriche.

∑ Fx=0   U_A=0     si annulla perché non ci sono altre reazioni!

∑ Fy=0   V_A + V_B – 60 = 0                          V_A + V_B= 60KN

Per la simmetria possiamo dire che: V_A = V_B =60/2= 30KN

 

METODO DELLE SEZIONI DI RITTER

Arrivati a questo punto facciamo 3 tagli sulla nostra struttura in modo da avere dei punti in cui le aste non concorrano allo stesso nodo:

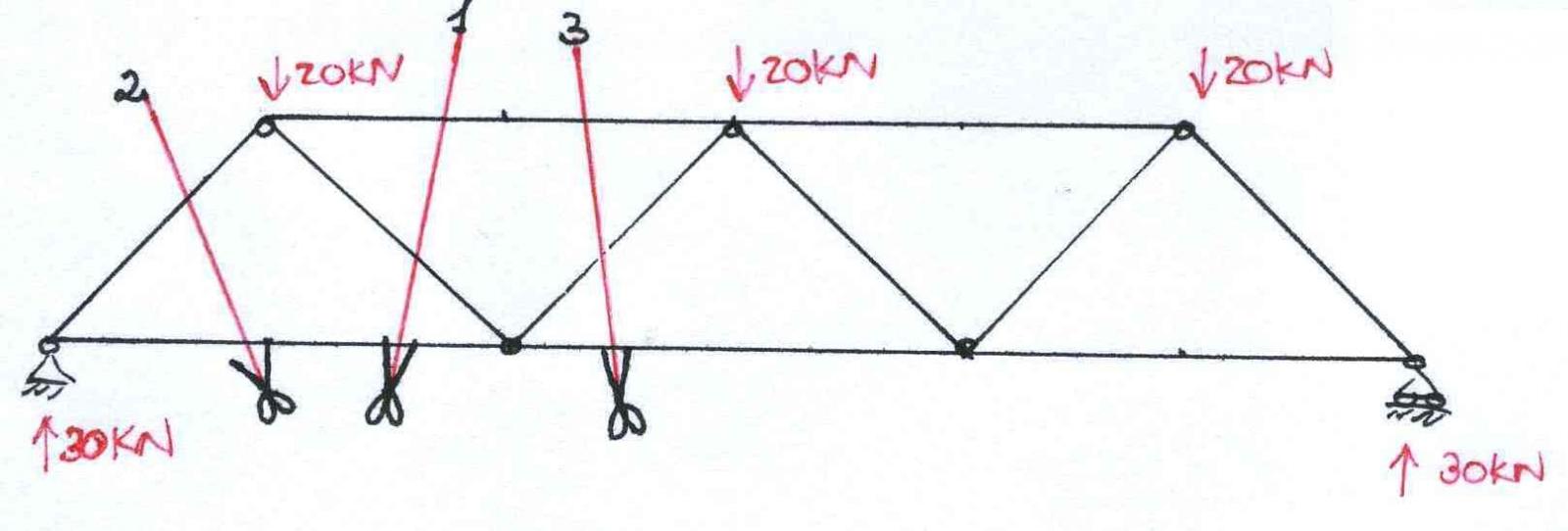
Ipotizzo i versi delle aste tagliate (le ipotizzo tese) e calcolo le reazioni vincolari, nel momento in cui otterrò dei risultati negativi, significa che avevo ipotizzato il verso sbagliato nella struttura! Quindi le mie aste potranno diventare dei puntoni o saranno dei tiranti.

Analizziamo la prima sezione

SEZIONE 1 :

Faccio l’equilibrio alla rotazione nel nodo C , in modo da avere solo una reazione da calcolare. Questo perché N₂  ed  N₃hanno braccio nullo in quanto la loro retta d’azione passa per C.

∑ Mc=0               -30*4+20*2-N₁*(2)=0     ->     -120+40-N₁*(2)=0   ->   N₁=-40KN

L’asta B-Dche avevo ipotizzato tesa, in realtà è compressa. Quindi è un puntone.

∑ M_B=0                -30*2+N₃*(2)=0           ->     N₃=30KN

L’asta A-Cè tesa, è un tirante.

 

Adesso faccio l’equilibrio lungo la componente verticale; posso osservare che N2 è disposta sulla diagonale di un quadrato, perciò la componente verticale e quella orizzontale saranno uguali: N_2x=N_2y=N₂*(√2/2).

∑ F_y=0                30-20-N₂ √2/2=0        ->      N₂= 10*2/√2=20/√2        ->   N₂= 10 KN   ho razionalizzato!

L’asta B-Cè tesa, è un tirante.

 

Svolgo lo stesso procedimento per le altre due sezioni

SEZIONE 2 :

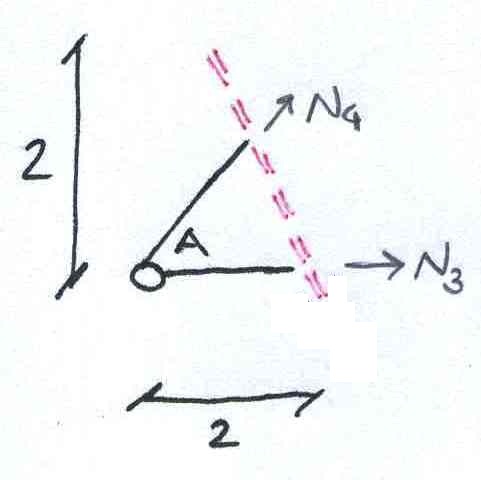
L’asta N₄è disposta in diagonale, anche qui la reazione verticale e orizzontale, saranno uguali: N_4x=N_4y=N₄*(√2/2).

∑ F_x=0                30+N₄√2/2=0     ->   N₄= -30*2/√2= -60/√2*√2/√2=-30√2KN

L’asta A-Bè compressa, è un puntone devo cambiare il verso delle frecce.

  

SEZIONE 3 :

Imposto l’equilibrio alla rotazione nel nodo D :

∑ M_D=0                N₅*(2)+20*(4)- 30*(6)=0      ->    N₅*(2)+80-180=0     ->     N₅= 50KN

Equilibrio lungo la componente verticale, con N₆ posto in diagonale quindi uso la formula della diagonale del quadrato.

∑ F_y=0                30-20+N₆√2/2=0        ->      N₆= -10*2/√2= -20/√2           ->   N₆= - 10√2KN    ho razionalizzato!

 

Ho risolto tutte le incognite delle aste! I risultati sono i seguenti:

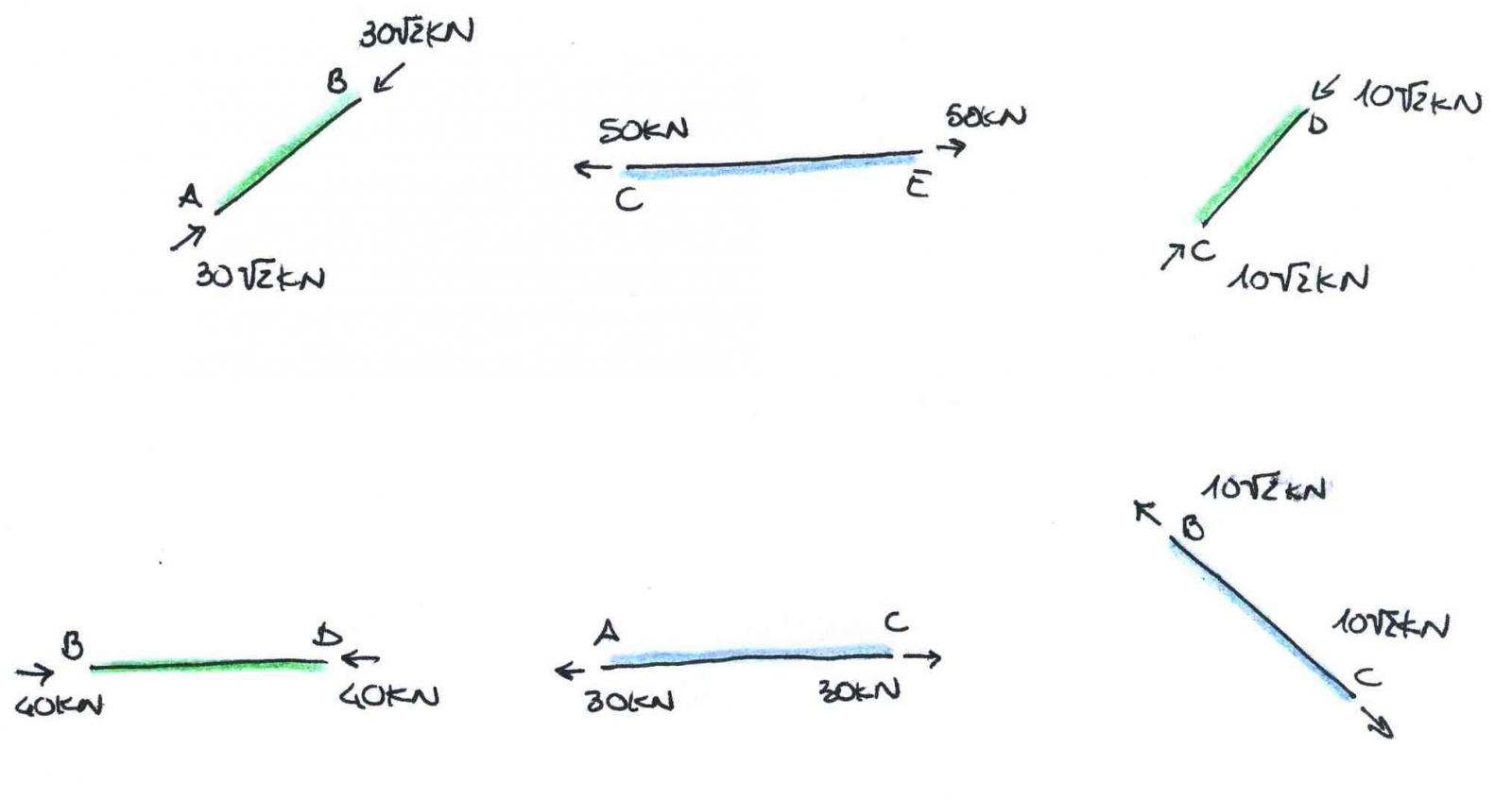
A questo punto ho tutti i dati che mi servono.

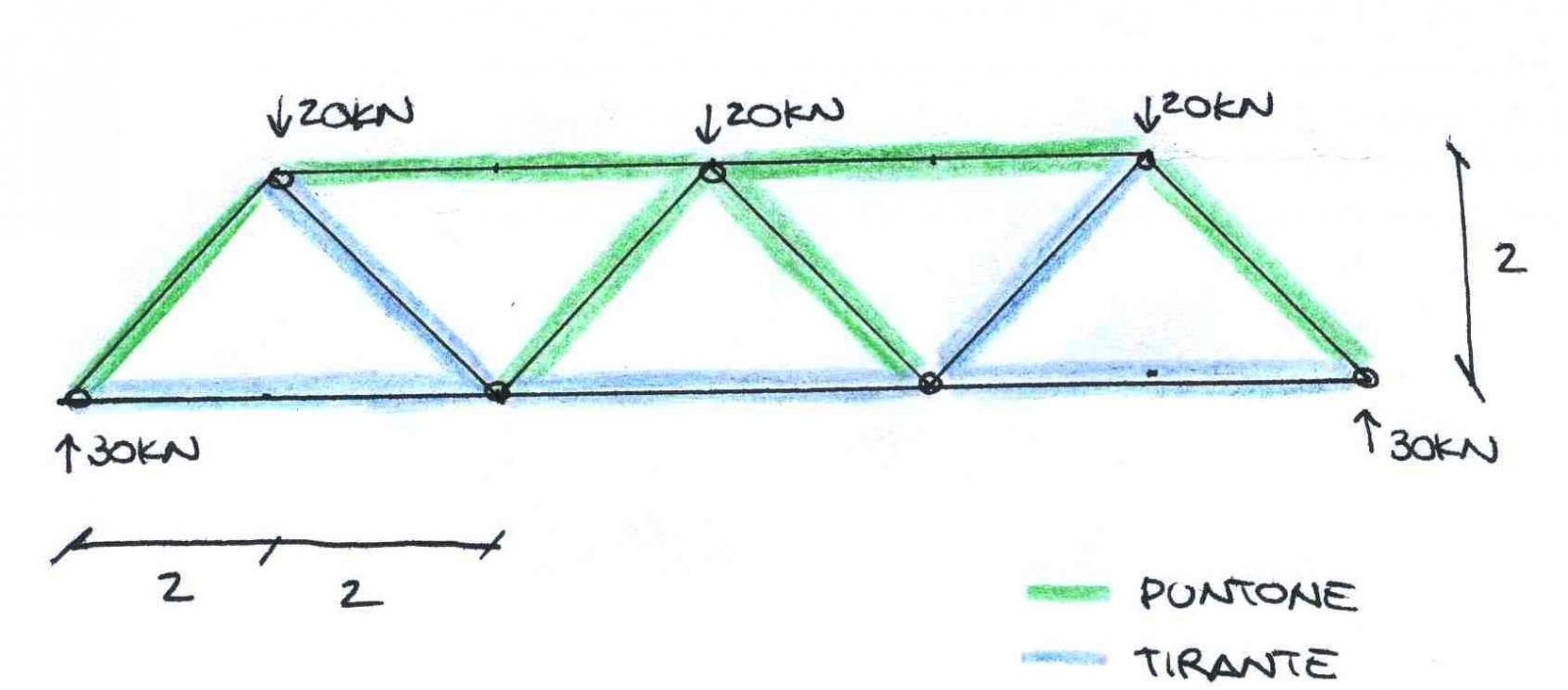
Adesso posso mettere in evidenza tutte le reazioni vincolari sia a destra che a sinistra dell’asse di simmetria.

 

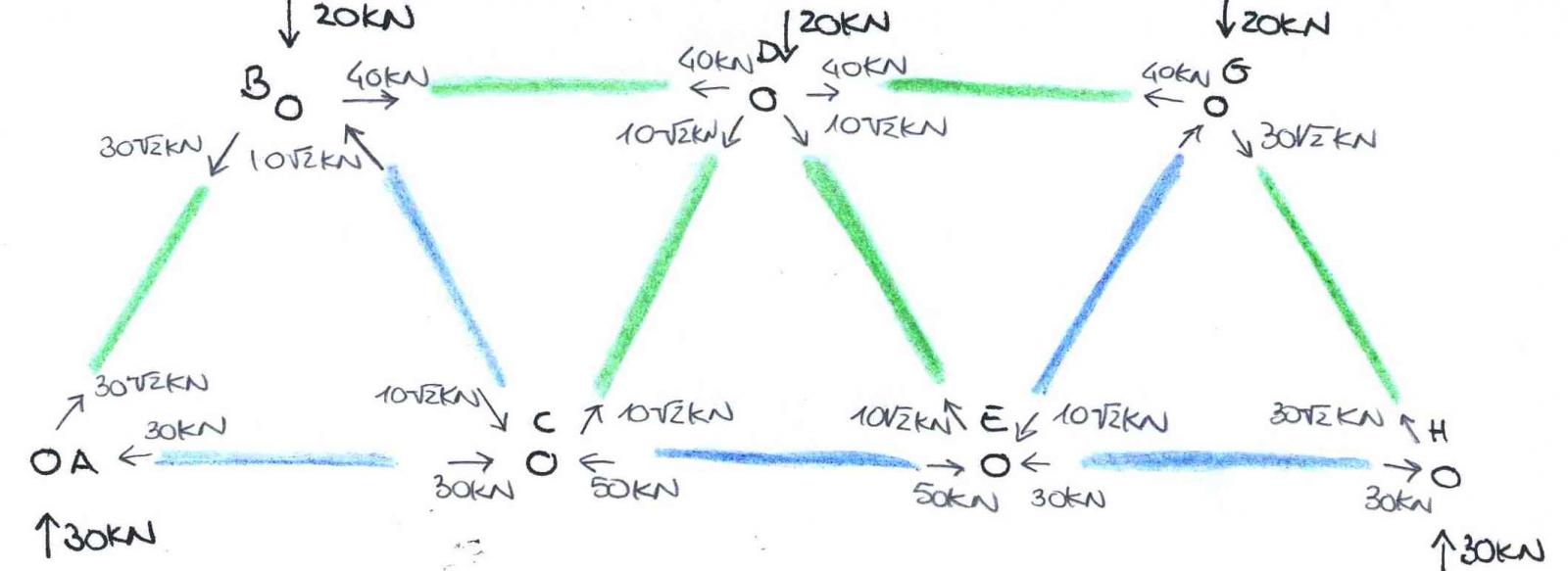
Ho risolto in questo modo la mia struttura calcolandola con il metodo delle sezioni di Ritter!

Adesso analizziamo la struttura utilizzando il programma di calcolo SAP2000.

Si crea un nuovo modello e si imposta la struttura su una griglia, si impostano le unità di misura (in questo caso KN, m , C ) si danno le misure di riferimento sugli assi

• x=7 perché abbiamo 7 interassi
• y=1 perché lavoriamo in 2D  
• z=2 perché abbiamo due assi uno superione e uno inferiore

Si impostano anche gli spazi che vengono impostati sul metro sugli assi XZ.

Per i vincoli faccio click con il tasto destro, metto in evidenza il nodo interessato e tramite assign ->Joint ->Restaints assegno un carrello e una cerniera (indicate dai relativi simboli). I carichi puntuali vanno invece definiti prima da define ->load patterns  e vanno aggiunti agli altri carichi. A questo punto li metto in evidenza e li assegno tramite Assign ->Joint Loads ->Forces.  Per assegnare il verso della forza dobbiamo mettere il segno meno davanti al carico che assegniamo, ed avremo carichi gravitazionali verso il basso. Avendo una trave reticolare, dobbiamo impostare sforzi assiali puri!  Quindi selezioniamo tutta la nostra strtuttura e da Assign -> Frame ->Releases/partial fixityspuntiamo start e end con moment 33 (major).

Adesso la nostra struttura è impostata.

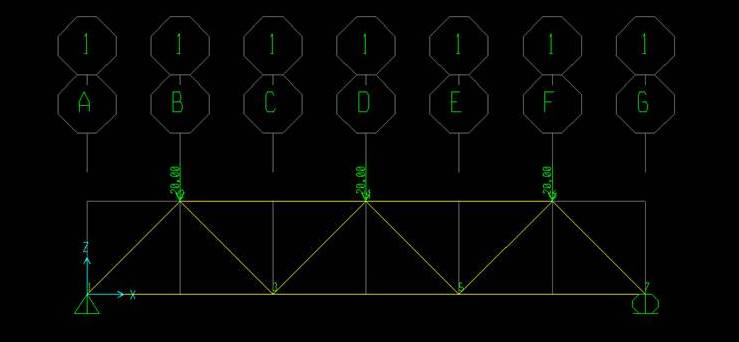
Per calcolarla dobbiamo fare click su Run Analysis e fare ilRun solo dei carichi concentrati che abbiamo impostato noi! I carichi Dead e Modal devono essere impostati su Do Not Run. A questo punto parte l’analisi che ci permetterà di verificare:

Le forze agenti sulla struttura:

 

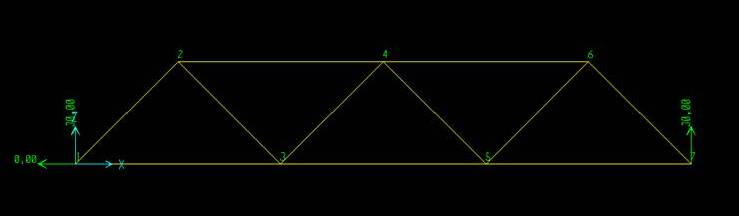
La deformata:

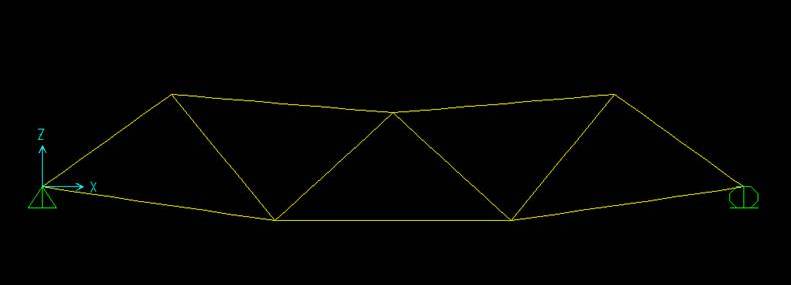
Gli sforzi assiali agenti sulla struttura e i diagrammi.

 

Chi era Amelie Emmy Noether?

È stata una fra i più importanti matematici di tutti i tempi. Il topologo russo Pavel Alexandrov la definì tout-court «il più grande matematico donna di tutti i tempi» e lo stesso Albert Einstein ne pubblica un apprezzamento sul New York Times poche settimane dopo la sua morte.

Amalie Emmy Noether(Erlangen, 23 marzo1882– Pennsylvania, 14 aprile1935) è stata una matematica tedesca di origini ebree. Si è occupata di fisica matematica, teoria degli anelli ed algebra astratta, ed il suo nome è indissolubilmente legato al celebre teorema di Noether del 1915, che mette in luce nel campo della fisica teorica una profonda connessione tra simmetrie e leggi di conservazione.

Figlia del già noto matematico Max Noether, nasce nella città bavarese di Erlangen, e fin dalla giovane età mostra spiccate capacità. Dopo aver passato gli esami necessari all'insegnamento del francese e dell'inglese, sceglie di rivolgersi allo studio della matematica all'Università di Erlangen, dove già il padre insegnava. Completata la tesi sotto la supervisione di Paul Albert Gordan, lavora all'Istituto di Matematica per sette anni, senza essere pagata.

Nel 1915 viene invitata da David Hilbert e Felix Klein a far parte del Dipartimento di Matematica dell'Università Georg-August di Gottinga. Alcuni membri della Facoltà di Filosofia si opposero, sostenendo che il titolo Privatdozent non potesse essere attribuito alle donne, e lei trascorse quattro anni tenendo lezione a nome di Hilbert. Nel 1919 le venne comunque alfine concesso di sostenere l'esame per l'abilitazione, che ottenne nel maggio dello stesso anno, continuando però ad insegnare senza percepire alcuno stipendio fino al 1923. Durante gli anni trascorsi a Gottinga ottenne rispetto e stima a livello mondiale per i suoi innovativi lavori in matematica, venendo invitata a tenere una conferenza plenaria al Congresso Internazionale dei Matematici di Zurigo, in Svizzera, nel 1932. L'anno seguente il governo nazista della Germania le vieta l'attività di insegnamento. Emmy emigra negli Stati Uniti d'America, dove ottiene un posto al Bryn Mawr College in Pennsylvania. Nel 1935 si sottopone ad un intervento chirurgico per una cisti ovarica e, nonostante i segni iniziali di ripresa, muore dopo quattro giorni.

 

ex_2) CALCOLO DI UNA STRUTTURA RETICOLARE ASIMMETRICA CON IL METODO DEI NODI

Ciao Ragazzi!

Questa volta ci occuperemo di una struttura reticolare ASIMMETRICA che risolveremo con il METODO DEI NODI.

VERIFICA DELLA STRUTTURA ISOSTATICA

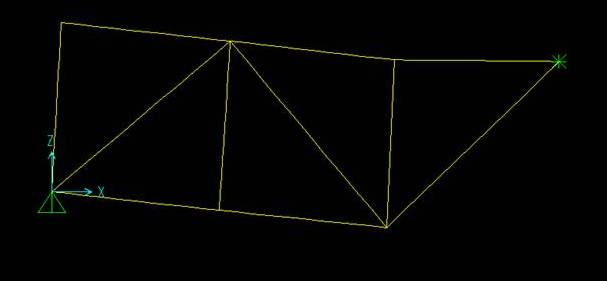
Considero la seguente struttura:

Per verificare che la struttura sia isostatica devo avere la seguente condizione: V= l

Il numero dei vincoli deve essere uguale al numero dei gradi di libertà della struttura.

Il numero di gradi di vincolo è dato dal numero di aste presenti nella struttura moltiplicato per il numero di gradi di libertà di ogni elemento.

l = 11 (aste) x3 (gradi di libertà) =33

La struttura ha dei vincoli esterni, in questo caso sono 3: due sono i gradi di libertà che blocca la cerniera a sinistra e uno è il grado di libertà che blocca il carrello ruotato a destra.

Per calcolare il numero di vincoli interni: V_i = 2*(n -1) n= numero di aste che arrivano alla cerniera interna.

La cerniera interna in A e H toglie 2 gradi di libertà : 2(2-1)=2

La cerniera interna in B – D ed E toglie 4 gradi di libertà : 2(3-1)=4

La cerniera interna in G toglie 6 gradi di libertà : 2(4-1)=6

La cerniera interna in C toglie 8 gradi di libertà : 2(5-1)=8

Quindi: V_i= 4+12+6+8=30

V=V_e+V_i

V= 3 V_e + 30 V_i = 33

V 33 = l 33

Oppure possiamo calcolare l’isostaticità della struttura con la seguente formula:

V_e+ N°aste = 2* N°nodi

3+11 = 2*7 è verificato!

La struttura è ISOSTATICA!

CALCOLO DELLE REAZIONI VINCOLARI

Adesso calcoliamo le reazioni vincolari esterne della struttura. Abbiamo una cerniera che porta una reazione verticale (R_vB) e una orizzontale (R_uB) e un carrello che porta una reazione orizzontale (R_uH). Poi abbiamo 2 carichi puntuali di 10KN sui nodi C ed E.

∑ Fx=0 U_B – U_H= 0 -> U_B = U_H

∑ Fy=0 V_B – F – F = 0 -> V_B= 20KN

Faccio l’equilibrio alla rotazione nel polo A:

∑ M_A=0 U_B*1 – 10KN*1 – 10KN *2 =0 -> U_B= U_H= 30KN

 

METODO DEI NODI

A questo punto consideriamo i singoli nodi della nostra struttura in modo da avere dei nodi con delle aste che hanno i versi ipotizzati da noi:

N.B:Vale la regola di prima! Nel momento in cui ho un risultato negativo, cambio il verso della freccia!

Adesso procedo analizzando tutti i nodi facendo l’equilibrio delle reazioni verticali e orizzontali :

∑ Fy=0 -> N₁₁*√2/2=0 Asta scarica! (Ricordandosi la regola della diagonale del quadrato!)

∑ Fx=0 -> N₁₀ +30KN=0 -> N₁₀ = -30KN Asta compressa!

∑ Fx=0 -> N₇ -30KN=0 -> N₇ = 30KN Asta compressa!

∑ Fy=0 -> N₉ -10KN=0 -> N₉ = 10KN Asta compressa!

∑ Fx=0 -> N₈ + N₆*√2/2=0 -> N₈ = -10KN Asta compressa!

∑ Fy=0 -> N₆*√2/2-10KN=0 -> N₆ = 10√2KN Asta tesa!

∑ Fy=0 -> N₅=0 Asta scarica!

∑ Fx=0 -> N₃ = 10KN Asta compressa!

∑ Fx=0 -> N₂*√2/2+30KN-10KN=0 -> N₂ = -20√2KN Asta compressa!

∑ Fy=0 -> N₁-20KN –20√2*√2/2=0 -> N₁=0 Asta scarica!

∑ Fx=0 -> N₄=0 Asta scarica!

∑ Fy=0 -> N₅ -10KN+10KN=0 -> N₅=0 Asta scarica!

∑ Fx=0 -> N₂*√2/2-30KN+10KN=0 -> N₂ = 20√2KN Asta compressa! (Riconfermiamo!)

 

Ho risolto tutte le incognite delle aste!

Adesso posso mettere in evidenza tutte le reazioni vincolari e vedere quali sono le aste compresse, quali quelle tese e quali risultano scariche.

 

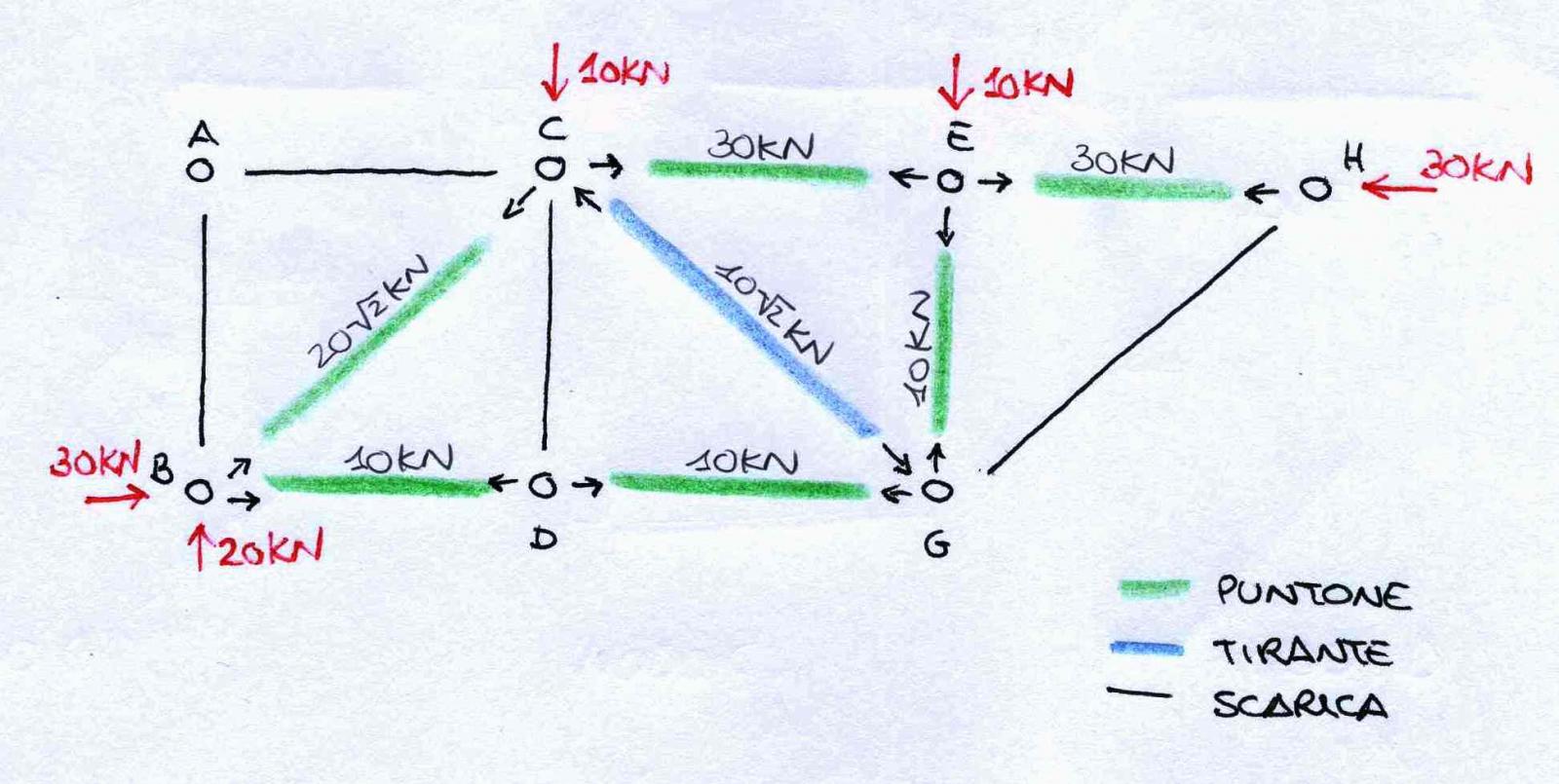
Ho risolto in questo modo la mia struttura calcolandola con il metodo dei nodi!

Adesso analizziamo la struttura utilizzando il programma di calcolo SAP2000.

Si crea un nuovo modello e si imposta la struttura su una griglia, si impostano le unità di misura (in questo caso KN, m , C ) si danno le misure di riferimento sugli assi

• x=4 perché abbiamo 7 interassi
• y=1 perché lavoriamo in 2D
• z=2 perché abbiamo due assi uno superione e uno inferiore

Si impostano anche gli spazi che vengono impostati sul metro (x=y=Z=1) sugli assi XZ.

Per i vincoli faccio click con il tasto destro, metto in evidenza il nodo interessato e tramite assign ->Joint ->Restraints assegno un carrello e una cerniera (indicate dai relativi simboli).Questa volta al carrello dobbiamo bloccare la traslazione lungo l’asse X! Infatti al posto del solito carrello apparirà un asterisco! I carichi puntuali vanno invece definiti prima da define ->load patterns e vanno aggiunti agli altri carichi. A questo punto li metto in evidenza e li assegno tramite Assign ->Joint Loads ->Forces. Per assegnare il verso della forza dobbiamo mettere il segno meno davanti al carico che assegniamo, ed avremo carichi gravitazionali verso il basso; in questo caso -10KN. Avendo una trave reticolare, dobbiamo impostare sforzi assiali puri! Quindi selezioniamo tutta la nostra struttura e da Assign -> Frame ->Releases/partial fixityspuntiamo start e end con moment 33 (major).

Adesso la nostra struttura è impostata.

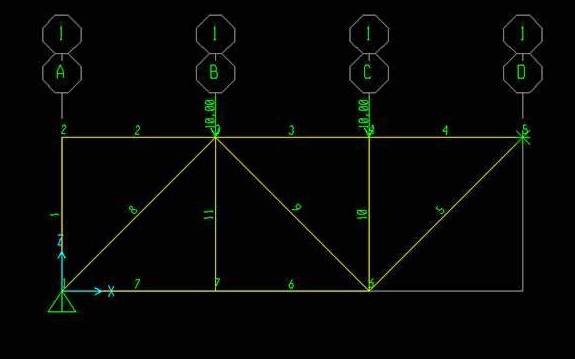
Per calcolarla dobbiamo fare click su Run Analysis e fare ilRun solo dei carichi concentrati che abbiamo impostato noi! I carichi Dead e Modal devono essere impostati su Do Not Run. A questo punto parte l’analisi che ci permetterà di verificare:

Le forze agenti sulla struttura:

La deformata:

Gli sforzi assiali agenti sulla struttura con il relativo diagramma.

 

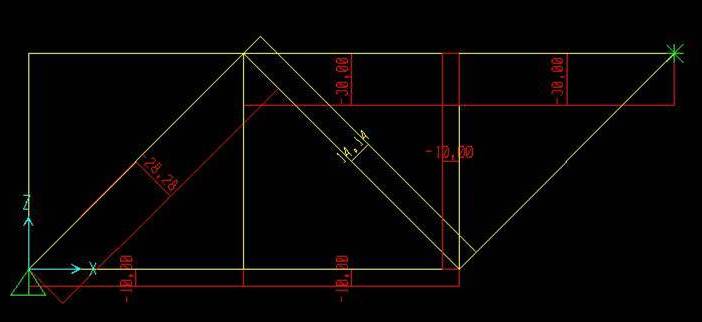
ex_3) CALCOLO DI UN PORTALE A TRE CERNIERE CON CARICO DISTRIBUITO A SINISTRA

Eccomi con un altro intervento sulle strutture ISOSTATICHE. Questa volta analizzo un portale con una cerniera e un carico distribuito. La struttura di per sé è simmetrica….ma vedremo che con il carico distribuito a sinistra qualcosa cambierà!

Prima cosa da fare è:

VERIFICA DELLA STRUTTURA ISOSTATICA

Considero la seguente struttura:

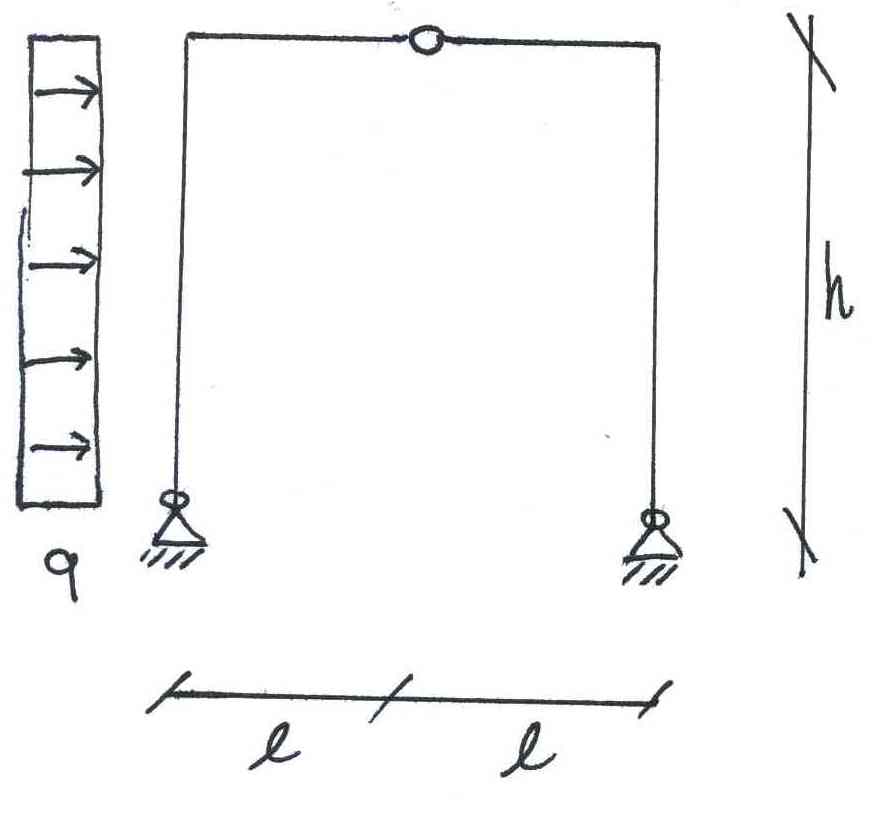
Calcolo l’isostaticità della struttura con la seguente formula: V= l

Il numero dei vincoli deve essere uguale al numero dei gradi di libertà della struttura.

l = 3 (aste) x 4 (gradi di libertà) =12

La struttura ha anche dei vincoli esterni che in questo caso sono 4 per per ogni cerniera.

Per calcolare il numero di vincoli interni: V_i = 2*(n -1) n= numero di aste che arrivano alla cerniera interna.

Per la cerniera interna in A abbiamo: 2(1-1)=0

Per la cerniera interna in B abbiamo: 2(2-1)=2

Per la cerniera interna in C abbiamo: 2(1-1)=0

Quindi: V_i= 2

V=V_e+V_i

V= 4 V_e + 2 V_i = 6

V 6 < l 12

LA NOSTRA STRUTTURA NON E’ ISOSTATICA!

ABBIAMO UNA STRUTTURA IPERSTATICA!!!! Perché…. IL NUMERO DI GRADI DI VINCOLO E’ MAGGIORE DEL NUMERO DI GRADI DI LIBERTA’!

V 6 > g 4

Niente pauraaa! Possiamo ricondurre questa struttura iperstatica ad una isostatica facendo il calcolo delle reazioni verticali considerando la struttura come un corpo unico!

Facciamo polo in A e calcoliamo l’equilibrio alla rotazione.

∑M_A=0 -> -qh*h/2 + 2lc = 0 c=qh²/4l

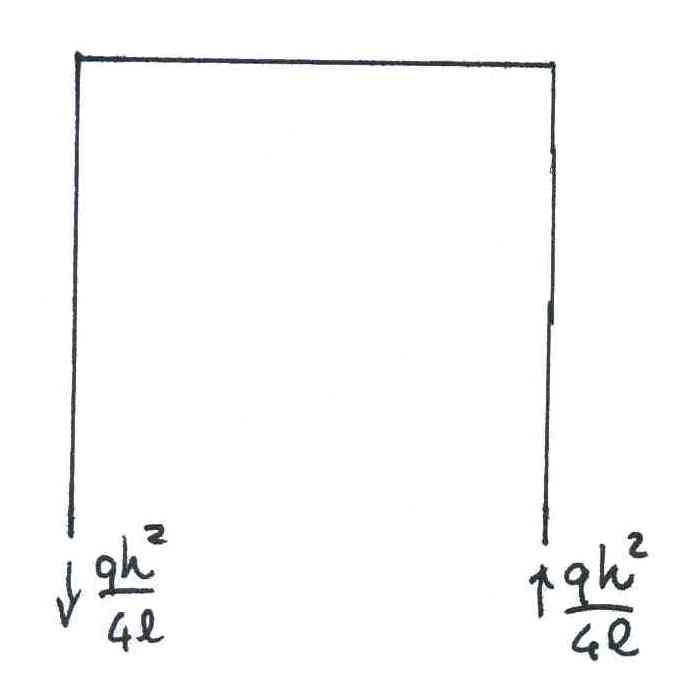
Ora divido la struttura in due parti perché mi servono altre informazioni per risolvere la struttura. Possiamo subito trovare f e sostituire perché siamo sull’asta orizzontale. Ricordandoci che in base alla convenzione positiva:

Gli spigoli portano discontinuità delle azioni di contatto! Quello che nell’asta verticale è un reazione verticale, sull’asta orizzontale diventa sforzo normale. T=N

 

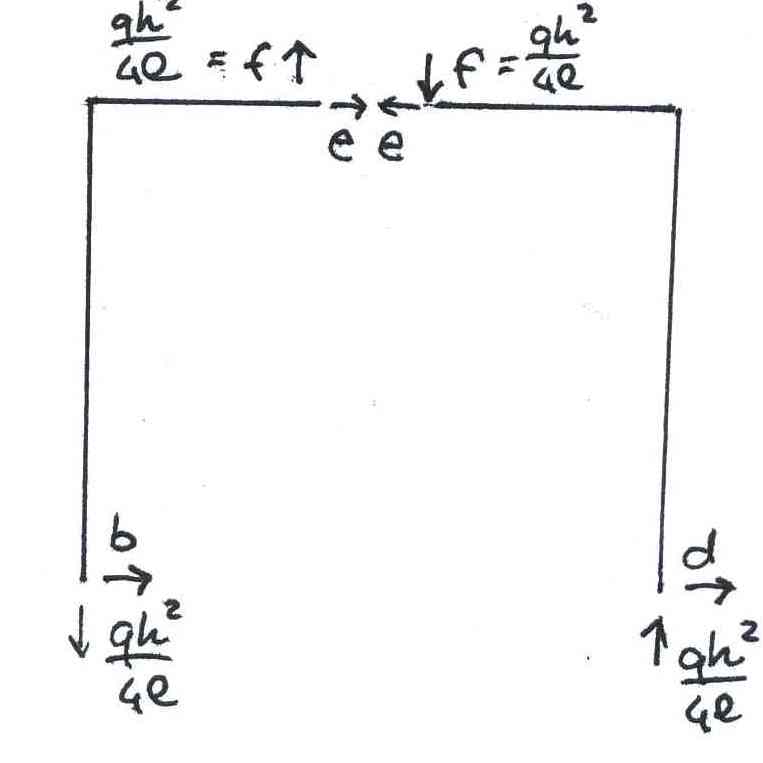
Ripeto l’equilibrio alla rotazione nel polo A:

∑M_A=0 -> -qh²/2 + qh²/4l*l-eh=0 -> e= -qh/4 cambio il verso nella struttura!

Adesso pongo tutte le reazioni nel sistema e mi assicuro che tutto sia in equilibrio! Possiamo notare però che la struttura risulta simmetrica se non per le reazioni orizzontali sulle aste verticali che devono bilanciare il carico distribuito laterale.

 

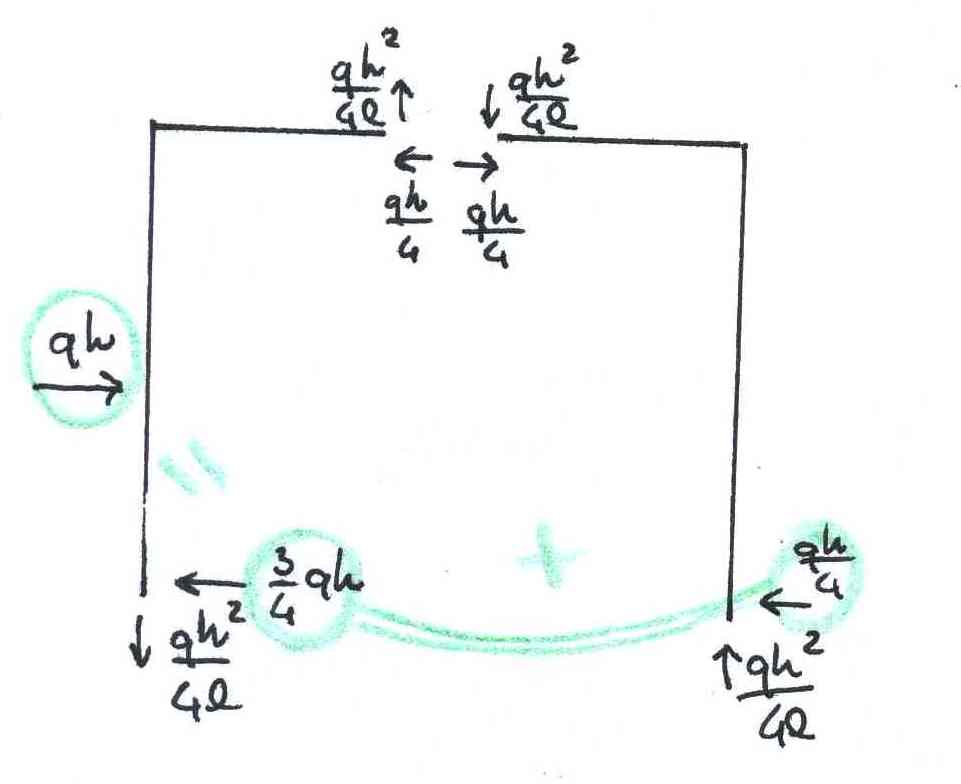
A questo punto posso disegnare con il metodo qualitativo i diagrammi di N, T e M.

Il diagramma della normale è costante poiché non vi sono carichi distribuiti che gravano assialmente sulle aste. Abbiamo valori positivi per la trazione e negativi per la compressione.

DIAGRAMMA N

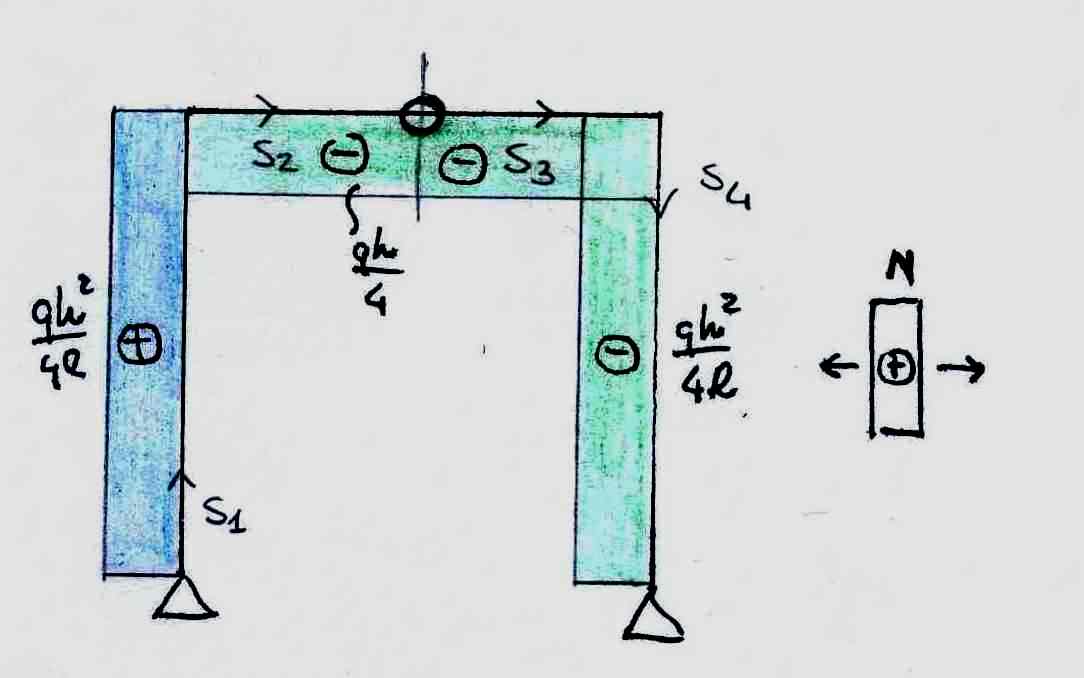
Il diagramma del taglio risulta costante per tutta la struttura tranne nel tratto verticale di sinistra dove abbiamo il carico distribuito. In questo caso il taglio diventa lineare (una retta in parole povere! In questo caso porta un “salto” a 3/4 di h partendo dal basso.

DIAGRAMMA T

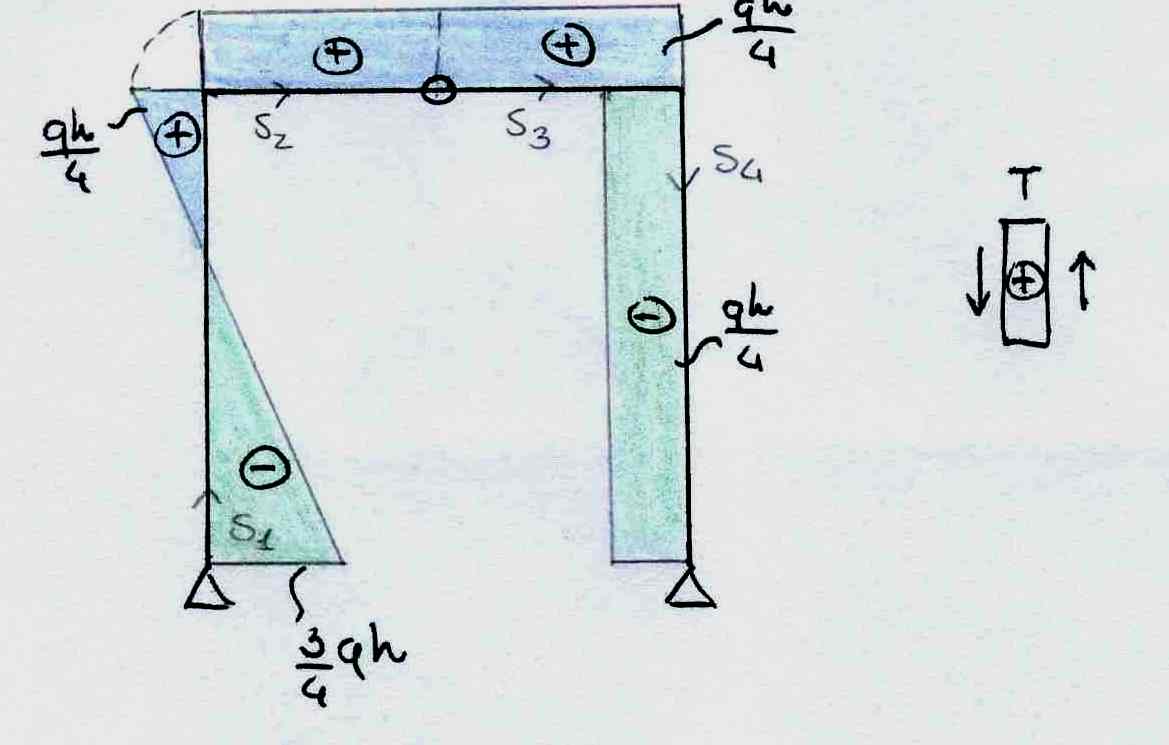
Per il diagramma del momento dobbiamo ricordare che il momento si disegna sempre dal lato delle fibre tese, e che quando:

TAGLIO COSTANTE = MOMENTO LINEARE

TAGLIO LINEARE = MOMENTO PARABOLICO

Il momento integra la funzione del taglio. (sale di un grado: x=x²). Dobbiamo inoltre ricordarci che quando il momento è massimo, il taglio è nullo e viceversa. In questo caso il momento massimo è M_max= -9/32qh²

DIAGRAMMA M

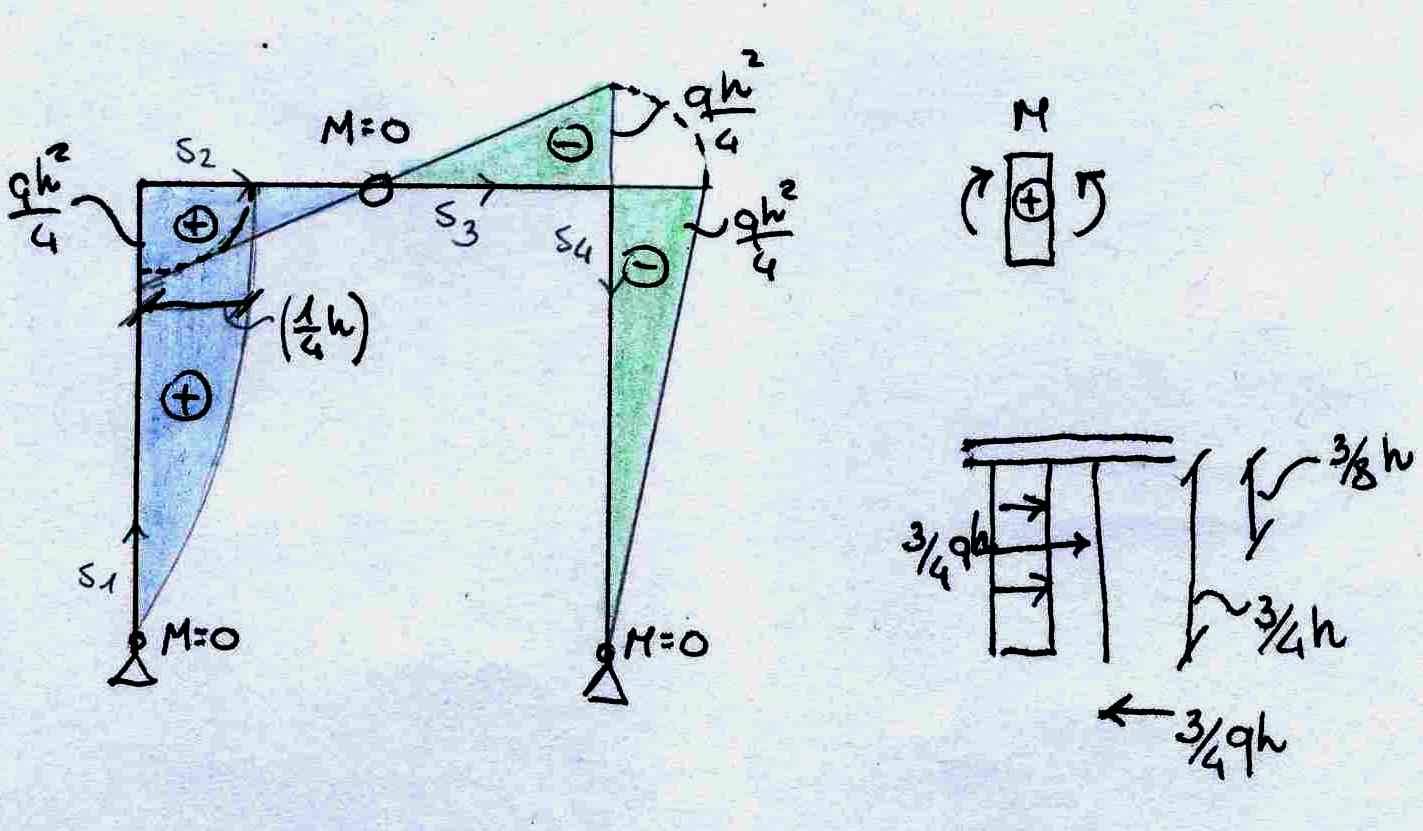
Adesso verifichiamo la struttura con SAP2000.

Ormai questa struttura si disegna in modo rapido! Dobbiamo ricordarci che questa volta il carico è distribuito e non puntuale. Dopo aver inserito il carico tramite define ->load patterns , assegno il carico distribuito tramite Assign ->Frame Loads -> Distribuited. Cosa importante! Come faccio a far riconoscere a Sap la cerniera???? Dopo aver inserito la cerniera, seleziono una volta l’asta orizzontale di sinistra e vado su Assign ->Frame Relases e spunto per il momento33 end; poi ripeto la stessa cosa per l’asta a destra della cerniera e questa volta però spunto start. Adesso posso far partire l’analisi.

Schema della deformata:

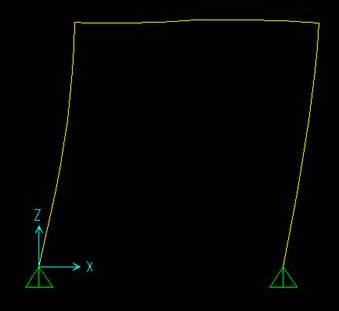
Questi sono i diagrammi:

 

ex_4) CALCOLO DI UN PORTALE A TRE CERNIERE CON CARICO PUNTULE VERTICALE

Analizziamo un portale con una cerniera e un carico puntuale. La struttura è simmetrica.

 

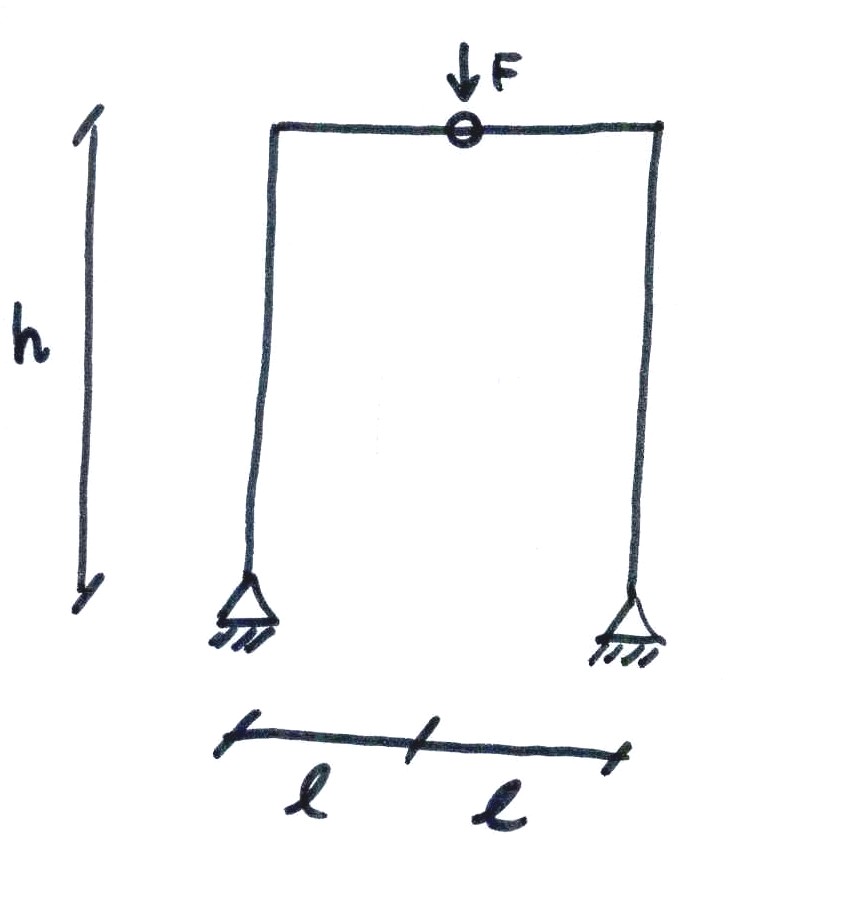
Anche in questo caso possiamo ricondurre questa struttura iperstatica ad una isostatica facendo il calcolo delle reazioni verticali considerando la struttura come un corpo unico! In questo caso poniamo una reazione verticale e una orizzontale sia per la cerniera a destra che per quella a sinistra, ed otteniamo le reazioni a,b,c,d. 

 

 

 

 

 

 

 

Notiamo in questo caso che la struttura essendo simmetrica mi permette di dividere la forza F verticale in due forze che si dividono quel carico in modo uguale e contrario! Quindi avremo la forza F ripartita tra a e c pari ad F/2.

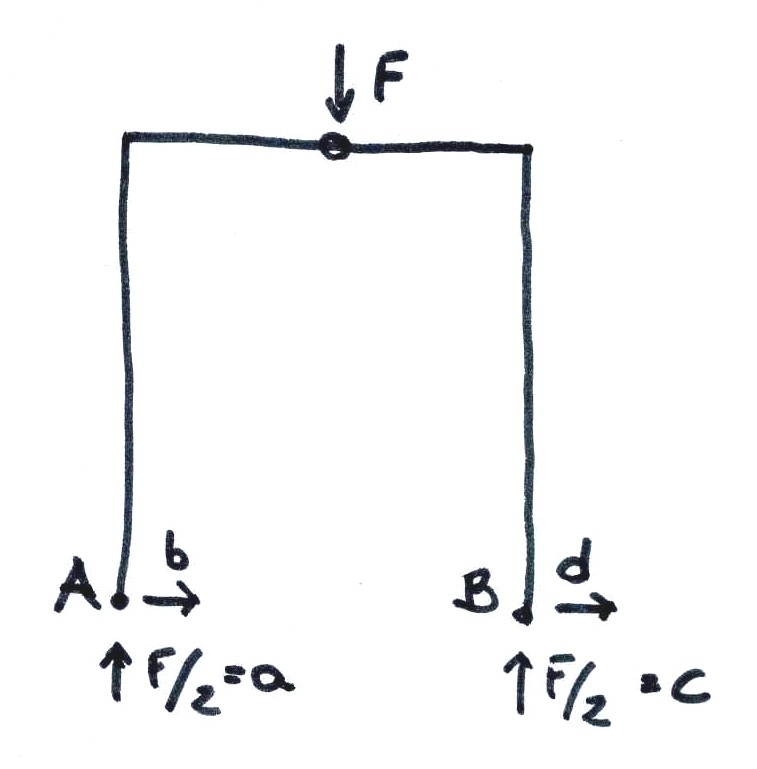
 Per controllo facciamo polo in A e calcoliamo l’equilibrio alla rotazione.

∑M_A=0     ->    c*2l-Fl=0      c=F/2

 

 

 

 

 

Ora spezzo la struttura in due parti perché mi servono altre informazioni per risolvere la struttura. Possiamo fare il calcolo per bilanciare il nodo:

∑F_x(B)=0   ->     -e-g=0    -> -e= -g

∑F_y(B)=0   ->     -F-f-h=0 ->  f= -F-h  ->  h= -F+F/2

 

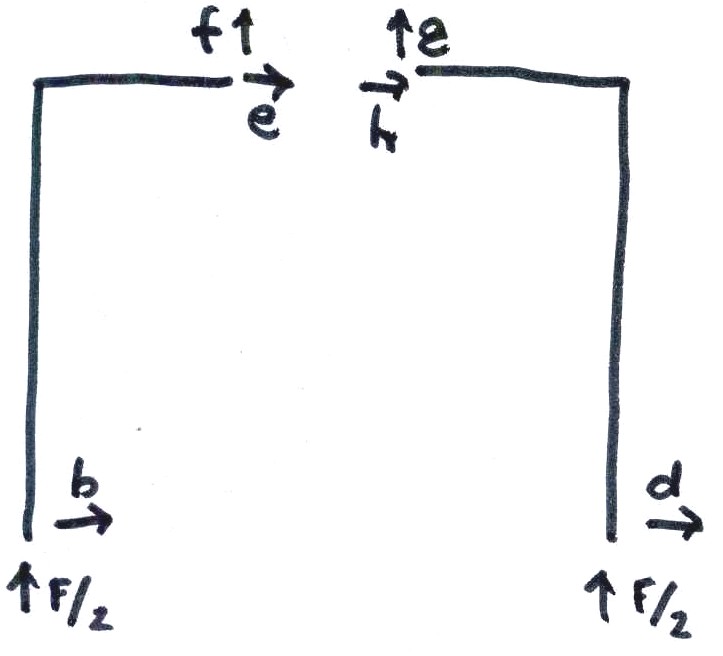
Ripeto l’equilibrio alla rotazione nel polo A per trovare le reazioni vincolari mancanti:

∑M_A=0     ->    -F/2*l -eh=0     ->  e= -Fl/2h   sostituisco   -e= -g   -> g=Fl/2h

 Adesso pongo tutte le reazioni nel sistema e mi assicuro che tutto sia in equilibrio! Dove ho ipotizzato verso negativo, cambio direzione alla freccia e rendo tutto positivo.

 

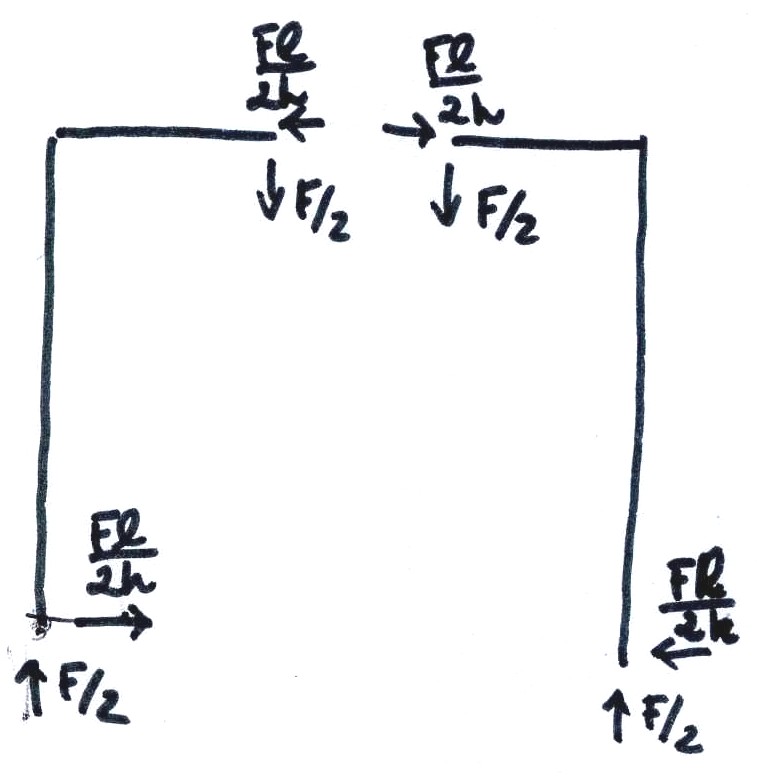
A questo punto posso disegnare con il metodo qualitativo i diagrammi di N, T e M.

Per studiare questi diagrammi possiamo utilizzare le equazioni di singolarità:

Fx = N negativo o di sinistra – N positivo o di destra

Fy= T negativo o di sinistra –  T positivo o di destra

C= M negativo o di sinistra – M positivo o di destra

Inoltre sappiamo che quando c’è una forza applicata, in quel punto ci sarà un “salto” con un punto di non derivabilità.

             

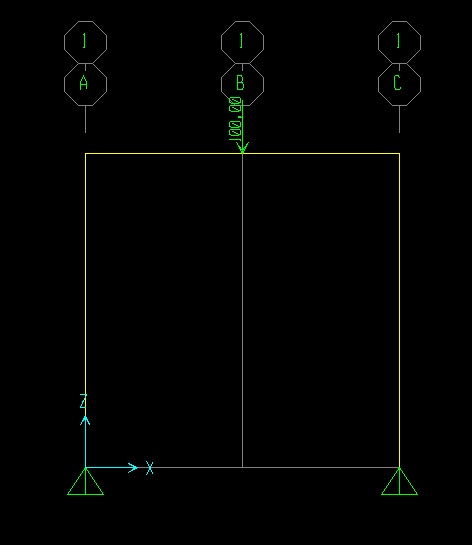
Ho svolto subito i calcoli con SAP2000 ricordando che per assegnare il carico puntuale vado su Assign ->Joint Loads ->Forces.  Per assegnare il verso della forza dobbiamo mettere il segno meno davanti al carico che assegniamo, ed avremo carichi gravitazionali verso il basso; in questo caso -100KN.

DIAGRAMMA N

 

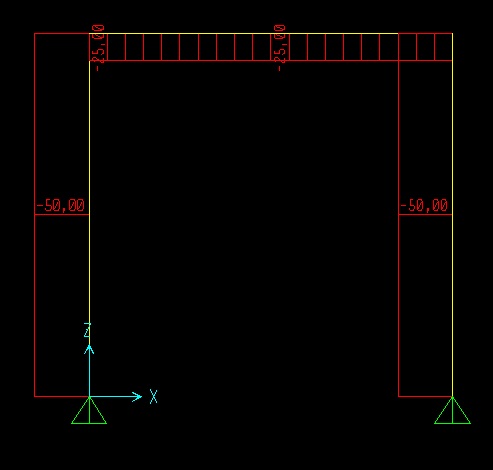
Il diagramma della normale è costante poiché non vi sono carichi distribuiti che gravano assialmente sulle aste, e il valore sarà pari alle reazioni vincolari che stanno ai bordi.

DIAGRAMMA T

 

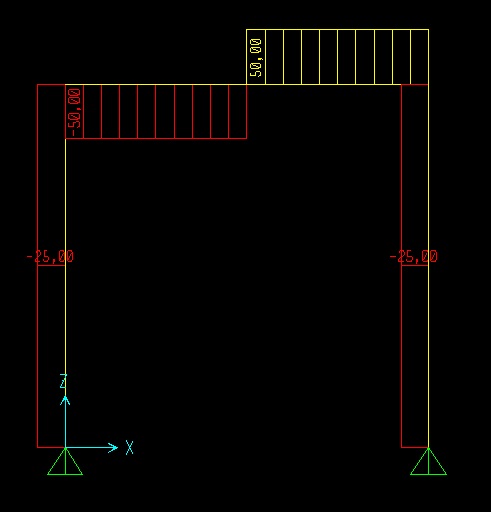
Il diagramma del taglio risulta costante per tutta la struttura tranne nel tratto orizzontale dove abbiamo la forza concentrata. In questo caso il taglio avrà un salto pari alla forza F applicata.

DIAGRAMMA M

 

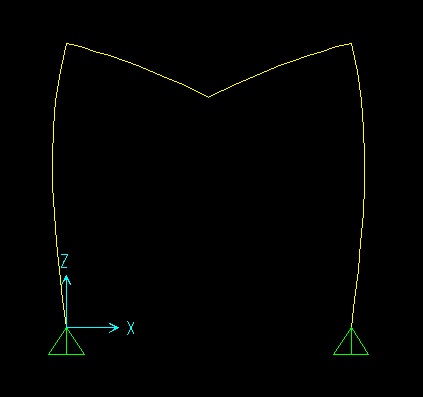
Avendo un TAGLIO COSTANTE ilMOMENTO saràLINEARE su tutte e tre le aste e pari a zero nelle tre cerniere.Negli spigoli della struttura avremo un valore lineare (triangolare) pari a Fl/2.

Il diagramma della deformata risulterà questo:

 

Qual è il primo edificio in calcestruzzo armato a Roma?

Il primo edificio in cemento armato è l’ex Gil di Luigi Moretti, situato nel quartiere di Trastevere e datato 1933-37. L’edificio accorpava in origine ben tre organismi relativamente autonomi dove si svolgevano attività di rappresentanza, sportive e sanitariee Anch’esso presenta un telaio in cemento armato. L’inedita tipologia delle bianche palestre all’aperto era ottenuta sovrapponendo pilastri e solai: ecco appunto la sintesi tra l’immagine voluta e la funzione necessaria, concretizzata attraverso il disegno di una struttura pura. Nella torre l’ossatura in cemento armato è, invece, nascosta per ottenere un volume chiuso e astratto: i quattro pilastri sono collegati da una tamponatura a cassetta costituita da laterizi posati a due teste e da una fila di laterizi intonacata all’interno. Oltre che per rilevanza dal punto di vista strutturale, esso è considerato una delle più importanti opere architettoniche  moderne della capitale, in quanto manifesto esplicito del razionalismo romano e dunque monumento significativo di confine tra l'architettura tradizionale e l'innovazione moderna di matrice europea.

 

 ex_5) DIMENSIONAMENTO TRAVI E TRAVETTI IN LEGNO, ACCIAIO E CALCESTRUZZO

 Per questa esercitazione dimensioneremo una trave con tre diversi materiali da costruzione: LEGNO, ACCIAIO e CALCESTRUZZO. Ho preso come impalcato di riferimento l’abitazione unifamiliare progettata per il Laboratorio di Progettazione1. Abbiamo una parte dell’impalcato coperta da una terrazza corrispondente ai pilastri B2 –B3 e C2 –C3 e una parte che prevede il piano superiore del duplex. Calcolo quindi la trave B1-B2 che porta il carico del solaio del piano superiore.

 

 

 

 

 

 

 

 

 

 

 

 

 

La trave presa in esame ha una luce di 4,7m e un interasse di 4,84m. L’area di influenza (ovvero il carico che la trave dovrà sopportare) sarà pari a metà dell’interasse a destra della trave in esame e metà sinistra per tutta la luce. Quindi:     

 AREA DI INFLUENZA-> 4,7m x (2,1m+2,75m) =22,795 mq        LUCE:  4,7m      INTERASSE: 4,85m

Dobbiamo considerare che per ogni tipo di materiale, abbiamo diversi carichi che incidono sulla struttura.

Uguale per tutti risulta il carico Qa= sovraccarico accidentale 2KN/mq

 Questo dato è stato preso dalle NTC (d.m. 14.01.2008) dalla tabella 3.1.II in cui c’è scritto che il carico d’esercizio per gli “Ambienti ad uso residenziale” di categoria A, è legato alla funzione dell’edificio,e tiene conto del numero di persone che passano nell’edificio, del peso dei mobili….

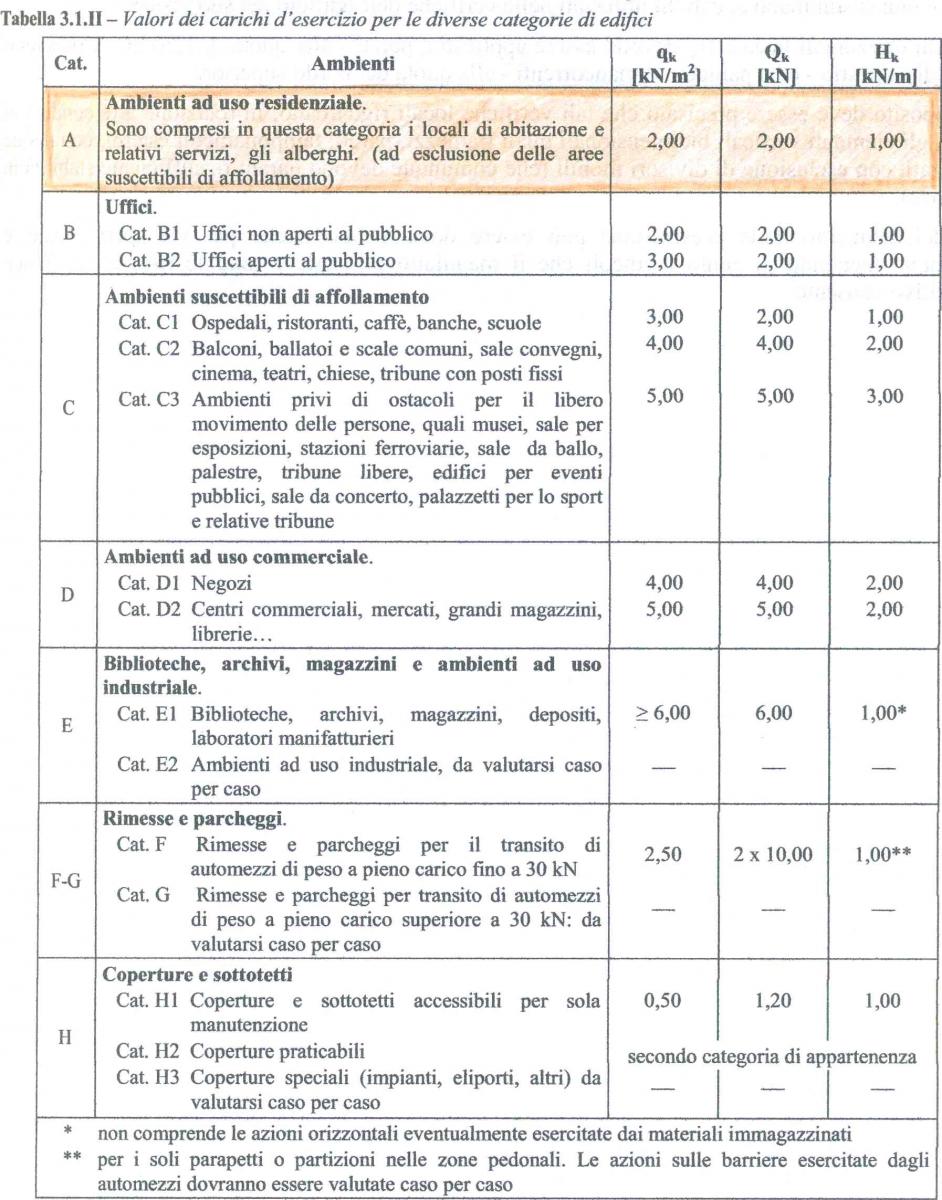
Poi abbiamo dei carichi Qs= carichi strutturali dati dal peso proprio della struttura (travetti, soletta, pignatte…)

 e dei carichi Qp= carichi non strutturali o permanenti sono quegli elementi che compongono il solaio, dati da massetto, pavimento, intonaco e si considerano anche gli impianti, i tramezzi…

Per trovare il carico Q_TOTdobbiamo sommare i carichi Q_TOT= Qa+Qs+Qp

Nel nostro caso l’impalcato risulta una trave doppiamente appoggiata con un carico Q_TOT. Il momento massimo della struttura è ql²/8dove lè la luce del progetto.

                                                                      

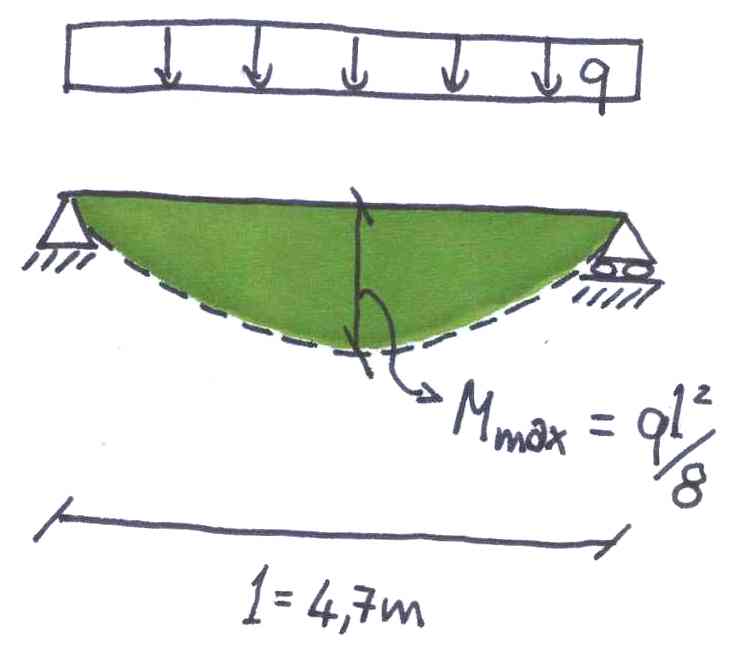
Adesso andiamo a calcolare la nostra struttura con i tre materiali:

LEGNO

Per il legno dobbiamo calcolare sia i travetti che la trave principale (in legno lamellare) per capire quale sarà la dimensione della nostra trave. Progettiamo il nostro solaio:

    

Per calcolare il nostro travetto, consideriamo la luce con la campata maggiore. Abbiamo una luce di 5,5 m (campata maggiore, pilastri A1-B1) e un interasse dei travetti di 0,50 m. Facciamo l’analisi dei carichi su un metro quadro di solaio:

DIMENSIONAMENTO DEL TRAVETTO

Sovraccarico accidentale

Qa= 2 KN/mq per civile abitazione (uguale per tutti i materiali)

Carico strutturale

 P (peso)= V (volume) * γ (peso specifico)

 

Tavolato (0,035*1*1)mc * 5,25 KN/mc = 0,18 KN

Qs=P/A = 0,21KN/1mq = 0,18 KN/mq

Oppure Qs= peso specifico*spessore = 5,25KN/mc * 0,035 m= 0,18 KN/mq

Sovraccarico permanente

• Pavimento in legno spessore di 2cm    qp 6,3KN/mc*0,02 m= 0,12KN/mq
• Massetto spessore di 2cm                   qp 24 KN/m³*0,02m = 0,48 KN/mq
• Isolante acustico spessore di 4cm        qp 4 KN/m³ *0,04m = 0,16 KN/mq
• Caldana spessore di 4cm                    qp 10 KN/m³ * 0,04m = 0,4 KN/mq
• Incidenza impianti                              qp= 0,5 KN/mq
• Incidenza tramezzi                                qp = 1 KN/mq

Qp= 0,12+0,48+0,16+0,4+0,5+1= 2,66 KN/mq

Adesso inserisco questi dati nel foglio Excel per trovare il carico totale e procedere con il dimensionamento dei travetti. Inserisco i valori dei tre carichi e quello dell’interasse. Per trovare il carico totale al metro lineare bisogna moltiplicare la somma dei carichi per l’interasse:

 

Interasse (m)	Qs (KN/mq)	Qp (KN/mq)	Qa (KN/mq)	Q (KN/m)
0,5	0,18	2,66	2,00	2,42

Q_TOT= interasse*(Qs+Qp+Qa) = 0,5*(0,18+2,66+2) = 2,42KN/m

A questo punto devo calcolare il momento massimo ricordandoci che stiamo calcolando una trave doppiamente appoggiata. Ricordiamoci che la luce dei travetti è pari a 5,5m.

 

q (KN/m)	luce (m)	M (KN*m)
2,42	5,5	9,150625

M_max= (Q*l^2)/8 = 9,15 KN*m

A questo punto devo progettare le dimensioni del mio travetto utilizzando la formula seguente:

                                                                                        

K_modè il coefficiente correttivo che tiene conto della durata del tempo e dell’umidità della struttura. I suoi valori possono esser scelti nella tabella presa dalla normativa; in questo caso vale 0,6 perché rispetta la classe di servizio 1 in cui l’umidità relativa non supera il 65% se non per poche settimane l’anno e la temperatura di equilibrio del materiale si mantiene tale intorno ai 20°C;

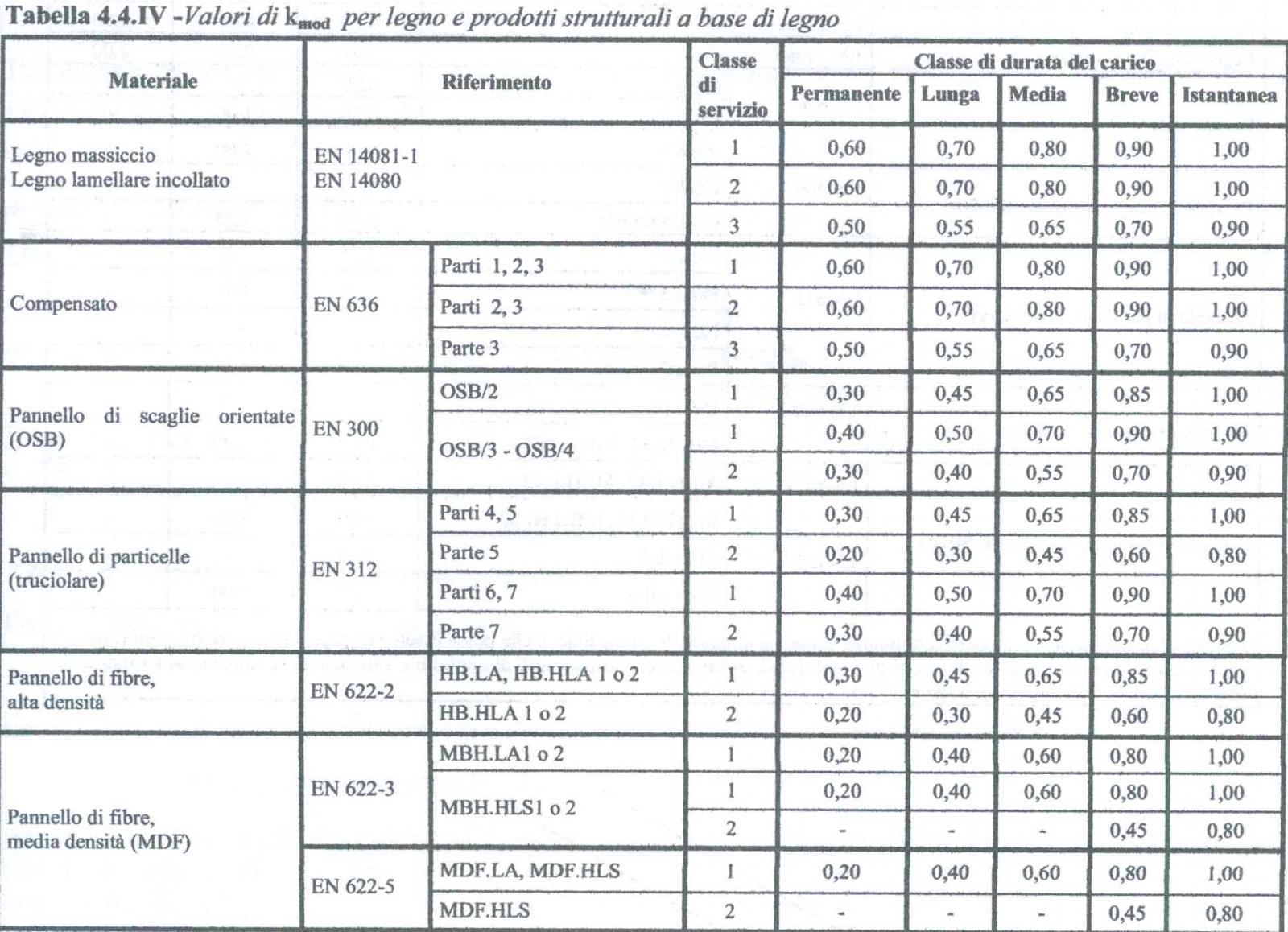
f_k  è il valore caratteristico della proprietà del materiale, detta anche tensione di snervamento del materiale, ed è quel valore che troviamo scritto vicino la classe di legno che scegliamo: in questo caso scegliamo una classe di resistenza intermedia GL 28h che corrisponde ad un valore di f_k= 28 N/mmq;

γ_m=1,45 è il coefficiente parziale di sicurezza che varia a seconda del materiale, qui sotto tabellato;

Ho scelto in questo modo laclasse di resistenza del legno lamellare.

Il nostro fD sarà pari a: (0,6*28)/1,45 =11,59 N/mmq

fm,k (N/mmq)	f_D (N/mmq)
28	11,59

Come possiamo vedere il valore della tensione di progetto, che di solito è dato dal valore di crisi diviso per un coefficiente di sicurezza, è ulteriormente dimezzato rispetto al valore di resistenza a flessione poiché, per un materiale viscoso come il legno, bisogna tener conto anche degli effetti del tempo e dell’umidità che incidono profondamente sulle prestazioni del materiale.

Ora, inserendo un valore di base (b=15cm), otteniamo il valore dell’altezza minima che dovrà avere il travetto h= ((6*M*1000)/(b*fd))^5= 13,77 cm.

Ipotizzo quindi un travetto con un’altezza maggiore rispetto al valore trovato per stare in sicurezza, quindi avrò un travetto di  h=20cm e b=15cm e procedo con la verifica.

Verifica

Qtra metro lineare= area sezione * peso specifico = 0,15m*0,2m*5,25KN/mc =0,157 KN/m

Qtr a mq= Qtr/interasse=0,157/0,5= 0,315KN/mq

Ripeto i calcoli sulla tabella Excel.

Aggiungo quindi al calcolo del carico strutturale anche il peso del travetto e ottengo che per la base scelta di 15cm avrei bisogno di un travetto alto minimo 18,02cm che è un valore comunque minore rispetto ai 20 cm del travetto ipotizzato,il dimensionamento del travetto è quindi corretto.->TRAVETTO IN LEGNO GL28h 15X20cm

DIMENSIONAMENTO TRAVE PRINCIPALE

Utilizzo lo stesso procedimento per calcolare la trave principale considerando che adesso il nostro interasse è di 4,85m e la luce è di 4,7m.

Sovraccarico accidentale

Qa= 2 KN/mq per civile abitazione (uguale per tutti i materiali)

Carico strutturale

• Tavolato (0,035*1*1)mc * 5,25 KN/mc = 0,18 KN
• Travetti                 0,02 m * 6 KN/mc  = 0,12 KN/mq

Qs=P/A = 0,18KN/1mq + 0,12KN/1mq = 0,30 KN/mq

Oppure Qs= peso specifico*spessore = 5,25KN/mc * 0,035 m= 0,18 KN/mq

Sovraccarico permanente

• Pavimento in legno spessore di 2cm      qp 6,3KN/mc*0,02 m= 0,12KN/mq
• Massetto spessore di 2cm                    qp 24 KN/m³*0,02m = 0,48 KN/mq
• Isolante acustico spessore di 4cm         qp 4 KN/m³ *0,04m = 0,16 KN/mq
• Caldana spessore di 4cm                      qp 10 KN/m³ * 0,04m = 0,4 KN/mq
• Incidenza impianti                               qp= 0,5 KN/mq
• Incidenza tramezzi                              qp = 1 KN/mq

Qp= 0,12+0,48+0,16+0,4+0,5+1= 2,66 KN/mq

Q_TOT= interasse*(Qs+Qp+Qa) = 4,85*(0,30+2,66+2) = 24,056KN/m

M_max= (Q*l^2)/8 = 24,056*4,7^2/8= 66,42KN*m

fD =(0,6*28)/1,45 =11,59 N/mmq

Ipotizzando la base 30 cm avremo un’altezza pari a 33,86cm che quindi può essere approssimata a 35cm. Ora verifico il risultato ottenuto:

Qtr al metro lineare= A x γ = 0,30 m x 0,35 m x 6 KN/m³= 0,63 KN/m

Qtr al metro quadro= Qtr / interasse = 0,63 KN/m / 4,85 m = 0,129 KN/mq

Qs = 0,30 KN/mq + 0,129 KN/mq = 0,429 KN/mq

Ottengo un’altezza pari a 34,30 cm quindiil dimensionamento della trave è corretto.->TRAVE IN LEGNO GL28h 30X35cm.

 

ACCIAIO

Per l’acciaio dobbiamo calcolare la IPE secondaria e capire quale sarà la dimensione della trave principale. Progettiamo il nostro solaio: 

   

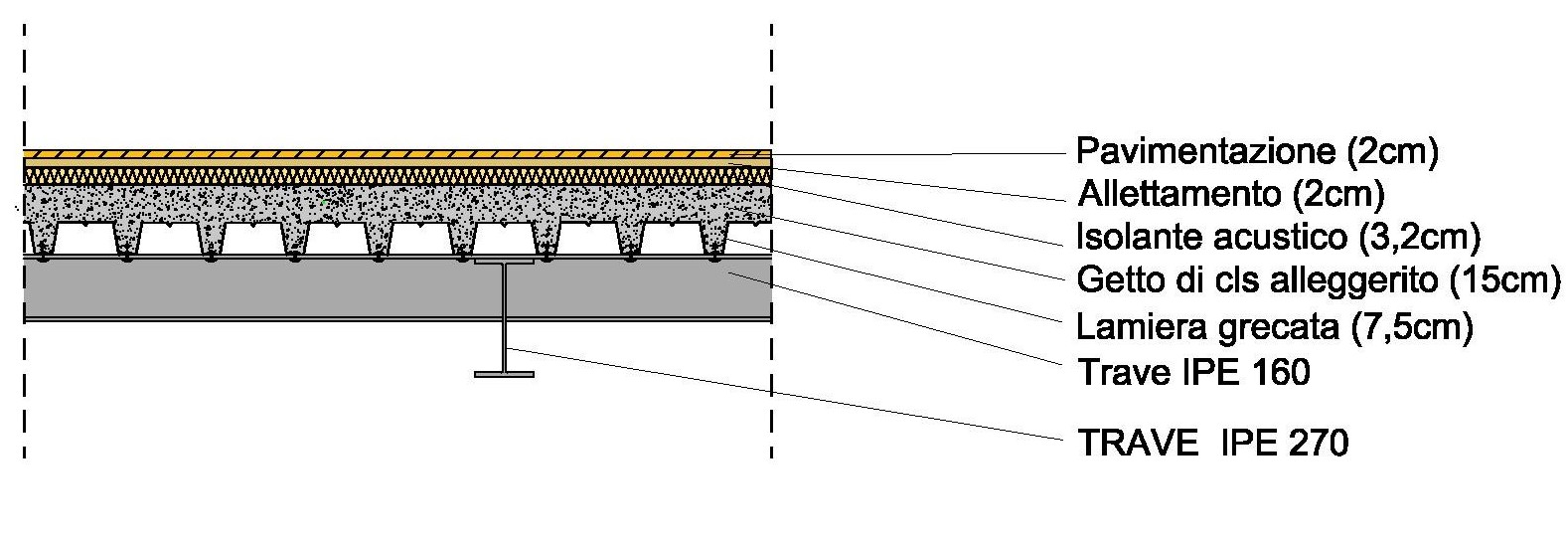
Per calcolare il nostro travetto, consideriamo la luce con la campata maggiore. Abbiamo una luce di 5,5 m e un interasse dei travetti di 1 m. Facciamo l’analisi dei carichi su un metro quadro di solaio:

DIMENSIONAMENTO DEL TRAVETTO

Sovraccarico accidentale

Qa= 2 KN/mq per civile abitazione (uguale per tutti i materiali)

Carico strutturale

Per il calcolo strutturale ci serviamo di una delle tabelle da normativa che ci illustrano che per una luce superiore ai 4,20m abbiamo una soletta di 15cm con  una lamiera grecata di 7,5cm.

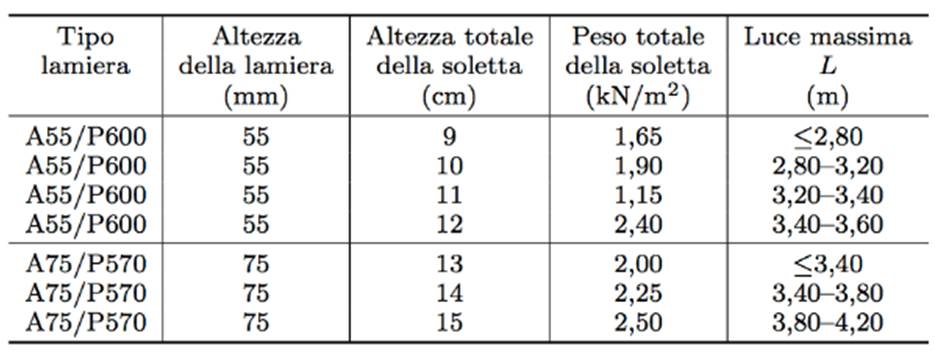
Qs= 2,50 KN/mq

Sovraccarico permanente

• Pavimento spessore di 2cm                    qp 5 KN/mc*0,02 m= 0,10 KN/mq
• Allettamento spessore di 2cm                 qp 18 KN/m³*0,02m = 0,36 KN/mq
• Isolante acustico spessore di 3,2cm        qp 4 KN/m³ *0,032m = 0,128 KN/mq
• Incidenza impianti                                 qp= 0,5 KN/mq
• Incidenza tramezzi                                qp = 1 KN/mq

Qp= 0,10+0,36+0,128+0,5+1= 2,088 KN/mq

Adesso inserisco questi dati nel foglio Excel per trovare il carico totale e procedere con il dimensionamento dei travetti. Inserisco i valori dei tre carichi e quello dell’interasse. Per trovare il carico totale al metro lineare bisogna moltiplicare la somma dei carichi per l’interasse:

interasse (m)	qs (KN/mq)	qp (KN/mq)	qa (KN/mq)	q (KN/m)
1	2,5	2,088	2,00	6,588

Q_TOT= interasse*(Qs+Qp+Qa) = 1 * (2,5+2,088+2) = 6,588 KN/m

A questo punto devo calcolare il momento massimo ricordandoci che stiamo calcolando una trave doppiamente appoggiata. La luce dei travetti è pari a 5,5m.

q (KN/m)	luce (m)	M (KN*m)
6,588	5,5	24,91088

 

M_max= (Q*l^2)/8 =  6,588*5,5^2/8= 24,91 KN*m

Classe di resistenza dell’acciaio

Per progettare le dimensioni del mio travetto utilizzo la seguente tabella con le classi di resistenza per l’acciaio appartenenti al primo gruppo che prevedono acciai non legati, cioè privi di altri metalli nella composizione della lega. Scelgo una classe di resistenza medio-bassa S275 con una tensione di snervamento pari a fyk=275 MPa.

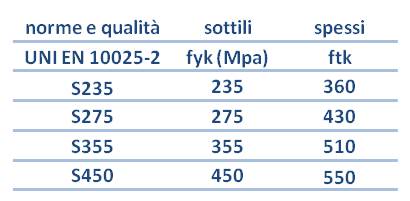
Il nostro fD sarà pari a: fyk/coefficiente di sicurezza dell’acciaio= 275/1,05 = 261,9 N/mmq

Ora calcoliamo il modulo di resistenza Wx = M/fD = 24,91KNm / 261,9 N/mmq * 1000 = 95,11 cmc.

M (KN*m)	fy,k (N/mmq)	F_D (N/mmq)	Wx (cm^3)
24,91088	275	261,90	95,11

Ottenuto questo valore, vado sul profilario delle IPE e cerco nella colonna del modulo di resistenza Wx un valore uguale o superiore a quello che ho ottenuto. Il valore più vicino è quello di una IPE160 con Wx=109cmc, in questo modo mi pongo in sicurezza.

Adesso vado ad aggiungere nei miei calcoli il peso della trave e inserisco nuovamente i dati nella tabella Excel per fare la verifica.

Verifica

Il peso della IPE lo troviamo sempre sul profilario P=15,8 Kg/m

Qtra metro lineare=0,158 KN/m

Qtr a mq= Qtr/interasse= 0,158 KN/m / 1 m= 0,158 KN/mq

Qs= 2,5 KN/mq + 0,158 KN/mq = 2,658 KN/mq

Inserisco nuovamente i dati sulla tabella Excel:

Non si supera il valore di 109cmc, il nostro travetto è dimensionato correttamente! Si conferma un TRAVETTO IPE 160

DIMENSIONAMENTO TRAVE PRINCIPALE

Per calcolare la trave principale adesso ho un interasse è di 4,85m e una luce è di 4,7m.

Sovraccarico accidentale

Qa= 2 KN/mq per civile abitazione

Carico strutturale

Qs= carico soletta + carico travetto = 2,5 KN/mq + 0,158 KN/mq = 2,658 KN/mq

Sovraccarico permanente

Qp= 0,10+0,36+0,128+0,5+1= 2,088 KN/mq

Q_TOT= interasse*(Qs+Qp+Qa) = 4,85*(2,658+2,66+2) = 32,71 KN/m

M_max= (Q*l^2)/8 = 32,71*4,7^2/8= 90,34 KN*m

fD =fyk/coefficiente di sicurezza= 275/1,05 =261,9 N/mmq

Wx= M/fD= 90,34/261,9= 344,95 cmc

La trave IPE  più vicina al valore e che mi permette di progettare in sicurezza è una IPE 270 con Wx= 429cmc

Verifica

Dal profilario calcolo il peso della IPE 270 che è P=36,1 Kg/m

Qtra metro lineare=0,361 KN/m

Qtr a mq= Qtr/interasse= 0,361 KN/m / 1 m= 0,361 KN/mq

Qs= 2,658 KN/mq + 0,361 KN/mq = 3,019 KN/mq

Inserisco nuovamente i dati sulla tabella Excel:

Non si supera il valore di 429cmc, la trave è dimensionata correttamente! Si conferma un TRAVE  IPE 270

 

CALCESTRUZZO ARMATO

Per il calcestruzzo dobbiamo calcolare la trave principale. Abbiamoun interasse è di 4,85m e una luce è di 4,7m.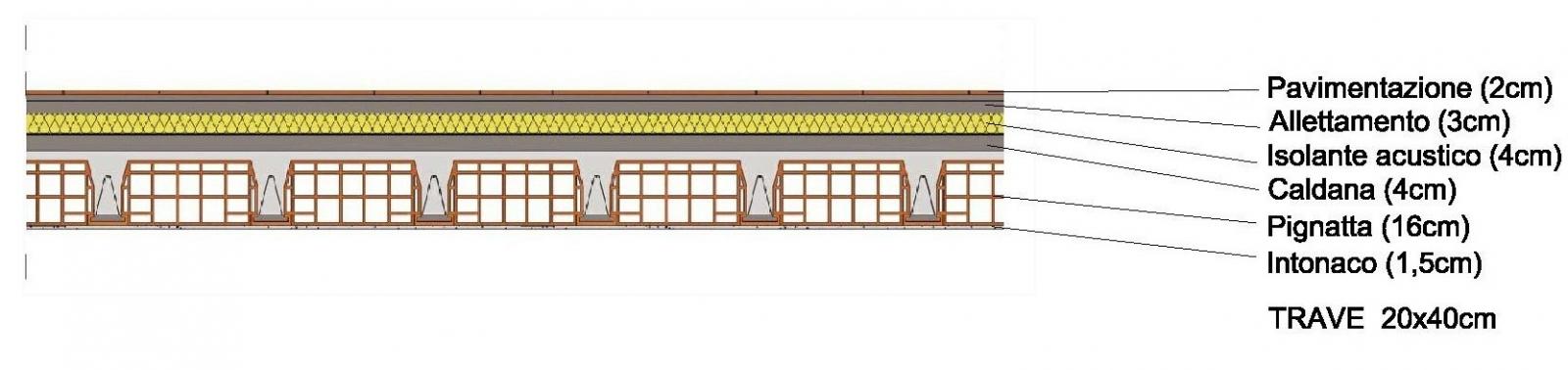

Sovraccarico accidentale

Qa= 2 KN/mq per civile abitazione (uguale per tutti i materiali)

Carico strutturale

Il carico è dato dalla somma delle Pignatte (16 cm) + Caldana (4cm) tenendo conto della luce del solaio. Dalla seguente tabella possiamo prendere i valori di riferimento in base alla nostra luce.

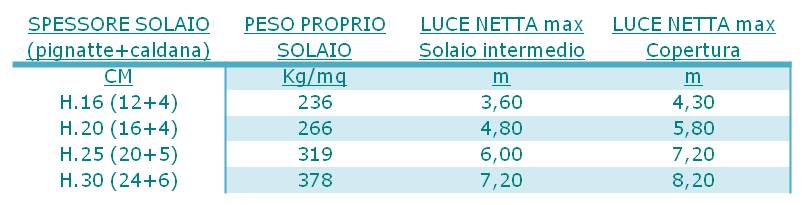
Qs= 2,66 KN/mq (per luci tra 3.60 e 48.0 m)

Sovraccarico permanente

• Pavimento spessore di 2cm               qp 5 KN/mc*0,02 m= 0,10 KN/mq
• Allettamento spessore di 3cm            qp 18 KN/m³*0,03m = 0,54 KN/mq
• Isolante acustico spessore di 4cm      qp 4 KN/m³ *0,04m = 0,16 KN/mq
• Intonaco spessore di 1,5cm               qp=0,3 KN/mq
• Incidenza impianti                            qp= 0,5 KN/mq
• Incidenza tramezzi                           qp = 1 KN/mq

Qp=0,1+0,54+0,16+0,3+0,5+1=2,60 KN/mq

Q_TOT= interasse * (Qs+Qp+Qa) =4,85 * ( 2,66 + 2,60 + 2) = 35,211 KN/m

interasse (m)	qs (KN/mq)	qp (KN/mq)	qa (KN/mq)	q (KN/m)
4,85	2,66	2,6	2,00	35,211

Calcolo del momento massimo

M_max= (Q*l^2)/8 = 35,211*4,7^2/8= 97,22 KN*m

Scelgo la classe di resistenza dell’acciaio

Per l’acciaio da calcestruzzo armato sono previste solo due categorie B450A e B450C che hanno lo stesso valore di tensione di snervamentofy=450 N/mmq ma una differente duttilità cioè si rompono a seguito di due diverse deformazioni e perciò sono associate a due diversi coefficienti di sicurezza.

Scelgo l’acciaio B450C più duttile ammesso in zona sismica che ha un coefficiente di sicurezza più basso pari 1,15.

Tensione di progetto dell’acciaio

fd_f= fy/γ_s= 450/1,15 = 391,30 N/mmq

Tensione di progetto del calcestruzzo

Il calcestruzzo presenta anche delle classi di resistenza cilindrica (che si riferiscono ai test fatti in laboratorio sui provini cilindrici e cubici). Le classi più usate sono la C20/25, C60/75  e la C40/50 come nel nostro caso. Inserisco il valore di resistenza cilindrica del calcestruzzo armato fck=40N/mmq

fd_c = 40/1,75= 22,85 N/mmq

dove 1,75 è il coefficiente di sicurezza del calcestruzzo armato.

Altezza utile

A questo punto devo trovare l’altezza della mia trave ed ipotizzo un valore di base b =20 cm, otteniamo così il valore di altezza utile hu che corrisponde alla distanza tra il lembo compresso della sezione e l’asse dell’armatura tesa.

Tramite il foglio Excel trovo prima il valore α e il valore r per determinare l’altezza utile:

α =  fd_c/ (fd_c+fd_s/15)= 0.47 (numero puro)

r =  ( 2/( α ( 1- α/3)))^0.5= 2.25 (numero puro)

hu= r √(M/ fD_c x b) = 32,84 cm

L’altezza totale H=hu+δ = 32,84 +5 = 37,84 cm

alfa	r	b (cm)	hu (cm)	delta (cm)
0,47	2,25	20	32,84	5

dove δ è la misura del copriferro che di solito misura 5cm.

Quindi se inizialmente potevo ipotizzare una trave alta 35cm, con il copri ferro, devo ipotizzare una trave di 40 cm per stare in sicurezza. Adesso faccio la verifica.

Verifica

Per fare la verifica prendo il valore finale del foglio Excel che mi indica il peso,

Qtra metro lineare= A * peso specifico= 1,89KN/m

Qtr a mq= Qtr/interasse= 1,89/4,7= 0,40KN/mq

Aggiungo quindi al calcolo del carico strutturale anche il peso della trave e ottengo un’altezza totale H=38,74cm che è un valore minore rispetto a H= 40cm scelta, il dimensionamento della trave è quindi corretto ->TRAVE 20x40cm

 

Il processo di produzione del legno lamellare

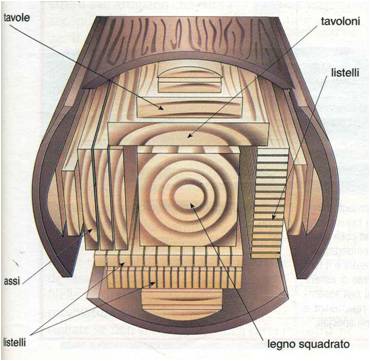Il processo di produzione del legno lamellare è l’insieme delle operazioni eseguite in appositi stabilimenti, che consistono essenzialmente nella riduzione del tronco in assi e nella loro ricomposizione, tramite incollaggio, fino a dare origine a elementi di forma e dimensione prestabilita.
                           
Il processo tecnologico consiste nelle seguenti fasi:

Scelta del legname

Le caratteristiche tecniche del prodotto finito dipendono dal materiale di base. E’ ovvio che per ottenere risultati attendibili, occorre partire da una materia prima avente caratteristiche il più omogenee e uniformi possibile.
Qualsiasi tipo di legname può essere potenzialmente utilizzato per tale tecnologia, anche se scelte tecnico-economiche indirizzano, di fatto, l’industria produttrice all’uso di legnami facilmente reperibili, incollabili e meno costosi, compatibilmente ai requisiti richiesti. In Europa si utilizza quindi quasi esclusivamente l’abete rosso, per lavorazioni speciali talvolta il pino silvestre, il larice e il rovere.
Le essenze legnose vengono suddivise, per il legno lamellare, in due categorie o classi, che ne individuano la qualità e le caratteristiche fisico-meccaniche e che condizionano i valori delle corrispondenti tensioni massime ammissibili.

Tali classi o categorie sono (secondo le DIN 1052):

categoria I: legno scelto senza traccia di putredine o danni di insetti, inclinazione massima della direzione delle fibre rispetto alla direzione della tavola non superiore al 10%, nodi sani, non raggruppati, con diametro massimo pari a 30 mm, peso specifico non superiore a 500 Kg/mc (al 20% di umidità) e spessore medio annuo di crescita del tronco non superiore a 3 mm.

categoria II: legno scelto con criteri meno rigidi, tuttavia senza traccia di putredine o danni di insetti, ma con tolleranze maggiori di diametro dei nodi (fino a 40 mm), inclinazione di fibre (fino al 12%), pesi specifici non inferiori a 400 Kg/mc (al 20% di umidità) e spessore medio annuo di crescita non superiore a 4 mm.

Dimensioni del materiale

La normativa DIN, mentre non fissa la lunghezza minima delle assi, ne limita invece lo spessore e la sezione trasversale e precisamente:a) l’area della sezione trasversale massima non deve superare 60 cm² (per legni di conifera), 50 cm² (per legni di latifoglia);
b) la massima larghezza consentita è pari a 25 cm per la singola lamella con uno spessore non superiore a 30 mm, anche se può essere aumentato fino a 40 mm in elementi costruttivi diritti, i quali non siano esposti a variazioni climatiche rilevanti.

Nella pratica costruttiva le lamelle hanno uno spessore finito intorno ai 33 mm e una larghezza pari a quella della sezione trasversale dell’elemento strutturale, normalmente variabile fra 10 e 22 cm, con variazioni modulari di 2 cm e lunghezza delle lamelle di 400-500 cm.

Essiccazione

L’essicazione è l’operazione tesa a ottenere quel grado di umidità del legno compatibile col tipo di colla e, soprattutto, confacente alla destinazione delle strutture. Generalmente essa deve essere compresa fra il 7 e il 16%. Fra due lamelle successive però la differenza di umidità non deve superare il 4%.

Gli impianti per la produzione del lamellare dispongono di essiccatoi. Il legname è messo nelle celle di essiccazione e portato al grado di umidità necessario alla lavorazione ed alla resistenza richiesta. Dopo l’essicazione, poiché il tasso di umidità non è regolare all’interno di una stessa lamella, essendo più basso in periferia che al centro, le lamelle vengono lasciate riposare per due, tre giorni all’interno dello stabilimento prima di essere portate alla linea di lavorazione.

Controllo della qualità delle tavole

Prima della giuntatura le tavole subiscono un controllo dell’umidità e della difettosità, più o meno automatizzato a seconda dell’azienda, il quale porta all’eliminazione dei difetti più gravi e delle eventuali sacche di umidità.

La verifica dell’umidità avviene sulle lamelle prima della loro intestazione per mezzo di test selezionatore tipo passa-non passa. Se l’umidità rilevata nelle lamelle è compresa fra i limiti prefissati, un segnale verde consente il proseguimento delle operazioni, altrimenti il segnale rosso lo arresta fino alla rimozione del pezzo fuori controllo. Le condizioni ambientali, invece, sono costantemente registrate su apposite carte che segnalano eventuali anomalie, evidenziando i valori che superano i limiti inferiori e superiori delle bande di controllo. Queste verifiche interessano tutto il reparto dove si svolgono le lavorazioni, che si succedono a cascata, dal deposito delle lamelle, alla loro intestazione, piallatura, incollaggio, sovrapposizione e pressaggio.
Contemporaneamente al controllo dell’umidità delle lamelle, viene effettuato quello visivo degli eventuali difetti del legno, come per esempio l’eccessivo numero di nodi, imbarcamenti, inclinazione delle fibre, cipollature, ecc. e vengono tagliate le estremità delle assi, eliminando screpolature e fessurazioni di testa. Questa fase deve essere affidata a maestranze qualificate e responsabili.

Giuntatura di testa

Per realizzare elementi strutturali di lunghezza maggiore della singola tavola o asse sono necessari giunzioni di testa. Di solito le giunzioni trasversali correnti fra le varie lamelle vengono effettuate con giunti detti a pettine o a dita, e vengono opportunamente sfalsate al fine di non indebolire una stessa sezione trasversale o una zona dell’elemento strutturale.Questo tipo di giunto è oramai nella prassi considerato come il più vantaggioso, in quanto   consente di ottenere un’ampia  superficie di incollaggio, una volta realizzata l’unione è auto serrante.
Successivamente alla fresatura si ha l’incollaggio di testa delle tavole, effettuato da apposite macchine che applicano forze di compressione variabili in relazione alla lunghezza dei denti dei giunti.

Piallatura e calibratura delle tavole

Le tavole così composte vengono piallate, in modo da offrire superfici piane in vista dell’incollaggio delle facce delle tavole per la successiva formazione della trave. Questo tipo di operazione, unitamente alla calibratura attraverso la quale si ottengono tavole di spessore costante, evita l’instaurarsi di tensioni che possono dare luogo alla formazione di cretti durante la pressatura. Inoltre la piallatura consente di ottenere superfici lisce, requisito molto importante in fase di incollaggio.

Incollaggio delle lamelle

Le colle e le operazioni di incollaggio costituiscono una fra le operazioni più importanti e delicate dal punto di vista operativo e tecnologico. Gli incollanti devono instaurare legami intermolecolari fra la colla stessa e le sostanze che costituiscono il legno, cioè le fibre di cellulosa e lignina, in modo da garantire, nel piano di incollaggio, lo stesso legame della corrispondente essenza legnosa. Le resistenze fisico-meccaniche del collante devono essere almeno eguali a quelle del legno, in modo che i piani di incollaggio non siano piani preferenziali di rottura.

Pressatura

Per realizzare l’incollaggio fra le lamelle bisogna sottoporre l’elemento strutturale a una pressione il più possibile uniforme; tale operazione viene effettuata in apposite presse. Le presse sono costituite da una struttura fissa sulla quale si fa agire un meccanismo di pressatura costituito normalmente da martinetti idraulici o pneumatici. L’operazione di posizionamento delle lamelle e di chiusura della pressa deve essere fatta il più rapidamente possibile, onde evitare che la colla cominci a indurire. Per la chiusura delle presse si procede dal centro verso le estremità. Le travi così realizzate rimangono in pressa per un periodo di 12 ore o più, secondo il tipo di colla, la temperatura e la forma della trave. La temperatura ambiente non deve comunque essere mai inferiore a 18° C. Il legname non deve variare il proprio contenuto idrometrico durante la produzione delle travi poiché il processo chimico che sta alla base della polimerizzazione delle colle è fortemente influenzato dalle condizioni termoigrometriche dell’ambiente in cui esso avviene.

Piallatura delle travi

Rimosse dalla pressa le travi sono lasciate 1-2 giorni a riposo all’interno dello stabilimento. Quindi fatte passare dentro una pialla fissa di forte capacità in modo da dare all’elemento lo spessore finito e rendere uniformi e lisce le superfici laterali.

 

 

 

Finitura e impregnazione

Nel reparto finitura la trave viene intestata realizzando le sagomature di progetto, i fori ed i tagli necessari per l’assemblaggio di elementi metallici.
L’ultima operazione in ordine di tempo consiste nell’applicazione di prodotti impregnanti tramite semplice spennellatura, sostanze cioè con funzione di preservare il legno da insetti, funghi, umidità e con un pigmento che conferisca alle travi il colore voluto. Tale operazione dovrebbe rientrare in seguito tra le operazioni di manutenzione ordinaria. L’applicazione della colla sulle lamelle avviene automaticamente e il sistema attualmente più utilizzato è quello della cosiddetta “incollatrice a fili” che consente di ottenere la realizzazione di un piano di incollaggio con distribuzione abbastanza uniforme della colla.

 

ex_6) ANALISI E DIMENSIONAMENTO DI UNA STRUTTURA RETICOLARE GEOMETRICA CUBICA DA AUTOCAD A SAP

Quando da piccoli giocavamo con i Geomag a nostra insaputa creavamo delle strutture reticolari spaziali, più o meno complesse…

Era semplice creare un bel cubetto, con le aste tese e al cubo aggiungere delle aste diagonali per renderlo più saldo, oppure facevamo delle piramidi a base quadrata… una delle configurazioni che anche se cadeva a terra al 90% rimaneva intatta! Queste due geometrie sono alla base delle strutture reticolari.

             

Con questa esercitazione disegneremo su Autocad una struttura reticolare cubica spaziale detta anche “piastra” che parte da un modulo: un cubo spaziale di 2m x 2m x 2m.

Siamo nello spazio disegno di Autocad in 2D, impostiamo come unità di misura i metri.

Dobbiamo pensare che questo disegno dovrà essere riportato su SAP! Quindi ci sono dei punti fondamentali da rispettare:

• Disegnare tutto in metri
• Disegnare le aste tutte su un unico layer nuovo che chiameremo ASTE
• Disegnare tutta la struttura partendo dall’origine degli assi(0,0,0) per importarla facilmente su SAP
• Disegnare una struttura chiusain modo che ogni modulo sia chiuso
• Disegnare la struttura in modo che nessuna linea si sovrapponga o sia ripetuta

Da AUTOCAD

STEP 1

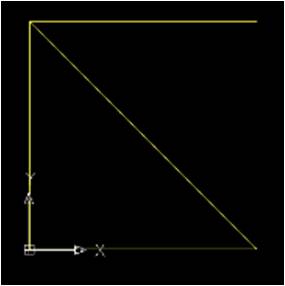
Disegniamo un quadrato mancante di un lato con una diagonale,con una polilinea.

Useremo questa figura come modulo per realizzare la nostra struttura.

Non disegneremo un quadrato completo altrimenti quando andremo a copiarlo in serie, avremo delle linee sovrapposte.

 

 

STEP 2

A questo punto passiamo dal 2D al 3D e utilizzando il comando ruota 3D, mettiamo la nostra figura in verticale: ruoto di 90° lungo l’asse x.

 

 

 

 

STEP 3

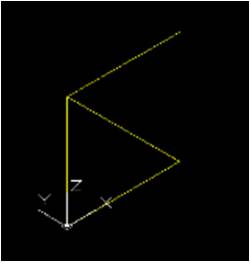
Con il comando UCS  punteremo la freccia prima in direzione di x (dove voglio vada x e faccio click), poi ripeto la stessa cosa per y e infine per z; in questo modo ruotiamo i tre assi di riferimento nelle direzioni che ci servono.

Per creare questa struttura ripeteremo diverse volte questo comando.

 

 

 

STEP 4

Orbitiamo la nostra figura e disegniamo le altre 3 aste che ci occorrono, ricordandoci sempre di non sovrapporle.

STEP 5

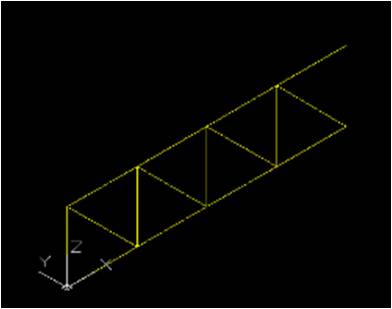
A questo punto abbiamo un primo modulo base in 3D, non ci resta che metterlo in serie! Seleziono le aste interessate e con il comando Array, facciamo una serie rettangolare che ci permette di ripetere il modulo quante volte vogliamo sia lungo l’asse x che y. In questo caso facciamo:

• 1 riga
• 4 colonne
• distanza tra un modulo e l’altro di 2m (dimensione del modulo)

 

 

A questa serie manca un’asta verticale, che adesso possiamo aggiungere con una linea singola.

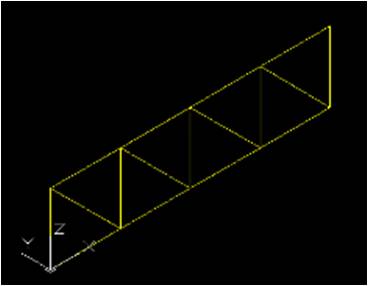
STEP 6

Ripetiamo la stessa cosa nell’altro verso imposto:

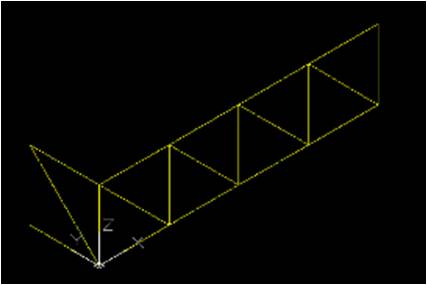
A questo punto ripetiamo in serie:

• 6righe
• 5colonne
• distanza tra un modulo e l’altro di 2m

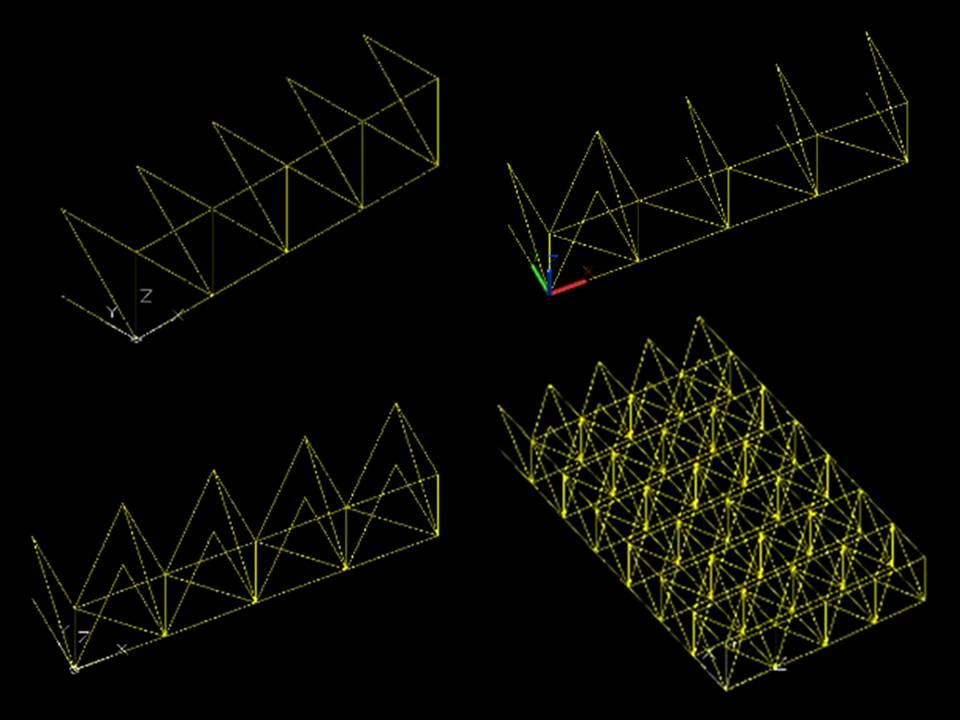
Ovviamente tutte le aste in più che non ci permettono di chiudere correttamente la figura, devono essere cancellate.Così è completata la nostra struttura reticolare spaziale! 

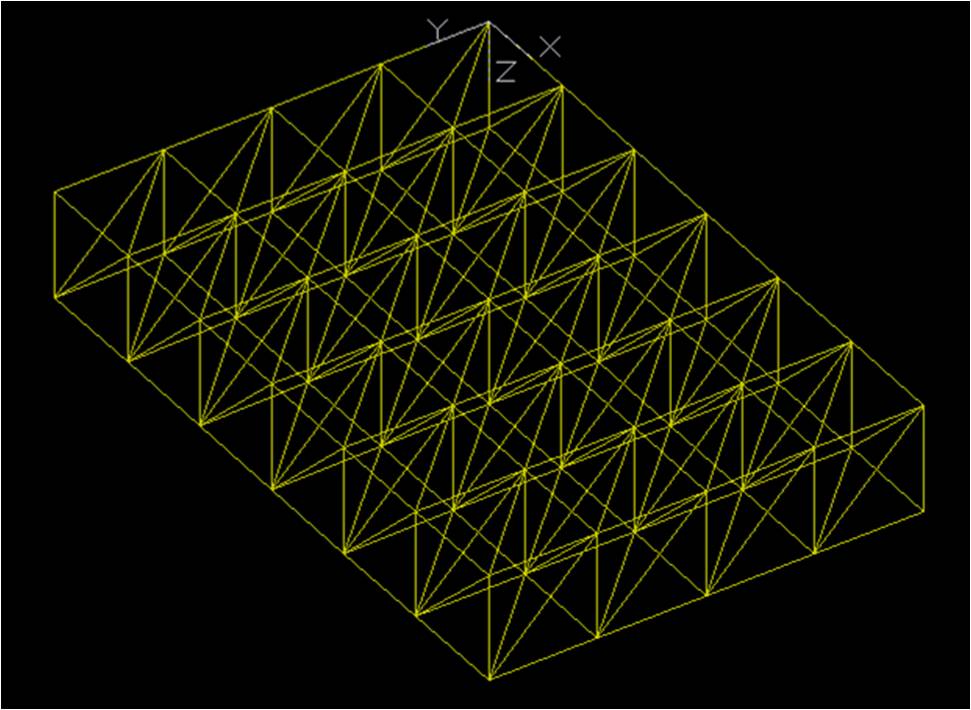
STEP 7

Ottenuta la figura, la dobbiamo esplodere. Seleziono tutta la figura e scrivo sulla barra di comando esplodi. 

STEP 8

Abbiamo la nostra struttura, dobbiamo ricordarci di salvarla in formato dxf che SAP riesce a leggere bene e in versione 2000 o 2004 per avere una maggiore compatibilità.

A SAP2000

Adesso riportiamo la nostra struttura su SAP per poterla calcolare. Abbiamo bisogno di far diventare tutte le nostre aste dei FRAMES. Questa è la prima cosa che ci viene chiesta su Sap quindi faccio diventare il layer ASTE -> FRAMES.

Definizione dei vincoli esterni

Aiutandoci con il comando ruota inseriamo i vincoli esterni. Poniamo quattro cerniere ai bordi della nostra struttura.Per i vincoli faccio click con il tasto destro, metto in evidenza i nodi interessati e tramite Assign ->Joint ->Restraints assegno le cerniere (indicate dal simbolo).

 

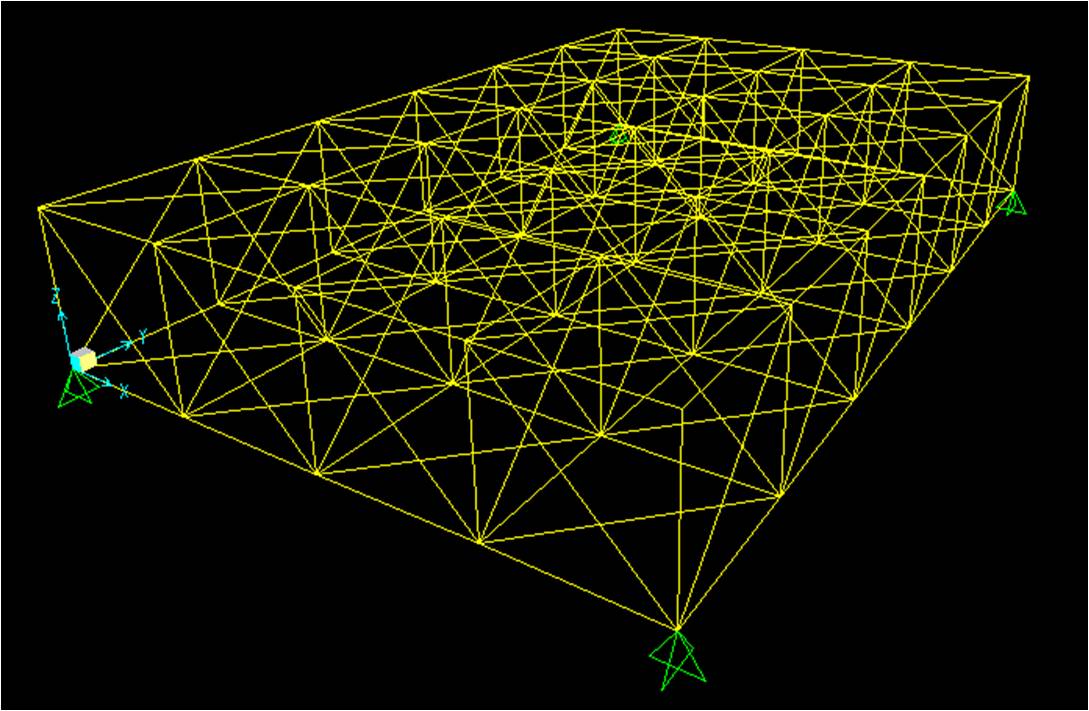
Definizione dei vincoli interni

Per definire i vincoli interni dobbiamo selezionare tutta la struttura e andare su assaign->frame->releases e assegnare il valore nullo all’inizio e alla fine del moment 22 e del moment 33. In questo modo Sap riconoscerà la struttura come reticolare.

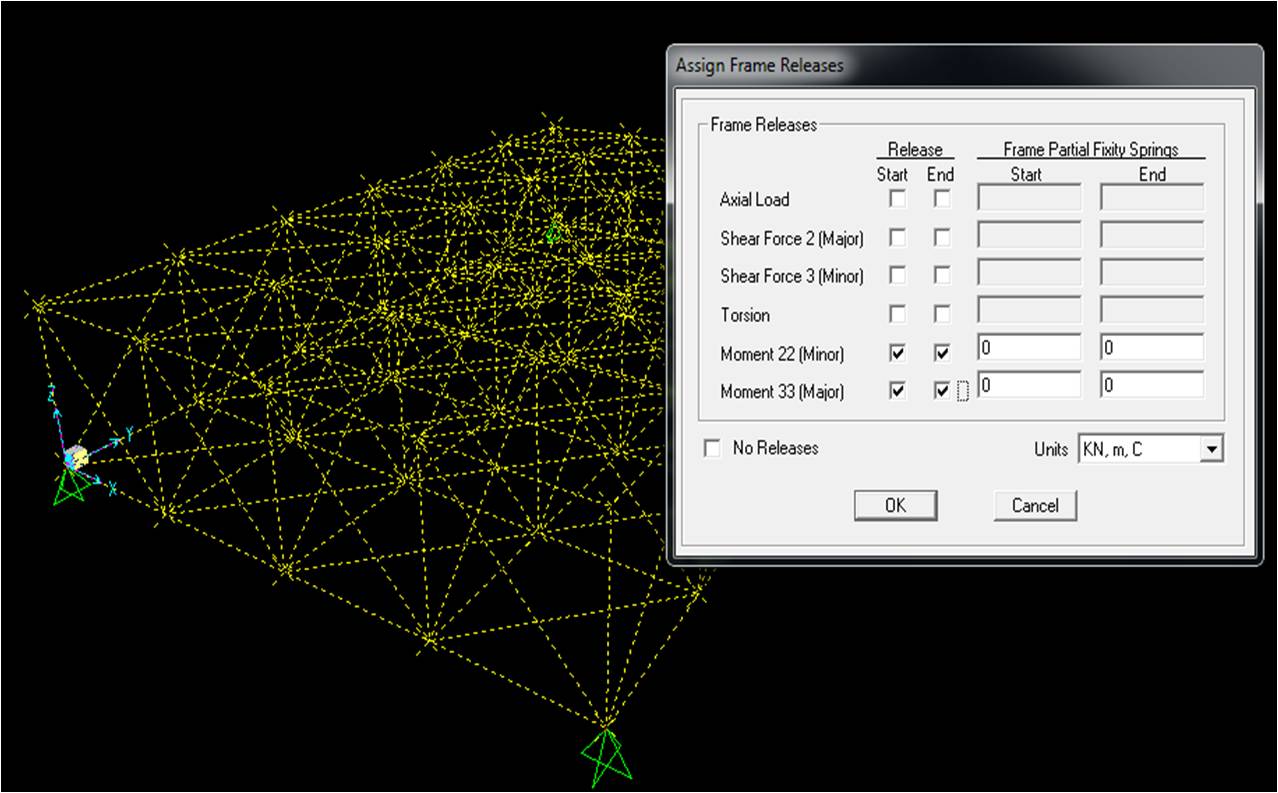
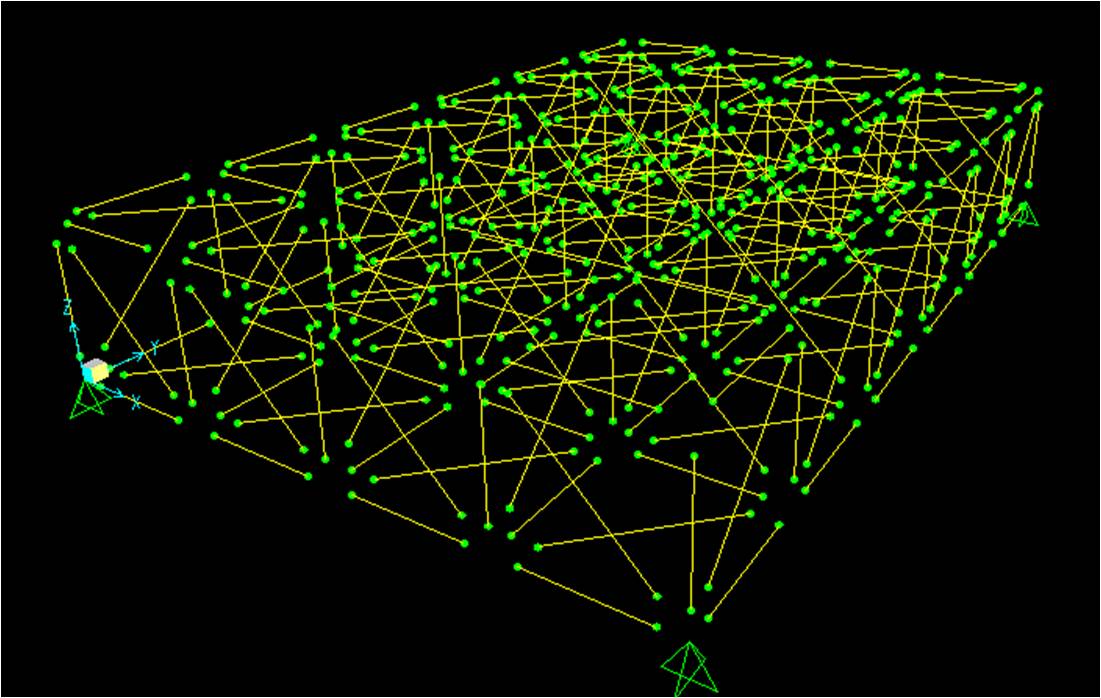
Definizione del materiale e della sezione

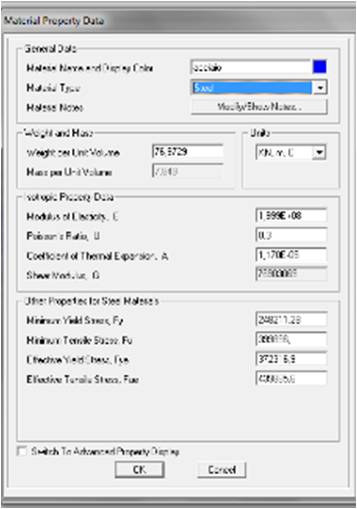
Per il materiale andiamo su Define->material->add new materiale rinominiamo come “acciaio”, scegliamo dal material type “steel” e lasciamo le caratteristiche fisiche e meccaniche predefinite.

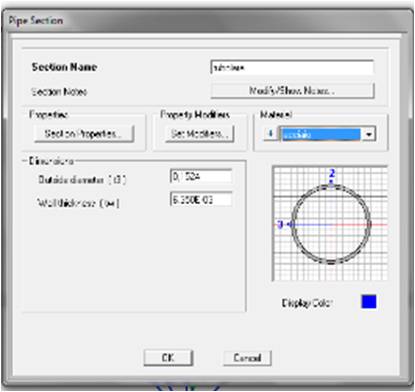
Per la sezione, andiamo su Define->sectione properties->frame sections->add new propertye scelgo la sezione “pipe” che rinominiamo come “tubolare” e diamo il materiale “acciaio”.

Selezioniamo tutta la struttura andiamo su ->assaign->frame->frame sections e scelgliamo la sezione definita.

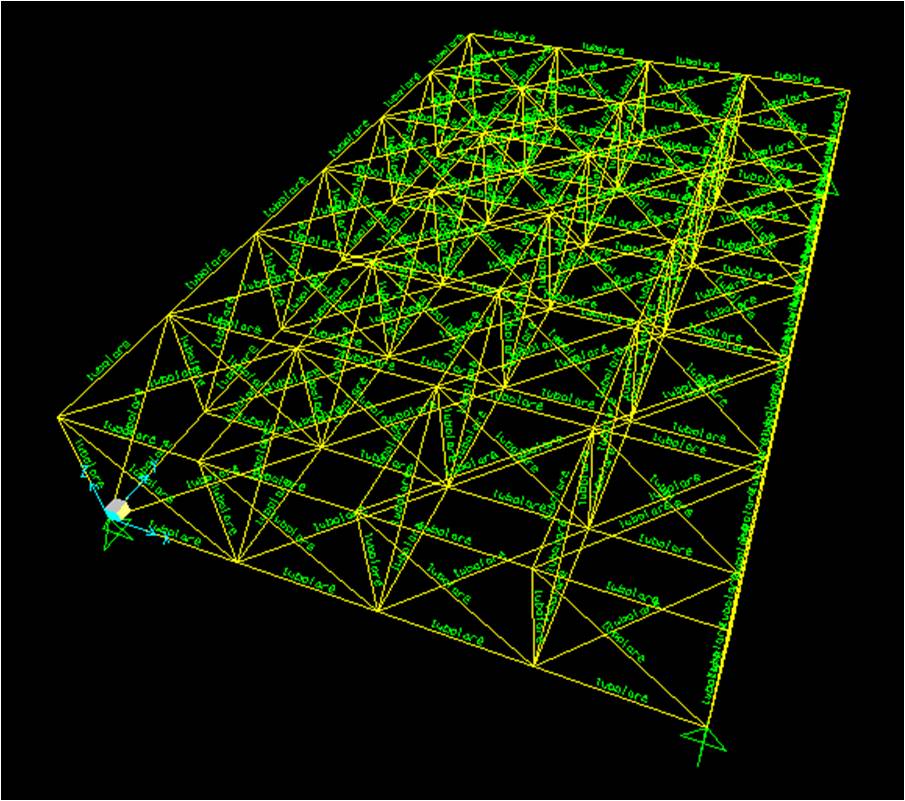
Aggiunta dei carichi

Per definire i carichi andiamo su Define->load patterns->add new load patternche rinomino come “puntuale” e impostiamo il valore “0” nel self weight multiplier.

Adesso dobbiamo assegnare il carico, ma solo ai nodi superiori! Quindi dobbiamo cercare di visualizzare solo i nodi superiori. Per farlo entriamo nella tavola di visualizzazione del piano xy e tra le opzioni spuntiamo le opzioni che mi permettono di avere nodi visibili e aste nascoste.

Per visualizzare solo i nodi superiori su una vista bidimensionale, andiamo su view->set 2D view->selezioniamo il piano superiore (quello con la z=2). Selezioniamo tutti i nodi sul piano xy , andiamo su Assaign->joint loads->forces e inserisco un valore di -40 KN a “force global Z”.

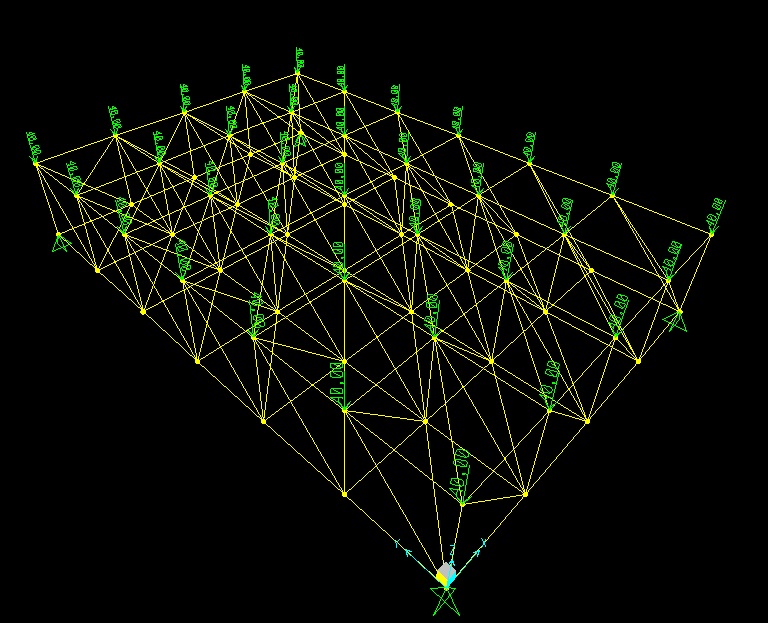
Run -> Analisi

Torniamo al display per visualizzare tutti i nodi e le aste e facciamo partire l’analisi.

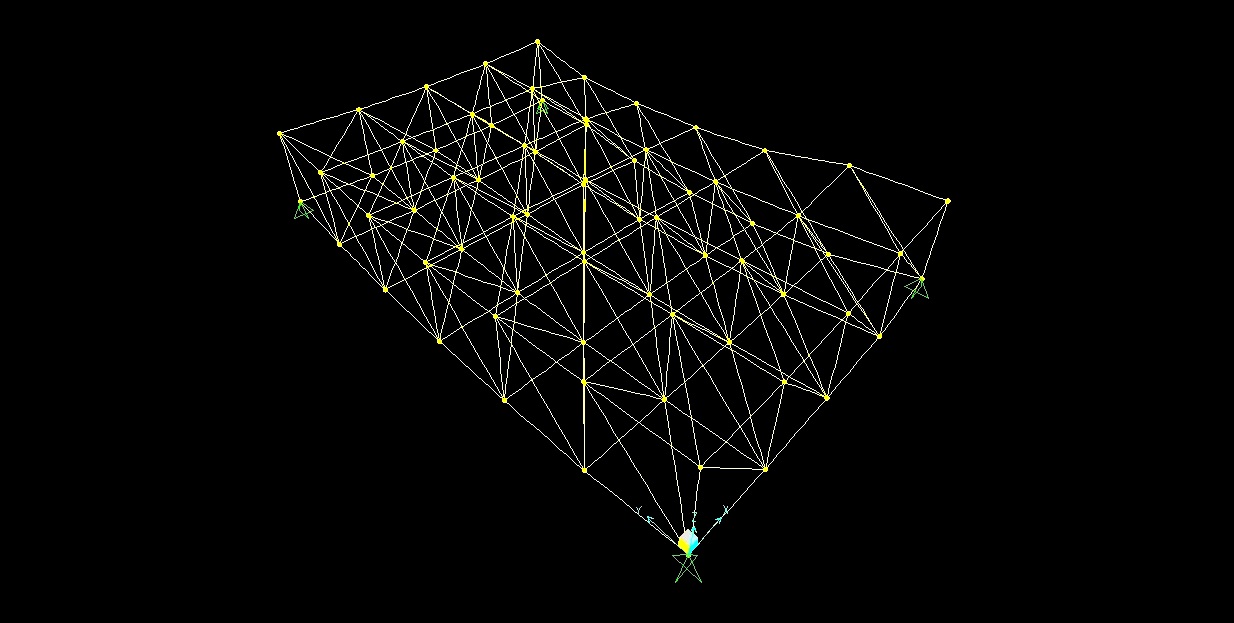
Dai diagramma dello sforzo normale, possiamo vedere quali sono le aste più sollecitate. Andiamo su display->show tables->analysis results. In questo modo possiamo visualizzare le tabelle che sintetizzano i dati delle analisi della struttura e soprattutto aprendo la tabella “element forces-frames”. In questa tabella abbiamo tutte le aste e possiamo facilmente individuare l’asta maggiormente tesa(N=258,934KN) e quella maggiormente compressa(N=-307,254KN).

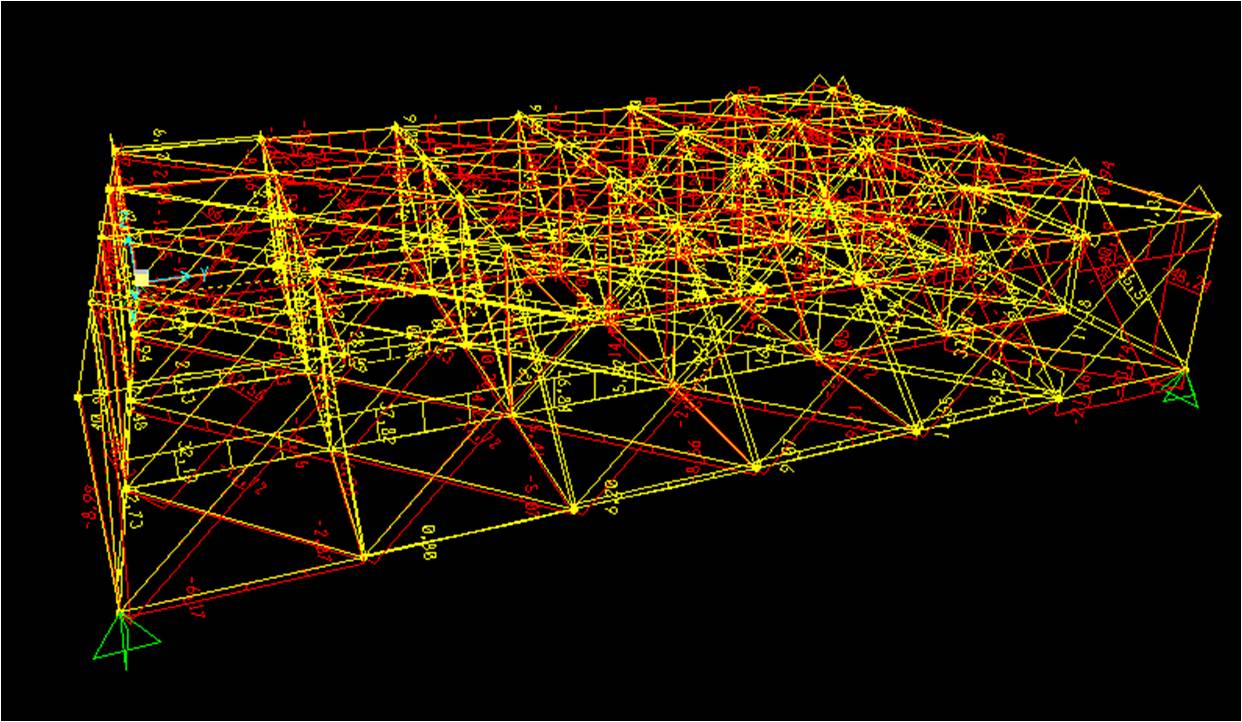
Dimensionamento asta maggiormente tesa e compressa

Per progettare le aste devo scegliere dai profilari un tipo di sezione per le aste, in questo caso scegliamo dei tubi circolari presi dal sito della OPPO (http://www.oppo.it/tabelle/profilati-tubi-circ.htm) e li scegliamo di un acciaio resistente del tipo Fe 510 con S355 quindi il nostro fyk=355 MPa

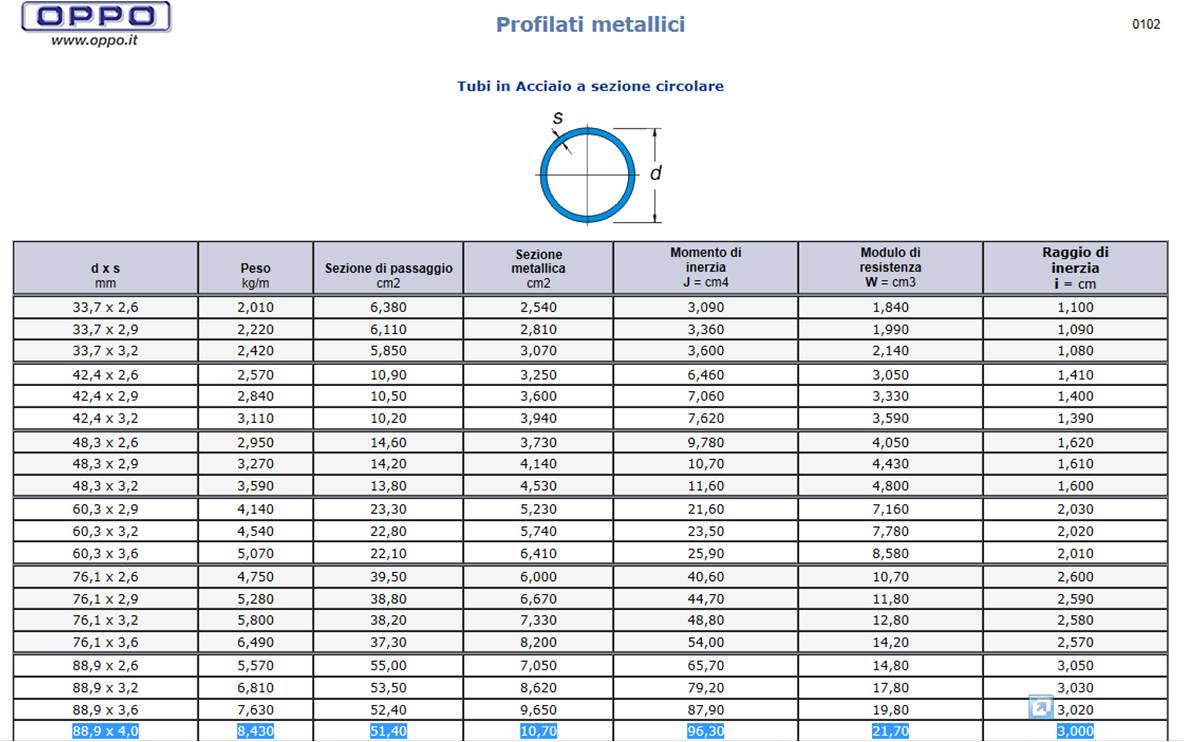
Progetto asta tesa

Fd=N/A la nostra incognita è A! dobbiamo trovare l’area minima della sezione per scegliere il nostro profilato.

Sappiamo che: Fd=fyk/γ_m1   ->355/1.15=308.7 N/mmq e dalla nostra tabella prendiamo il valore trovato di N=258,934 KN.

A=N/fd= 258,934*1000/308.7=838,79mmq=8,39cmq

Sul nostro profilario scegliamo un tubolare con area maggiore di quella trovata, quella direttamente superiore è di A=965mmq=9,65cmq

Dobbiamo verificare che con questi dati la seguente disequazione sia vera:

N/A<fd

258934N/965mmq=268,32N/mmq >Fd    non è verificata!

Provo con una sezione con area maggiore A=1070mmq=10,70cmq

258934N/1070mmq=241,994N/mmq <Fd  -> L’ASTA TESA È VERIFICATA!

Progetto asta compressa

Ripetiamo gli stessi calcoli per l’asta maggiormente compressa:

Fd=308.7 N/mmq

Questa volta N=-307,524 KN

A=N/fd=307,524*1000/308.7=996,19mmq=9,96cmq

Scelgo un profilato con sezione tubolare maggiore A=1070mmq =10,70cmq

Facciamo la verifica: N/A<fd 307524N/1070mmq=287,40N/mmq <Fd   -> È VERIFICATA!

Ma per l’asta compressa oltre a questa verifica, dobbiamo procede con la verifica a snellezza e quella a stabilità.

Verifica a snellezza

Si definisce lunghezza d’inflessione la lunghezza l₀= β lda sostituire nel calcolo del carico critico elastico Ncr alla lunghezza l dell’asta quale risulta dallo schema strutturale. Il coefficiente β deve essere valutato tenendo conto delle effettive condizioni di vincolo dell’asta nel piano di inflessione considerato.

                 

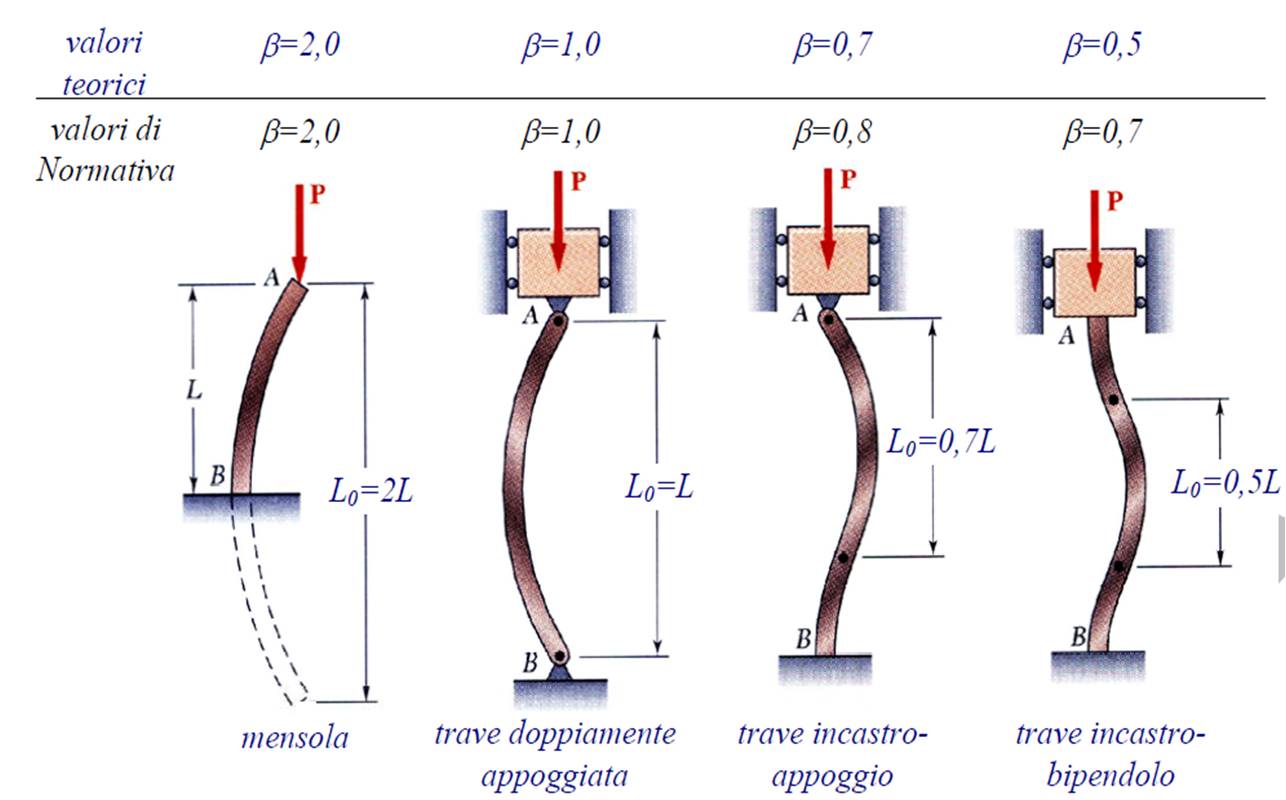
La snellezza non ha dimensione fisica e misura il rapporto tra la lunghezza e la larghezza del profiloλ=l₀/ρ_min

l₀₌lunghezza dell’asta=2,82m

ρ_min=giratore d’inerzia=3cm

λ=282cm/3cm=94<200  -> OK! È VERIFICATO!

Verifica a stabilità

Adesso dobbiamo verificare che  ->  Nd≤ Nbrd che è la resistenza a instabilità.

                         

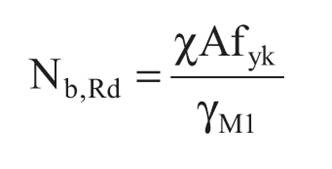
Da questa formula si susseguono delle formule che partendo dal carico critico Euleriano ci permettono di verificare che il carico di compressione di progetto, sia minore della resistenza a instabilità.

                      

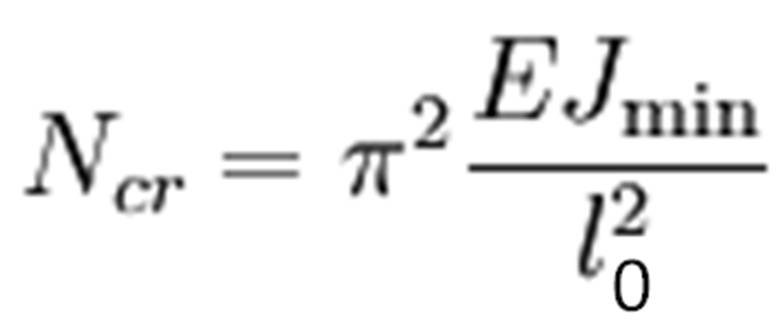
E=modulo di elasticità 210.000Mpa

J_min=momento di inerzia minimo della sezione=96,30cm⁴=963000mm⁴ (valore tabellato)

l_o=lunghezza libera di inflessione che dipende dal tipo di vincolo, nel caso di cerniera e carrello

l= l_o=2√2=2,82m (poiché l’asta maggiormente compressa è una diagonale del quadrato)

N_cr= π²*210000N/mm²*963000mm⁴/7952400mm²=250730,2N~250,73KN

Trovato il carico critico Euleriano, devo trovare il valore:

               

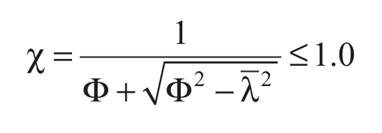
Dove : Φ=0,5*[1+λ²+α(λ-0,2)]

α=0,21 valore tabellato dalle norme tecniche

                   

λ =1,52

quindi Φ=0,5*[1+λ²+α(λ-0,2)]=0,5*[1+2,29+(0,21*1,32)]=1,67

Χ=1/[1,67+√( 1,67²-1,52²)]=1/2,36=0,42

N_brd=0,42*1070*355/1,05=151940 N= 151,94 KN< N_d   LA SEZIONE NON È VERIFICATA!

Ripeto la verifica scegliendo una sezione con area maggiore! Abbiamo visto che il valore è nettamente inferiore! Quindi possiamo scegliere una sezione più grande di qualche centimetro. Proviamo con A=1540mmq =15,40cmq

Facciamo la verifica: N/A<fd 307524N/1540mmq=199,69N/mmq <Fd   -> È VERIFICATA!

λ=282cm/4,8cm=58,6<200  -> È VERIFICATO!

N_cr=π²*210000N/mm²*3570000mm⁴/7952400mm²=929498,2N~929,5KN

λ=√(A*fyk)/N_cr=0.77

Φ=0,5*[1+λ²+α(λ-0,2)]=0,5*[1+0,59+(0,21*0,57)]=0,85

Χ=1/[Φ+√( Φ²-λ²)]=1/[0,85+√( 0,85²-0,59²)]=0,68

N_brd=A*Χ*fyk/γ_m0=1540*0,68*355/1,05=354053,33 N= 354,05KN  N_d<N_brd-> LA SEZIONE È VERIFICATA!

 

ex_7) RIPARTIZIONE DELLE FORZE SISMICHE

Con questo esercizio vedremo come si ripartiscono le forze sismiche su un telaio di un piano avendo di base dei telai shear-type che creano dei controventi per tutta la struttura. Grazie anche agli ultimi avvenimenti non possiamo sicuramente dimenticare il fatto che siamo un PAESE SISMICO! Quindi nella progettazione dobbiamo rispettare le norme antismiche ormai obbligatorie dal 2008. Dobbiamo verificare che le nostre strutture sopportino non solo le forze dei carichi verticali (quindi il peso della struttura stessa) ma anche le forze orizzontali date ad esempio dal vento e dai sismi che arrivano dirette sulla struttura.

Controventi: sono dei vincoli che impediscono alla struttura di effettuare uno spostamento o una rotazione dovuta da una forza orizzontale. Questi hanno un comportamento elastico e vengono rappresentati come delle molle dove la rigidezza di ognuna di esse rappresenta proprio la rigidezza di ogni telaio. Nel caso di una sollecitazione orizzontale (sisma, vento) la forza è applicata nel centro di massa (baricentro) della struttura. Quando si progetta una struttura bisogna pensare alla posizione di tutti i controventi (e alla rigidezza di ognuno) e a far coincidere il più possibile il centro di massa con il centro delle rigidezze (punto attorno al quale la struttura ruota) per diminuire il braccio della forza orizzontale e quindi il momento dovuto ad essa.

La struttura è IPERSTATICA, ma posso risolverla facilmente con il metodo delle rigidezze riconducendola ad una isostatica, considerando i nostri controventi come dei vincoli elastici (molle) che rispondono alle forze esterne applicate. Grazie alla presenza delle Shear Type si comporta come un corpo rigido e ha quindi solo  modi per muoversi: traslando verticalmente, traslando orizzontalmente o ruotando, i suoi vincoli sono proprio i controventi. Per il calcolo delle molle è valida la legge di Hooke che ci permette di comprendere come si distribuiscono le rigidezze in pianta: entrano in gioco le forze di sollecitazione orizzontale.

f=k*δ

 k= rigidezza della molla

δ=lo spostamento elastico

In base all’altezza dei pilastri, al modulo elastico del materiale con cui sono costruiti e al modulo di inerzia di ciascun pilastro che a sua volta dipende dalla forma e dalle dimensioni della sezione, abbiamo una rigidezza traslante diversa.

La nostra struttura è composta da 12 pilastri a sezione rettangolare in cemento armato quindi il loro un modulo elastico sarà pari a E=21000N/mm², con dimensioni 30x55cm e un interpiano di 3,50m. Le sezioni rettangolari dei pilastri hanno due diversi momenti di inerzia, uno rispetto all’asse x e uno rispetto all’asse y:

I_y=(hb³)/12=(55*30³)/12=123750cm⁴

I_x=(bh³)/12=(30*55³)/12=415937,5cm⁴

Dobbiamo ricordare che in base a dove abbiamo la campata con la luce maggiore, dobbiamo girare i pilastri nel verso opportuno affinché portino il momento flettente maggiore.

STEP 1 CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DELL’EDIFICIO

Calcoliamo la rigidezza traslante per tutti i telai con la seguente formula: Kt=12E*(I₁+I₂+I₃...)/h².

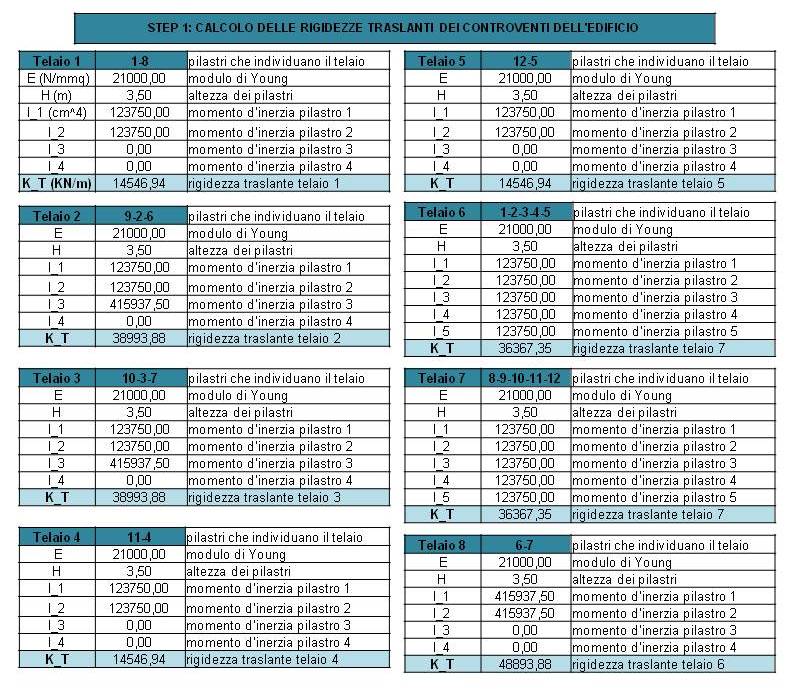
STEP 2 TABELLA SINOTTICA RIGIDEZZE CONTROVENTI E DISTANZE

Ricopiamo in questa tabella le rigidezze dei telai e le distanze orizzontali e verticali di ciascun telaio dal punto di origine 0.

STEP 3 CALCOLO DEL CENTRO DI MASSA

Per calcolare le coordinate del centro di massa G utilizziamo le seguenti formule:

X_G=(Area₁*X_G1+Area₂+*X_G2)/(Area₁+Area₂)

Y_G=(Area₁*Y_G1+Area₂+*Y_G2)/(Area₁+Area₂)

A₁A₂ = aree in cui è diviso l’impalcato

X_G1 Y_G1  ; X_G2 Y_G2= coordinate del baricentro di ciascuna delle due aree.

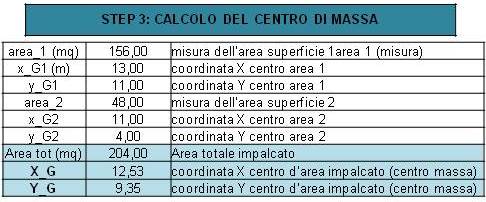
Possiamo disegnare l’impalcato con le due aree individuate e le molle che rappresentano i controventi.

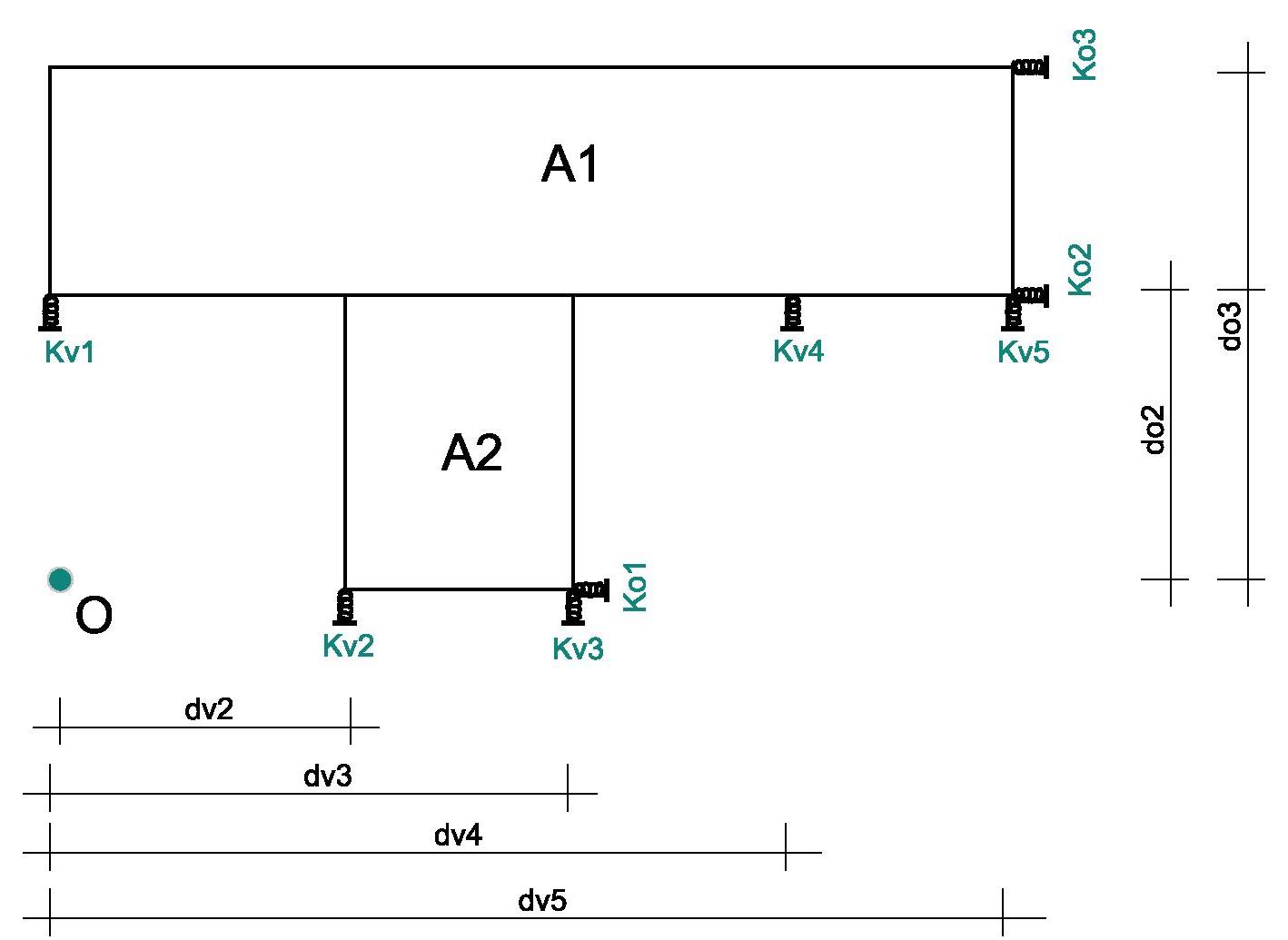
STEP 4 CALCOLO DEI CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI

Adesso troviamo il centro delle rigidezze C con le formule:

X_c = [Σ_i (Kv_i*dv_i)]/Kv_tot

Y_c = [Σ_i (Ko_i*do_i)]/Ko_tot

e le distanze di ciascun controvento dal centro delle rigidezze e la rigidezza torsionale  K_φ=Σ_i(K_i*dd_i²).

 

STEP 5 ANALISI DEI CARICHI SISMICI

Partiamo dalla formula della forza sismica:

F=m*a = m*g*c = c(m*g) = c*P

 a=c*gfrazione dell’accelerazione di gravità con c<1->coefficiente di intensità sismica

m*g  è la formula del peso P della struttura quindi possiamo dire che la forza sismica è una “frazione del peso della struttura”.

Per calcolare il peso di una struttura:

P = G+ψ*Q

G= (qs+qp)*A_tot -> somma del carico strutturale e quello permanente per l’area dell’impalcato.

Q= qa*A_tot ->carico accidentale per l’area dell’impalcato

Ψ=o,80-> coefficiente di contemportaneità o di partecipazione che per normativa è <1

Quindi possiamo trovare la forza sismica  F=P*c.

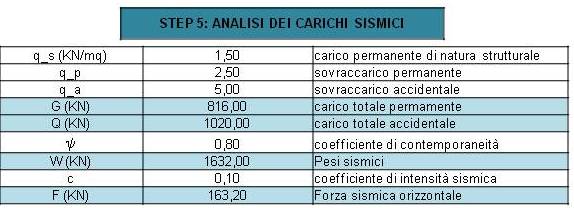
STEP 6/7 RIPARTIZIONE FORZA SISMICA LUNGO x/y

Con questa tabella verifichiamo sia in direzione x che in direzione y quali potrebbero essere le conseguenze di un possibile sisma. Il momento torcente nelle due direzioni èM_x= F (XC - XG) e M_y= F (YC - YG)  con XC-XG e YC-YG che sono i bracci della forza sismica applicata lungo le due direzioni.

Una volta calcolati i momenti torcenti, la rotazione e le traslazioni orizzontali e verticali possiamo calcolare come la forza sismica si ripartisce su ogni controvento in entrambe le direzioni.

Lungo x:

per i controventi orizzontali Ri^o= Ki^o * (uo + ϕdi^o)

per i controventi verticali Ri^v= Ki^v * ϕdi^v

Lungo y:

per i controventi orizzontali Ri^o= Ki^o * ϕdi^o

per i controventi verticali Ri^v= Ki^v * (uv + ϕdi^v)

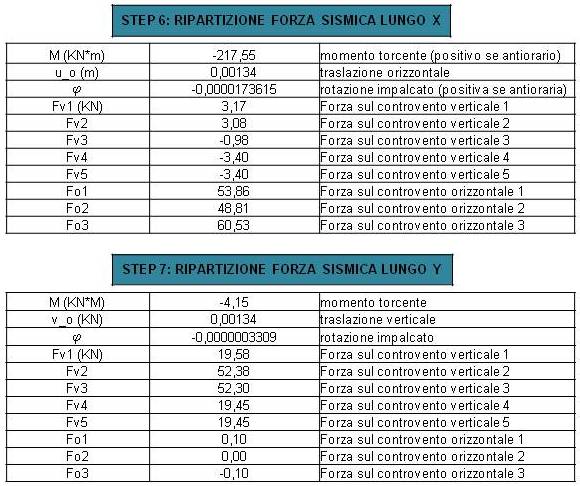
La nostra struttura non essendo simmetrica avrà il centro delle rigidezze che non coincide con il centro delle masse e quindi in caso di sisma si genererà un momento torsionale intorno al punto C con una rotazione minima ed una leggera traslazione.

 

 

Costruzioni antisismiche: la casa Sofie

SOFIE - Sistema Costruttivo Fiemme- è un progetto di ricerca sull'edilizia sostenibile condotto dall'Istituto IVALSA del Consiglio Nazionale delle Ricerche con il sostegno della Provincia Autonoma di Trento. SOFIE ha lo scopo di definire le prestazioni e le potenzialità di un sistema per la costruzione di edifici a più piani, realizzato con struttura portante di legno trentino di qualità certificata e caratterizzato da elevate prestazioni meccaniche e basso consumo energetico, ottimi livelli di sicurezza al fuoco e al sisma, comfort acustico e durabilità nel tempo: il sistema X-LAM (pannelli lamellari di legno massiccio a strati incrociati). Nata in Germania meno di dieci anni fa, questa tecnica costruttiva si basa sull'utilizzo di pannelli lamellari di legno massiccio di spessore variabile dai 5 ai 30 cm realizzati incollando strati incrociati di tavole di spessore medio di 2 cm. I pannelli vengono tagliati a seconda delle esigenze architettoniche completi di aperture per porte, finestre e vani scala e in seguito issati e collegati tra loro in opera con angolari metallici, chiodi a rilievi tronco-conici e viti autoforanti. I pannelli sono realizzati interamente con legno proveniente dalle foreste della Valle di Fiemme e delle altre valli del Trentino.

Statica

I pannelli a base di legno di tipo X-lam sono elementi di parete, di solaio e/o di copertura realizzati incollando fra loro, a pressione, strati sovrapposti di lamelle di legno. Ogni lamella è formata dalla giunzione a dita, testa contro testa, di tavole di legno strutturale (cioè individualmente classificate e selezionate secondo la resistenza meccanica). La direzione delle lamelle di uno strato del pannello è perpendicolare a quella delle lamelle degli strati adiacenti. Questa disposizione incrociata conferisce una notevole stabilità dimensionale e di forma al pannello stesso, nonché buone caratteristiche meccaniche in tutte le direzioni. Il tipo di incollaggio, l’esecuzione a regola d’arte dei giunti a dita e della pressatura del pannello nonché l’uso esclusivo di tavole classificate secondo la resistenza meccanica, rappresentano altrettante condizioni indispensabili affinché il pannello X-lam possa essere impiegato nelle costruzioni.

Sisma

Nel 1995 in Giappone si è verificato quello che sia per numero di vittime che per tipologia di danno è considerato il terremoto più distruttivo per le opere civili. La terrà tremò per quasi 30 secondi, sconquassando un’intera regione e provocando quasi 6 mila morti. Proprio a Kobe, dopo la tragedia, il Governo giapponese ha deciso di realizzare, con una spesa di 4 miliardi di dollari, il più importante centro di sperimentazione antisismico del mondo. Dal 2004 vengono testati i prototipi in scala reale di centinaia di abitazioni, ponti, palazzine e opere civili e industriali. La lista d’attesa per accedere all’E-Defence, così viene chiamato il laboratorio con la sua piattaforma di simulazione dove americani, inglesi, tedeschi e cinesi fanno la coda per ottenere la certificazione antisismica giapponese, l’unica riconosciuta in tutto il mondo. Proprio a Kobe nel 2007 durante una simulazione, una struttura interamente di legno ha resistito ad una simile forza d’urto. A riuscirci è stata una palazzina alta 23,5 metri realizzata e progettata in Italia.

Ivalsa ha effettuato una serie di prove sperimentali volte a caratterizzare il comportamento strutturale di edifici con struttura portante di pannello di legno di tipo X-lam con particolare riguardo al loro comportamento nei confronti delle azioni sismiche. A questo proposito è stato intrapreso un programma di ricerca in collaborazione con il Laboratorio prove materiali e strutture della Facoltà di Ingegneria di Trento, il National Institute for Earth Science and Disaster Prevention (NIED), il Building Research Institute (BRI), l'Università di Shizuoka e il Centre for Better Living in Giappone, che si è sviluppato attraverso alcune fasi principali:

• prove monotòne e cicliche su giunti;
• prove monotòne e cicliche su pannelli parete con diverse configurazioni di giunti, aperture, dimensioni dei pannelli e aliquota di carichi verticali applicati condotte presso i laboratori Ivalsa;
• prove pseudo-dinamiche su un provino di edificio a un piano in dimensioni reali con 3 differenti configurazioni delle aperture nelle pareti esterne parallele alla direzione di applicazione del terremoto condotte presso l'Università di Trento;
• prove su tavola vibrante su un edificio di tre piani con dimensioni in pianta di m 7x7 e 10 m di altezza totale con copertura a due falde in 3 differenti configurazioni delle aperture nelle pareti esterne parallele alla direzione di applicazione del terremoto e con tre diversi terremoti applicati in serie (Kobe, El Centro e Nocera Umbra) condotte presso il NIED di Tsukuba in Giappone;
• prove su tavola vibrante 3D full-scale su edificio di sette piani con dimensioni in pianta di m 15x7.7 e 23,5 m di altezza totale, copertura a singolo spiovente e masse aggiuntive su ciascun solaio pari al 30% del carico di esercizio, come previsto dai codici europeo e italiano per le combinazioni di carico sismiche (peso totale dell'edificio: 285 tonnellate circa), condotte presso l'E-Defense del NIED di Miki in Giappone, mediante l'applicazione in serie di due diversi terremoti (Niigata-Chuetsu-Oki e Kobe).

http://www.youtube.com/watch?feature=player_embedded&v=W4q_ytmwyzY

l'esercitazione dell'arco parabolico con le immagini dei grafici di Sforzo Normale, Taglio e Momento (errore di SAP2000)

Mario Desideri, ospite all'Università di Architettura L. Quaroni, Roma 4 Aprile 2005

Qui sotto il video:

http://www.nitrosaggio.net/H/Saggio/formazione/desideri.mov

 

maggiori info: http://www.arc1.uniroma1.it/saggio/colti/vatori.html

Segue l'elenco degli e delle esonerati/e dalla prova scritta per l'esame di progettazione strutturale B. Si è già tenuto conto della frequenza. Non saranno effettuate prove orali a non iscritti regolarmente al portale dello studente, sistema ESSE3.