blog di benedetta.ranazzi

 

 Lo scopo di questa esercitazione è quello di calcolare come viene ripartita una forza orizzontale, che sia essa considerata come la forza del vento o quella di un sisma, che agisce su una stuttura in cemento armato, costituita da telai Shear-Type, attraverso il metodo delle rigidezze.

La struttura si compone di sette telai, quattro paralleli all'asse x, e tre paralleli all'asse y:

- telaio 1v     pilastri 1-5

- telaio 2v     pilastri 2-6

- telaio 3v     pilastri 3-7-9

- telaio 4v     pilastri 4-8-10

- telaio 1o     pilastri 1-2-3-4

- telaio 2o     pilastri 5-6-7-8

- telaio 3o     pilastri 9-10

Poichè questi telai sono modellati come telai Shear-Type, è possibile calcolare la loro rigidezza in questo modo:  

                                                                       

                  

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi un’adeguata rigidezza.

Facendo riferimento ai risultati ottenuti nella quarta esercitazione EXE4 - Dimensionamento di un pilastro, i momenti d'inerzia dei pilastri saranno i seguenti:

                                    

 

Nello STEP 1 del file excel viene calcolata la rigidezza traslante associata a tutti i controventi

 

Nello STEP 2 vengono riportate tutte le rigidezze traslanti calcolate nello STEP 1, e le distanze dei controventi da un'origine arbitratria considerata come origine del sistema di riferimento O.

 

Lo STEP 3 prevede il calcolo del centro di massa che, nel caso di un impalcato con densità di massa uniforme, coincide con il centro d'area. Esso corrisponde al punto in cui verrà applicata la forza sismica.

Per rendere possibile questa operazione è necessario suddividere l'impalcato in due figure geometriche elementari, calcolarne il valore delle aree e la distanza di ognuno dei due centri d'area dall'origine O.

 

A questo punto, attraverso lo STEP 4, è possibile calcolare:

- le rigidezze totali, sia verticali che orizzontali;

- il centro delle rigidezze, con rispettive coordinate;

- la rigidezza torsionale, necessaria per il successivo calcolo della rotazione 

 

Lo scopo di questa esercitazione è il dimensionamento di un pilastro nelle tre diverse tecnologie: Legno, Acciio e Calcestruzzo armato.

Osservando le piante, appare subito evidente che il pilastro più sollecitato risulti essere quello centrale, perchè quello con area di influenza maggiore A = L₁ x L₂ = m 5,00 x 4,00 = 20 m².

Poichè il foglio di calcolo necessita di alcune informazioni relative ai carichi che gravano sui solai, faranno riferimento la prima e la terza esercitazione EXE1_Dimensionamento di una trave per un solaio in legno, acciaio e calcestruzzo armato e EXE3_Verifica a deformabilità di una trave a sbalzo.

 

LEGNO

La prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, moltiplicando l'area della sezione della trave per il peso specifico del materiale di cui quest'ultima è composta.

Area sezione = (0,30 x 0,55) m

Peso specifico = 8 KN/m³

Di conseguenza:

Trave_p = (0,30 x 0,55) m x 8 KN/m^{3 =} 1,32 KN/m

Trave_s = (0,30 x 0,55) m x 8 KN/m^{3 =} ​1,32 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

Carico strutturale (Qs) = 0,265 KN/m²

Carico permanente (Qp) = 2,66 KN/m²

Carico accidentale (Qa) = 2,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi. Per ottenere ciò, devo essere inseriti alcuni parametri:

- La resistenza a flessione caratteristica con fibre di legno parallele f_c0,k = 21 MPa;

- Il coefficiente di durata del carico k_mod = 0,8;

- Il coefficiente parziale di sicurezza del materiale γ_m = 1,45

 La terza parte del foglio di calcolo è incentrata sulla definizione della base b e dell'altezza h.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 8.800 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Ora è possibile calcolare una delle due dimensioni della sezione del pilastro, ossia la base minima b_min. Questo valore dovrà però essere ingegnerizzato, dovrà cioè essere scelto un valore della base b superiore ad b_min. A questo punto, nota una delle due dimensioni, potrà essere definita anche l'altra, l'altezza h_min, che andrà a sua volta ingegnerizzata, per ottenere un valore h_min < h.

L'ultima operazione consiste nella fase di verifica. 

Infatti, dopo aver definito i valori di base e altezza della sezione del pilastro, con b < h, il foglio Excel individuerà anche l'area di progetto A_design. La sezione risulterà verificata se, e solo se, A_design > A_min

700 cm² > 529 cm²

LA SEZIONE E' VERIFICATA!

 

ACCIAIO

 

Come nel caso del legno, anche per il dimensionamento di un pilastro in acciaio, la prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, quindi:

Trave_p (IPE 400) = 66,3 Kg/m = 0,66 KN/m

Trave_s (IPE 160) = 15,8 Kg/m = 0,16 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

Carico strutturale (Qs) = 2,03 KN/m²

Carico permanente (Qp) = 2,95 KN/m²

Carico accidentale (Qa) = 2,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi. Per ottenere ciò, devo essere inseriti alcuni parametri:

- La tensione di snervamento f_yk = 275 MPa;

- Il coefficiente parziale di sicurezza del materiale γ_m = 1,05

 La terza parte del foglio di calcolo è incentrata sulla definizione del momento di inerzia minimo I_min.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 210.000 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3 m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Ora è possibile calcolare il momento d'inerzia minimo I_min = A x (ρ_min)²

Attraverso l'ingegnerizzazione dei valori di ρ_min e I_min sarà possibile scegliere il profilo HEA adatto. Bisognerà dunque vedere sulla Tabella Profilati metallici, qual è quello che riporta i valori di raggio minimo di inerzia e momento di inerzia minimo superiori rispetto a quelli del foglio di calcolo.

Il profilo scelto è un HEA 160. A questo punto, dopo aver inserito l'area di progetto A_design, il momento di inerzia minimo di progetto I_design e il raggio minimo d'inerzia ρ_min, il profilo risulterà verificato se, e solo se 

A_design > A_min

IL PROFILO E' VERIFICATO!

 

 

CALCESTRUZZO ARMATO

 

Come nel caso del legno e dell'acciaio, anche per il dimensionamento di un pilastro calcestruzzo armato, la prima parte del foglio Excel è impostata sul calcolo dello sforzo normale di compressione N agente sul pilastro.

Per definire questo valore è necessario prima di tutto individuare il carico dovuto al peso proprio delle travi, moltiplicando l'area della sezione della trave per il peso specifico del materiale di cui quest'ultima è composta.

Area sezione = (0,30 x 0,50) m

Peso specifico = 25 KN/m³

Di conseguenza:

Trave_p = (0,30 x 0,50) m x 25 KN/m^{3 =} 3,75 KN/m

Trave_s = (0,30 x 0,50) m x 25 KN/m^{3 =} ​3,75 KN/m

Si inseriscono a questo punto i valori dei carichi gravanti sul solaio e il numero dei piani n = 4

 

Carico strutturale (Qs) = 2,54 KN/m²

Carico permanente (Qp) = 2,35 KN/m²

Carico accidentale (Qa) = 3,00 KN/m²

La successiva parte del foglio di calcolo prevede di definire l'area minima A_min che la sezione del pilastro deve avere per evitare che il materiale entri in crisi, e di conseguenza anche la dimensione minima della base b_min. Per ottenere ciò, deve essere inserita la tensione di snervamento f_ck = 40 MPa;

La terza parte del foglio di calcolo è incentrata sulla definizione del momento di inerzia minimo I_min.

Per fare ciò bisogna inserire ancora alcuni dati:

- Il modulo di elasticità del materiale E = 21.000 N/mm²;

- Il coefficiente adimensionale che riflette l’influenza dei vincoli β = 1;

- L'altezza del pilastro l = 3 m.

Attraverso l'utilizzo di questi parametri si riesce a calcolare:

- Il valore massimo della snellezza λ_max;

- Il vaolre minimo del raggio d'inerzia ρ_min.

Dopo aver determinato una delle due dimensioni della sezione del pilastro, ossia la base minima b_min si potrà ingegnerizzare, dovrà cioè essere scelto un valore della base b superiore ad b_min. A questo punto, nota una delle due dimensioni, potrà essere definita anche l'altra, l'altezza h_min, che andrà a sua volta ingegnerizzata, per ottenere un valore h_min < h.

L'ultima operazione consiste nella fase di verifica. 

Infatti, dopo aver definito i valori di base e altezza della sezione del pilastro, con b < h, il foglio Excel individuerà anche l'area di progetto A_design. La sezione risulterà verificata se

                                                                                A_design > A_min    (1)

In questo caso però è necessaria un’ulteriore verifica della sezione, poiché nel cemento armato il nodo tra trave e pilastro, essendo realizzato con un incastro, trasmette momento, sottoponendo il pilastro a presso-flessione.

E' per questo motivo che oltre alla (1), bisogna imporre anche che

                                                                                  σ_max ≤ f_cd

Poichè tutte e due le condizioni risultano soddisfatte

LA SEZIONE E' VERIFICATA!

 

 

Questa esercitazione prevede il dimensionamento di una mensola nelle tre diverse tecnologie: Legno, Acciaio e Calcestruzzo armato.

Osservando la pianta, risulta evidente che la trave a sbalzo più sollecitata è quella centrale, perchè quella con area d'influenza maggiore.

Si procede, dunque, con il dimensionamento della mensola, basandosi sugli stessi carichi e le stesse stratigrafie di solaio dell' EXE1_Dimensionamento di un solaio per un solaio in legno, acciaio e calcestruzzo armato.

 

SOLAIO IN LEGNO

Carico strutturale (Qs) = 0,265 KN/mq

Carico permanente (Qp) = 2,66 KN/mq

Carico accidentale (Qa) = 2,00 KN/mq

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

A questo punto, dopo ver scelto la tipologia di legno, legno lamellare GL 24h, bisogna inserire il valore di resistenza a flessione caratteristica fm,k = 24 MPa.

Si ottiene così la tensione ammissibile sig_d (N/mm²) = 0,8 x kmod / 1,45, dove:

- 0,8 è il coefficiente della durata del carico (kmod);

- 1,45 è il coefficiente parziale di sicurezza del materiale (γm).

Impostando un'ipotetica base b = 20 cm, si ottiene l'altezza minima h_min, ossia il valore minimo che deve avere l’altezza della sezione

Questa altezza minima deve però essere ingegnerizzata, deve cioè essere scelto un valore di altezza superiore ad hmin. 

Si inserisce quindi anche il valore del modulo elastico E = 8.000 N/mm².

In questo modo il foglio Excel determina:

- il momento d’inerzia I_x = b x h³/12;

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata. 

LA SEZIONE E' VERIFICATA!

 

SOLAIO IN ACCIAIO

 

Carico strutturale (Qs) = 2,028 KN/mq

Carico permanente (Qp) = 2,95 KN/mq

Carico accidentale (Qa) = 2,00 KN/mq

 

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

 A questo punto si inserisce la tensione di snervamento del Fe 430/ S275, fy,k = 275 MPa, e si ottiene così:

- la tensione di progetto f_d = 293,13 N/mm²

- il modulo di resistenza W_x = 226,18 cm³.

Dopo aver ottenuto il modulo di resistenza, bisogna ingegnerizzare la sezione. Quindi si inserisce il valore del momento d’inerzia I_x del profilo, che ha come modulo di resistenza W_x, un valore maggiore di quello trovato

Dopo aver scelto il profilo, che in questo caso è una trave IPE 220, non resta altro che inserire il valore del modulo elastico E = 210.000 N/mm².

In questo modo il foglio di calcolo determina:

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata.

LA SEZIONE E' VERIFICATA!

 

SOLAIO IN CALCESTRUZZO ARMATO

Carico strutturale (Qs) = 2,536 KN/mq

Carico permanente (Qp) = 2,345 KN/mq

Carico accidentale (Qa) = 3,00 KN/mq

Dopo aver inserito i valori dei carichi sul foglio Excel, e avendo così ottenuto il carico totale Q, inserendo anche la luce l = 2 m, si ricava  il valore del Momento massimo che, trattandosi di una mensola, è definito dall'equazione:

M_max = ql²/2.

A questo punto si sceglie la tipologia di acciaio per l'armatura del cls, B450C, e si inserisce la tensione di snervamento fy = 450 MPa; in questo modo si ottiene la tensione di progetto fd_f.

Si inserisce inoltre anche fck = 60 MPa, e si considera una base b = 20 cm

Si ottiene in questo modo un'altezza minima  H = 25,30 cm. Questa altezza va ingegnerizzata, deve cioè essere scelto un valore di altezza superiore ad H. Quindi l'altezza della sezione della trave sarà uguale a Hd = 35 cm.

L'ultimo passaggio è l'inserimento del modulo elastico dell'acciaio dell'armatura E = 21000 N/mm².

In questo modo il foglio di calcolo determina:

- il momento d’inerzia I_x = b x h³/12;

- l’abbassamento massimo v_max = q x l⁴/ 8 x E x I_x

- il suo rapporto con la luce l/v_max.

Se quest'ultimo valore soddisfa la condizione l/v_max ≥ 250 la sezione può definirsi verificata. 

LA SEZIONE E' VERIFICATA!

 

 

 

A completamento dell'esercitazione sulla struttura reticolare (STRUTTURA RETICOLARE 3D), postata in data 31/03/2014, segue la parte di analisi per il dimensionamento delle aste.

 

Si estrae da SAP2000 una tabella che riporta e i valori di Sforzo normale (N) agenti su ogni asta, con relativa lunghezza (L).

 

A questo punto, è essenziale differenziare le aste tese da quelle copresse, perchè i parametri da tenere in considerazione per il dimensionamento sono diversi a seconda del che si tratti delle une o delle altre.

ASTE TESE

Per calcolare l’area minima (A_min)  è necessario definire alcuni parametri.

Dunque, dopo aver scelto il tipo di acciaio dalla Normativa Tecnica, sono necessari:

- La resistenza a tensione di snervamento fyk = 235MPa;

- Il coefficiente di sicurezza del materiale γm = 1,05;

- La resistenza a tensione di progetto: fd = fyk/γm

In base all'area minima calcolata (A_min = N/fd), si scelgono dalla Tabella Profilati metallici i profili che soddisfano la condizione:

A_design > A_min.

In questo caso sono state divise tutte le aste in qattro macrogruppi, ognuno con le seguenti specifiche:

A_design = 2,54 cm²

A_design = 5,74 cm²

A_design = 17,10 cm²

A_design = 33,60 cm²

A questo punto l'ultimo passaggio consiste nel procedere con la fase di verifica.

Si prende in considerazione l'asta più sollecitata

e si impone la seguente condizione: N/A_design ≤ fd

186,24 N/mm² ≤ 223,81 N/mm²

LA SEZIONE E' VERIFICATA!

 

ASTE COMPRESSE

 

Come nel caso delle aste tese, per calcolare l’area minima (A_min) si utilizzano gli stessi parametri:

- Resistenza a tensione di snervamento fyk = 235MPa

- Coefficiente di sicurezza del materiale γm = 1,05;

- Resistenza a tensione di progetto: fd = fyk/γm

Quindi A_min = N/fd.

Per consedirare la sezione dell'asta verificata non è sufficiente soddisfare la condizione N/A_design ≤ fd, ed è per questo che nel foglio di lavoro Excel vengono introdotti ulteriori paramentri:

 

- Il modulo di elasticità del materiale E = 210000 MPa (acciaio);

- La lunghezza dell’asta l = 2 m o 2,83 m;

- Il coefficiente del vincolo β= 1;

- Momento d’inerzia minimo I_min (cm⁴);

- Il raggio d’inerzia del profilo  ρ_design (cm);

A questo punto, come nel caso delle aste tese, si sceglgono dalla Tabella Profilati Metallici i profili che soddisfano la condizione A_design > A_min.

Quindi anche le aste compresse vengono suddivise in qattro macrogruppi, ognuno con le seguenti specifiche:

A_design = 5,74 cm² 

A_design = 12,50 cm²

A_design = 25,70 cm²

A_design = 47,00 cm²

Adesso, prendendo in esame l'asta più sollecitata

oltre alla disequazione N/A_design ≤ fd (209,11N/mm² < 223,81 N/mm²) che risulta essere verificata, è necessario imporre un'altra condizione, ossia che la SNELLEZZA (λ) risulti minore o uguale a 200.

Poichè in questo caso λ < 200

LA SEZIONE RISULTA VERIFICATA!

Questa esercitazione prevede il dimensionamento di una trave nelle tre diverse tecnologie di un solaio in legno, uno in acciaio ed uno in calcestruzzo armato.

Per dimensionare una trave è necessario analizzare i carichi che agiscono su di essa, e possono essere macro categorie:

 - Carichi strutturali (Q_S), corrispondenti al peso delle parti strutturali del solaio, escludendone la trave principale, essendo      essa l’incognita del problema.

 - Carichi permanenti (Q_P), corrispondenti al peso delle parti non strutturali del solaio, compreso il peso dei tramezzi e degli    impianti.

 - Carichi accidentali (Q_A), che dipendono dalla destinazione d’uso dell'edificio.

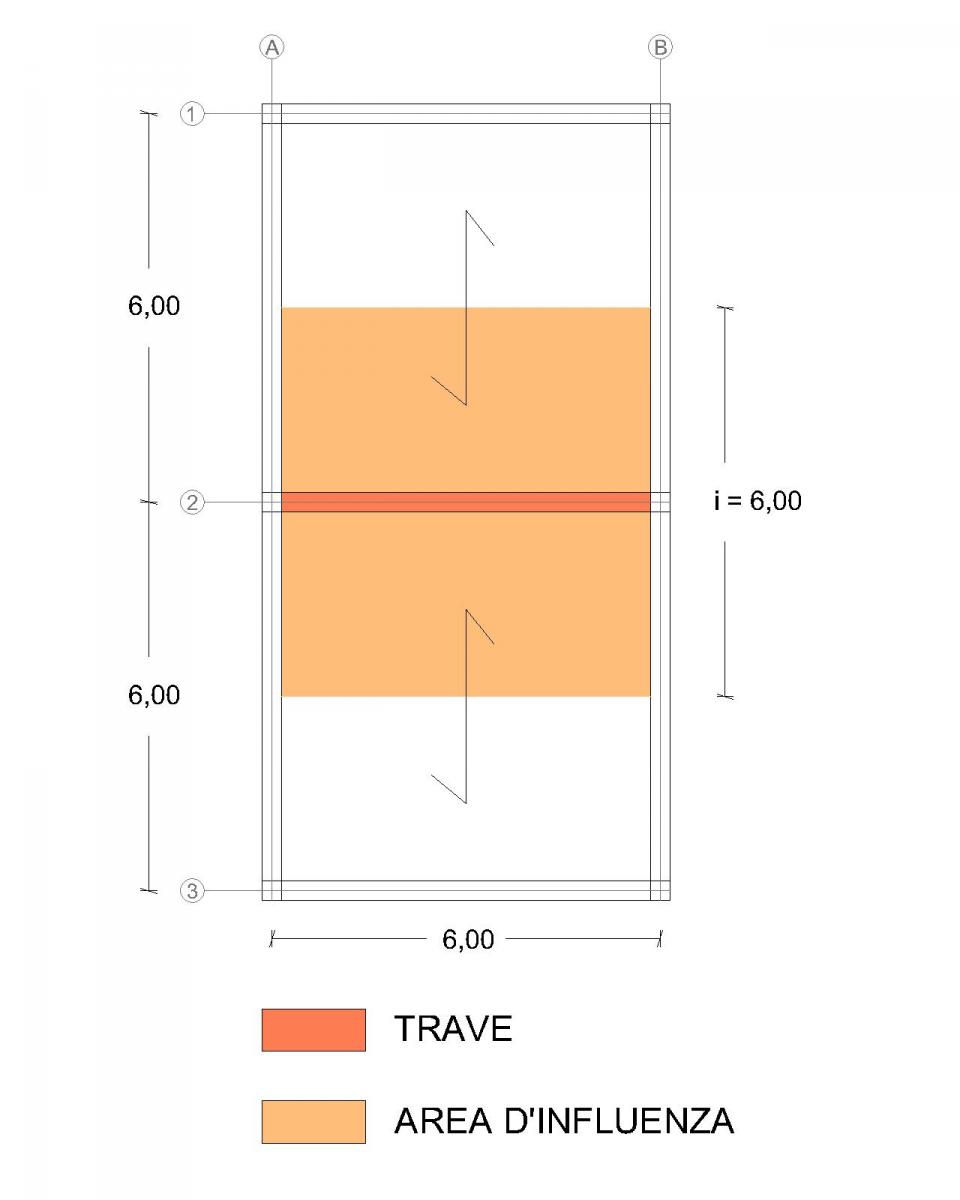
Osservando la pianta di questo impalcato-tipo, capiamo immediatamente che la trave centrale è quella più sollecitata, perchè risulta essere quella con area d'influenza maggiore.

Infatti luce = 6 m ; interasse = 6 m, quindi area di influenza = 36mq. 

Si procede quindi ad esaminare nel dettaglio ognuna delle tre differenti tecnologie di solaio.

 

SOLAIO IN LEGNO

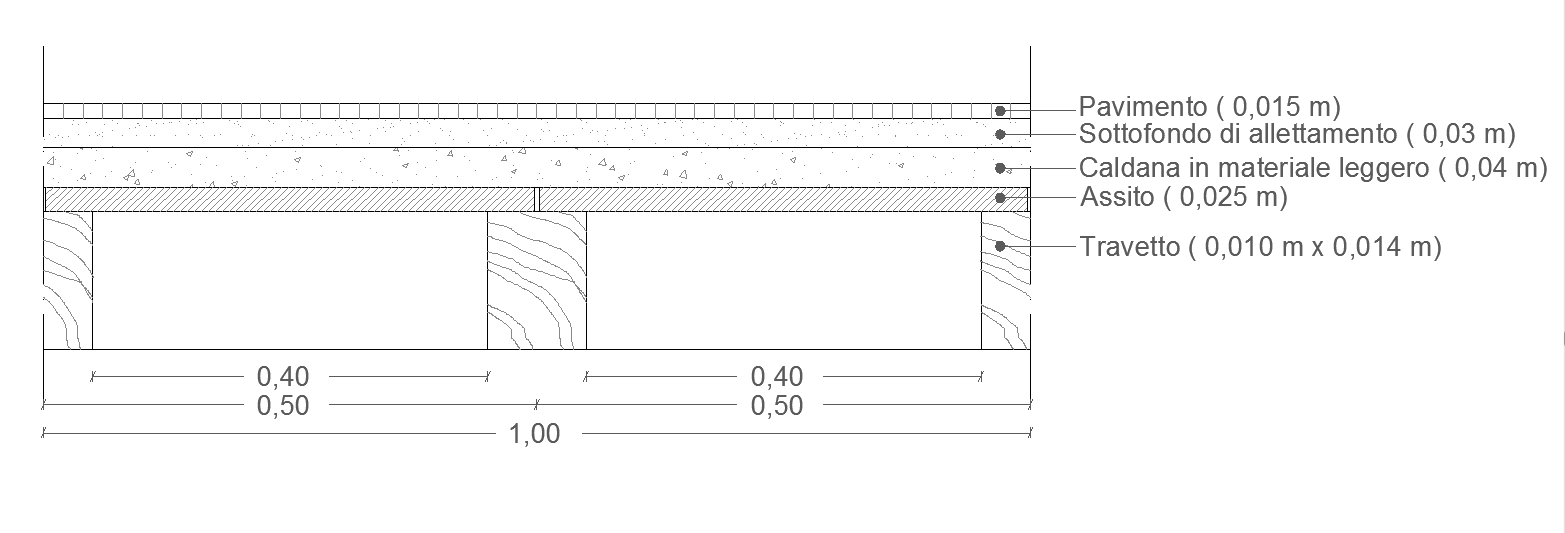
CARICHI STRUTTURALI (Qs)

ASSITO IN LEGNO DI PIOPPO

 spessore = 0,025m

 peso specifico = 5 KN/mc

 Q_s1 = m 0,025 x 5 KN/mc= 0,125 KN/mq

TRAVETTI IN LEGNO DI PIOPPO

 dimensioni = 0,10 m x 0,14 m

 peso specifico = 5KN/mc

Q_s2 = 2( 0, 10 x 0,14)m x 5 KN/mc = 0,14 KN/mq

Q_s= Q_{s1 +} Q_s2 = KN/mq 0,125 +  0,14 = 0,265 KN/mq

 

CARICHI PERMANENTI (Qp)

PAVIMENTO IN COTTO

spessore = 0,015 m

peso specifico = 16 KN/mc

Q_p1= m 0,015 x 16 KN/mc = 0,24 KN/mq

SOTTOFONDO DI ALLETTAMENTO IN MALTA DI CALCE

spessore = 0,03 m 

peso specifico = 21 KN/mc

Q_p2= m 0,03 x 21 KN/mc = 0,64 KN/mq

CALDANA IN MATERIALE LEGGERO

spessore = 0,04 m

peso specifico = 7 KN/mc

Q_p3= m 0,04 x 7 KN/mc = 0,28 KN/mq

TRAMEZZI

Q_p4 = 1 KN/mq

IMPIANTI

Q_p5 = 0,5 KN/mq

Q_p = Q_p1 + Q_p2 + Q_p3 + Q_p4 + Q_p5 = KN/mq 0,24 + 0,64 + 0,28 + 1 + 0,5 = 2,66 KN/mq

 

CARICHI ACCIDENTALI (Q_A)

Q_A = 2 KN/mq

Stabilito da normativa per ambienti ad uso residenziale.

 

Inseriamo questi valori nel foglio di calcolo Excel ed otteniamo così il carico totale Qu (KN/mq).

Inserendo la dimensione della luce che equivale a 6 m, si ricava il momento massimo di una trave doppiamente appoggiata, ossia Mmax = ql²/8.

Adesso bisogna completare il foglio di calcolo con :

  - la tipologia di legno

    (Legno lamellare GL 24h con resistenza a flessione caratteristica fm,k = 24 MPa    

 – il coefficiente della durata del carico kmod = 0,8 (stabilito dalla normativa)

 – coefficiente parziale di sicurezza del materiale

    ( Legno lamellare γm = 1,45 )

Ipotizziamo la base della trave pari a 0,030 m, per ottenere una h_min che equivale all'altezza minima della trave. 

Questa altezza minima deve essere ingegnerizzata, bisogna scegliere quindi un'altezza superiore ad h_min, cioè H = 0,55 m.

Infine bisogna effettuare la verifica, ossia aggiungere al carico totale Q_u il peso proprio della trave.

La sezione 30 x 55 cm è verificata perchè, dopo aver aggiunto al carico totale il peso proprio della trave, h_min < H.

 

 

SOLAIO IN ACCIAIO

  

 

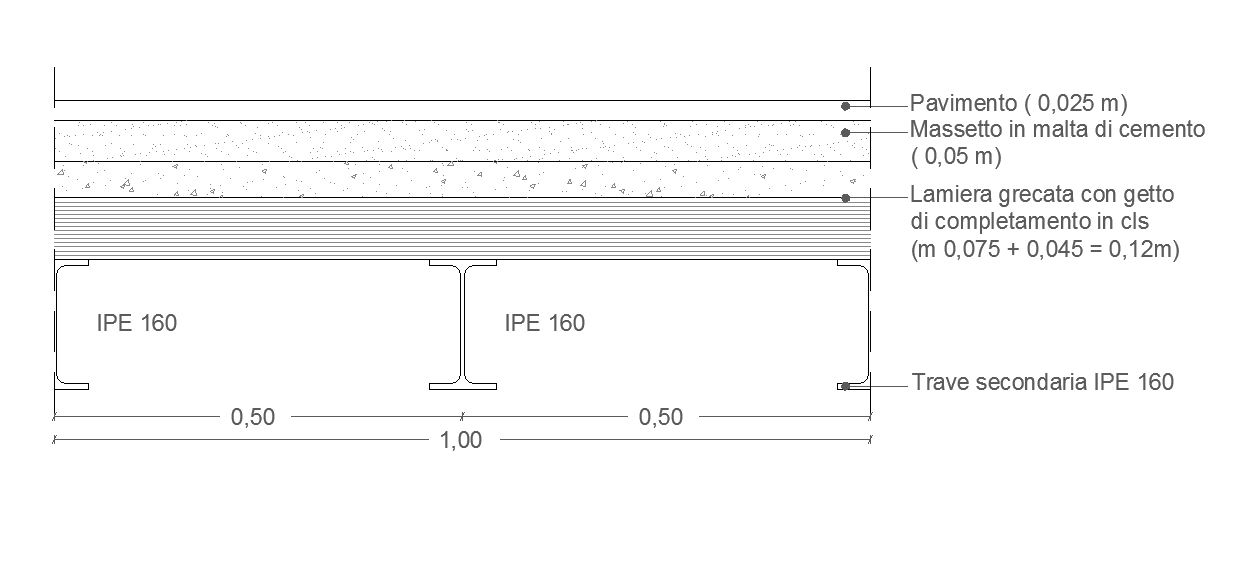
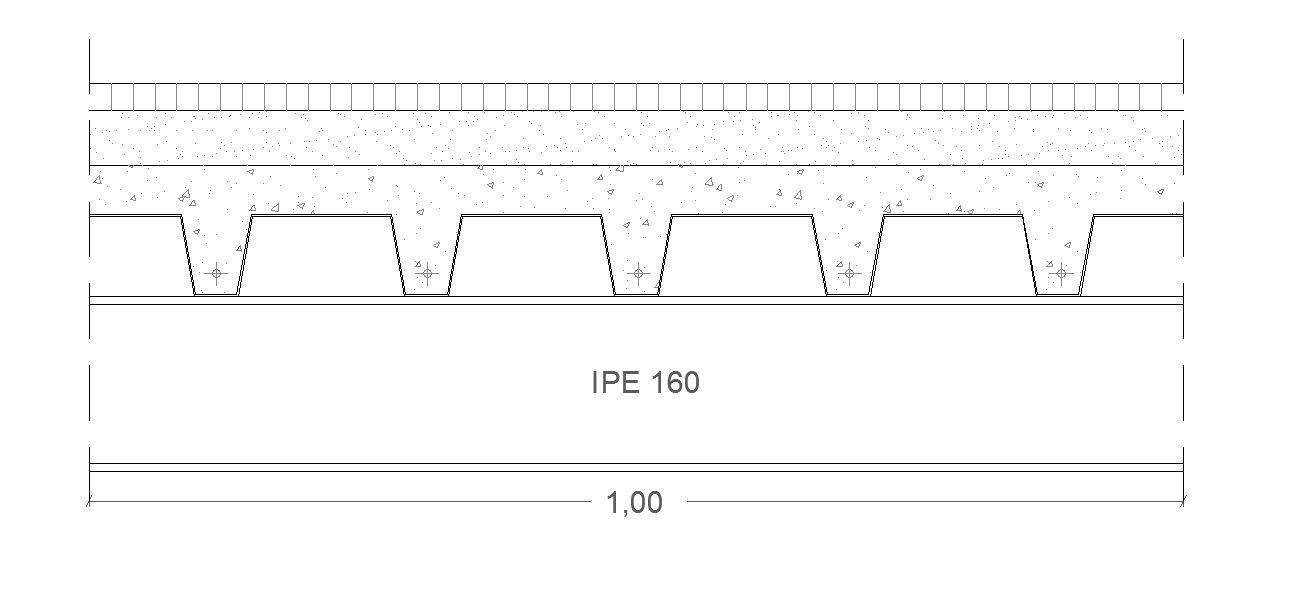
CARICHI STRUTTURALI (Qs)

TRAVE SECONDARIA IPE 160

 area sezione = 0,00201mq

 peso specifico = 78,5 KN/mc

 Q_s1 =( 2 x 0,00201 mq) x 78,5 KN/mc = 0,315 KN/mq

LAMIERA GRECATA

FM 75/750 = 0,165 KN/mq (da scheda tecnica)

 Q_s2 = 0,165 KN/mq

GETTO IN CLS

 area sezione = 0,0645 mq

 peso specifico = 24 KN/mc

 Q_s3 = m 0,0645 x 24 KN/mc = 1,548 KN/mq

Q_s = Q_s1 + Q_s2 + Q_s3 = KN/mq 0,315 + 0,165 + 1,548 = 2,028 KN/mq 

 

CARICHI PERMANENTI (Qp)

PAVIMENTO IN COTTO

spessore = 0,025 m

peso specifico = 16 KN/mc

Q_p1= m 0,025 x 16 KN/mc = 0,40 KN/mq

MASSETTO IN MALTA DI CEMENTO

spessore = 0,05 m 

peso specifico = 21 KN/mc

Q_p2= m 0,05 x 21 KN/mc = 1,05 KN/mq

TRAMEZZI

Q_p3 = 1 KN/mq

IMPIANTI

Q_p4 = 0,5 KN/mq

Q_p = Q_p1 + Q_p2 + Q_p3 + Q_p4 = KN/mq 0,40 + 1,05 + 1 + 0,5 = 2,95 KN/mq

 

CARICHI ACCIDENTALI (Q_A)

Q_A = 3 KN/mq

Stabilito da normativa per ambienti suscettibili di affollamento.

 

Inseriamo questi valori nel foglio di calcolo Excel ed otteniamo così il carico totale Qu (KN/mq).

Inserendo la dimensione della luce che equivale a 6 m, si ricava il momento massimo di una trave doppiamente appoggiata, ossia Mmax = ql²/8.

Adesso bisogna completare il foglio di calcolo con :

 - la tensione di snervamento del Fe 430/ S275, fy,k = 275 MPa

Dai risultati ottenuti con modulo di resistenza pari a W_xmin = 1131,21 cm³, scelgo un profilo con  W_x > W_xmin.

Scelgo dunque una IPE 400.

 

SOLAIO IN CALCESTRUZZO ARMATO

 

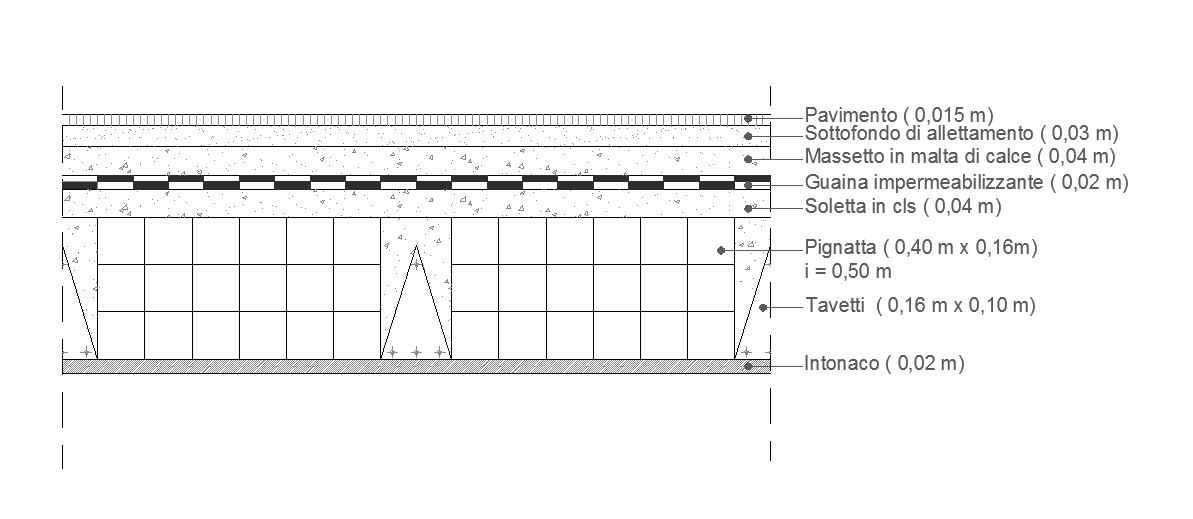
CARICHI STRUTTURALI (Qs)

PIGNATTE

 dimensioni = 0,40 m x 0,16 m 

 peso specifico = 9 KN/mc

 Q_s1 = 2( 0,40 x 0,16)m x 9 KN/mc = 1,152 KN/mq

SOLETTA IN CLS

 spessore = 0,04 m

 peso specifico = 25 KN/mq

 Q_s2 = m 0,04 x 25 KN/mc = 1 KN/mq

TRAVETTI

 dimensioni = 0,16 m x 0,10 m 

 peso specifico = 24 KN/mc

 Q_s3 = ( 0,16 X 0,10) m  x 24 KN/mc = 0,384 KN/mq

 Q_s = Q_s1 + Q_s2 + Q_s3 = KN/mq 1,152 + 1 + 0,384 = 2,536 KN/mq 

 

CARICHI PERMANENTI (Qp)

PAVIMENTO IN PARQUET DI BAMBOO

 spessore = 0,015 m

 peso specifico = 7 KN/mc

 Q_p1= m 0,015 x 7 KN/mc = 0,105 KN/mq

SOTTOFONDO DI ALLETTAMENTO IN MALTA DI CALCE

 spessore = 0,03 m 

 peso specifico = 18 KN/mc

 Q_p2= m 0,03 x 18 KN/mc = 54 KN/mq

GUAINA IMPERMEABILIZZANTE

 spessore = 0,02 m

 peso specifico = 0,01 KN/mc

 Q_p3 = m 0,02 x 0,01 KN/mc = 0,0002 KN/mq

INTONACO

 spessore = 0,02 m

 peso specifico = 10 KN/mc

 Q_p4 = m 0,02 x 10 KN/mc = 0,2 KN/mq

TRAMEZZI

Q_p5 = 1 KN/mq

IMPIANTI

Q_p6 = 0,5 KN/mq

Q_p = Q_p1 + Q_p2 + Q_p3 + Q_p4 + Q_p5 + Q_p6 = KN/mq 0,105 + 0,54 + 0,0002 + 0,2 + 1 + 0,5 = 2,345 KN/mq

 

CARICHI ACCIDENTALI (Q_A)

Q_A = 3 KN/mq

Stabilito da normativa per ambienti ad uso uffici.

 

Inseriamo questi valori nel foglio di calcolo Excel ed otteniamo così il carico totale Qu (KN/mq).

Inserendo la dimensione della luce che equivale a 6 m, si ricava il momento massimo di una trave doppiamente appoggiata, ossia Mmax = ql²/8.

Adesso bisogna completare il foglio di calcolo con :

 - le specifiche dell'acciaio per l'armatura, tensione di snervamento f_yk = 450 MPa

 - resistenza di calcolo a compressione del calcestruzzo f_ck = 50 MPa.

Ipotizziamo la base della trave pari a 0,030 m, per ottenere una h_min che equivale all'altezza minima della trave. 

Questa altezza minima deve essere ingegnerizzata, bisogna scegliere quindi un'altezza superiore ad h_min, cioè H = 0,50m.

La sezione 30 x 50 cm è verificata perchè, dopo aver aggiunto al carico totale il peso proprio della trave, h_min < H.

 

Ho scelto di disegnare i mio modello direttamente su SAP 2000.

 

Selezionare la griglia preimpostata_Grid only_ e determinare le unità di misura KN, m, C.

Si aprirà una tabella in cui inserire il numero di linee della griglia e la lunghezza delle aste_Number of Grid Lines_Grid Spacing

Disegno un cuboall'interno della griglia che mi servirà da modulo base per la struttura reticolare.

Copio il cubo specificando la coordinata dell'ascissa.

 

Ripeto la stessa operazione, questa volta specificando l'ordinata.

 

Poichè il software riconosce i punti interni come degli incastri, vado ad assegnare le cerniere interne.

Seleziono tutte le aste, _Assign_Frame_Release Partial Fixity e spunto Start e End nel momento 33, con valore 0.

Adesso posso assegnare i carichi: dopo aver selezionato i punti in cui voglio che siano applicate le forze_Assign_Joint Loads_Forces

aggiungo la mia FORZA_F al Load Patterns e gli attribuisco come peso proprio 0 (Self Weight Multiplier)

Dopo aver selezionato dal menù a tendina il mio carico, posso attribuire un'intensità alle forze assegnate

 

Vincolo la mia struttura in alcuni punti, quindi li seleziono e con i comandi _Assign_Joint_Restraints_ scelgo delle cerniere

Prima di poter avviare l'analisi assegno una sezione alle aste _Assign_Frame_Frame Sectinos_ e scelgo una sezione circolare_Pipe

 

A questo punto avvio l'analisi e specifico di analizzare soltanto  la deformazione dovuta al carico FORZA_F

Adesso mi è possibile vedere la deformata

Posso inoltre visualizzare i grafici finali, con particolare attenzione allo sforzo normale

Tramite il comando _Set Display Options_ posso verificare numeramente i risultati

Non resta altro che esportare i risultati su una tabella Excel _File_Export Current Table_To Excel 

 

Ho scelto di disegnare i mio modello direttamente su SAP 2000.