blog di SOFIA FRANCIOSINI

In questa quinta esercitazione dobbiamo calcolare la spartizione di una forza orizzontale (forza sismica o del vento) sui diversi telai che compongono la struttura che ho preso in esame, applicando il metodo delle rigidezze.

Come modello di studio prendo in esame un generico edificio con struttura in telai shear-type in cemento armato, che riesce a svolgere il ruolo di controvento oltre che trasmettere i carichi verticali a terra.

PRIMO STEP

Per prima cosa prendiamo in esame la pianta di carpenteria dell'edificio e andiamo ad individuare i telai orizzontali e verticali. Nel mio caso individuo un totale di 14 telai, divisi in:
-7 telai verticali
-7 telai orizzontali

I pilastri hanno sezione 30 cm x 50 cm. Divido i telai in:

v₁ = pilastri 1,8,15                                        o₁ = pilastri 1,2,3,4,5,6,7

v₂ = pilastri 2,9,16                                        o₂ = pilastri 8,9,10,11,12,13,14

v₃ = pilastri 3,10,17                                      o₃ = pilastri 15,16,17,18,19,20,21

v₄ = pilastri 4,11,18                                      o4 = pilastri 22,23,24

v5 = pilastri 5,12,19,22,25,28,31                    o5 = pilastri 25,26,27

v₆ = pilastri 6,13,20,23,26,29,32                    o₆ = pilastri 28,29,30

v₇ = pilastri 7,14,21,24,27,30,33                    o7 = pilastri 31,32,33

Indico nella struttura i controventi, rappresentandoli in pianta come delle molle. Sono un particolare tipo di vincolo che esercitano una forza reattiva ma allo stesso tempo subiscono una deformazione, tra la forza reattiva e la deformazione vi è una diretta proporzione. 

In questo primo step mi devo ricavarela rigidezza traslante di ogni telaio (k = 12 EI/ h³ + 12 EI/ h³). Bisogna stare attenti al diverso orientamento dei pilastri poichè questi offrono un momento d’inerzia diverso in base al loro orientamento (bh^3/12).  

I due valori possibili sono 112500.00 cm⁴ e 312500.00 cm⁴.

SECONDO STEP

Nella seconda tabella sono riportate le rigidezza dei controventi analizzati precedentementi, e la distanza di ciascuno di essi dall'origine.

TERZO E QUARTO STEP

In questo passo dobbiamo calcolare il centro di massa dell'impalcato. Per semplificare questo calcolo, divido la forma della mia pianta in figure geometricamente semplici ( la L dell'edificio viene divisa in due rettangoli). Misuro l’area di questi e la distanza dei loro centri d’area con l’origine fissata precedentemente. 
Con questi dati applico la formula per ottenere le due coordinate del centro di massa dell'impalcato:

X_g= A₁*X_g1 + A₂*X_g2 + A₃*X_g3 / A_tot

Y_g= A₁*Y_g1 + A₂*Y_g2 + A₃*Y_g3 / A_tot

Il mio centro di massa G ha come cordinate ( XG =18,48; Y_G= 10,68). A questo punto vado a sostituire nella formula del centro di massa, la rigidezza dei telai al posto delle aree e la loro distanza dall'origine degli assi, al posto di x_G1, x_G2, y_G1 e y_G2. E' possibile ora trovare le coordinate del centro delle rigidezze C dell'impalcato.

Il centro delle rigidezze ha come coordinate Xc= 18.51 m; Yc= 10.95 m. In questo caso il centro di massa e il centro delle rigidezze si trovano molto vicini. Ciò implica che l’impalcato colpito da una forza lungo X o da una forza lungo Y subirà semplicemente una traslazione, senza subire una rotazione. Invece se i due punti fossero capitati molto più distanti, questa distanza sarebbe servita come "braccio" del momento, sia in caso di una forza orizzontale, che nel caso di una forza verticale.

QUINTO STEP

Nella quinta tabella utilizziamo l'analisi dei carichi sismici per ricavare il valore della forza sismica complessiva agente sul centro di massa. A questo punto vado a riprendere i valori di q_s, q_p e q_a che ho ottenuto nella prima esercitazione, mentre la destinazione ad uso residenzia dell'edificio mi determina un coefficiente di contemporaneità di ψ = 0,3.

Il coefficiente di intensità sismica c viene determinato dall'area geografica dell'impalcato ed è pari a  c = 0,10.

F = 130, 32 KN è il valore della forza sismica da applicare in entrambe le direzioni (x;y)

SESTO E SETTIMO STEP

Negli ultimi due step le tabelle determinano la ripartizione della forza sismica sui vari telai e gli effetti che va a provocare sul telaio.

Nello specifico la sesta tabella prende in esame la traslazione e la rotazione scaturite da Fx, mentre la successiva analizza gli stessi effetti legati a Fy

Ripartizione forza sismica lungo X

Ripartizione forza sismica lungo Y

Gli effetti dell'azione sismica legati a Fx sono i seguenti:

Gli effetti dell'azione sismica legati a Fy sono i seguenti:

Per questa esercitazione è richiesto il dimensionamento, con seguente verifica, di un pilastro, immaginandolo nei soliti materiali: legno, acciaio e cemento armato.

Prendo in considerazione, in un'ipotetica struttura in pilastri e travi di tre piani, il pilastro più sollecitato, quello a terra, che olre al peso del solaio soprastante, deve sorreggere anche il resto della struttura, quindi i due pilastri con i rispettivi solai. 

considerando le aree di influenza, il pilastro più sollecitato risulta quello centrale.

PILASTRO IN LEGNO

Possiamo dividere il procedimento in due parti: la prima ci fornisce le informazioni realtive all'area di influenza (m²) del pilastro e lo sforzo Normale (KN) agento sul pilastro stesso. Prendiamo in esame il solaio già utilizzato per la prima esercitazione (vd. ESERCITAZIONE I: dimensionamento di una trave) così da poterci ricavare i dati relativi ai carichi delle travi, del qs,qp e qa. Tutto deve poi essere moltiplicato per il numero dei piani della struttura. In questo modo ci troviamo lo sforzo normale agente sul pilastro.

A questo punto bisogna fornire i dati propri del materiale che andiamo a utilizzare, in modo da poterci calcolare le dimesioni minime di base e altezza della sezione del pilastro. Nel mio caso b_min= 12.84 cm, però la porto ad una dimensione maggiore per poter stare in sicurezza (b= 20 cm), per l'altezza mi comporto nello stesso modo ( h= 30 cm).

A questo punto verifichiamo che l'area di design sia maggiore dell'area minima ( 20000 cm² > 478.3cm²).

PILASTRO IN ACCIAIO

Come nel caso precedente possiamo dividere il procedimento in due parti: la prima ci fornisce le informazioni realtive all'area di influenza (m²) del pilastro e lo sforzo Normale (KN) agento sul pilastro stesso. Prendiamo in esame il solaio già utilizzato per la prima esercitazione (vd. ESERCITAZIONE I: dimensionamento di una trave) così da poterci ricavare i dati relativi ai carichi delle travi, del qs,qp e qa. Tutto deve poi essere moltiplicato per il numero dei piani della struttura. In questo modo ci troviamo lo sforzo normale agente sul pilastro.

A questo punto bisogna fornire i dati propri del materiale che andiamo a utilizzare, in modo da poterci calcolare le dimesioni di A_min, ro_min e I_min.  Dai dati risultanti mi trovo le dimensioni di design dell'area, del raggio di inerzia e del momento d'inerzia. Ulteriore verifica da controllare riguarda il valore di snellezza max che non si deve superare:
- λ = 96.23. Il profilato che viene fuori è un HEA 160.

PILASTRO IN CEMENTO ARMATO

Come prima  possiamo dividere il procedimento in due parti: la prima ci fornisce le informazioni realtive all'area di influenza (m²) del pilastro e lo sforzo Normale (KN) agento sul pilastro stesso. Prendiamo in esame il solaio già utilizzato per la prima esercitazione (vd. ESERCITAZIONE I: dimensionamento di una trave) così da poterci ricavare i dati relativi ai carichi delle travi, del qs,qp e qa. Tutto deve poi essere moltiplicato per il numero dei piani della struttura. In questo modo ci troviamo lo sforzo normale agente sul pilastro.

A questo punto bisogna fornire i dati propri del materiale che andiamo a utilizzare, in modo da poterci calcolare le dimesioni minime di area e di base della sezione del pilastro. Nel mio caso A_min= 249.0 cm², e b_min= 15.8 cm. Considero in questo modo, sempre per problemi di sicurezza, una base di 30cm. Ci calcoliamo il valore di h_min= 8.30 cm, che portiamo a 40 cm, così da avere un pilastro di dimensioni 30x40. 

La verifica da fare è che  σ_max   <  f_cd  ( 22.74 Mpa < 34.0 Mpa).

Per questa esercitazione bisogna dimensionare una mensola, usando tre tipi diversi di materiale (legno, acciaio, cemento armato), usando il programma Excel.

Riprendo la stessa pianta di carpenteria dell' Esercitazione I ( http://design.rootiers.it/strutture/node/1735 ) , una struttura composta da pilastri e travi, con l'aggiunta però dello sbalzo della mensola. La struttura è data da tre travi di luce 8m, delle quali 2m in aggetto. Prendo in esame la mensola maggiormente sollecitata, quella centrale.

Il foglio elettronico che prendiamo è diviso in due parti. Una parte uguale a quella della prima esercitazione, e quindi riguardanti problemi legati allo SLU, mentre nella seconda parte, quella che riguarderà la deformabilità, quindi ci troviamo in campo elastico, SLE.

Ovviamente le due analisi presuppongono coefficienti di sicurezza diversi, perchè nello stato limite ultimo si analizza il collasso, mentre nello stato limite di esercizio si considerano i fenomeni di deformabilità, ovvero fenomeni che non compromettono il funzionamento generale della struttura.

SOLAIO IN LEGNO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

Mi risulta quindi che: qu= 33,472 KN/m

e dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 66,944 KN*m

Imposto ora i dati relativi al materiale di riferimento:

Scelgo un legno di classe C24, che ha come caratteristiche:

fmk = 24 N/mm2 (tensione caratteristica)

Kmod = 0.8

γ m = 1.45

ci troviamo a questo punto la tensione di progetto fd (N/mm2) = (Kmod x fmk) / γ m = 13.24

e ottengo per una base di 25cm un altezza minima di 34,83 cm che ingegnerizzo a 40cm.

Ora inizia la parte relativa allo SLE, ci troviamo il carico relativo al campo elastico qe.

Imposto il Modulo elastico pari a 8000 MPa ed ottengo una Ix = 133333 cm⁴

Infine arrivo a calcolarmi il mio spostamento massimo v_max= 0,35cm, che mi conferma il progetto poiché Ix/v_max >250.

SOLAIO IN ACCIAIO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

Mi risulta quindi che: qu= 39.508 KN/m

e dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 79.016 KN*m

Imposto ora i dati relativi al materiale di riferimento:

Scelgo un acciaio di classe S235, che ha come caratteristiche:

fyk = 235 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m ₀= 223.81 (con γ m ₀= 1.05)

Troviamo così il modulo di resistenza a flessione minimo uguale al rapporto Mmax/fd 

Wx,min = 353.05 cm³

Prendo la tabella delle sezioni IPE per trovare le dimensioni della trave portante, sapendo che la resistenza a flessione deve essere più grande di quella trovata.

Prendo una IPE 270, della quale il valore Ix= 5790 cm⁴

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e =  23.921 KN/m
Come risultato avrò un v_max = 0,393 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

SOLAIO IN CEMENTO ARMATO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 83.66 KN*m

Scelgo un acciaio di classe S450, che ha come caratteristiche:

fyk = 450 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m = 391.30 (con γ m = 1.15)

Prendo un cls che abbia come tensione caratteristica fck = 60 N/mm^2, così da trovare la tensione di progetto

fcd= (0.85 x fck) / γm, con γm pari a 1.5.

Prendo il valore di β=0.57 e di r=2.09

Prendo un valore della base pari a 20cm per poi riuscire a trovare il valore di hu = 23.15 cm, con un copriferro δ di 4cm. L'Hmin viene di 27.15 cm che approssimo ad un altezza di 30cm.

Il foglio elettronico di excel verifica allora con i dati ottenuti se la trave presa in considerazione ha una tensione di progetto pari alla massima tensione esercitata in campata. In questo caso la trave è verificata.

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 26.70 KN/m
Imposto il Modulo elastico del c.a. pari a 21000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 45000 cm⁴
Come risultato avrò un v_max = 0,57 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

In questa esercitazione bisogna prendere in esame una trave reticolare. Utilizzo il programma SAP 2000, per la modellazione della trave stessa, per poi dimensionarla aiutandomi con un file Excell.

1. Modellazione

Scelgo una griglia modulare, basata su 6 quadrati di lati 2m x 2m, con riferimenti X = 3, Y= 4, Z = 2. Su questa griglia decido di costruirmi una trave reticolare a base quadrangolare. Per disegnarla mi sono costruita un cubo che poi ho copiato più volte per comporre la struttura. A questo punto devo verificare di non aver copiato più volte uno stesso segmento e quindi di non aver creato doppioni. Vado su  Edit_Merge duplicate, dopo aver selezionato tutta la struttura, e mi accerto di non avere doppi. Un altra verifica che è opportuno fare è la verifica di tolleranza dei nodi. Seleziono tutta la struttura e vado su Edit_Edit points_Merge joints e confermo il valore pari a 0,1.

 2. Materiale e Carichi

A questo punto la mia struttura è finita e quindi posso passare a porre i miei vincoli. Decido di mettere 4 cerniere agli appoggi. Dato che la struttura reticolare lavora a sforza normale di trazione o compressione, bisogna svincolare i nodi al momento. Seleziono quindi tutta la struttura e poi vado su Assign_Frame_Release/Partial Fixity e blocco Moment (2-2) e Moment (3-3).
Procedo con la caratterizzazione della mia struttura definendo il materiale (tubolare in acciaio) ed assegno ai nodi superiori una forza F pari ad F=-150 KN (Assign_Joints Load).

3. Analisi

La trave reticolare è caratterizzata da solo sforzo normale, quindi devo verificare che siano assenti sforzi di taglio e di momento. Vado a vedere le sollecitazioni N,T,M. Constato che sia il taglio che il momento sono nulli, mentre gli sforzi normali sono presenti e diversi asta per asta. Esporto tutti i dati relativi alla mia struttura su un foglio di calcolo elettronico Excel per procedere con il dimensionamento delle aste.

4. Dimensionamento

Dopo aver ordinato il foglio Excel , ho per ogni singola asta il valore dello sforzo normale di trazione (+) o compressione (-). Ovviamente non ho tutte aste di dimensioni uguali, infatti all'infuori del mio quadrato ho anche la dua diagonale.
- Aste orizzontali = 2 m
- Aste diagonali = 2.83 m
- Aste inclinate = 2 m
 

4.1 Trazione  
Devo riportare tutti i valori di N di trazione all'interno del mio file Excel, a aggiungo le caratteristiche dell'acciaio scelto (f_yk=235 MPa) ed il coefficiente γ_m=1,05. A questo punto ottengo una A_min (cm²)=(N*10)/f_yd. Ora posso scegliere i profileti tubolari prendendo i profili in base a questi valori ingegnerizzandoli.

4.2 Compressione
Per la compressione la questione varia. La prima parte rimane identica al procedimento per la trazione, ma bisogna anche considerare il fenomeno di instabilità.
Aggiungo quindi i valori di E=210000 MPa, beta=1, e la lunghezza dell'asta considerata. Arrivo così ad ottenere i tre dati fondamentali per poter dimensionare le mie aste.

-Lambda= pi*sqrt(E/f_cd)
-Rho_min= (l₀*100)/Lambda
-I_min= E*(Rho_min)².

Inizio il dimensionamento delle aste in base ai valori di Rho_min e I_min. L'ultima verifica di cui devo tenere conto è la Lambda finale che deve risultare <200.

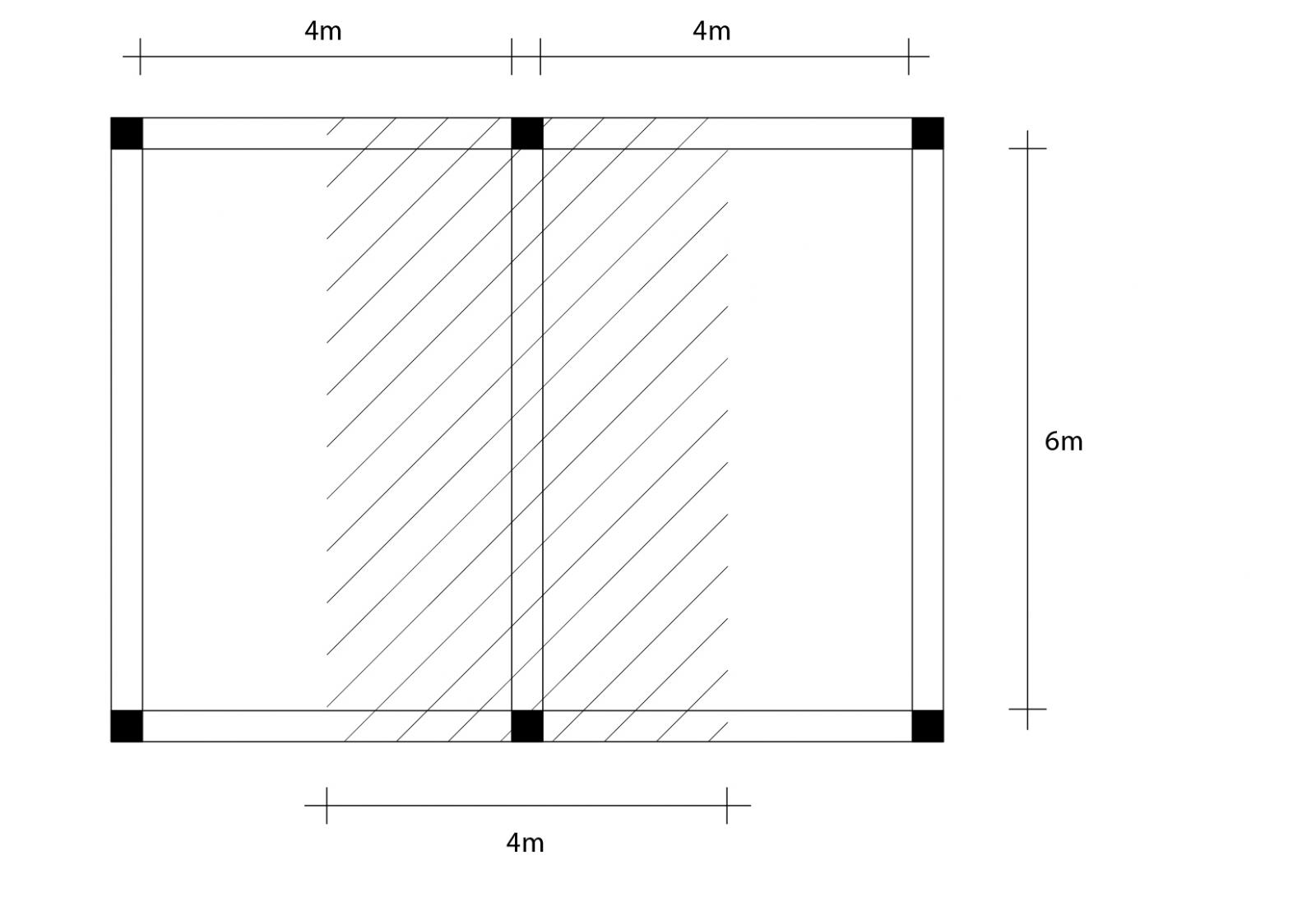
Prendiamo in esame una struttura composta da pilastri e travi. Nel mio caso si stratta di una struttura formata da tre travi di luce 6m doppiamente appoggiate. Prendo in considerazione la trave maggiormente sollecitata, quella centrale, e quindi la sua area d'influenza. 

SOLAIO IN LEGNO

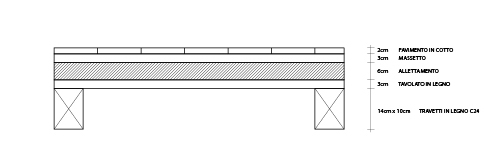
Considero un solaio in legno, appoggiato sulla trave centrale, composto dagli elementi presenti nel disegno soprastante. Dobbiamo quindi colcolare il carico ( qu) che grava su questa struttura. Per far ciò dobbiamo vedere quanto possa pesare in termini di KN il solaio stesso. 

PESI SPECIFICI (da schede tecniche) espressi in KN sapendo che 1KN=100Kg

Pavimento in cotto : 40 Kg/mq --> 0.4 KN/mq
Massetto : 1900 Kg/mc --> 19 KN/mc
Allettamento : 1400 Kg/mc --> 14 KN/mc
Tavolato in legno : 530 Kg/mc --> 5.3 KN/mc
Travetti in legno: 530 Kg/mc --> 5.3 KN/mc

devo a questo punto esprimere i valori al mc in mq, in quanto devo trattare il carico linearmente, all'interno della mia porzione di solaio espessa in 1 mc. Quindi:

Pavimento  --> [( 19 KN/mc x 1m x 1m x 0.03m) / 1mq] = 0.57 KN/mq

Allettamento  --> [( 14 KN/mc x 1m x 1m x 0.06m) / 1mq] = 0.84 KN/mq

Tavolato   --> [( 5.3 KN/mc x 1m x 1m x 0.03m) / 1mq] = 0.159 KN/mq

Travetti  --> [ 2x( 5.3KN/mc x 1m x 0.1m x 0.14m) / 1mq] = 0.15 KN/mq

A questo punto inizio a calcolare i diversi carichi. Il carico strutturale è composto dalla somma dei pesi specifici dei travetti e del tavato in legno.

qs= 0.15 KN/mq + 0.159 KN/mq = 0.31 KN/mq

il carico permanente è composto dal resto degli elementi del solaio più 1 KN/mq per i tramezzi portati e 0.5 KN/mq per gli impianti.

qp= 0.4 KN/mq + 0.57 KN/mq + 0.84 KN/mq + 1 KN/mq +0.5 KN/mq = 3.31 KN/mq

In più ci prendiamo un valore già stabilito per il carico accidentale, in quanto l'edificio ha come destinazione d'uso delle residenze

qa= 2 KN/mq

A questo punto mettiamo tutti i valori trovati all'interno del file excel.

Vediamo subito il valore del carico ultimo pari a 33.47 KN/m. Da qui ci calcoliamo il valore di Mmax in campata pari a qu(l²)/8 quindi pari a 150.62 KNm.

Scelgo un legno di classe C24, che ha come caratteristiche:

fmk = 24 N/mm2 (tensione caratteristica)

Kmod = 0.8

γ m = 1.45

ci troviamo a questo punto la tensione di progetto fd (N/mm2) = (Kmod x fmk) / γ m = 13.24

scelgo una base di 30cm, e trovo una hmin = 47.70cm, in fine posso prendere la H definitiva della mia trave, pari a 50cm.

SOLAIO IN ACCIAIO

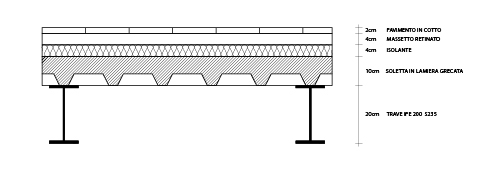
Considero un solaio in acciaio, appoggiato sulla trave centrale, composto dagli elementi presenti nel disegno soprastante. Dobbiamo quindi colcolare il carico ( qu) che grava su questa struttura. Per far ciò dobbiamo vedere quanto possa pesare in termini di KN il solaio stesso. 

PESI SPECIFICI (da schede tecniche) espressi in KN sapendo che 1KN=100Kg

Pavimento in cotto : 40 Kg/mq --> 0.4 KN/mq
Massetto : 1900 Kg/mc --> 19 KN/mc
Isolante : 0.2 KN/mc
Soletta in lamiera grecata: 1.86 KN/mq
IPE 200: 78.5 KN/mc, di area 0.0028mq

devo a questo punto esprimere i valori al mc in mq, in quanto devo trattare il carico linearmente, all'interno della mia porzione di solaio espessa in 1 mc. Quindi:

Pavimento  --> [( 19 KN/mc x 1m x 1m x 0.04m) / 1mq] = 0.76 KN/mq

Isolanti  --> [( 0.2KN/mc x 1m x 1m x 0.04m) / 1mq] = 0.008 KN/mq

Travetti  --> [ 2x( 78.5KN/mc x 0.0028mq x 0.1m ) / 1mq] = 0.43KN/mq

A questo punto inizio a calcolare i diversi carichi. Il carico strutturale è composto dalla somma dei pesi specifici delle travette in acciaio e della lamiera grecata

qs= 0.43 KN/mq + 0.86 KN/mq = 2.29 KN/mq

il carico permanente è composto dal resto degli elementi del solaio più 1 KN/mq per i tramezzi portati e 0.5 KN/mq per gli impianti.

qp= 0.4 KN/mq + 0.76 KN/mq + 0.008 KN/mq + 1 KN/mq +0.5 KN/mq = 2.6 KN/mq

In più ci prendiamo un valore già stabilito per il carico accidentale, in quanto l'edificio ha come destinazione d'uso delle residenze

qa= 2 KN/mq

A questo punto mettiamo tutti i valori trovati all'interno del file excel.

Vediamo subito il valore del carico ultimo pari a 39.51 KN/m. Da qui ci calcoliamo il valore di Mmax in campata pari a qu(l²)/8 quindi pari a 177.79 KNm.

Scelgo un acciaio di classe S235, che ha come caratteristiche:

fyk = 235 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m ₀= 223.81 (con γ m ₀= 1.05)

Troviamo così il modulo di resistenza a flessione minimo uguale al rapporto Mmax/fd 

Wx,min = 794.36 cm³

Prendo la tabella delle sezioni IPE per trovare le dimensioni della trave portante, sapendo che la resistenza a flessione deve essere più grande di quella trovata. 

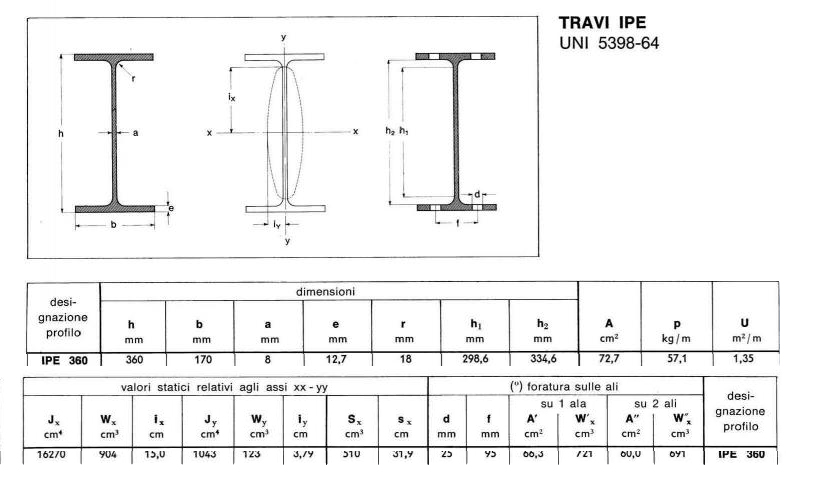
Prendo una IPE 360, della quale il valore Wx= 904 cm³

SOLAIO IN CEMENTO ARMATO

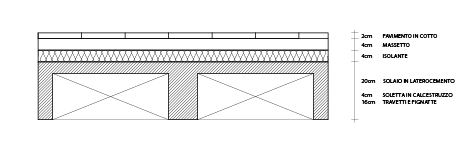
Considero un solaio in cemento armato, appoggiato sulla trave centrale, composto dagli elementi presenti nel disegno soprastante. Dobbiamo quindi colcolare il carico ( qu) che grava su questa struttura. Per far ciò dobbiamo vedere quanto possa pesare in termini di KN il solaio stesso. 

PESI SPECIFICI (da schede tecniche) espressi in KN sapendo che 1KN=100Kg

Pavimento in cotto : 40 Kg/mq --> 0.4 KN/mq
Massetto : 1900 Kg/mc --> 19 KN/mc
Isolante : 0.2 KN/mc
Solaio in latero cemento : travetti 24 KN/mc; soletta 24 KN/mc
Intonaco (1cm) : 18 KN/m

devo a questo punto esprimere i valori al mc in mq, in quanto devo trattare il carico linearmente, all'interno della mia porzione di solaio espessa in 1 mc. Quindi:

Pavimento  --> [( 19 KN/mc x 1m x 1m x 0.04m) / 1mq] = 0.76 KN/mq

Isolante  --> [( 0.2KN/mc x 1m x 1m x 0.04m) / 1mq] = 0.008 KN/mq

Travetti  -->  [( 24KN/mc x 1m x 1m x 0.04m) / 1mq] = 0.96 KN/mq

Soletta  -->  [2 x ( 24KN/mc x 0.1m x 0.16m x 1m) / 1mq] = 0.77 KN/mq

Pignatte (8)  --> 8x (9.1 Kg)/1mq = 72.8 Kg/mq = 0.728 KN/mc

A questo punto inizio a calcolare i diversi carichi. Il carico strutturale è composto dalla somma dei pesi specifici del solaio in latero cemento.

qs= 0.96 KN/mq + 0.77 KN/mq + 0.728 KN/mq = 2.46 KN/mq

il carico permanente è composto dal resto degli elementi del solaio più 1 KN/mq per i tramezzi portati e 0.5 KN/mq per gli impianti.

qp= 0.4 KN/mq + 0.76 KN/mq + 0.008 KN/mq + 0.18 KN/mq + 1 KN/mq +0.5 KN/mq = 2.668 KN/mq

In più ci prendiamo un valore già stabilito per il carico accidentale, in quanto l'edificio ha come destinazione d'uso delle residenze

qa= 2 KN/mq

A questo punto mettiamo tutti i valori trovati all'interno del file excel.

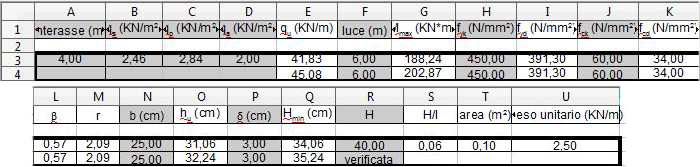
Vediamo subito il valore del carico ultimo pari a 41.83 KN/m. Da qui ci calcoliamo il valore di Mmax in campata pari a qu(l²)/8 quindi pari a 188.24 KNm.

Scelgo un acciaio di classe S450, che ha come caratteristiche:

fyk = 450 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m = 391.30 (con γ m = 1.15)

Prendo un cls che abbia come tensione caratteristica fck = 60 N/mm^2, così da trovare la tensione di progetto

fcd= (0.85 x fck) / γm, con γm pari a 1.5.

Prendo il valore di β=0.57 e di r=2.09

Prendo un valore della base pari a 25cm per poi riuscire a trovare il valore di hu= 31.06 cm, con un copriferro δ di 3cm. L'Hmin viene di 34.06 cm che approssimo ad un altezza di 40cm.

Il foglio elettronico di excel verifica allora con i dati ottenuti se la trave presa in considerazione ha una tensione di progetto pari alla massima tensione esercitata in campata. In questo caso la trave è verificata.