Blog

Prima esercitazione : Struttura reticolare simmetrica

Le strutture reticolari sono strutture composte da tiranti( aste tese) e puntoni (aste compresse), collegate tra di loro da cerniere interne.
 Per la risoluzione di questa struttura reticolare simmetrica e con carichi ripartiti in ugual modo nel nodo B , D e G  abbiamo cercato di utilizzare il metodo di Ritter al fine di calcolare lo sforzo assiale a cui sono sottoposte tutte le aste.

Il primo passo consiste nel verificare che la struttura sia isostatica, poiche se fosse iperstatica non sarà possibile utilizzare il metodo di Ritter.

Verfica isostaticità
La struttura è isostatica se il numero di vincoli è pari al numero dei gradi di libertà della struttura.  n°gdv=n°gdl

Verifica dell' isostaticità della struttura:

·         Gradi di libertà si ricava moltiplicando il numero degli elementi per il numero dei gradi di libertà.
Gd l= 11 x 3 = 33

·         Gradi di vincoli si ricava sommando il numero i vincoli esterni e i vincoli interni  
V = V_{E +} Vi  

I vincoli esterni della struttura sono in tutto 3  
V_E = 3

I vincoli interni della struttura si calcola applicando a ogni nodo
V_i = 2 (n - 1)
dove n è il numero delle aste che convergono nel nodo

In particolare in:

A e H 2( 2-1)= 2  ; B e G 2(3-1)= 4 ; D C ed E 2(4-1)= 6

Il grado di vincolo interno sarà quindi:

V_{i =} 2 + 2 + 4 +4 + 6 +6 +6 = 30

Quindi:

Gdv = V_{E +} V_I = 30 +  3 = 33

La struttura quindi risulta isostatica  n°gdl=n°gdv

Verfica isostaticità
Inoltre si può fare un ulteriore verifica che consiste nel

V_E + a = 2 x nodi  ( vincoli esterni + n° aste = 2 x n° nodi ) 
3 + 11 = 2 x 7 =14 ( verificato)

Quindi possiamo dire che le condizioni di isostaticotà sono verificate e si può procedere calcolando i vincoli tramite le equazioni di bilancio.

Mi disegno le reazioni vincolari V_A  e   V_B

imponendo le equazioni alla traslazione verticale si possono trovare i valori di V_A  e   V_B dovute alla cerniera ed al carello.

Σ Fy =0

V_A+ V_{B –} 3F= 0   
Le reazioni verticali VA e VB della struttura che essendo applicata a una struttura simmetrica ripartiscono equamente il carico applicato ai nodi superiori e bilanciano le forze esterne pari a 60 kN.

Quindi:   
V_A   =  V_B  = 3/2 F   = 3/2 x 20 KN = 30 KN  (uguali proprio perché la struttura è simmetrica).

Adesso possiamo effettuare un taglio virtuale della struttura in due parti tramite una sezione di Ritter, cioè dobbiamo sezionare in modo da tagliare tre aste che non convergono verso uno stesso nodo. E cosi possiamo mettere in evidenza le azioni di contatto.

Dal primo taglio virtuale, posso mettere in ivedenza gli sforzi normale aggenti sulle sezioni delle aste tagliate. Si ipotizza un verso uscente dalla sezione e quindi come se le considerassimo le aste siano sottoposte a trazione e a seconda del risultato delle equazioni di equilibrio a confermare il verso oppure no.

In questo caso abbiamo tre incognite N_{1  ,}N₂  e  N₃ e tre sono equazioni di bilancio, quindi il problema è risovibile.

Scrivendo le 3 equazioni di equilibrio a rotazione, cambiando ogni volta il polo scelto nel punto di incontro di due della altre aste per poi ricavare una delle incognite.

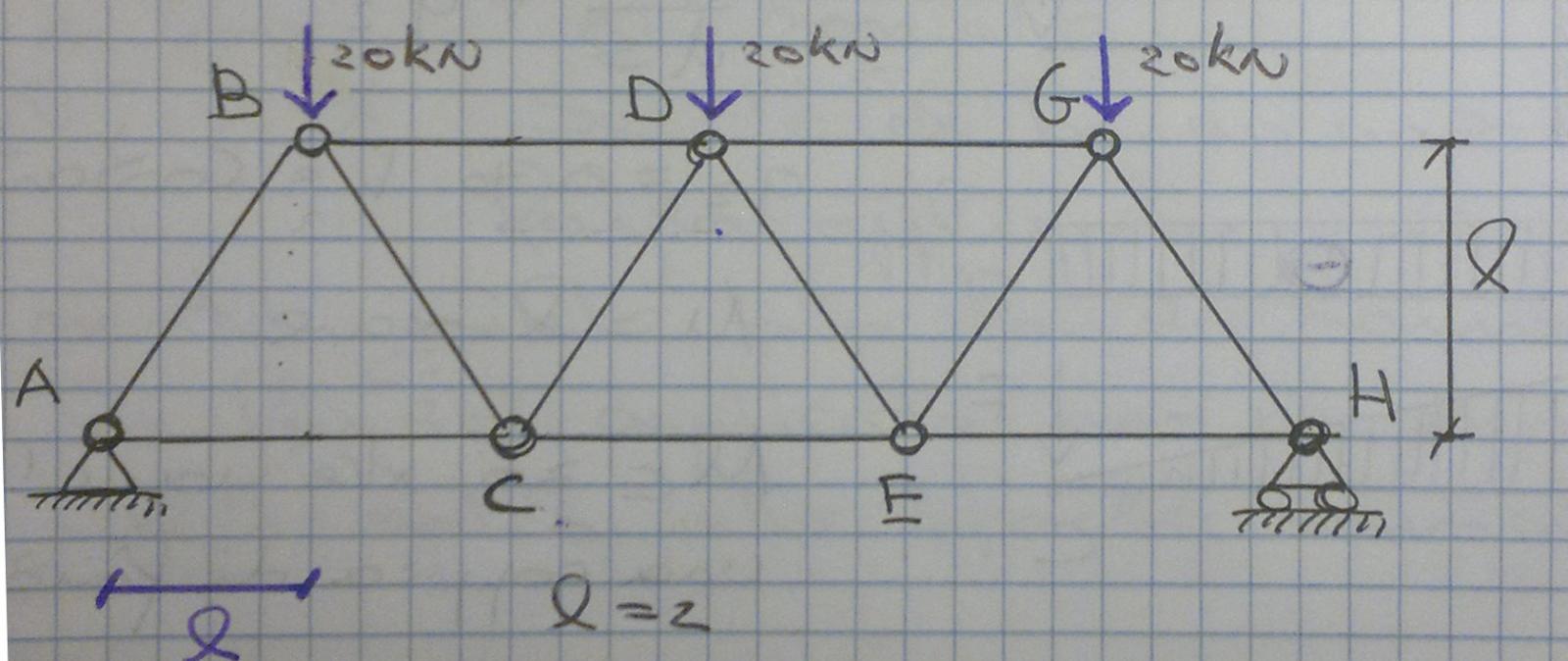
Facendo l' equilibrio al momento in C  in cui convergono due delle tre aste sezionate possiamo poi ricavare la forza N₁ incognita

ΣMc=0

- 3/2 F · 2l + F · l - N_{1 · l} =0

N₁ = F - 3F = -2F

Il segno negative comporta di cambiare il verso a priori presupposto e quindi è un puntone.

Facendo l' equilibrio in B ricavo N₃

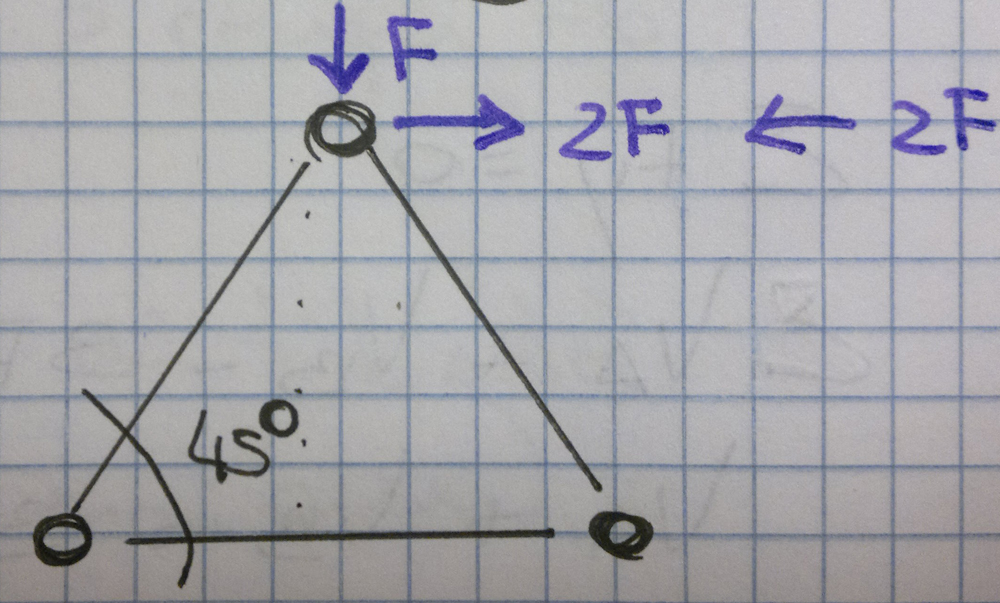
Equilibrio al momento in B
ΣMB=0

- 3/2 F · l + N_{3 · l =} 0   N_{3 =} 3/2 F

Cosi posso ricavare anche facendo equilibrio alla traslazione verticale

 

Equilibrio verticale, ricordando la scomposizione della forza nelle sue componenti orizzontali e verticali e imponendo le equazioni di equilibrio alla traslazione otteniamo

 

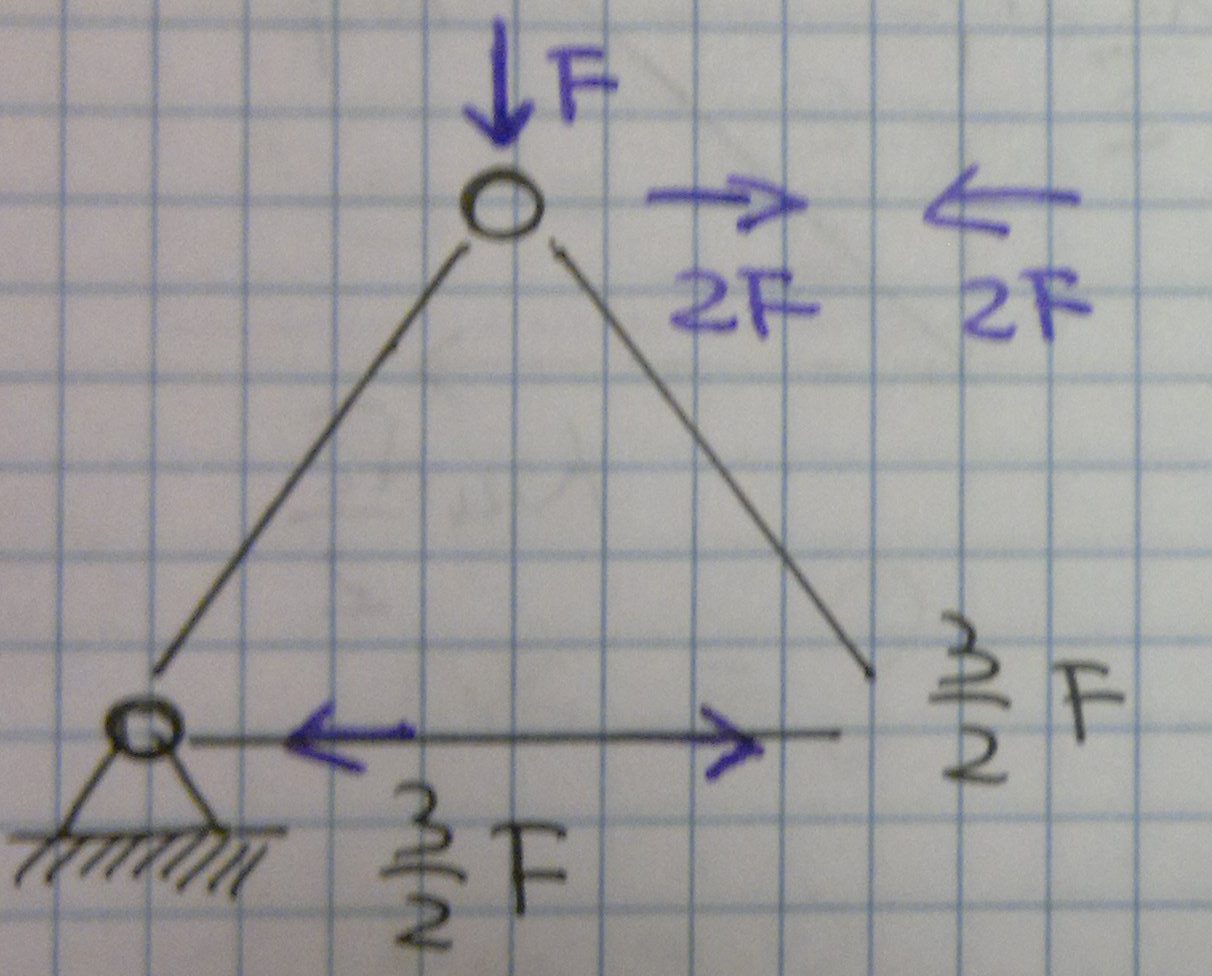
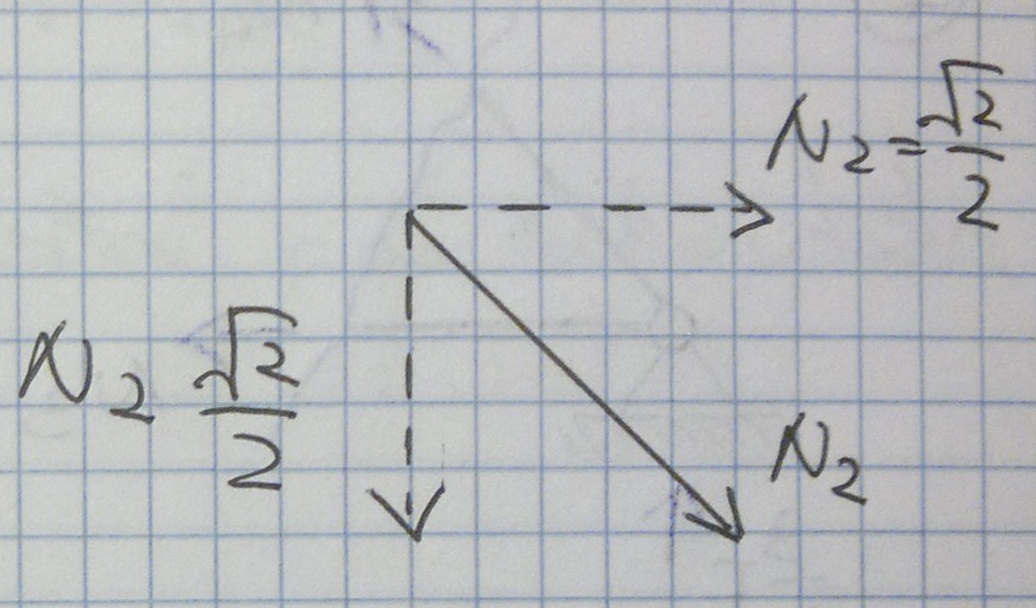
Σ Fy =0

3 / 2 F - F - N₂ 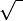 2/ 2 = 0  Quindi   N_{2 =} F 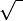2/ 2 

A questo punto effettuo un altro taglio per rivacarmi  N₄ l’ unico valore che ancora non conosciamo della parte sinistra della trave reticolare.

la N₄ la possiamo scomporre nei suoi due componenti:

 

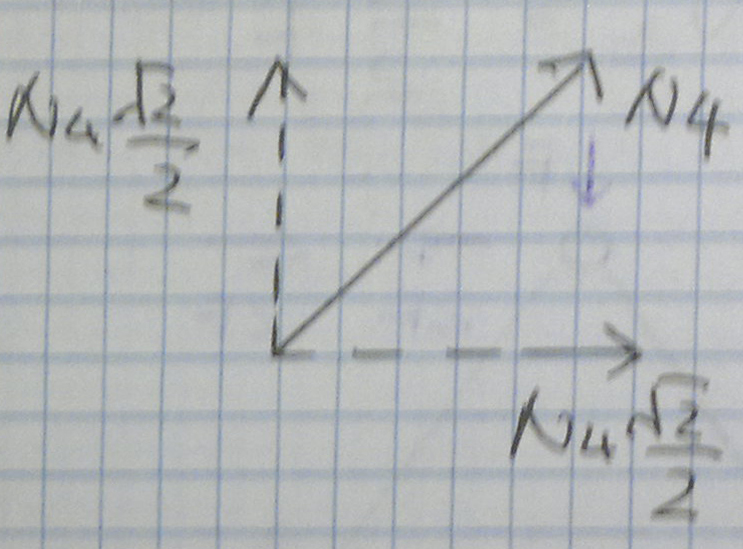
Conoscendo il valore di N₃ possiamo scrivere l’equilibrio alla traslazione verticale

  Equilibrio verticale:

3/2 F + N₄ 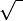2/ 2=0

 N_{4 =} - 3 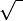2/ 2 · F

Quindi mettendo insieme i risultati, abbiamo

 

 

Continuando a effettuare un altro taglio ricaviamo:

Dall’equilibrio del momento in D

ΣMD=0

N_{5 ·} l + F · 2l - 3/2 F · 3 / 2 F · 3 l = 0

N_{5 =} 5/2 F  Infatti questa è l'asta più sollecitata

Infine mediante l' equilibrio verticale ricaviamo N₆

N₆ 2/ 2 + 3/2 F - F =0

N_{6 =} -  F2/ 2 (cambio verso)

 

 

Seconda Esercitazione : Struttura reticolare asimetrica

La struttura reticolare asimetrica può essere risolto questa volta utilizzando il metodo dei nodi.

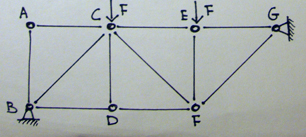
Per iniziare, come nel primo esercizio, bisogna verificare che la struttura sia isostatica

La struttura è isostatica se il numero di vincoli è pari al numero dei gradi di libertà della struttura.  n°gdv=n°gdl

Verifica dell' isostaticità della struttura:

La struttura è isostatica se il numero di vincoli è pari al numero dei gradi di libertà della struttura.  n°gdv=n°gdl

·         Gradi di libertà si ricava moltiplicando il numero delle aste per il numero dei gradi di libertà.
          Gd l= 11 x 3 = 33

·         Gradi di vincoli si ricava sommando il numero i vincoli esterni e i vincoli interni 
           V = V_{E +} Vi  

I vincoli esterni della struttura sono in tutto 3 
V_E = 3

I vincoli interni della struttura si calcola applicando a ogni nodo
V_i = 2 (n - 1)
dove n è il numero delle aste che convergono nel nodo

In particolare in:

A e G    2( 2-1)= 2  ;

B ,D e E    2(3-1)= 4

F     2(4-1)= 6

C    2 (5-1)=8

Il grado di vincolo interno sarà quindi:

V_{i =} 2 x 2 + 4 x 2 + 6 + 8= 30

Quindi:

Gdv = V_{E +} V_I = 30 +  3 = 33

La struttura quindi risulta isostatica  n°gdl=n°gdv

 

Calcolo delle reazioni vincolari
Ora possiamo procedere analizzando le reazioni vincolari RuA , RvA e RuG.

Imponendo l’equazione di bilancio alla traslazione verticale

∑Fy = 0  

 RvA = 20

Attraverso l’equazione di bilancio ai momenti M(B) ottengo RuA

∑MG = 0

RuA ∙ 1 –(10 ∙1)- (10∙2)= 30  RuA = 30

Imponendo l’equazione di bilancio alla traslazione orizzontale ottengo  RuG

∑Fx = 0  

 RuA = RuG

 

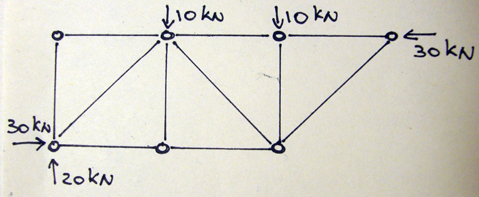
Calcolo delle azioni di contatto
Applichiamo il metodo dei nodi per ricavare le forze lungo le aste, in cui dobbiamo assumere che ai nodi ci siano delle forze concentrate sui nodi e possiamo analizzarli  attraverso l’equilibrio al nodo oppure con il metodo geometrico utilizzando la regola del parallelogramma per scomporre le forze.
 

Nodo A

Le incognite  in questo caso sono N₁ e N₂  i quali risultano aste le aste 1 e 2 entrambe  scariche.

N₁ =0

N₂ =0

 

Nodo B
 

 

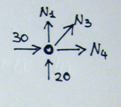
In questo caso è possibile scomporre N₃ nelle sue due componenti e poi imponendo l’equilibrio alla traslazione orizzontale e verticale si ottengono i valori di N₃ e N₄

∑Fx =0   30+ N₃√2 /2 +N₄ = 0

∑Fy =0   20 + N₃ √2 /2 =0      

              N₃= - 20 ∙  2 /√2  = - 20 √2  kN

Posso ricavare N_4:    

30 – (20 √2∙√2/2) + N₄ = 0

30- 20 + N₄ = 0

N₄ = -10 kN ( cambio verso )

 

Nodo D

 

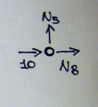
10 + N₈ = 0

N₈ = - 10

N₅ = 0

Nodo C

     

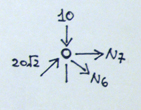
Possiamo scomporre i  contributi dell’asta 6 e 5, per poi ricavare dall’equilibrio alla traslazione verticale e orizzontale i valori di N₆ e N₇

∑Fy = 0    10 + N₆ √2/2 -20√2-√2/2=0

                10+N₆ ∙√2/2 -20 = 0

               N₆ = 10√2  kN

∑Fx = 0     N₇+ N₆ √2/2 + 20√2 - √2/2 = 0

                 N₇ + 10√2∙√2/2 +20 = 0

                 N₇= -20-10 = -30 kN

L’asta 6 è tesa e l’asta 7 è compressa

 

Nodo E

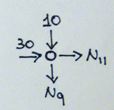
Facendo equilibrio alla traslazione verticale e orizzontale possiamo ricavare

N₉ = -10 kN

N₁₁ = -30 kN

Cambiando il verso presupposto, le aste 9 e 11 sono tutti e due compresse.

 

Nodo F

 

Possiamo anche qui scomporre i contributi dell’asta 10  e si ricava che l’asta 10 sia scarica.

N₁₀  √2/2 + 10 -10√2 ∙ √2/2 = 0

N₁₀ √2/2 = -10 +10 = 0

N₁₀ =0

Nodo G

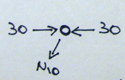
L’asta 10 essendo scarica l’ incognita risulta essere N₁₁

N₁₁ = 30

L’asta 11 è anch’essa compressa.

 

Dopo aver analizzato i nodi attraverso equazioni equilibrio verticale e orizzontali possimo rappresentare graficamente quali aste sono compresse, quali sono tese e quali scariche.

Quindi successivamente è stato utile verificare i risultati ottenuti utilizzando il programma SAP ottenendo questi risultati:

La deformata

Lo sforzo assiale

Quindi i risultati sono verificati.

 

 

Dimensionamento del Solaio

 

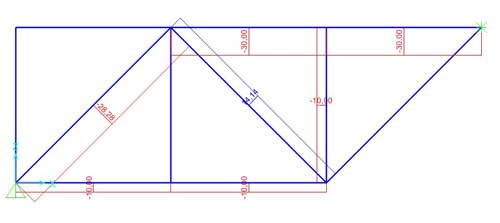
Il progetto preso in analisi è un semplice impalcato, realizzato durante il triennio.

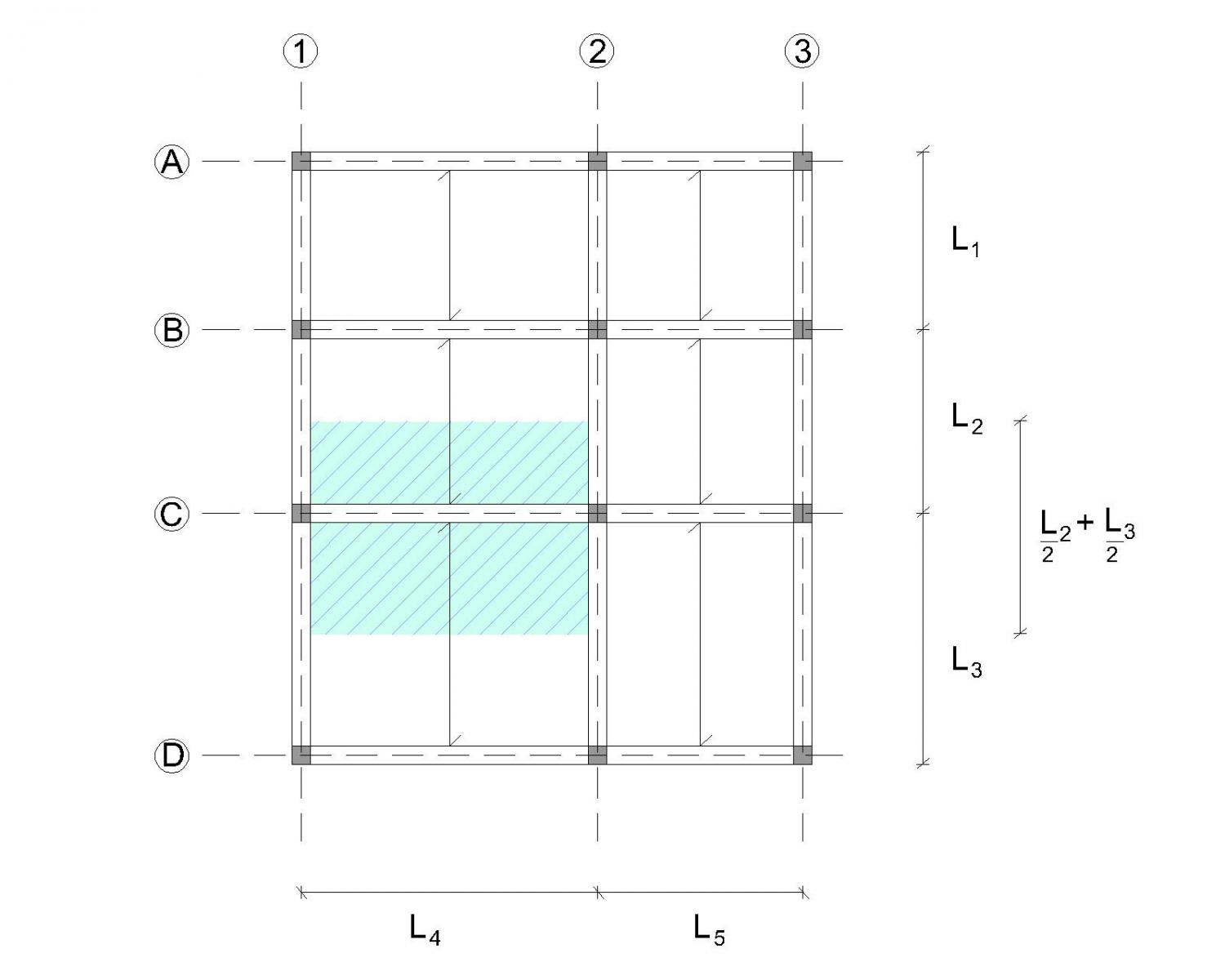
Dall’impalcato ho cercato di evidenziare la trave più sollecitata evidenziata nel disegno : trave  C1-C2.

 

Soggetta a un carico di cui l’ area di influeneza  è pari a: 

A= luce x interasse =  L₄  x (L₂/2 + L₃/2)  =    4.80 x (3.00/2 + 4.10/2) =   17.04  m

L₁ =  2.90 m

L₂ =  3.00 m

L₃ =  4.10 m

L₄ =  4.80 m

L₅ =  3.3 0 m

   Il primo passo importante è quello di calcolare il carico totale del Solaio per unità di lunghezza a cui è soggetto la trave più sollecitata. In particolare secondo le Norme Tecniche per le costruzioni 2008 la classificazione delle azioni avviene secondo la variazione delle loro intensità nel tempo

a)      Permanenti (Q) : azioni che agiscono durante tutta la durante tutta la vita nominale della costruzione, la cui variazione di intensità nel tempo è lenta da poterle considerare con sufficiente approssimazione nel tempo:

-          Peso proprio di tutti gli elementi strutturali (Qs)

-          Peso proprio di tutti gli elementi non strutturali (Qp)

 

b)   Variabili (q_k) comprendono i carichi legati alla destinazione d’uso dell’opera che nel caso del mio edificio di uso residenziale  prendiamo come valore q_k = 2.00  kN/m²

I carichi strutturali e non strutturali sono espressi in mq ,è dato dalla somma del carico di ogni elemento del nostro pachetto che hanno un loro peso specifico espresso in kN /m³ e moltiplicati per la loro altezza m, ottenendo così il carico Q in kN/m².

 

Progetto di un solaio in legno a doppia orditura

Il progetto del solaio in legno qui sotto rappresentato consiste nel  dimensionare prima  i travetti, che influenzano poi sul dimensionamento della sezione della trave principale (in questo caso la trave più caricata è la C1-C2 ) affinché sia in grado di resistere a tutti carichi agenti su di essa.

 

   Luce trave C1-C2 = 4.80 m

   Interasse trave = 3.55 m 

·   Luce travetto = 4.10 m

     Interasse travetto = 0.90 m

 

 

 

 

 

 

Scelgo di utilizzare  tra le travi  lamellare in commercio la classe GL24 (BS11)

 

·    Pesi permanenti strutturali

       Calcolo del carico totale al metro lineare ottenuto facendo:

1-      Area dell’elemento nelle sue dimensioni in un m²            A = (B X H)      [ m²]

2-      Calcolare il suo volume di 1m       V=  A x 1m      [m³]

3-      Ricavare il peso ( kN) moltiplicando il peso specifico per il volume      P = V x peso specifico ( kN/m³ )        [kN]

4-      Trovare il carico a metro lineare        Q_s = 1 (m²) / interasse (m) x  P (kN)    [ kN/m² ]

·         Carico variabile come dettato dalle norme tecniche del le costruzioni del 2008, precedentemente individuato è pari aq_k = 2.00  kN/m²    

 

Progetto travetti lamellari  classe GL24

Il progetto dei travetti vengono effettuati partendo da:

Analisi dei carichi

·         Carichi agenti totali per unità di superficie  pari alla somma tra i carichi strutturali e non          strutturale:

              Q_s + Q_{p +} q_{K =}    0.21 + 2.35 + 2.00 = 4.56 kN/m²

·         Carico sui travetti si ricava dividendo il carico espresso in densità lineare

 q = 4.80 kN/m² x 0.9 m ( interasse ) = 4.1 kN/m

Ricavare il momento massimo flettente

·  Il   momento massimo di una trave appoggiatasi si trova in mezzaria e ha un valore pari a   ql²/8, quindi ricavo il momento massimo:

M = ql²/8 =  4.1kN/m  x (4.1 m)² /8 m = 8.62 kN*m

Analisi delle tensioni di progetto

Per trovare il valore di progetto : fD = K_{mod x} f_k / ɣ_m

 dobbiamo tenere in considerazione sia i vari valori di resistenze f_k che variano a seconda della se si tratta di valore di resistenza a trazione, flessione o compressione. Divise a loro volta in direzione parallela o perpendicolare , in cui i valori possono cambiare anche di molto.

 

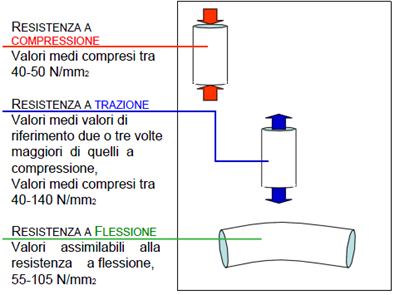
In questo caso scelgo la classe di legno GL24 (BS11) con resistenza a flessione  pari a :

fm,k = 24N/mm²

 

Inoltre si deve tener conto del Kmod un  coefficiente correttivo che tiene conto dell’effetto, sui parametri di resistenza, sia della durata del carico sia dell’umidità della struttura.

Prendo kmod pari a 0.6

Invece il ɣ_m  è un coefficiente parziale di sicurezza relativo al materiale, che nel caso del legno lamellare vale    ɣ_m =1.45

Quindi   fD = = K_{mod x} f_k / ɣ_m = 0,6 x 24 N/mm²/ 1.45 = 9.93 N/mm²

Cosi fissato la base dei travetti a 10 cm si ricava in questo modo l’altezza minima che possimo adottare pari a 22,83 cm, cosi controllando nelle schede dei produttori possono decidere di scegliere una sezione dei travetti lamellari  GL24  pari a 10 x 24.

A questo punto bisogna

·         Verificare il peso proprio del travetto in base alla sezione che abbiamo scelto:

Progetto della trave classe GL24

La trave maggiormente sollecitata è C1-C2

·         Luce trave C1-C2 = 4.80 m

          Interasse trave C1-C2  = 3.55 m 

Importante è ricordarsi che di aggiungere ai carichi strutturali anche quelli dei travetti appena calcolati:

·    Carico variabile come dettato dalle norme tecniche del le costruzioni del 2008, precedentemente individuato è pari aq_k = 2.00  kN/m²     

Inserendo i carichi nella tabella Exel usando lo stesso procedimento usato per i travetti ricavo consultando sempre i produttori una trave 20 x 40.

 

 

Solaio in acciaio

In questo caso si è scelto di adottare la tecnologia del  solaio in lamiera grecata e laterizi. In cui il progetto consiste nel dimensionare le dimensioni prima dei travetti e poi della trave ( come è stato fatto per il solaio in legno ) in base alla sommatoria dei carichi che gravano su di esse.

Progetto travetti

Luce: 4.01 m

In terasse: 0.90 m

·         Carico permanente strutturale

         della lamiera grecata e laterizi è pari a:  Qsdi 1.80 KN/mq

·         Carico variabile pari a  q_k = 2.00  kN/m²    

Inserendo cosi i dati ricavati nella tabella di calcolo exel posso trovare il carico a metro lineare gravante sui travetti facendo la somma tra:

 Q_s + Q_p + q_K = ( 1.8 kN/m² + 2.35  kN/m² + 2.00 kN/m²)  x 0.9m =      5.50 kN/m (carico a metro lineare)

Dopodiché  si può ricavare il momento massimo agente sul travetto di luce pari a 4.10 m in cui sappiamo che il valore del valore massimo del momento è a

M= ql² / 2  =   6.15 x (4.10)² / 2 = 11.,6 kN m

La tensione di snervamento è dato dalla classe dell’acciaio che si sceglie di adottare che nel mio caso scegliendo la classe Fe 360 s235

 fyk = 235 N/mmq

Da cui ricavo  il valore della tensione di progetto Fd pari al rapporto tra fyk e il coefficiente di sicurezza adimensionale utilizzato per l’acciaio da carpenteria pari a 1.05  (dato dalla normativa ) che tiene conto di tutte le incertezza del materiale.

Fd= fyk / 1.05 = 235 N/mmq / 1.05 =  223.81  N/mmq

Ottenendo cosi in fine valore del modulo di resistenza a flessione W_X pari a

W_x  = M/Fd = 12.9 kNm / 223.81  N/mmq = 56.91 cm³

Quindi posso prendere dal sagomario un profilo che ha un modulo di resistenza superiore, quindi scelgo  un IPE 140 con valore W_x pari a 77,3 cm³

In fine ottengo il carico dei travetti  = 12.9 kg/m =0.129 kN/m

 

Progetto trave  C1-C2

Luce: 4.80 m

Interasse: 3.55 m

·  Carico permanente strutturale

         della lamiera grecata e laterizi più il peso dei travetti è pari a: 

       Qs = 1.80 KN/mq + 0.129 kN/m = 1.93 kN/m

·         Carico variabilepari a  q_k = 2.00  kN/m²     

 

·    Carico permanenti non strutturali  pari a

     Q_P  = 2.35kN/m²                                                                     

Inserendo cosi i dati ricavati nella tabella di calcolo exel posso trovare il carico a metro lineare gravante sui trave facendo la somma tra:

 Q_s + Q_p + q_K = ( 1.938 kN/m² + 2.35  kN/m² + 2.00 kN/m²)  x 3.55m =    22.3kN/m (carico a metro lineare)

Dopodiché  si può ricavare il momento massimo agente sul travetto di luce pari a 4.80 m in cui sappiamo che il valore del valore massimo del momento è a

M= ql² / 2  =   22.3 x (4.80)² / 2 = 64.2 kN m

La tensione di snervamento è dato dalla classe dell’acciaio che si sceglie di adottare che nel mio caso scegliendo la classe Fe 360 s235

 fyk = 235 N/mmq

Da cui ricavo  il valore della tensione di progetto pari al rapporto tra fyk e il coefficiente di sicurezza adimensionale utilizzato per l’acciaio da carpenteria pari a 1.05  (dato dalla normativa ) che tiene conto dell’ incertezza del materiale.

Fd= fyk / 1.05 = 235 N/mmq / 1.05 =  223.81  N/mmq

Ottenebdo cosi in fine valore del modulo di resistenza a flessione pari a

W_x  = M/Fd = 64.2 kNm / 223.81  N/mmq = 314.15 cm³

Quindi posso prendere dal sagomario un profilo che ha un modulo di resistenza superiore, quindi scelgo  un IPE 240 con valore W_x pari a 324 cm³

 

 

 

Solaio in Cls

In questo caso ho pensato di verificare il mio pacchetto di solaio in cls  precedentemente progettato durante il laboratorio di costruzioni.

Progetto  della travi C1-C2

Luce: 4.80 m

Interasse: 3.55 m

·    Carico variabilepari a  q_k = 2.00  kN/m²     

Inserendo cosi i dati ricavati nella tabella di calcolo exel posso trovare il carico a metro lineare gravante sui trave facendo la somma tra:

 q = (Q_s + Q_p + q_K ) x interasse = ( 0.88 kN/m² + 2.35  kN/m² + 2.00 kN/m²)  x 0.5m =     

       2.6 kN/m (carico a metro lineare)

Dopodiché  si può ricavare il momento massimo agente sul travetto di luce pari a 4.10 m in cui sappiamo che il valore del valore massimo del momento è a

M= ql² / 2  =   2.6 x (4.80)² / 2 = 7.5 kN m

 

Il calcestruzzo  è contraddistinto dal valore  caratteristico della sua resistenza a compressione, misurata su provini cilindrici e indicata cin il simbolo fck il quale rappresenta la resistenza cilindrica o  secondo Rck è la resistenza cubica . Il valore caratteristico ha una probabilità del 5 % che la resistenza effettiva sia minore di esso. Le classi di resistenza del Cls piu usati vanno dal C20/25 fino  C50/60, nel mio caso ho scelto si usare il    C25/30 .

Si può ricavare la resistenza dell’acciaio delle armature con il valore della tensione di snervamento che è dato dalla classe dell’acciaio che si sceglie di adottare , nel mio caso scegliendo un acciaio B450C ( unico ammesso in zona sismica ) con fyk = 450 Mpa

Da cui ricavo  il valore della tensione di snervamento Fd  pari al rapporto tra fyk e il coefficiente di sicurezza adimensionale utilizzato per l’acciaio da barre pari a 1.15  (dato dalla normativa ) che tiene conto dell’ incertezza del materiale.

Fd= fyk / 1.15 = 450 N/mmq / 1.15 =  391,3  N/mmq

Per trovare l’altezza utile pari al prodotto del fattore r per la radice del momento fratto la base,  d =r √ M/b in cui se la base e il momento sono noti l’incognita da trovare è r.

r  dipende dalla resistenza del calcestruzzo e dal dal fattore α che a sua volta dipende da n che è il coefficiente di normalizzazione per ricavare che la tensione dell’acciaio è n volte quella del calcestruzzo

σ_s= nσ_c

Infatti possiamo ricavare il valore normalizzato n pari a :

n= Ef/Ec = 210000 Mpa /30000Mpa = 7  ,  in cui si evidenzia  che la tenzione σ_s =  7 volte di σ_c,  ma se si tiene conto della viscosità si prende un valore doppio che le norme per attenersi a una regola consolidata la considera pari a : n = 15.  Quindi l’area dell’acciaio darà considerata n volte quella del cls ( Area omogeneizzata)

Possiamo ricavare

α =fc /(fc + fdf /n) = 20Mpa/(20 Mpa + 450Mpa /15) = 0.34

r= 2/ (α x (1- α/3 ) ^0.5 = 2.58

Cosi la mia altezza utile sarà 15 cm ed con base 15 cm l’altezza totale sarà  20 cm.

 

 

 

 

Struttura reticolare spaziale

Le strutture reticolari vengono utilizzate per realizzare grandi coperture per stadi, ospedali in quanto consentono di coprire grandi luci con altezze e pesi contenuti che altre strutture non potrebbero essere realizzate. Ci sono vari tipi e quello che cercheremo di realizzare è chiamato schema cubico, realizzata su una base quadrata, formata da tiranti puntoni e diagonali, formando cosi tante maglie reticolari e costituiti da moduli di reticolari che si ripetono nelle tre dimensioni.

• Disegno della struttura reticolare su autocad

Si parte con un nuovo file di autocad , e con la creazione di un nuovo layer chiamandolo aste.

 

Si disegna una polilinea, in zero assoluto per facilitare quando  esportazione in sap, immaginiamo di disegnare la faccia principale del nostro cubo semplificato di dimensione 2m x 2m x 2m,  lasciandolo aperto, in modo tale che poi usando il comando di autocad di “ copia in serie” non ci siano aste doppie sovrapposte, in quanto poi non sarà possibile fare analisi della struttura con SAP.

Poi disegniamo la diagonale, andando poi nella vista 3D di autocad lo ruotiamo di 90 gradi.

   

a questo punto possiamo fare il comando “ARRAY”, immaginando che dovremmo realizzare una piccola pensilina 4 x 6.
Quindi imposteremo come valori di questa copia serie  inserendo 1 riga 4 colonne perché voglio 4 elementi in direzione X  poste a direzione 2 m .

Si ottiene cosi la prime riga di trave reticolare .

Per disegnare le altre maglie della faccia laterale  bisogna cambiare il sistema di riferimento UCS, in quanto su autocad 3d siamo sempre vincolati a disegnare nel piano X  e Y   .
Utilizzando nuovamente il comando polilinea si  disegna una maglia sempre 2m x 2m x 2m e la sua diagonale.

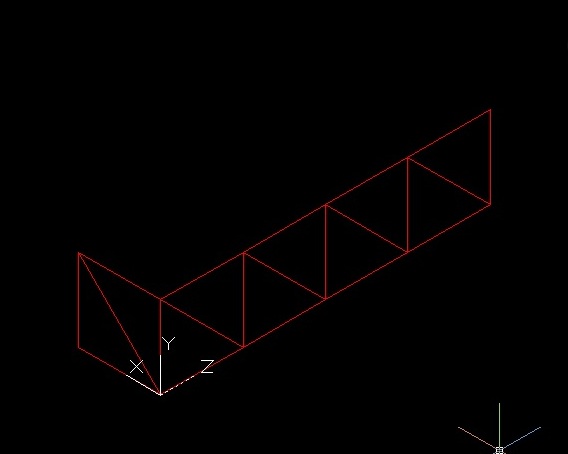
Applico nuovamente il comando Array per il modulo trasversale in modo tale che si ripete per tutti gli spigoli  impostando questa volta 1righe e 5 colonne a distanza di 2 m.

Dobbiamo disegnare le diagonali sopra e sotto e copiarlo lungo tutte le altre meglie.

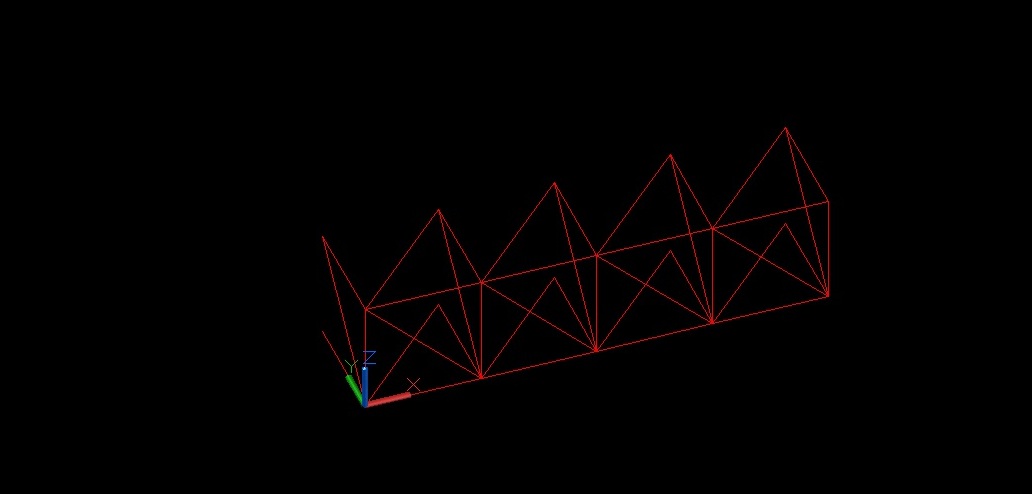
Cambiando di nuovo UCS applichiamo un latra volta il comando “array”  inserendo 7 colonne a distanza 2 metri , anche se abbiamo bisogno di 6 elementi  per evitare di chidere poi difficilmente il modello , sarà più facile cancellare.

Prima di passare su SAP bisogna esplodere tutto in modo che siamo tutti elementi separati, e affinche si possa poi fare analisi si SAP.
Quindi questo è la nostra reticolare spaziale

 

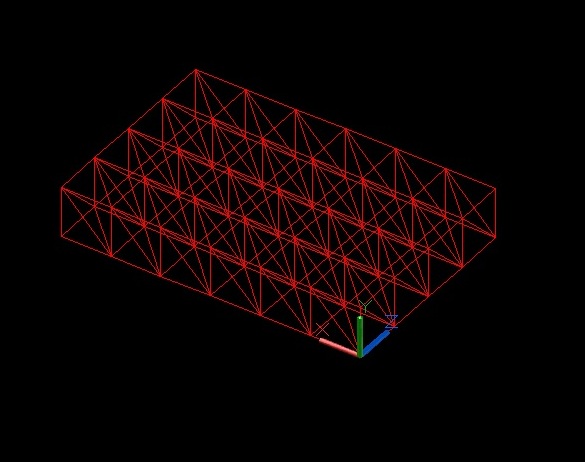
Salviamo il disegno in dxf2000, evitando cosi problemi di compattibilità con SAP.

 

 

• Analisi della struttura reticolare su SAP
   

Importiamo la struttura reticolare su SAP 2000. Impostiamo l’unità di misura IN KN mC, andare si import - autocad dxg file, apparirà una finestra di traduzione di elementi di autocad su sap, e quindi tutti gli elementi che sono sul layer aste diventerà frame.

Sul piano XY lo potremmo vedere in 3D, impostiamo il modello cominciando mettere dei vincoli di base, quindi immaginiamo questa struttura reticolare non abbia bisogno di pilastri intermedi ma che abbia solo alcuni pilastri, quindi mettiamo i nostri vincoli esterni , in tutte le  4 cerniere esterne.

Poi indiamo a mettere i vincoli interni andando a disegnare i nodi non disegnati su autocad, selezionando tutto, e assegnare il rilascio dei momenti interni 2.2 e 3.3, come se imponiamo alle aste a lavorare solo allo sforzo normale.

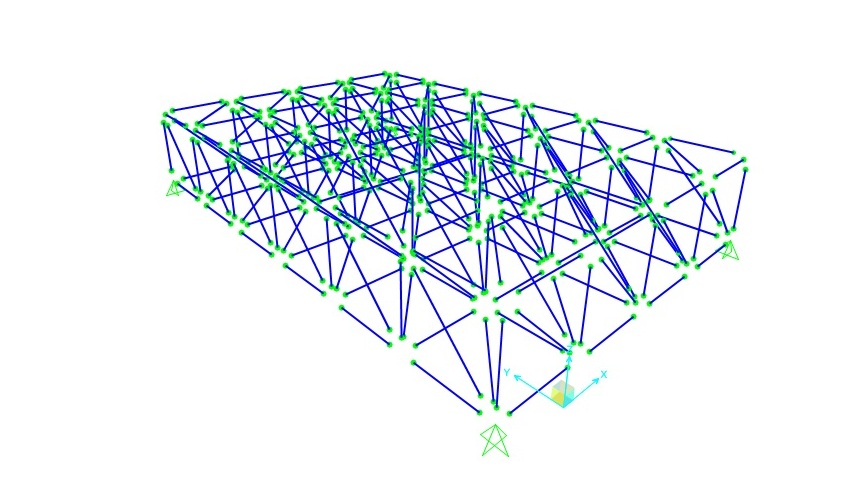
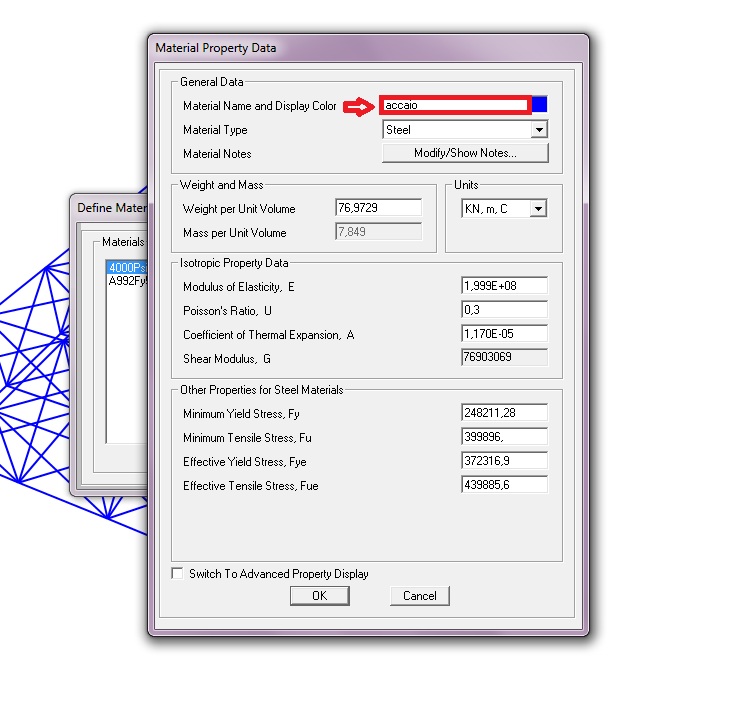
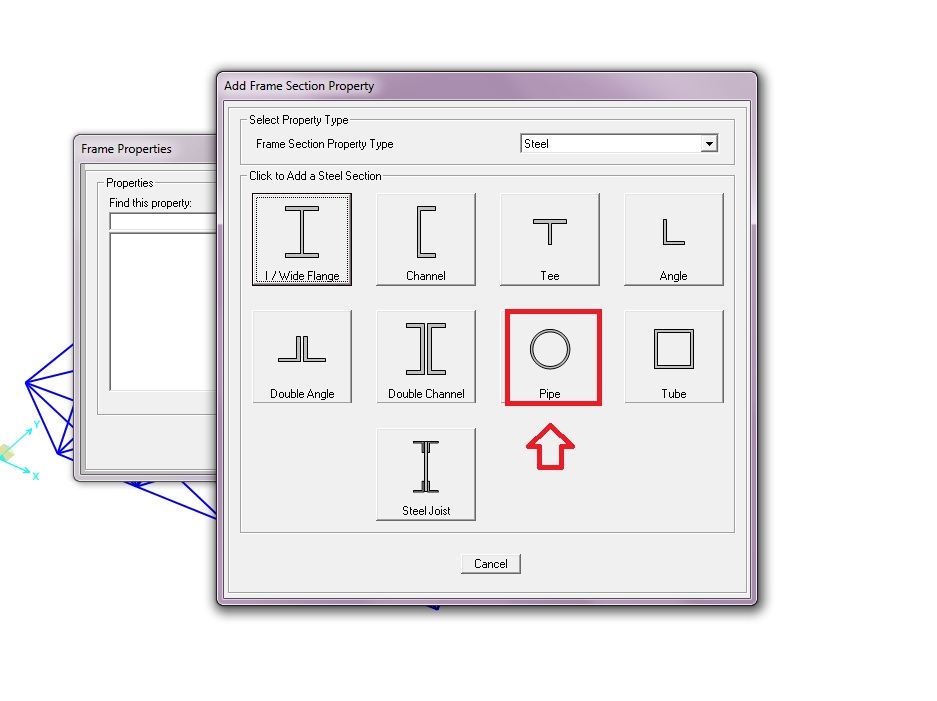
Fondamentale differenza con le 2 dimensioni è fondamentale assegnare materiale e assegnare le sezioni. E asegnarlo a tutti gli elementi realizzati ipotizzando in acciaio a sezione tubolare .

Andando poi a creare un carico concentrato che andrà  segnato solo ai nodi superiori.

A questo punto si può salvare e passare all'analisi della struttura.
Rcaviamo la deformata

La struttura risulta essere asimmetrica, infatti i diagrammi non sono simmetrici perché la geometria della nostra struttura non è simmetrica.

Possiamo andare a controllare i diagrammi dei momenti e taglio che devono essere zero in quanto le nostre aste lavorano solo a sforzo normale.

 

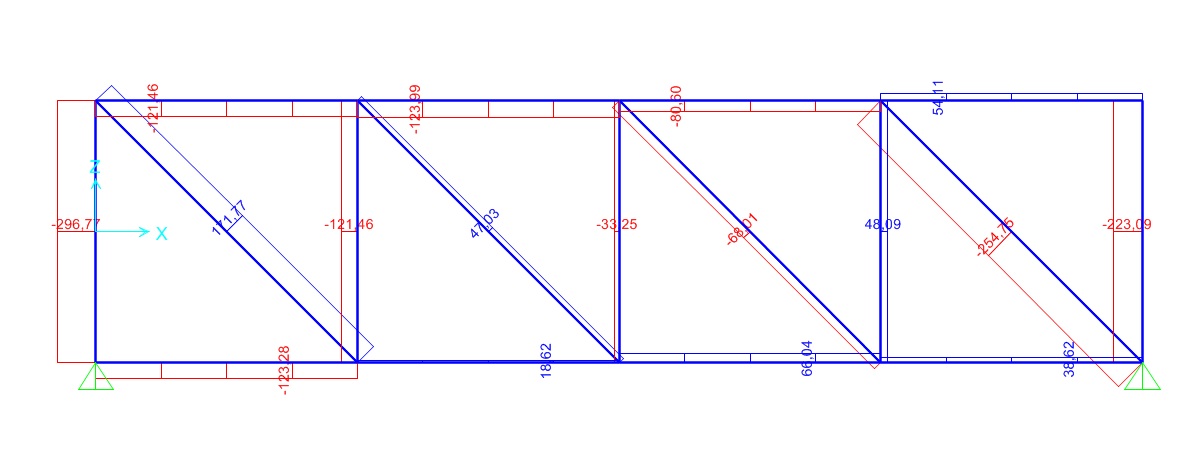
Per visualizzare i risultati delle aste intemedie si può fare un click direttamente sull’asta, o altrimenti andando su display- show tables -  analysis results -> element output -> file -> export current table -> to excel). Da questa tabella esportata su exel possiamo conoscere il valore di ogni asta della struttura attraverso la tabelle è inoltre possibile individuare l’asta maggiormente sollecitata a trazione e a compressione .

• Progetto dell’asta a trazione massima

Dopo aver individuato lasta a trazione massimo è possibile progettare l’asta trovando l’area minima necessaria utilizzando la formula di Navier

A = N/ Fd

A= area minima necessaria

N= sforzo assiale

Fd= è la resistenza di progetto pari al rapporto tra Fy/ γm

γm= è  il coefficiente di sicurezza pari a 1,05

L’area minima necessaria  per un il tipo di acciaio scelto Fe360S235 è pari a 11,57 cm²

  Allora scelgo il profilato più adatto con area sezione pari 12,50 cm²

 

• Progetto asta a compressione

Nelle aste compresse a differenza del'asta a trazione importante è verificare la lunghezza dell'asta causa di instabilità eureliano dovuto all'eccesso di snellezza. Il carico critico eureliano assiale non sia superiore del carico agente

Se l’asta maggiormente compressa ha uno sforzo assiale pari a : N = 307 kN

L’area minima necessaria  per un il tipo di acciaio scelto Fe360S235 è pari a 13,26 cm²

  Allora scelgo il profilato più adatto con area sezione pari a 13,90 cm²

Allora scelgo il profilato più adatto con area sezione pari a 13,90 cm²

Per l’asta compressa è soggetta un carico di punta carico critico eureliano che diventa molto rischioso per profili troppo snelli che tendono a incurvarsi fino a rottura.
 Si possono quindi effettuare tre tipi di verifica del profilo scelto:

·         Verifica a resistenza

·         Verifica a stabilità

·         Verifica a snellezza

Verifica a resistenza
La sezione scelta sarà verificata se rapporto tra lo sforzo normale 307 kN e l’area del nuovo profilo sarà minore della resistenza di progetto fD

307000 N / 1390 mm² = 220,8 N / mm²  < 223.81 N / mm²  (Verificato)

Verifica a snellezza
La snellezza dell’asta è data dal rapporto tra la luce libera di inflessione  l₀ (distanza tra due punti di flesso successivi della deformata flessionale ₎ e il raggio d’inerzia ρ .

λ = l₀ /ρ 

La normativa impone limiti alla snellezza massima negli elementi in cui possa essere presente uno sforzo normale di compressione:

λ_max ≤ 200 per le membrature principali

λ_max ≤ 250 per le membrature secondarie

Lo schema dell'asta incernierata porta ad avere un valore di lo= l, mentre il raggio d'inerzia ρ è pari a 3,9 cm.

λ = l₀ /ρ = 1x282 /3,9 = 72,3 < 200 (verificato)

 

Verifica a stabilità
Il problema di stabilità è molto rilevante nella progettazione di strutture in acciaio. Importante è ricordare il carico critico eureliano ovvero il valore della forza normale il cui superamento comporta perdita di stabilità dell’equilibrio dell’asta.

E = 210000 N/mm²

A = 13.9 cm² = 1390 mm²

     Λ= 72,3 ² =

N_{cr =} (3.14)² x 210000 N/mm² x 1390mm ² / 72,3 ²  = 550 kN

Ai fini della verifica, abbiamo bisogno di valori uniformi e quindi λ diventa un parametro adimensionale

A = 13.9 cm² = 1390 mm²

fyk = 235 N/mmq

Ncr = 550000 N

Il lambda adimensionale = √1390 mm₂ x 235 N/mm² / 550000 N = 0.77

Trovato il lambda adimensionale possiamo trovare il coefficiente X

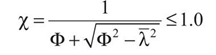
Dove Φ = 0.5 [1 + α (λ - 0.2) + λ² 
in cui α è il fattore di imperfezione diverso per le diverse curve di instabilitàe vale 0.21.

 

Φ = 0.5[1 + 0.21 ( 0.77 - 0.2) + (0.77)²] =0.86 

X = 1 / 0.8563 + √(0.86)² - (0.77)² = 0.815 <1

Per la normativa italiana e eurocodice 3

Nd ≤N_brd

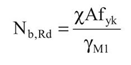
N_{brd =}  0,815 x 1390 mm ² x 235 N/mm ²  /1,05 = 253542 N = 253 KN < 550 KN

Il profilo scelto è verificato.

 

 

Ripartizione delle forze sismiche
Svolto con: Nanni Beatrice,Muglia Andrea e Valdarnini Flavia.

Per tutte gli edifici realizzati in zona sismica (Italia è quasi del tutto sismica), importante è valutare come avviene la ripartizione delle forze orizzontali in caso di sisma e come ogni singola struttura reagisce.
Le forze orizzontali vengono sopportate dai vincoli orizzontali e resistono perché sono rigidi ed  grazie all’ elasticità dei materiali, fa sì che l’edificio resista.
Sarà opportuno tenere nelle fasi progettuali disporre all’interno della struttura i cosiddetti controventi.

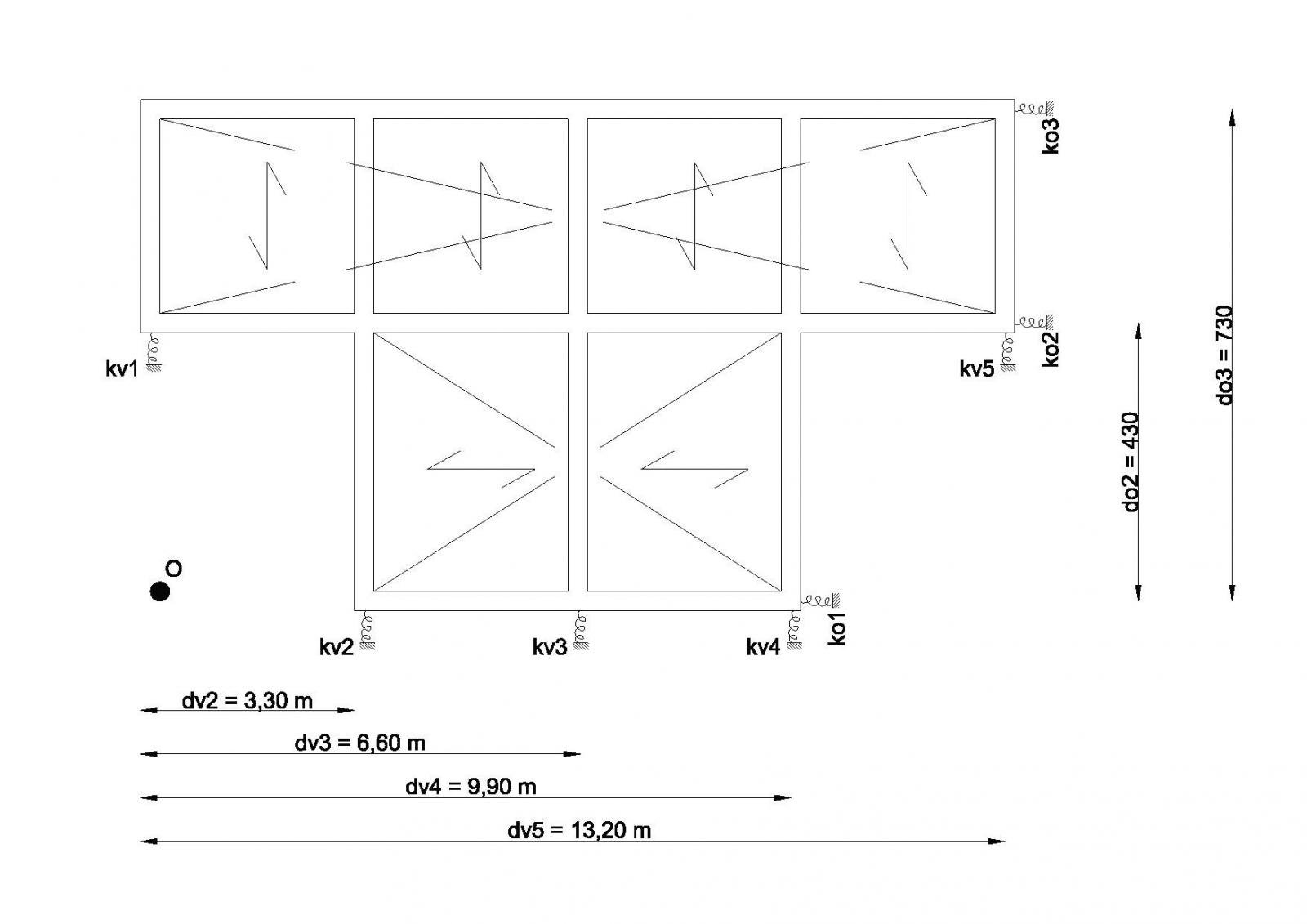
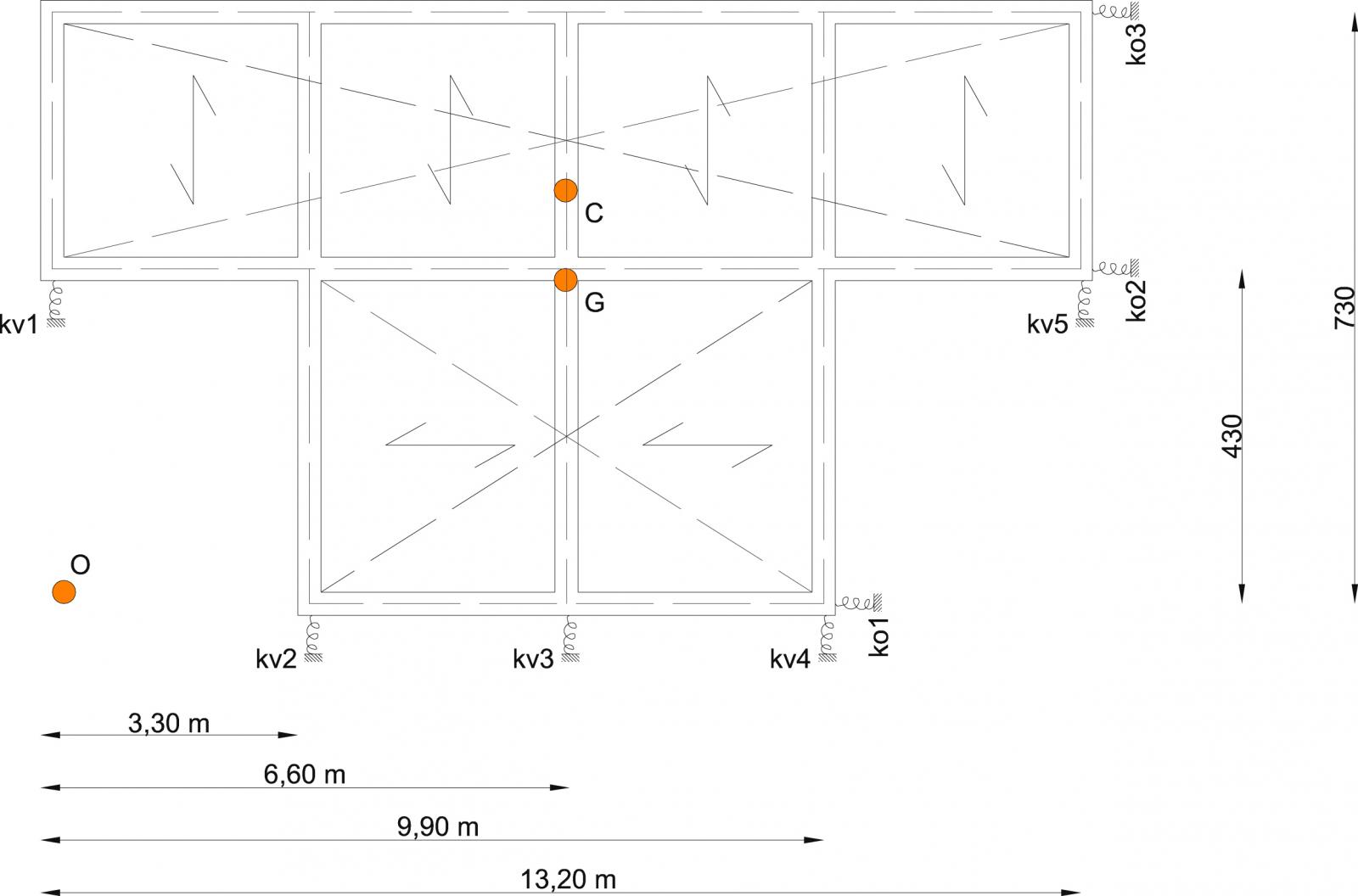
L’impalcato preso in considerazione è una struttura simmetrica composta da 5 controventi verticale e 3 controventi orizzontali.

 

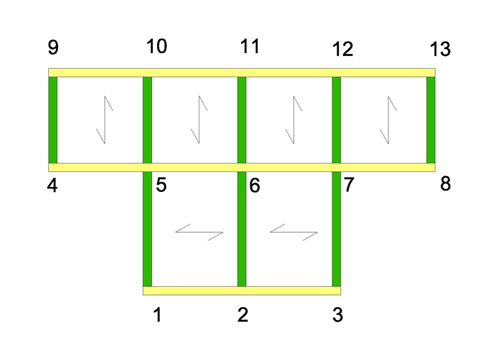
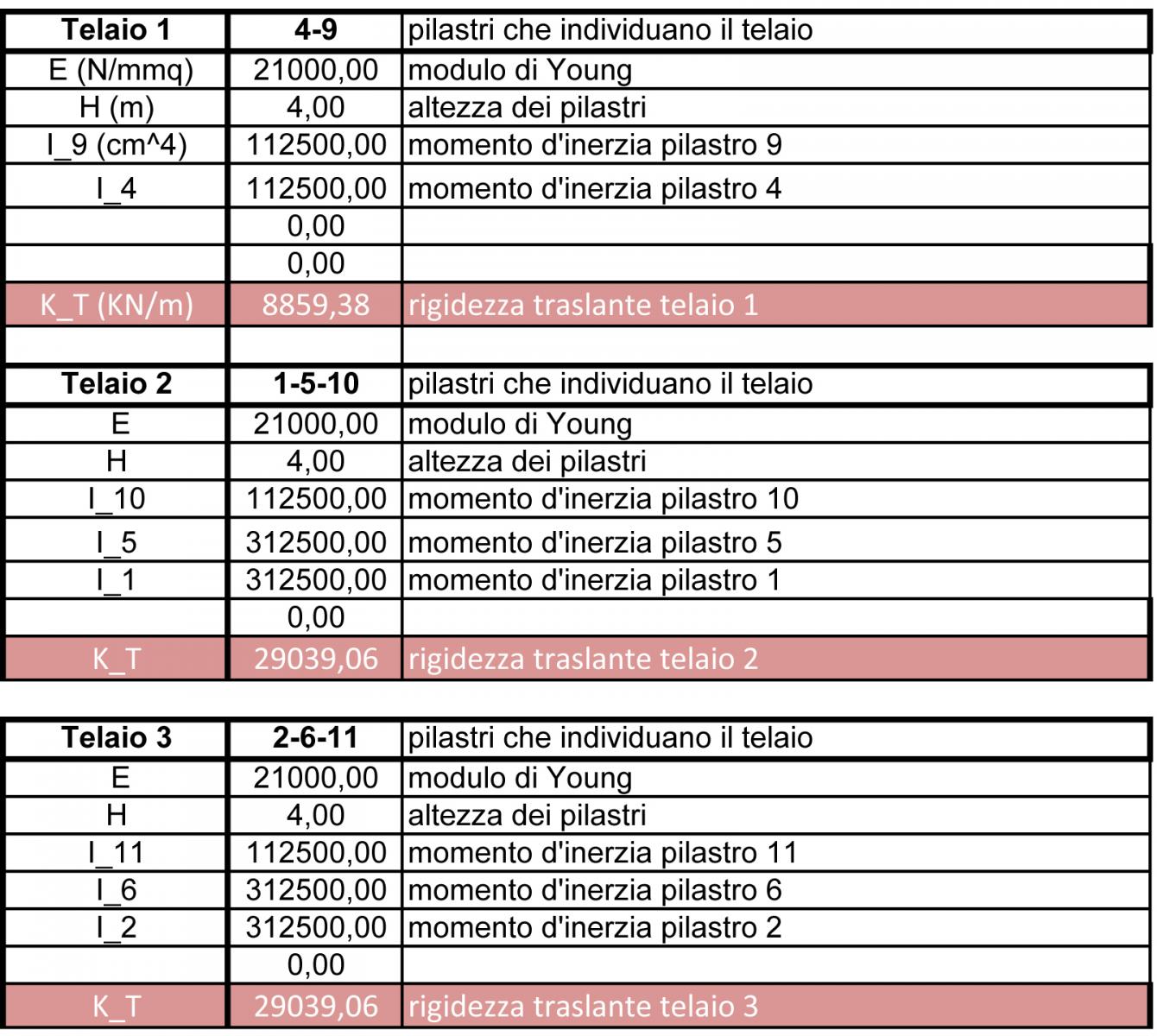
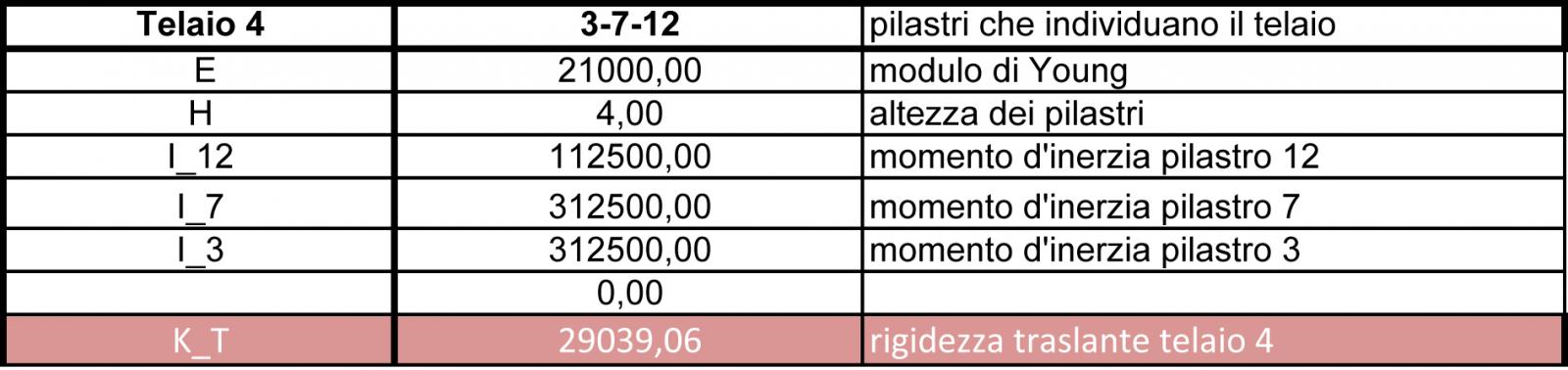
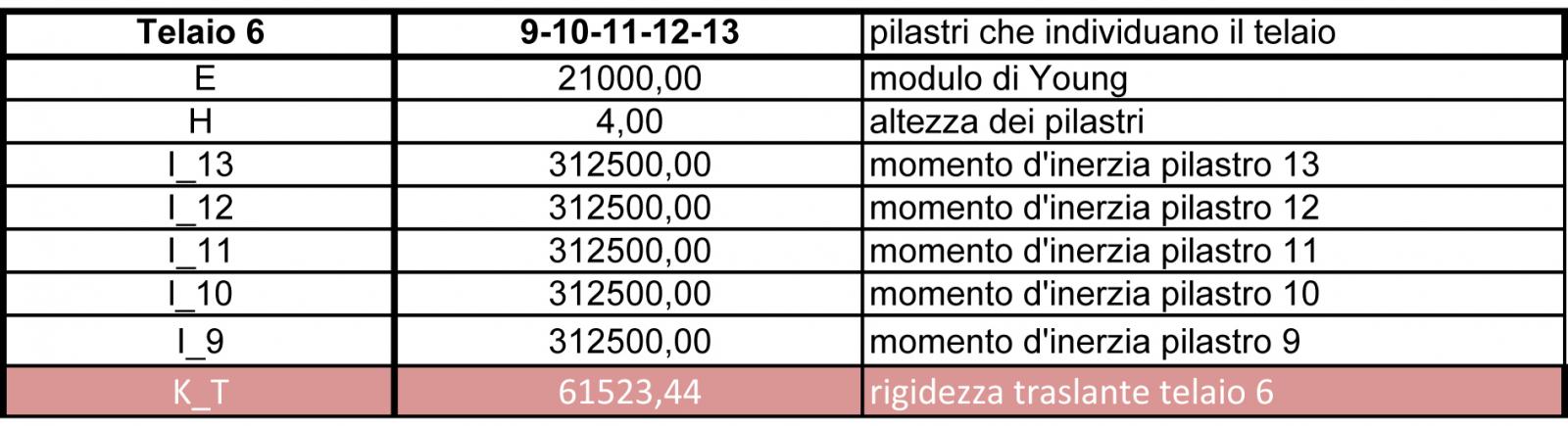
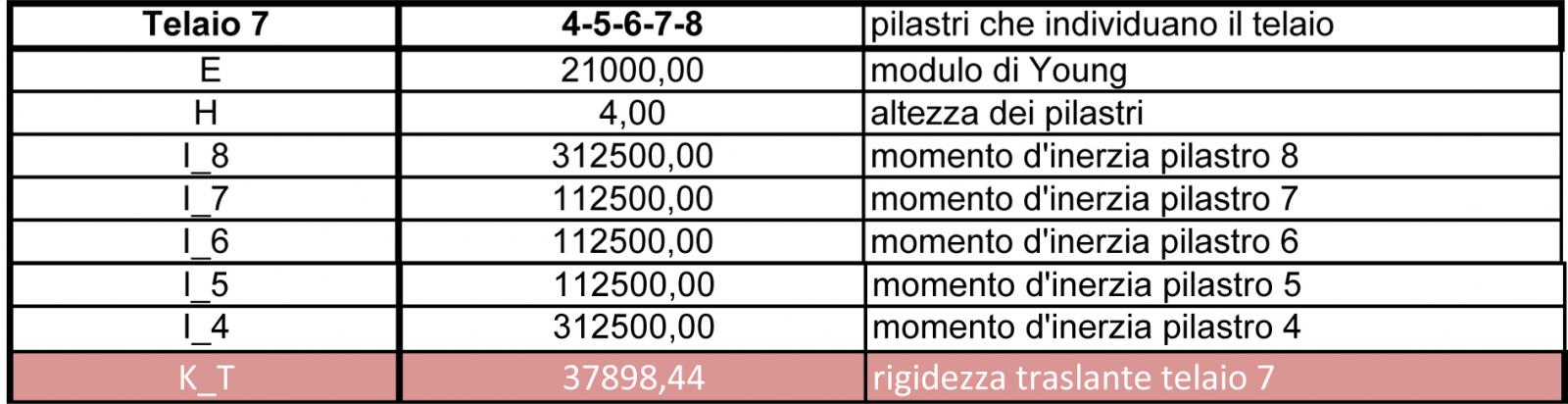
Considerando che la tecnologia dell’impalcato sia la stessa, quello che conta sono le rigidezze relative, quanto cioè quanto è rigido il controvento rispetto a un altro e cosi nelle otto tabelle dello step 1 ci saranno le rigidezze dei otto controventi dell’impalcato.
Ogni controvento è individuato dai suoi pilastri di cui è composto , ed il modello che c ‘è dentro è un modello shear type, ovvero una tipologia di telaio infinitamente rigida.
 

In questa ipotesi di orditura scelta ci saranno alcuni pilastri che saranno quelli principali che portano il solaio e cosi travi che portano il solaio e travi secondarie.
In particolare  le travi che portano il solaio saranno queste evidenziate in arancione:

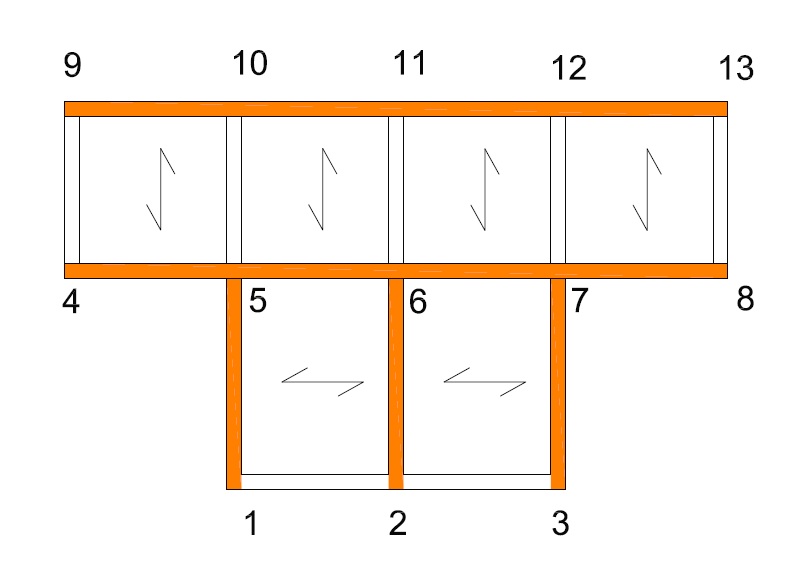
 Cosi questi controventi oltre essere un controvento porta anche  il solaio e poi ci sono quelli che mezzi portano il solaio e mezzi non, allora in questo caso, ma sicuramente quelli che portano il solaio hanno bisogno di una maggiore inerzia termica, quindi a seconda vengono orientati in un certo modo il pilastro in modo da sfruttare una maggiore inerzia flettente.

Quando arriva una forza orizzontale tutti i pilasti si inflettono e la forza verticale dipende da come i pilastri sono stati orientati. Infatti i pilastri che portano il solaio ricevono un grande carico verticale che oltre a inflettere le travi inflette i pilastri e ho bisogno di disporre il lato lungo per sfruttare il momento d’ inerzia maggiore.

I pilastri non sono sempre compressi, la compressione è  dominante , ma quando essa è collegato a delle travi e se esse si inflettono per la continuità del nodo anche i pilastri si inflettono abbastanza. Quindi le travi che si infletteranno di più sono quelle che portano il solaio e l’inerzia maggiore servirà nella direzione in cui questi pilastri collegano le travi che portano i solai .

In particolare i pilastri in cui ho più incertezza sono il pilastro 5 , 6 e 7 che sono collegati a travi che portano il solaio e quelli che non portano il solaio quindi si deciderà di orientarli nella direzione della trave che porta il solaio più lunga che sviluppa maggiore momento flettente.
 
I  pilatri 5-6-7 saranno stati orientati in base alla lunghezza della trave con luce maggiore che porta il solaio che si inflette di più rispetto alla trave di luce minore.  Allora secondo la direzione della flessione dominante si decide di disporre tali pilastri con questo orientamento.
Acciaio        pilastri HE  200A                                                                      

 

Calcetruzzo pilasri 30x50

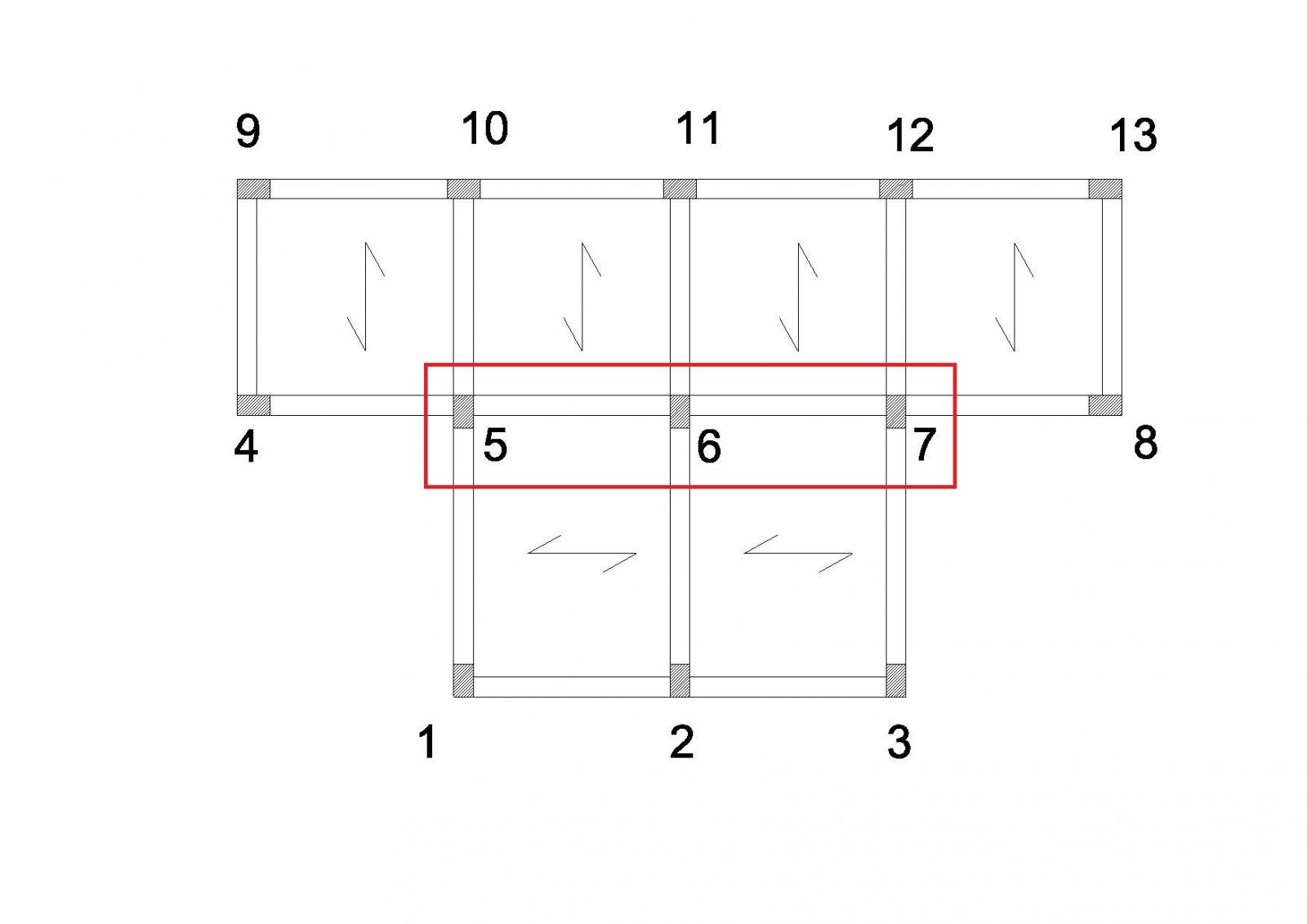
I pilatri del controvento 1-5-10, 2-6-11, 3-7-12, a parità di area hanno un’inerzia diverso se si considera in direzione X o Y.
ES. pilastro cls

Inerzia I_x  = 1/12 x b x h³ = 1/12 x 50 X 30³= 112500 cm⁴

Inerzia I_y  = 1/12 x h x b³ = 1/12 x  30 X 50³= 312500 cm⁴

Tecnologia in Acciaio

Step 1
La scelta dei pilastri in accaio comporta di usare nella prima parte delle otto tabelle:

^-                      modulo di young dell’acciaio pari a E= 210.000 N/mm²

^-                     H è l’altezza dei pilastri 4 m

^-                     I_n  pari ai valori del momento d’inerzia dei pilastri ( in un profilo in acciaio ad esempio HE il momento d’inerzia più grande è quello che distanzia il più possibile dalle ali , quelle in cui le ali hanno la massima distanza dall’asse)

Per il pilastri HE 200A abbiamo un I_{X =} 1336 cm⁴ e un Iy = 3692 cm⁴

 

In particolare  la riga  in arancione delle tabelle sono la somma delle rigidezze traslanti data dalla formula

K_T= 12 EI /h³

Step 2
La tabella sinottica dei controventi e distanze, sono una serie di dati, i valori delle rigidezze traslanti dei controventi sono stati ricavati dalle tabelle dello step 1, in più sono segnati le distanze divise in verticale ed orizzontale  partendo  da punto O, in questo caso d_v1 non è presente perché coincidono , cosi come non esiste d_o1.
Mi disegno la struttura mettendo in evidenzia non la tecnologia ma disegnando le molle chiamate le rigidezze rispettivamente K_o e K_{v .}

Step 3
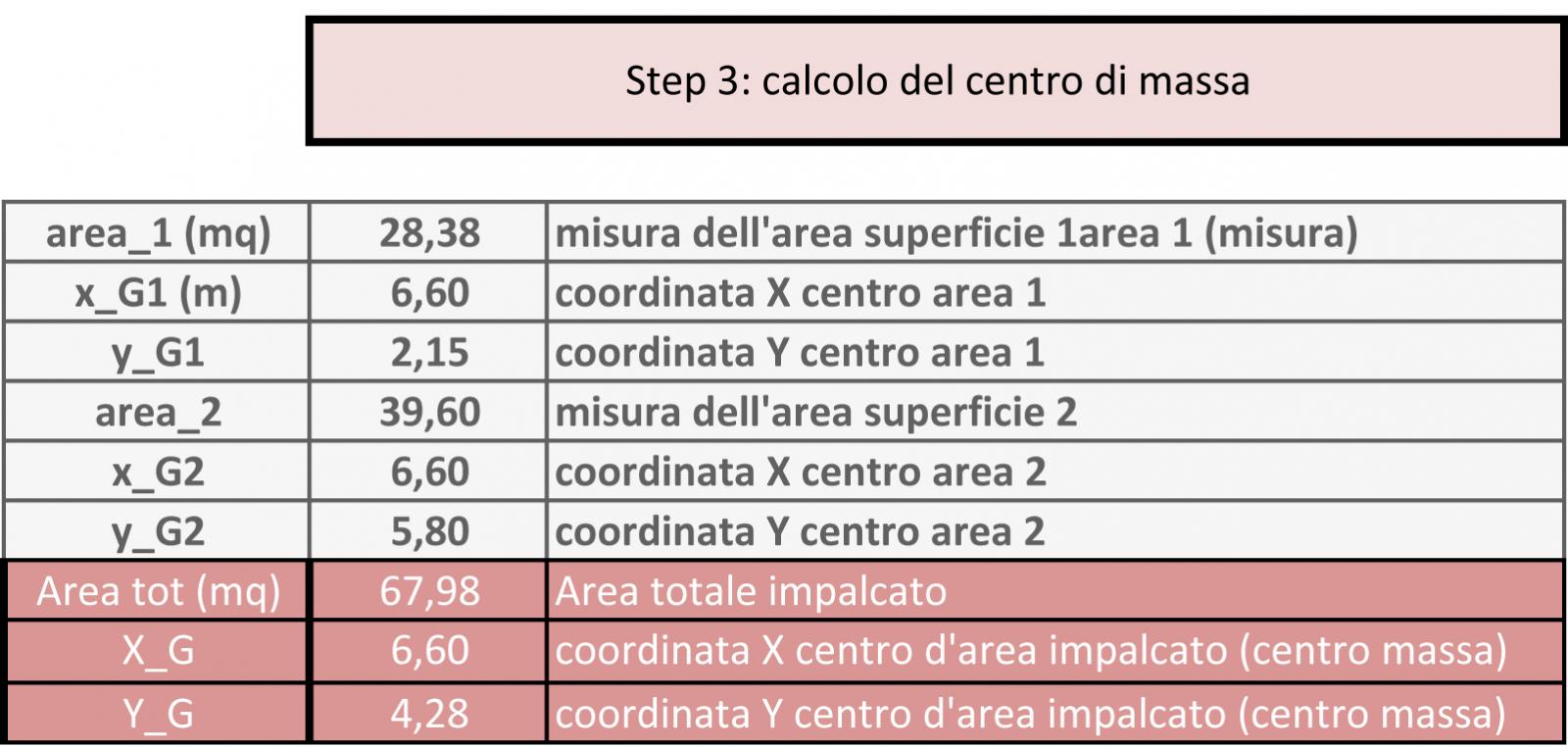
Calcolo del centro della masse.

La forza sismica è una forza d’inerzia effetto della massa per accelerazione,  dovuta a un accelerazione di trascinamento in cui il suolo comincia a ballare e tutto quello che c’è sopra balla a sua volta, quindi è proporzionale alla massa della  struttura.

La forza sismica è il prodotto di una massa  per un accelerazione   F = m a , è una forza.  Le strutture divese in molto rigide e flessibili si comportano in modo diverso.
Quelle molto rigide prendono tutto il moto di trascinamento invece la strutture flessibili  quando il terreno si muove ed assume un moto suo ,  si prende solo una frazione dell’accelerazione di gravità.

La forza sismica è applicata nel centro di massa

Il modo più semplice anche quando l’impalcato è più complicato conviene sempre generalizzare dividendo in più aree ad esempio in questo caso in A1 e A2, in cui sicuramente il centro di massa sarà al centro delle aree, di ogni rettangolo poi indicare le coordinate  del centro rispetto a un sistema di riferimento.

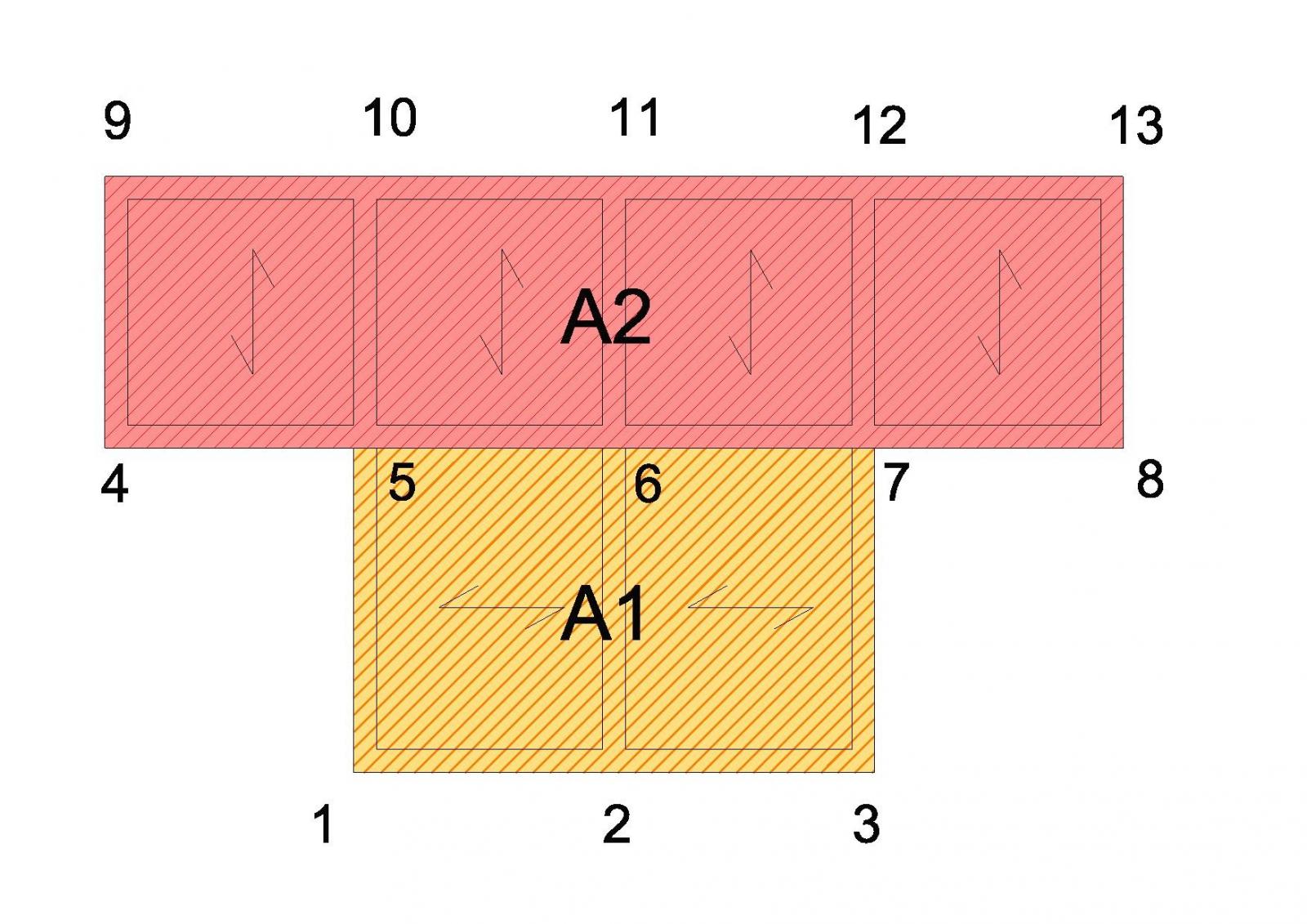
Automaticamente ottengo l’area totale dell’ impalcato e trovare poi X_G e  Y_G:

X_{G =}  A1 ∙X_G1 + A2 ∙X_G2 / A1 + A2

Y_G = A1 ∙ Y_G1 + A2 ∙ Y_G2 / A1 + A2

 

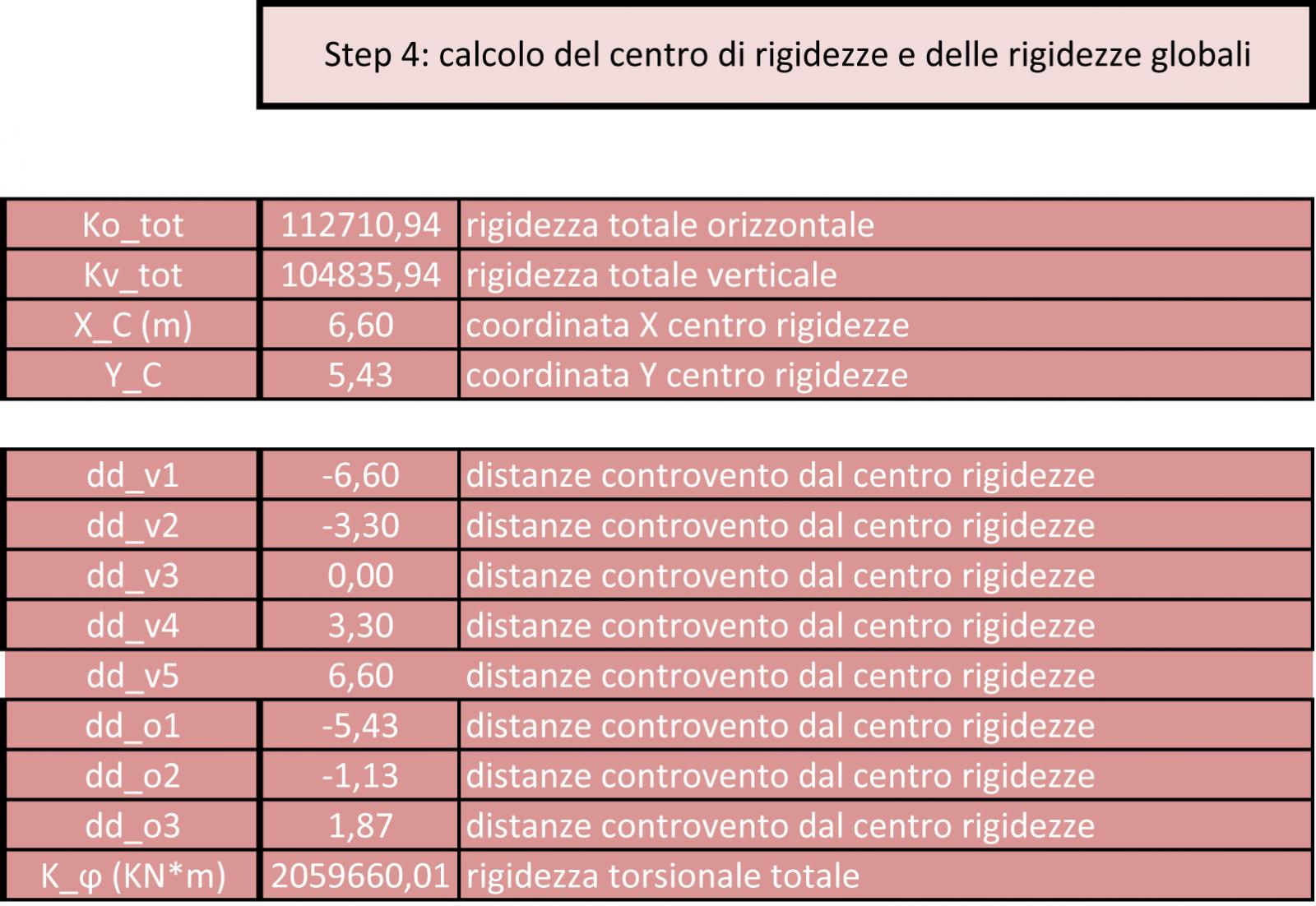
Step 4
Calcolo del centro di rigidezze e delle rigidezze globali

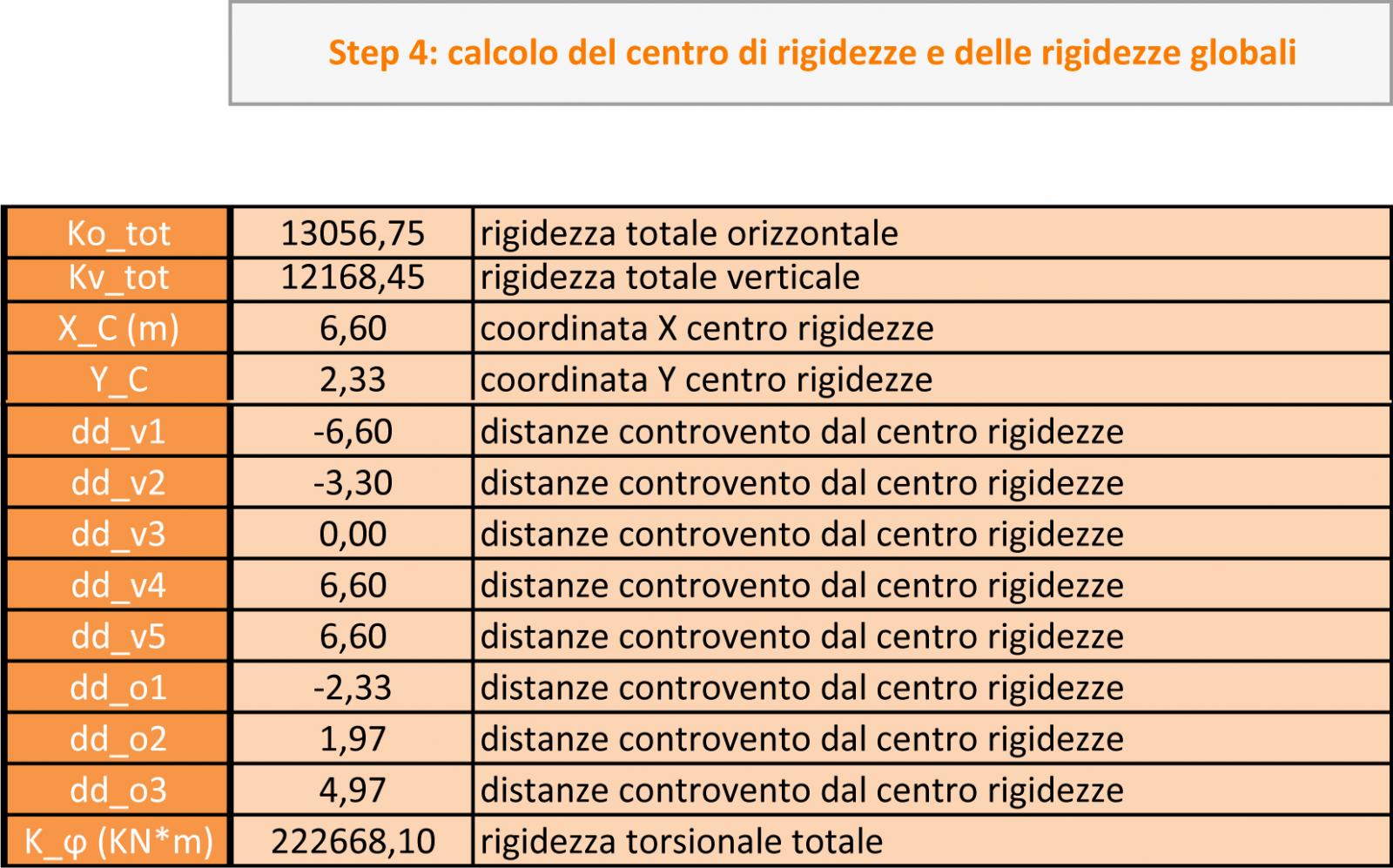
In questo caso i risultati sono tutti automatici e dipendono dai dati precedentemente ottenuti.
K_o tot è la somma delle rigidezze orizzontali = k₀1 + K ₀2 + K_O3 

K_v tot è la somma delle rigidezze verticali = k_V1 + K _V2 + K_V3+  k_V4 + K_V5

La coordinata X_C del centro delle rigidezze è stata ricavata:
X_c = K _v2 ∙ d₂ + K _v3 ∙ d₃ + K _v4 ∙ d₄ / Kv tot
(in cui k _v1 ∙ d ₁ = 1)

Y_c = K o2 ∙ d₂ +  k o3 ∙ d₃ + K o4 ∙ d₄ / Ko tot
(in cui k o1 ∙ d 1 = 1)

Una volta trovato il centro delle rigidezze C che è il punto in cui l’implacato ruota se la forza non passa per il centro, ma in questo caso il centro C avrà il suo braccio b.
Molto spesso il centro delle rigidezze capito vicino ai controventi più rigidi infatti si nota che sta vicino ai controventi più rigidi ( setti murari).

In particolare le distanze hanno alcuni segni negativi e positivi a seconda della rotazione oraria o antioraria e cosi le molle si accorciano a o si allungano .

In fine abbiamo K ϕ è la rigidezza torsionale totale è una grandezza pari alla somma di tutti i  controventi di tutte le rigidezze per le loro distanze , ed è una quantità sempre positiva.

Si nota infatti che lungo l'asse Y, il centro di massa e il centro delle rigidezze coincidano: di conseguenza, alla presenza di una forza sismica verticale l'impalcato sarà soggetto una traslazione.

 

Step 5
Analisi dei carichi sismici
Lo scopo è valutare la forza sismica che la struttura subisce pari al prodotto tra
F= m ∙ a  (massa per accelerazione)

  a = è l’accelerazione che il corpo subisce per effetto del trascinamento dato dalla normativa
In particolare l' accelerazione a è una frazione dell’accelerazione di gravità dato dal prodotto  a = c ∙ g
in cui C è un coefficiente di intensità sismica, costante dato dalla normativa e  vale  C < 1, frazione molto piccola.

Quindi:
F= m ∙ a = m ∙ c ∙ g = c ( mg )  
in questo modo  P = mg è il peso della struttura pari al prodotto della massa per l’accelerazione di gravità.  Quindi la forza sismica non è altro che una frazione del peso della struttura infatti è per questo che le strutture più sono pesanti e più è vulnerabile.

P (o W) si trova sommando il peso proprio della struttura più il sovraccarico permanente più il sovraccarico accidentale (legato alla funzione) moltiplicato per un coefficiente di contemporaneità Ψ (generalmente pari a 0,80).

Ora, attraverso l’individuazione di questi valori che sono obbligatori da normativa, si procede con il calcolo della Forza Sismica Orizzontale, che nella nostra struttura è pari a 38, 07 KN.
 
G è il carico totale permanente, pai alla somma tra q_s è il sovraccarico strutturale e q_p il sovraccarico permanente,  moltiplicato per l’area totale.
G =(q_s + q_p) A_T

Q è il carico totale accidentale prodotto tra q_a per l’area totale.
Q= q_a ∙ A_T

G e Q  sommate e moltiplicate per il coefficiente Y di contemporaneità (data dalla normativa ) ci permette di trovare il valore di W, il peso sismico.
W= ( G+Q ) Y

Infine F è la forza sismica orizzontale pari a
F= c ∙ W

 

Step 6 e Step 7
Ripartizione forza sismica lungo X e Y
Qui si entra nella probabilità aleatoria del sisma, per capire quale possa essere l’atteggiamento nei confronti dell’azione sismica, infatti noi cerchiamo di simulare in quale direzione e la normativa ci impone di verificare lungo almeno due direzioni perpendicolari, quindi X e Y.
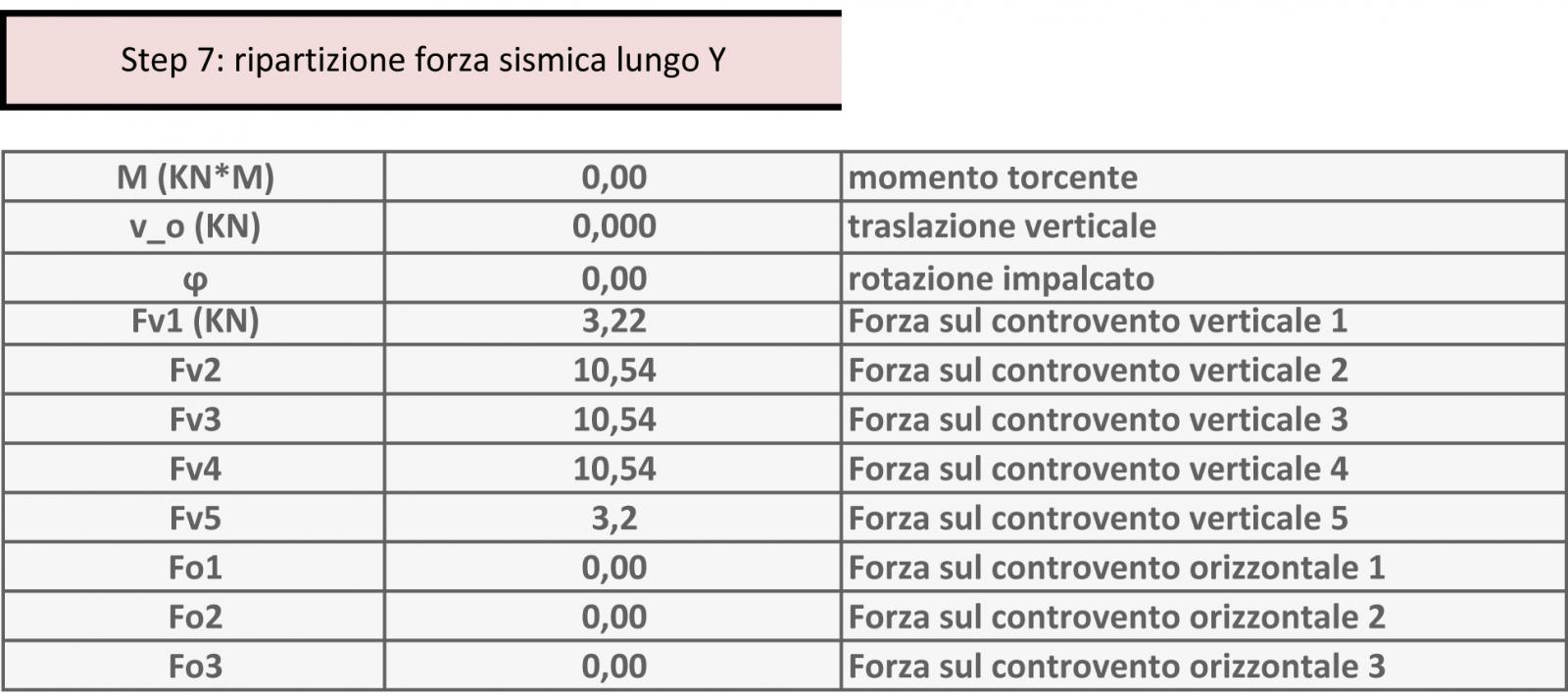
Quindi in queste tabelle cerchiamo di inserire prima forza in direzione orizzontale  e il quale viene ripartita nei controventi e poi  si inserisce una forza in direzione verticale e anch’essa ripartita nei controventi.
 Non è detto che la forza orizzontale viene ripartito solo ai controventi orizzontale e la forza verticale solo ai controventi verticali, perché nella maggior parte dei casi ogni azione sismica non è diretta verso il centro delle rigidezze quindi poi provoca torsione, quindi  l’impalcato oltre  traslare, ruota e quando ruota la forza si ridistribuisce  ballano tutti gli altri impalcati.
Avviene la torsione perché il centro di massa non coincide con il centro delle rigidezze.

 

In questo caso nella tabella 6 il momento torcente è negativo quindi antiorario.
Il momento torcente è il prodotto tra la forza sismica per il braccio , il braccio è la distanza  tra il baricentro precedentemente calcolato il centro delle rigidezze.

La traslazione orizzontale (dove tutto il corpo si muove allo stesso modo) è pari alla forza orizzontale diviso la somma delle rigidezze in direzione orizzontale.
u_o = F/ Ko_TOT

La rotazione d’impalcato ϕ è invece pari al momento torcente indotta da una forza esterna per il braccio b ( distanza tra il centro di massa e il centro delle rigidezze ).
ϕ =  Fb/ K ϕTot

Quindi in base ai valori trovati di U_o e ϕ  ognuno dei controventi orizzontali e verticali avranno una reazione, una forza d’implacato pari a:

Controventi orizzontali
Ri⁰= Ki⁰ x (uo + ϕdi⁰)
Controventi verticali
Ri^V= Ki^V x (ϕdi^V)

 Tutti gli altri valori F_vn e F_on saranno tutti gli altri valori che ricevono i controventi nella ripartizione. Quindi abbiamo ricavato i valori che riceve ognuna dei controventi .

Nella tabella 7 sarà la ripartizione lungo Y con i relativi  valori della traslazione verticale.

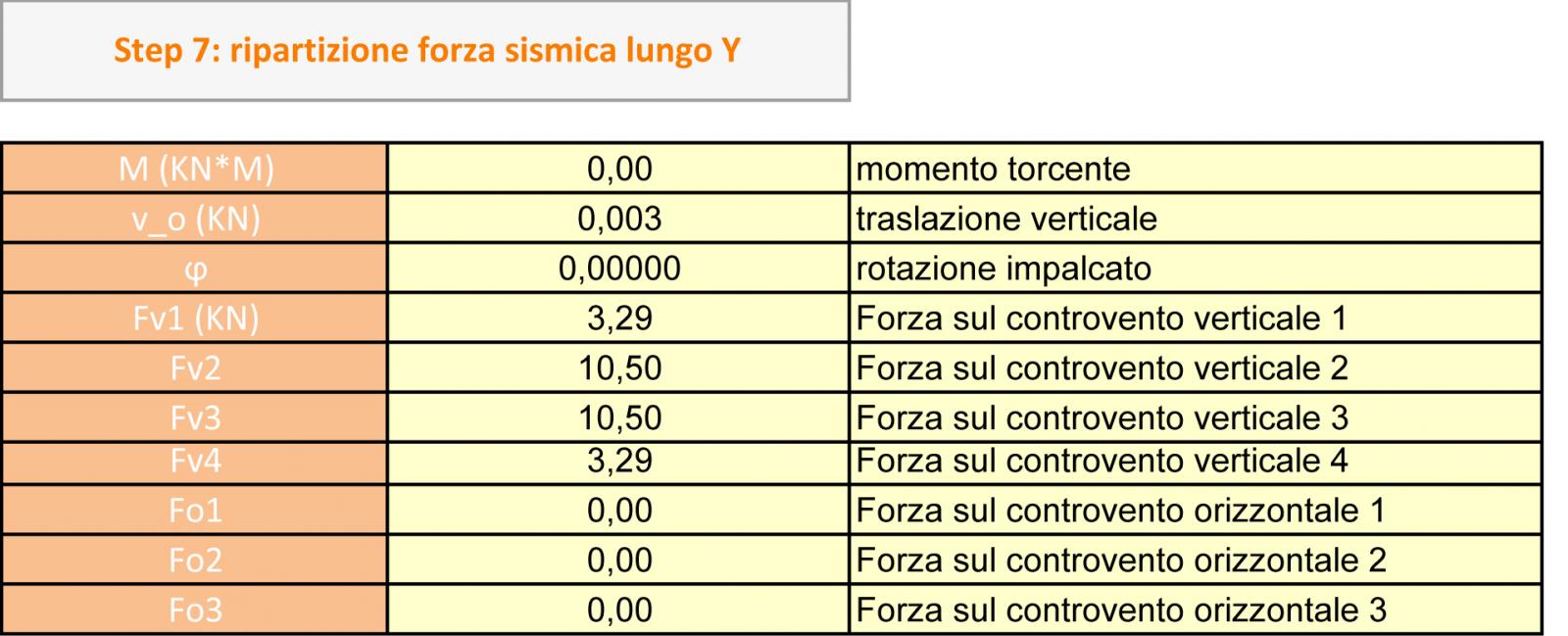
Si nota che nonostante  le forze nei controventi orizzontali sono più piccole delle forze dei controventi verticale.

Tecnologia in C.A
In caso si ipotizza di utilizzare dei pilastri in C.A  30 x 50 cm  con altezza pari a 4 m
I momenti d'inersia da inserire saranno rispettivamnete:

I_x = 1/12 x b x h³ = 1/12 x 50 x 30³ = 112500 cm⁴
Iy = 1/12 x h³ x b = 1/12 x 30 x 50³ = 312500 cm⁴
E = 21000 N/mmq

Step 1
Possiamo calcolarci le rigidezze dei controventi verticali ed orizzontali

Step 2
Dai dati ricavati dalle tabelle dello step 1, si inseriscono le distanze divise in verticale ed orizzontale  partendo  da punto O, in questo caso d_v1 non è presente perché coincidono , cosi come non esiste d_o1.
Mi disegno la struttura mettendo in evidenzia non la tecnologia ma disegnando le molle chiamate le rigidezze rispettivamente K_o e K_{v .}

Step 3
Inserisco i dati relative alle due aree dell'impalcato con le relative cordinate in x e y e automaticamente ottengo l’area totale dell’ impalcato e trovare poi X_G e  Y_G dell'intero impalcato:

X_{G =}  A1 ∙X_G1 + A2 ∙X_G2 / A1 + A2

Y_G = A1 ∙ Y_G1 + A2 ∙ Y_G2 / A1 + A2

 

 

Step 4

Automaticamente grazie ai dati ottenuti dalle taabelle precedenti ricavo le cordinate del centro delle rigidezze dell'impalcato.

 

Si nota infatti che lungo l'asse Y, il centro di massa e il centro delle rigidezze coincidano: di conseguenza, alla presenza di una forza sismica verticale l'impalcato sarà soggetto una traslazione.

 

Step 5

Si inseriscono i  valori dei carichi: strutturali, permanenti, accidentali e li moltiplicandoli per l'area totale dell'impalcato, si ottiene il carico permanente totale e il carico accidentale totale.

G e Q  sommate e moltiplicate per il coefficiente Y di contemporaneità (data dalla normativa ) ci permette di trovare il valore di W, il peso sismico.
W= ( G+Q ) Y

Infine F è la forza sismica orizzontale pari a
F= c ∙ W =  38.07 kN

 

Step 6 -7
Infine sarà possibile verificare la risposta della struttura alla forza sismica esterna lungo due direzionilungo l'asse X o Y .
L'unico valore rilevante è la rotazione dell'implacato lungo la X.
 

 

###base64###

 

VERIFICA DELL'ISOSTATICITA':
il numero dei gradi di libertà deve essere uguale al numero dei gradi di vincolo.

Ve (vincoli esterni) + a (n delle aste) = 2 x n (n dei nodi)     3 + 11= 2 x 7   14= 14  la struttura è isostatica.

CALCOLO DELLE REAZIONI VINCOLARI:

Considerando che la struttura è simmetrica le reazioni saranno anch'esse simmetriche.

Va= 30 KN; Vb= 30 KN

CALCOLO DELLE AZIONI DI CONTATTO:

Calcolo gli sforzi lungo le aste usando il metodo delle sezioni di RITTER. Taglio la struttura in più parti tramite sezioni che prendono un numero di aste che non concorrono nello stesso modo; poi si dovrà vedere se le aste saranno soggette a compressione o trazione ( N>0 TIRANTE), (N<0 PUNTONE)

SEZIONE N 1

Faccio l'equilibrio dei momenti intorno a C

∑M (c) = 0      -30KN X 4m + 20KN X 2m - N₁ X 2m = 0

N₁ = -40 KN (negativo è un PUNTONE)

Per trovare N₃   faccio l'equilibrio intorno a B

∑M(b) = 0     -30KN x 2m + N₃ x 2m =0    N₃ = 30KN (positivo è un TIRANTE)

Per trovare N₂  lo scompongo come se fosse la diagonale di 1 quadrato.

∑y= 0    30KN -20KN - N₂ √2/2 = 0  N₂ = 10√2 KN ( N>0 )

SECONDA SEZIONE:

∑y= 0    N₃ + N₄ √2/2 = 0        30KN + N₄ √2/2= 0   N₄ = -30√2 KN

 

 

 

 

TERZA SEZIONE:

∑M(d) = 0         N₆  x 2m + 20KN x 4m - 30KN x 6m = 0     N₆ = 50 KN

Trovo N₅       

∑y =0         30KN- 20KN + N₅ √2/2 = 0       N₅ = -10 √2 KN

ESERCITAZIONE SU SAP

La deformazione della trave

I DIAGRAMMI N,T,M

 

 

ESERCITAZIONE N 2

CALCOLO DELLE REAZIONI VINCOLARI:

Primo corpo

∑y=0       ya+yb=0   ya= -yb

∑M(a)=0    -50+yb x 6m    yb= 50/6 = 8,33    quindi  ya= -8,33

Secondo corpo

∑y= 0       -yb+yc=0    yb=-yc

∑M(b)=0    50 + Yc x 6m=0     yc= -8,33  quindi yb= 8,33

DIAGRAMMI CON SAP

 

 

 

 

ESERCITAZIONE DIMENSIONAMENTO TRAVI IN CLS, LEGNO E ACCIAIO

 

L'impalcato in esame è un'abitazione ad uso residenziale.

In questa esercitazione si vuole dimensionare la trave più sollecitata, all'interno dell'area di influenza, in tre diverse tipologie: legno, acciaio e cls.

ACCIAIO

• calcolo dei travetti

 

Luce della campata maggiore: 3,30 m

Interasse: 1 m

 

I sovraccarichi accidentali Qa sono quelli legati alla funzione dell'edificio. Riporto qui la tabella con le categorie di locali previste dalla normativa per la definizione di tali carichi.

 

Nel mio caso, avendo un'abitazione ad uso residenziale, avrò 2KN/mq

 

Carichi permanenti:

• peso proprio della struttura Qs 1,86KN/mq che comprende la soletta e la lamiera grecata (10 cm)

• 

• Sovraccarichi permanenti Qp 2,3472 KN/mq che comprende il pavimento in gres porcellanato 0,2 KN/mq; massetto 0,64 KN/mq ed isolante 0,00072 KN/mq, più il carico relativo agli impianti che è 0,50KN/mq e quello dei tramezzi 1KN/mq

•  

• Per trovarmi il carico totale al metro lineare farò: Qa + Qp + Qs x 1 m = 6,21 KN/mq

  Utilizzo il foglio excel per trovarmi Wx ovvero il modulo di resistenza che mi indicherà il tipo di profilo da utilizzare per i miei travetti.

• 

Wx = 37,77 cm ³

 

Secondo la tabella devo utilizzare una IPE 120 con un peso di 0,104 KN/mq. Ora devo verificare che il modulo di resistenza che viene, sommando il Q con il peso dell'ipe, non sia superiore al modulo di resistenza dell'ipe stessa.

 

0,104 KN/mq + 6,21 KN/mq = 6,314 → Wx = 38,40 ‹ 52,96 LA VERIFICA è SODDISFATTA!

 

 

• Calcolo della trave principale

 

Luce: 3,40 m

Interasse: 2,90 m

Qa: 2 KN/mq

Qs: 1,964 KN/mq (1,86 + 0,104 KN/mq)

Qp: 2,3472 KN/mq

 

Wx= 118,17 cm³ → IPE 180 che pesa 18,8 kg/m

 

Q + 0,188KN/mq = → Wx = 119,12 m³ < 146,3 m³ LA VERIFICA è SODDISFATTA

 

 

• Calcolo dei travetti

 

Luce : 3,30 m

 

Interasse: 0,5 m

 

Qa: 2 KN/mq

 

Qs: tavolato: 350 kg/m³ (legno forte) x 0,035 m (spessore) = 12,25 kg/mq → 0,1225 KN/mq

 

Qp: pavimento (cotto 28 kg/mq) 0,28KN/mq; massetto (1800kg/mc x 0,05 m) 0,9KN/mq; impianti 0,50KN/mq e incidenza tramezzi: tramezzo 8 cm, intonaco 1 cm; peso specifico laterizio 800 kg/mc x 0,08m = 0,64KN/mq – peso specifico intonaco 2000 kg/mc x 0,01m = 0,2 x2 (intonaco da entrambe le parti del tramezzo) = 0,4 KN/mq

 

TOTALE TRAMEZZI: 0,64KN/mq + 0,4 KN/mq x H (altezza) / i (interasse) = 1,07 KN/mq

 

 

Qa + Qs + Qp = 2,32KN/mq

 

Inserisco i dati nel foglio excel e ipotizzo la base del mio travetto di 10 cm, otterrò un h di 15,13cm.

Scelgo una sezione di 10x16 e un legno GL24h, ora devo aggiungere il peso del travetto al Q e verificare che la nuova altezza risulti entro i limiti di quella ipotizzata.

 

Il legno GL 24h ha una massa volumica di 380Kg/m³, quindi per un travetto di 10x16cm avrò:

3,8KN/mc x 0,1m x 0,16m x 1m = 0,060KN/m x 2 (perchè in un metro ci sono due travetti) = 0,12 KN/m

Sommando il peso del travetto al Q iniziale ottengo un h di 15,52 che è < di 16 quindi la verifica è soddisfatta.

 

 

Trave principale

Luce: 3,40 m

Interasse: 2,9 m

Qa: 2KN/mq

Qp: 2,75 KN/mq

Qs: 0,1225 KN/m + 0,12KN/m = 0,2425KN/mq

 

Dal foglio excel, ipotizzando una base di 25 cm ho un h di 28,02 cm. Scelgo quindi una sezione di 20x30cm

Il legno GL 28h ha una massa volumica di 410 kg/m³. Mi calcolo il suo peso: 4,1KN/mc x 0,2m x 0,3m x 1m = 0,246 KN che vado a sommare a Q. Di seguito avrò la nuova h che è di 28,26cm < a 30 cm. LA VERIFICA è SODDISFATTA.

 

CLS

 

 

 

Luce: 3,40m

Interasse : 2,9m

 

acciaio B450c, cls C40/50

 

Qa: 2KN/mq

Qs: Peso delle pignatte : 66,4 kg/mq → la mia pignatta è lunga 25 cm e pesa 8,3 kg quindi sapendo che in 1 mq ce ne sono 8 basta fare 8 x8,3 kg = 66,4 kg/mq 0,664KN/mq

Peso dei travetti: per calcolarmi i travetti ho preso la loro larghezza (12 cm) l'ho moltiplicata per la loro altezza (H-s vedi figura) per il peso del c.a. → 25 kg/m³ x 0,12m x0,16m x 1m = 0,48 KN

Aggiungo anche il peso della soletta sopra (s) 25 kg/m³ x0,04m = 1KN/mq

Qp: pavimento in cotto: (28 kg/mq) 0,28KN/mq; massetto (1800kg/mc x 0,04 ) 0,72 KN/mq, essendo un solaio intermedio ci aggiungerò anche l'intonaco 10KN/mc 10 x 0,01 m = 0,1 KN/mq ed infine l'incidenza tramezzi 1KN/mq e impianti 0,50 KN/mq

Mettendo i dati sul foglio, ipotizzando una base di 30cm ottengo un H (che è l'altezza totale) di 17,86 cm. Avrò una sezione 30 x 20 (bxh) che ha un peso di 1,34 KN/m; lo aggiungo al Q e verifico che la nuova altezza non superi i 20 cm → H di 18,13cm < a 20 cm.

 

STRUTTURA RETICOLARE SPAZIALE

Nell'esercitazione in classe del 18/04 abbiamo costruito in Cad una reticolare in 3D, l'abbiamo successivamente importata in SAP e analizzata.

 

AUTOCAD: siamo partiti dal disegnare con una polilinea un quadrato di lato 2m (con un lato aperto che ci servirà in seguito) e la sua diagonale. Passiamo in 3d e facciamo ruotare il quadrato nello spazio (con ruota 3d).

Con il comando "serie" ( diciamo al comando di realizzare 4 colonne a 2 metri di distanza) copiamo la nostra figura lungo l'asse x, e chiudiamo la nostra struttura (prima infatti avevamo lasciato un lato del quadrato aperto per non farci sovrappore le linee in seguito al comando serie).

Disegnamo, con l'UCS nella posizione opportuna, le due aste orizzontali e quella obliqua, dando poi di nuovo il comando serie lungo l'asse x ( colonne distanti 2 m)

 

Ora non ci resta che disegnare, ricordandosi di cambiare sempre l'UCS, le aste oblique per completare la campata; vado a fare l'ultima serie di 7 colonne a distanza 2 m (abbiamo creato una campata in più per poi eliminare solo una parte e chiudere la struttura con facilità)

ABBIAMO QUINDI UNA RETICOLARE SPAZIALE DI 4 X 6 CAMPATE.

 

SAP: 

Abbiamo importato in SAP il nostro file, precedentemente salvato in DXF, e settato le unità di misura (KN M C)

 

Per prima cosa andiamo ad assegnare i vincoli di base. (assign, joint restraints).

Sappiamo che in una struttura reticolare, dove le forze solo applicate solo sui nodi, c'è solo SFORZO ASSIALE. Quindi selezioniamo le nostre aste e gli diamo il momento (cioè rilascio il momento perchè le aste non sono incastrate).

 

Definiamo poi il materiale (define, material, add new material - acciaio) e la geometria (assegnandogli il tubolare)

Definisco anche il carico CONCENTRATO (define, load patterns, add new load pattern) e poi lo vado ad assegnare solo ai nodi superiori (in dispay option for active window levo la spunta ad invisible e la metto a frame not in view per selezionare con facilità tutti i miei nodi superiori).

Faccio l'analisi. Questa è la deformata.

Ovviamente (come detto anche prima) notiamo che i diagrammi del momento e del taglio sono nulli perchè le aste agiscono solo con sforzo normale.

Qui sono riportati i diagrammi di N IN XZ E YZ

 

Possiamo vedere tutte le nostre aste numerate con annessi anche i diagrammi N. Nella tabella (che troviamo in dispay, show tables, element output) possiamo vedere l'asta maggiormente sollecitata.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ESERCITAZIONE SUL DIMENSIONAMENTO DELLA TRAVE

 Prima esercitazione - trave reticolare simmetrica

1) Per prima cosa si verifica l'isostaticità della trave, ovvero si calcola se il numero dei gradi di libertà sia pari al numero dei gradi di vincolo.

l=V ( n° gradi di libertà= n° gradi di vincolo)

l=3 x11 (3 x numero di corpi)

V= V_e +V_i (vincoli esterni + vincoli interni)

V_e= 3       V_i= 2(n-1)  

A=H=2       B=G=4         C=D=E=6        

V_i=4+8+18=30

V=3+30=33        l=33

 

2) Successivamente si calcolano le reazioni vincolari.

∑F_y=0

V_a +V_h - 3F=0

V_a +V_h - 60KN=0

V_a +V_h =60KN ------> V_a = V_h =30KN

La reazione vincolare nel nodo A è uguale a 0 perchè non vi sono altre forze orizzontali che la bilanciano.

 

3) Adesso bisogna calcolare le azioni di contatto. Il metodo scelto in questo caso è stato il metodo di Ritter o metodo delle sezioni, in cui si sceglie di sezionare la trave in un punto tale che tagli tre aste non convergenti nello stesso punto.

    ------>      

Per ricavare lo sforzo normale N₁ è stato fatto l'equilibrio dei momenti rispetto al punto C.

∑M_c=0

-30KNx4m + 20KNx2m - N₁x2m =0   ---->    N₁= -40KN

Il verso ipotizzato per lo sforzo normale è sbagliato, l'asta BD risulta perciò compressa

Per ricavare lo sforzo normale N₃ è stato fatto l'equilibrio dei momenti rispetto al punto B.

∑M_b=0

-30KNx2m + N₃x2m =0   ---->    N₃= 30KN            L'asta AC è tesa

Per ricavare lo sforzo normale N₂ è stato fatto l'equilibro delle forze verticali scomponendo N₂ per ricavare la sua componente verticale, poichè l'asta BC è inclinata a 45°.  (N₂ √2/2)

∑F_y=0

30KN - 20KN - N₂ √2/2 = 0 ----> N₂ = 10√2 KN        L'asta BC è tesa

 

Anche l'asta AB è inclinata a 45° e per trovare lo sforzo a cui è sottoposta si fa una sezione che tagli le aste convergenti nel nodo A in modo da sezionare così l'asta incognita e una già calcolata (AC), potendo così fare l'equilibrio delle forze orizzontali.

       ------->     

∑F_x=0

30KN + N₄ √2/2 = 0 ----> N₄ = -30√2 KN

Il verso ipotizzato per lo sforzo normale N₄ risulta sbagliato, perciò l'asta AB è compressa

 

Sezionando dopo il nodo C si tagliano le due aste di cui ancora si è calcolato lo sforzo normale, l'asta CE e l'asta CD

    ---->    

Facendo l'equilibrio dei momenti rispetto al nodo D si ottiene lo sforzo normale N₅

∑M_d=0

-30KNx6m + 20KNx4m + N₅x2m =0   ---->    N₅= 50KN    L'asta CE è tesa

Infine sfruttando l'equilibrio delle forze verticali si ottiene il valore dello sforzo N₆

∑F_y=0

N₆ √2/2 + 30KN -20KN = 0 ----> N₆ = -10√2 NK   ---->     L'asta CD è compressa

 

Poichè la trave è di tipo simmetrico sia nella ripartizione dei carichi che nella disposizione delle aste, per capire se le aste mancanti sono puntoni  o tiranti e ricavare il valore dello sforzo normale basta riportare in modo simmetrico i  dati ottenuti dal calcolo della prima metà della trave.

Verifica con sap2000:

Per riprodurre la struttura su Sap2000 sono partita dal modello di una trave reticolare che ha di default gli stessi vincoli dell'esercizio, ho definito il numero e la dimensione delle campate, ho posto il momento all'inizio e alla fine di ogni asta uguale a 0, ho definito il carico e applicato le forze puntuali  in corrispondenza dei nodi B, D e G ed ho avviato l'analisi:

Ottengo così l'immagine della deformata:

E i diagrammi con i valori dello sforzo assiale (rosso=aste copresse, giallo =aste tese):

 

---

Seconda esercitazione - trave reticolare asimmetrica

1) La prima cosa da fare è la verifica dell'isostaticità della trave, calcolando il numero dei gradi di libertè e il numero dei gradi di vincolo.

l=V ( n° gradi di libertà= n° gradi di vincolo)

l=3 x11 (3 x numero di corpi)

V= V_e +V_i (vincoli esterni + vincoli interni)

V_e= 3       V_i= 2(n-1)  

A=H=2       B=D=E=4         C=8      G=6    

V_i=4+12+8+6=30

V=3+30=33        l=33  ---> la struttura è isostatica

 

2) Il secondo passo è quello di trovare le reazioni vincolari facendo l'equilibrio delle forze verticali per ricavare la reazione verticale, e l'equilibrio dei momenti rispetto al nodo A per ricavare le reazioni orizzontali che riuslteranno uguali ed opposte esserndo le uniche presenti.

∑F_y=0  

V_B - 10KN -10KN =0 ----> V_B=20KN

∑M_A=0 

U_Bx1m - 10KNX1m - 10KNx2m =0 ---> U_B =30KN = U_H

                                 

3) Le azioni di contatto sono state trovate utilizzando questa volta il metodo dei nodi, facendo cioè solamente l'equilibro delle forze verticali ed orizzontali per ottenere lo sforzo assiale che arriva sulla cerniera, isolando di volta in volta ogni nodo, In queso caso, non essendo una struttura simmetrica, è necessarico svolgere il procedimento per ogni nodo.

Partendo dal nodo A si nota subito che le due aste AC e AB sono scariche

Dall'equilibrio delle forze verticali del nodo B, scomponendo la forza poichè l'asta BC è a 45°, si ottiene lo sforzo assiale N₄ = -20√2 KN, il verso ipotizzato è perciò sbagliato e l'asta BC risulta compressa

Dall'equilibrio delle forze verticali si ottiene incece N₃ = -10KN e anche in questo caso il verso ipotizzato è sbagliato e l'asta BD è compressa

Lo stesso procedimento è stato utilizzato per i nodi restanti, in particolare l'asta DC e l'asta GH risultano scariche poichè nel nodo D N₆=0  perchè non vi sono altre forze verticali che la equilibrano e nel nodo G N₁₁=0

Tutte le aste sono compresse fatta eccezione per l'asta CG che è tesa con sforzo normale di trazione N₈ =10√2 KN

N₅=N₃= 10KN   DG asta compressa

N₇= 30KN  EC asta compressa

N₁₀= 10KN  EG asta compressa

N₉= 30KN  EH asta compressa

Nel nodo H facendo l'equilibrio alle forze orizzontali si verifica il valore dello sforzo di compressione dell'asta EH

 

Verifica con sap2000:

Per riprodurre la trave su Sap2000 in questo caso ho utilizzato il modello della griglia, definedo numero e dimensione delle campate, disegnando poi le singole aste e applicando i vincoli nei nodi B ed H assegnando però al carrellino nel nodo H la sola traslazione verticale essendo posizionato verticalmente nell'essercizio. Ho poi posto il momento all'inizio e alla fine di ogni asta unguale a 0, ho definito e applicato i carichi puntuali nei nodi C ed E ed ho avviato l'analisi:

Si ottiene così l'immagine della deformata:

E i diagrammi con i valori dello sforzo assiale (rosso=aste copresse, giallo =aste tese):

 

 

 

---

Terza esercitazione - dimensionamento travi (svolto con Francesca Perusini)

Il solaio analizzato è quello di una casa a schiera progettata nel corso del Laboratorio di Progettazione1.
Essendo un edificio di civile abitazione il sovraccarico accidentale, legato alla funzione, sarà di 2 KN/m². La trave da progettare sarà una trave doppiamente appoggiata in cui il momento massimo è ql²/8. L'esercitazione prevede il calcolo del solaio con tre diverse teconologie: acciaio, legno e calcestruzzo armato.

 

 STRUTTURA IN ACCIAIO:

Dimensionamento della trave IPE:

Carico accidentale qa: 2KN/m²

Carico strutturale qs:

lamiera grecata tipo A75/P570: 2KN/m²

Sovraccarico permanente qp:

Isolante termoacustico: 360 Kg/m³ x 0,01 m = 3,6 Kg/m²  ------>  0,036 KN/m²

Massetto: 2000 Kg/m³ x 0,04 m = 80 Kg/m²  ------>  0,8 KN/m²

Piastrelle in Gres Porcellanato: 1540 Kg/m³ x0,013 m = 20 Kg/m²  -------> 0,2 KN/m²

Controsoffitto: 800 Kg/m³ x 0,03 m = 24 Kg/m² ------> 0,24 KN/m²

Incidenza tramezzi :  1KN/m²

Incidenza impianti : 0,5 KN/m²

q_p TOT = 0,036 KN/m² + 0,8 KN/m² + 0,2 KN/m² + 1KN/m² + 0,5 KN/m² = 2, 536 KN/m²

 

Inserendo questi valori nel foglio di calcolo excel si ottiene il valore della resistenza W_x= 350,51 cm³

E' stata scelta perciò  da profilario una trave IPE 270 il cui valore W_x = 429 cm³

 

 STRUTTURA IN LEGNO:

Dimensionamento travetto in legno:

Carico accidentale qa: 2KN/m²

Carico strutturale qs:

Tavolato in castagno 840 Kg/m³(Peso specifico )  x 0,03 m (Spessore)  = 25,2 Kg/m² -------> 0,25 KN/m²

Sovraccarico permanente qp:

Massetto: 2000 Kg/m³ x 0,05 m = 100 Kg/m² -------> 1 KN/m²

Parquet in  rovere: 720 Kg/m³x 0,02 m = 14,4 Kg/m² --------> 0,144 KN/m²

Incidenza tramezzi: 1KN/m²

Incidenza impianti: 0,5 KN/m²

q_p TOT= 1 KN/m² + 0,144 KN/m² + 1KN/m² + 0,5 KN/m² = 2,644 KN/m²

Dati:

Legno GL28h                f_k = 28 MPa

Interasse = 0,9 m

Luce = 3 m

b  = 0,1 m

Inserendo questi dati nel foglio di calcolo excel si ottiene l'altezza del travetto:

E' stato perciò scelto un travetto di sezione 10cm x 20cm, poichè l'altezza minima necessaria risulta di 17, 65 cm

 

Dimensionamento trave in legno:

Carico accidentale qa: 2KN/m²

Carico strutturale qs:

Travetti in legno: 500 Kg/m³ x 0,1 x 1 = 50 Kg/m² ------> 0,5 KN/m²

Tavolato in castagno: 0,25 KN/m²

q_s TOT= 0,5 KN/m² + 0,25 Kn/m² = 0,75 KN/m²

Sovraccarico permanente qp: 2,644 KN/m²

Dati:

Legno GL28h                f_k = 28 MPa

Interasse = 3 m

Luce = 6 m

b = 0,2 m

Modificando i valori dell'interasse, luce, qp e b nel foglio excel, tenendo conto perciò anche del peso strutturale dei travetti, si ottiene l'altezza della trave:

La trave scelta ha una sezione di 20m x 50cm, essendo il valore minimo dell'altezza di 47,81 cm.

 

 STRUTTURA IN CALCESTRUZZO ARMATO:

 

Dimensionamento trave:

Carico accidentale qa: 2KN/m²

Carico strutturale qs:

Travetti: 2500 Kg/m³ x 0,18 m x 0,1 m =  45 Kg -----> 0,45 KN x 2 (n° travetti in 1 m²)= 0,9 KN/m²

Pignatte: 550 Kg/m³ x 0,18 m x 0,4 m = 40 Kg ------>  0,4 KN x 2 (n° pignatte in 1 m²) = 0,8 KN/m²

Caldana: 2500 Kg/m³ x 0,04 m = 1 KN/m²

q_s TOT= 0,9 KN/m² + 0,8 KN/m² + 1 KN/m² = 2,7 KN/m²

Sovraccarico permanente qp:

Massetto:  2000 Kg/m³ x 0,04 m = 80 Kg/m² ----->  0,8 KN/m²

Isolante termoacustico: 360 Kg/m³ x 0,01 m = 3,6 Kg/m²  ------>  0,036 KN/m²

Piastrelle in Gres Porcellanato: 1540 Kg/m³ x0,013 m = 20 Kg/m² ------->  0,2 KN/m²

Intonaco:  200 Kg/m³ x 0,01 m =2 Kg/m² ------->  0,02 KN/m²

q_p TOT= 0,8 KN/m²  +  0,036 KN/m² + 0,2 KN/m² + 0,02 KN/m² = 1,056 KN/m²

Dati :

Calcestruzzo C 25/30      fck = 30 MPa

base = 25 cm

copri ferro = 3 cm

 

Inserendo questi dati nel foglio di calcolo excel si ottiene l'altezza della trave:

Il valore minimo dell'altezza risulta essere 31,38 cm, la trave scelta ha perciò una sezione di 25cm x 35cm.

 

---

Quarta esercitazione - piastra reticolare spaziale

Disegno di una struttura reticolare spaziale su AutoCAD per poi importarla su Sap2000 in modo da poterla analizzare.

Disegno con AutoCad :

Si parte dal disegno di un modulo quadrato 2m x 2m costituito da tiranti, puntoni e diagonali in modo tale da poterlo riprodurre in serie.Si inizia a disegnare partendo dall’origine degli assi 0,0,0 utilizzando una polilinea per rappresentare le 3 aste e la diagonale, non chiudendo il quadrato in modo da non avere aste ripetute e sovrapposte dopo aver utilizzato la riproduzione in serie. Questo perchè il programma Sap2000 in cui si importerà il disegno non riconosce le aste sovrapposte.

A questo punto è necessario passare dal piano 2D allo spazio 3D in modo da poter rappresentare gli elementi mancanti del modulo cubico (2m x2m x2m) da riprodurre in serie.

Prima di utilizzare il comando “serie” il disegno va ruotato nuovamente.

Fatto questo si selezionano le 4 aste e utilizzando il comando serie (array) ,che permette di fare copie in serie rettangolari, si fa la prima asta reticolare definendo una serie di 4 colonne con distanza l’una dall’altra di 2 m.

Alla reticolare così ottenuta va disegnata l’asta verticale finale assente nel modulo di base.

Ora si disegna il modulo base delle 3 aste e diagonale anche nella direzione dell’asse y e si riproduce in serie nello stesso modo usato precedentemente( con il comando serie/array). E’ necessario cambiare l’UCS, mettendo l’asse X lungo la direzione del nuovo array (UCS > invio > seleziona origine > seleziona direzione asse x > seleziona direzione asse y).

 

Si completa poi la prima campata disegnando le aste oblique superiori ed inferiori del primo modulo e duplicandole sempre con il comando serie/array, dopo aver opportunamente cambiato UCS.

A questo punto si cambia nuovamente UCS (l’asse x deve essere sempre nella direzione della serie) e tutta la prima “riga” (modulo definitivo) viene selezionata e riprodotta con il comando serie/array  con una serie di 7 colonne distanziate sempre di 2 m (dimensione del modulo base).

Si ottiene così una struttura reticolare spaziale con 4 capate lungo l’asse z e 7 lungo l’asse x. Dovendo quest’ultime essere 6, si cancellano le aste in eccesso; questo procedimento risulta più semplice rispetto alla riproduzione in serie del modulo solo per 6 colonne, dovendo poi disegnare tutte le aste di chiusura mancanti.

  

Prima di importare il disegno su Sap2000 si separano le polilinee con il comando “esplodi”.

Analisi su Sap2000:

Per importare il file, è necessario un salvataggio in formato .dxf2000. Una volta importato il file su Sap, sulla finestra che si aprirà automaticamente, bisogna selezionare alla voce “Frame” il layer usato su AutoCad per le aste (in questo caso il layer “aste”).

Successivamente si selezionano i 4 vertici della struttura per assegnare i vincoli (Assign > Join > Restraints ). 

E’ poi necessario rilasciare i momenti nei nodi, in quanto cerniere interne, per assicurarsi che le aste siano sollecitate solo assialmente. Per fare questo, dopo aver selezionato tutto, si rilasciano i momenti all’inizio e alla fine di ciascun’asta (Assign > Frame> Partial Fixity).

  

Prima di procedere con l’analisi della struttura è fondamentale definire il materiale e la sezione delle aste.

Define > Materials > Add New > “Steel”

Define > Section Proprieties > Frame Section > Add new > “Tubolare”(Pipe)---àMaterials > “Steel”

Definito questo si assegna alla struttura la sezione scelta con il relativo materiale (Assign > Frame > Frame Section > “Tubolare”).

Anche il carico deve essere prima definito e poi assegnato. A questo punto perciò si definisce un carico concentrato gravitazionale da applicare poi solamente nei nodi superiori opportunamente selezionati. Il carico verrà applicato sull’asse z con un valore di - 40 KN.

Fatto questo si può avviare l’analisi.

Poiché taglio e momento devono essere nulli, visto che le aste lavorano solamente a sforzo assiale, si ottengono solamente i diagrammi dello sforzo normale.

Diagramma sforzo assiale sul piano zx:

Diagramma sforzo assiale sul piano zy:

Spuntando la voce “Label”, nella tabella che si aprirà da set display options,tutte le aste verranno numerate; da display > show tables selezionando poi element output si aprirà una tabella con i dati di tutte le aste numerate. Per ciascuna asta sono presenti 3 valori che corrispondono alle sollecitazioni alle due estremità e nel mezzo. Alcune aste sono lunghe 2m ed avranno i 3 valori sotto la voce “station” di 0-1-2m, mentre altre(quelle diagonali) sono lunghe 2√2m ed avranno come misure 0-1,41-2,83m. I valori dello sforzo di taglio e momento come previsto risultano nulli.

Esportando la tabella su Excel sarà più facile ordinare le aste in base a quelle soggette a maggiore sforzo normale sia di trazione (positivo) che di compressione (negativo). Dopo aver individuato queste due, si passa al progetto e verifica delle aste.

Progetto asta tesa:

Scelgo l’asta maggiormente tesa in modo da mantenermi in sicurezza; questa risulta essere la n°124  con un valore N=258,93KN.

Utilizzando la formula di Navier posso dimensionare l’asta.

Sapendo quindi che f_d = N / A 

A=N/f_d                dove f_d= f_yk/γ_m

                     f_yk = resistenza a snervamento

                     γ_m=1,05  = coefficiente di sicurezza

 

Scelgo un acciaio Fe360 S235 e trovo un valore dell’area minima per poter resistere pari a:

A=258934 N/ (235 MPa/1.05) = 1157mm² = 11,57cm²

Nel profilario dei tubi in acciaio a sezione circolare cerco un profilo che abbia un’area superiore a quella ottenuta.

Scelgo perciò il profilo: d x s = 114,3x3,6 mm

                                A’= 12,50 cm² > 11,57cm².

 

Verifica a resistenza:

(N/A’)< f_d          

 258934 N/1250 mm²= 207,14 MPa < 223,81 MPa

Asta verificata a resistenza.

 

Progetto asta compressa:

Lo stesso procedimento applicato all’asta maggiormente tesa, viene utilizzato per il progetto dell’asta compressa.

Le aste compresse possono però essere anche soggette a carico critico euleriano che le porta ad un’inflessione dell’asta fino al collasso. Questa è strettamente legata alla snellezza, ovvero quando il rapporto tra l’altezza e la lunghezza dell’elemento è molto grande.

Sono perciò necessarie anche verifiche a snellezza e a stabilità.

 

Scelgo l’asta maggiormente tesa in modo da mantenermi in sicurezza; questa risulta essere la n°10  con un valore N= -307,25KN.

Scelgo un acciaio Fe430 S275 e trovo un valore dell’area minima per poter resistere pari a:

A=N/f_d    

A=307254 N/ (275 MPa/1.05) = 1173mm²  = 11,73cm²

Nel profilario dei tubi in acciaio a sezione circolare cerco un profilo che abbia un’area superiore a quella ottenuta.

Scelgo perciò il profilo: d x s = 114,3x3,6 mm

                                 A’= 12,50cm² > 11,73cm²

 

Verifica a resistenza:

(N/A’)< f_d         

  307254 N/1250 mm²= 245,80 MPa < 261,90 MPa

Asta verificata a resistenza.

 

Verifica a snellezza:

λ<200             λ =l_o/ρ

                      l_o = luce libera di inflessione che dipende dal tipo di vincolo dell’asta.

                      In questo caso abbiamo un’asta doppiamente incernierata

                      b=1

                      l=283 cm (asta diagonale)

                      l_o=b*l=1*l;

                      ρ =raggio d’inerzia = 3,92cm (da tabella)

 

λ =283/3,92=7 2,19 < 200  

Asta verificata a snellezza.

                

Verifica a stabilità:

Devo trovare il carico critico euleriano N_cr e verificare che lo sforzo assiale Nd sia minore della resistenza a stabilità Nd<Nbdr

N_cr =  π² x E x Jmin / l₀²

Dove: E = modulo elastico a compressione = 210000 N/mm²

            Jmin= momento di inerzia minimo della sezione (da profilario) = 192 cm⁴ = 1920000 mm⁴

            l₀ = luce libera di inflessione, ovvero quanto è larga l'onda sinusoidale che definisce lo sbandamento,che dipende dai vincoli. In questo caso i i vincoli sono cerniere perciò l₀ = l. l = √2 m = 2,83 m (asta diagonale).

N_cr = π²x 210000 N/mm² x 1920000 mm⁴ / (2830 mm)²=

      = 9,86x 210000 N/mm² x 1920000 mm⁴ / 8008900 mm²= 496371,6 N = 496,37 KN

N_d < N_bdr 

dove N_bdr = resistenza all'instabilità = χ* A* fyk / γm

        χ = 1 / (φ + √φ²-λ²)  <  1

        φ = 0,5 (1 + α (λ_ - 0.2) + λ_²)

        α = fattore di imperfezione = 0,21

        λ_= √(A * fyk / N_cr)

Inserendo queste formule in un foglio Excel il calcolo sarà più immediato

Le caselle in bianco sono quelle in cui i dati vanno inseriti, quelle in azzurro sono quelle in cui il valore viene calcolato.

Ottengo N_brd = 254,31 KN > N_d =307,25 KN  

Asta non verificata a stabilità.

Scelgo perciò una sezione maggiore e ricalcolo il valore di N_cr inserendo il relativo momento d'inerzia. Utilizzando il foglio di calcolo excel è possibile vare rapidamente più prove fino ad arrivare al profilo che soddisfi la verifica a stabilità.

Secondo tentativo: asta non verificata

Terzo tentativo: asta verificata

Profilo scelto: d x s = 114,3x4,5 mm

                                 A’= 15,50cm²

N_cr = π²x 210000 N/mm² x 2430000 mm⁴ / (2830 mm)²=

      = 9,86x 210000 N/mm² x 1920000 mm⁴ / 8008900 mm²= 604952,9 N = 604,95 KN

N_d < N_bdr

Ottengo N_brd = 313,57 KN > N_d =307,25 KN  

Asta verificata a stabilità.

 

---

 

Quinta esercitazione - RIPARTIZIONE DELLE FORZE SISMICHE (svolto con Francesca Perusini)

La forza sismica è una forza d’inerzia che arriva alla struttura per effetto di un’accelerazione di trascinamento. Dipende dal prodotto della massa della struttura per l’accelerazione massima che la struttura riceve quando viene scossa dal terreno; infatti maggiore sarà la massa dell’edificio, maggiore sarà la forza sismica agente su di esso.

F = m*a

a è una frazione dell’accelerazione di gravità:

a = c g             dove c < 1 è coefficiente di intensità sismica

La forza sismica è perciò:

F = m*cg = c (mg)  dove mg = forza peso P  ---->  F = cP.

Per contrastare la forza sismica è necessario prevedere nella struttura dell’edificio dei controventi che permettano di resiste anche alle sollecitazioni orizzontali.

Per analizzare l’azione della forza sismica si considera che il solaio in esame si comporti come un corpo rigido e perciò possa subire una traslazione verticale, traslazione orizzontale e rotazione. I telai inoltre si comportano come dei corpi elastici (delle molle) che ricevono la forza sismica e la restituiscono come forza di richiamo.

La forza sismica agisce sul centro di massa e determina una traslazione del corpo rigido.

E’ molto importante la distribuzione delle rigidezze in pianta perché la struttura può subire anche una rotazione intorno al centro delle rigidezze sempre dovuta all’effetto della forza orizzontale. Questo accade nel caso in cui il centro delle rigidezze non coincide con il centro di massa; in questa situazione si crea un momento dato dalla forza sismica per il braccio, ovvero per la distanza tra il centro di massa e il centro delle rigidezze.

La struttura analizzata è in acciaio ed è composta da 5 controventi verticali e 4 controventi orizzontali.

La sezione dei pilastri è una HE 160 con valori di momento d’inerzia:

I_x = 1673 cm⁴

I_y = 616 cm⁴

I pilastri sono disposti in pianta con l’anima parallela alla trave principale, con le ali perpendicolari alla trave principale poiché devono anche portare il solaio; per questo motivo i due pilastri centrali dell’impalcato (3,5) sono posizionati diversamente rispetto agli altri. Bisogna tenere conto di questo nella scelta del momento d’inerzia da inserire nelle tabelle per il calcolo delle rigidezze in quanto si sceglierà quello rispetto all’asse y per tutti i pilastri ad eccezione di dei pilastri centrali per i quali si utilizzerà il momento d’inerzia rispetto all’asse x.

 

Step 1 : CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DEL’EDIFICIO

Utilizzando il foglio di calcolo excel si trovano i valori delle rigidezze traslanti dei 9 telai della struttura, inserendo opportunamente i diversi momenti d’inerzia, come sopra descritto.

La rigidezza totale si trova:

K_T =( 12E *Σ_i I_i ) / h³

                             E = modulo di Young = 210000 N/mm2 per l’acciaio

                             h = altezza dei pilastri

                             Σ_i I_i = sommatoria dei momenti di inerzia di tutti i pilastri della struttura.

Step 2 : TABELLA SINOTTICA CONTROVENTI E DISTANZE

Nella tabella sono riportati i valori delle rigidezze calcolate precedentemente  e le relative distanze dal punto O.

Step 3 : CALCOLO DEL CENTRO DI MASSA

La forza sismica viene applicata nel centro di massa. Si calcola perciò il valore delle tre aree in cui abbiamo diviso l’impalcato e le coordinate dei rispettivi centri di massa (X_G,,Y_G). Per  trovare il centro di massa dell’area totale dell’impalcato so sommano i prodotti delle tre aree per le rispettive coordinate x e y e si divide per l’area totale.

X_G = (A₁ x_G1 + A₂ x_G2 + A₃ x_G3) / (A₁ + A₂ + A₃) = Σ_iA_i*x_i/ A_tot  

Y_G = (A₁ y_G1 + A_2 yG2 + A₃ y_G3) / (A₁ + A₂ + A₃) = ΣiA_i*y_i/ A_tot

 

Step  4 : CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI

A questo punto tramite il foglio excel si calcolano le rigidezze totali verticali ed orizzontali e le relative coordinate del centro delle rigidezze (X_c , Y_c):

Σ_iK_xi = rigidezza totale orizzontale (K_{x tot})

Σ_iK_yi = rigidezza totale verticale (K_{y tot})

 

X_c = Σ_iK_xi*d_yi/ k_yitot.   sommatoria delle rigidezze dei controventi orizzontali per le relative distanze verticali dal punto  0

Y_c = Σ_iK_yi*d_xi / k_xitot.  sommatoria delle rigidezze dei controventi verticali per le relative distanze orizzontali dal punto 0

Il centro delle rigidezze è il punto attorno a cui l’impalcato ruota ne caso in cui la forza esterna (sismica) non passi per ques’ultimo.

 

Si calcola ora la rigidezza torsionale totale :

K_φtot  = Σ_iK_yi*dd_yi²  + Σ_iK_xi*dd_xi²

dove dd_y e dd_x  sono le distanze dei controventi dal centro delle rigidezze ed hanno segno positivo o negativo in base alla rotazione positiva o negativa che subiscono (molle si allungano o si accorciano per effetto della rotazione).

 

Step 5 : ANALISI DEI CARICHI SISMICI

La forza sismica, come già detto, è data dalla forza peso per il coeff.  d’intensità sismica:

F = cP

E’ perciò una frazione della forza peso (poiché c < 1).

Per calcolare la forza sismica è necessario perciò calcolare il peso della struttura (P), definendo carichi strutturali, sovraccarico permanente e carico accidentale (q_s , q_p, q_a).

P = G + ψ Q

G = carico totale permanente = (q_s + q_p) *A_tot

Q = carico totale accidentale = q_a *A_tot

ψ = coefficiente di contemporaneità, dato dalla normativa, che diminuisce il carico accidentale (ψ=0,80).

Adesso si può calcolare il valore di F assumendo c=0,20

Step 6_7 : RIPARTIZIONE DELLA FORZA SISMICA LUNGO X  E LUNGO Y

 A questo punto si analizza la ripartizione della forza sismica sia lungo x che lungo y; questo perché l’azione del sisma è incerto e non possiamo sapere a priori in quale direzione si svilupperà.

Il foglio di calcolo excel riporta il calcolo di:

-Momento torcente: M = F (XC - XG)     

                             M = F (YC - YG)  

dove (XC - XG) è il braccio della forza, ovvero la distanza tra la coordinata Y del centro delle rigidezze e quella del centro di massa, nel caso in cui il centro di massa non coincida con il centro delle rigidezze.

-Traslazione:  u_x = F/K_{x tot}

                     u_y = F/K_{y tot}

-Rotazione rigida: φ = F*b / K_φtot   (Momento torcente/rigidezza totale)

 

Ora si può calcolare come la forza sismica si ripartisce su ogni controvento in relazione alle loro rigidezze:

R_xi = K_xi (u_x + φ dd_xi)  controventi orizzontali

R_yi = K_yi (u_y + φ dd_yi) controventi verticali

 

Ripartizione della forza sismica lungo x:

Ripartizione della forza sismica lungo y:

In questo caso la rotazione risulta nulla. Questo  è dovuto al fatto che l’impalcato scelto è simmetrico perciò il centro di massa (punto di applicazione della forza sismica) coincide con il centro delle rigidezze e di conseguenza il braccio della forza sismica , responsabile della rotazione sarà nullo.

penso di esserci riuscito XD

Esercizio relativo ad una trave reticolare asimmetrica risolto col metodo dei nodi e seguente verifica con il software Sap2000