SdC(b) (LM PA)

ESERCIZIO 1

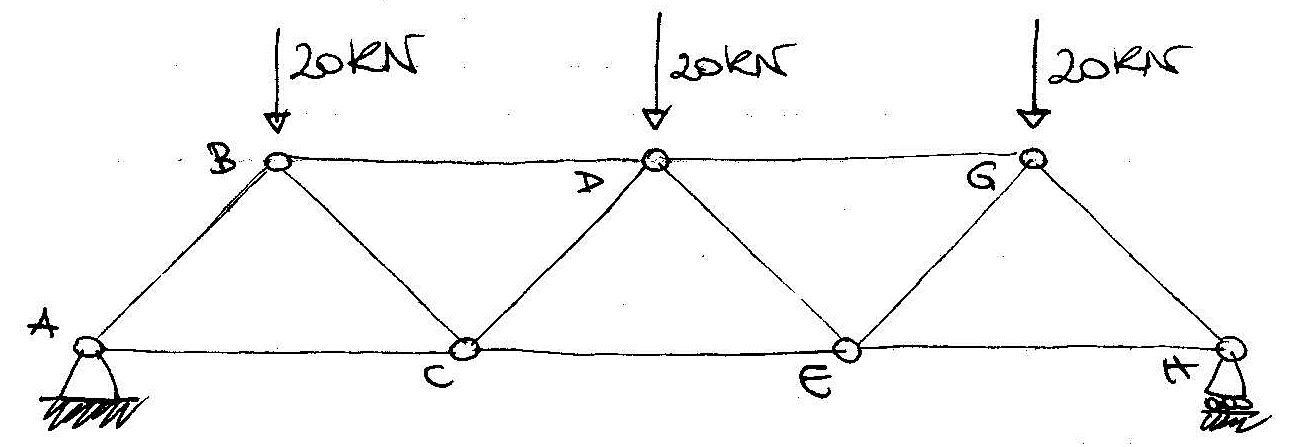
Verifica dell’isostaticità:

Gradi di libertà 11x3=33

Nodi A, H : 2 aste -> il nodo da 2 x (2 – 1) = 2 gradi di vincolo

Nodi B, G : 3 aste -> il nodo da 2 x (3 – 1) = 4 gradi di vincolo

Nodi C, D, E : 4 aste -> il nodo da 2 x (4 – 1) = 6 gradi di vincolo

Vincoli interni = 30

Vincoli esterni = 2 (cerniera) + 1 (carrello) = 3

V = 30 + 3 = 33 -> struttura isostatica.

Controllo

Vesterni + Naste = 2 x Nnodi

3 + 11 = 2 x 7 -> struttura isostatica.

Reazioni vincolari:

La struttura è simmetrica quindi le reazioni vincolari dovranno essere altrettanto. Di conseguenza sicuramente non ci sarà reazione orizzontale alla cerniera (perché il carrello è impossibilitato a produrre una reazione orizzontale) e le due reazioni verticali saranno pari alla somma delle forze esterne applicate diviso 2. Quindi 20 x 3 / 2 = 30 kN

Sollecitazioni:

Usando il metodo delle sezioni di ritter considero solo una parte della struttura. Le azioni di contatto vengono trovate mettendo in equilibrio la parte della struttura considerata.

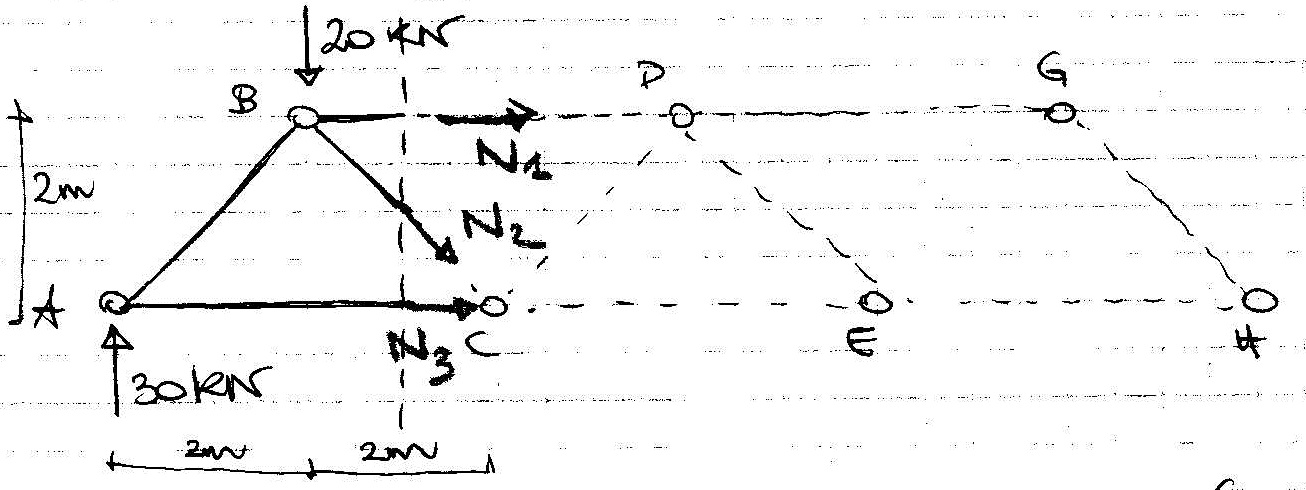
Per equilibrio momenti intorno a C (dove N2 e N3 non hanno braccio e non fanno momento) trovo N1 pari a -40 kN.

Per equilibrio dei momenti intorno a B trovo N3 pari a 30kN

Per equilibrio a traslazione verticale trovo N2 pari a 10 (radice di) 2 kN

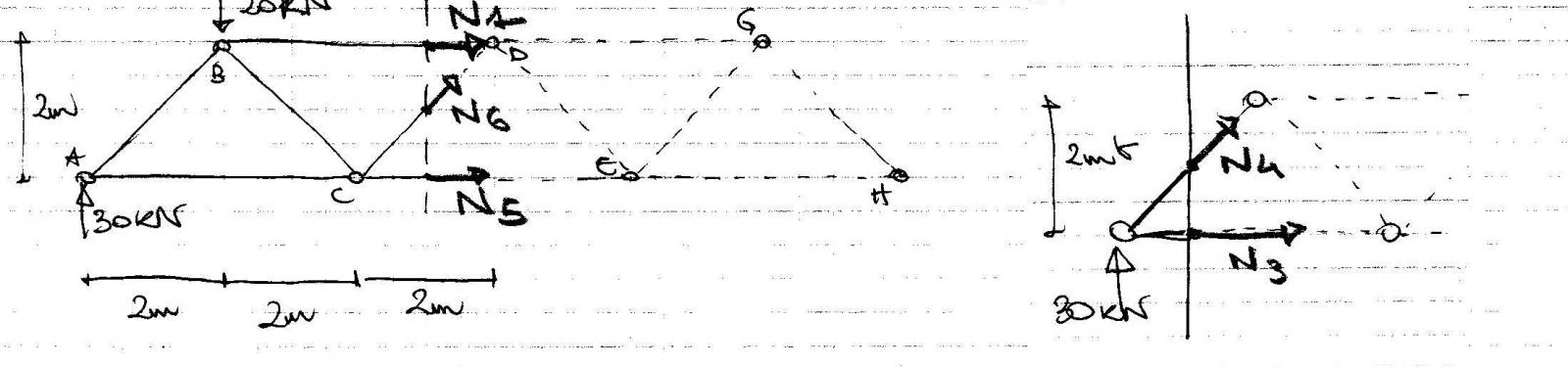
Con altre due sezioni e con lo stesso principio secondo il cui ogni singola parte della struttura è in equilibrio con le azioni di contatto trovo le altre reazioni normali:

N4 = -30 (radice di)2 kN

N5 = 50 kN

N6 = -10 (radice di)2 kN

Ho ipotizzato un verso della normale considerandola sempre tesa, in modo che nel caso di risultati negativi l’asta sarà compressa.

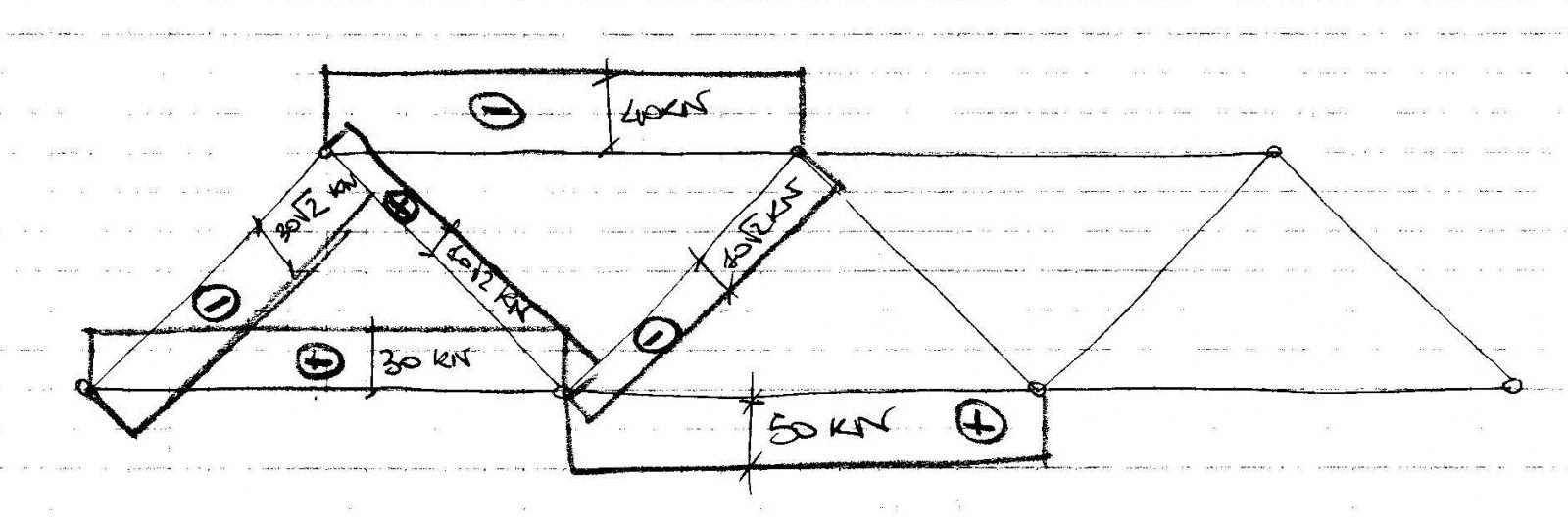
Per simmetria non è necessario fare altro tagli in quanto le azioni di contatto saranno specchiate come le reazioni vincolari e i carichi applicati.

Nel diagramma delle sollecitazioni si nota come le aste superiori siano tutte compresse mentre le aste inferiori siano tutte tese.

 

ESERCIZIO 2

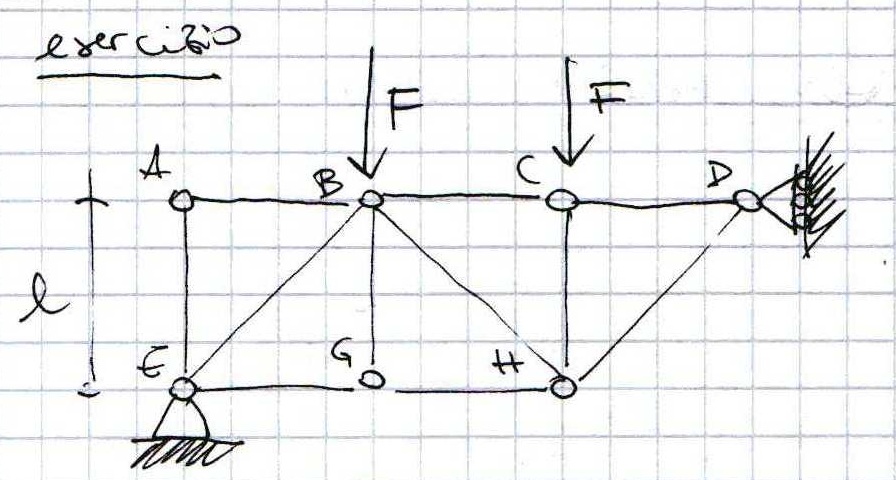
Come prima procedo alla verifica dell’isostaticità:

A,D -> 2 gradi di vincolo

E,C,G -> 4 gradi di vincolo

H -> 6 gradi di vincolo

B -> 8 gradi di vincolo

Vesterni = 3

Gradi di libertà: 11x3=33

Gradi di vincolo: 30+3=33 -> struttura isostatica.

Per calcolare le reazioni vincolari metto in equilibrio la struttura a rotazione (in E), e a traslazioni verticali e orizzontali. Ho 3 equazioni in 3 incognite (le tre reazioni) quindi sono sufficienti per risolvere il sistema, che ha risultato:

Ve = 2F

Od = 3F

Oe = 3F

A differenza del metodo precedente delle sezioni, utilizzo il metodo dei nodi, seguendo lo stesso principio: ogni parte della struttura deve essere in equilibrio con le azioni di contatto, sia essa una sezione della struttura o un nodo.

Metto quindi in equilibrio tutti i nodi:

Dal diagramma delle sollecitazioni si nota che alcune aste sono scariche e solamente una delle aste è tesa.

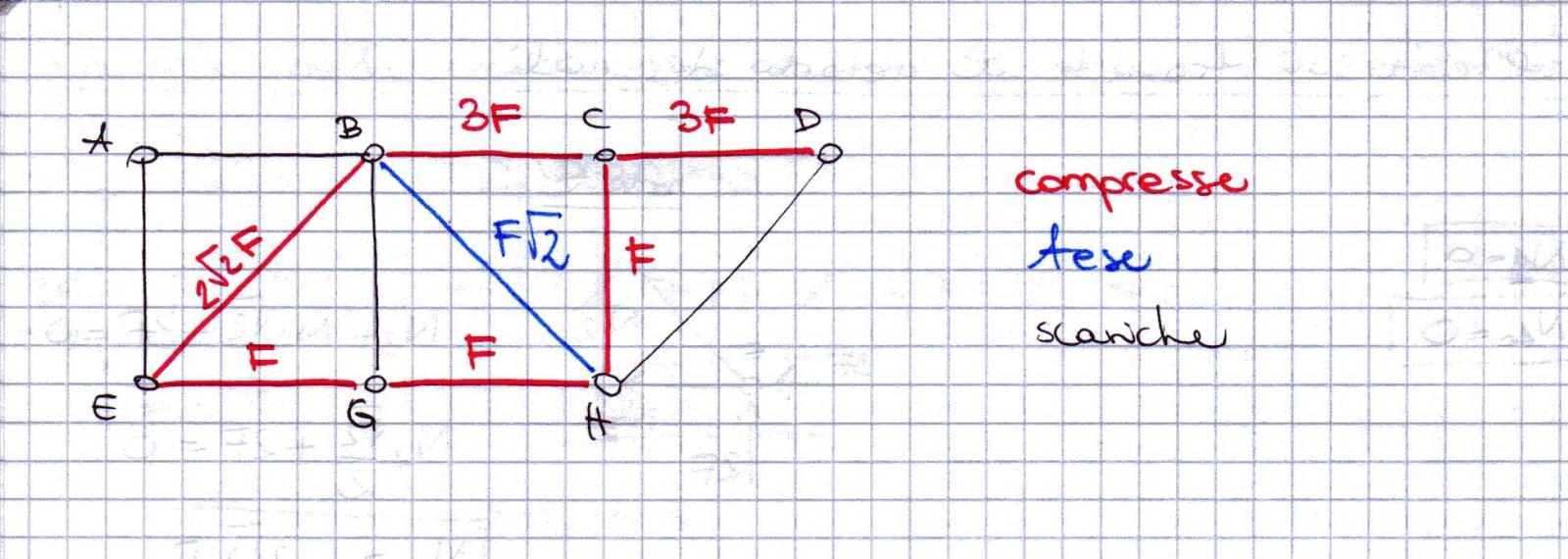
Verifico il risultato che ho trovato con il software SAP inserendo dati numerici:

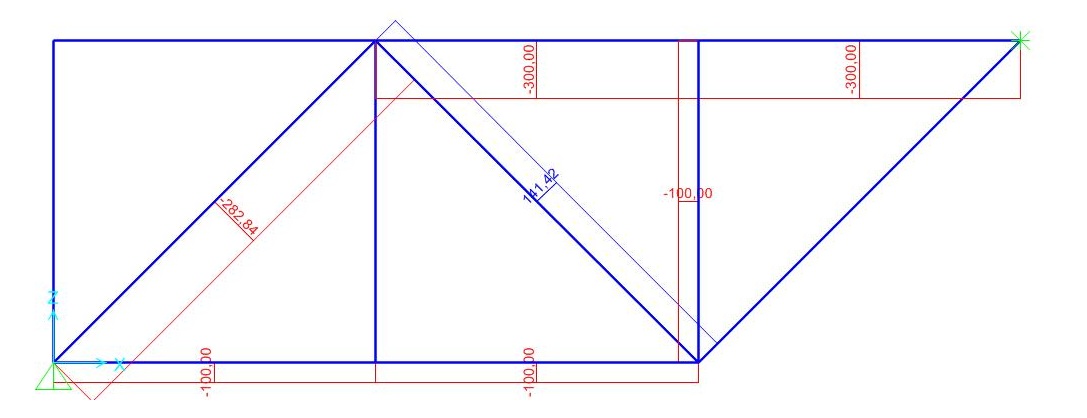
I risultati sono analoghi a quelli calcolati analiticamente.

ESERCIZI SUI TELAI PIANI

La serie di esercizi che riporto ha come obiettivo la risoluzione in maniera qualitativa delle azioni di contatto della struttura isostatica e il controllo tramite il software SAP2000 dei risultati ottenuti.

Esercizio 1 – arco a tre cerniere

REAZIONI VINCOLARI

Essendo la struttura simmetrica la cerniera interna (che interrompe la continuità) non può avere reazioni verticali diverse da 0 altrimenti sarebbe contraddittoria con la simmetria.

Il carico q distribuito su una luce 2l per equilibrio a traslazione verticale genererà due reazioni vincolari alle cerniere pari a ql verso l’alto.

La reazione e il carico creano una coppia di forze di braccio non nullo (il carico può essere pensato come una forza pari a ql con distanza l/2 dalla cerniera interna) e genereranno un momento ql²/2.

Per equilibrare questo momento la cerniera interna e la cerniera alla base reagiranno con delle forze orizzontali pari al momento fratto il loro braccio, quindi ql²/2h. Nello specifico la parte di sinistra genera una coppia antioraria e la parte di destra una coppia oraria.

SOLLECITAZIONI

Secondo le equazioni di equilibrio, il carico distribuito perpendicolarmente all’asse della trave è la derivata del taglio. Essendoci un carico uniforme, il taglio sarà quindi lineare.

Sappiamo che alla cerniera interna dovrà essere 0 (perché non trasmette reazioni verticali) mentre al nodo sarà ql. La funzione taglio è lineare e sulla parte sinistra negativa e destra positiva.

Nelle aste il taglio sarà costante (assenza di carico distribuito) e pari al valore della reazione orizzontale in cerniera, quindi ql²/2h.

Verifico con SAP il risultato:

Con l=6m, h=12m, q=10 kN/m.

Nota: pur non essendoci nessuna forza concentrata il taglio non è continuo in quanto il nodo tra trave e pilastro rappresenta una singolarità che fa scambiare i valori al taglio e alla normale.

Essendo il taglio sulla trave lineare il momento sarà parabolico. In particolare alla cerniera interna sarà nullo e al nodo sarà ql²/2. Il nodo non rappresenta una singolarità per il momento che non salta, seppur non derivabile in quel punto. Nei pilastri il taglio è costante, il momento sarà quindi lineare e varrà 0 in cerniera e sempre ql²/2 al nodo.

La normale sarà costante sia nel pilastro che nella trave (nessun carico orizzontale distribuito) e prenderà quindi i valori delle reazioni vincolari:

sul pilastro sarà ql (come la reazione verticale della cerniera alla base) e sulla trave sarà ql²/2h (come la reazione orizzontale della cerniera interna). Come preannunciato al nodo i valori di normale e taglio si scambiano

Esercizio 2

Come variante dell’esercizio precedente, il carico non viene distribuito sulle aste orizzontali ma sul pilastro.

REAZIONI VINCOLARI

La struttura non è simmetrica quindi nel punto B la cerniera interna trasmetterà anche reazione verticale.

Per trovare le reazioni vincolari faccio l’equilibrio dei momenti attorno alle due cerniere alla base:

∑M (A) = - qh²/2 + V_B l + O_B h = 0

∑M (C) = V_B l - O_B h = 0

Da queste ricavo che O_B =  ¼ qh     e      V_B = qh²/4l

Per equilibrio a traslazione orizzontale trovo O_A = qh – ¼ qh = ¾ qh

Per equilibrio a traslazione verticale trovoV_A = V_B = qh²/4l

Nella parte destra per equilibrio a traslazione trovo che V_C – V_B = 0 e O_C – O_B =0.

Quindi V_C = qh²/4l     e      O_C = ¼ qh.

Anche i momenti sono equilibrati in quanto la coppia ¼ qh ha braccio h e produce momento orario pari a ¼ qh²e la coppia qh²/4l ha braccio l e produce momento antiorario pari a ¼ qh².

SOLLECITAZIONI:

Non c’è nessun carico distribuito orizzontale, la normale sarà quindi sempre costante.

Nel pilastro di sinistra sarà pari a V_A, quindi  qh²/4l e sarà di trazione. Le aste orizzontali avranno normale pari a O_B, quindi  ¼ qh. Il pilastro destro avrà normale pari a qh²/4l dicompressione.

Con l=6m, h=12m, q=10 kN/m.

Il taglio avrà un andamento lineare nel pilastro di sinistra e costante nelle altri parti della struttura. Per conoscere i valori controllo quali sono le reazioni ai bordi (cerniere e nodi)

In A dovrà valere ¾ qh (negativo) mentre al nodo dovrà essere ¼ qh. Nelle aste orizzontali sarà costante pari a qh²/4l e nel pilastro di destra sarà ¼ qh (negativo)

Il momento avrà funzione parabolica nel pilastro a sinistra e lineare negli altri elementi e 0 nelle tre cerniere. Nel pilastro di sinistra il momento avrà tangenza nulla all’altezza di  ¾l dove si azzera il taglio. Nel pilastro di destra la funzione momento sarà lineare con valore al nodo di qh²/4. Per continuità anche sulle aste avrà valori alle estremità di qh²/4. Il momento massimo ¾h varrà 9/32 qh²

Esercizio 3

REAZIONI VINCOLARI

Procedo con il calcolo dei momenti nel punto A e C:

∑M (A) = -F h/2 – V_B l/2 + O_B h = 0

∑M (C) = - F h/2 – V_B l/2 – O_B h =0

Da cui      V_B = Fl/2h     e    O_B = 0

Per equilibrio a traslazione in A e in C ci saranno due forze orizzontali pari a F in direzione opposta alla forza applicata, e per equilibrio a traslazione verticale in A ci sarà una forza pari a Fl/2h verso il basso e in C una forza di pari intensità verso l’alto.

 

SOLLECITAZIONI

La normale sarà costante in tutti gli elementi data l’assenza di carico distribuito assialmente. Nei due pilastri sarà pari alla reazione verticale alla base, quindi Fl/2h e sarà di trazione al pilastro sinistro e compressione al pilastro destro. Dato l’assenza di reazione orizzontale alla cerniera interna la normale sulle aste orizzontali è nulla.

Con l=6m, h=12m, F=10 kN

Il taglio sarà sempre costante (data l’assenza di carico distribuito perpendicolare) ma avrà dei punti di salto dove sono applicate le forze concentrate. Alla base dei pilastri avrà valore pari a F data la reazione delle cerniere per poi a h/2 saltare di un valore pari a F data la forza applicata, diventando nullo nel tratto superiore prima del nodo. Nelle aste orizzontali avrà valore pari a Fl/2h, ovvero la reazione verticale in B ma anche la normale nei pilastri.

Il momento avrà andamento lineare dove è presente taglio e costante dove è assente. Nelle 3 cerniere dovrà essere 0. Quindi partendo da A dove è 0, sarà lineare fino a h/2 dove varrà Fh/2. Continuerà fino al nodo in maniera costante, per poi riprendere l’andamento lineare nelle aste orizzontali, dove varrà Fh/2 ai nodi e 0 in cerniera. Analogamente il pilastro di sinistra avrà momento Fh/2 costante nel tratto in alto e lineare fino alla cerniera dove varrà 0 e tenderà le fibre verso destra.

Esercizio 4

La struttura non è simmetrica dato il pilastro di sinistra lungo 2h mentre quello di destra è lungo h. La cerniera in B potrà quindi avere reazione verticale.

REAZIONI VINCOLARI

∑M (A) = O_B 2h – V_B l/2 – ql²/8 =0

∑M (C) = ql²/8 – V_B l/2 – O_B h = 0

Da cui      VB = ql/12   e    OB = ql²/12h

Per equilibrio alla traslazione verticale e orizzontale trovo le altre reazioni vincolari alle cerniere A e C:

V_A = 7/12 ql        O_A = ql²/12h       V_C = 5/12 ql            O_C=ql²/12h

SOLLECITAZIONI

Non essendoci carico distribuito orizzontale la normale sarà sempre costante.

In A varrà quanto la forza verticale V_A, quindi 7/12ql. Al nodo ci sarà un salto e prenderà il valore della forza orizzontale della cerniera interna, ql²/12h. Nell’ultimo tratto verticale prende il valore di V_C, quindi 5/12ql. In ogni tratto sarà di compressione.

Con l=6m, h=6m, q=10 kN/m

Il taglio sarà costante nei pilastri e lineare nelle travi orizzontali.

Partendo da A, nel pilastro avrà il valore della forza orizzontale O_A, quindi ql²/12h e sarà positivo. Al nodo ci sarà un salto e avrà valore negativo di 7/12 ql. La diagonale del diagramma non passa per la cerniera, dove avrà valore ql/12, e all’altro nodo varrà 5/12ql positivo. Nel pilastro a destra prenderà valore costante di intensità O_C, quindi ql²/12h, negativo.

Il momento avrà andamento lineare nei pilastri e quadratico sulla trave.

Nel pilastro di sinistra varrà 0 in A e al nodo varrà il valore del taglio ql²/12h per il braccio 2h quindi ql²/6.

Analogamente nel pilastro di destra sarà 0 in C e al nodo varrà ql²/12h per il braccio h quindi ql²/12.

Per continuità del nodo incastro la parabola che descrive il momento sarà asimmetrica e varrà ql²/6 al nodo di sinistra e ql²/12 al nodo di destra.

 

ESERCIZI SUL DIMENSIONAMENTO DELLE TRAVI DI UN SOLAIO:

Struttura scelta: trave con doppio appoggio.

Momento massimo: ql²/8 in mezzeria

Interasse: 4m

Luce: 6m

LEGNO:

Scelgo un solaio in legno a una orditura, dove il peso strutturale è rappresentato da trave, travetti e tavolato. Per scegliere una sezione di trave consona al solaio decido di fare una stima dei carichi ipotizzando che tutto il carico strutturale pesi 1 kN/mq

Carico Strutturale:

 1kN/mq (trave, travetti,tavolato) – provvisorio per calcolare una sezione tipo della trave lignea.

Carico Accidentale:

2kN/mq come da nuove norme tecniche per le costruzioni (DM 14 gennaio 2008, pubblicato sulla  Gazzetta Ufficiale n. 29 del 4 febbraio 2008 - Suppl. Ordinario n. 30) 

Carico Permanente:

pavimento: Gres Porcellanato

CARATTERISTICHE TECNICHE:

SPESSORE da 6,5 A 12 mm

PESO 20 kg/m²

REAZIONE AL FUOCO Classe 0 secondo DM 26.6.84

Fonte:http://www.itc.cnr.it/corsi/pavimenti/immagini/pavimento%20pdf/finiture.pdf

Materiale	Peso al mc	Spessore	Peso al mq
Massetto malta bastarda	19 kN/mc	0,06	1,14 kN/mq
Pavimento in gres porcellanato	25 kN/mc	0,008 m	0,20 kN/mq
Impianti			0,50 kN/mq
Incidenza tramezzi			1,00 kN/mq

 

Totale: 2,84 kN/mq

 

Peso del solaio:

1+2+2,84= 5,84 kN/mq

Ipotizzo la sezione della trave:

Stima del carico al metro lineare (interasse 4 m): 5,84 * 4 =23,36 kN/m

L’azienda fa basi di abete rosso (500 kg/mc) di cm 8 - 10 -12 - 14 -16 - 18 - 20 - 22 – 24

fonte: http://www.tecsol.it/prodotti_tecsol_travi_legno_lamellare.htm

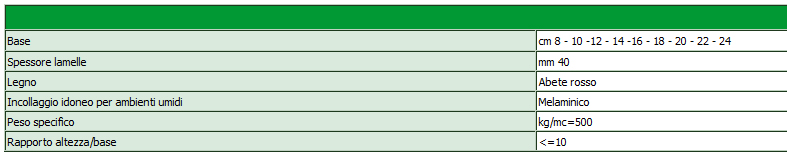
Scelgo una trave 24 x 45 cm

Area della sezione: 0.108 mq

Volume per 1m di trave: 0.108 mc/m

Peso di 1m di trave: 0.108 x 500 = 54 kg/m = 0,54 kN/m

In ogni mq ci sono 1/interasse travi, quindi 1/4 x 0.54 = 0.135 kN/mq -> incidenza delle travi sul peso a mq

Ipotizzo la sezione del travetto:

Interasse: 0.5m

Luce: 4m

Stima del Carico a metro lineare:  5,84 (peso del solaio) x 0.5 = 2,92  kN/m

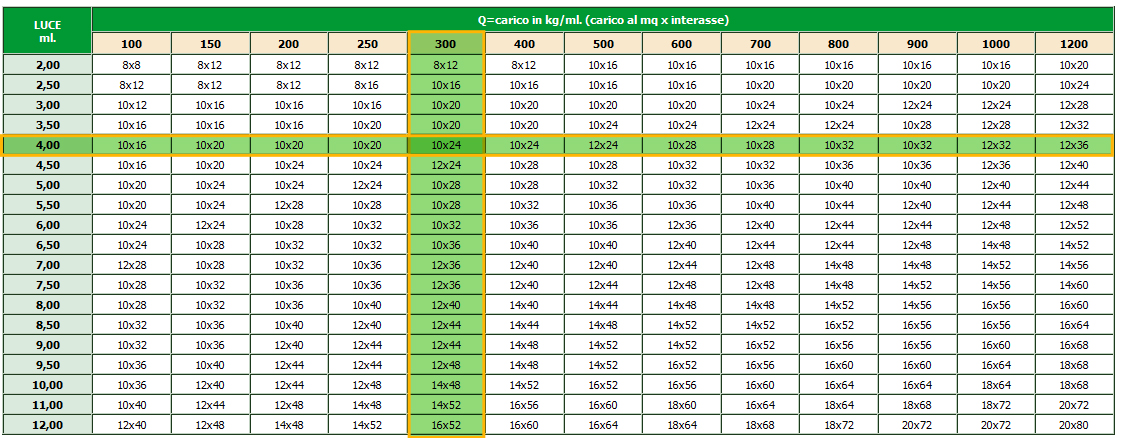
Dalle tabelle dell’azienda scelgo un travetto di: 10x24 cm

Volume di 1 m di travetto: 0.024 mc/m

Peso: 500*0.024 = 12kg/m = 0.12 kN/m

In ogni mq ci sono 1/0.5 travetti quindi 2* 0.12 = 0.24 kN/mq -> incidenza dei travetti sul peso a mq

Tavolato:

spessore: 0.03 m

Peso specifico: 500 kg/mc

Peso al mq: 500x0.03=15kg/mq = 0.15 kN/mq

 

Peso totale della struttura ipotizzata:  0.135 + 0.24 + 0.15 =0.525 kN/mq

 

Verifica trave:

Dopo aver calcolato l’effettivo qs della struttura ipotizzata, inserisco i dati in tabella verificando se le dimensioni sono corrette:

Altezza minima richiesta 40,26 cm. La trave che ho ipotizzato è 24 x 45, è quindi opportunamente dimensionata nel caso utilizzassi una classe del legno GL32h o GL36h. Per classi inferiori la trave non è opportunamente dimensionata.

Verifica travetto:

Il qs per la verifica del travetto non considera il peso proprio delle travi.

Altezza minima: 14,51 cm.

Il travetto ipotizzato è 10 x 24 e risulta essere sovradimensionato per classe di legno GL36h. Si può quindi utilizzare una classe di legno più bassa come la GL24h dove l’altezza minima richiesta diventa 17,78 cm.

n.b. : per il calcolo delle tensioni ammissibili sono stati introdotti i coefficienti di sicurezza delle Nuove Norme Tecniche per le Costruzioni dove gamma = 1,45 e Kmod = 0,6

ACCIAIO:

Ipotizzo un solaio a una orditura con travi e travetti di acciaio, lamiera grecata, soletta armata con rete elettrosaldata. Il solaio è controsoffittato.

Come per il legno ipotizzo un carico strutturale per fare un dimensionamento di massima delle travi, poi calcolo il carico strutturale del solaio ipotizzato e verifico se le sezioni scelte sono opportunamente dimensionate.

Stima dei carichi:

Carico Strutturale:

ipotizzo un Qs di 2 kN/mq

Carico Permanente:

Considero lo stesso solaio utilizzato nell’esempio precedente aggiungendo però la controsoffittatura:

Materiale	Peso al mc	Spessore	Peso al mq
Massetto malta bastarda	19 kN/mc	0,06 m	1,14 kN/mq
Pavimento in gres porcellanato	25 kN/mc	0,008 m	0,20 kN/mq
Impianti			0,50 kN/mq
Incidenza tramezzi			1,00 kN/mq
Controsoffitto	20 kN/mc	0,015 m	0,30 kN/mq

 

Totale: 3,14 kN/mq

Carico Accidentale:

2kN/mq come da nuove norme techine per le costruzioni (DM 14 gennaio 2008, pubblicato sulla  Gazzetta Ufficiale n. 29 del 4 febbraio 2008 - Suppl. Ordinario n. 30) 

Stima totale:

2+2+1,84= 7,14 kN/mq

Ipotizzo la sezione della trave:

luce 6m, interasse 4m

inserendo i dati per il dimensionamento di massima nel foglio excel il risultato è un Wx minimo di 574,24 cm3

scelgo un profilato Ipe330 (Wx=713,1 cm3)

fonte: http://www.oppo.it/tabelle/profilati_ipe.htm

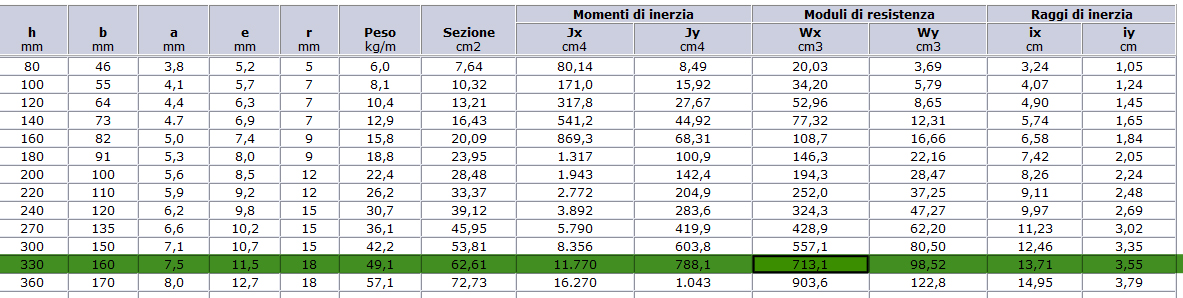
Ipotizzo la sezione del travetto:

luce 4m, interasse 2m

Per il dimensionamento del travetto serve un profilato con un Wx minimo di 127,61 cm3

scelgo un profilato Ipe180 (Wx=146,3 cm3)

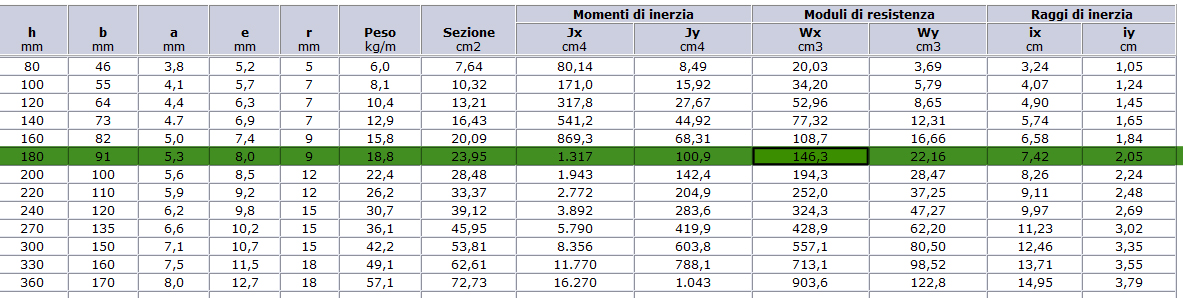
Calcolo del qs effettivo:

trave:

da tabella: 49,1 kg/m = 0,491 kN/m.

In un mq ci sono 1/interasse travi quindi ¼ x 0.49 1 = 0.123 kN/mq

Travetti:

da tabella: 18,8 kg/m = 0,188 kN/m

in un mq ci sono 1/interasse travetti quindi ½ x 0,188 = 0,094 kN/mq

lamiera grecata:

fonte: http://www.edilpanel.it/lamgrecate.htm

il carico sopra la lamiera è qa+qp = 2 + 3,14= 5,14 kN/mq = 514 kg/mq

scelgo la lamiera S/C 2000 spessore 1mm peso 11,94 kg/mq= 0,12 kN/mq

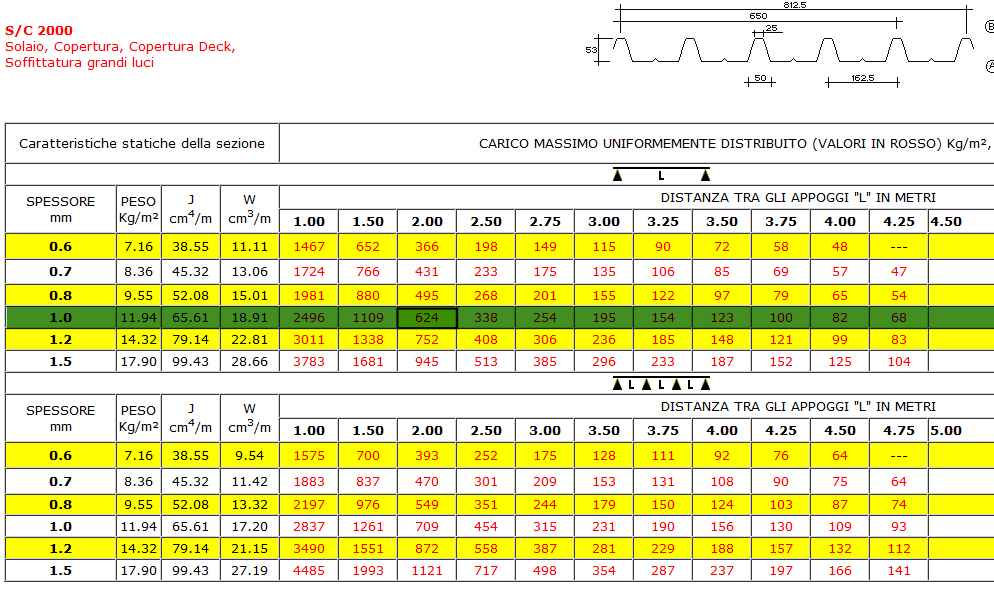
dalle tabelle dell’azienda scelgo una lamiera che si appoggia sui travetti, quindi distanza tra gli appoggi = 2m e spessore 1mm (così che il carico agente 514kg/mq sia inferiore di quello che la lamiera può sopportare 624kg/mq)

soletta armata:

cls:

peso circa 23kN/mc

spessore di progetto: 0,08m.

peso: 23 x 0.08 = 1,84 kN/mq

rete elettrosaldata:

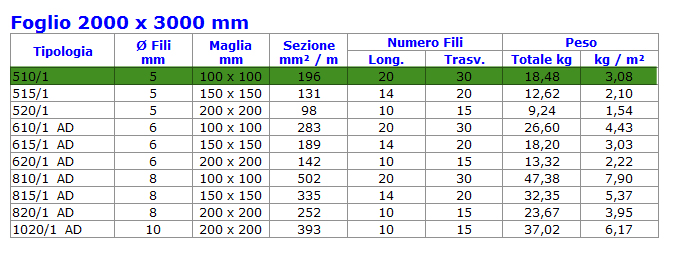
fonte: http://www.studiopetrillo.com/tabella-del-peso-rete-elettrosaldata-per-cemento-armato,70.html

tipo 510/1 peso al mq: 3,08 kg/mq = 0.03 kN/mq

 

calcolo del qs effettivo:

0,123 + 0,094 + 0,12 + 1,84 + 0,03 =2,2 kN/mq

Verifica del solaio con il qs effettivo:

Trave:

Wx minimo = 590,32 cm3

La IPE330 ipotizzata ha Wx = 713,1 cm3, quindi è verificata.

travetto:

NB: Il qs considerato per il travetto non tiene conto del peso proprio delle travi

Wx minimo = 128,86 cm3

La IPE180 ipotizzata ha Wx = 146,3 cm3 quindi è verificata.

CEMENTO ARMATO:

Ipotizzo un solaio composto da travi in cemento armato e travetti di 10 cm di base.

Il carico strutturale è quindi composto da travi, travetti, pignatte e getto di completamento. Non conoscendo le reali dimensioni necessarie per questi elementi, inizio un'analisi preliminare ipotizzando un Qs di 3 kN/mq

Carico Permanente:

Materiale	Peso al mc	Spessore	Peso al mq
Massetto malta bastarda	19 kN/mc	0,06	1,14 kN/mq
Pavimento in gres porcellanato	25 kN/mc	0,008 m	0,2 kN/mq
Intonaco			0,3 kN/mq
Tramezzi			1,0 kN/mq
Impianti			0,5 kN/mq   3,14 kN/mq

Carico Accidentale:

2kN/mq come da nuove norme techine per le costruzioni (DM 14 gennaio 2008, pubblicato sulla  Gazzetta Ufficiale n. 29 del 4 febbraio 2008 - Suppl. Ordinario n. 30) 

Stima totale:

3+2+3,14= 8,14 kN/mq

--------

Classe delle barre d’acciaio: B450C, la cui tensione di snervamento è 450 N/mmq.

Fonte: http://www.ferriere.pittini.it/schede_tecniche/BARRESPF201.pdf

 

Le Norme Tecniche per le costruzioni impongono una classe minima di C16/20 per strutture semplicemente armate. Per classi superiori a C45/55 c’è l’obbligo di una sperimentazione preventiva e la produzione deve seguire delle specifiche procedure per il controllo della qualità, scelgo quindi una classe intermedia C32/40 per cemento armato non precompresso.

Con questi dati procedo a un dimensionamento di massima delle travi del solaio:

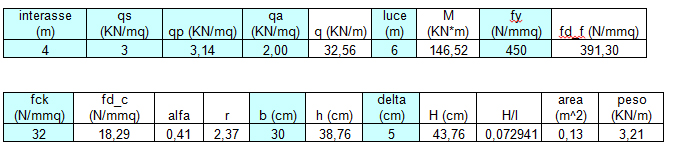
Una trave che può sostenere questo solaio (con Qs ipotizzato) ha sezione 30 x 50 cm (5 cm copriferro). Procedo ora al calcolo del Qs effettivo:

Trave:

calcestruzzo:  23 kN/mc

Volume della trave 30x50 = 0,15 mc/m

Peso: 0,15 x 23 = 3,45 kN/m

Incidenza a MQ: 3,45 / 4 (interasse) = 0,8625 kN/mq

Pignatte:

fonte: http://www.ilap.it/pignatte.htm

scelgo le pignatte SH16 (33 x 35 x 16) che hanno peso di 6,7 kg = 67 N.

In 1 metro ci sono (1/0,35)= 2,86 pignatte/m. Il peso al metro lineare è quindi 67 x 2,86 = 191,62 N/m = 0,19 kN/m

l’interasse delle pignatte è 33 cm (base pignatta) + 10 cm (base travetto) = 0,43 m

l’incidenza delle pignatte sul solaio è quindi: (1/0,43) x 0,19 = 0,442 kN/mq

travetti:

Volume: 0,16 x 0,1 = 0,016 mc/m

Peso al metro lineare: 23 x 0,016 = 0,368 kN/m

L’interasse dei travetti è lo stesso delle pignatte, quindi 0,43m.

L’incidenza al MQ è quindi: (1/0,43) * 0,368 =0,856 kN/mq

Getto di cls:

spessore di progetto:  4 cm.

Peso al MQ: 23 x 0,04 = 0,92 kN/mq

Qs effettivo:

0,8625 + 0,442 + 0,856 + 0,92 = 3,0805 kN/mq

Verifica della trave:

Dato il lieve incremento del valore di carico strutturale effettivo (3,08 kN/mq) rispetto a quello ipotizzato (3 kN/mq) il foglio di calcolo restituisce un valore di altezza utile minima di 38,95 cm. (solo qualche mm in più)

Sommando il copriferro (5 cm), l’altezza minima della trave è 43,95. La trave ipotizzata di 30 x 50 è quindi opportunamente dimensionata.

 

ESERCIZIO SUL DIMENSIONAMENTO DELLE ASTE TESE E COMPRESSE E VERIFICA A INSTABILITA':

L’esercitazione ha come obiettivo il calcolo della sezione di aste soggette solo a sforzo assiale disegnate tramite il software autoCAD, caricate tramite il software SAP che indica anche i valori di sforzo normale delle travi.

Parte 1 – disegno della struttura tridimensionale

Disegnare il modulo a partire dall’origine degli assi così da farla coincidere con quella di sap. Va fatto un layer apposito per le aste in quanto il layer0 di default di autocad non viene letto da sap.

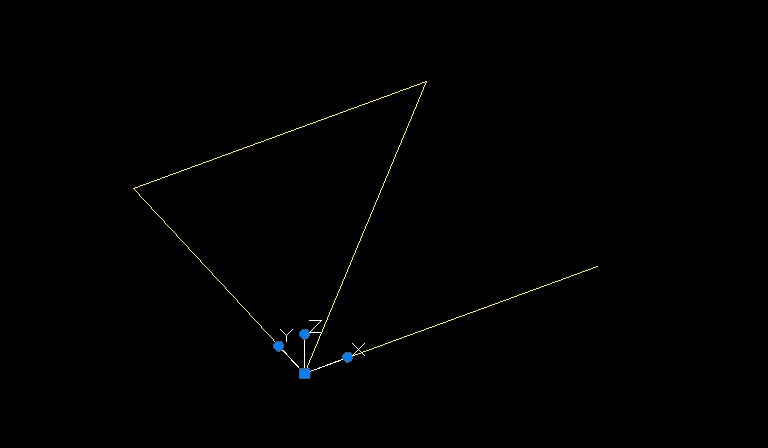
Usare il comando “serie rettangolare” di autocad per copiare il modulo creato.

Nb – la versione 2012 di autocad non apre la finestra di dialogo ma i dati (numero di copie, distanze ecc.) vanno inserite dal prompt dei comandi

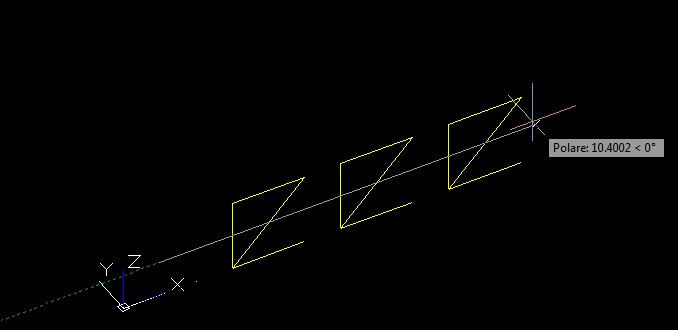
Una volta creata la successione lineare vanno disegnate le aste lungo l’altro asse perpendicolare (nel mio caso l’asse Y) e il modulo 3D va quindi copiato sempre con il comando Serie Rettangolare in modo da creare tutta la struttura. è importante evitare che ci siano sovrapposizioni tra aste, inoltre ogni singola asta deve essere rappresentata da una linea, quindi nel caso (come di autoCAD 2012 che con il comando serie crea dei blocchi) di polilinee o blocchi, basta selezionare tutto il modello e usare il comando Esplodi.

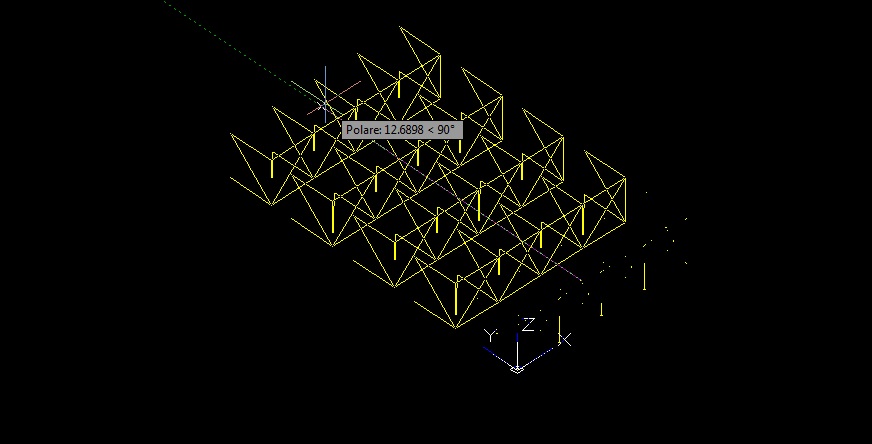
Il file va salvato da autoCAD in formato .dxf, così da poter essere aperto con SAP.

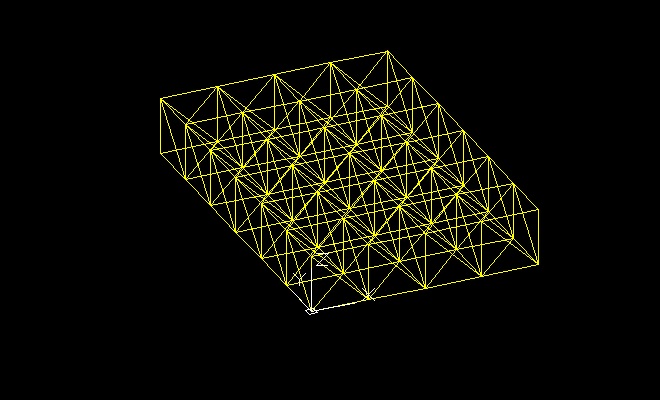
Parte 2 – Analisi su SAP

Una volta importato il modello e scelte le unità di misura, va comunicato a sap che il layer “aste” (o qualsiasi sia il nome dato su autoCAD) debba essere letto come FRAMES.

Si procede quindi a impostare i vincoli (4 cerniere ai 4 angoli della struttura), scaricare le aste a momento per imporre le cerniere interne a tutti i nodi e a caricare la struttura tramite una forza negativa (verso l’asse gravitazionale) di 40kN su ogni nodo superiore.

Riporto l’analisi di sap della deformata:

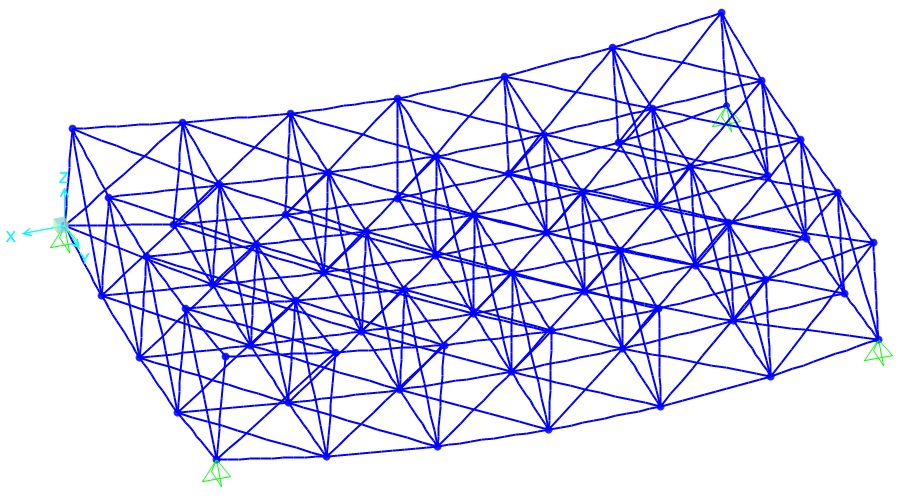
Parte 3 – Analisi degli sforzi normali

L’obiettivo è quello di progettare le sezioni delle aste più sollecitate a sforzo normale.

Per progettare l’asta a trazione basterà prendere il valore della normale più alto e fare un progetto a resistenza del materiale tramite la formula di Navier.

Per progettare a compressione si dovranno controllare gli sforzi normali massimi sia nelle aste corte (lungo gli assi principali) che quelle oblique. Questo perché va fatta la verifica a instabilità euleriana, dove viene calcolato il carico di punta massimo che l’asta compressa può sopportare prima di sbandare, chiamato Pcritico che dipendedalla lunghezza libera di inflessione che è diversa a nell’asta lunga e nell’asta corta.

Per avere chiaro quali sono gli sforzi agenti sulla mia struttura esporto da sap una tabella excel con i dati relativi agli sforzi assiali, e tramite quest’ultimo ordino le righe secondo sforzi assiali decrescenti.

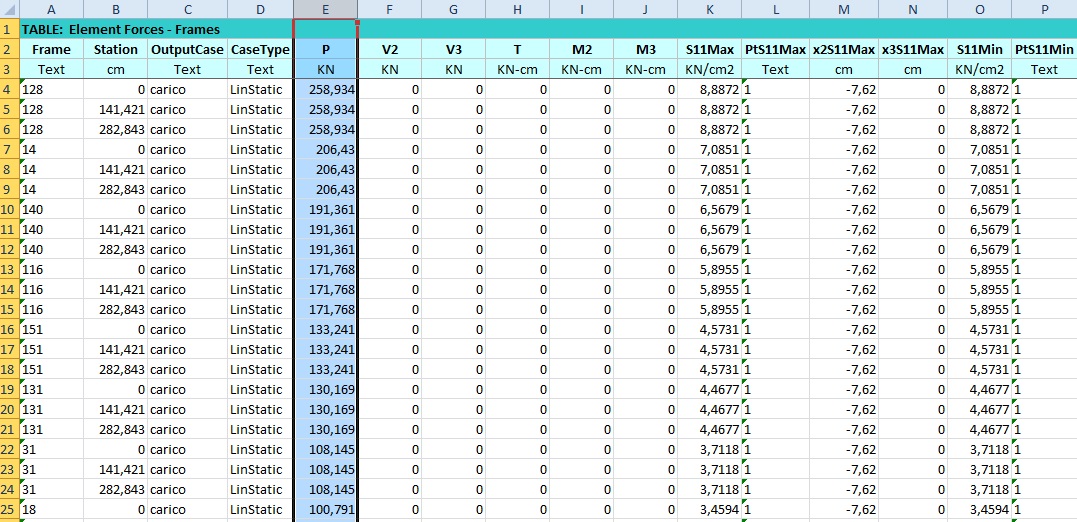
Per la lettura della tabella va considerato che sap restituisce il valore normale all’inizio dell’asta, in mezzeria e alla fine, quindi vanno lette tre righe alla volta. Per esempio l’asta più tesa (che si vede dall’immagine) è un’asta obliqua ( infatti la sua lunghezza è 2 √2 ovvero la lunghezza impostata precedentemente da autoCAD (le aste corte sono lunghe 2m)) che ha sforzo normale di 258,934 kN.

Riporto una tabella con i valori di sforzo assiale massimi trovati da excel:

Parte 5 – progetto dell’asta a trazione

L’asta a trazione non ha bisogno di una verifica a instabilità euleriana quindi il progetto (o la verifica) può essere eseguito tramite la formula di Navier per calcolare l’area minima necessaria.

A = N/Fd

Dove A è l’area minima che mi servirà per scegliere la sezione della trave, N è lo sforzo normale calcolato con SAP e Fd è la resistenza del materiale calcolata dalla tensione di snervamento (Fy) ridotta da un coefficiente di sicurezza (γm=1,05)

Tramite un foglio Excel calcolo le varie aree minime necessarie per sopportare la sollecitazione. Non sapendo che tipo di acciaio mi è più utile, calcolo l’area minima per tutte e tre le classi di resistenza Fe360S235, Fe430S275 e Fe510S355.

La N è uguale a258,934 kN come da tabella precedente

Secondo le tabelle dei profilati tubolari:

fonte: http://www.oppo.it/tabelle/profilati-tubi-circ.htm

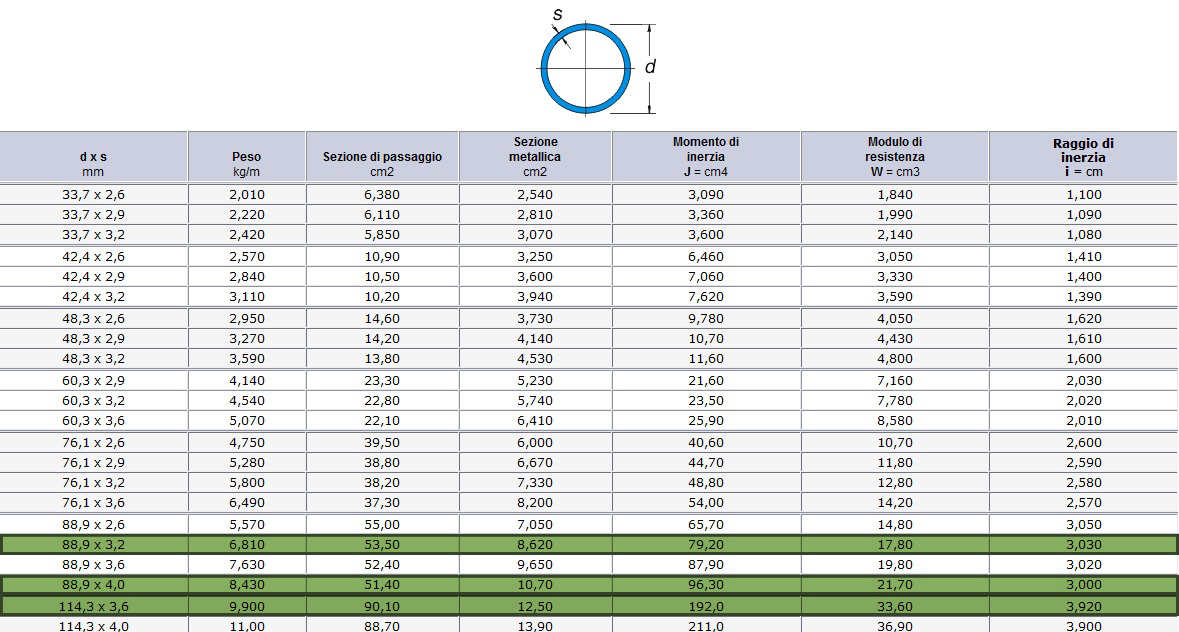
Progetto dell’asta:

Parte 6 – progetto dell’asta corta a compressione

Per le aste compresse non è sufficiente progettare a resistenza del materiale, ma va verificato che il carico critico assiale che l’asta può sopportare sia superiore del carico agente.

Per far ciò, prima progetto l’asta a compressione con N = -296,771 kN

Sempre seguendo la tabella dei tubolari:

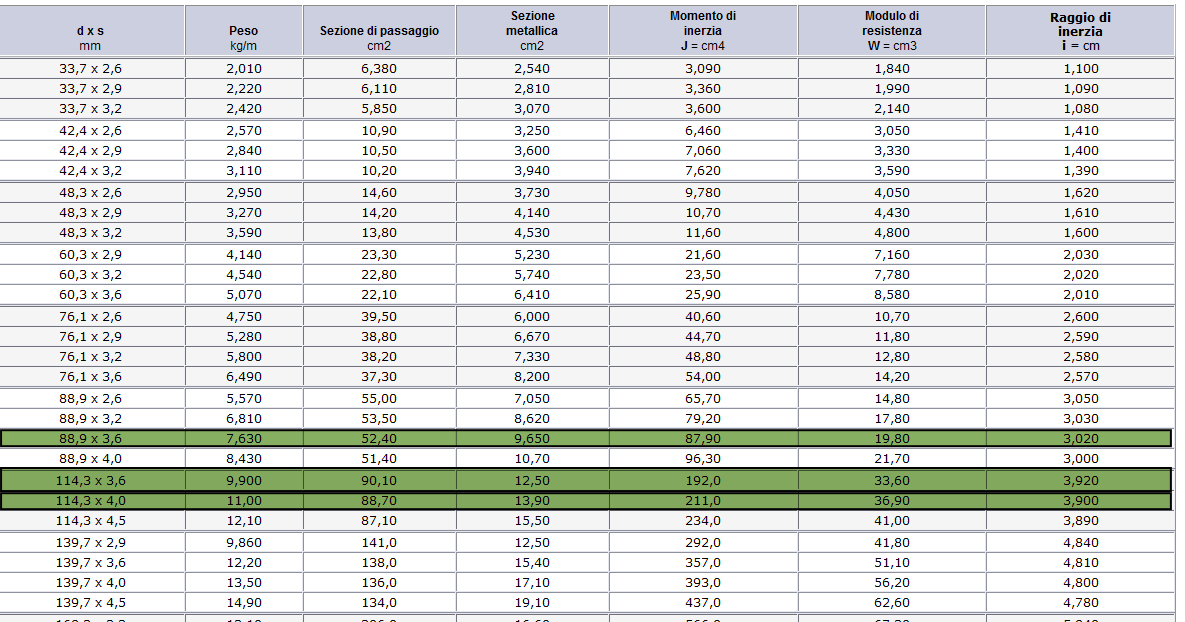
Applicando la formula del carico euleriano verifico per ogni sezione se è in grado di sopportare lo sforzo assiale a cui è sottoposta.

Pcrit = (π² x E x J_min)/l₀²

 A seconda della classe di resistenza della sezione, anche il modulo di Young E è diverso

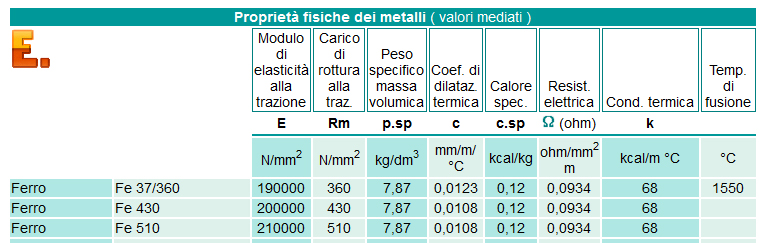
Fonte: http://www.engineerplant.it/tab_metalprop.htm

Essendo tutte le aste doppiamente incernierate la lunghezza libera di inflessione l₀ coincide con la lunghezza effettiva dell’asta.

Avendo scelto una sezione tubolare il momento d'inerzia J è uguale per entrambi gli assi, infatti nelle tabelle ne compare uno solo.

 

Con un foglio excel calcolo il carico critico per ogni sezione e verifico che la normale agente 296,771 kN è minore in tutti e tre i casi, quindi tutte e tre sono plausibili sezioni opportunamente dimensionate.

OSSERVAZIONE il carico critico calcolato utilizzando la classe più resistente è molto minore degli altri 2, in quanto aumentando la classe diminuisce l’area della sezione e quindi il momento d’inerzia, snellendo l’asta.

Parte 7 – progetto dell’asta lunga a compressione

Sforzo assiale agente: -307,254 kN

Come nel caso precedente, calcolo l’area minima con la formula di Navier:

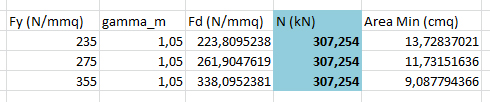
Consultando quindi le tabelle dei profilati:

NB: i risultati sono analoghi a quelli delle aste corte, dato che l’area minima necessaria è piuttosto simile visto che il valore della normale che ha poca variazione. Ho scelto comunque una sezione più grande per l’asta a classe di resistenza minore perché l’area della sezione minima (13,73 cmq) era troppo vicina a quella della sezione precedente di progetto (13,90 cmq)

Passo ora alla verifica a instabilità:

ATTENZIONE!!! L’asta progettata a classe di resistenza Fe510S355 è troppo snella ed è INSTABILE. È opportuno quindi nel caso si voglia utilizzare questa classe di resistenza scegliere una sezione diversa con un momento d’inerzia maggiore

Le altre due aste sono invece opportunamente dimensionate.

 

ESERCIZIO SUL CALCOLO DELLA RIPARTIZIONE DELLE FORZE SISMICHE

(esercizio svolto con Emanuel Dad Khan e Sara Forlani)

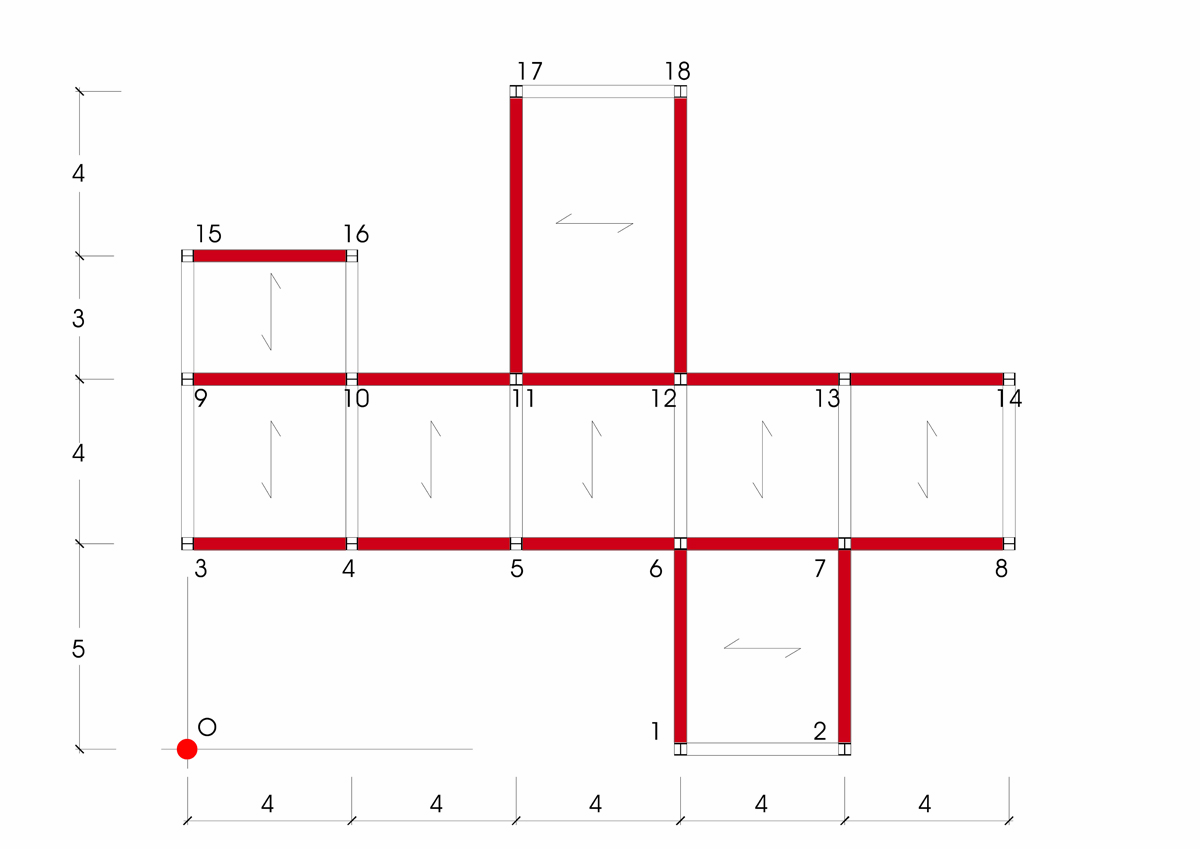
L’esercitazione ha come obiettivo quello di calcolare come la forza sismica si ripartisce nei controventi di questo impalcato.

Ipotizzo che la tecnologia costruttiva dell’impalcato sia la stessa (acciaio) e i pilastri siano HEB120.  

Questi ultimi sono opportunamente orientati per avere il momento d’inerzia maggiore in asse con la trave portante con luce maggiore che sarà quindi più sollecitata a momento flettente. Considero trave e pilastri incastrati, quindi per continuità del momento anche i pilastri saranno soggetti allo stesso momento flettente della trave (al nodo).

STEP1 – calcolo delle rigidezze traslanti dei controventi dell’edificio.

Calcolo la rigidezza traslante di ciascun controvento considerando la formula:

K_t =  12 E (∑I ) / h³

Dove E è il modulo di Young dell’acciaio (210.000 N/mmq), h è l’altezza dei pilastri (3,2 m) e I sono i momenti d’inerzia di tutti i pilastri.

Avendo orientato i pilastri secondo la loro necessità di resistenza a momento flettente  trasferito dalla trave, in ogni controvento bisognerà prendere in considerazione il momento d’inerzia riferito all’asse del controvento. Per esempio nel controvento 3 -4-5-6-7-8 avremo diversi momenti d’inerzia così disposti:

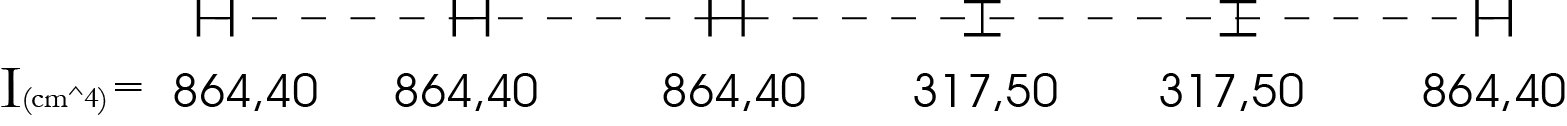
Calcolo così tutte le rigidezze di tutti i controventi orizzontali e verticali:

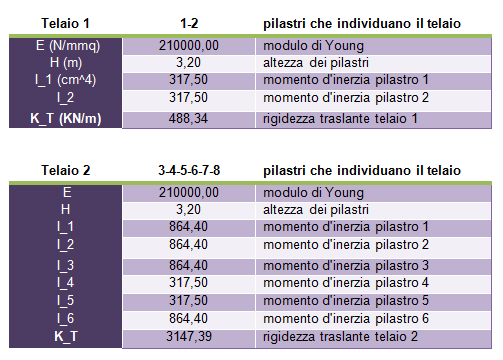
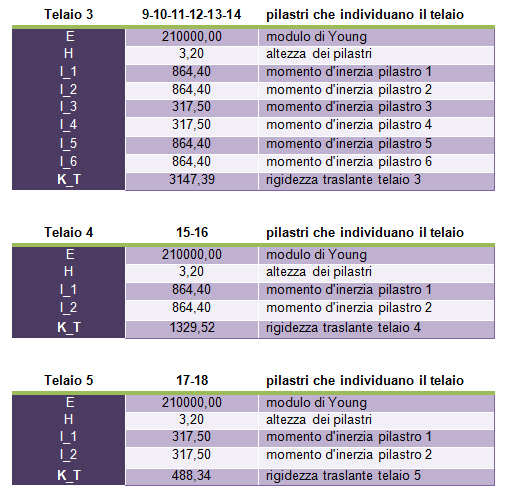
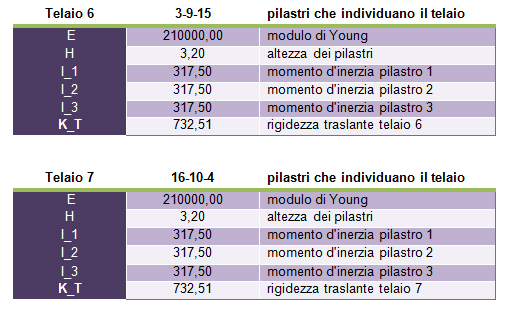
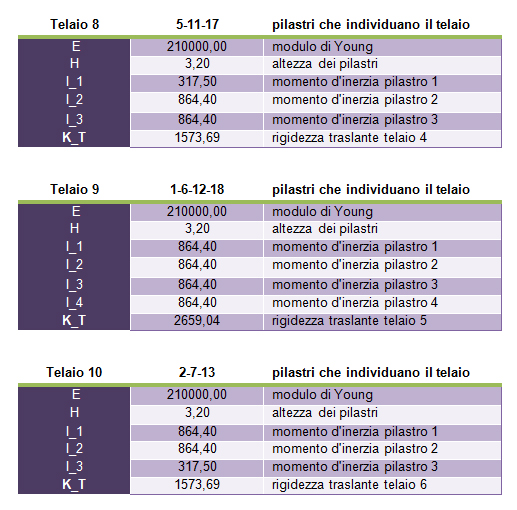
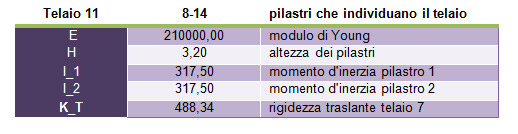
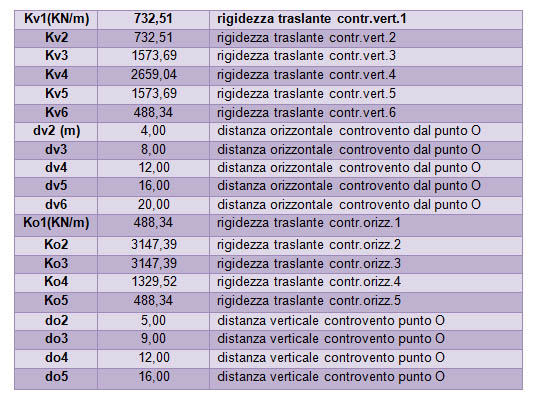
STEP 2 – tabella sinottica dei controventi e distanze

Scelgo un sistema di riferimento che ha origine nel punto O (segnato nella pianta dell’impalcato).

In questa tabella vengono riportate tutte le rigidezze traslanti dei vari controventi e ad ognuna viene attribuita una distanza dall’origine.  Questi dati serviranno successivamente per il calcolo del centro delle rigidezze.

STEP 3 – Calcolo del centro di massa

Il calcolo del centro di massa è fondamentale in quanto la forza sismica si identifica come una forza concentrata applicata a questo punto. Più il centro di massa e il centro delle rigidezze sono distanti tra loro (avendo quindi un maggiore braccio) più l’impalcato tende a ruotare nel caso di un evento sismico.

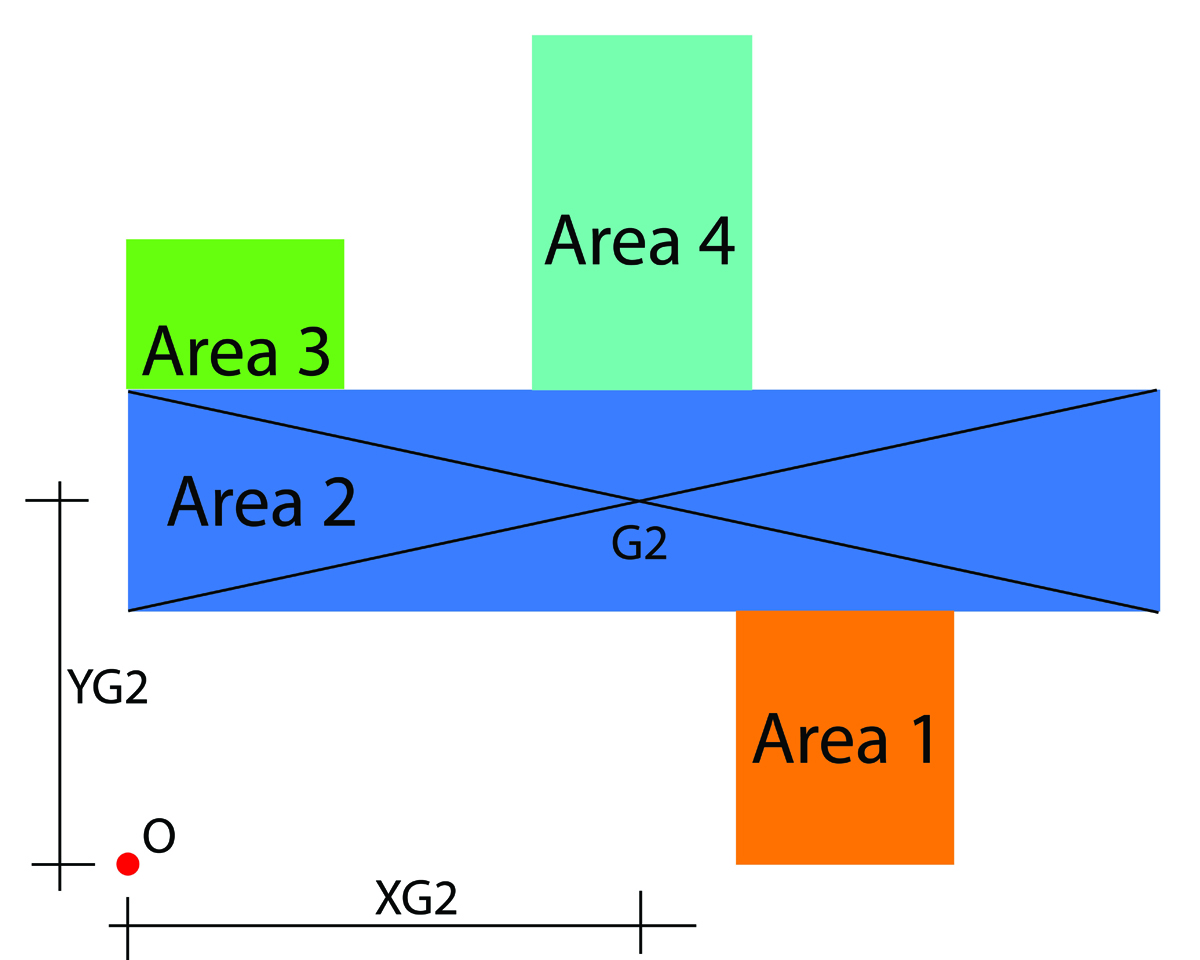
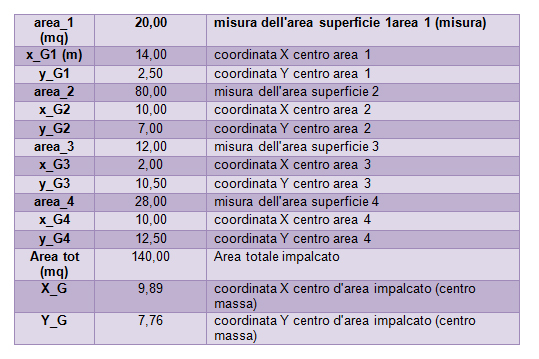
Il centro di massa è il centro delle aree dell’impalcato. Va quindi considerato quest’ultimo diviso in aree rettangolari (aventi proprio centro di massa all’incrocio delle diagonali) e calcolato il centro delle aree con questa formula:

X_G= ∑A_i X_Gi / ∑ A_i

Y_G= ∑A_i Y_Gi / ∑ A_i

STEP 4 – Calcolo del centro delle rigidezze e rigidezze globali

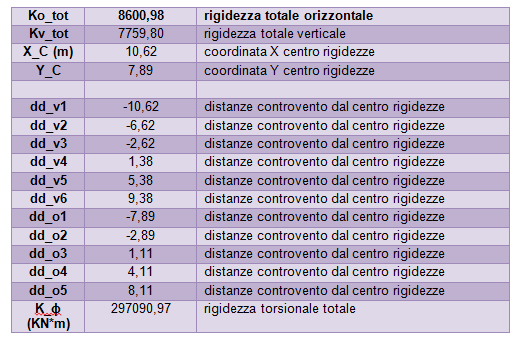
Analogamente al calcolo del centro di massa si procede al calcolo del centro delle rigidezze considerando tutti i controventi e la loro distanza dal centro di riferimento O iniziale:

X_c= ∑k_vi d_vi / ∑ k_vi

Y_c= ∑k_oi d_oi / ∑ k_oi

Trovato il centro delle rigidezze posso calcolare la distanza dei controventi da quest’ultimo.

dd_vi = d_vi - X_c

dd_oi = d_oi - Y_c

Calcolo la rigidezza torsionale totale che è la sommatoria delle rigidezze moltiplicate per la loro distanza al quadrato dal centro delle rigidezze (dd)

K_ϕ= Σ_iK_idd_i²

STEP 5 – Analisi dei carichi sismici

Per la seconda legge di Newton la forza è data da una massa a cui è impressa un’accelerazione.

Quindi per la forza sismica si avrà:

Forza sismica = Massa edificio x accelerazione per effetto del moto di trascinamento.

Questa accelerazione è minore della forza di gravità g (9,81 m/s²) che è ridotta da un coefficiente c chiamato coefficiente di intensità sismica. Maggiore è c più il sisma è di grande entità.

Quindi l’accelerazione può essere definita come

a = c g

Sostituendo alla formula precedente:

F_sismica = c g m

Dove massa per accelerazione gravitazionale è proprio il peso della struttura

F_sismica = c P

Da cui se ne deduce che strutture pesanti sono più vulnerabili al sisma in quanto la forza impressa sarà maggiore.

Va quindi calcolato il Peso sismico della struttra (W) che si ricava:

W = G + yQ

Dove G sono i carichi permanenti e strutturali, Q sono i carichi accidentati e y è un coefficiente di contemporaneità.  I carichi G e Q sono espressi in KN, vanno quindi moltiplicati i carichi distribuiti qs, qp e qa (espressi in kN/mq) per l’area totale dell’impalcato.

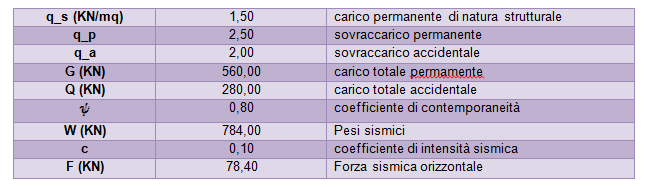
STEP 6 – ripartizione forza sismica lungo X

La forza sismica ha una natura aleatoria, non sappiamo quindi quale sia la direzione secondo cui viene applicata. Da normativa vanno verificate almeno due direzioni e per ognuna di queste intervengono sia i controventi disposti nella stessa direzione della forza, sia quelli disposti ortogonalmente, in quanto la forza sismica provoca torsione all’impalcato (se non passa per il centro delle rigidezze) e per contrastarla anche i controventi ortogonali avranno una reazione.

Ipotizziamo la forza sismica applicata in direzione orizzontale. (lungo X)

Susciterà quindi una traslazione orizzontale:

U₀ = F / K_{o tot}

e una rotazione rigida dell’impalcato:

ϕ  = F b / K_ϕ

 

ognuno dei controventi orizzontali avrà una reazione:

R_oi = K_io ( U₀ + ϕ dd_oi)

Essendo la forza sismica orizzontale, ai controventi verticali non compare il contributo dovuto alla traslazione dell’impalcato ma solamente il contributo per contrastare la torsione di questo:

R_vi = K_vi ϕ dd_vi

Dove K è la rigidezza del controvento, U₀ è la traslazione dell’impalcato dovuta alla forza sismica, ϕ è la rotazione dell’impalcato dovuta alla forza sismica e dd è la distanza del controvento dal centro delle rigidezze.

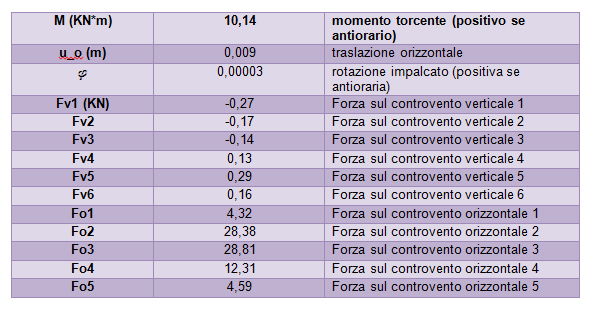
STEP 7 – ripartizione forza sismica lungo Y

Analogamente alla direzione orizzontale, procedo al calcolo della ripartizione delle forze sismiche nel caso la forza sia lungo Y.

Nonostante la forza abbia la stessa intensità sia traslazione che rotazione sono diverse in quanto la rigidezza traslante totale verticale è diversa da quella orizzontale e il braccio del centro di massa e il centro delle rigidezze è diverso nelle due direzioni, andando a generare momenti torcenti differenti.

Anche in questo caso nel calcolo delle reazioni dei controventi nella direzione parallela alla forza sismica si considera sia il contributo a spostamento che quello a rotazione mentre per i controventi in direzione X si considera solo il contributo a rotazione.

  

ES.1 STRUTTURA RETICOLARE SIMMETRICA_METODO DELLE SEZIONI DI RITTER

Per la risoluzione di questa struttura reticolare mi sono servita del metodo delle sezioni di Ritter al fine di calcolare gli sforzi normali ai quali sono sottoposte le aste. Per prima cosa bisogna verificare che la struttura sia esternamente ISOSTATICA (numero dei gradi di libertà deve essere uguale al numero dei gradi di vincolo).

Una volta verificata la condizione di isostaticità della struttura, posso calcolare le REAZIONI VINCOLARI tramite le EQUAZIONI DI BILANCIO (equilibrio esterno).

Uso il METODO DELLE SEZIONI DI RITTER per calcolare le AZIONI DI CONTATTO. Quando seziono le aste, metto in evidenza gli sforzi normali e faccio un ipotesi a priori sostenendo che siano tutte tese. Applico l'equilibrio alla rotazione prendendo come poli i punti dove si incontrano tutte le aste tranne una. Se il segno dello sforzo normale che ho calcolato è negativo, allora l'asta è compressa e dovrò cambiarle il verso.

Sfruttando la simmetricità della struttura e delle forze applicate su di essa si può risolvere metà della struttura in quanto gli sforzi normali saranno anch'essi simmetrici.

Il diagramma di sollecitazione mostra i correnti superiori compressi e quelli inferiori tesi. (tipico delle STRUTTURE RETICOLARI APPOGGIATE).

 

 

ES.2 STRUTTURA RETICOLARE ASIMMETRICA_METODO DEI NODI

Dopo aver verificato l'isostaticità della struttura e calcolato le reazioni vincolari, calcolo le azioni di contatto delle forze normali alle quali è sottoposta ogni asta.

Come per il metodo delle sezioni, anche per quello dei nodi bisogna fare un'ipotesi sul comportamento delle aste (tese o compresse). Di seguito sono riportati alcuni esempi:

- nel nodo A abbiamo il caso in cui entrambe le aste sono scariche.

- nel nodo E ipotizzo che l'asta 9 sia un puntone. Facendo l'equilibrio alla traslazione verticale si ottiene che N9=F. Dato che il segno della normale risulta positivo, allora l'ipotesi iniziale è corretta.

- viceversa nel nodo B, l'ipotesi che l'asta 2 sia un tirante è errata e ciò perché il segno della normale risulta essere negativo.

Di seguito è riportata l'analisi globale delle sollecitazioni a cui sono sottoposte le aste e la verifica fatta con SAP2000 applicando alle forze dei valori numerici.

 

__________________________________________________________________

 

 

 

DIMENSIONAMENTO TRAVI (LEGNO, ACCIAIO E CLS ARMATO)

PROGETTO DI UNA TRAVE DI UN IMPALCATO DI UN HOTEL

TRAVE:     Area di influenza= 32,60 mq    |    Interasse= 4m    |     Luce= 8m

Per prima cosa risolvo la struttura isostatica per ricavare la formula del momento che andrò ad inserire nel foglio excel per il dimensionamento di massima della trave.

qp=2,65KN/mq

 Valori presi dalle schede tecniche delle aziende (http://www.artechint.com/prezziario/solai.html) e dalle Nuove Norme Tecniche per le Costruzioni.

- carichi accidentali qa legati alla  funzione dell'edificio, trai quali i carichi variabili e quelli di natura aleatoria (es. neve, sisma). Si deve fare riferimento alleNuove Norme Tecniche per le Costruzioni (DM 14 gennaio 2008, pubblicato sulla  Gazzetta Ufficiale n. 29 del 4 febbraio 2008- Suppl. Ordinario n. 30).

qa: 2KN/mq

PROGETTO DI UNA TRAVE IN LEGNO

Solaio in legno a doppia orditura, composto da travi (interasse di 4 m), travetti (interasse 0,50 m), tavolato, massetto con relativi impianti e pavimentazione in parquet. Si vuole progettare una delle travi portanti di tale solaio.

Una volta ottenuto il carico a metro lineare ipotetico (22,56 KN/m) vado a consultare le tabelle utili per i dimensionamenti di travi e travetti dell'azienda Tecsol.  http://www.tecsol.it/prodotti_tecsol_travi_legno_lamellare.htm.