blog di tommaso.passerini

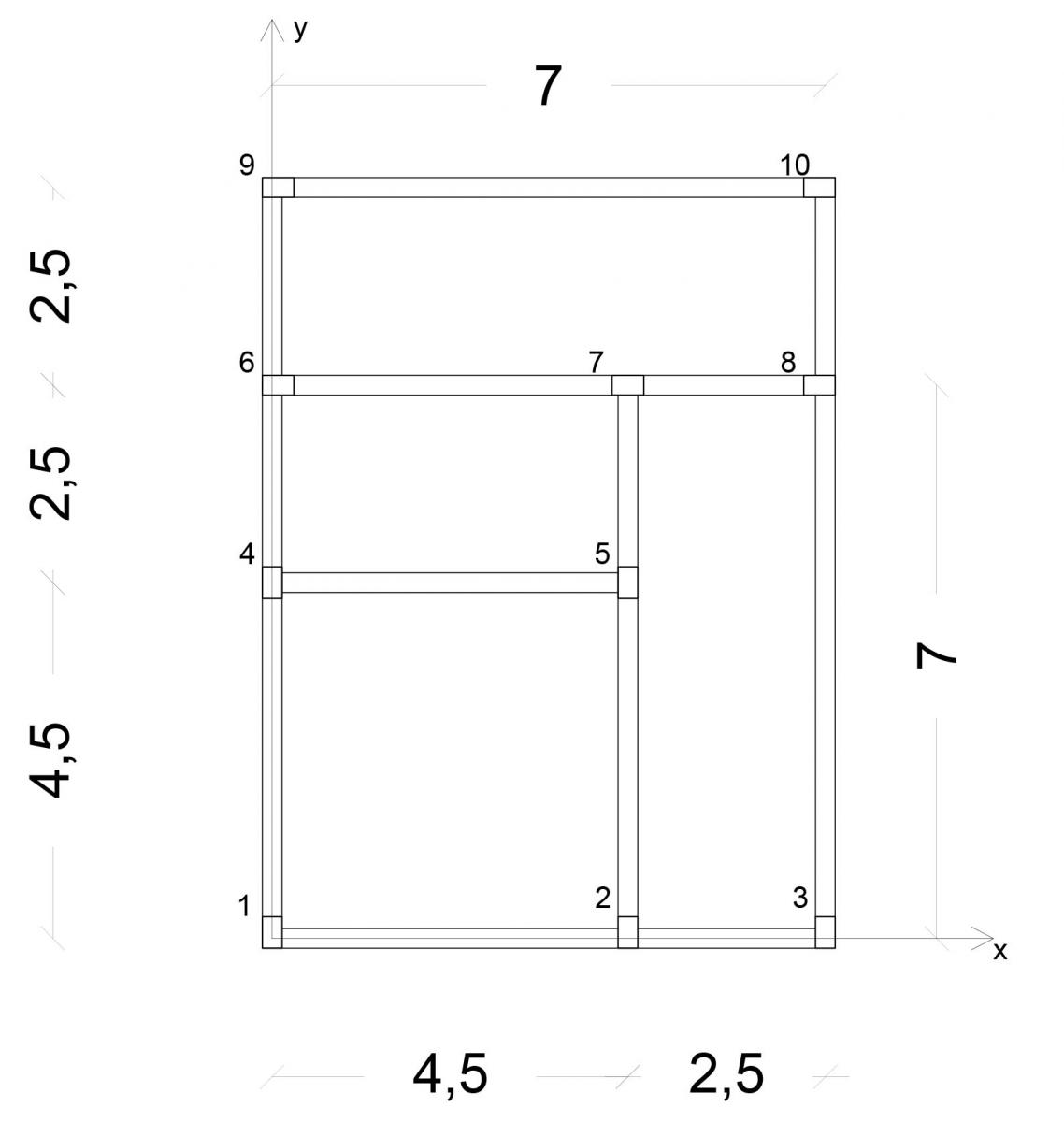
Questa esercitazione consiste nel calcolare come viene riparita una forza orizzontale (data dal vento o dal sisma) in un implacato. Vedremo quindi anche la modalità con il quale colare il centro d’area ed il centro delle rigidezze.

 L’impalcato analizzato è di un generico edificio di un solo piano costituito da telai piani in cls armato con tipologia di controventi modello shear-type : i telai Shear-Type sono un modello teorico che hanno la capacità di possedere travi infinitamente rigide, questo fa si che le estremità dei pilastri non possono ruotare. La rotazione impedita porta a deformare i pilastri stessi come travi doppiamente incastrate. In questo caso la deformata si avvicina alla deformata di una trave deformabile per solo taglio.

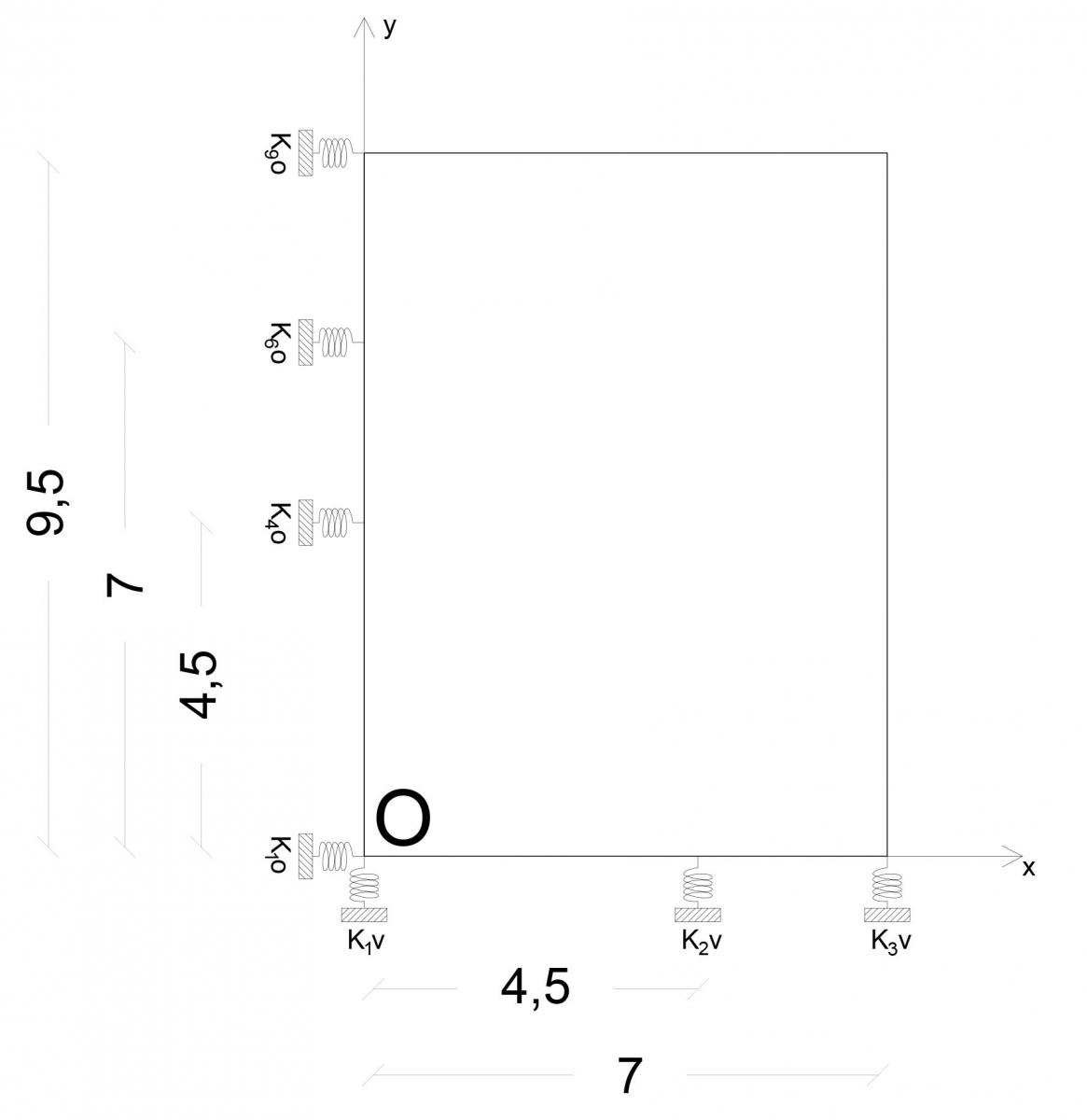
Poniamo l’impalcato in un piano cartesiano che ha come origine il punto più in basso a sinistra ed notiamo l’esistenza di 3 telai verticali, ovvero paralleli all’asse y, e 4 orizzontali, cioè paralleli allesse x :

Telaio 1v composto da: Pilastri 1, 4, 6, 9

Telaio 2v composto da: Pilastri 2, 5, 7

Telaio 3v composto da: Pilastri 3, 8, 10

Telaio 1o composto da: Pilastri 1, 2, 3

Telaio 2o composto da: Pilastri 4, 5

Telaio 3o composto da: Pilastri 6, 7, 8

Telaio 4o composto da: Pilastri 9, 10

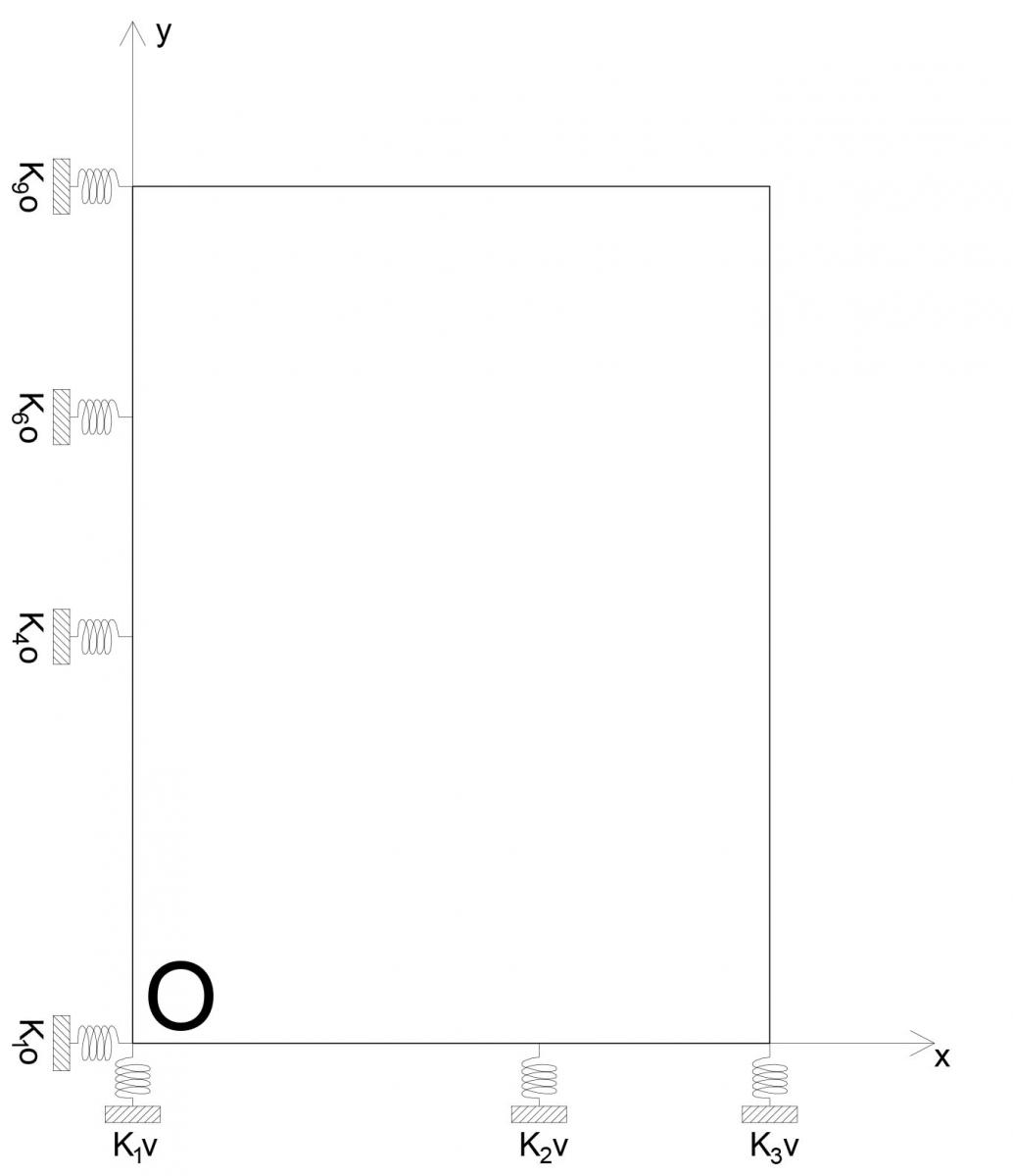
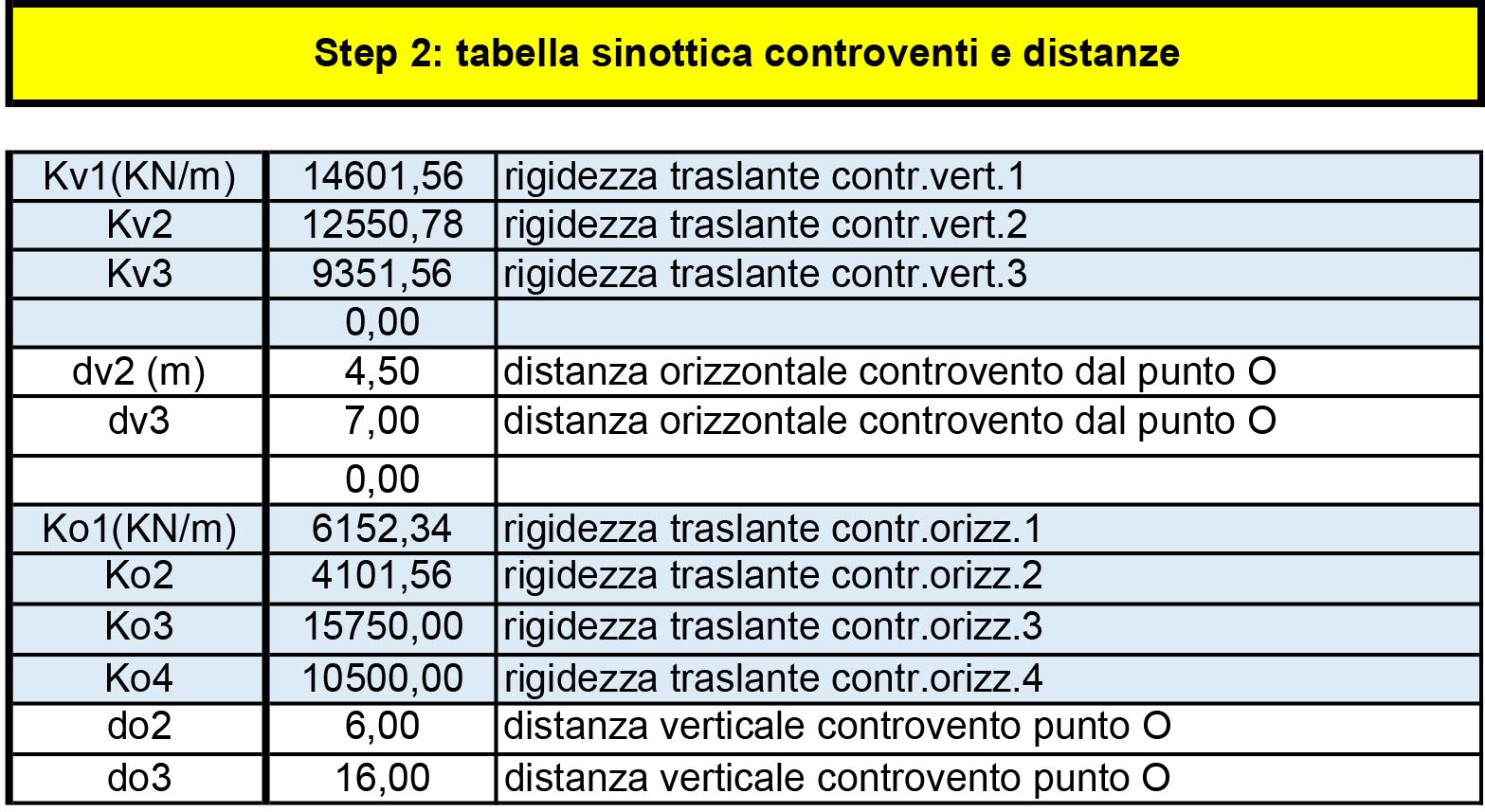
I controventi saranno rappresentati come molle, aventi la loro adeguata rigidezza, essendo possibili vincoli cedevoli elasticamente dell’impalcato.

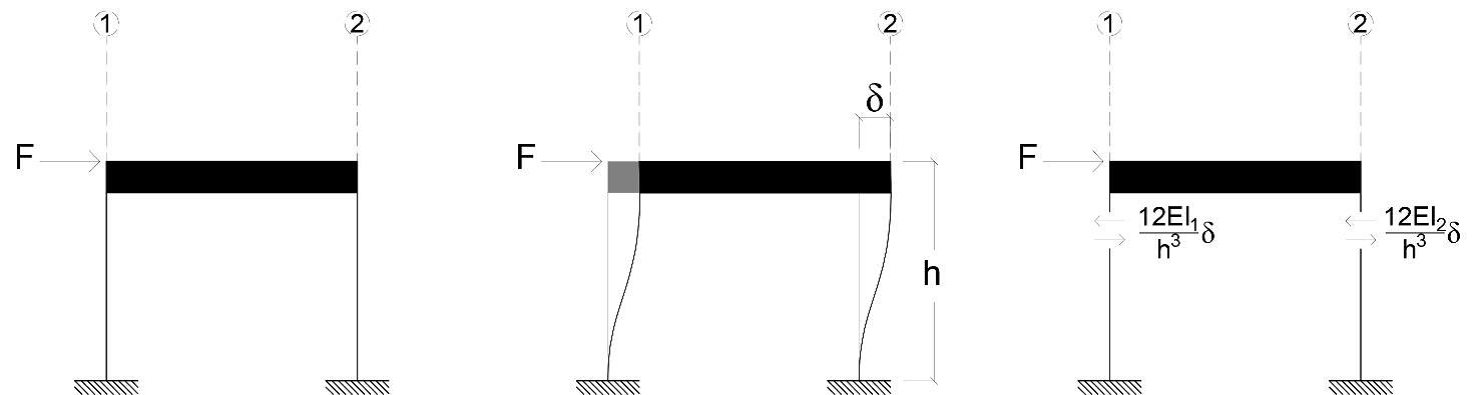
Procedo con il calcolarmi le rigidezze traslanti dei vari controventi. Essendo un modello shear type la rigidezze si ricaverà con:

F = (12EI₁ / h₃ + 12EI₂ / h₃) δ

F = k δ

k = 12EI₁ / h₃ + 12EI₂ / h₃

Generalizzando la formula da 2 ad n pilastri :

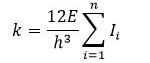
Dove E è il modulo elastico del cls armato (21000 MPa) ed I è il momentro d’inerzia che può essere, a seconda di come è disposto il pilastro:

I_x = bh³ / 12

I_y = b³h / 12

Una volta trovate le rigidezze traslanti dei telai procediamo calcolandoci le loro distanze dal punto di origine O.

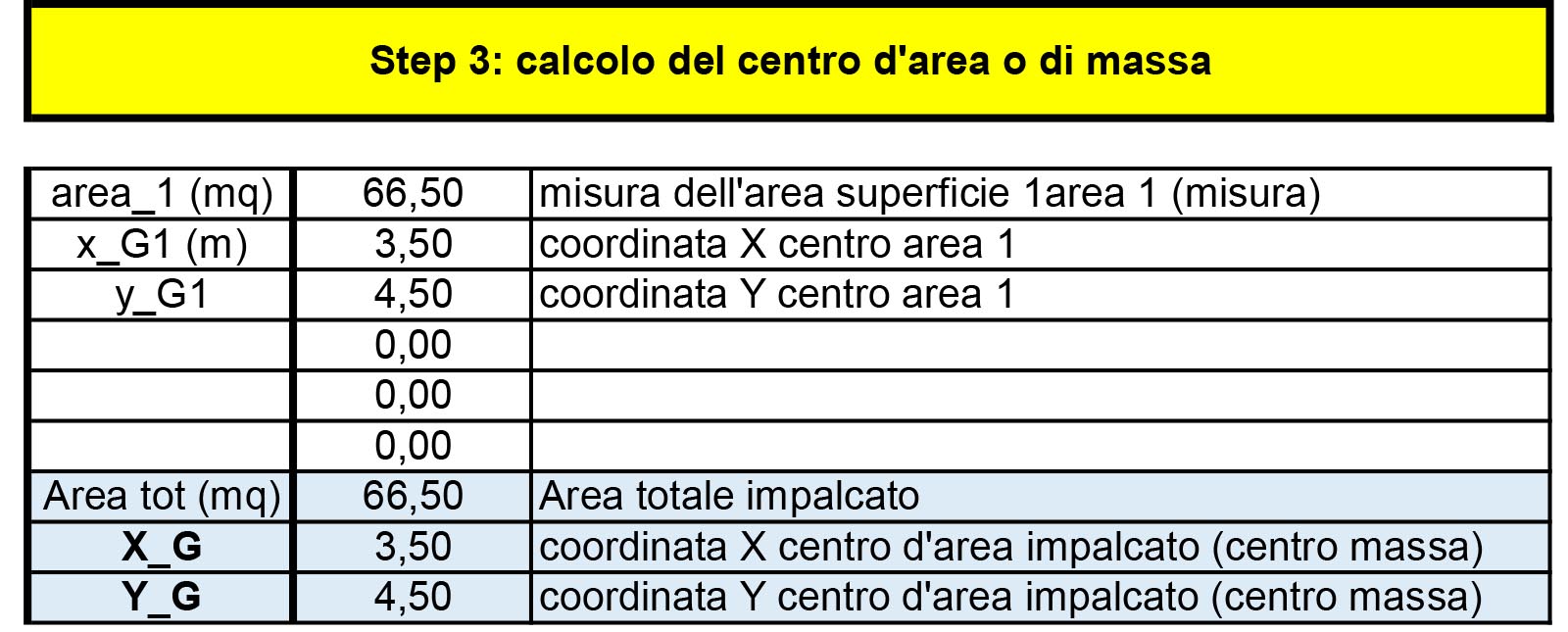
Andiamo ora a calcolare e trovare il centro d’area dell’edificio. Nel nostro caso l’impalcato è un semplice rettangolo quindi il centro d’area si troverà esattamente all’incrocio delle 2 bisettrici.

Se la forma fosse stata complessa si proceva con il suddividere l’area totale in aree semplici trovando i centri di area di ognuna di esse (che equivarrà al centro geomentrico), successivamente di dovranno applicare 2 formule per trovare i 2 assi che si incontrano nel centro d’area :

x_G = ΣA_i x_Gi / A_tot

y_G = ΣA_i y_Gi / A_tot

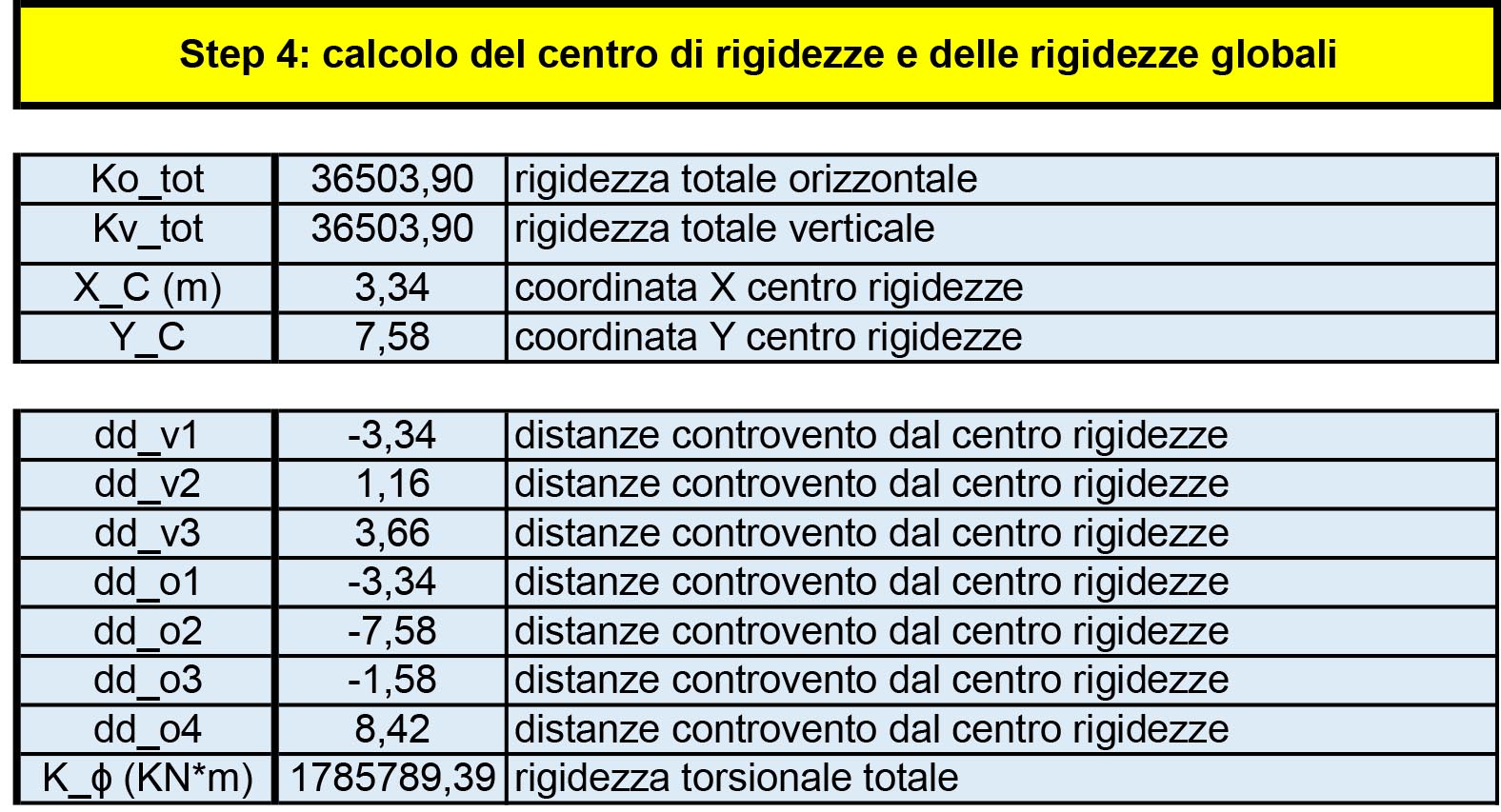
Procediamo ora con il calcolarci la rigidezza totale orizzontale, rigidezza totale verticale, rigidezza torsionale ed il centro delle rigidezze individuato anch’esso da 2 assi cartesiani di grazie alle formule:

x_C = Σk_vi d_vi / k_{v_tot}

y_C = Σk_oi d_oi / k_{o_tot}

Calcolandoci tutte le distanze dei controventi dell’impalcato dal centro delle rigidezze C possiamo trovare il valore della rigidezza torsionale dato dalla formula:

kφ = Σk_vi dd²_vi+Σk_oi dd²_oi

Vediamo dove sono posizionati i due centri nell’impalcato:

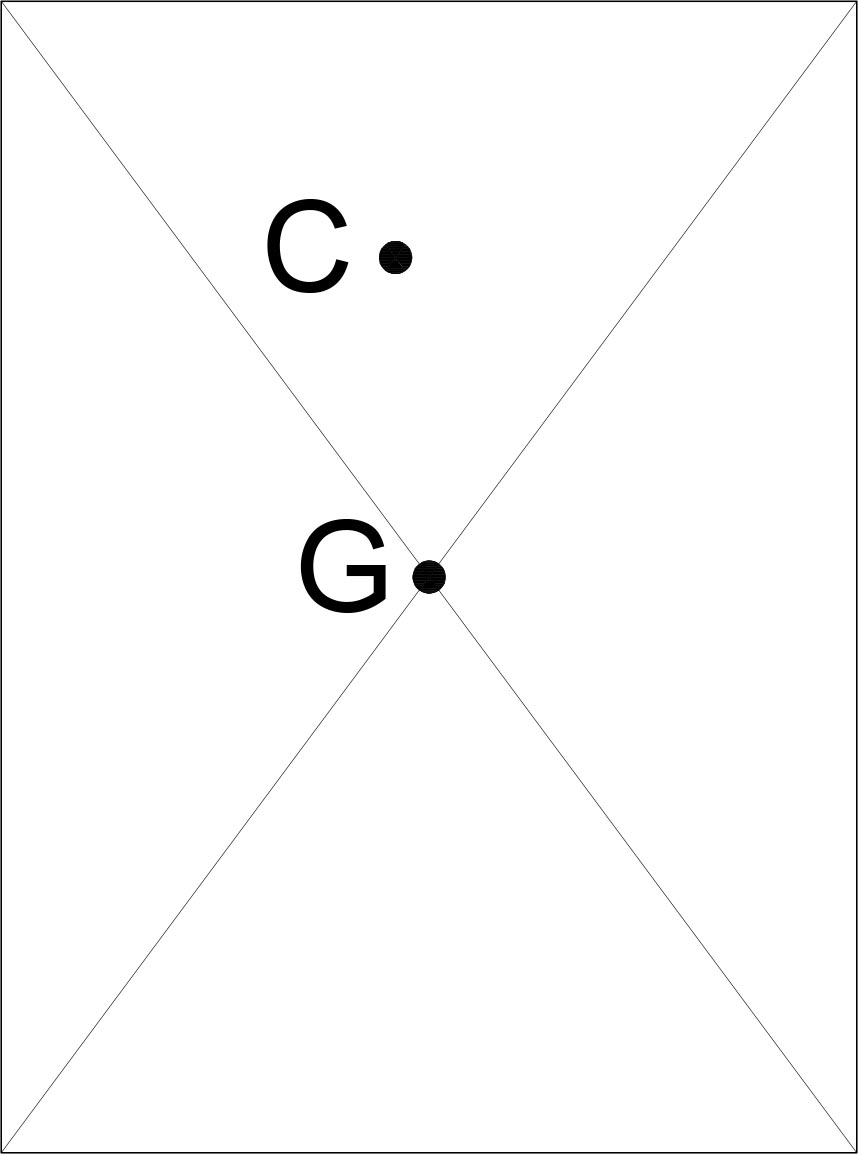
Notiamo che il centro delle rigidezze è situtato molto in altro rispetto l’asse y ed è quindi abbastanza distante dal centro d’area, questo è dato per un irrigidimento eccessivo nella parte alta. Sapendo che la forza sismica che andremo a trovare verrà applicata nel centro d’area G vorrà dire che questa non coincidenza tra G e C provocherà delle rotazioni dell’impalcato.

Andiamo adesso a trovarci la forza sismica da applicare in G. Dobbiamo prima di tutto difinire i tre carichi distribuiti (q_s , q_p e q_a )in modo da calcolarci il carico totale permanente G_k ed il carico permanente accidentale Q_k :

G_k = (q_s + q_p ) A_tot

Q_k = q_a A_tot

Da normativa utilizziamo la combinazione sismica per calcolare i pesi sismici:

W = G_k + ψ_2j Q_k

Dove ψ _2j è il coefficiente di contemporaneità tabellato nella normativa.

Il peso sismico W rappresenta la forza peso dell’edificio, ovvero il rapporto tra massa ed accelerazione gravitazionale. Essendo l’accelerazione del sisma, però, minore dell’accelarazione gravitazionale, viene introdotto un coefficiente d’intensità sismica c che dipende dalla zona dove è collocato l’edificio. In questo modo possiamo trovarci la forza sismica:

F = c W

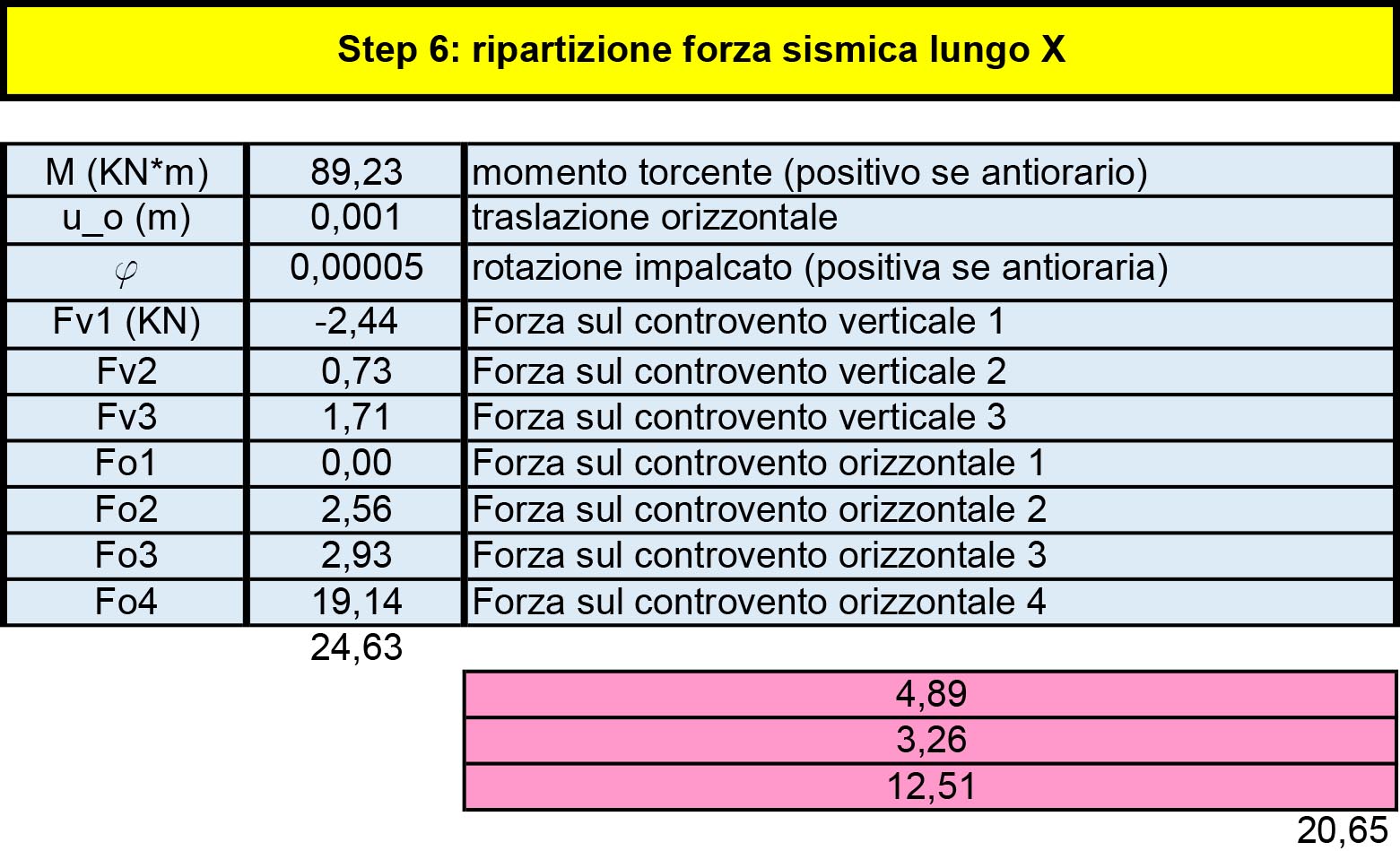
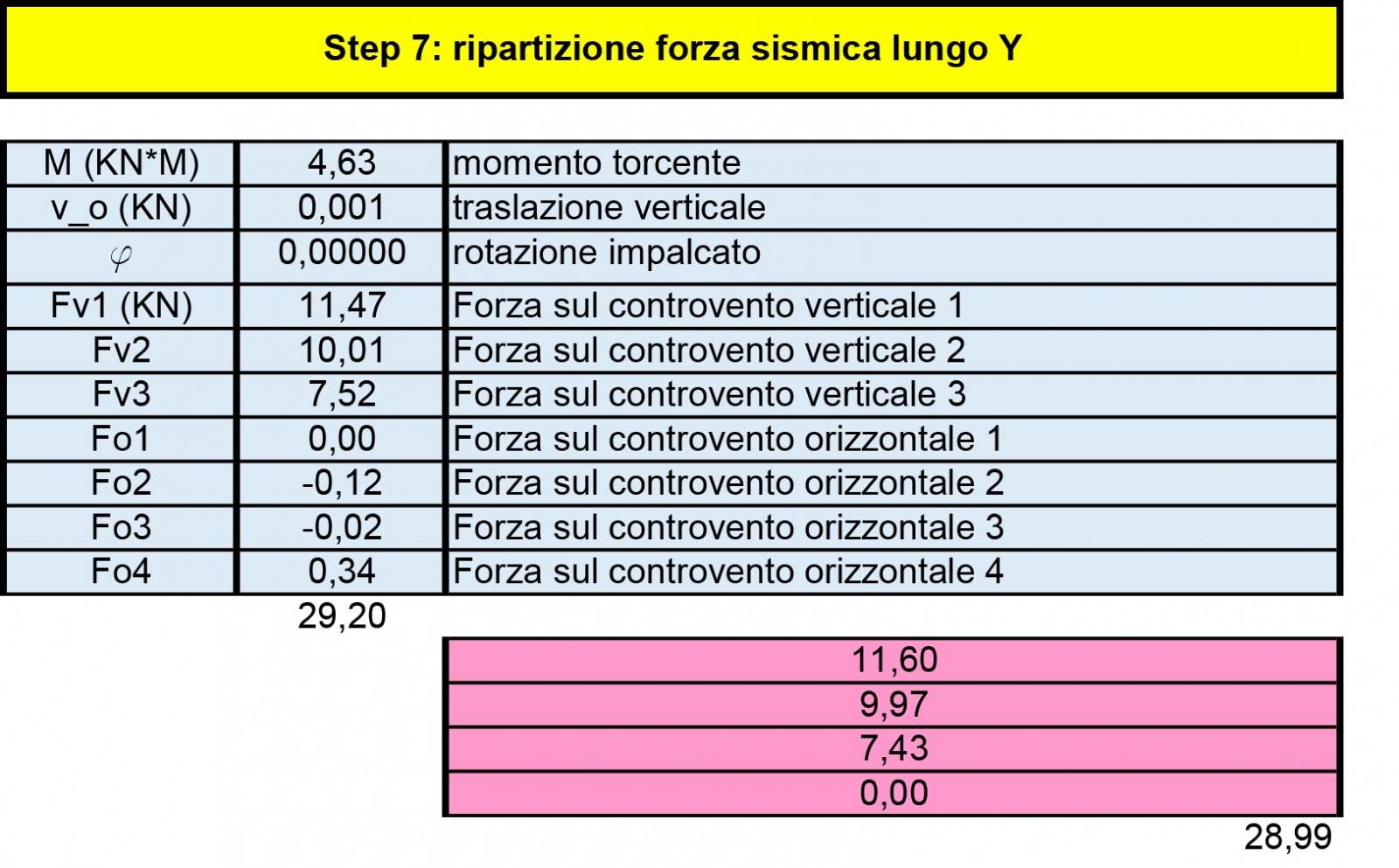
Ora che abbiamo tale forza la andiamo ad applicare nel centro d’area creando 2 casi:

• forza applicata in direzione x, che comporterà ad possibile rotazione e traslazione orizzontale dell’impalcato
• forza applicata in direzione y, che comporterà ad possibile rotazione e traslazione verticale dell’impalcato

Lo spostamento orizzontale, che chiamiamo u, è pari a:

u = F / k_{o_tot}

Lo spostamento verticale, che chiamiamo v, è uguale a:

v = F / k_{v_tot}

La rotazione φ impressa all’impalcato si trova con la seguente formula:

φ = M_c / kφ

Dove M_c è il momentro torcente dato dal rapporto tra forsa simica F per il braccio, ovvero la distanza tra G e C.

Possiamo infine ricavarci la forza sui singoli controventinei due casi di carico.

Quando la forza sarà applicata in direzione x, la reazione elastica dei controventi orizzontali sarà pari a:

F_{o_n} = k_{o_n} (u + φ dd_{o_n})

Mentre nei vericali sarà :

F_{v_n} = k_{v_n} φ dd_{v_n}

Quando la forza sarà applicata in direzione y, la reazione elastica dei controventi verticali sarà pari a:

F_{v_n} = k_{v_n} (v + φ dd_{v_n})

Mentre negli orizzontali sarà :

F_{o_n} = k_{o_n} φ dd_{o_n}

In questa esercitazione ci troviamo davanti al problema di dimensionare la sezione di una trave a sbalzo in legno, calcestruzzo armato e acciao.

L’impalcato di riferimento si rifà a quello dell’esercitazione precedente modificato per realizzare l’aggetto: questo grazie l’arretramento della fila di pilastri di destra di 2,5 metri.

INTERASSE = 3,5 m

LUCE = 2,5 m

AREA INFLUENZA = 8,75 m²

Passo 1: Trovata l’area d’influenza maggiore tra le travi a sbalzo il procedimento di dimesionamento iniziale è lo stesso utilizzato nell’esercitazione precedente (link) con due modifiche sostanziali:

• Il momento massimo M_MAX sarà quello di una mensola quindi uguale a q_ul²/2 ;
• Il carico accidentale q_a sarà equivalente a 4 kN/m² , coefficiente dato dalla Normativa per carici accidentali su balconi (categoria C2).

Passo 2: Dopo aver dimensionato la sezione, dobbiamo effettuare la verifica a deformabilità controllando che l’abbassamento massimo della trave in rapporto con la sua luce deve essere maggiore di 250 (valore dato da Normativa):

                                            l/ v_max > 250

Dove :

                                            v_max = ql⁴/8EI

Per trovare v_max è necessario utilizzare il metodo della linea elastica, vediamo i passaggi:

• Il momento flettente nella generica sezione x è uguale a M = -qx²/2
• Ci troviamo la curvatura χ = (qx²/2) (1/EI)
• Integriamo χ e troviamo la rotazione ϕ = (qx³/6) (1/EI) + C₁
• Integriamo nuovamente trovando lo spostamento v = (qx⁴/24) (1/EI) + C₁x + C₂
• Osserviamo che in corrispondenza dell’incastro B (x=l) devono essere nulli tanto l’abbassamento quanto la rotazione.
• Quindi per x=l si ottiene  C₁ = -ql³/6  e C₂ = ql⁴/8
• Infine sostituendo le due costanti d’integrazione a v ci troviamo l’abbassamento massimo v_max = ql⁴/8EI

Questo procedimento vale per tutte e tre le tecnologie e si effettua allo SLE quindi i carichi sulla struttra verrano ricombinati con la combinazione di carico agli SLE data da normativa.

Andiamo ora a dimensionare le tre tecnologie strutturali ( i solai sono gli stessi dell’esercitazione precedente)

CALCESTRUZZO ARMATO

Fatto il passo 1 la sezione della mia trave in calcestruzzo armato equivale a 30x50 cm.

Come nell’esercitzione precedente riverifico che la sezione sia verificata aggiungendo nel q_u il peso della trave.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max

LEGNO

Fatto il passo 1 la sezione della mia trave in legno equivale a 25x45 cm.

Non c’è bisogno di verificare il peso proprio della trave poichè il legno ha peso specifico basso.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max

ACCIAIO

Fatto il passo 1 il profilato preso è di un IPE 300.

Successivament controllo che la sezione sia verificata aggiungendo nel q_u il peso della trave.

Applico la combinazione di carico agli SLE ed inserisco il modulo di elasticità del cls armato in modo da trovarmi il momento d’inerzia I_x .

Ora abbiamo tutti gli elementi per calcolarci il v_max

L’esercitazione parte analizzano un impalcato stuttutrale di un edificio composto da telai piani, ovvero travi su pilastri. Premetto che, in questa esercitazione, i pilastri possono essere considerati come vincoli di appoggio semplice. Successivamente si dimensionerà la trave più sollecitata nelle tre diverse tecnologie : C.A., acciaio e legno.

La pianta di carpenteria presa come riferimento è del solaio superiore del mio appartamento.

1 : Individuo, grazie alla tessitura dei solai, le travi principali da quelle secondarie. Successivamente descrivo le aree di influenza di ogni trave principale ed individuo la trave maggiormente sollecitata, ossi quella con area di influenza maggiore.

N.B.: a parità di aree di influenza la trave più sollecitata sarà quella con più luce.

LUCE = 7,00 m

INTERASSE = 3,50 m

AREA = 24,50 mq

2 : Per ognuna delle tre tecnologie costruttive, procediamo con l’analisi dei carichi distribuiti (kN/m²) che si dividono in:

q_s carichi strutturali: comprendono tutti gli elementi con funzione strutturale (escludendo il peso proprio della trave)

q_p carichi permanenti: comprendono tutti gli elementi presenti sul solaio ma che non hanno una funzione strutturale

q_a carichi accidentali: nominati dalla normativa tecnica e dipendono dalla destinazione d’uso (commerciale, residenziale ecc). Da normativa, per edificio residenziale , esso equivale a 2kN/m².

3 : I tre carichi dovranno essere sommati tra loro con l’utilizzo però di coefficenti moltiplicativi sui singoli cairichi imposti dalla normativa NTC2008- Norme tecniche per le costruzioni- D. M. 14 Gennaio 2008.

Questa somma fornirà il carico totale come una combinazione di carico, espressa con la seguente formula:

I coefficenti moltiplicativi di sicurezza considerati sono tabellati nella normativa a seconda dello stato limite che si deve analizzare, nel nostro caso SLU (Stato Limite Ultimo).

Andiamo ora ad analizzare i carichi e a dimensionare la trave maggiormente sollecitata nelle tre diverse tecnologie costruttive: i solai utilizzati sono stati scelti sull’abaco dei modelli UNI10355.

DIMENSIONAMENTO TRAVE IN CALCESTRUZZO ARMATO

1 : Trovati q_s, q_p, q_a, calcolo il carico totale distribuito sulla trave q_u (kN/m²)  dato dalla combinazione di carico per l’interasse.

2 : Inserisco luce della trave in modo da trovarmi il momento massimo agente sulla trave. Avendo premesso che i pilastri vengono considerati come appoggi, il modello sarà quello di una semplice trave appoggiata appoggiata pertanto il momento massimo è in mezzeria ed equivale a q_ul²/8.

3 : Seleziono la classe di resistenza dell’acciaio da armatura B450C che possiede una resistenza caratteristica f_yk di 450 MPa (N/mm²) e la classe di resistenza del calcestruzzo per uso ordinario C25/30 che possiede una resistenza caratteristica f_ck di 25 MPa. In questo modo mi trovo la tensione di progetto dell’acciao f_yd = f_yk/γ_s e la tensione di progetto del calcestruzzo compresso f_cd = α_ccx f_ck/γ_c  (α_cc è il coefficiente di degrado a lunga durata e γ_c è il coefficiente parziale di sicurezza del calcestruzzo armato).

4: Trovati i valori delle tensioni di progetto ed il momento massimo, fisso la base della trave b così mi trovo l’altezza utile della sezione h_u da cui poi ricaverò l’altezza minima della sezione A_min sommando ad h_u la distanza tra il baricentro dell’armatura ed il filo del CLS (δ).

La trave ingegnerizzata finale ha una sezione di 30x60 cm. Anche se l’altezza minima trovata è di 50,04 cm ho dovuto prendere un’altezza pari a 60 cm poichè, nel calcestruzzo armato, avendo elevato peso specifico (2500 Kg/m³), dopo aver dimensionato la trave bisogna aggiungere al carico totale distrubito q_u il peso proprio della trave, e ricontrollare quanto viene H_min.

DIMENSIONAMENTO TRAVE IN LEGNO

Eseguo i primi 2 step in maniera equivalente a quelli del calcestruzzo armato

3 : A questo punto devo decidere che tipologia di legno utilizzare , ovvero legno massiccio o legno lamellare, in modo tale da ricavarmi la tensione caratteristica a flessione f_mk del legno scelto. Il ho optato per un legno massiccio di classe C24 che avrà quindi una f_mk = 24 MPa. Travato f_mk posso trovarmi, secondo la normativa, la tensione di progetto f_md = k_modx f_mk/γ_m (k_mod è il coefficiente diminutivo dei valori di resistenza del materiale, che tiene in conto l’effetto della durata del carico e delle condizioni di umidità in cui la struttura si troverà ad operare, mentre γ_m è il coefficiente parziale di sicurezza del legno).

4: Trovato il valore della tensione di progetto ed il momento massimo, fisso la base della trave b in modo tale da ricavere l’altezza minima che deve avere la sezione h_min = 42,27 cm.

La trave ingegnerizzata finale ha una sezione di 30x45 cm. Non c’è bisogno come per il calcestruzzo armato di rifare i calcoli aggiungendo al carico totale il peso della trave poichè il legno ha un peso specifico basso (710 Kg/m³).

DIMENSIONAMENTO TRAVE IN ACCIAIO IPE

Eseguo i primi 2 step in maniera equivalente a quelli del calcestruzzo armato

3 : Si sceglie poi una delle tre classi di acciaio strutturale (S235, S275, S355), nel mio caso S235, che mi dara il valore della tensione caratteristica di snervamento f_yk . Grazie ad essa posso trovarmi, da norma, la tensione di progetto f_yd = f_yk/γ_s (γ_s è il coefficiente parziale di sicurezza dell’acciaio).

4: Trovato il valore della tensione di progetto ed il momento massimo mi trovo il modulo di resistenza minimo rispetto l’asse x W_x,min = 779,14 . Grazie ad esso mi trovo la sezione della trave IPE da sagomario che sarà di una IPE360.

Anche se il peso specifico dell’acciaio è elevato (7850 Kg/m³), l’acciaio è un materiale intrinsecamente senello ma ad alta resistenza, quindi c’è bisogno di rifare i calcoli aggiungendo al carico totale il peso della trave.

La struttura analizzata è una superficie rigata a curvatura negativa definita come “paraboloide iperbolico”. Si è voluta scegliere poichè io ed il mio collega, Valerio Minella, l’abbiamo studiata, calcolata e costruita nel corso singolo “Geometrie e Modelli” delle professoresse Tedeschini Lalli-Magrone. Avevamo quindi il desiderio di capirne il funzionamento con la natura di reticolare spaziale.

Vorrei premettere da subito che io ed il mio collega abbiamo realizzato 2 modelli di paraboloide iperbolico completamente differenti l’uno dall’altro.

Il mio modello è stato realizzato in Rhinoceros grazie all’utilizzo di 4 “rette sghembe” che fungono da direttrici della superficie descritta da un insieme finito di rette che. Ovviamente, il mio modello è un’approssimazione della superficie : sia perchè avranno un certo spessore quando gli assegnerò una sezione, sia perchè il loro numero è tutt’altro che infinito.

Passo 1: Esporto il file nel formato.dxf e lo importo su SAP2000 (non c’è stato bisogno di passare per AutoCAD perchè Rhinoceros esporta già di suo i .dxf del 2004). Ovviemente ho fatto in modo che il modello si trovi sull’origine degli assi (0,0,0) e che abbia come asse veticale l’asse z.

Passo 2: Una volta inserito selezione tutti i frame del modello è gli assegno delle cerniere interne con il rilascio dei momenti sulle tre dimensioni dandogli così comportamento di reticolare spaziale.

Passo 3: Si passa poi all’asssegnazione dei vincoli esterni, “cerniere”, in maniera arbitraria sui nodi alla base del modello. Per far ciò sono dovuto rimanere sulla visualizzazione 3d poichè SAP2000 lavora sulla visualizzazione 2d dei piani.

Passo 4: Mi semplfico le tabelle finali selezionando tutti i frame del modello e assegnandogli un valore minimo di Stazioni pari ad 1: questo farà in modo che le tabelle delle analisi finali sulle sollecitazioni interne avranno solamente un valore all’inizio e alla fine asta, poichè essendo una reticlore spaziale avrà solamente sforzo Normale Costante.

Passo 5: Assegno a tutti i frame la sezione tubolare cava in avviaio di default di SAP2000

Passo 6: Successivamente passo all’assegnazione dei carichi sulla struttura: seleziono, sempre mediante la visulizzazione 3d, tutti i i nodi della superficie superiore, tranne quelli al bordo, è gli assegno una forza F, senza peso proprio, di direzione –z e di valore 100 kN, ai restanti nodi al bordo assegno la forza F sempre in direzione –z  con valore dimezzato, cioè 50 kN, questo perchè, essendo la natura del carico è distribuita, l’area di influenza dei nodi ai bordi è minore o uguale alla metà.

Passo 7: A questo punto sono pronto per avviare l’analisi della struttura e appare subito lo schema della deformata.

Passo 8: 

Controllo subito se c’è sforzo di Taglio o Momento flettente nella struttura: se ciò accadesse vuol dire che c’è stato un errore nella modellazione della struttura o nell’inserimento delle cerniere interne. Il risultato è positivo poichè i valori non esistono.

Controllo il diagramma dello sforzo Normale (il valore in rosso è di compressione, quello in blu di trazione).

Passo 9: L’ultimo lavoro che facciamo con SAP2000 è quello di farci tabellare in valori delle solecitazioni interne (in questo caso solo sforzo Normale). A questo punto esportiamo la tabella in excel e lasciamo SAP2000.

Passo 10: Prendendo spunti dalla tabella esportata da SAP2000 e dalla tabella esercitazione_pilastri.xls nel materiale scaricabile sul sito, realizzo uno file excel con 2 schede, una per aste compresse ed una per aste tese.

Passo 11: 

Inserisco, per le aste compresse, il valore dello sforzo normale di compressione (rendendolo positivo) e la lunghezza libera d’inflessione di ogni frame: quest’ultima sarà uguale alla lunghezza di dell’asta stessa poichè, avendo come vincoli agli estremi 2 cerniere, ha un coefficente di vicolo β pari ad 1.

                               _l0 = β l                                                                     (1)

                               _l0 = l                                                                        (2)

Passo 11: Specifico che voglio utilizzare un acciaio S235 andando ad inserire la tensione caratteristica di progetto f_yk ed il coefficente di sicurezza γ_m pari a 1,05. Grazie a questi due valori mi trovo la resistenza di progetto f_yd (3).Succesivamente trovo l’area minima A_min della sezione grazie alla formula di Saint Venant (4).

                               _fyd = f_yk / γ_m                                                                   (3)

                               A_min= N / f_yd                                                                   (4)

Passo 12:  Inserisco il modulo dei elasticità E dell’acciaio in modo tale che posso trovarmi la massima snellezza λ* possiblie che la trave compressa deve avere affinche l’instabilità non si inneschi prima dello schiacciamento (5). Da questa ci ricaviamo automaticamente il raggio d’inerzia minimo ρ_min (6) e, successivamente, il momento d’Inerzia minimo I_min (7).

                               λ*= π (E/f_yd)^1/2                                                              (5)

                               ρ_min= l₀ / λ*                                                                   (6)

                              I_min= A_min  ρ²_min                                                             (7)

Passo 13: Trovati A_min e I_min andiamo a prendere il sagomario dei profilati mettalici a sezione circolare cava dal sito www.oppo.it ed iniziamo ad assegnare le sezioni che abbiano un valore superiore a tutti e 2 (attenzione, l’Area da prendere in considerazione è l’area della sezione metallica). Scelto il profilato da assegnare scrivo i nuovi valori di Area A_design Momento d’Inerzia I_design e raggio d’inerzia ρ_design in modo tale da ricalcolarmi la snellezza λ, da normativa tale valore deve essere inferiore a 200 (coefficiente adimensionale poichè la snellezza è il rapporto di due lunghezze).

Passo 13: Ripeto lo stesso procedimento per le aste in acciao tese fermandomi all’Area minima poichè l’acciao teso non ha problemi di instabiltà.

Il passo successivo sarà quello di riassegnare le sezioni su SAP2000 e rimandare l’analisi.