blog di Giordana Panella

Gruppo: Panella Giordana e Ilaria Quagliani

Il progetto è situato a Roma in un lotto trapezoidale delimitato su due lati da via Ostiense e via del Porto Fluviale, a nord dalla ferrovia e ad ovest da una preesistenza.

L'edificio si articola su 8 piani:

• 2 piani interrati, dove troviamo un piano di parcheggi e la prima parte di zona commerciale
• piano terra dedicato ad altri servizi per il pubblico
• primo piano adibito ai servizi per gli uffici (reception, mensa...)
• 4 piani di uffici

I primi quattro piani sono strutturalmente sorretti da un telaio in cemento armato e gli altri 4 da una reticolare spaziale in modo da creare una grande terrazza pensata per rendere più piacevole la pausa pranzo degli impiegati. Inoltre questo tipo di struttura ci ha permesso di svuotare l'angolo all'incrocio di Via Ostiense e Via del Porto Fluviale in modo da alleggerire il fronte stradale già saturo nel quartiere.

La reticolare è sorretta da tre vani in cemento armato posizionati appositamente in modo da bilanciare tutta la struttura. Essi sono giuntati dal telaio in modo da non compromettere la staticità dell'edificio.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Gruppo: Panella Giordana, Quagliani Ilaria

L’esercitazione prevede la realizzazione del progetto di massima di un graticcio.

Per dimensionare il graticcio partiamo da una piastra alta 100 cm di dimensioni 200 x 200 cm sostenuta da pilastri angolari 100x100 cm e pilastri perimetrali 60 x 120 cm.

Scegliamo un cls 50/60 ad alte prestazioni in quanto il graticcio è una struttura speciale.

Ipotizziamo che la piastra sostenga 3 piani con un carico qu= 12,31 KN/mq quindi la piastra porta un Qu= 14772 KN.

I nodi angolari si prendono un carico di 2,31 KN, i perimetrali di 4,62 KN e i centrali di 9,23 KN.

Dopo aver mandato l’analisi ricaviamo Mmax = 1817,204 KNm/m.

Risulta sovradimensionata di circa il 30%  dunque possiamo andare avanti.

Anche l’abbassamento viene verificato risultando 1/200 della luce, u = 0,5 cm.

Dopo aver fatto tutte le verifiche necessarie scegliamo  il passo che vogliamo dare alle travi del nostro graticcio, lo poniamo pari a 250 cm, quindi ci calcoliamo il momento d’inerzia di una fascia alta 100 e larga 250 cm.

Ix = bh³ / 12 = 2,5 x 1³/12 = 0,21 m⁴

Dopo di che decidiamo la base che vogliamo dare alle travi b = 50 cm per trovare la loro altezza:

h = (Ix * 12/b)^1/3 = 1,71 m

Quindi le travi che comporranno il graticcio sono 50 x 175 cm.

Applichiamo ai nodi centrali 230,81 KN, ai perimetrali 115,41 KN e agli angolari 57,70 KN.

Con questo tipo di struttura Mmax del pilastro risulta di 4291 KNm e Mmax della trave di bordo risulta essere circa 4000 KNm per aiutare la struttura a diminuire i momenti che potrebbero interferire con le strutture adiacenti abbiamo deciso di aumentare la base delle travi di bordo di 100 cm.

In questo modo risulta un Momento massimo delle travi di 3366 KNm con cui andiamo a verificare le travi del graticcio. Il Mmax dei pilastri perimetrali risulta 3906 KNm e quello degli angolari è 1082 KNm con cui andiamo a verificare i pilastri a flessione in quanto risultano essere tutti in grande eccentricità.

Dopo aver verificato che alcuni elementi risultano sovradimensionati andiamo a sostituirli.

Le nuove dimensioni sono:

Travi del graticcio 50 x 100 cm

Trave di bordo 150 x 175 cm

Pilastri perimetrali 60 x 110 cm

Pilastri d’angolo 100 x 100 cm

Con queste nuove dimensioni andiamo a verificare le tensioni della trave di bordo:  τmax = α Mt/ ba² = 2,23 Mpa < 8 Mpa

Dove Mt = 3037,89 KNm e α = 3 + 1,8 a/b = 4,08

 

 

 

 

Gruppo: Panella Giordana, Quagliani Ilaria

Il nostro progetto al terzo e quarto piano si compone di due vierendeel di modulo 3x3 m lunghe 18 metri che permettono di avere uno spazio al piano terra senza appoggi. Le vierendeel si appoggiano a due setti disposti longitudinalmente di lunghezza 4 metri e spessore 30 cm.

Pianta Vierendeel                                     

Prospetto

Pianta telaio

ANALISI DEI CARICHI

Solaio

Combinazione di carico allo stato limite ultimo SLU:  qu= 25,96 KN/m

Qu: 25,96 x 3 = 77,88 KN

Sapendo che il cemento armato pesa molto abbiamo aggiunto il peso proprio della struttura: pp = 30,68 KN

Il carico totale applicato puntualmente su ogni nodo è:  F= (77,88 + 30,68) x 3= 325,68 KN

ANALISI STATICA DELLA TRAVE VIERENDEEL

Poiché la trave vierendeel si comporta come un telaio shear type ribaltato  i correnti hanno le stesse caratteristiche dei pilastri del telaio e i montanti quelle del traverso.

In virtù di ciò siamo riuscite a calcolare deformata, taglio e momento dei correnti:

questi sono i diagrammi che ci aspettiamo poi usciranno dall'analisi su sap

MODELLO SU SAP

Su sap sono state applicate le sezioni alle travi, di 30 x 40, e ai pilastri, 30 x 80. Le travi che collegano le vierendeel sono di 25 x 30. La classe del cls scelta è C28/35.

Il modello teorico della trave di Vierendeel è assimilabile a quella del telaio shear type infatti applichiamo rigidezza infinita al pilastro modificando il fattore moltiplicativo del momento d’inerzia.

Applichiamo i carichi definiti in precedenza e i vincoli. Per assicurarci che tra la trave e il setto ci fosse effettivamente un nodo rigido è stato applicato il Constraint Body.

Mandata l'analisi abbiamo ottenuto quello che ci aspettavamo:

Deformata

Taglio

Momento

Sforzo Assiale

VERIFICA

Una volta ricavati i sforzi abbiamo verificato i pilastri a presso flessione e le travi a flessione:

 

 

 

 

 

 

 

Gruppo: Panella Giordana, Quagliani Ilaria

Poiché dobbiamo verificare che il telaio regga alla forza sismica abbiamo pensato di utilizzare dei pilastri rettangolari, che abbiamo predimensionato:

Pilastri piano terra 30 x 60 cm

Pilastri primo piano 30 x 40 cm

Pilastri secondo piano 30 x 25 cm

Sono stati orientati in modo da avere il momento d’inerzia maggiore per aumentare la rigidezza del telaio.

Per completezza dell’esercitazione abbiamo aggiunto le tamponature esterne:

Q_tomp. in presenza di finistre: 3,4 x 2,95 x 0.80 = 8 KN/m

Su sap2000 avevamo già definito Qs,Qp e Qa, ora facciamo la nostra analisi aggiungendo Q_tomp.

Questo è il diagramma che ricaviamo dopo aver predimensionato tutti gli elementi e aver aggiunto ai carichi lineari la tamponatura esterne. Ora possiamo mandare l’analisi.

Di conseguenza abbiamo dimensionato e verificato i pilastri, le travi e le mensole come nell' esercitazione precedente (alleghiamo le tabelle).

Vento

Abbiamo considerato un contributo del vento pari a 0,50 KN/m^2.  

Abbiamo calcolato l’area di interasse per ogni pilastro ora possiamo calcolarci il carico distributivo verticale agente su ognuno di esso:

26,25 mq x 0,5 = 13,125 KN/m

57,75 mq x 0,5 =  28,875 KN/m

52,50 mq x 0,5 = 26,25 KN/m

Ora possiamo verificare se effettivamente le travi e pilastri che abbiamo messo possono reggere questa sollecitazione:

Pilastri

Per sicurezza abbiamo verificato anche le travi e le mensole di cui allegheremo le tabelle.

Sisma

Per la forza sismica usiamo un modello strutturale che viene identificato con il nome di telaio shear-type dove gli elementi hanno Momento ma curvatura nulla e hanno Sforzo Normale ma deformazione nulla, infatti si ha rigidezza flessionale infinita e rigidezza assiale infinita.

Infatti su Sap  per rendere l’impalcato un corpo rigido vengono applicati i diaphragm stando attente ad assegnare uno diverso per piano, in quanto in caso di azione sismica ogni solaio deve essere libero di ruotare autonomamente.

 

Centro di massa

Per calcolare il centro di massa abbiamo considerato il rettangolo delle scale e il rettangolo dell’impalcato ricavando di ognuno il centro geometrico e l’area, da inserire nella formula per le coordinate del centro di massa:

x_c = A₁*x₁-A₂*x₂/ A₁-A₂

y_c= A₁*y₁-A₂*y₂/ A₁-A₂

Per il calcolo della forza sismica si inizia calcolando i vari carichi per poi sommarli, solo il carico accidentale viene moltiplicato per il coefficiente di contemporaneità (indicato in normativa) e il coefficiente di intensità sismica (c= 0,10) che tiene conto della sismicità del luogo dove siamo.

Q_s = np x Ap x qs = 2012, 4 KN

Q_p  = np x Ap x qp = 2631,6 KN

Q_a = np x Ap x qa = 2322 KN

Fs = c (Q_s + Q_p + 0.80 Q_a) = 650,12 KN

In quanto la forza sismica si distribuisce in  modo diverso ai vari piani ci andiamo a calcolare per ogni piano la forza sismica da applicare al centro delle rigidezze:

Fi = (hi / Ʃhi) Fs

F_TP = 108,35 KN

F_P1 = 216,71 KN

F_P2 = 325,06 KN

Applichiamo queste forze su sap in direzione x ed y:

Ecco cosa succede al nostro impalcato in direzione X:

Ecco cosa succede al nostro impalcato in direzione Y:

In pianta si riconosce molto bene l'effetto di traslazione e rotazione che ci aspettavamo come risultato della forza sismica

Ora possiamo verificare cosa succede agli elementi del nostro impalcato:

• combinazione 1: carico sismico in direzione X

• combinazione 2: carico sismico in direzione Y

Anche per la forza sismica sono state verificate le travi e le mensole per sicurezza, risultano tutte verificate, alleghiamo le tabelle.

I pilastri non verificati sono stati aumentati di sezione. Ci siamo rese conto che la struttura ha un buon comportamento per la forza sismica proveniente dalla direzione Y per questo potremmo pensare di controventare in miglior modo la struttura nella direzione X.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Gruppo: Panella Giordana, Quagliani Ilaria

La struttura ipotizzata è un telaio di 3 piani ciascuno alto 3,50 m con 2 m di sbalzo su di un lato che ricorre per ogni piano. Andiamo ad inserire all’interno di un modulo il vano scale.

Analisi dei carichi

Prima di iniziare il dimensionamento andiamo ad evidenziare gli elementi che hanno un area di influenza maggiore.

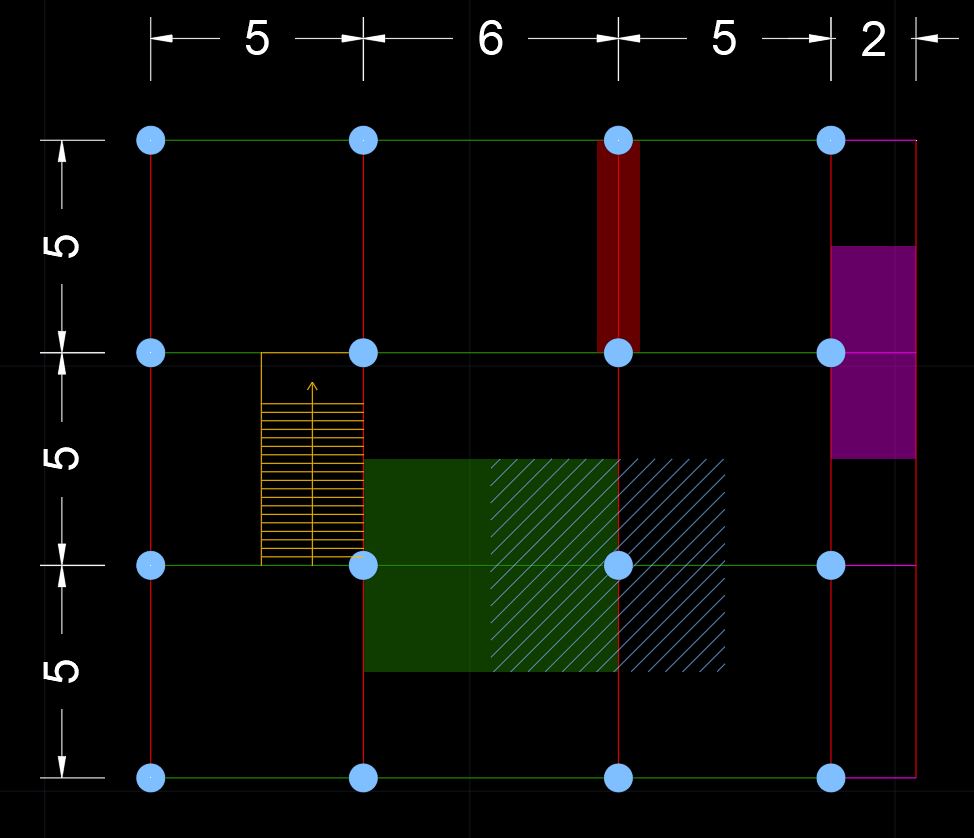
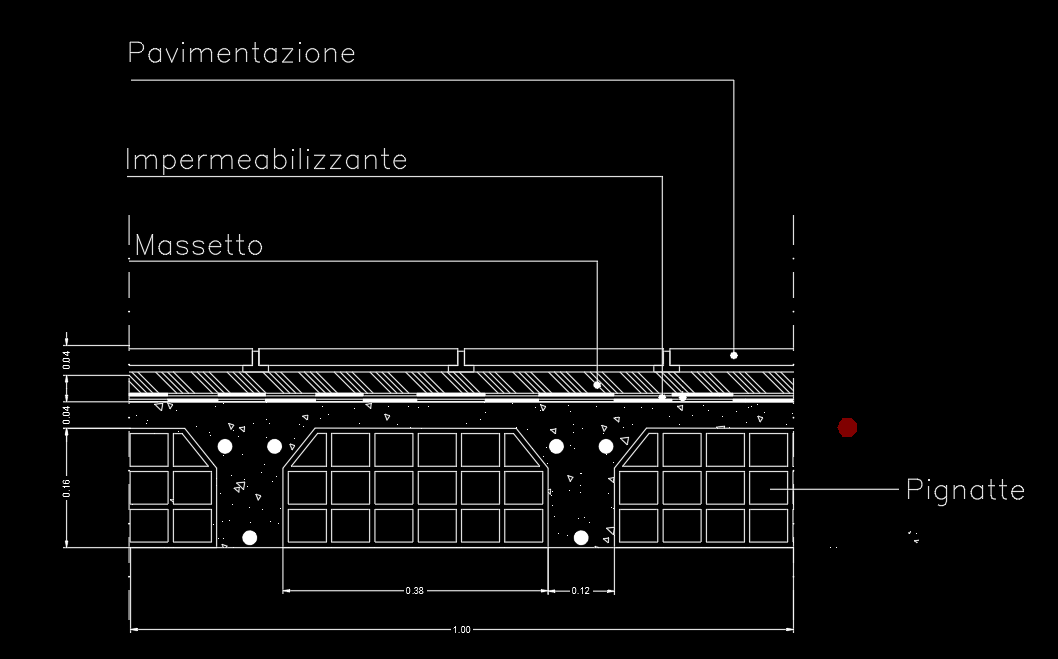
I solai che costituiscono i piani dell’edificio sono in latero-cemento.

Definendo i vari strati calcoliamo qs,qp e qa che saranno uguali per ogni dimensionamento in modo da poterli inserire nelle tabelle excel per poi calcolare il qu specifico per ogni gruppo di elementi.

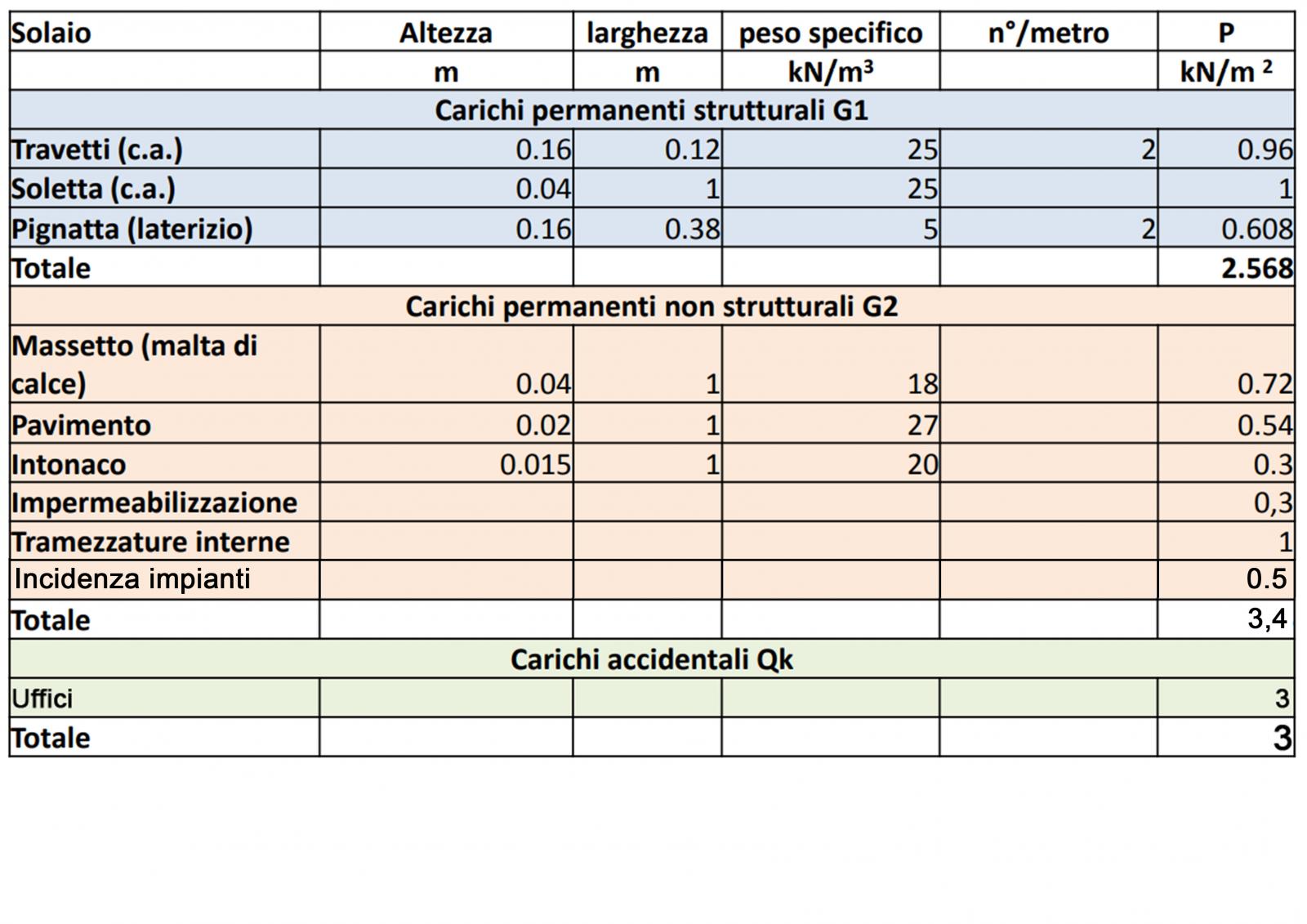
Ora possiamo passare su SAP. Come prima cosa è stata disegnata la struttura del primo livello, impostando i vincoli a terra che sono incastri, poi copiata in altezza.

   

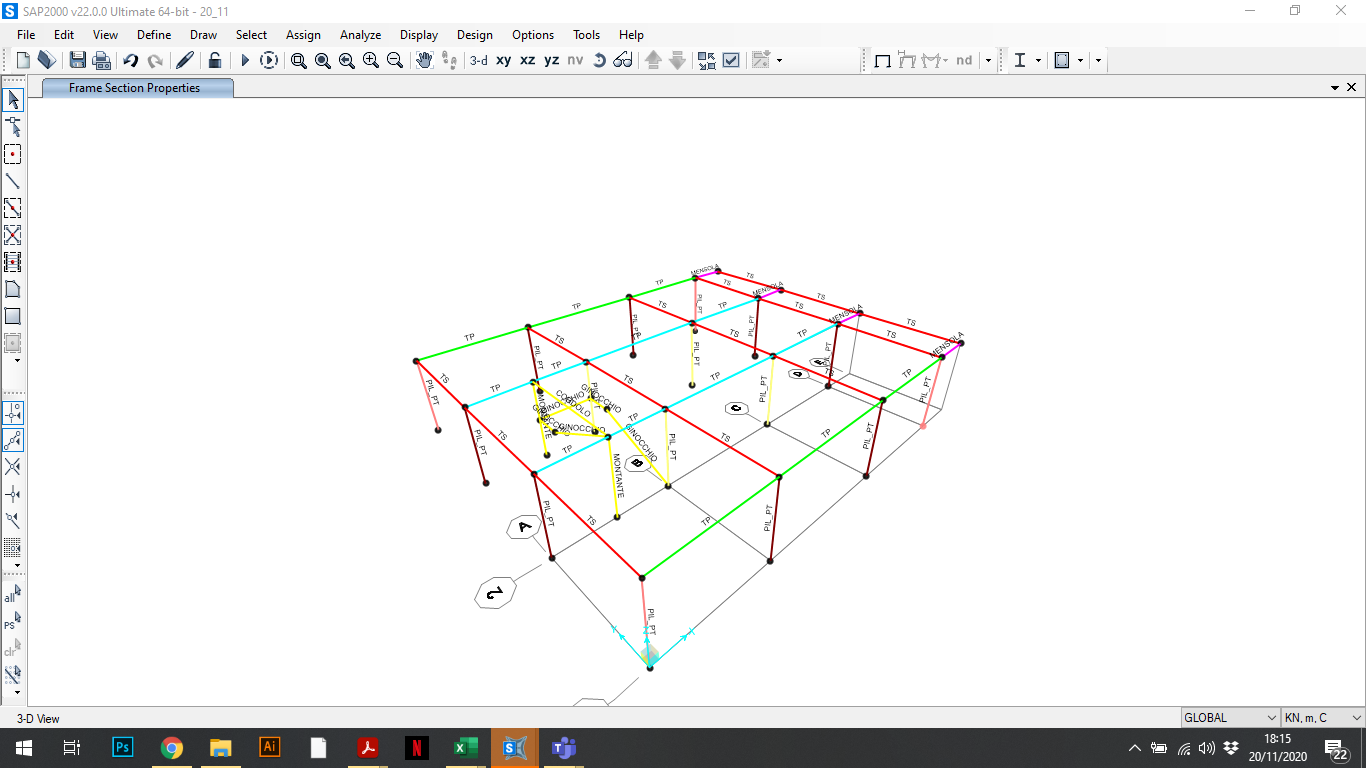
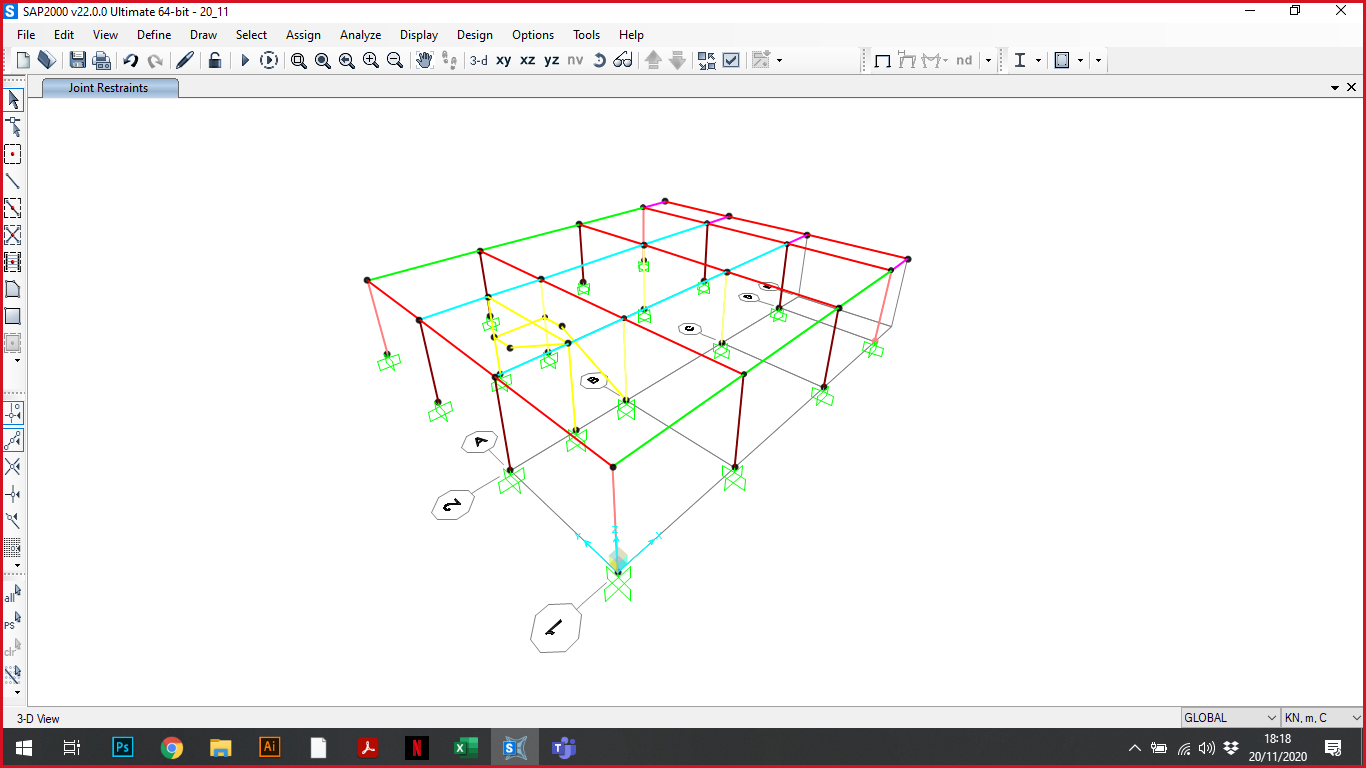
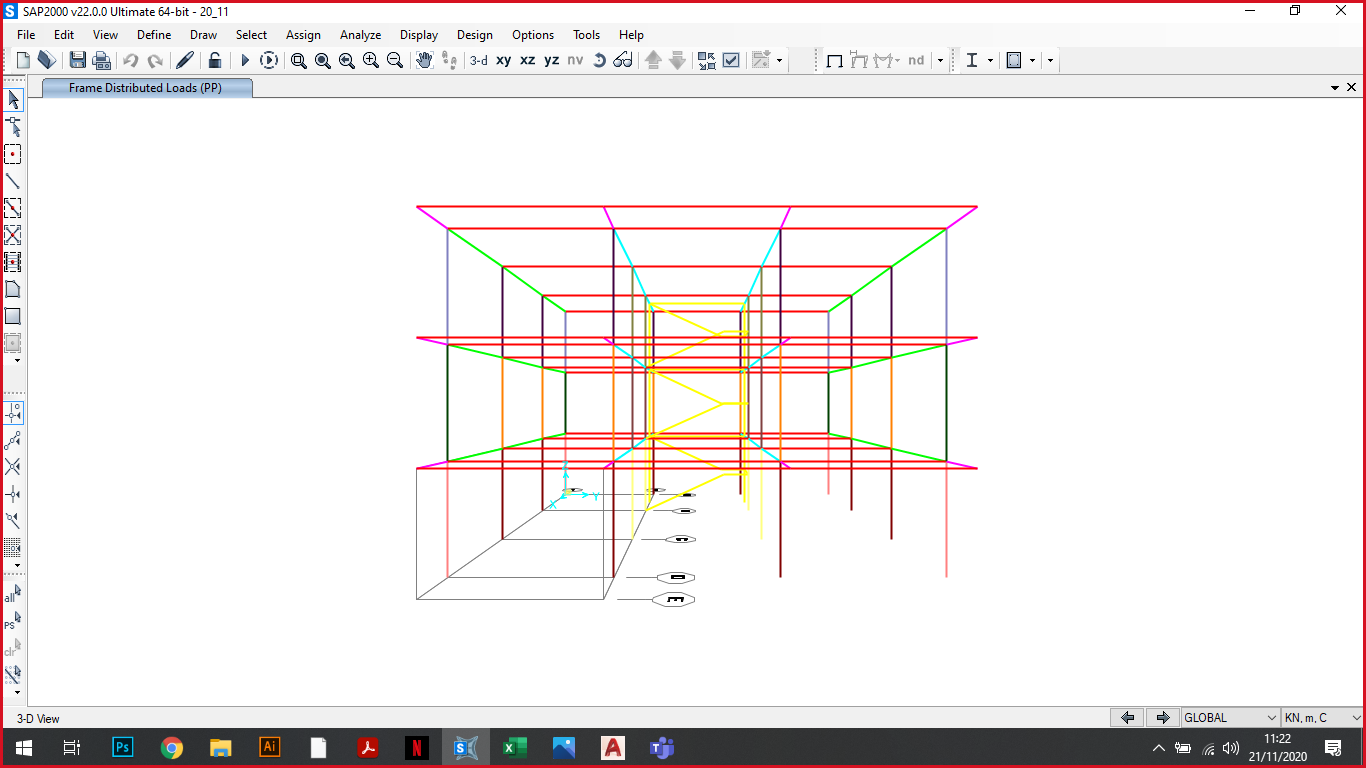
Poi è stato impostato come materiale il calcestruzzo C28/35, con modulo elastico E= 32308 MPa (calcolato con la formula Ecm. = 22000 ∙ ((f ck. + 8) / 10)0,3. [N/mm2]) e definiti ed assegnati ad ogni elemento dei gruppi di appartenenza in modo che sia più facile poi andare ad applicare  le sezioni e  riconoscerle immediatamente.

La struttura dell’edificio è divisa in travi principali centrali TP_C, travi principali perimetrali TP_P, travi secondarie TS, mensole e pilastri.

Predimensionamento

• Predimensionamento trave

Grazie alle aree di influenza evidenziate prima sappiamo l’interasse delle travi maggiormente sollecitate.

Abbiamo anche tutti i carichi in modo da poterli combinare per il carico allo Slu.

Il momento massimo viene calcolato in base al modello di trave doppiamente appoggiata infatti va inserita la luce della trave.   

Prima decidendo che cls utilizzare abbiamo automaticamente definito anche la sua resistenza caratteristica (fck=28 N/mm²). Ora è necessario scegliere anche quella dell’acciaio da armatura B450C  (fyk= 450 N/mm²).

Adesso è possibile calcolare le tensioni di progetto del calcestruzzo e dell’acciaio da cui determiniamo hu, che deriva dalle ipotesi di progetto che entrambi i materiali attingono contemporaneamente alla tensione di progetto e che le sezioni rimangono piane ricordando il digramma delle tensioni dei due materiali serve un procedimento di omogeneizzazione.

A questo si aggiunge il copriferro per arrivare ad un’altezza minima da cui poi si parte per decidere un altezza di design.

Il peso proprio di una trave in cemento armato incide molto infatti nella tabella excel è possibile rendersi conto se si sta predimensionando in modo corretto.

Osserviamo come Hmin<Hdesign e quindi le sezioni sono verificate.

Trave principale 70 x 30 cm

Trave secondaria 35 x 25 cm

• Predimensionamento pilastro

Anche qui stesso discorso per i carichi e per l’area di influenza. Oltre a questo sul pilastro gravano il peso della trave principale e della trave secondaria infatti lo sforzo normale N è la somma del carico qu e del peso delle travi moltiplicato per il numero dei piani sopra il pilastro.

Per considerare il contributo a flessione che genera momento nel predimensionamento prendiamo la resistenza di progetto fcd dimezzata da cui ricaviamo l’area minima.

Nell’ultima parte della tabella si tiene conto dell’instabilità del carico di punta che ci permette di ricavare la base minima.

L’altra misura da tenere sotto controllo è l’altezza, in modo che poi l’area di progetto sia superiore all’area minima calcolata in precedenza.

Pilastri piano terra 45 x 45

Pilastri primo piano 40 x 40

Pilastri secondo piano 30 x 30

• Predimensionamento mensola

Per una prima parte il predimensionamento dello sbalzo è come quello delle travi, l’unica differenza è la formula del momento massimo in quanto lo schema statico è quello della mensola.

Per completare il dimensionamento bisogna verificare a deformabilità cioè l’abbassamento e va aggiunto il peso proprio della trave.

Mensola 50 x 30

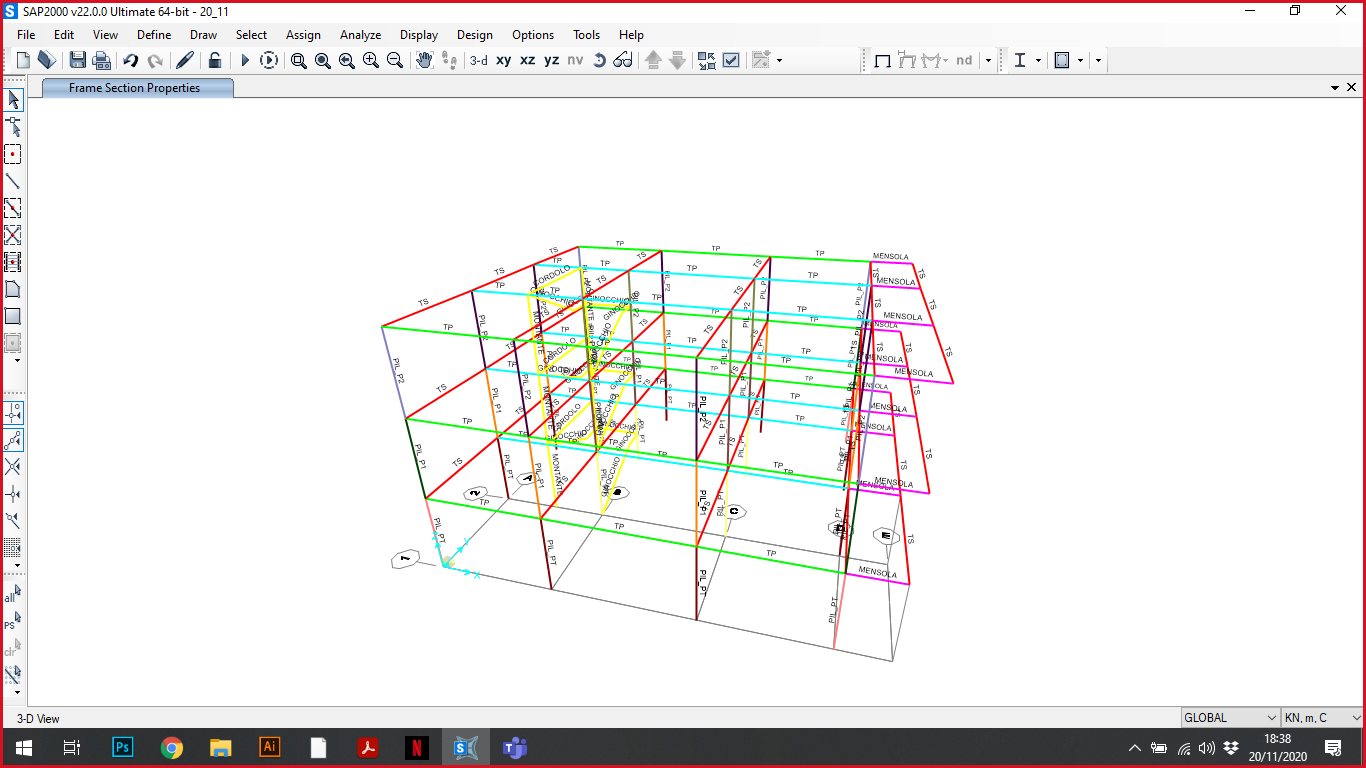
Carico lineare

Per ottenere il carico lineare da applicare sulle travi principali centrali abbiamo moltiplicato il carico al metro quadro per la larghezza di influenza e per le travi principali perimetrali l’abbiamo diviso:

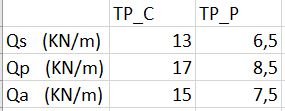
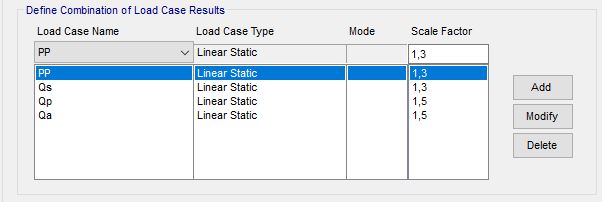
Su sap2000 quando definiamo qs,qp e qa moltiplichiamo per i fattori di scale che equivale a mettere i coefficenti parziali per la combinazione SLU.

 

• Vano scale

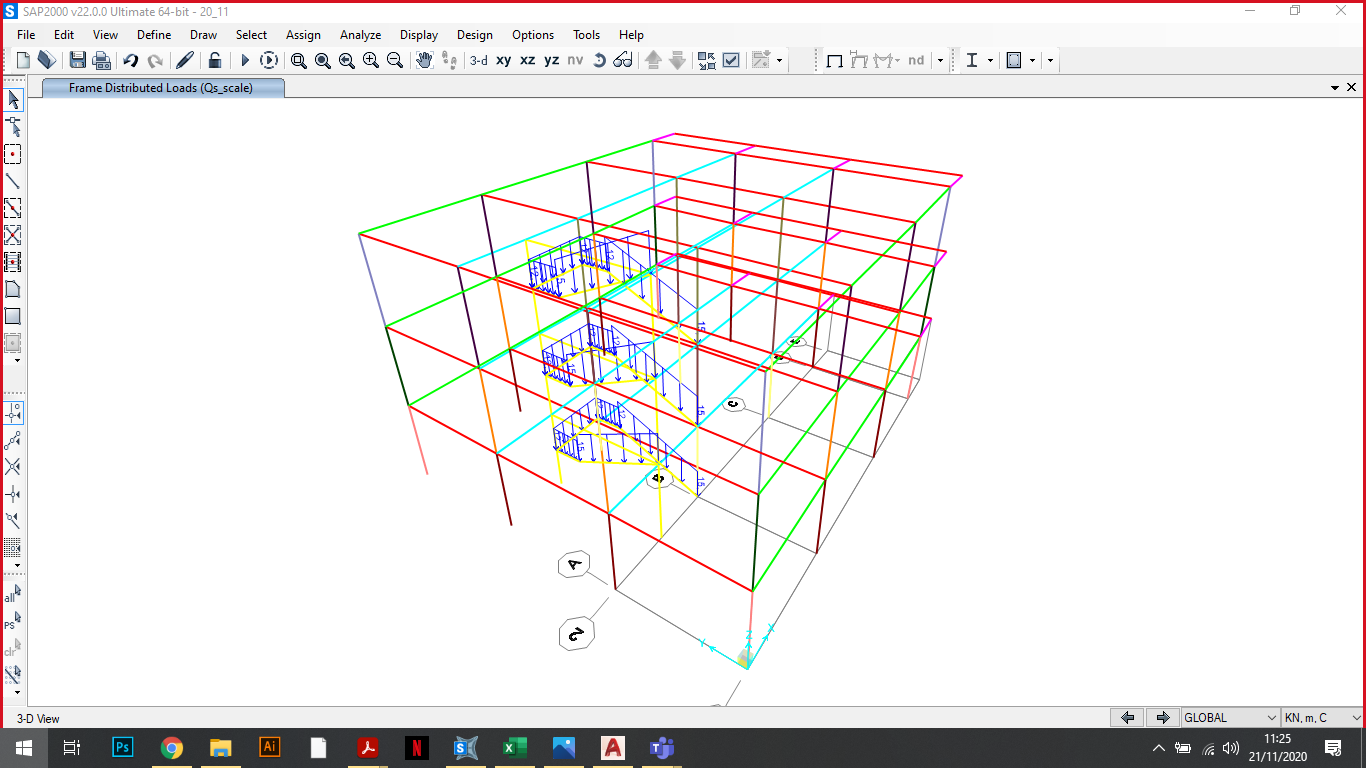
Abbiamo dato delle dimensioni ipotetiche per la scala:

Trave a ginocchio 45x30 cm

Cordolo 30x20 cm

Montanti 30x30 cm

Per poter poi applicare i carichi calcolati in questo modo:    

Qp rampe= 5,5 KN/m

Qa rampe= 5,1 KN/m

Qu=  15 KN/m

Qp pianerottolo= 1,5 KN/m

Qa pianerottolo= 6 KN/m

Qu pianerottolo= 12 KN/m

Questo è il diagramma che ricaviamo dopo aver dimensionato tutti gli elementi e aver messo i carichi lineari.

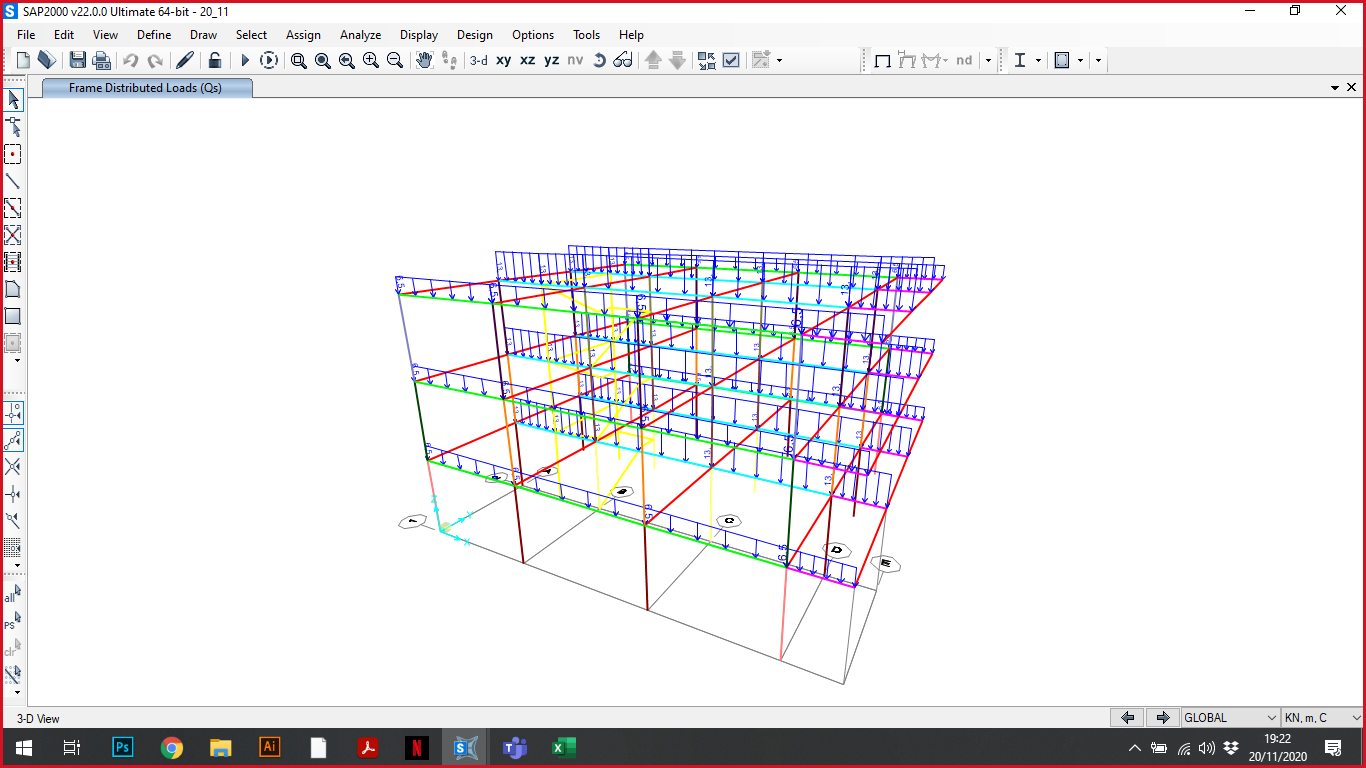
Ora possiamo iniziare l'analisi con la combinazione allo SLU:

Sforzi assiali                                                                                                           Taglio                                                                                                                  

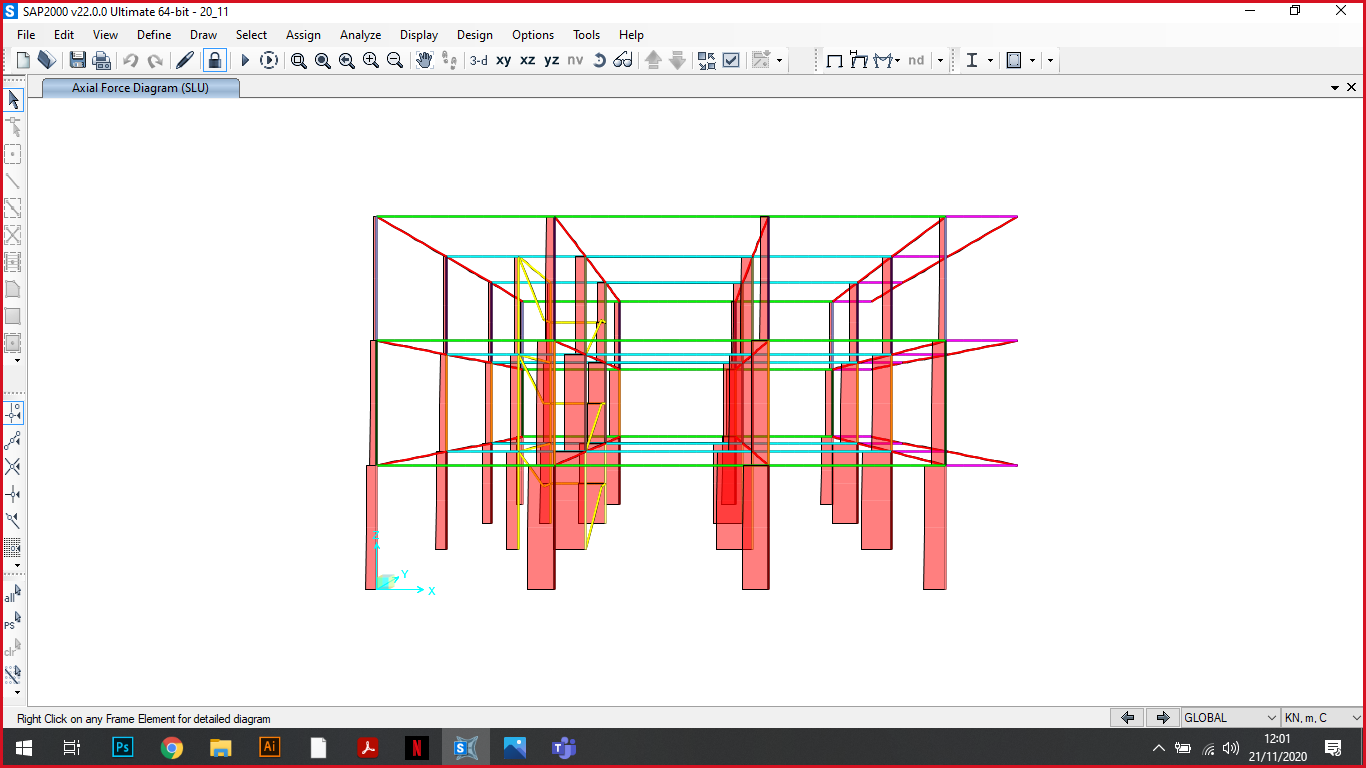
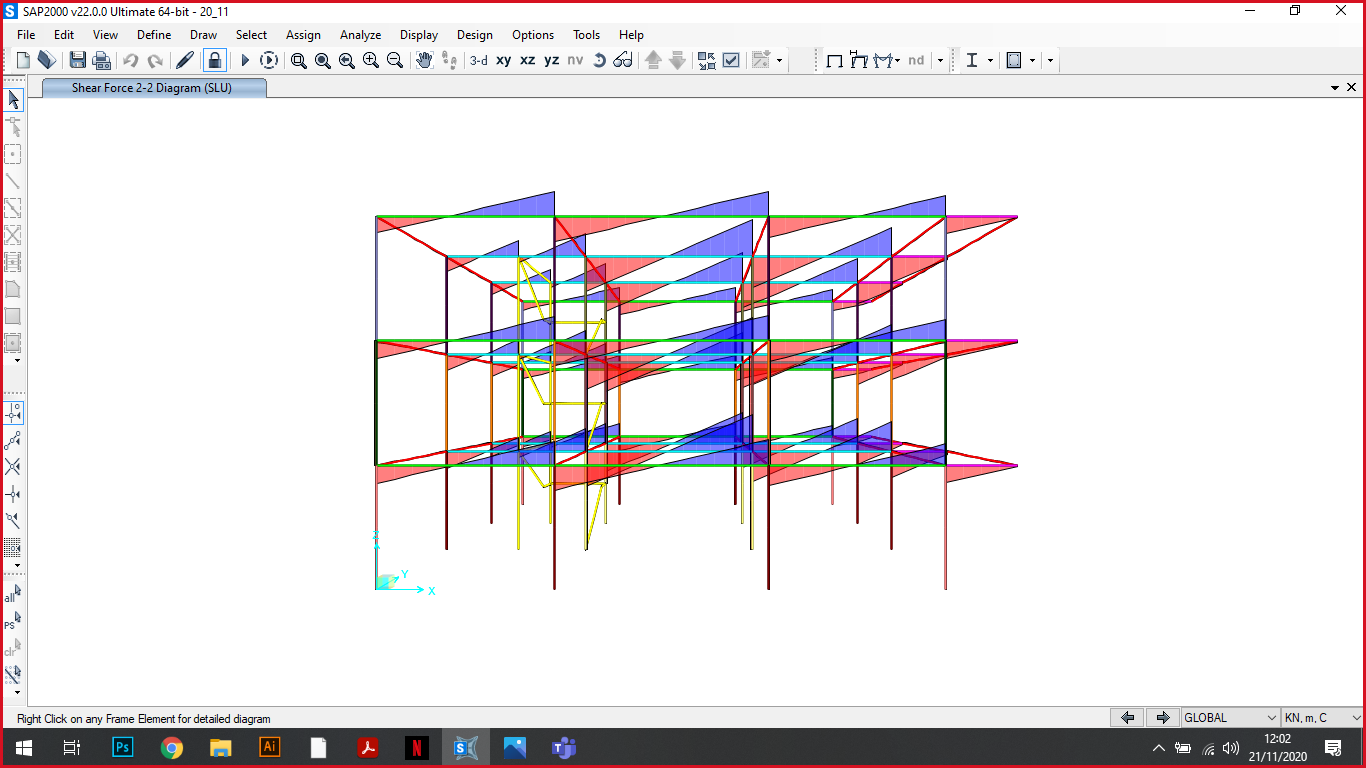
Momento                                                                                                                Deformata

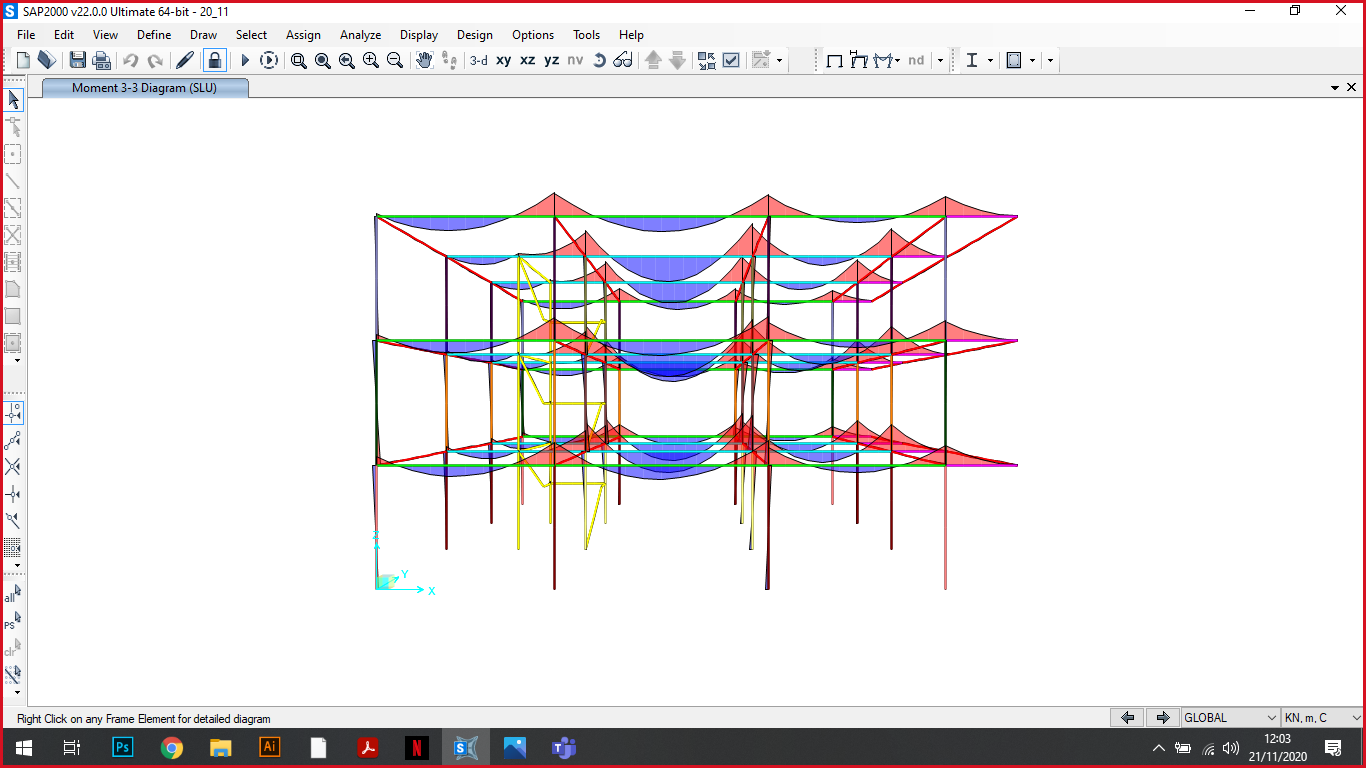
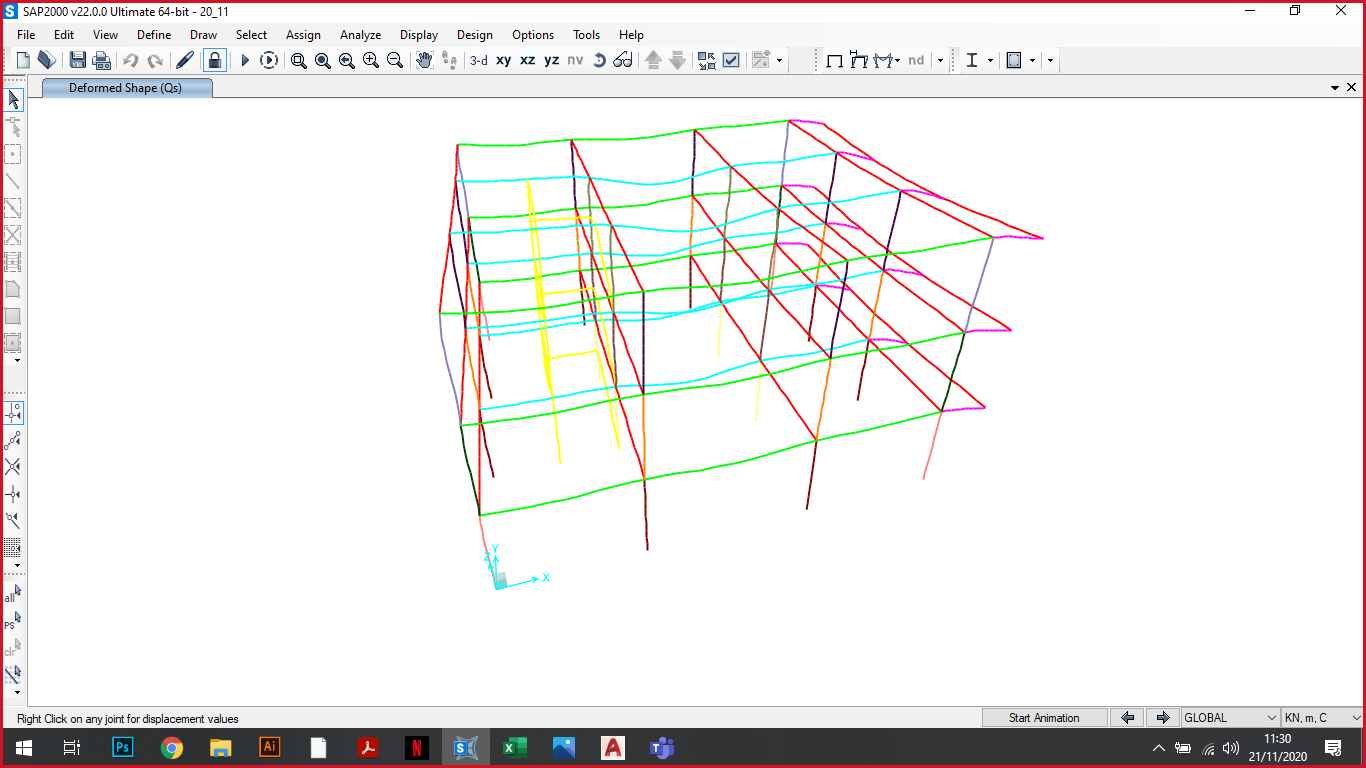
Dimensionamento e verifica

• Verifica pilastri

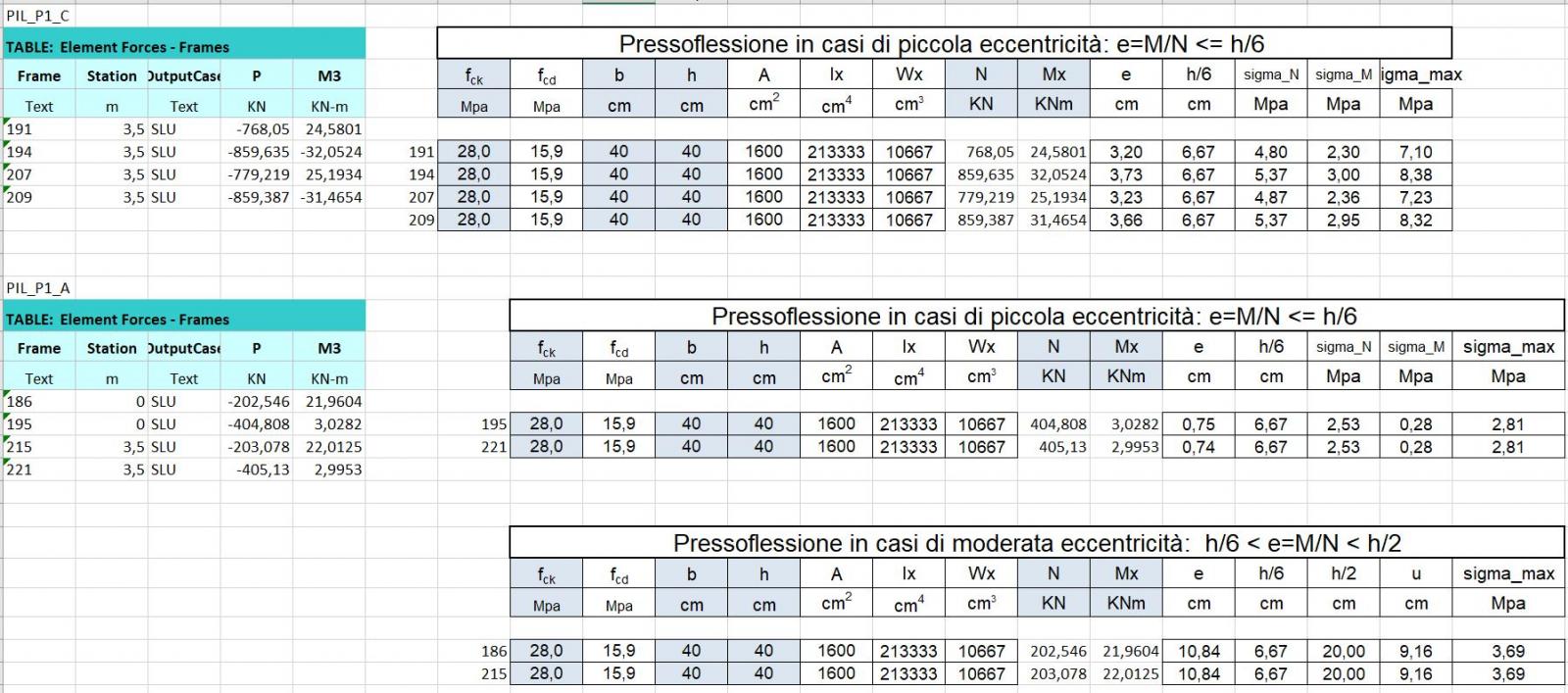
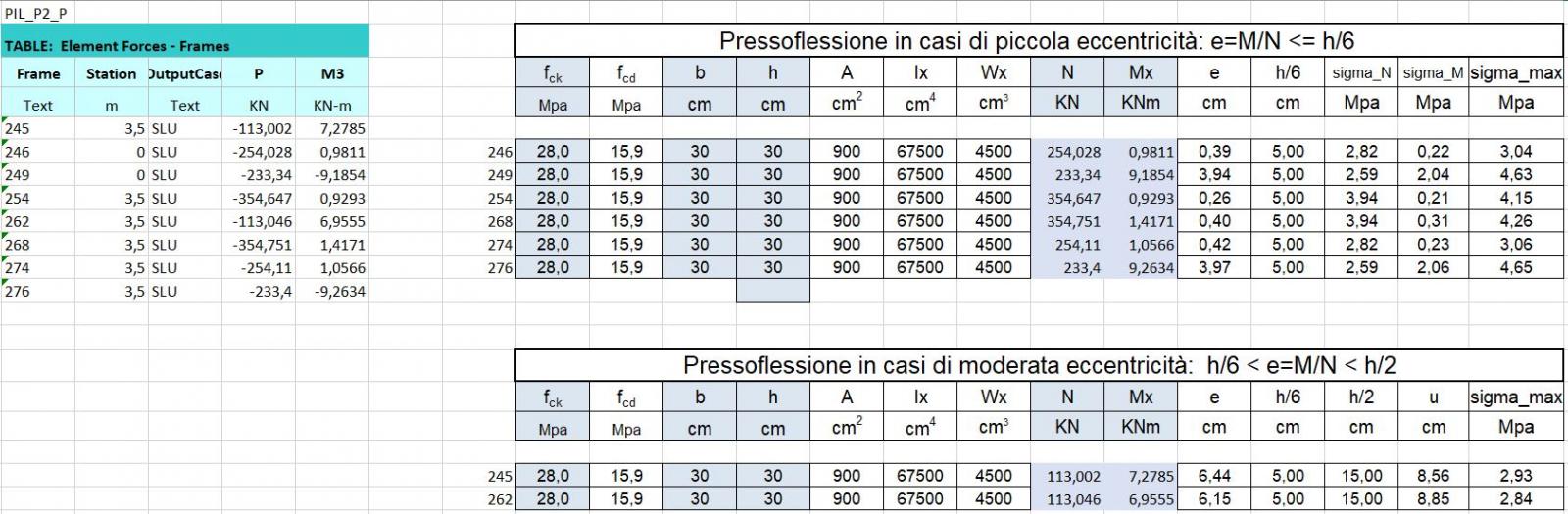
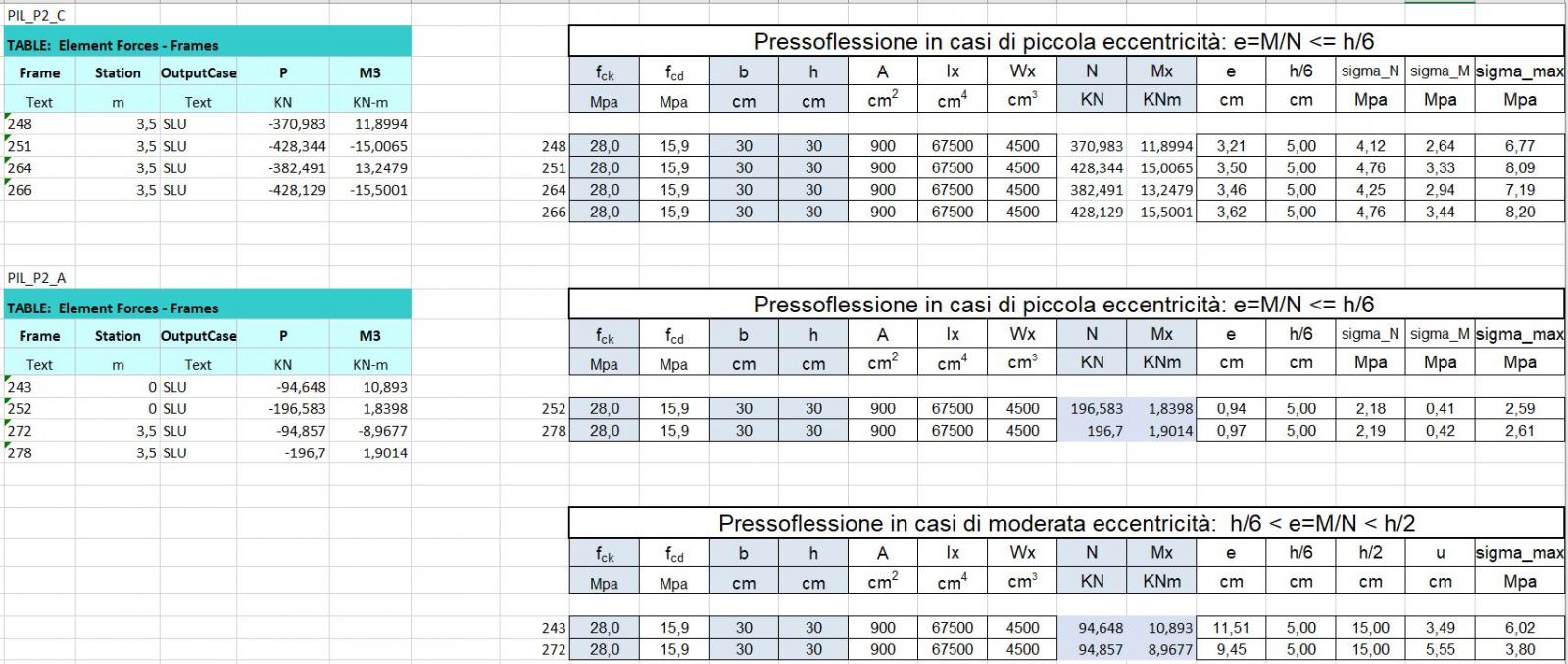
Le tabelle excel sono state esportate da sap per piani per poi dividerle in pilastri centrali, perimetrali ed angolari. I pilastri sono stati verificati con Nmax e Mmax.

Il pilastro viene verificato a pressoflessione perché il nodo trave-pilastro è rigido cioè trasmette momento per questo si verifica che σmax sia minore di fcd.

I pilastri in piccola eccentricità risultano verificati in quanto σmax= N/A + M/N < fcd.

I pilastri in moderata eccentricità risultano verificati in quanto σmax= 2/3 x N/bu < fcd.

• Verifica travi

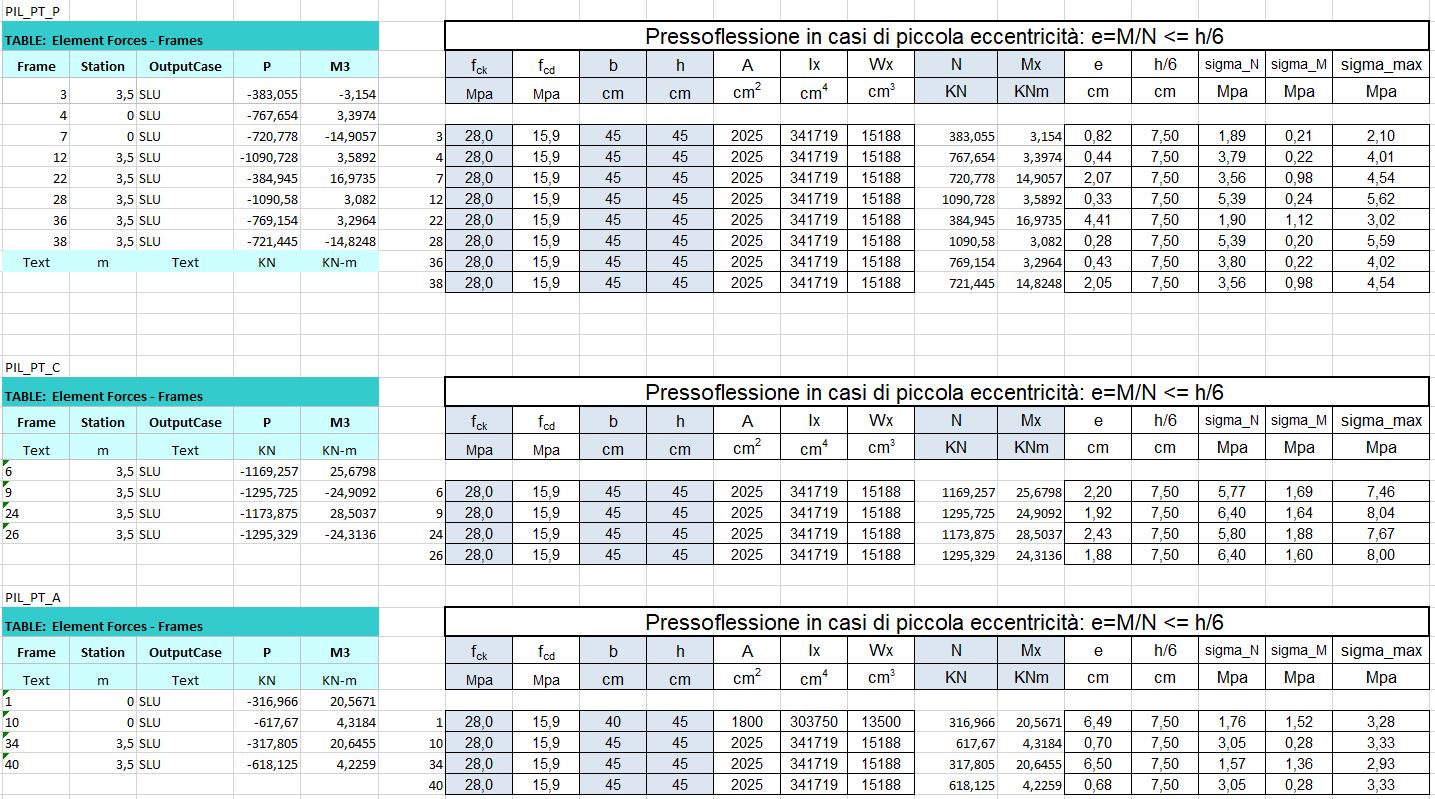
Le tabelle esportate da sap sono state divise in travi principali centrali e perimetrali e uguale per le travi secondarie.

Sono state dimensionate sostituendo in tabella Mmax per ogni trave. Successivamente teniamo conto del peso proprio della trave per verificare se l’altezza scelta è maggiore di Hmin.

Trave principale centrale

Trave principale perimetrale

Trave secondaria centrale

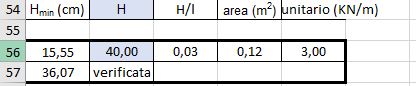
Trave secondaria perimetrale

• Verifica mensole

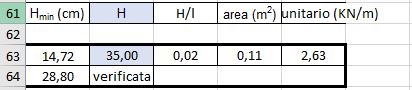
Anche le tabelle excel delle mensole sono state divise in centrali e perimetrali, in modo da sostituire Mmax con quello di ogni mensola.

Durante questo passaggio ci siamo rese conto di aver sovradimensionato le mensole laterali di conseguenza è stata cambiata la sezione su excel verificandolo a deformabilità.  

Mensola centrale

Mensola perimetrali

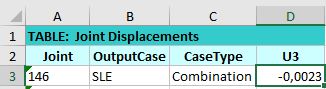
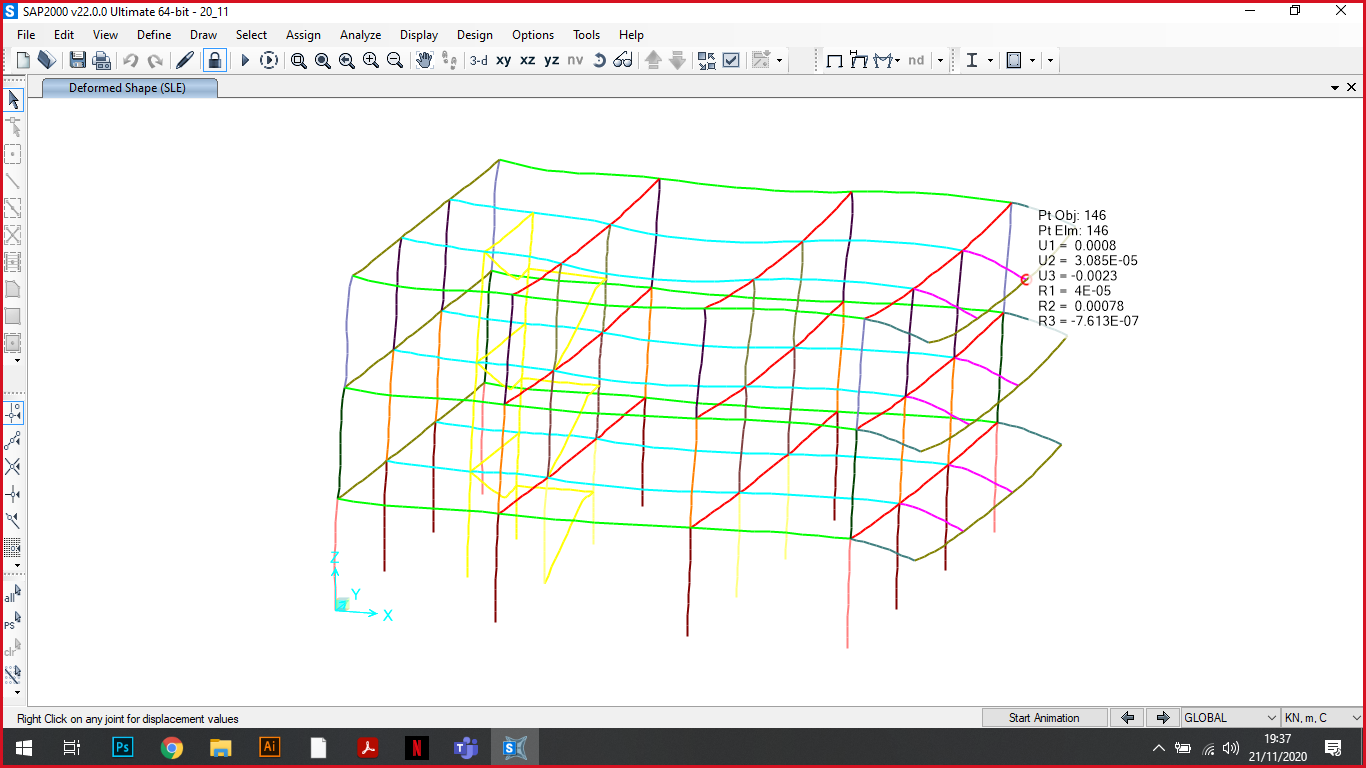
Finito il procedimento di verifica sono state modificate le sezioni risultate sovradimensionate su Sap e abbiamo effettuato l’analisi con la combinazione allo SLE per verificare la deformata.

 

 

 

 

 

 

 

 

 

Gruppo di lavoro: Giordana Panella, Quagliani Ilaria

1. Disegno di una trave reticolare tridimensionale

Abbiamo disegnato la trave reticolare tridimensionale su Autocad con un modulo di 3x3x4 metri. Sul lato più lungo si ripete per 14 volte e sul lato più corto per 4 volte.

L'edificio si sviluppa su 5 piani che appoggiano su due setti. I solai sono appesi tramite 20 pilastri.

2. Analisi dei carichi

Una volta ipotizzata la composizione dei solai è stata calcolata la distribuzione di carico ultimo: qu=  γs qs + γp qp + γa qa

qs 

Lamiera grecata: 0,105 KN/mq

Soletta in cls armato: 2,5 KN/mq

Travetti Ipe 270: 0,361 KN/mq

Travi scatolari 50x30: 0,25 KN/mq

qp

Pavimentazione: 0,19 KN/mq

Massetto: 0,38 KN/mq

Controsoffitto: 0,35 KN/mq

Impianti: 0,5 KN/mq

Tramezzi:1 KN/mq

qa

Destinazione d'uso uffici: 3 KN/mq

qu: 12,31 KN/mq

Aree di influenza:

A1,A4,F4,F1= 4,5 mq

A2,A3,F2,F3= 13,5 mq

B1,C1,D1,C4,D4,E4 = 9 mq

B2,C2,D2,C3,D3,E3 = 27 mq

Setti = 108 mq

In seguito sono state moltiplicate le aree di influenza per il numero dei piani e qu. 

3. Progetto della reticolare su SAP 2000

Una volta importato il file .dxf e definito il materiale (acciaio S355), una sezione forfettaria e i vincoli esterni e  interni. 

I carichi sono stati applicati in corrispondenza dei pilastri appesi e dei setti.

Dopo di che è stata avviata l'analisi dei carichi, che ci ha permesso di visualizzare la deformata a SLU. Poichè la trave reticolare non deve essere soggetta a momento è stato verificato che l'unico sforzo presente all'interno delle aste fosse quello assiale.

4. Dimensionamento delle aste 

A seguire sono state estrapolate le tabelle excel con i valori delle sollecitazioni che abbiamo diviso in compressione e in trazione. Le aste soggette a compressione sono state a loro volta suddivise in base alla lunghezza di inflessione e successivamente in range di 900 KN. Lo stesso ragionamento è stato fatto per le aste tese solo che sono state divise in un range di 400 KN. 

 

I profili scelti sono stati poi importati su SAP.

5. Verifica di deformabilità 

Per controllare gli spostamenti verticali è stato necessario realizzare la combinazione dei carichi PP = 1073,92 KN (peso proprio della trave reticolare) e qe= 8,64 KN/mq (distribuzione di carico di esercizio), che è stato sempre moltiplicato per le aree di influenza e per i piani dell'edificio.

Da questa analisi è stato riscontrato che l'abbassamento massimo contenuto all'interno della struttura è di 0,039 m; poichè la luce tra le due cerniere è pari a 24 m dalla formula L/200 la struttura risulta verificata.