La seconda esercitazione prevede il dimensionamento della trave più sollecitata del telaio in FIG.01 nelle tre tecnologie: legno; acciaio e cemento armato.
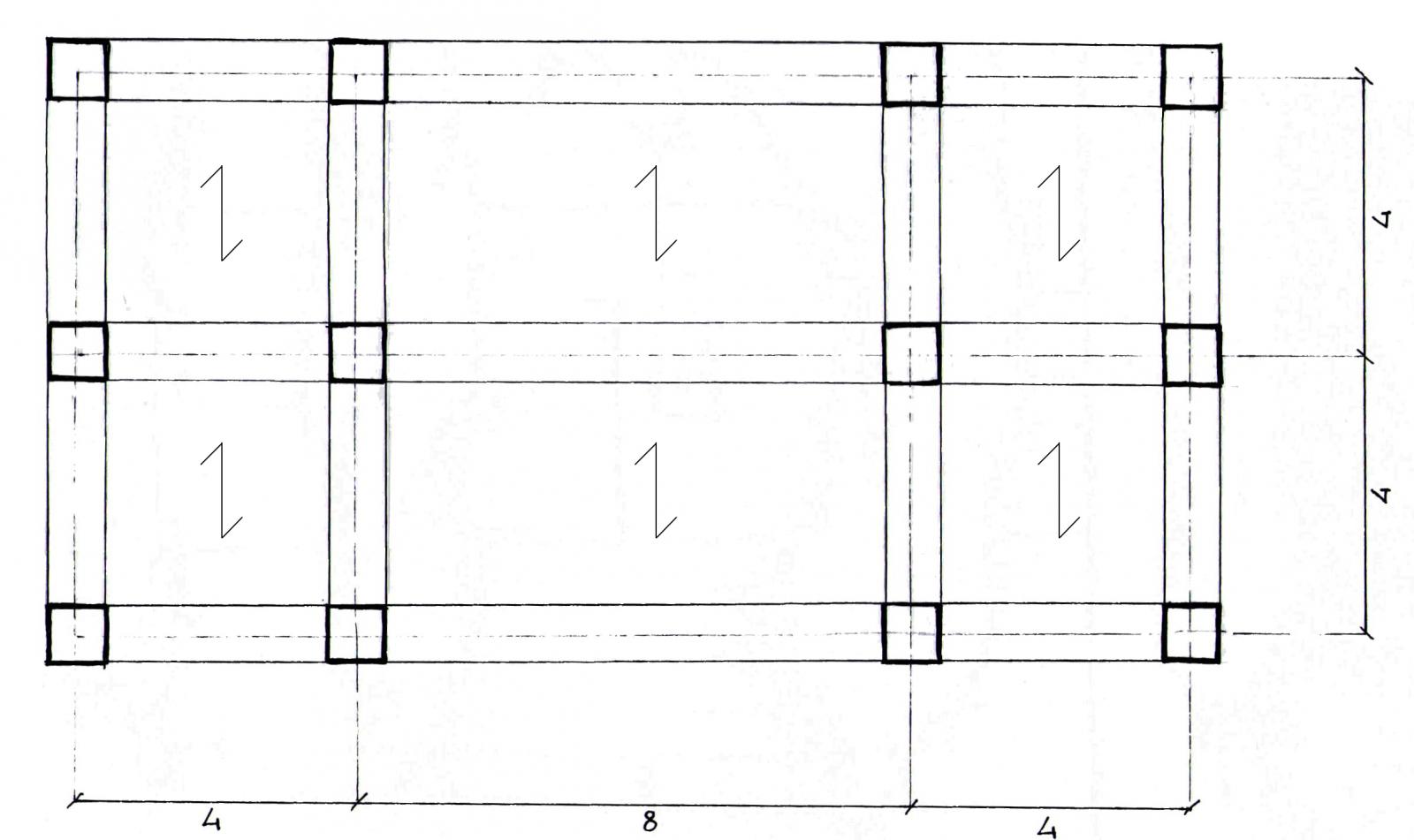
FIG.01
Osservando la struttura è evidente che la trave su cui grava più carico è quella centrale poichè la sua area di influenza è pari a 32 m2, ossia 8 m di luce x 4 m di interasse. (FIG.02)
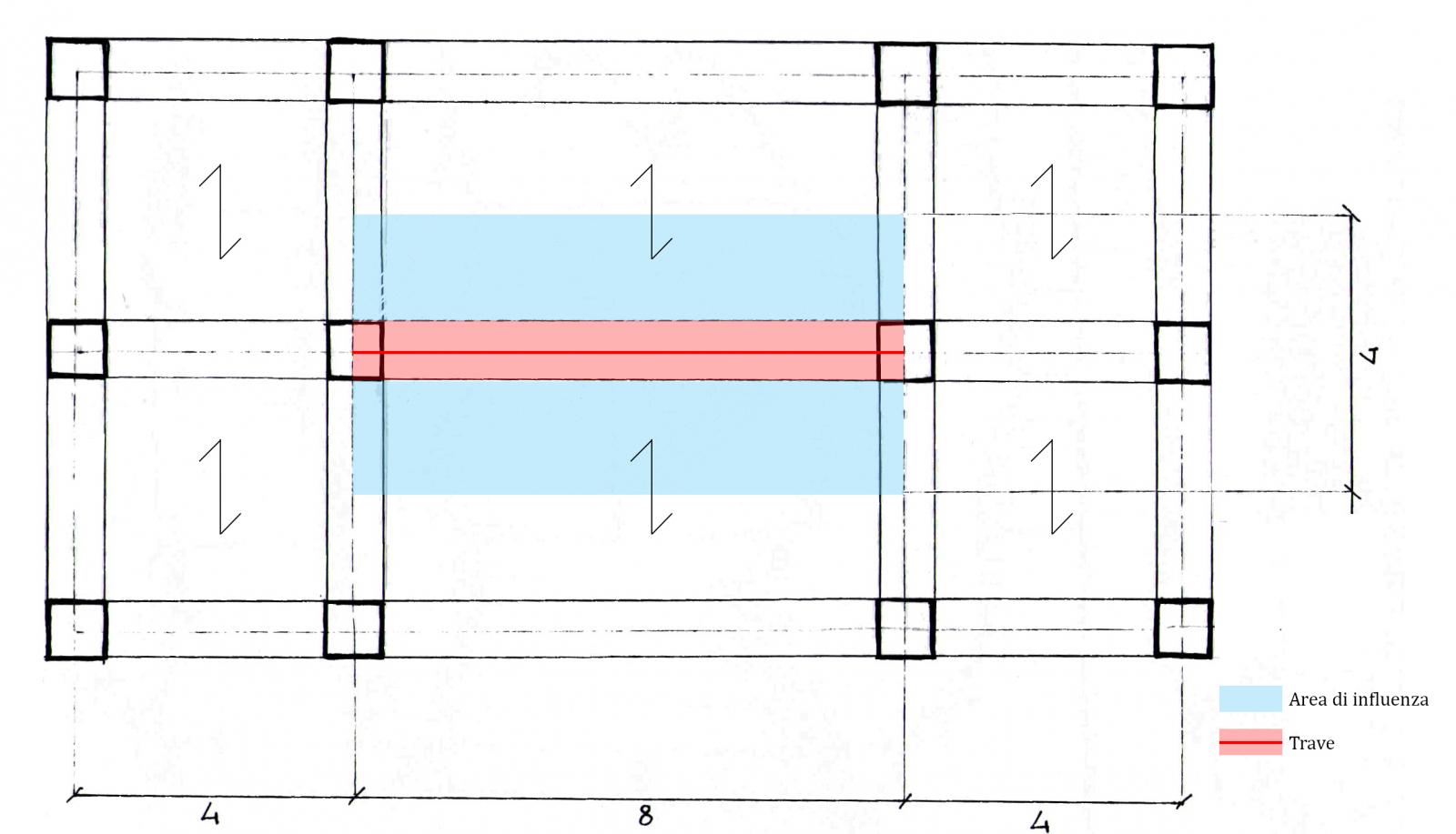
FIG.02
LEGNO
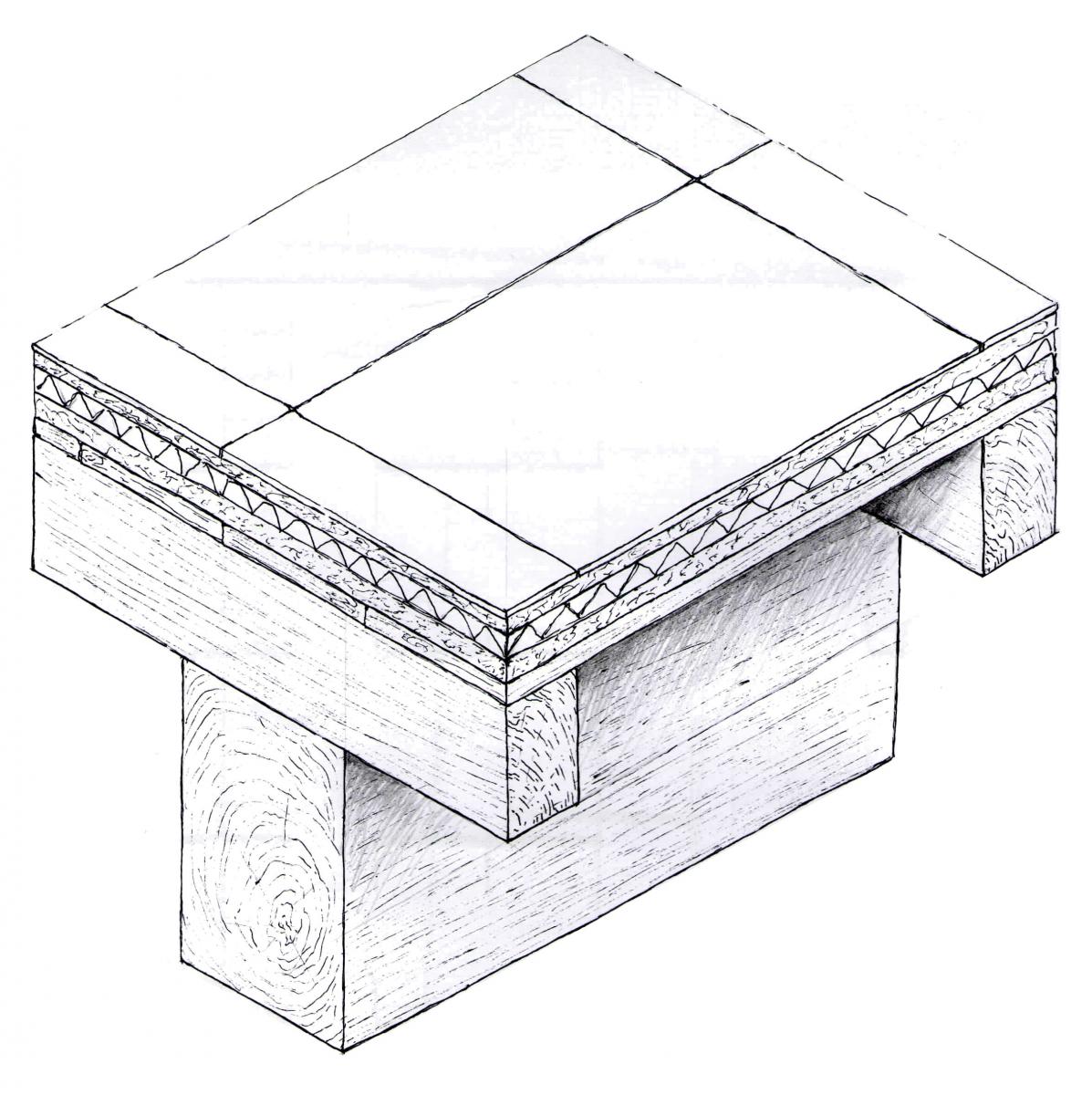
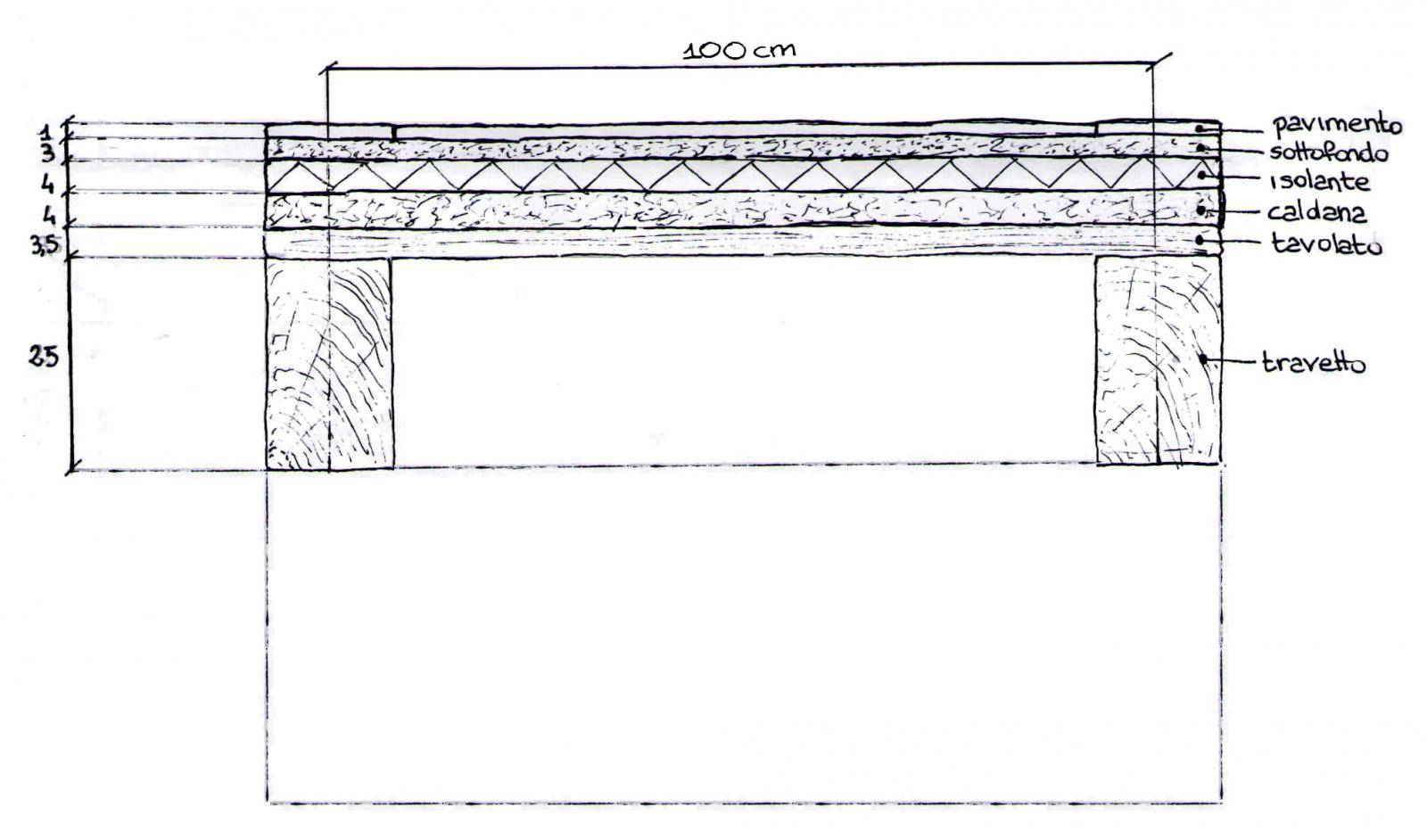
FIG.03
Supponendo un solaio in legno con un'orditura semplice (FIG.03) composto da:
travetti con sezione 15X25 cm e con un peso specifico pari a 5 kN/m3
tavolato spesso 3,5 cm e con peso pari a 0,21 kN a m2
caldana alta 4 cm e con peso pari a 0,28 kN a m2
isolante alto 4 cm e con peso pari a 0,0072 kN a m2
sottofondo alta 3 cm e con peso pari a 0,54 kN a m2
pavimento alta 1 cm e con peso pari a 0,20 kN a m2
Si calcola il carico strutturale (qs) escludendo il peso proprio della trave, il carico permanente (qp) e il carico accidentale (qa).
travetti (0,15 x 0,25 x 1)m/m2 x 5 kN/m3 = 0,0375 m3/m2 x 5 kN/m3 = 0,19 kN/m2
tavolato 0,21 kN/m2
qs = (0,19+0,21)kN/m2 = 0,40 kN/m2
caldana 0,28 kN/m2
isolante 0,0072 kN/m2
sottofondo 0,54 kN/m2
pavimento 0,20 kN/m2
qp = (0,28 + 0,0072 + 0,54 + 0,20 +1,00 + 0,50) kN/m2 = 2,53 kN/m2
ambiente ad uso residenziale 2 kN/m2
qa = 2 kN/m2
Tali valori possono essere ora inseriti in un foglio di calcolo excel che a partire dal qs, dal qp e dal qa ricaverà q (kN/m) tenendo conto di un fattore di accrescimento pari a 1,3 per i carichi permanenti strutturali e non strutturali (qs e qp) e 1,5 per i carichi accidentali (qa) e dell'interasse pari a 4m.
Conoscendo il carico gravante sulla trave e la luce di questa si può facilmente ricavare il momento della trave appoggiata (M = q x l2/8).
In fase progettuale viene scelto il tipo di legno che si vuole utilizzare, in questo caso è stato preso in considerazione un legno lamellare GL 24h la cui resistenza caratteristica fm,k è pari a 24 MPa. Ora è possibile calcolare la tensione ammissibile sigam e impostando la base b, ricavare l'altezza h. (FIG.04)

FIG.04
Non avendo considerato il peso proprio della trave è opportuno sovradimensionare la sezione scegliendo un profilo 35 x 60 cm.
A questo punto si reputa opportuno dimensione il carico dovuto al peso proprio della trave p e aggiungerlo nella tabella excel per verificare se effettivamente la trave dimensionata con una sezione 35 x 60 cm risulta adeguata.
p = (0,35 x 0,60 x 1)m3/m x 7 kN/m3 = 1,47 kN/m

FIG.05
Il peso p moltiplicato del fattore di sicurezza 1,3 è stato aggiunto nella casella E3 dei carichi q [kN/m] (FIG.05). Il nuovo carico, comprensivo anche del peso proprio della trave, può essere assorbito da una trave con h = 54,94 cm. Considerando che una trave con una sezione 35 x 55 cm avrà un peso p sicuramente inferiore a quello di una trave con sezione 35 x 60 cm, possiamo concludere il capitolo di questa esercitazione sul legno, notando un eccessivo sovradimensionamento iniziale e scegliendo un profilo rettangolare 35 x 55 cm per la nostra trave in legno lamellare.
La sezione 35 x 55 cm è stata verificata!
ACCIAIO
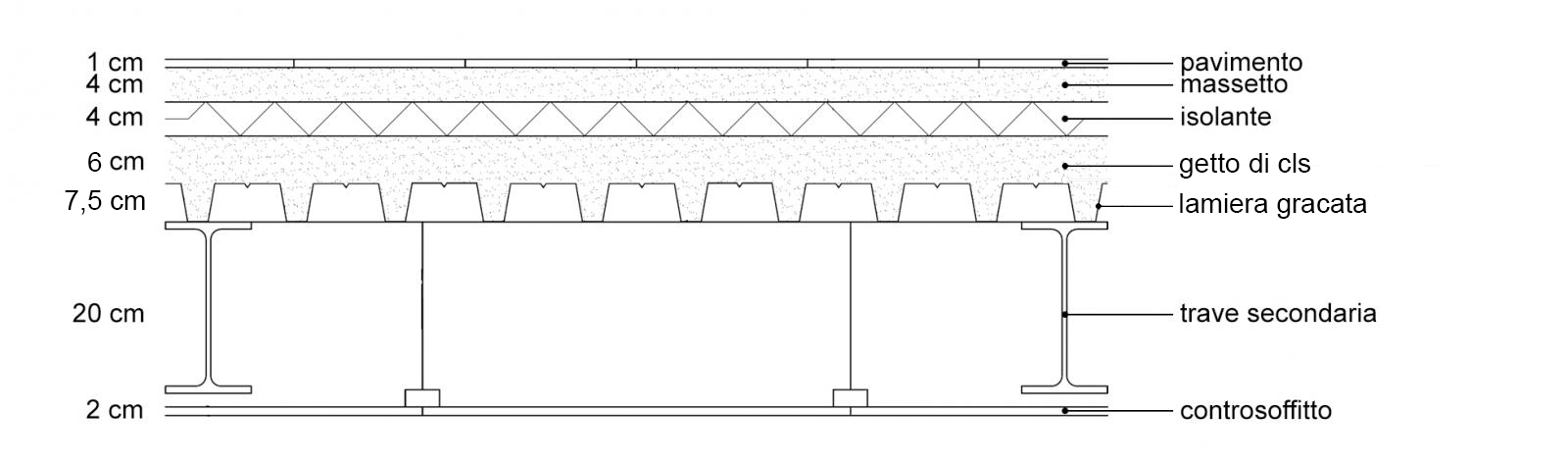
FIG.06
Supponendo un solaio in acciaio come in FIG.06 composto da:
controsoffitto spesso 1 cm e con peso specifico pari a 13 kN/m3
travi secondarie (IPE 200) con peso specifico pari a 78,5 kN/m3,
getto di cls spesso 6 cm e con peso specifico pari a 24 kN/m3,
lamiera grecata h 75 mm con peso pari a 0,11 kN/m2,
isolante alto 4 cm e con peso pari a 0,0072 kN a m2
massetto alto 4 cm e con peso pari a 0,64 kN a m2
pavimento dello spessore di 1 cm e con peso pari a 0,2 kN a m2
Si calcola il carico strutturale (qs) escludendo il peso proprio della trave, il carico permanente (qp) e il carico accidentale (qa).
travi secondarie (0,00285 x 1)m3/m2 x 78,5 kN/m3 = 0,224 kN/m2
getto di cls V x p= 0,035 m3/m2 x 24 kN/m3 = 0,84 kN/m2
lamiera grecata 0,11 kN/m2
qs = 0,224 + 0,84 + 0,11 kN/m2=1,174 kN/m2
isolante 0,0072 kN/m2
massetto 0,64kN/m2
pavimento 0,2kN/m2
controsoffitto (0,02 x 1 x 1)m3/m2 x 13 kN/m3 = 0,26 kN/m2
qp = (0,0072 + 0,64 + 0,2 + 0,26) kN/m2 = 2,61 kN/m2
ambiente ad uso residenziale 2 kN/m2
qa = 2 kN/m2

FIG.07
I risultati restituiti dalla tabella excel riportano un valore del modulo di resistenza Wx pari a 1059,73 cm3, è perciò opportuno selezionare come profilo un IPE 400 in cui Wx è pari a 1160 cm3.
Anche per la trave in acciaio è opportuno calcolare nuovamente il carico q aggiungendo il peso proprio della trave p, maggiorato di un fattore pari a 1,3.
Trave IPE 400 con sezione pari a 84,50 cm2, e peso specifico dell'acciaio pari a 78,5 kN/m3.
p = (84,50 x 10-4 x 1) m3/m x 78,50 kN/m3 = 0,663 kN/m

FIG.08
Dalla FIG.08 possiamo notare come nonostante nel primo predimensionamento non era stato considerato il peso proprio della trave, il profilo scelto sarebbe risultato comunque idoneo per coprire la luce di 8 metri, supponendo un solaio come quello della FIG.06 .
Il profilo IPE 400 è stato verificato!
CLS
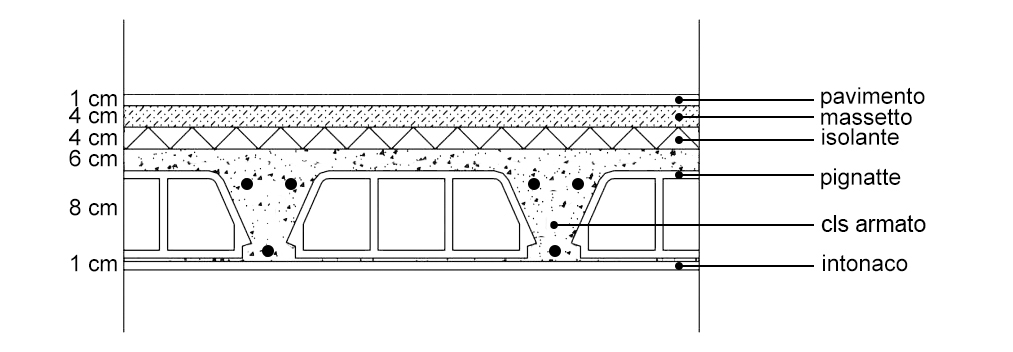
FIG.09
Supponendo un solaio in latero-cemento come in FIG.09 composto da:
intonaco spesso 1 cm e con peso specifico pari a 18 kN/m3
pignatte n° 2 di dimensioni 8x40x25 cm e con peso pari a 1,32 kN a m2
cls armato con una sezione pari a 840 cm2 in un metro e con peso pari a 25 kN/m3
massetto alto 4 cm e con peso pari a 0,64 kN a m2
pavimento alta 1 cm e con peso pari a 0,20 kN a m2
Si calcola il carico strutturale (qs) escludendo il peso proprio della trave, il carico permanente (qp) e il carico accidentale (qa).
pignatte 1,32 kN/m2
cls armato ( 0,084 x 1) m3/m2 x 25 kN/m3 = 2,10 kN/m2
qs = 1,32 kN/m2 + 2,10 kN/m2 = 3,42 kN/m2
isolante 0,0072 kN/m2
massetto 0,64kN/m2
pavimento 0,2kN/m2
intonaco (0,01 x 1 x 1)m3/m2 x 18 kN/m3 = 0,18 kN/m2
qp = (0,0072 + 0,64 + 0,2 + 0,18) kN/m2 = 2,56 kN/m2
ambiente ad uso residenziale 2 kN/m2
qa = 2 kN/m2


FIG.10
Come si può apprezzare dalla FIG.10, scegliendo un acciaio per le armature con una resistenza caratteristica fy pari a 450 MPa e un calcestruzzo con resistenza a compressione Rck pari a 50 MPa e impostando la base b della nostra trave su i 30 cm, avremo un altezza utile h pari a 43,42 cm, che diventa H = 48,52 cm aggiungendo il delta = 5 cm. Arrotondiamo a 55 cm per una sezione finale della trave in cemento armato pari a 30 x 55 cm.
Come per la trave in legno e per quella in acciaio è opportuno calcolare il carico q aggiungendo il peso proprio della trave p,moltiplicato per un fattore pari a 1,3.
p = (0,35 x 0,55 x 1)m3 x 25 kN/m3= 4,125 kN/m


FIG.11
Dalla FIG.11 possiamo notare come aggiungendo il peso proprio della trave p ai carichi q la sezione predimensionata con un profilo 30 x 55 cm risultati idonea per coprire la luce di 8 metri, supponendo un solaio come quello della FIG.09.
La sezione 30 x 55 cm è stata verificata!
Commenti recenti