
Prendendo ad esempio questa pianta di carpenteria ipotetica, possiamo dedurre che la trave maggiormente sollecitata è la C: è sicuramente una trave principale che sostiene l’orditura del solaio ed è quella con l’area di influenza maggiore (32mq), determinata dal prodotto della luce (8m) per l’interasse (4m).

Come prima cosa possiamo inserire nei fogli excel per tutte e tre le tecnologie le dimensioni (luce e interasse) determinate dalla pianta di carpenteria

[legno]

[acciaio]

[cls]
PREMESSA:
Prescindendo dal tipo di tecnologia e dalla stratigrafia specifica di ogni solaio, sappiamo che per conoscere a che tipo di sollecitazione è sottoposta la trave dovremo necessariamente calcolare i diversi carichi agenti sul solaio espressi come densità di carico superficiale [kN/mq].
Calcoleremo i diversi carichi (q) in base alla loro classificazione:
qs: carico degli elementi strutturali
qp: carico permanente degli altri elementi presenti con funzione non strutturale, a cui va aggiunto il carico dovuto ai tramezzi (1 kN/mq) e quello dovuto agli impianti (0,5 kN/mq)
[ vengono utilizzati questi valori approssimati per l’incidenza di questi due elementi sia per la difficoltà di effettuare precisamente il calcolo, sia perché la loro distribuzione interna e quantità spesso cambiano nella vita di una costruzione]
qa: carichi accidentali. Sono regolati dalla normativa (NTC2008- Norme tecniche per le costruzioni- D. M. 14 Gennaio 2008), comprendono anche fenomeni naturali queli sisma, vento o precipitazioni nevose. In questa esercitazione terremo conto solamente dei carichi di esercizio (legati alla destinazione d’uso dell’edificio). Nello specifico considereremo un edificio residenziale che secondo normativa appartiene alla categoria A (ambienti ad uso residenziale: locali di abitazione e relativi servizi, alberghi ad esclusione di aree suscettibili ad affollamento) e per il quale è previsto un valore tabellato di 2kN/mq
-----------------------------------------------------------------------------------------------------------------------------
DIMENSIONAMENTO:
LEGNO
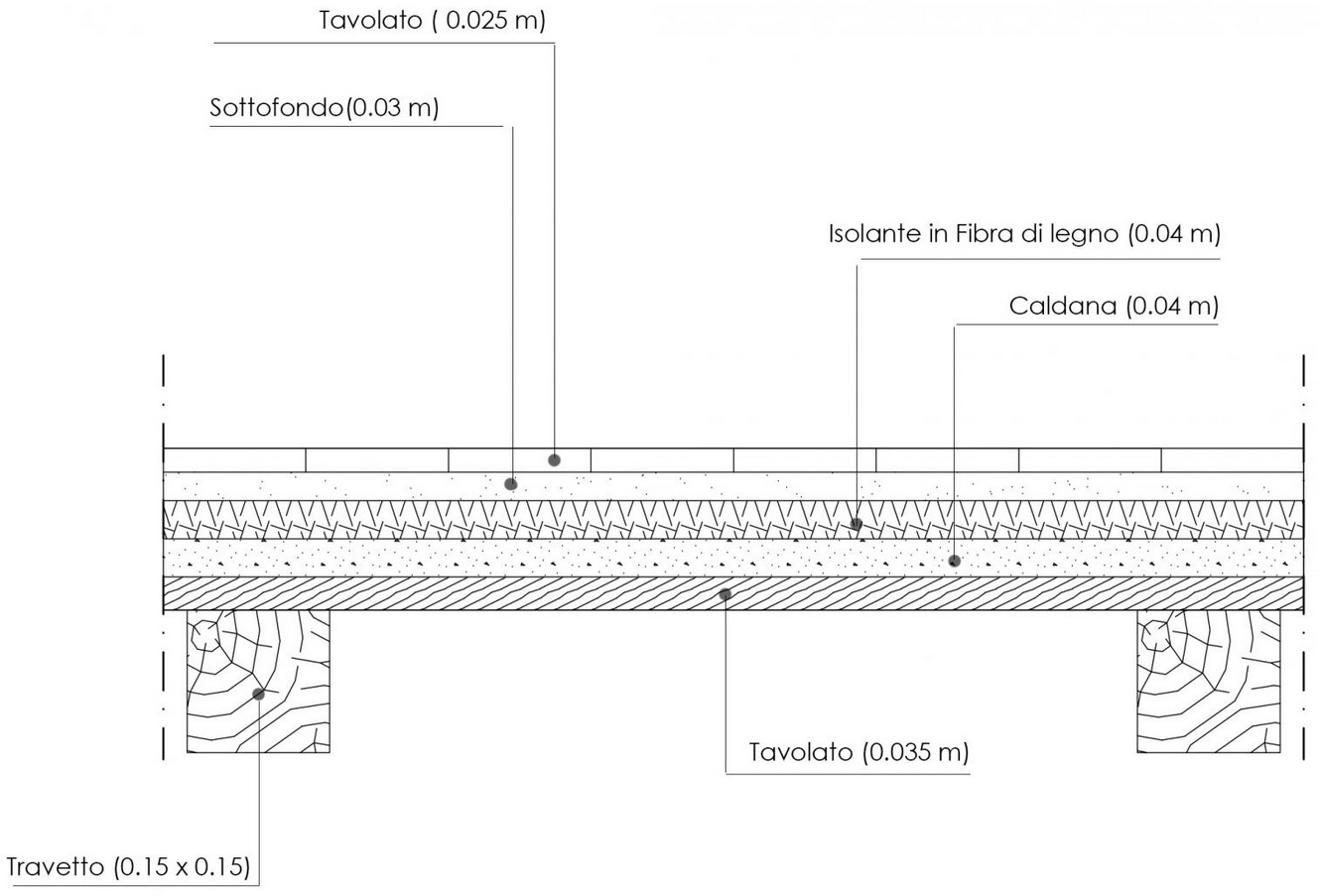
una volta ipotizzata la stratigrafia e la composizione del solaio è necessario prendere in considerazione il peso specifico di tutti i materiali che la compongono che sarà poi necessaio per il calcolo delle varie densità di carico.
materiale dimensioni(spessore/sezione) [cm] peso specifico [kN/mc]
1 travetto abete [qs] 15x15 7
2 tavolato abete [qs] 3,5 7
3 caldana malta di cemento [qp] 4 21
4 isolante fibra di legno [qp] 4 0,48
5 sottofondo malta di calce [qp] 3 18
6 tavolato (pav.) abete [qp] 2,5 7
Dopo aver raccolto tutti i dati possiamo calcolare la densità di carico, cioè il carico superficiale per 1 mq di solaio.
Seguendo la premessa, calcoleremo questi valori suddividendoli per categorie, per ognuna delle quali saranno attribuiti dei coefficienti moltiplicativi di sicurezza differenti che sono riportati in normativa in funzione dello stato limite che si intende considerare: nel nostro caso allo stato limite ultimo.
carico strutturale qs:
1 travetto (0,15 x 0,15 x 1) m³/m² x 7 kN/m³ = 0,157 kN/m²
2 tavolato (0,035 x 1 x 1) m³/m² x 7 kN/m³ = 0,245 kN/m²
qs = 0,157 + 0,245 kN/m² = 0,402 kN/m² ( in questa fase non stiamo considerando il peso proprio della trave che stiamo dimensionando)
carico permanente qp:
3 caldana (0,04 x 1 x 1) m³/m² x 21 kN/m³ = 0,84 kN/m²
4 isolante (0,04 x 1 x 1) m³/m² x 0,48 kN/m³ = 0,192 kN/m²
5 sottofondo (0,03 x 1 x 1) m³/m² x 18 kN/m³ = 0,54 kN/m²
6 tavolato (pav.) (0,025 x 1 x 1) m³/m² x 7 kN/m³ = 0,175 kN/m²
qp = 0,84 + 0,192 + 0,54 + 0,175 kN/m² = 1,75 kN/m²
a cui dobbiamo aggiungere 1,5 kN/m² dovuti agli impianti e ai tramezzi
qp = 1,75 + 1,5 kN/m² = 3,25 kN/m²
carico accidentale qa:
come abbiamo detto considereremo un edificio in classe A e quindi assumiamo
qa = 2 kN/m²
L’inserimento dei risultati ottenuti nel foglio excel produrrà un valore qu, carico lineare, generato dal prodotto del singolo valore di carico per il proprio coefficiente moltiplicativo secondo la formula:
qu = [(qs x 1,3) + (qp x 1,5) + (qa x 1,5)] x interasse = [(0,402 x 1,3) + (3,25 x 1,5) + (2,00 x 1,5)] x 4 = 33,59 kN/m

E’ denominato qu perchè rappresenta la combinazione di carico per Stato Limite Ultimo determinato dalla normativa.
Inserendo questo valore nella formula per il calcolo del momento massimo di una trave doppiamente appoggiata e la luce che abbiamo impostato , otterremo il valore della sollecitazione per cui stiamo progettando la trave.
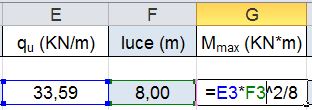
Possiamo quindi iniziare a inserire i dati relativi al progetto.
il primo valore da inserire è quello relativo alla resistenza caratteristica a flessione fm,k che è riferito alla tecnologia (massiccio o lamellare)
Si incontrano poi dei coefficienti che sono necessari per il calcolo della tensione di progetto:
Kmod e gamma.
Kmod è un coefficiente diminutivo dei valori di resistenza del materiale, che tiene in conto l’effetto della durata del carico e delle condizioni di umidità in cui la struttura si troverà ad operare.
Gamma è il coefficiente parziale di sicurezza relativo al materiale e i suoi valori sono tabellati.
Nel nostro caso ipotizzeremo un Kmod relativo a una durata media (0,8) e un valore gamma per un legno lamellare incollato (1,45).
Dopo aver inserito le informazioni geometriche, le caratteristiche del materiale e aver determinato la tensione di progetto, possiamo dimensionare la sezione rettangolare della trave semplicemente scegliendo una base di progetto e quindi determinando l’altezza.
Questo metodo prevede infatti che l’altezza (h) sia l’unica incognita da determinare per il dimensionamento, e che si considerino date la base (b) ,il momento massimo e la tensione di progetto.

Come possiamo vedere, ipotizzando una base di 35 cm e una classe di resistenza GL24c, che l’altezza minima necessaria è 58,98 cm: arrotondata sceglieremo un’altezza di 60cm
qualora volessimo diminuire questo valore possiamo ipotizzare una classe di resistenza più elevata. Iterando il processo possiamo vedere che per ridurre di dieci centimetri l’altezza dobbiamo arrivare ad una classe di resistenza GL36c

A questo punto però, data la grande luce della trave, è opportuno verificare che la sezione risulti verificata anche aggiungendo a qs il peso proprio della trave:
qs trave = (0,35 x 0,6 x 1) m³/m² x 7 kN/m³ = 1,47 kN/m²
aggiungendo questo valore al qs calcolato in precedenza:
qstot = 1,47 + 0,402 kN/m² = 1,872 kN/m²

si nota che matenendo la stessa classe di resistenza del legno (GL24c) la sezione non risulta verificata è necessario portare la classe di resistenza a GL32c.

-----------------------------------------------------------------------------------------------------------------------------
ACCIAIO

materiale dimensioni(spessore/sezione) [cm] peso specifico [kN/mc]
1 controsoffitto cartongesso [qp] 2 7,6
2 travi secondarie IPE200 [qs] 28,50cm2 78,5
3 lamiera grecata [qs] 0,75 0,11 (kN/mq)
4 getto cls malta di cemento [qs] 6 24
5 isolante lana di roccia [qp] 4 0,4
6 massetto cemento cellulare [qp] 4 11,7
7 piastrelle (pav.) cotto [qp] 2,5 18
Dopo aver raccolto tutti i dati possiamo calcolare la densità di carico, cioè il carico superficiale per 1 mq di solaio.
carico strutturale qs:
2 travi secondarie (0,00285 x 1) m3/m2 x 78,5 kN/m3 = 0,224 KN/m2
3 lamiera grecata 0,11KN/m2
4 getto cls (0,035 x 1) m3/m2 x 24 kN/m3 = 0,84 KN/m2
qs = 0,224 + 0,11 + 0,84 kN/m² = 1,174 kN/m²
carico permanente qp:
1 controsoffitto (0,02 x 1 x 1) m³/m² x 7,6 kN/m³ = 0,152 kN/m²
5 isolante (0,04 x 1 x 1) m³/m² x 0,4 kN/m³ = 0,016 kN/m²
6 massetto (0,04 x 1 x 1) m³/m² x 11,7 kN/m³ = 0,468 kN/m²
7 pavimento (0,025 x 1 x 1) m³/m² x 18 kN/m³ = 0,45 kN/m²
qp = 0,152 + 0,016 + 0,468 + 0,45 kN/m² = 1,086 kN/m²
a cui dobbiamo aggiungere 1,5 kN/m² dovuti agli impianti e ai tramezzi
qp = 1,086 + 1,5 kN/m² = 2,58 kN/m²
carico accidentale qa:
come abbiamo detto considereremo un edificio in classe A e quindi assumiamo
qa = 2 kN/m²

Ora possiamo inserire i valori relativi al materiale:
Il valore che distingue un acciaio da un altro è la tensione caratteristica di snervamento fy,k (i pedici y e k significano rispettivamente yield/snervamento e k/caratteristico), che individua la classe di resistenza del materiale.

La tensione di progetto fyd si calcola a partire dalla tensione di snervamento dell’acciaio prescelto, tenendo conto di un coefficiente parziale di sicurezza γs, che in questo caso è pari a 1,05:

Il foglio di calcolo fornirà ora il dato Wxmin calcolato tramite il valore del momento massimo (Mmax = ql2/8) e della tensione di progetto, secondo l’equazione Wxmin = Mmax / fyd


Una volta ottenuto il valore minimo del modulo di resistenza della sezione possiamo scegliere tra i profili esistenti sul mercato. Ovviamente non troveremo un valore pari a quello che otteniamo precisamente dai nostri calcoli, dovremo scegliere un profilo che abbia un modulo di resistenza superiore a quello ottenuto.
nel nostro caso Wx,min= 1025,86 cm3. Il profilo che soddisfa la nostra necessità è quello di una IPE400, il cui Wx è pari a 1160 cm3.

E’ opportuno verificare che la sezione sia verificata anche tenendo in considerazione il peso proprio della trave: (sezione: 84,5cm², densità 78,5 kN/m³)
qs trave = (0,00845 x 1) m³/m² x 78,5 kN/m³ = 0,663 kN/m²
aggiungendo questo valore al qs calcolato in precedenza
qstot = 1,174 + 0,663 kN/m² = 1,837 kN/m²

Notiamo che il nuovo valore Wxmincalcolato considerando il peso della trave, rientra nel valore previsto per il profilo selezionato.

-----------------------------------------------------------------------------------------------------------------------------
CLS
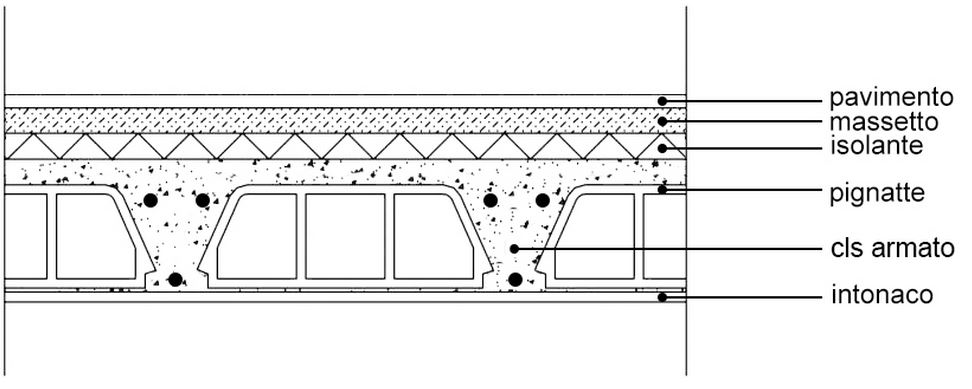
materiale dimensioni(spessore/sezione) [cm] peso specifico [kN/mc]
1 intonaco [qp] 1 18
2 cls armato [qs] 840cm2 25
3 pignatte laterizio [qs] 8x40x25 1,32 (kN/mq)
4 isolante lana di roccia [qp] 4 0,4
5 massetto cemento cellulare [qp] 4 11,7
6 parquet (pav.) larice [qp] 2,5 7
Dopo aver raccolto tutti i dati possiamo calcolare la densità di carico, cioè il carico superficiale per 1 mq di solaio.
carico strutturale qs:
2 cls armato (0,084 x 1) m3/m2 x 25 kN/m3 = 2,1 KN/m2
3 pignatte 1,32KN/m2
qs = 2,1 + 1,32 kN/m² = 3,42 kN/m²
carico permanente qp:
1 intonaco (0,01 x 1 x 1) m³/m² x 18 kN/m³ = 0,18 kN/m²
4 isolante (0,04 x 1 x 1) m³/m² x 0,4 kN/m³ = 0,016 kN/m²
5 massetto (0,04 x 1 x 1) m³/m² x 11,7 kN/m³ = 0,468 kN/m²
6 pavimento (0,025 x 1 x 1) m³/m² x 7 kN/m³ = 0,175 kN/m²
qp = 0,18 + 0,016 + 0,468 + 0,175 kN/m² = 0,839 kN/m²
a cui dobbiamo aggiungere 1,5 kN/m² dovuti agli impianti e ai tramezzi
qp = 0,839 + 1,5 kN/m² = 2,339 kN/m²
carico accidentale qa:
come abbiamo detto considereremo un edificio in classe A e quindi assumiamo
qa = 2 kN/m²

Il foglio di calcolo relativo al cemento armato ha bisogno di più informazioni per dimensionare l’altezza della sezione rettangolare di una trave; questo può essere spiegato dal fatto che si tratta di un materiale non omogeneo, composto da calcestruzzo e da acciaio.
Proprio per questo motivo in fase progettuale è necessario scegliere sia la resistenza caratteristica dell’acciaio (fyk) , che quella del calcestruzzo (fck).

Avendo scelto le resistenze caratteristiche, è possibile ricavare da queste la tensione di progetto del calcestruzzo compresso (fcd) e quella dell’acciaio (fyd), che da normativa sono:
fyd= fyk/γs
Con γs che è il coefficiente parziale di sicurezza relativo all’acciaio ed assume il valore di 1,15 per gli acciai da armatura.
fcd= αcc fck/γc
Con αcc che rappresenta il coefficiente riduttivo per le resistenze di lunga durata, pari a 0,85; e γc, il coefficiente parziale di sicurezza relativo al calcestruzzo, uguale a 1,5.
Utilizzando questi valori calcolati e ipotizzando una base, scelta progettuale, della trave (in questa ipotesi 30cm), possiamo ottenere il valore delle hu


come sappiamo l’altezza minima della trave in calcestruzzo armato è definita dalla formula
Hmin = hu + δ
dove δ è l’altezza dello strato copriferro (nel nostro caso 5cm)

da cui

la nostra scelta ricade quindi su un’altezza di 50 cm (approssimando per eccesso).
Più ancora che per i precedenti casi, che solitamente configurano strutture leggere, e per i quali abbiamo effettuato la verifica prevalentemente a causa della grande luce da superare, nel caso del calcestruzzo armato ,che viene considerato una struttura pesante, è necessario effettuare la verifica considerando il peso proprio della trave,
in questo caso il foglio excel già contiene delle celle di calcolo atte a questa veriifca.
le prime tre calcolano il peso unitario della trave:

nel nostro caso 3,75kN/m.
La riga sottostante aggiunge il peso al valore di carico ultimo qu, mantentedo tutti i valori progettati in precedenza (le tensioni e la geometria), calcolando una nuova altezza utile (hu) e una conseguente altezza minima (Hmin).

dopodichè, se la nuova Hmin risulterà inferiore a quella ipotizzata nella casella H della riga precedente, il foglio comunicherà che la sezione della trave è verificata.
Commenti recenti