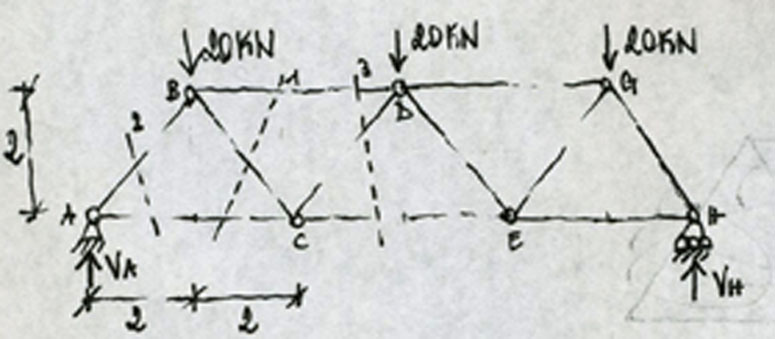
Per calcolare le azioni di contatto agenti sulla struttura come prima cosa occorre verificare l’isostaticità della struttura, in modo tale che le reazioni possano essere determinate attraverso le solo condizioni di equilibrio. La struttura sarà isostatica se il numero di gradi di libertà eguaglierà il numero dei gradi di vincolo, e quindi se L=V (dove V è uguale al numero dei gradi di vincolo esterni più i gradi di vincolo interni):
L = numero aste x 3
V = Ve + Vi
Ve = gradi di vincolo del carrello + gradi di vincolo della cerniera = 3
Vi = 2 ( n - 1 ) ; dove n è il numero di aste nel nodo che sto considerando
Nodi A-H: 2 ( n - 1 ) = 2 ( 2 - 1 ) = 2
Nodi B-G: 2 ( n - 1 ) = 2 ( 3 - 1 ) = 4
Nodi C-D-E: 2 ( n - 1 ) = 2 ( 4 - 1 ) = 6
Vi = nodoA + nodoB + nodoC + nodoD + nodoE + nodoG + nodoH = 30
V = Ve + Vi = 3 + 30 = 33
L = V → 33 = 33 ISOSTATICITA’ VERIFICATA
Una volta verificata l’isostaticità della struttura, si può procedere col calcolo delle reazioni vincolari. Per simmetria della struttura e dei carichi, le reazioni vincolari verticali della cerniera e del carrello saranno uguali tra loro, quindi ciascuna sarà uguale a metà del carico totale:
Va = Vh = 3 * 20KN / 2 = 30KN
Mentre la reazione vincolare orizzontale della cerniera applicata nel nodo A sarà pari a zero poichè non ci sono altre forze orizzontali in grado di bilanciarla.
Per calcolare le azioni di contatto abbiamo scelto di utilizzare il metodo delle sezioni di Ritter, andando a sezionare idealmente la struttura e facendo attenzione a non intersecare più di tre aste che non convergano nello stesso punto. Inoltre le forze applicate alla struttura dovranno essere equilibrate dalle azioni di contatto nelle aste tagliate.
PRIMA SEZIONE
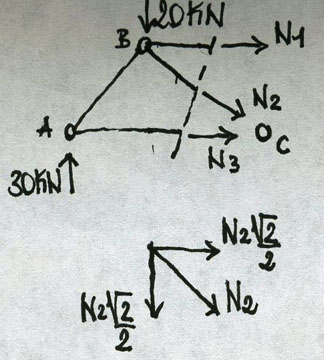
Attraverso l’equilibrio dei momenti in C ottengo il valore dello sforzo normale N1:
∑Mc = - 30*4 + 20*2 - N1*2 = 0
N1 = ( - 30*4 + 20*2 ) / 2 = - 40KN → avevo supposto per convenzione un N1 positivo di trazione, poiché il valore è venuto negativo questo vuol dire che lo sforzo normale è di compressione e pari a 40KN
Attraverso l’equilibrio dei momenti nel nodo B ottengo il valore dello sforzo normale N3:
∑Mb = - 30*2 + N3*2 = 0
N3 = 30*2/2 = 30KN → il valore è venuto positivo, questo vuol dire che il verso supposto inizialmente è corretto quindi l’asta è tesa
Per trovare il valore dello sforzo normale sull’asta 2 devo scomporre il valore di N2 in una componente verticale e una orizzontale, quindi tramite l’equilibrio delle forze verticali posso trovarmi il valore di N2:
∑Fy = 30 - 20 - N2*√2/2 = 0
N2 = ( 30 - 20 ) * 2/√2 * √2/√2 = 10√2KN → il valore è positivo quindi l’asta è tesa
Facendo altre sezioni e applicando lo stesso procedimento posso calcolare il valore dello sforzo normale su tutte le aste.
SECONDA SEZIONE
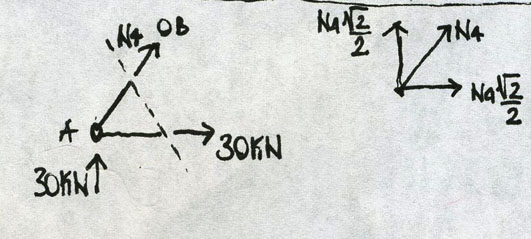
Scompongo lo sforzo normale N4 in una componente orizzontale e una verticale e tramite l’equilibrio delle forze orizzontali determino il valore di N4:
∑Fx = 30 + N4*√2/2 = 0
N4 = - 30 * 2/√2 * √2/√2 = - 30√2KN → il valore è negativo quindi l’asta è compressa
TERZA SEZIONE
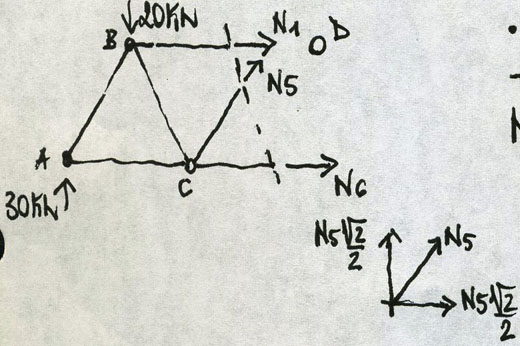
Attraverso l’equilibrio dei momenti nel nodo D ottengo il valore di N6:
∑Md = - 30*6 + 20*4 + N6*2 = 0
N6 = ( 30*6 - 20*4) / 2 = 50KN → il valore è positivo quindi l’asta è tesa
Scompongo lo sforzo normale N5 in una componente orizzontale e una verticale, quindi attraverso l’equilibrio delle forze verticali determino il valore di N5:
∑Fy = 30 - 20 + N5*√2/2 = 0
N5 = ( - 30 + 20 ) * 2/√2 * √2/√2 = - 10√2KN → il valore è negativo quindi l’asta è compressa
La struttura è simmetrica quindi non ho bisogno di altre sezioni per determinare gli altri sforzi normali, infatti i risultati trovati possono essere estesi al resto della struttura:
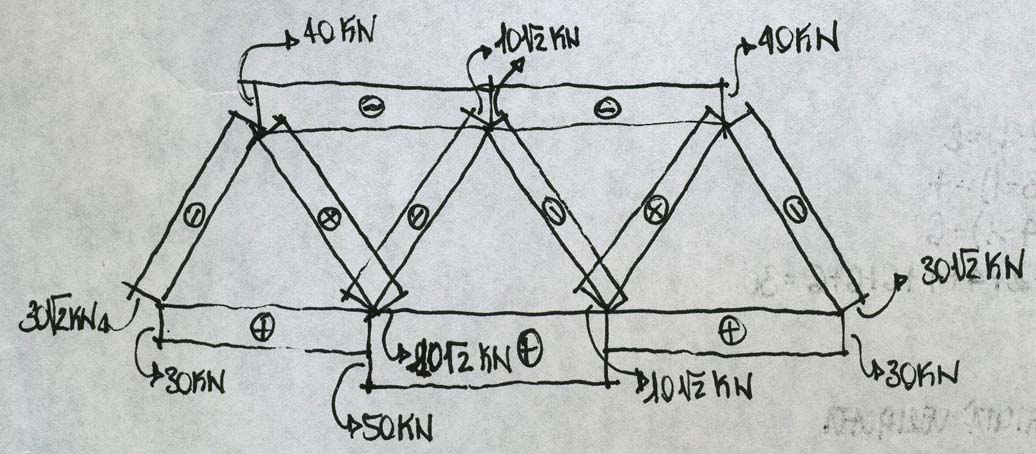
Utilizzando il software SAP2000, disegnando quindi la struttura, assegnandogli i vincoli e le forze esterne, ho potuto verificare i risultati ottenuti nel calcolo a mano:
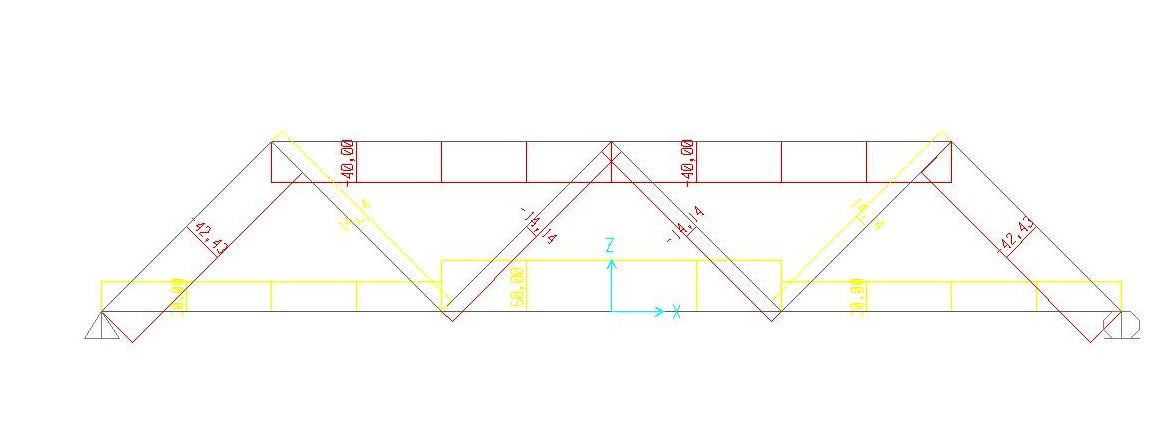
TRAVATURA RETICOLARE ASIMMETRICA

Per prima cosa verifico l’isostaticità della struttura, così da poterla risolvere con le semplici equazioni di equilibrio. Rispetto all’esercizio precedente utilizzo un metodo più rapido: l’isostaticità sarà verificata se Ve + a = 2 * n , dove Ve è il numero dei gradi di vincolo esterni, “a” è il numero delle aste e “n” è il numero di nodi.
Ve = gradi di vincolo del carrello + gradi di vincolo della cerniera = 3
a = numero delle aste = 11
n = numero di nodi = 7
Ve + a = 2 * n → 3 + 11 = 2 * 7 → 14 = 14 → ISOSTATICITA’ VERIFICATA
Ora posso procedere col determinare le reazioni vincolari. Attraverso l’equilibrio delle forze verticali posso trovare il valore di Rvb:
∑Fy = Rvb - 10 -10 = 0
Rvb = 20 KN
Per determinare invece il valore delle reazioni vincolari orizzontali devo fare l’equilibrio dei momenti, in questo caso decido di farlo rispetto al nodo B:
∑Mb = -10*1 - 10*2 + Roh*1 = 0
Roh = 10 + 20 = 30 KN
Ora sapendo il valore di Roh posso determinare facilmente il valore di Rob, infatti poiché unica forza orizzontale in grado di equilibrare Roh, Rvb avrà stesso valore ma verso opposto.
Per determinare il valore delle azioni di contatto utilizzo il metodo dei nodi, che consiste nell’isolare i singoli nodi della struttura indicando gli sforzi normali agenti sul nodo e le eventuali forze esterne, e poi attraverso l’equilibrio delle forze, risolvendo semplici equazioni ad una sola incognita, si determinano i valori degli sforzi assiali.
NODO A
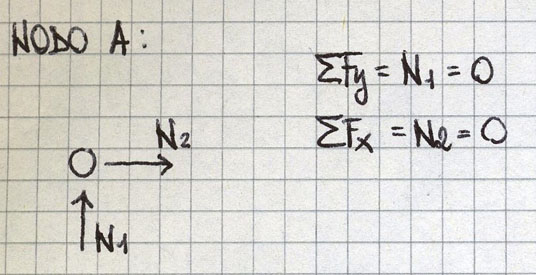
Per l’equilibrio delle forze orizzontali e verticali le aste 1 e 2 sono scariche:
∑Fy = N1 = 0
∑Fx = N2 = 0
NODO B

Per trovare il valore dello sforzo normale sull’asta inclinata devo scomporre N3 in una componente orizzontale e in una verticale, così attraverso l’equilibrio delle forze verticali trovo il valore di N3 e attraverso quello delle forze orizzontali trovo il valore di N4:
∑Fy = 20 + N3*√2/2 = 0
N3 = - 20 * 2/√2 * √2/√2 = - 20√2 KN → Il valore è venuto negativo, quindi lo sforzo normale ha verso opposto rispetto a quello supposto: l’asta è compressa
∑Fx = 30 + N4 + N3*√2/2 = 0
N4 = - 30 - N3*√2/2 = -30 + 20*√2 * √2/2 = - 10KN → Il valore è negativo quindi l’asta è compressa
NODO C
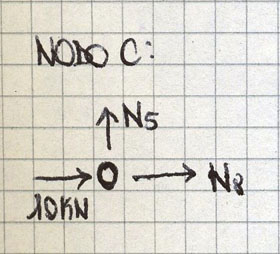
N5 è pari a zero perché non ci sono altre forze verticali in grado di equilibrarla:
∑Fy = N5 = 0
Il valore di N8 si può invece facilmente trovare attraverso l’equilibrio delle forze orizzontali:
∑Fx = 10 + N8 = 0
N8 = - 10KN → il valore è negativo quindi l’asta è compressa
NODO D
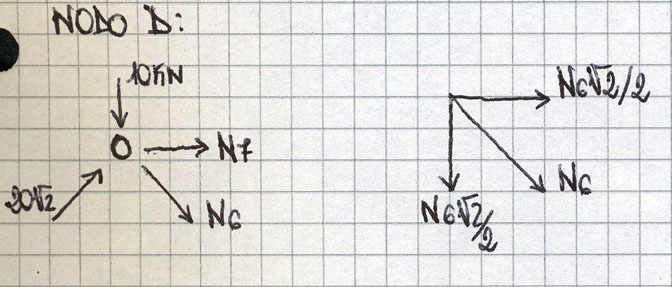
Attraverso l’equilibrio delle forze verticali, quindi considerando anche il contributo verticale dello sforzo normale sull’asta 3, trovo il valore di N6:
∑Fy = - 10 - N6*√2/2 + 20 = 0
N6 = ( -10 + 20 ) * 2/√2 * √2/√2 = 10√2Kn → il valore è positivo quindi l’asta é tesa
Attraverso l’equilibrio delle forze orizzontali, dove avrò il valore di N7 e i contributi orizzontale dello sforzo normale sulle aste 3 e 6, ottengo il valore di N7:
∑Fx = N7 + 20 + 10 = 0
N7 = - 30KN → il valore è negativo quindi l’asta è compressa
NODO E

L’asta 11 è scarica poiché lo sforzo normale sull’asta 8 e il contributo orizzontale dello sforzo normale sull’asta 6 sono già equilibrati, infatti facendo l’equilibrio delle forze orizzontali ottengo:
∑Fx = 10 + N11*√2/2 - 10 = 0
N11 = 0 → l’asta è scarica
Attraverso l’equilibrio delle forze verticali, considerando sempre anche il contributo verticale di N6, ottengo il valore di N9:
∑Fy = N9 + 10 = 0
N9 = -10KN → il valore è negativo quindi l’asta è compressa
NODO G

N10 ha valore pari a N7 e verso opposto, poiché è l’unica forza orizzontale in grado di equilibrarla:
∑Fx = 30 + N10 = 0
N10 = - 30KN → il valore è negativi quindi l’asta è compressa
Riassumendo i risultati ottenuti:
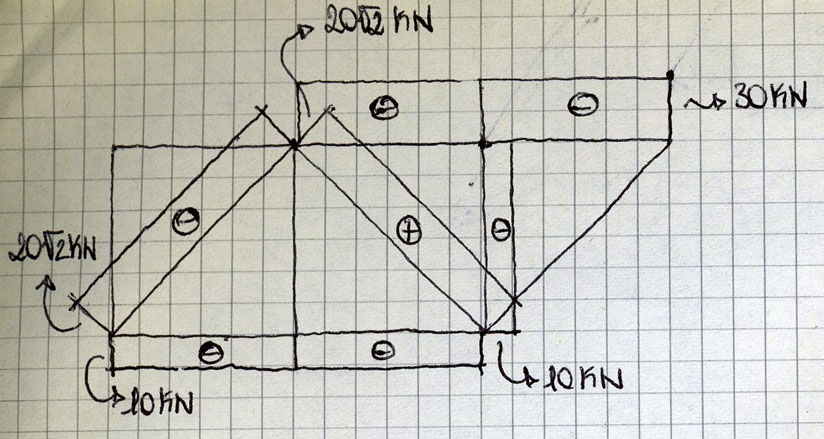
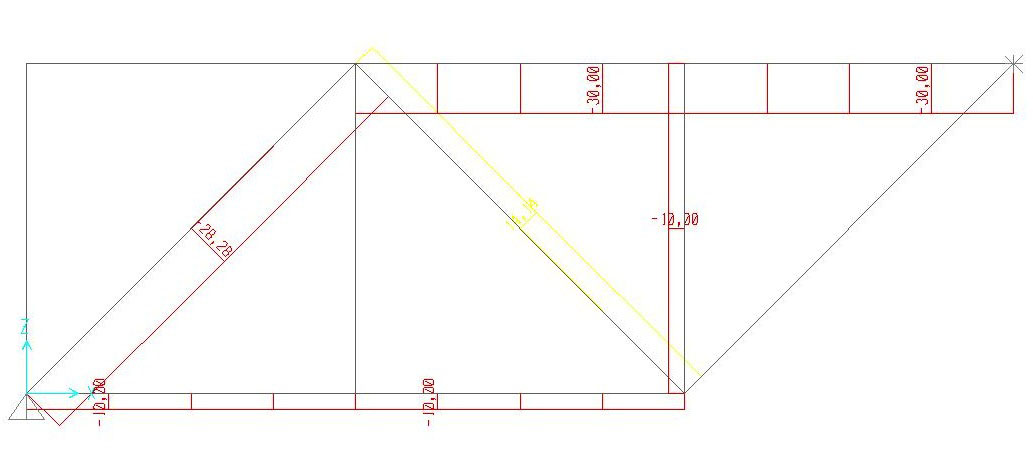
Ancora una volta, utilizzando il software SAP2000 ho potuto verificare i risultati:
DIMENSIONAMENTO TRAVI

L’esercizio prevede il dimensionamento di una trave in acciaio, legno e calcestruzzo armato di un edificio ad uso residenziale tramite l’uso di un foglio di calcolo excel. La trave che verrà dimensionata è quella evidenziata in rosso, dobbiamo quindi tener conto di una luce di 6 metri e di un interasse di 3 metri.
Per calcolare lo stato di tensione interno alla trave, in modo da poter poi scegliere la sezione opportuna, occorre conoscere il valore delle forze che la struttura deve sostenere. Il primo passo sarà quindi quello di calcolare queste forze che si dividono in:
-
qs: peso proprio della struttura
-
qp: sovraccarico permanente (costituito da elementi che non hanno una funzione strutturale ma che sono parte integrante dell’edificio come ad esempio tramezzi, pavimenti, ecc.)
-
qa: sovraccarico accidentale (costituito da mobili, occupanti, ed altre attrezzature; perciò dipende dalla destinazione d’uso dell’edificio)
Per quanto riguarda qs e qp questi vanno calcolati in base alle dimensioni degli elementi e ai pesi specifici dei materiali, mentre qa è tabellato in base alla destinazione d’uso dell’edificio.
TRAVE IN ACCIAIO

-
1.Dimensionamento del travetto secondario:
qp:
- pavimentazione in gres (spessore 2 cm; peso 20KN/mc):
0,02m*20KN/mc = 0,40 KN/mq
-
massetto (spessore 5cm; peso 19KN/mc):
0,05m*19KN/mc = 0,95 KN/mq
-
controsoffitto (spessore 1,5 cm; peso 8KN/mc):
0,015m*8KN/mc = 0,12 KN/mq
-
tramezzi (mattoni forati + intonaco di spessore 1,5 cm per lato):
mattoni forati (spessore 12 cm; peso 7KN/mc): 0,12m*7KN/mc*2,7m = 2,27 KN/m
intonaco (spessore 1,5 cm per lato; peso 20KN/mc):0,015m*2*20KN/mc*2,7=1,62KN/m
totale tramezzi: 2,27KN/m + 1,62KN/m = 3,89KN/m
Le norme italiane affermano che: “Per gli orizzontamenti degli edifici per abitazioni e uffici, il peso proprio di elementi divisori interni potrà essere ragguagliato a un carico permanente portato uniformemente distribuito”, “Il carico uniformemente distribuito ora definito dipende dal peso proprio per unità di lunghezza delle partizioni nel modo seguente”:
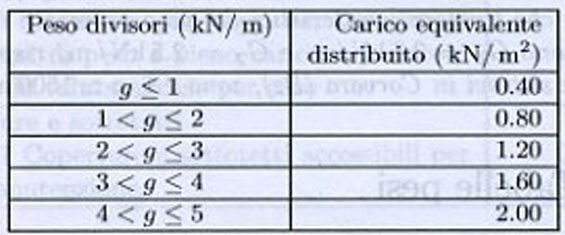
quindi nel nostro caso si può assumere un carico distribuito pari a 1,60KN/mq
qp totale: 0,40KN/mq + 0,95KN/mq + 0,12KN/mq + 1,60KN/mq + 0,5KN/mq = 3,57KN/mq
qs:
-
lamiera grecata con soletta collaborante (altezza soletta 12cm; spessore lamiera 1mm): 2,40 KN/mq
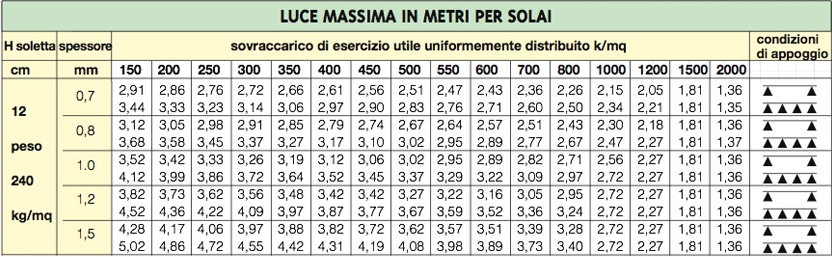
qa:
-
ambienti ad uso residenziale: 2 KN/mq
Una volta calcolati i carichi agenti sul travetto li inserisco nel foglio excel nella loro relativa colonna, così nella colonna 5 vengono sommati e moltiplicati per l’interasse in modo da ottenere il valore di “q” in KN/m; cioè il valore dei carichi agenti sulla struttura come se fossero uniformemente distribuiti sulla travetto.
Ottenuto il valore di “q” e conoscendo il valore della luce che deve coprire il travetto, nella colonna 7 ottengo il valore del momento massimo (nel caso della trave appoggiata-appoggiata Mmax = ql^2/8, se avessi un caso più complesso potrei calcolarmi il momento massimo su SAP e poi riportarlo nel foglio excel). Conoscendo il valore del momento massimo e della tensione di design (tensione di snervamento caratteristica dell’acciaio/coefficiente di sicurezza ϒm) nell’ultima colonna ottengo il valore del modulo di resistenza della sezione Wx minimo che deve avere la sezione da scegliere in modo tale che non venga superata la tensione di design:

Scelgo quindi per il travetto un IPE120 con un Wx = 52,96 cm^3 e un peso = 10,4kg/m:
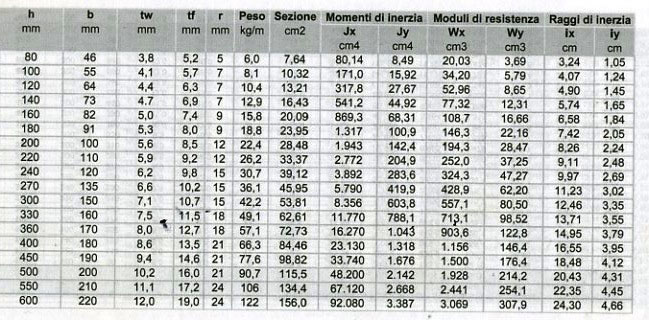
Ora inserisco il peso dell’IPE120 nel peso proprio della struttura e ricalcolo il Wx minimo che deve avere la sezione, in modo tale da verificare che il Wx dell’IPE scelta sia sempre superiore a quello minimo:
-
peso del travetto: 10,4kg/m = 0,104KN/m = 0,104/interasse = 0,104KN/mq
qs= 2,40KN/mq + 0,104KN/mq = 2,504KN/mq
Reinserisco i dati nella tabella excel e verifico che Wx sia inferiore del Wx della sezione scelta:

-
2.Dimensionamento della trave:
qp: 3,57 KN/mq (è uguale a quello calcolato in precedenza per il travetto)
qs:
-
lamiera grecata con soletta collaborante (altezza soletta 12cm; spessore lamiera 1mm): 2,40 KN/mq
-
travetto: 0,104 KN/mq
qs totale: 2,40KN/mq + 0,104KN/mq = 2,504KN/mq
qa:
-
ambienti ad uso residenziale: 2 KN/mq
Procedendo come abbiamo fatto in precedenza con il travetto inserisco i dati nel foglio excel e ottengo un Wx minimo di 533,40 cm^3:

Scelgo quindi per la trave un IPE300 con un Wx = 557,1 cm^3 e un peso = 42,2kg/m.
Ora inserisco il peso dell’IPE300 nel peso proprio della struttura e ricalcolo il Wx minimo che deve vere la sezione, in modo tale da verificare che il Wx dell’IPE scelta sia sempre superiore a quello minimo:
-
peso della trave: 42,2kg/m = 0,422KN/m = 0,422/interasse = 0,147KN/mq
qs= 2,504KN/mq + 0,147KN/mq = 2,651KN/mq
Reinserisco i dati nella tabella excel e verifico che Wx sia inferiore del Wx della sezione scelta:

TRAVE IN LEGNO
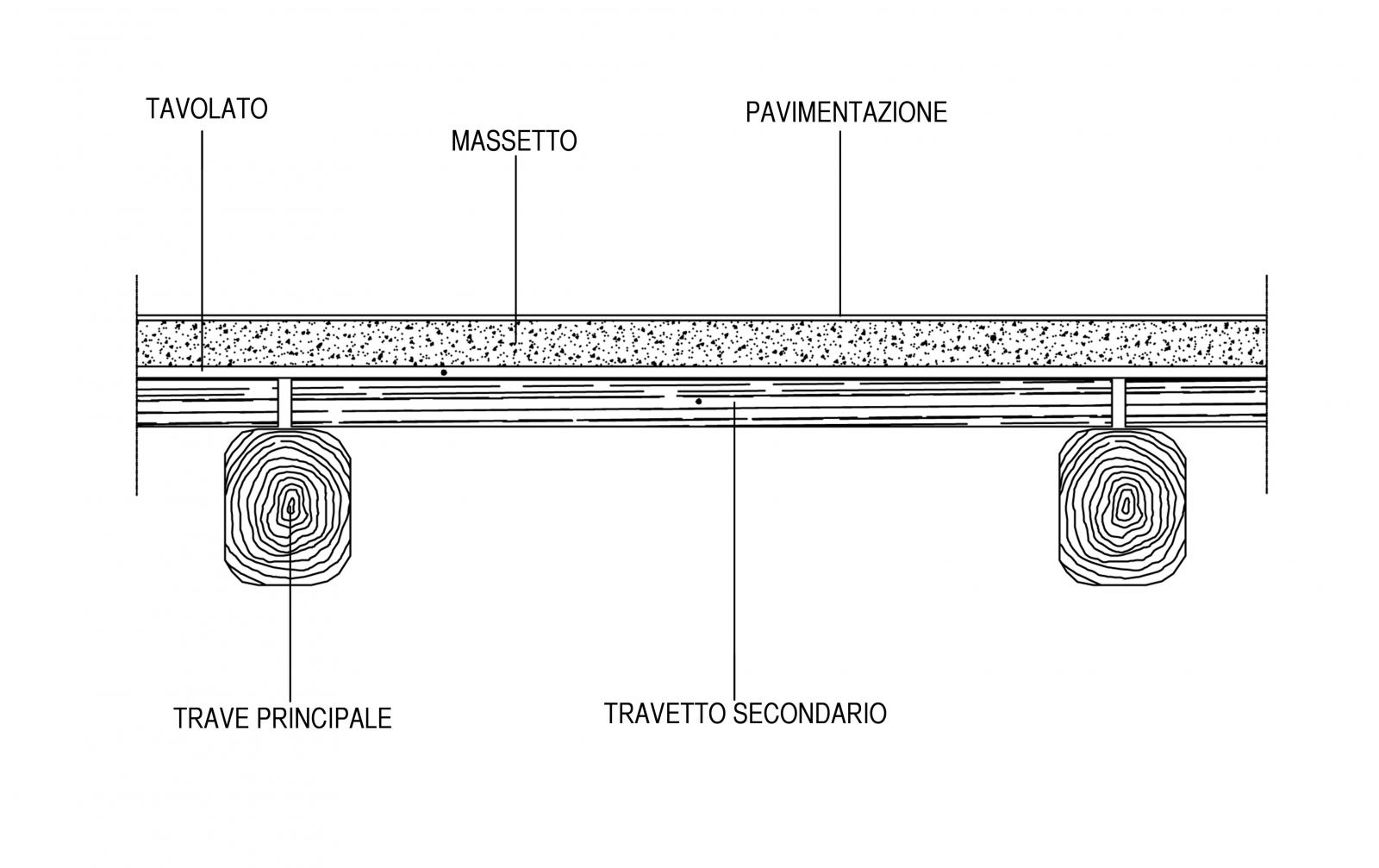
-
1.Dimensionamento del travetto secondario:
qp:
-
pavimentazione in parquet (spessore 0,015m; peso 7,60KN/mc):
0,015m*7,60KN/mc = 0,114 KN/mq
-
massetto (spessore 5cm; peso 19KN/mc):
0,05m*19KN/mc = 0,95 KN/mq
-
tramezzi (mattoni forati + intonaco di spessore 1,5 cm per lato):
mattoni forati (spessore 12 cm; peso 7KN/mc): 0,12m*7KN/mc*2,7m = 2,27 KN/m
intonaco (spessore 1,5 cm per lato; peso 20KN/mc):0,015m*2*20KN/mc*2,7=1,62KN/m
totale tramezzi: 2,27KN/m + 1,62KN/m = 3,89KN/m
Le norme italiane affermano che: “Per gli orizzontamenti degli edifici per abitazioni e uffici, il peso proprio di elementi divisori interni potrà essere ragguagliato a un carico permanente portato uniformemente distribuito”, “Il carico uniformemente distribuito ora definito dipende dal peso proprio per unità di lunghezza delle partizioni nel modo seguente”:

quindi nel nostro caso si può assumere un carico distribuito pari a 1,60KN/mq
qp totale: 0,114KN/mq + 0,95KN/mq + 1,60KN/mq + 0,5KN/mq = 3,164KN/mq
qs:
-
tavolato in castagno ( spessore 3cm; peso 7KN/mc):
0,03m*7KN/mc = 0,21KN/mq
qa:
-
ambienti ad uso residenziale: 2 KN/mq
Una volta calcolati i carichi agenti sul travetto li inserisco nel foglio excel nella loro relativa colonna, così nella colonna 5 vengono sommati e moltiplicati per l’interasse in modo da ottenere il valore di “q” in KN/m; cioè il valore dei carichi agenti sulla struttura come se fossero uniformemente distribuiti sulla travetto.
Ottenuto il valore di “q” e conoscendo il valore della luce che deve coprire il travetto, nella colonna 7 ottengo il valore del momento massimo (nel caso della trave appoggiata-appoggiata Mmax = ql^2/8, se avessi un caso più complesso potrei calcolarmi il momento massimo su SAP e poi riportarlo nel foglio excel). Ora bisogna calcolare la tensione di design, che per il legno ha la seguente formula:
fd = Kmod*fmk/ϒm; dove Kmod è un fattore moltiplicativo < 1che tiene conto della viscosità del legno, fmk è la resistenza caratteristica a flessione del legno e ϒm è il coefficiente di sicurezza (ϒm = 1,45 per il legno lamellare e ϒm = 1,5 per il legno massello). Nel nostro caso:
-
Kmod = 0,7 → per carichi permanenti su solai in legno lamellare
-
fmk = 28 MPa → per il castagno
-
ϒm = 1,45 → per il legno lamellare
Conoscendo il momento massimo e la tensione di design ora possiamo ricavare le dimensioni minime che deve avere il travetto. Sapendo che per una sezione rettangolare:
Wx = bh^2/6 ricavo che h^2 = 6*Wx/b → h = (6*Wx/b)^1/2
inoltre sapendo che Wx = Mx/fd e sostituendo nella formula precedente ottengo:
h = (6*Mx/b*fd)^1/2
Inserendo quindi i dati nel foglio ecxel, supponendo una base del travetto pari a 12cm ottengo un’altezza minima pari a 14,95cm:

Scelgo nella tabella della casa produttrice HolzAlbertani un travetto di dimensioni 12cmx16cm:
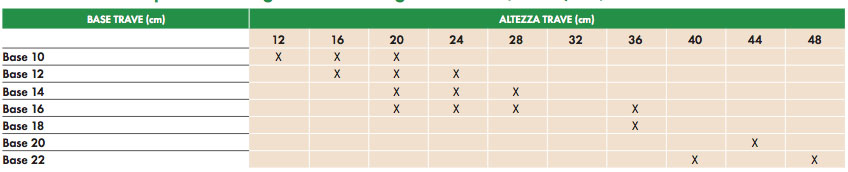
Ora inserisco il peso del travetto scelto nel peso proprio della struttura e verifico che l’altezza minima sia comunque minore di quella del travetto scelto:
-peso del travetto:
(0,12m*0,16m*4,9KN/mc)/interasse = (0,12*0,16*4,9)/1 = 0,094KN/Mq
qs = 0,21KN/mq + 0,094KN/mq = 0,304KN/mq
Reinserisco i dati nel foglio excel e verifico che l’altezza minima sia inferiore di quella del travetto scelto:

-
-
2.Dimensionamento della trave:
qp: 3,164 KN/mq (è uguale a quello calcolato in precedenza per il travetto)
qs:
-
tavolato in castagno ( spessore 3cm; peso 7KN/mc):
0,03m*7KN/mc = 0,21KN/mq
qs totale: 0,21KN/mq + 0,094KN/mq = 0,304KN/mq
qa:
-
ambienti ad uso residenziale: 2 KN/mq
Procedendo come abbiamo fatto in precedenza con il travetto inserisco i dati nel foglio excel e ottengo un’altezza minima della trave pari a 38,59cm:

Scelgo nella tabella della casa produttrice HolzAlbertani una trave di dimensioni 22cmx40cm:

Ora inserisco il peso della trave scelta nel peso proprio della struttura e verifico che l’altezza minima sia comunque minore di quella della trave scelta:
-peso della trave:
(0,22m*0,40m*4,9KN/mc)/interasse = (0,22*0,40*4,9)/3 = 0,14KN/mq
qs = 0,304KN/mq + 0,14KN/mq = 0,44KN/mq
Reinserisco i dati nel foglio excel e verifico che l’altezza minima sia inferiore di quella della trave scelta:

TRAVE IN CALCESTRUZZO ARMATO
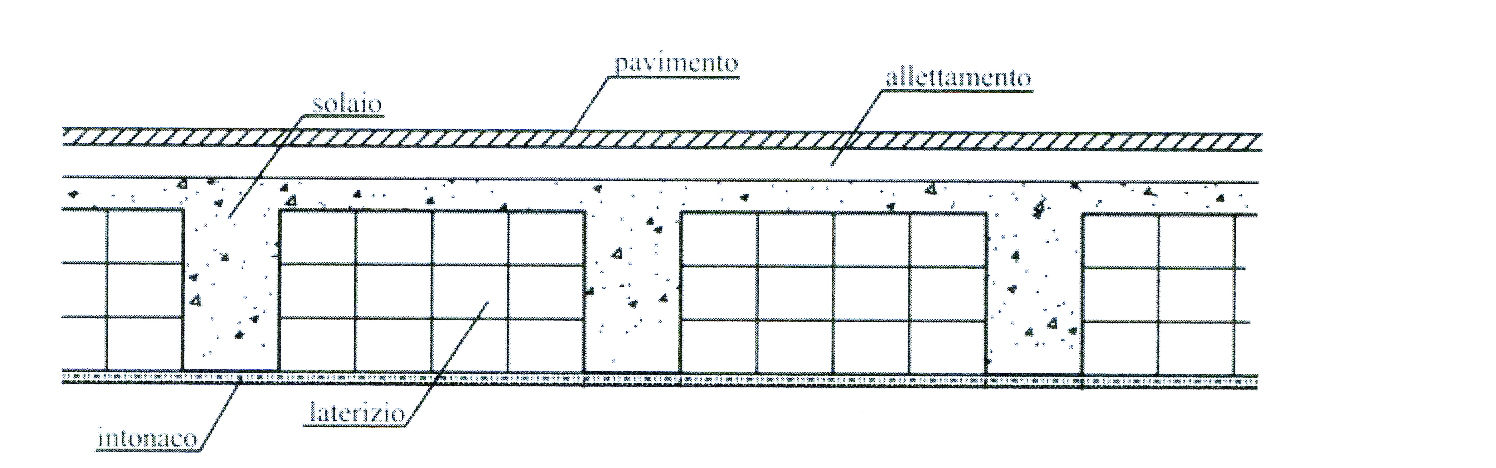
1.DIMENSIONAMENTO DELLA TRAVE:
qp:
- pavimentazione in gres (spessore 2 cm; peso 20KN/mc):
0,02m*20KN/mc = 0,40 KN/mq
-
massetto (spessore 5cm; peso 19KN/mc):
0,05m*19KN/mc = 0,95 KN/mq
-
intonaco (spessore 1,5cm; peso 20KN/mc):
0,015*20KN/mc = 0,30 KN/mq
- tramezzi (mattoni forati + intonaco di spessore 1,5 cm per lato):
mattoni forati (spessore 12 cm; peso 7KN/mc): 0,12m*7KN/mc*2,7m = 2,27 KN/m
intonaco (spessore 1,5 cm per lato; peso 20KN/mc):0,015m*2*20KN/mc*2,7=1,62KN/m
totale tramezzi: 2,27KN/m + 1,62KN/m = 3,89KN/m
Le norme italiane affermano che: “Per gli orizzontamenti degli edifici per abitazioni e uffici, il peso proprio di elementi divisori interni potrà essere ragguagliato a un carico permanente portato uniformemente distribuito”, “Il carico uniformemente distribuito ora definito dipende dal peso proprio per unità di lunghezza delle partizioni nel modo seguente”:
quindi nel nostro caso si può assumere un carico distribuito pari a 1,60KN/mq
qp totale: 0,40KN/mq + 0,95KN/mq + 0,30KN/mq + 1,60KN/mq + 0,5KN/mq = 3,75KN/mq
qs:
-
peso pignatte(12cm) + travetti(12cm)+ soletta(4cm) = 2,20KN/mq valore tabellato
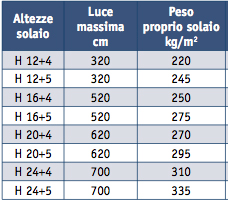
qa:
-
ambienti ad uso residenziale: 2 KN/mq
Una volta calcolati i carichi agenti sulla trave li inserisco nel foglio excel nella loro relativa colonna, così nella colonna 5 vengono sommati e moltiplicati per l’interasse in modo da ottenere il valore di “q” in KN/m; cioè il valore dei carichi agenti sulla struttura come se fossero uniformemente distribuiti sulla trave.
Ottenuto il valore di “q” e conoscendo il valore della luce che deve coprire la trave, nella colonna 7 ottengo il valore del momento massimo (nel caso della trave appoggiata-appoggiata Mmax = ql^2/8, se avessi un caso più complesso potrei calcolarmi il momento
massimo su SAP e poi riportarlo nel foglio excel).
Per procedere con il progetto della trave in cls devo scegliere il tipo di acciaio per l’armatura. L’acciaio che si usa nel cls è costituito da tondini ad aderenza migliorata e si utilizzano solo due classi di acciaio: B450A e B450C entrambi con fy = 450MPa; la differenza tra questi due tipi di acciaio sta nel punto di rottura, uno ad una deformazione del 3% rispetto la lunghezza iniziale e uno al 7%, quindi uno è più duttile e uno meno duttile. Scelgo di utilizzare l’acciaio B450C, unico ammesso in zona sismica poiché quello con intervallo di duttilità maggiore, e con coefficiente di sicurezza ϒm = 1,15.
Ora occorre scegliere il tipo di calcestruzzo da utilizzare. Il calcestruzzo si divide in circa 15 classi a seconda della sua resistenza, le prime 2-3 classi non possono essere utilizzate nel calcestruzzo armato ma sono solitamente utilizzate nei magroni di fondazione, mentre dalla classe C50/60 in poi sono calcestruzzi estremamente performanti per l’uso dei quali occorre un’autorizzazione del Ministero dei Lavori Pubblici. Le classi di calcestruzzo più utilizzate sono quelle che vanno dalla classe C20/25 alla C60/75, dove il primo numero indica la resistenza cilindrica e il secondo la resistenza cubica espresse in N/mm^2 = MPa. Scelgo di utilizzare un calcestruzzo C40/50 con fck = 40N/mm^2 e quindi corrispondente tensione di design fd,c = fck/ϒ = 40/1,75 = 22,86KN/mm^2.
Una volta definite le caratteristiche dei materiali posso calcolarmi l’altezza utile della sezione: hu = r*√(Mmax/b) dove “r” è un coefficiente dove compare il fattore alfa = fd,c/(fd,c + fd,f/n) e dove n è il coefficiente di omogenizzazione pari al modulo di elasticità dell’acciaio diviso quello del calcestruzzo. Supponendo una base della trave pari a 25cm ottengo un’altezza utile pari a 30,87cm, a cui dobbiamo aggiungere l’altezza del copriferro per ottenere un’altezza minima totale della trave pari a 35,87cm:

Ovviamente si dovrà arrotondare per eccesso l’altezza minima ottenuta in base alle travi standard in produzione, quindi la mia trave avrà base = 25cm e altezza = 40cm.
Ora inserisco il peso della trave scelta nel peso proprio della struttura e verifico che l’altezza minima sia comunque minore di quella della trave scelta:
-peso della trave:
(0,25m*0,40m*25KN/mc)/interasse = (0,25*0,40*25)/3 = 0,83KN/Mq
qs = 2,20KN/mq + 0,83KN/mq = 3,03KN/mq
Reinserisco i dati nel foglio excel e verifico che l’altezza minima sia inferiore di quella della trave scelta:

TRAVATURA RETICOLARE SPAZIALE
DISEGNO DELLE ASTE SU AUTOCAD:
1. creo un nuovo layer dove andrò a disegnare la struttura, poiché se disegnassi sul layer 0 poi SAP non lo riconoscerebbe
2. disegno le aste di lunghezza 2m utilizzando il comando pollilinea e digitando come punto iniziale 0,00 in modo tale da iniziare dallo zero assoluto e da non perdermi poi il disegno quando lo importo su SAP
3. disegno le aste creando una serie aperta in modo tale che poi utilizzando il comando array non si sovrappongano gli elementi
4. utilizzo comando array andando a selezionare le aste disegnate e impostando i valori della serie rettangolare con 1 riga e 4 colonne poste ad una distanza di 2m
5. chiudo la serie con un’asta verticale
6. vado sulla finestra a tendina “view”, poi su “3D view” e scelgo la vista “SW isometric” in modo da passare alla vista 3D
7. utilizzo il comando “ruota 3D” in modo da ruotare la figura in verticale, quindi seleziono la figura, indico l’asse x come asse di rotazione e ruoto di 90°

8. cambio l’UCS in modo da disegnare le altre aste sul piano yz, facendo attenzione a disegnare sempre un modulo aperto in modo tale che poi utilizzando il comando array non si sovrappongano delle pollilinee
9. utilizzo il comando array per duplicare il modulo lungo l’asse x ad una distanza di 2m:
10. disegno le aste inclinate superiori e inferiori del modulo
11. utilizzo il comando array per duplicarle lungo la struttura

12. utilizzo ancora una volta il comando array per duplicarmi il modulo disegnato lungo l’asse y, andando a impostare 1 riga e 7 colonne (non 6 colonne poiché successivamente sarà più facile cancellare gli elementi in eccesso piuttosto che chiudere la serie con le aste in 3D)
13. volendo ottenere come risultato finale una travatura reticolare spaziale composta da 4 moduli lungo l’asse x e 6 moduli lungo l’asse y, vado a cancellare gli elementi in più dovuti alla duplicazione del modulo per 7 colonne e ottengo la travatura reticolare finale

14. salvo in AutoCAD 2000/LT2000 DXF per poi importare il disegno su SAP
DISEGNO DELLA STRUTTURA SU SAP:
1. Vado su “File”/ “Importa”/ “AutoCAD.dxf File” e seleziono il file da importare disegnato precedentemente su Autocad
2. Imposto come unità di misura KN, m, C e su “telai” imposto “aste” in modo tale che tutto ciò che ho disegnato su Autocad sul layer aste venga importato come telai.

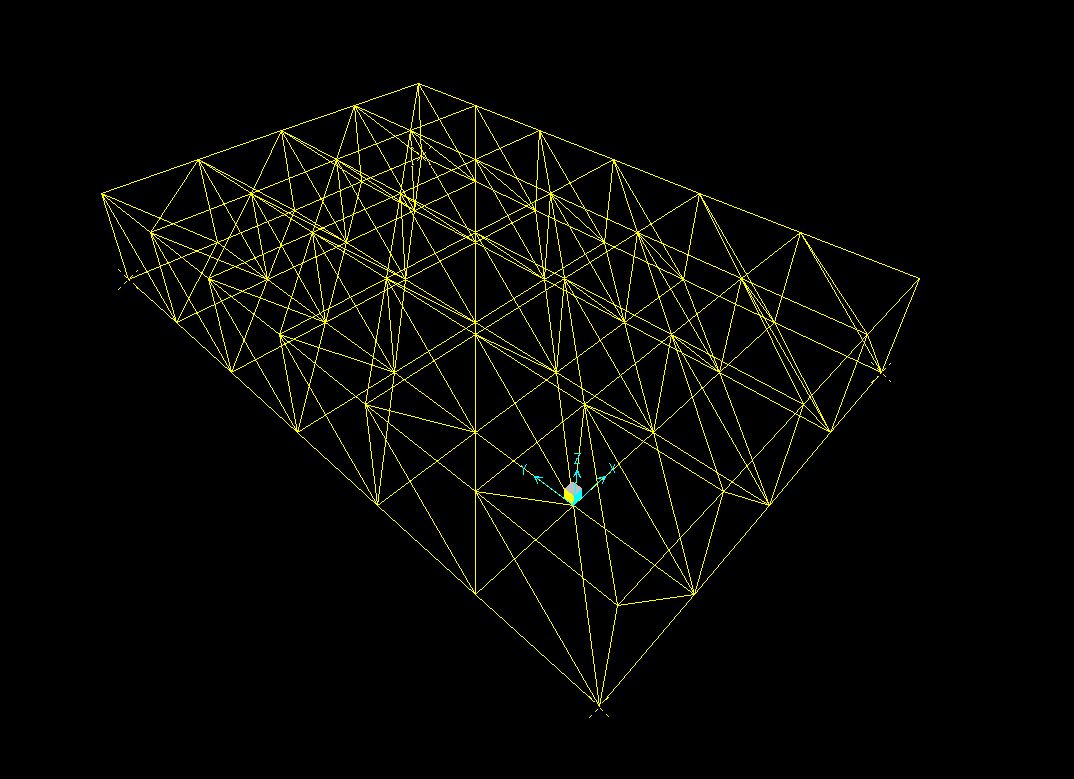
3. mi metto sulla vista 3D
4. Assegno i vincoli immaginando che i pilastri siano solo ai 4 angoli della piastra, quindi seleziono i nodi a cui assegnare i vincoli, vado su “Assegna”/ “Nodo”/ “Vincoli Esterni” e scelgo di assegnare delle cerniere

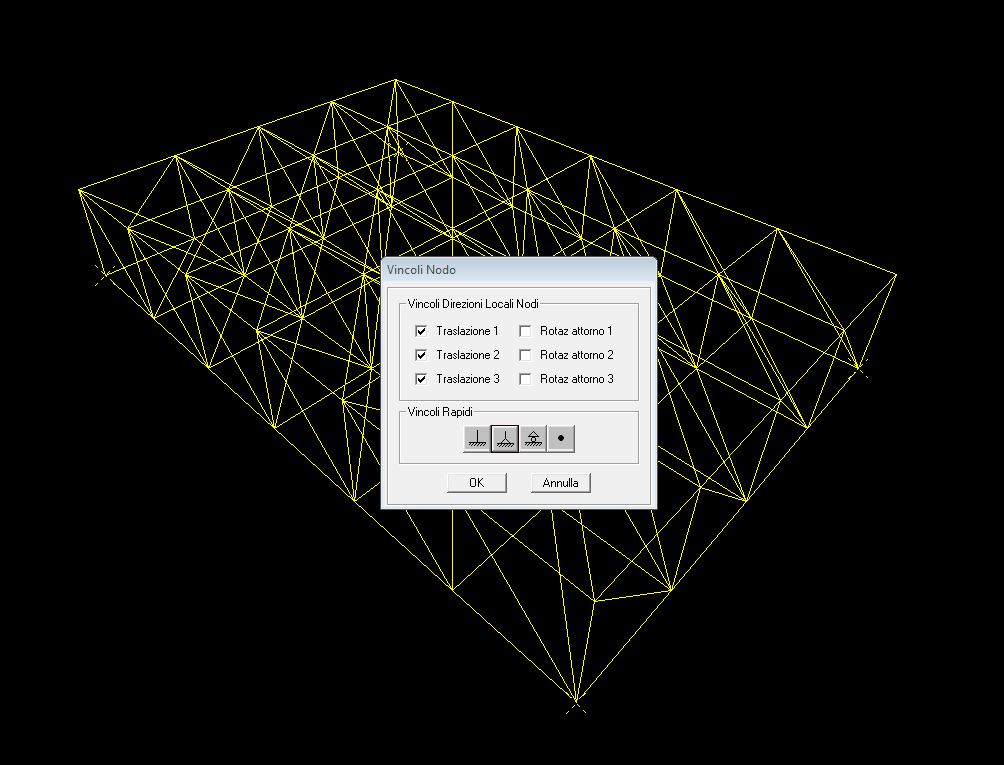

5. Metto le cerniere interne in modo che le aste lavorino a solo sforzo normale, quindi seleziono tutta la struttura e vado su “Assegna”/ “Frame”/ “Rilasci” e rilascio i momenti 22 e 33 sia all’inizio che alla fine
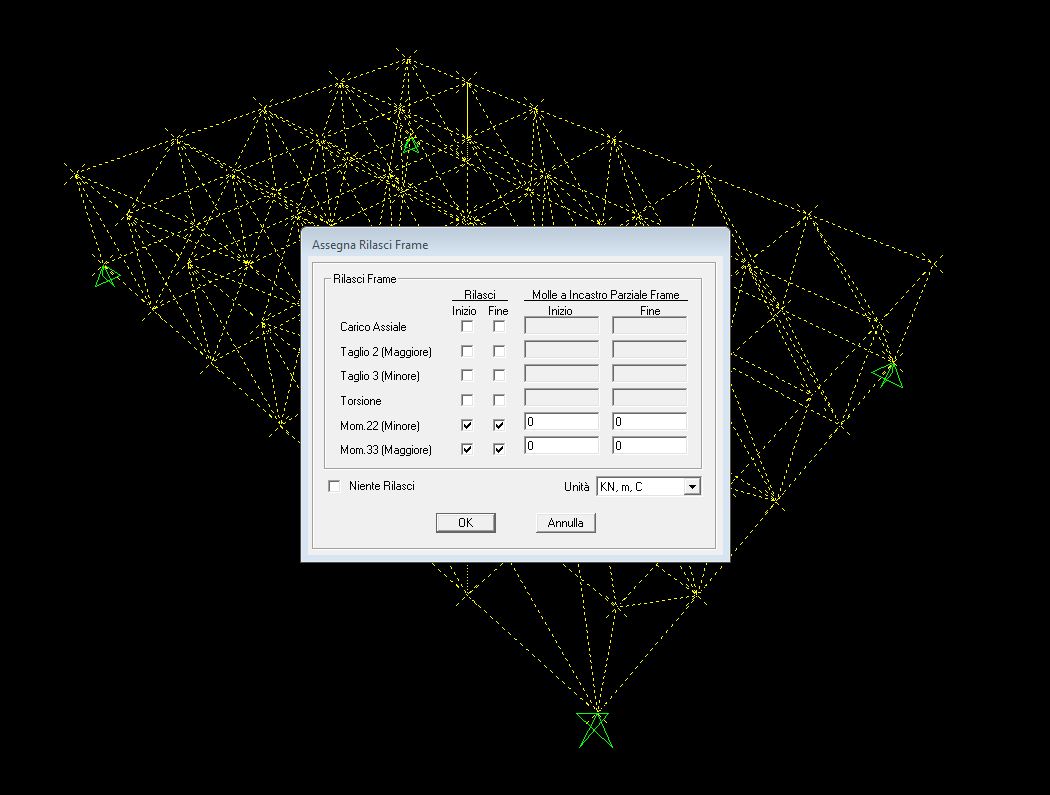
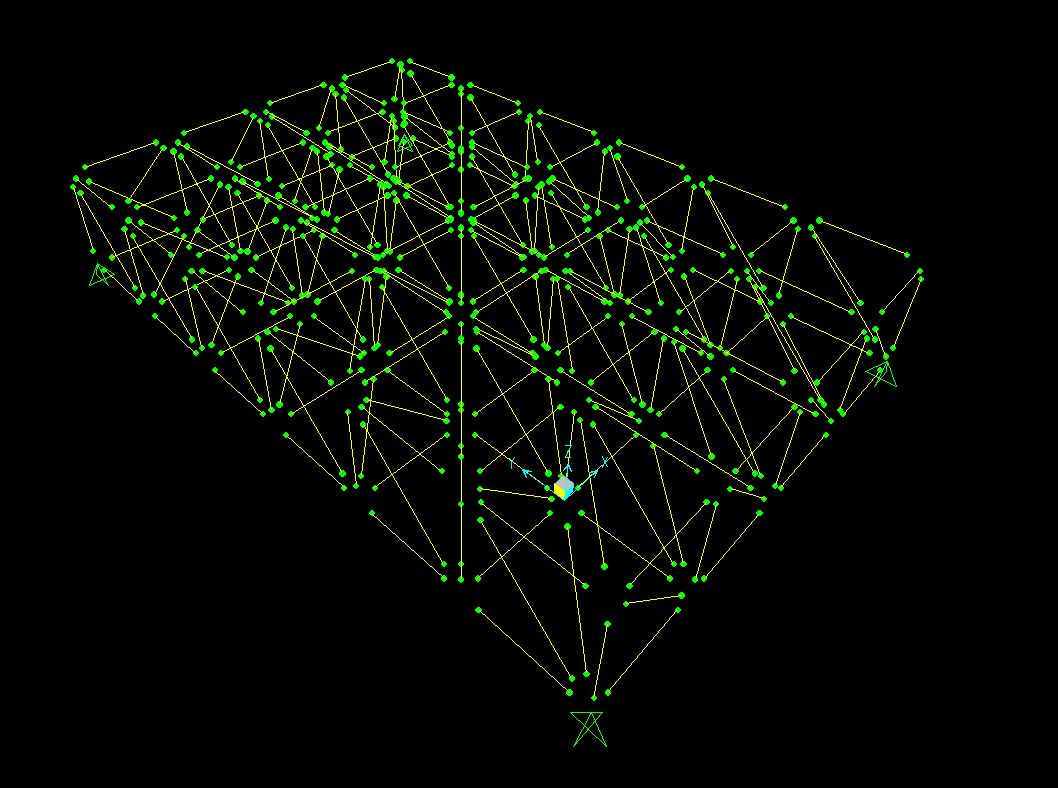
6. Vado a definire il materiale per poi assegnarlo alla struttura, quindi vado su “Definisci”/ “Materiali”/ “Aggiungi Nuovo Materiale” gli assegno “stell” e lo chiamo “acciaio”
7. Vado ad assegnare all’acciaio un sezione tubolare, quindi vado su “Definisci”/ “Proprietà Sezione”/ “Aggiungi Nuova Proprietà” e su “Proprietà Tipo Sezione Frame” seleziono l’acciaio e gli assegno la sezione tubolare, poi come materiale gli assegno “acciaio” cioè il materiale che ho creato in precedenza
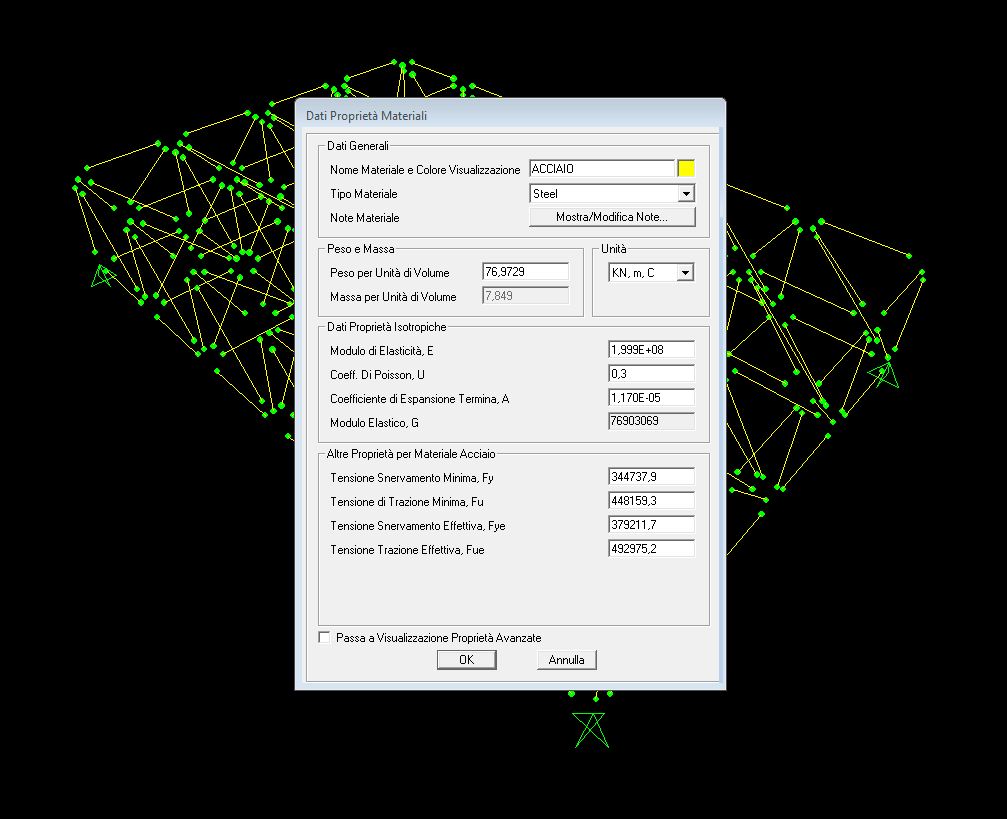
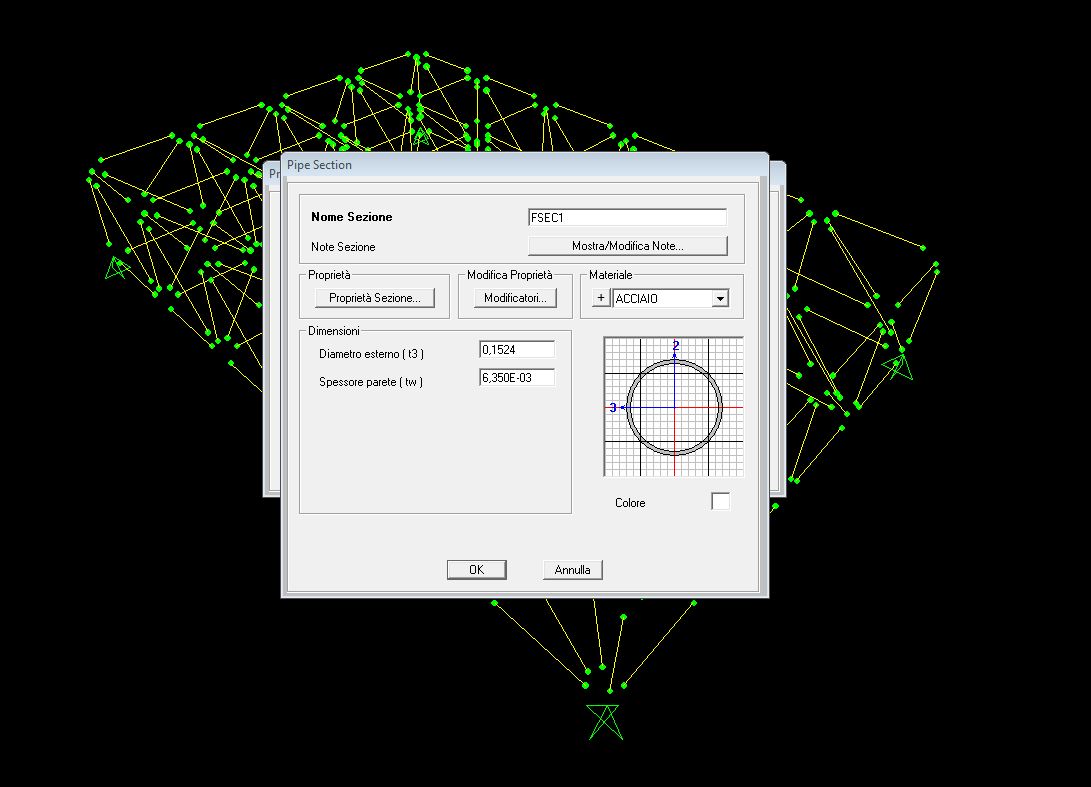
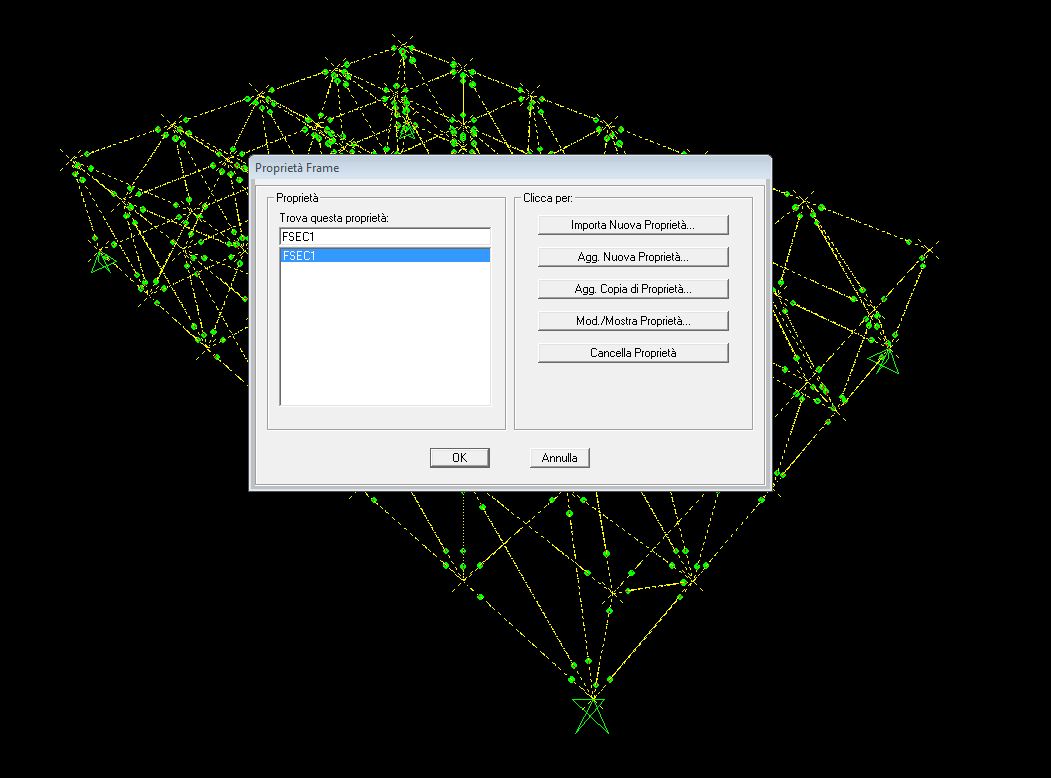
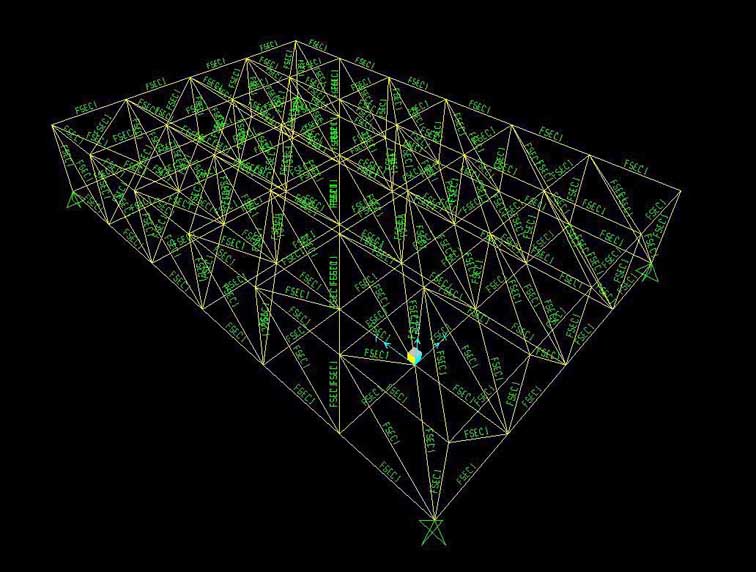
8. Vado ad assegnare la sezione tubolare d’acciaio a tutta la struttura, quindi seleziono tutta la struttura e vado su “Assegna”/ “Frame”/ “Sezioni Frame” e gli assegno la sezione FSEC1 che è quella creata precedentemente
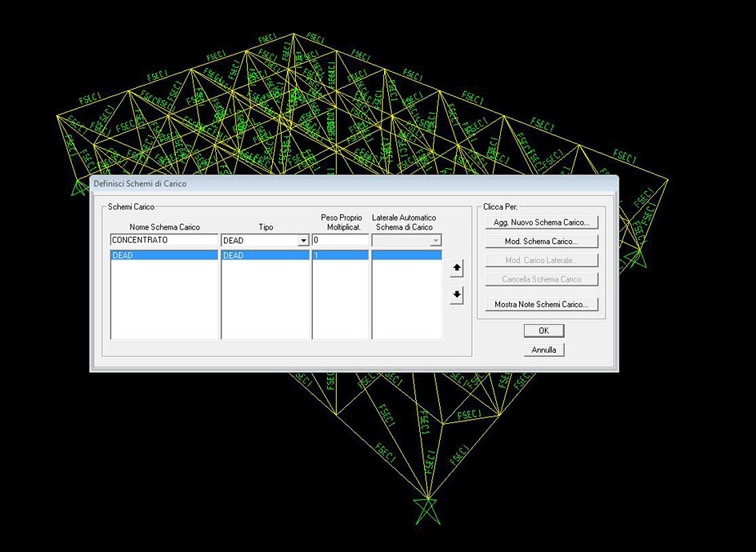
9. Definisco il carico che poi assegnerò alla struttura, quindi vado su “Definisci”/ “Schemi di Carico” e creo un nuovo carico chiamandolo “Concentrato” e assegnandogli con “Peso Proprio Moltiplicat.” zero. Ora vado su “Aggiungi Nuovo Schema di Carico” e me lo aggiunge sulla lista dei carichi.
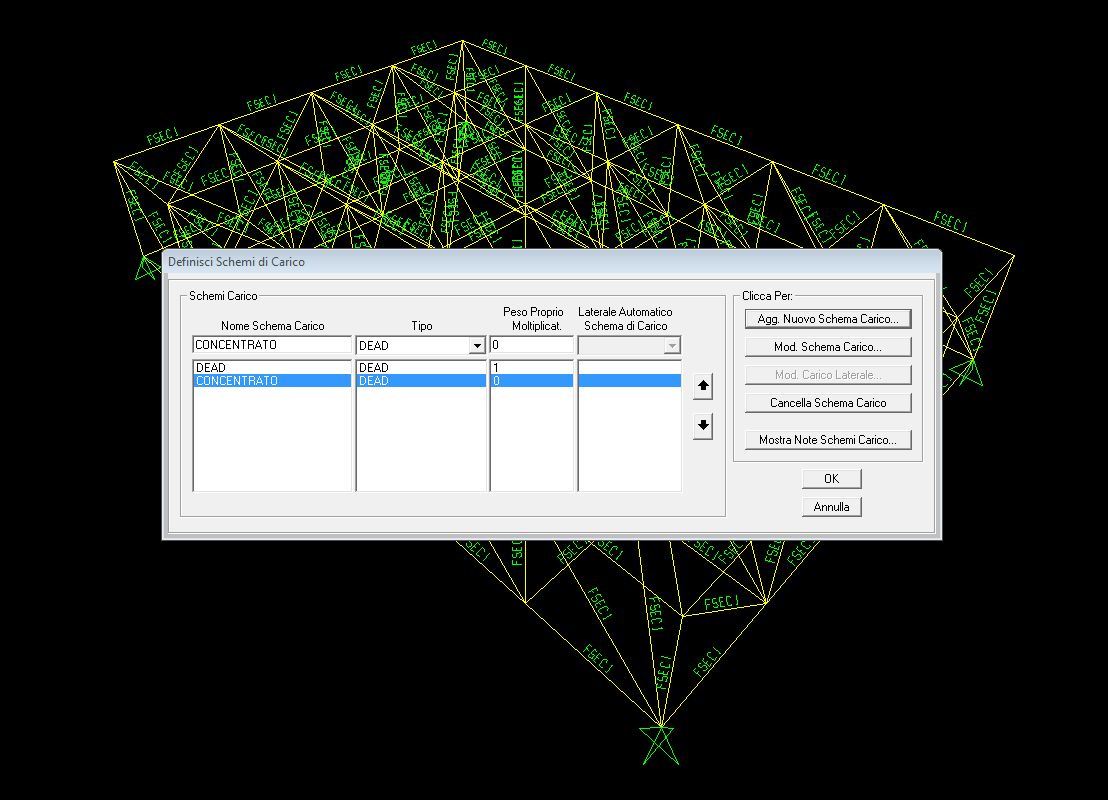
10. Devo assegnare alla struttura il carico definito in precedenza, ma mi devo assicurare di assegnare il carico solo ai nodi superiori, quindi mi metto sul piano xy, poi vado su “Imposta Opzioni Visualizzazione” e nella colonna “Nodi” deseleziono “Invisibile” mentre nella colonna “Frame” seleziono “Frame non in vista”

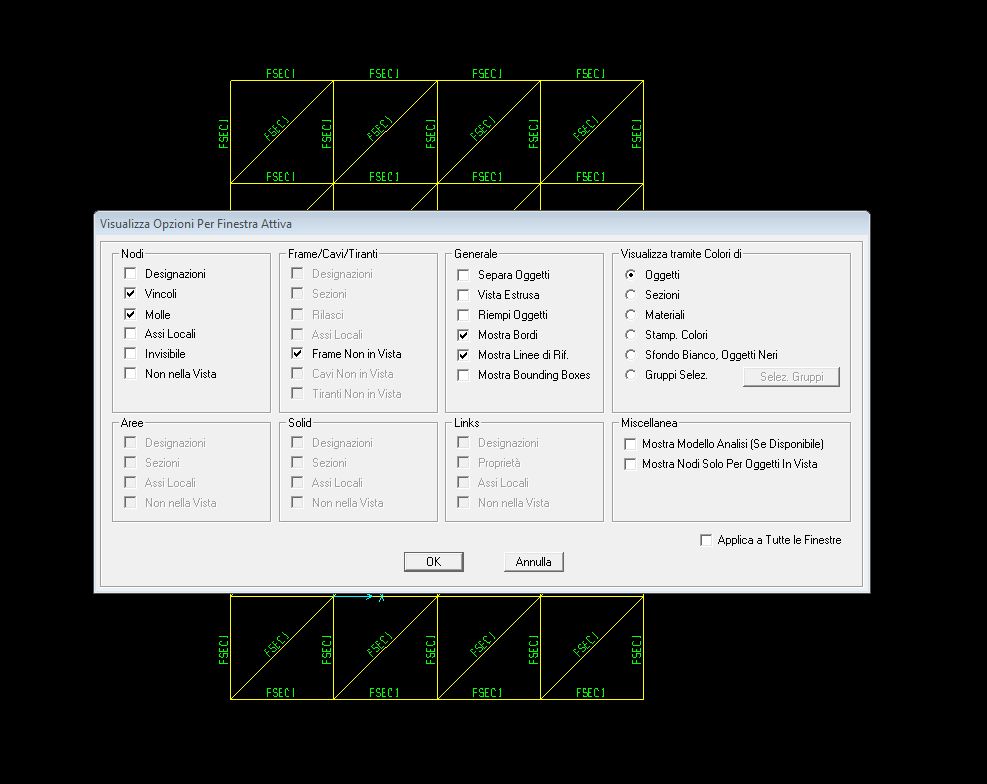
11. Seleziono tutti i nodi e poi mi metto sul piano xz in modo da assicurarmi di aver selezionato solo i nodi superiori, quindi vado su “Assegna”/ “Carichi Nodo”/ “Forze”, su “Nome schema di carico” assegno “Concentrato” e su “Forza Globale z” assegno -40KN


12. Rivado su “Imposta Opzioni Visualizzazione” e nella colonna “Nodi” seleziono “Invisibile” mentre nella colonna “Frame” deseleziono “Frame non in vista”
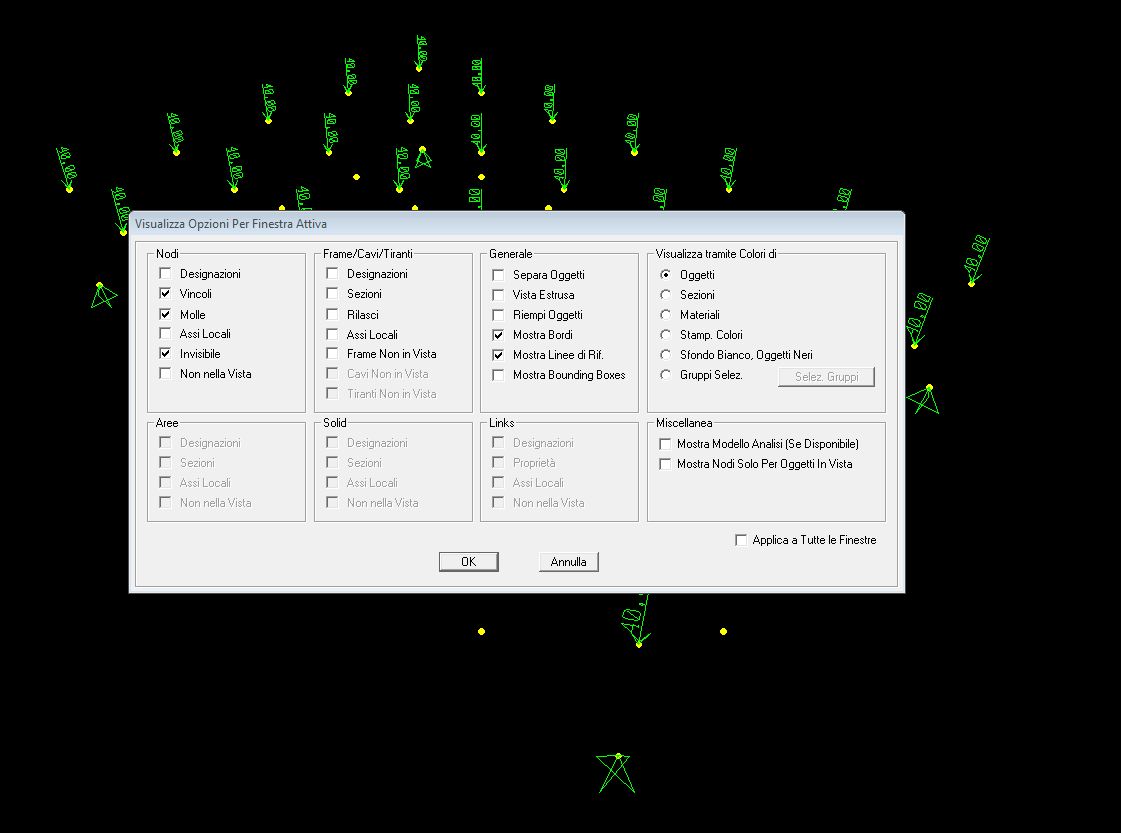
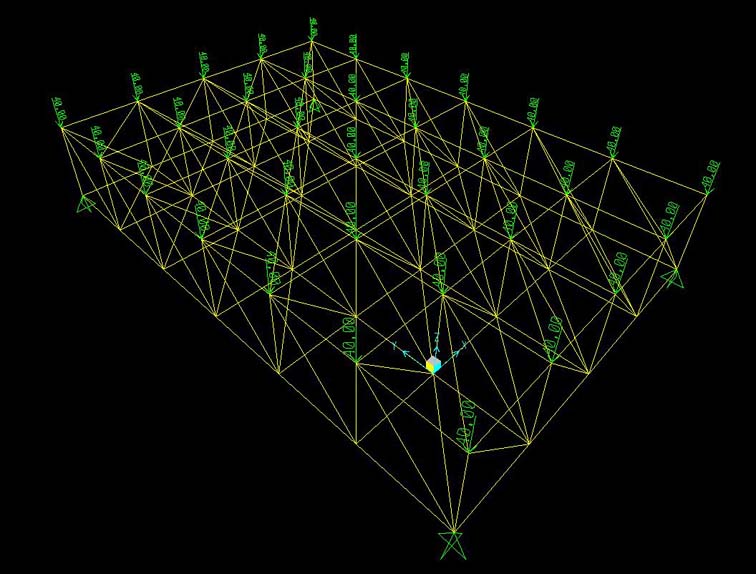
13. Ora che la struttura è disegnata vado su “Lancia Analisi” e selezionando “DEAD” e MODAL” vado su “Non eseguire caso” poi clicco su “Esegui ora” e ottengo la deformata della struttura disegnata
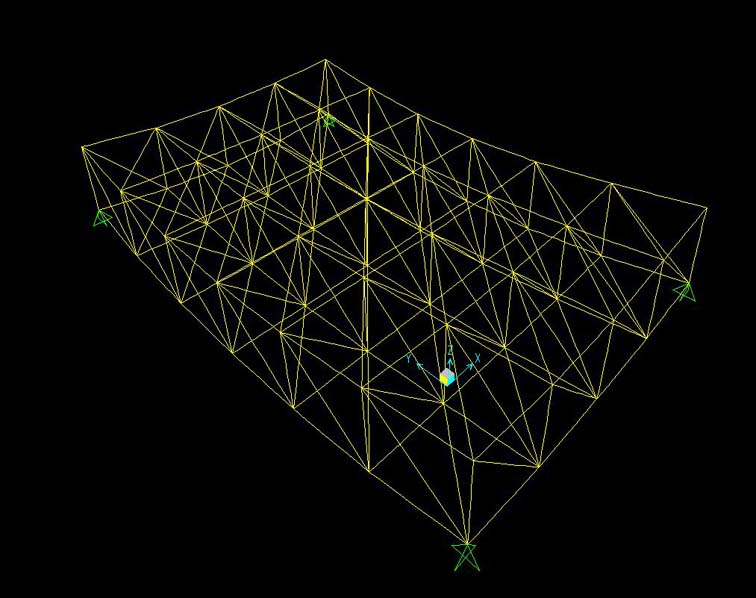
14. Verifico di aver disegnato bene la struttura andando a vedere i grafici del momento e del taglio, che dovranno risultare pari a zero, quindi vado su “Mostra sollecitazioni/tensioni”/ “Frame/Cavi”/ “ e poi seleziono il taglio e il momento
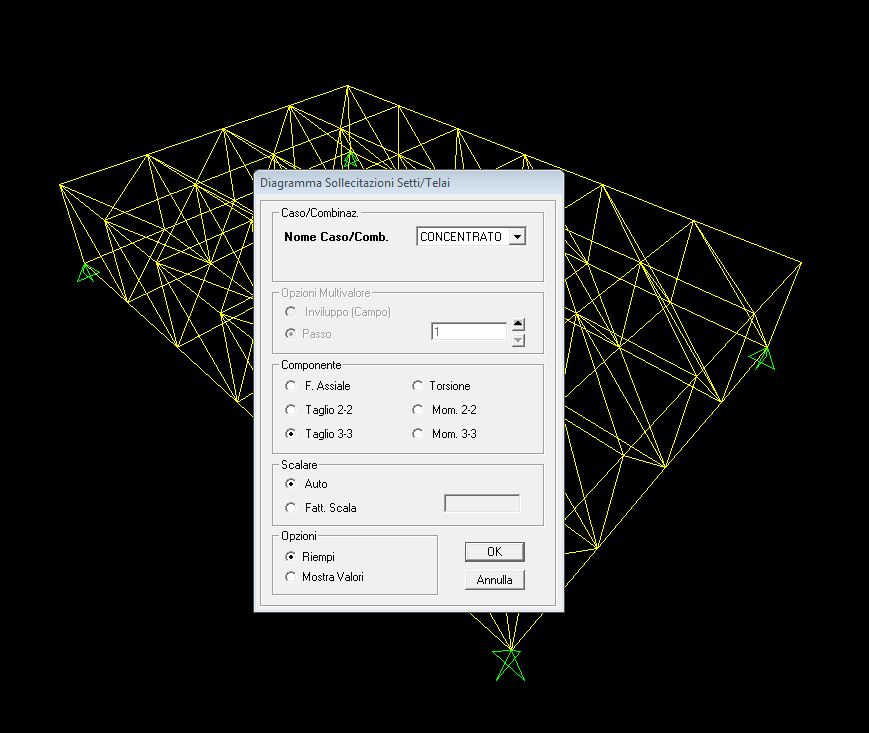
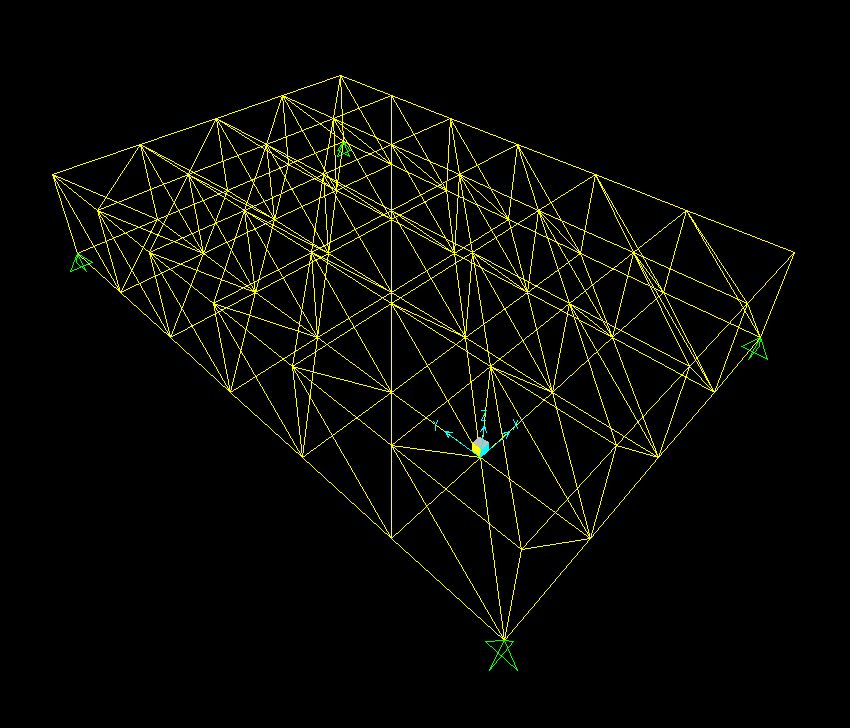
15. Ora invece vedo i valori dello sforzo assiale per poi progettare la struttura, quindi vado su “Mostra sollecitazioni/tensioni”/ “Frame, cavi” e poi seleziono lo sforzo assiale

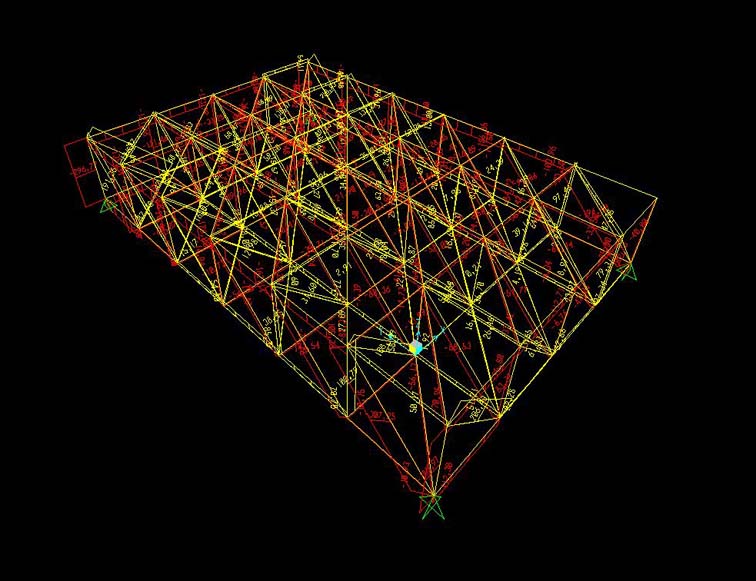
16. Per visualizzare tutti i valori dello sforzo normale sulle varie aste, per poi ottenere il massimo valore di trazione e compressione, vado su “Visualizza”/ “Mostra Tabelle” e in “Risultati dell’analisi” seleziono “Output Elemento” quindi vado su “ok”
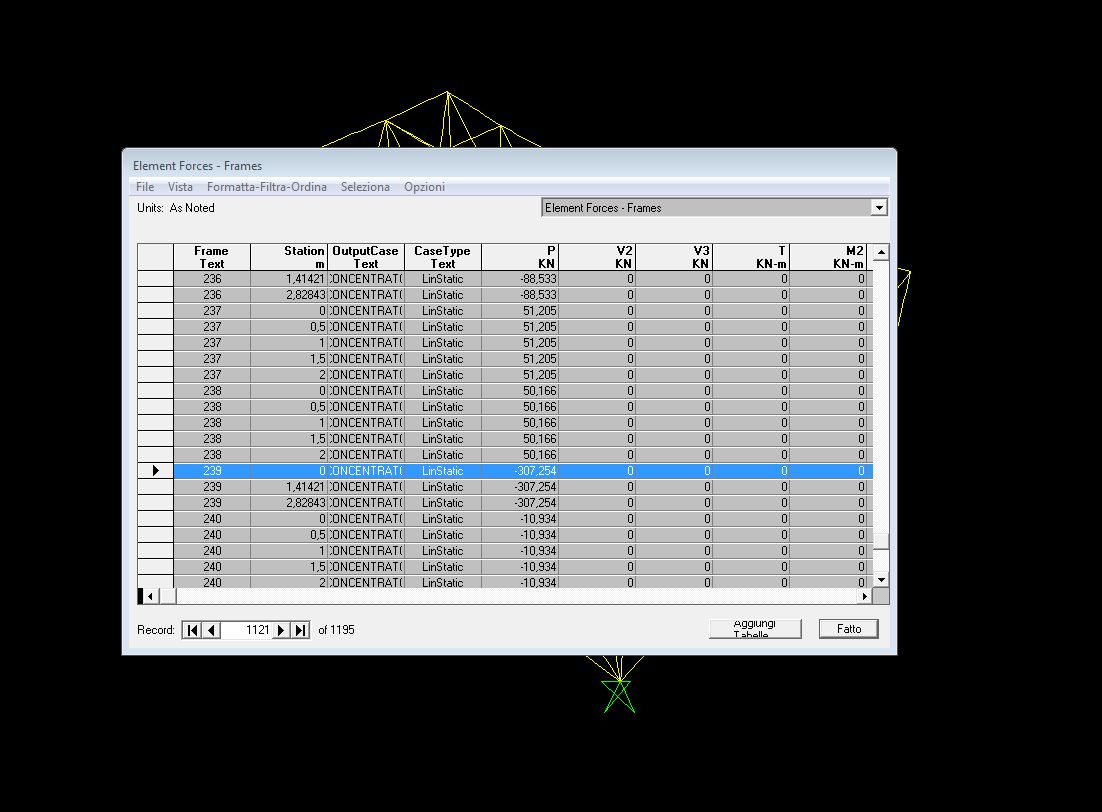
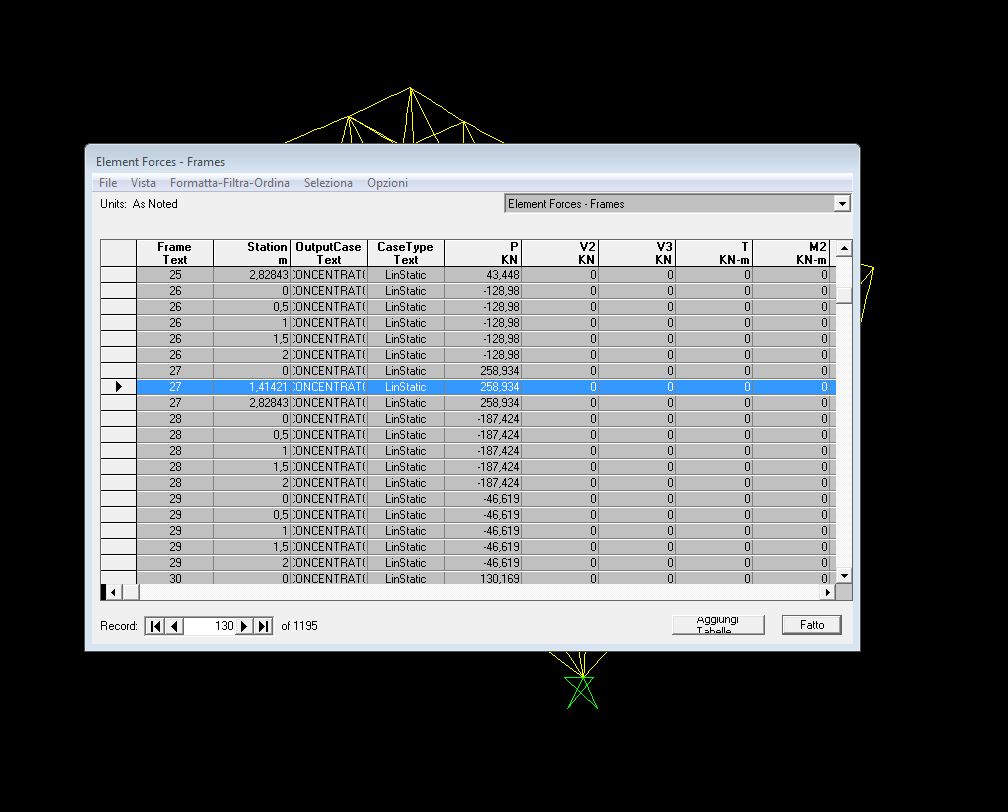
Una volta conosciuto su SAP lo sforzo normale massimo di trazione (258,934 KN) e compressione (307,254 KN) vado a calcolare la sezione minima da scegliere.
-Progetto a trazione:
Sapendo che σ = fD = N/A posso ricavare l’area minima della sezione dell’asta in modo che non venga superata la tensione di design (tensione di snervamento ridotta attraverso un coefficiente di sicurezza):
A = N/fD
Per calcolare l’area minima mi resta solo da conoscere fD, scelgo quindi di utilizzare un acciaio Fe430 S275 (dove il primo numero indica la tensione di rottura espressa in MPa, e il secondo numero la tensione di snervamento sempre in MPa):
fD = fy/ϒm = 275/1,05 = 261,90 MPa
A = Nmax(trazione)/fD = 258934N / 261,90N/mmq = 988,67 mmq = 9,89 cmq
L’area calcolata è quella minima per non superare lo snervamento, sceglierò quindi tra i profilati quello con un’area subito più grande dell’area minima calcolata:
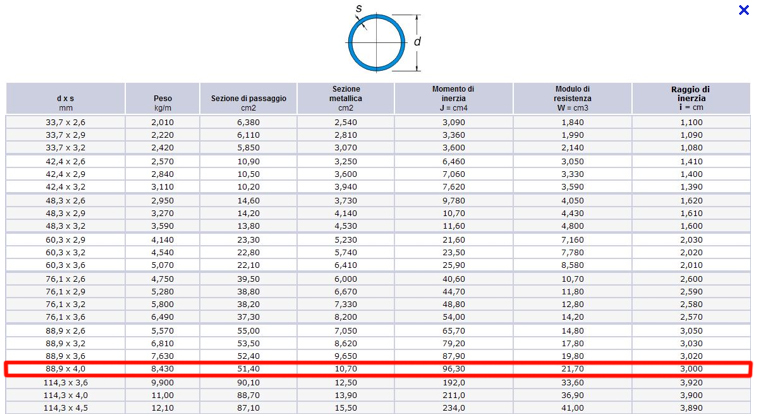
Per il progetto dell’asta compressa utilizzo lo stesso procedimento utilizzato in precedenza per l’asta tesa:
A = Nmax(compressione)/fD = 307254N / 261,90N/mmq = 1173,17 mmq = 11,73 cmq
L’area calcolata è quella minima per non superare lo snervamento, sceglierò quindi tra i profilati quello con un’area subito più grande dell’area minima calcolata:

Nell’asta soggetta a compressione, inoltre, occorre verificare che l’asta non sia troppo snella (quando il rapporto tra altezza dell’asta e larghezza della sezione è alto) per non incorrere in uno sbandamento laterale. Attraverso la formula di Eulero posso calcolarmi il valore del carico critico Pcrit per cui si innesca il fenomeno dello sbandamento:
-
Se Nmax ≥ Pcrit → Asta instabile
-
Se Nmax < Pcrit → Asta stabile
Pcrit = (∏² * E * Jmin) / l₀² dove: E = modulo elastico a compressione
Jmin = momento d’inerzia minore, poichè l’asta sbanda di
più nella direzione in cui il momento d’inerzia è
minore (nel nostro caso è uguale sia rispetto
l’asse x che rispetto l’asse y)
l₀ = lunghezza libera d’inflessione, rappresenta la
modalità in cui sbanda l’asta e dipende dall’altezza
dell’asta e dalle condizioni di vincolo
Nel nostro caso i vincoli sono costituiti solo da cerniere per cui l₀ = l, dove l è la lunghezza dell’asta quindi pari a 2,828m (poiché l’asta soggetta a massimo sforzo di compressione è una delle aste inclinate)
Pcrit = (3,14² * 210000N/mm² * 1920000 mm⁴) / 2828² mm = 497074N = 497,074 KN
Nmax = 307,254KN < Pcrit = 497,074KN → la sezione è verificata
Commenti recenti