PROGETTO DI TRAVE
Dato uno schema strutturale di un solaio come quello rappresentato in figura è necessario procedere con il dimensionamento della trave più sollecitata, che in questo caso è quella centrale. Il dimensionamento avverrà per tre diverse tecnologia : CEMENTO ARMATO, ACCIAIO e LEGNO.
Indivisuata la trave più sollecitata vado a delimitare la sua area di influenza: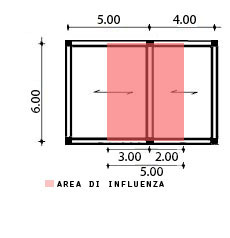
PROGETTO DI TRAVE IN CEMENTO ARMATO
Sezione trasversale schematica di un generico solaio misto in latero-cemento. La normativa (D.M.09/01/96, par.7) fornisce precise indicazioni sul suo predimensionamento:
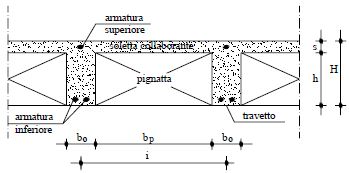
Prendo a questo punto in analisi un metro quadro (m2) di solaio rappresentato in sezione:
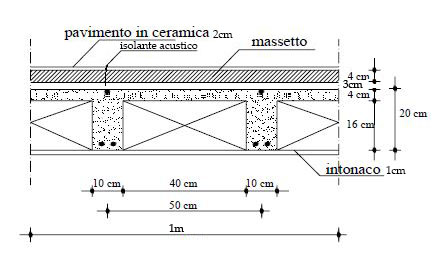
Vado ora ad analizzare i diversi tipi di carichi che agiscono sulla struttura individuandone i loro pesi specifici:
Calcolo il peso di ogni singolo elemento del solaio al metro quadro: moltiplico il suo peso specifico in kN/m3 per il suo stesso volume e lo divido per un metro quadrato.
A questo punto posso calcolarmi il momento massimo M agente sulla trave avendo il carico lineare qu, la luce che copre la mia trave che è 6 (il braccio ) e sapendo che il momento max di una trave appoggiata è ql2/8.
Mmax = qu x l2/8= 50.84x(6)2/8= 228,79kNm
PROGETTO DELLA TRAVE :
Dopo aver trovato il carico lineare totale che graverà sulla mia trave e il momento massimo vado a dimensionarmi la trave:
Per il cemento armato avrò due tensioni di progetto essendo un materiale non omogeneo, una per l’acciaio fyd, dove y sta per yield ossia snervamento,e una per il calcestruzzo fcd.
La tensione di progetto per l’acciaio che deve resistere a trazione si calcola cosi:
Ora per trovare l’ H min della sezione della trave ho bisogno di :
b=30 cm
così mi ricavo hu che è l’altezza utile della sezione reagente in calcestruzzo e
si trova al di sopra dell’ armatura
Hu= r √Mmax/b = 35.37 cm
PROGETTO DI TRAVE IN ACCIAIO
Prendo in analisi un metro quadro (m2) di un solaio di una struttura in acciaio rappresentato in sezione:
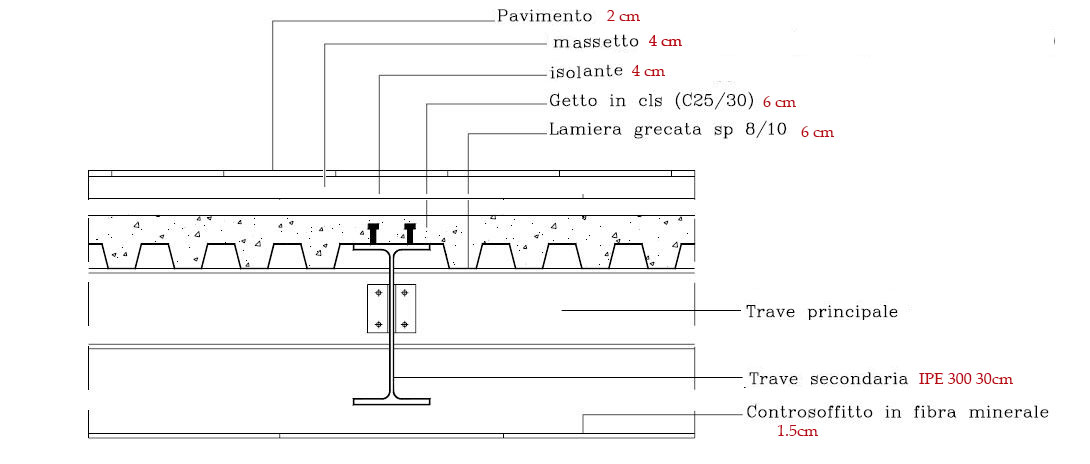
Vado ora ad analizzare i diversi tipi di carichi che agiscono sulla struttura individuandone i loro pesi specifici:
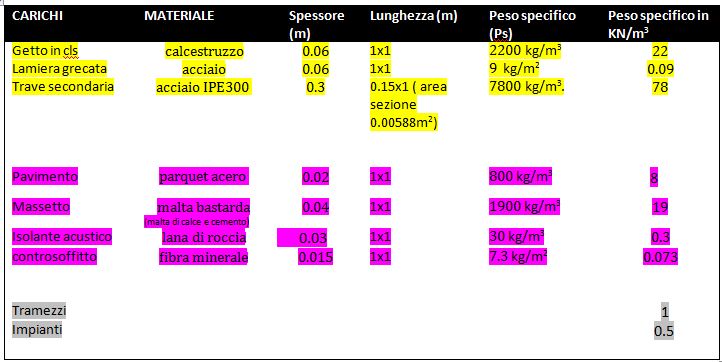
Calcolo il peso di ogni singolo elemento del solaio al metro quadro: moltiplico il suo peso specifico in kN/m3 per il suo stesso volume e lo divido per un metro quadrato.
A questo punto posso calcolarmi il momento massimo M agente sulla trave avendo il carico lineare qu, la luce che copre la mia trave che è 6 (il braccio ) e sapendo che il momento max di una trave appoggiata è ql2/8.
Mmax = qu x l2/8= 45.91 x (6)2/8= 206,61kNm
Ora non mi resta che scegliere il valore caratteristico di snervamento per l’acciaio fyK che mi individua la classe di resistenza del materiale , in questo caso scelgo un acciaio medio (classe Fe430/s275) di resistenza 275 Nmm2.
Mi calcolo così la tensione di progetto fd ( tensione ammissibile) dividendo fyk per un il coefficienti di sicurezza per la resistenza delle membrature e la stabilità, γs = 1,05 :
Fd = 275/1.05= 261.90
Mi calcolo infine il MODULO DI RESISTENZA A FLESSIONE Wxmin, per poi andare a scegliere il profilato appropriato sulla tabella dei profili in acciaio.
Wxmin:= M/fd = 788,88 cm3
Questa formula me la ricavo direttamente dalla formula di Navier e divide il momento flettente max per la tensione di progetto.
La tabella di calcolo mi ha ora trovato il Wxmin cioè il valore minimo che la sezione che sceglierò dovrà avere affinchè nessuna fibra del materiali superi la tensione di progetto.
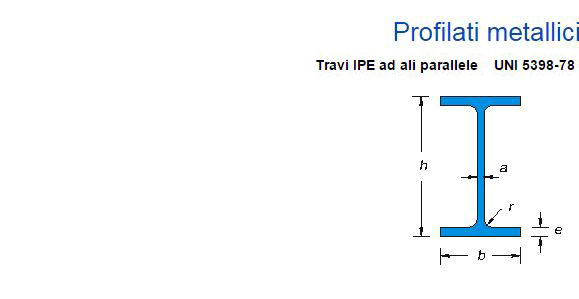
Nella tabella dei profili metallici (sotto riportata) scelgo un profilo adatto che abbia un modulo di resistenza a flessione Wx maggiore di quello da me trovato: IPE 360
7
La tensione di progetto fd e la resistenza a flessione wx sono inversamente proporzionali quindi più piccola scelgo la resistenza del materiale a snervamento più grande dovrò scegliere la sezione del profilato e viceversa.
PROGETTO DI TRAVE IN LEGNO
Prendo in analisi un metro quadro (m2) di un solaio di una struttura in acciaio rappresentato in sezione:
Vado ora ad analizzare i diversi tipi di carichi che agiscono sulla struttura individuandone i loro pesi specifici:
per progettare il mio solaio scelgo di utilizzare un legno lamellare incollato GL28h, GL sono le classi di resistenza e la cifra che la segue corrispondono al valore caratteristico della resistenza a flessione, h invece sta a significare che il legno lamellare è omogeneo, ossia le lamelle utilizzate appartengono alla stessa classe di resistenza.
Calcolo il peso di ogni singolo elemento del solaio al metro quadro: moltiplico il suo peso specifico in kN/m3 per il suo stesso volume e lo divido per un metro quadrato. 
A questo punto posso calcolarmi il momento massimo M agente sulla trave avendo il carico lineare qu, la luce che copre la mia trave che è 6 (il braccio ) e sapendo che il momento max di una trave appoggiata è ql2/8.
Mmax = qu x l2/8= 38.96 x (6)2/8= 175.30 kNm
Per calcolare la TENSIONE DI PROGETTO Fd per quanto riguarda il legno dobbiamo procurarci alcuni dati:
ricordo che ho scelto un legno lamellare incollato GL28h.
Fmk: resistenza a flessione caratteristica del legno 28 N/mm2
Kmod: è un coefficiente che riduce i valori della resistenza che tiene conto della durata del carico e delle condizioni di umidità e cambia a seconda del materiale prescelto , nel mio caso: classe di servizio 2, classe di durata del carico media =0.80
Inserendo questi dati nella tabella di calcolo mi ricavo Fd= kmod x fmk / γm
Rimane ora da inserire nel foglio di calcolo la base b=35 ipotizzata per trovare l’altezza minima della trave di legno che era l’unica incognita nel nostro progetto.
L’altezza minima viene 44 cm e con una ingenierizzazione arrivo ad un altezza della trave in legno di 55cm
Ora passo alla seconda fase dell’ esercitazione in cui verifico la deformabilità dello sbalzo.
Calcolo il peso di ogni singolo elemento del solaio al metro quadro: moltiplico il suo peso specifico in kN/m3 per il suo stesso volume e lo divido per un metro quadrato.
Commenti recenti