Blog

DIMENSIONAMENTO DI UNA TRAVE RETICOLARE 3D

Prendo come esempio una pensilina composta da una  travatura reticolare piramidale a base quadrata.

Al fine di dimensionare le aste di questa struttura ho ipotizzato che essa debba sostenere un carico di 40 KN.

Per completare la mia esercitazione avrò bisogno del softwar SAP2000 e di un foglio di calcolo Excel.

 1- Disegno direttamente su SAP2000 il mio modello di struttura reticolare: determino innanzitutto        l'unità di misura in KN,m,C andandola a modificare in basso a sinistra nel menù a tendina; dopo di che FILE→NEW MODEL e scelgo dalla finestra GRID ONLY, così da crearmi una griglia misurare su cui disegnare.

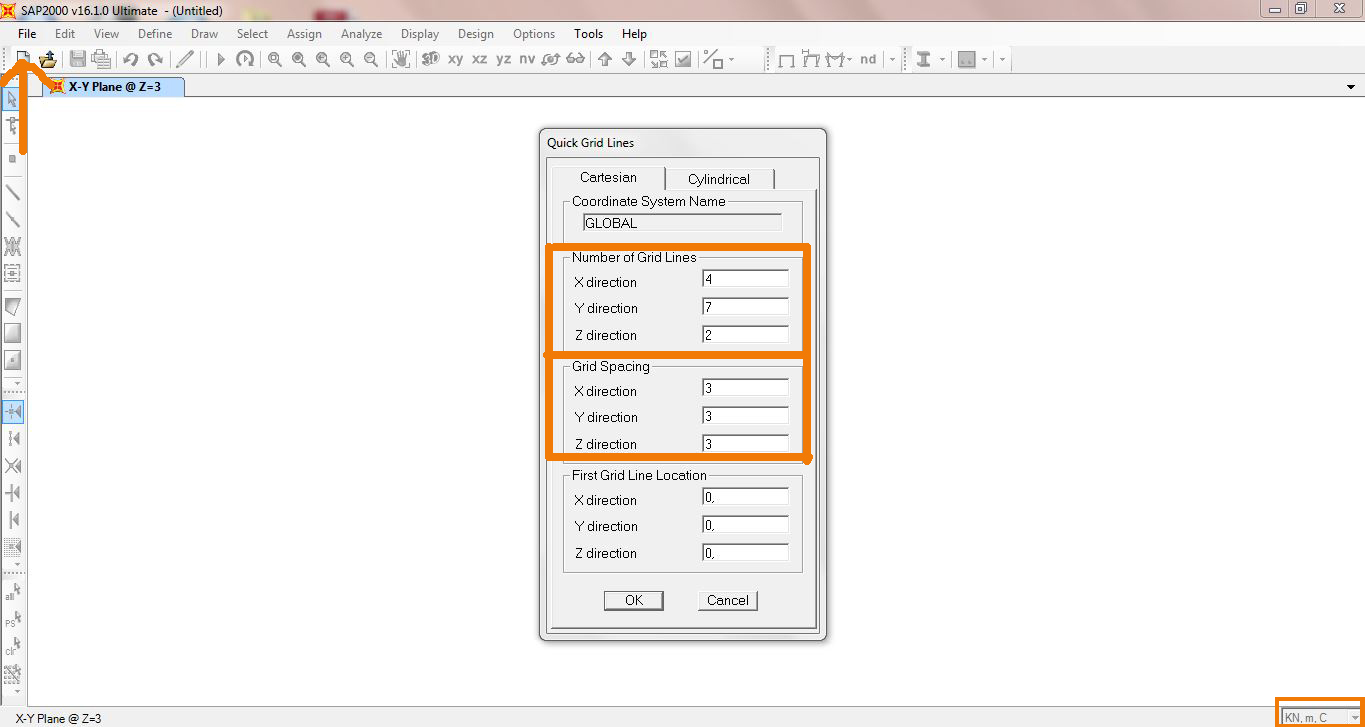
Vado a inserire in Number of Grid Lines il numero di campate secondo gli assi x,y,z i quali mi determineranno la griglia e in Grid Spacing la lunghezza delle mie aste che sarà di 3m in tutte e tre le direzioni.

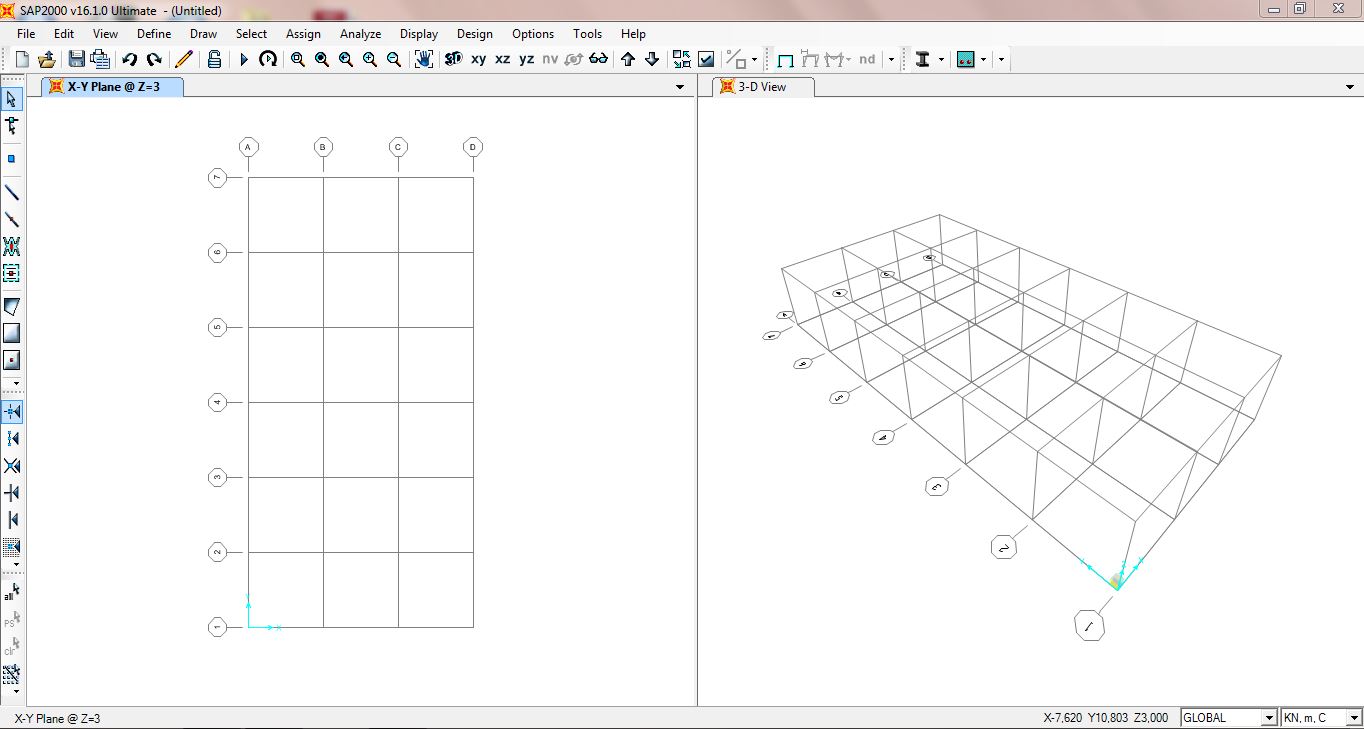
Con il comando FRAME , linea, disegno un modulo della trave piramidale controventata alla base.

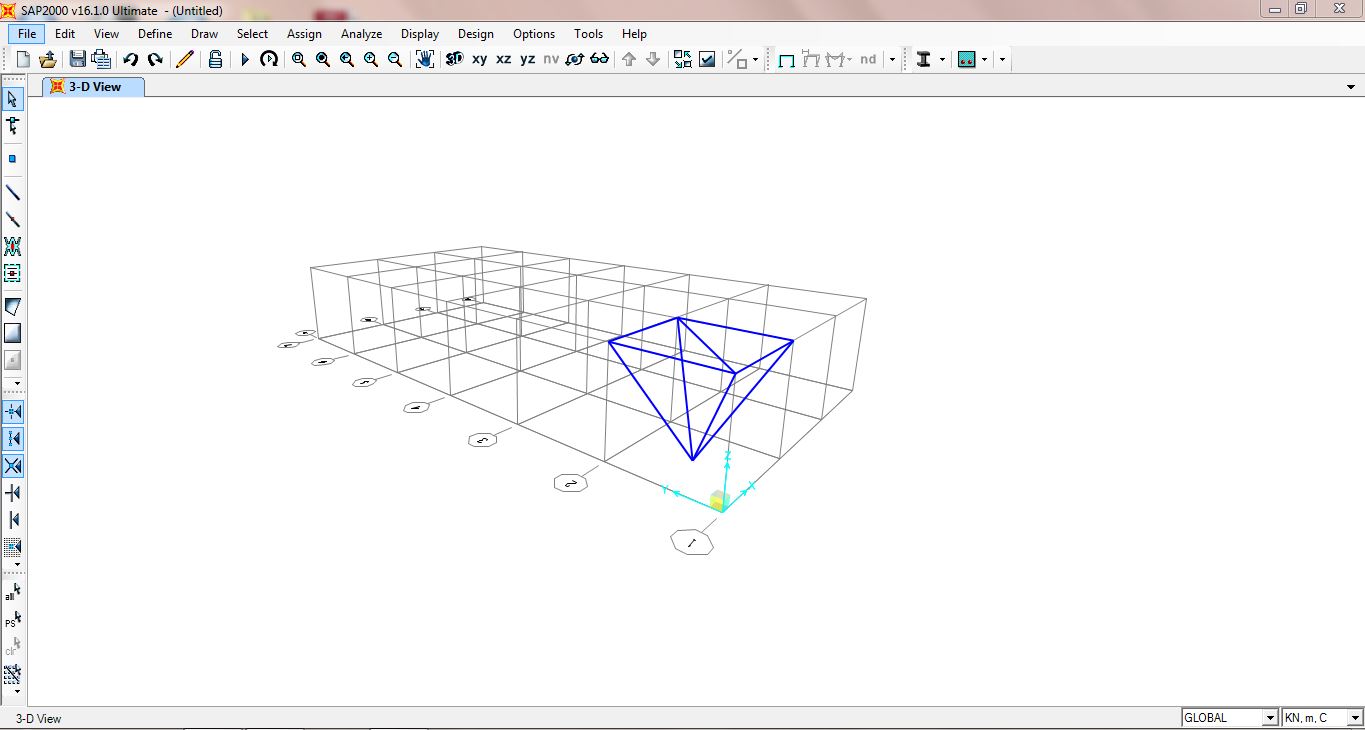
Attraverso il comando copia Ctrl+C  Ctrl+V  sarà ripetuto inserendo le coordinate sugli assi x e y formando una struttura rettangolare 3x6 m.

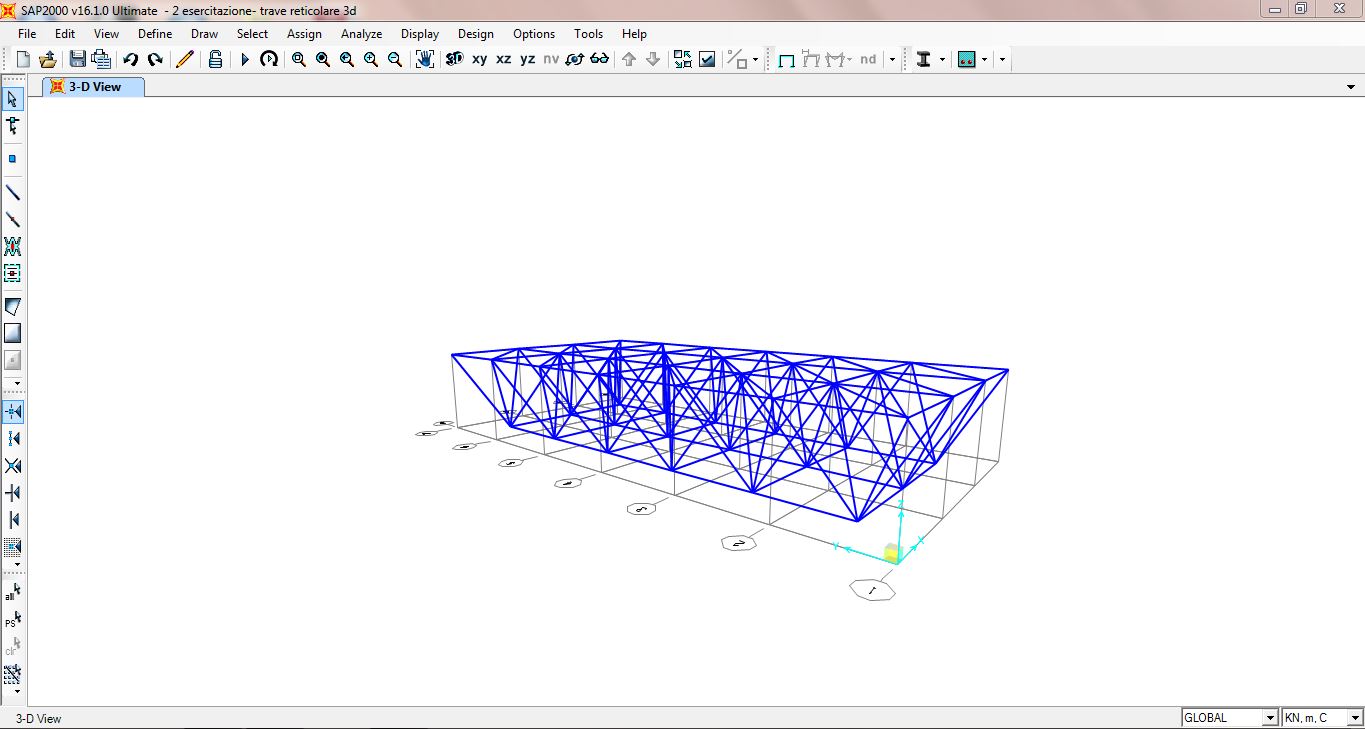
Controllo che non ci siano aste duplicate: selezione tutto, EDIT→EDIT  POINTS→MERGE JOINTS

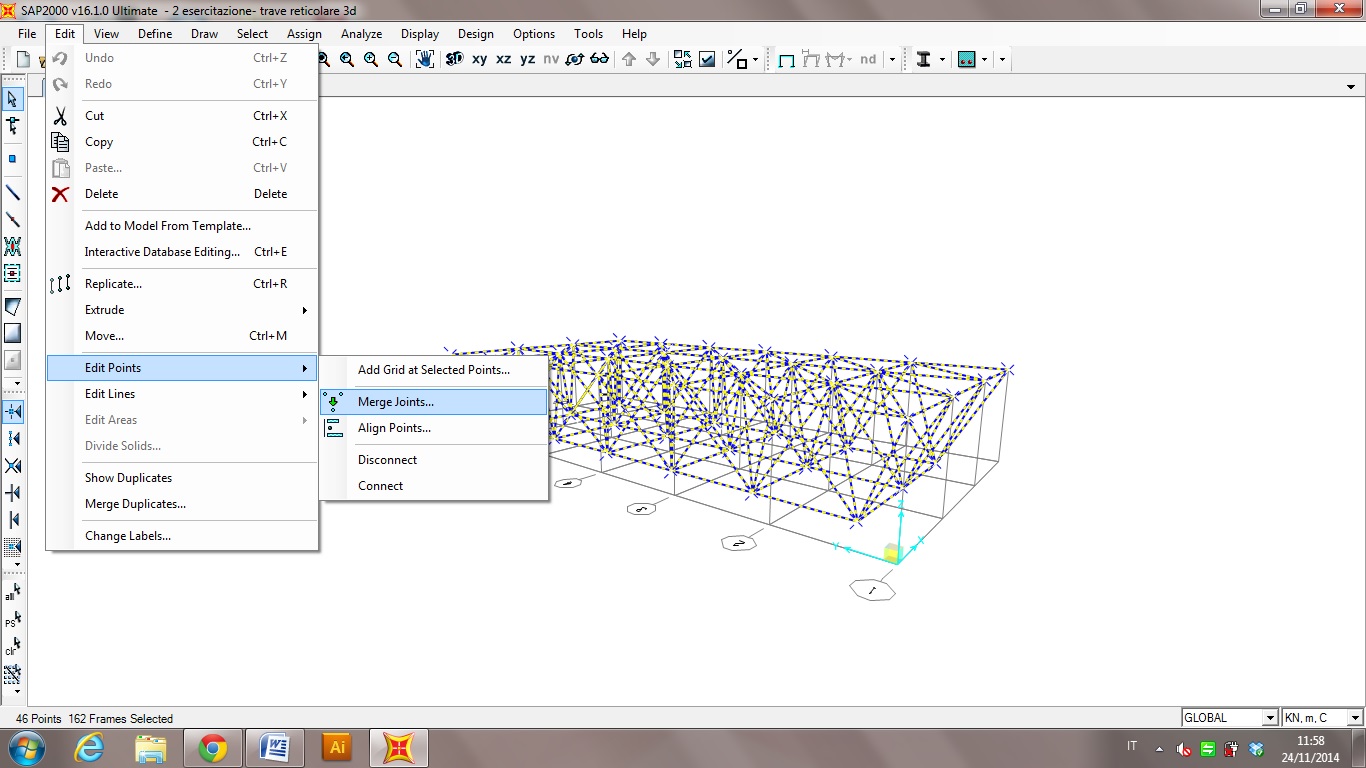
A questo punto la modellazione della struttura è terminata

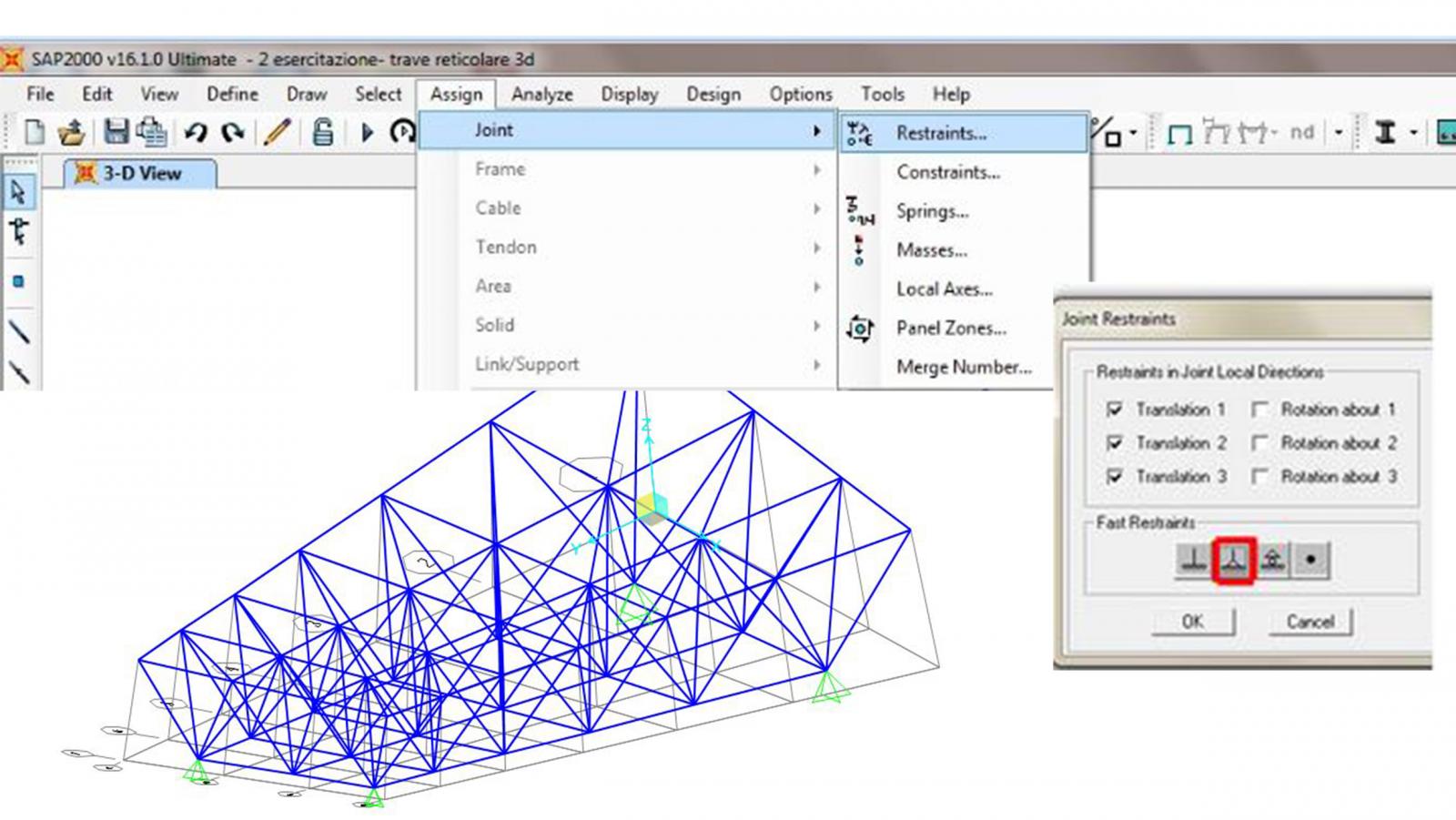
2- Andiamo ad assegnare i vincoli esterni : seleziono i 4 vertici estremi della travatura piramidale, ASSIGN→JOINT→RESTRAINTS , dalla finestra che mi si apre seleziono il vincolo Cerniera.

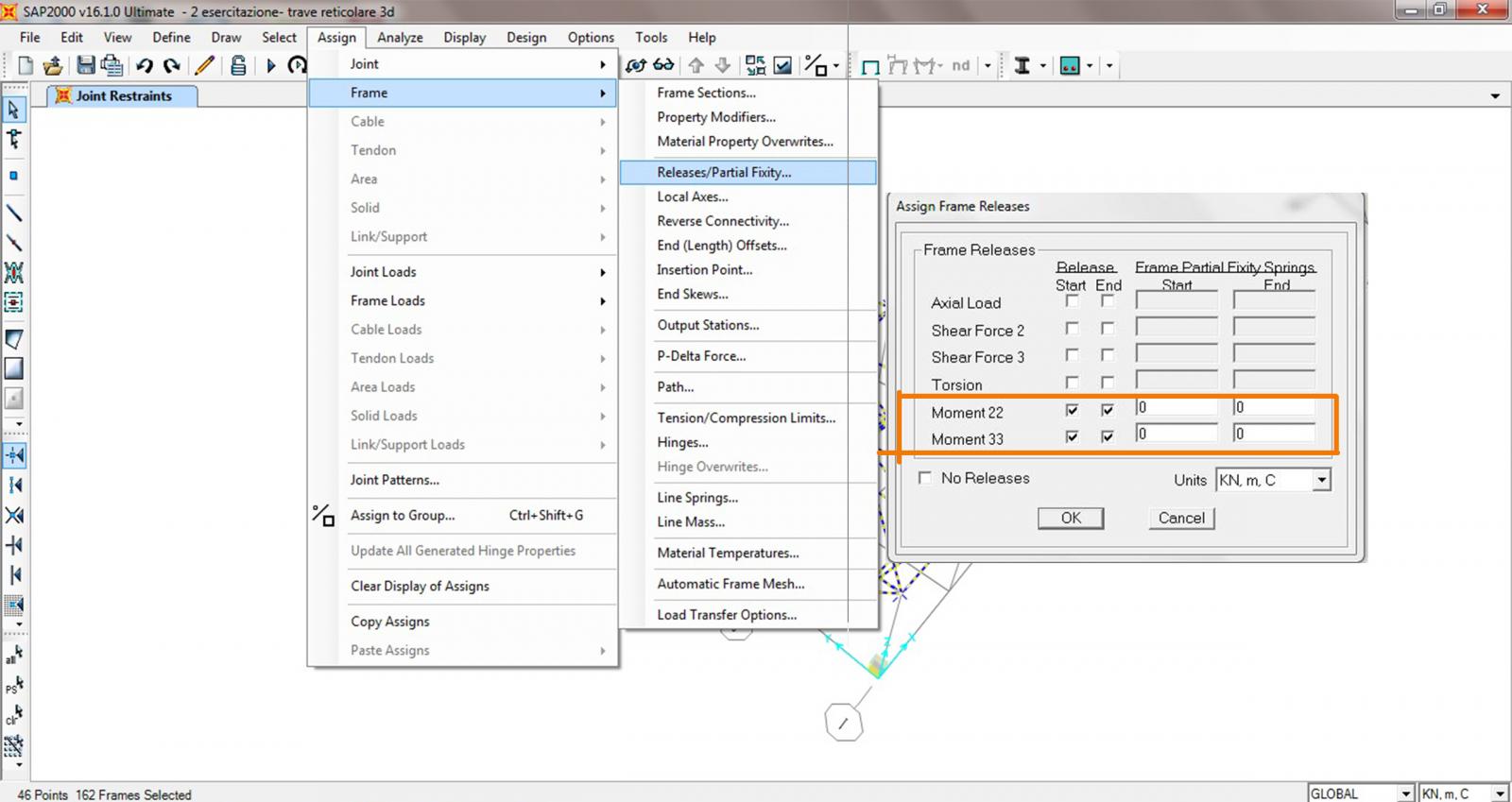
Assegno ora i vincoli interni che rappresentano i nodi di ogni asta: seleziono la struttura,  ASSIGN→FRAME→RELEASES/PARTIAL FIXITY, nella finestra andrò a a spuntare  Moment 22 e Moment 33 sia su Start sia su End  mettendo a entrambe zero, così da riprodurre il vincolo di cerniera interna rendendo libera la rotazione.

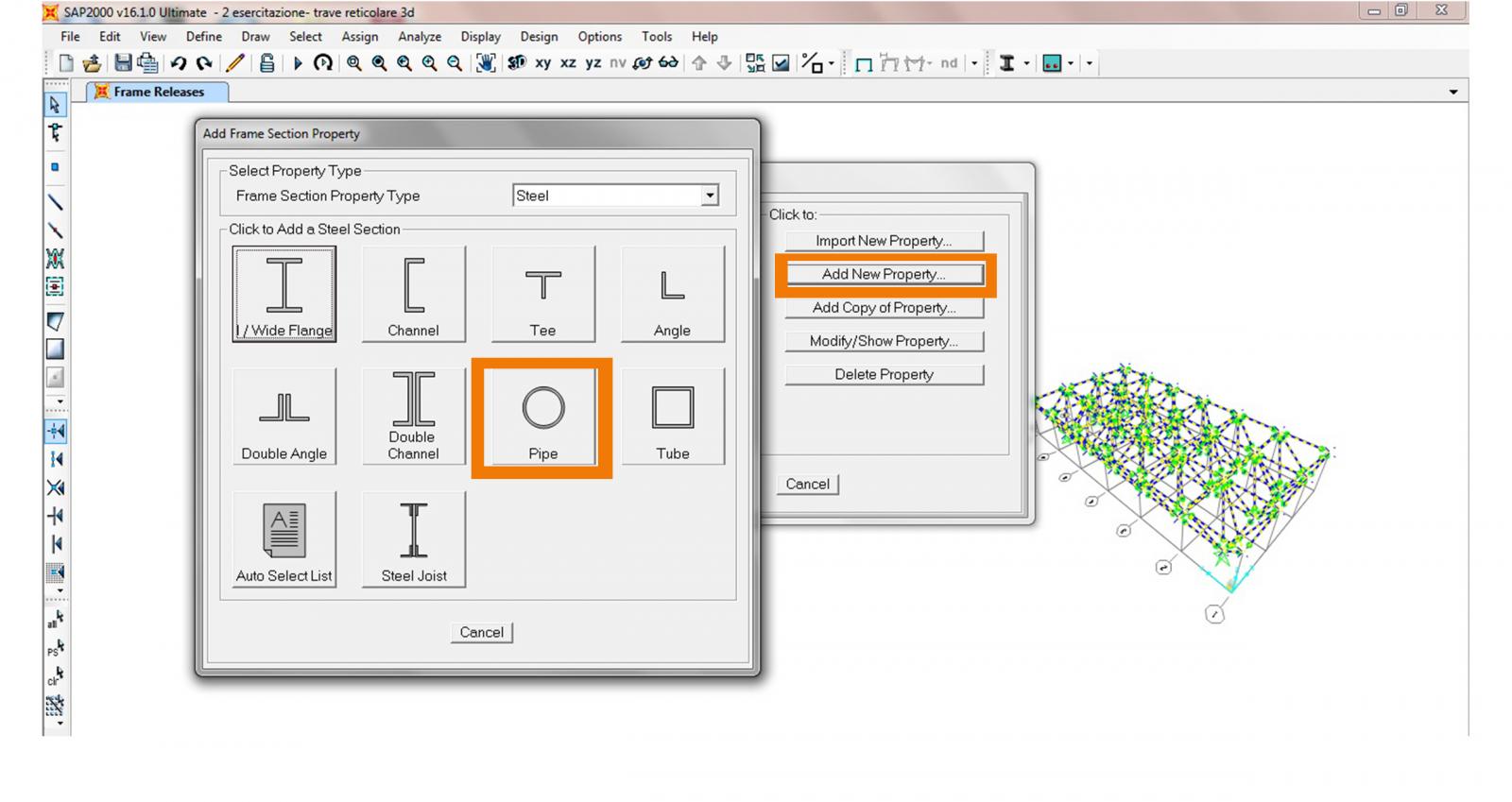
3- andiamo ad assegnare il materiale e la sezione alle aste: seleziono tutta la struttura, ASSIGN→FRAME→FRAME SECTION poi a sx clicco su Add New Property, in Frame Section Proprerty Type scelgo il materiale  steel (acciaio) e clicco sul profilo Pipe, si aprieà una finestra in cui inserisco in Section Name  Pipe diamo poi ok per due volte .

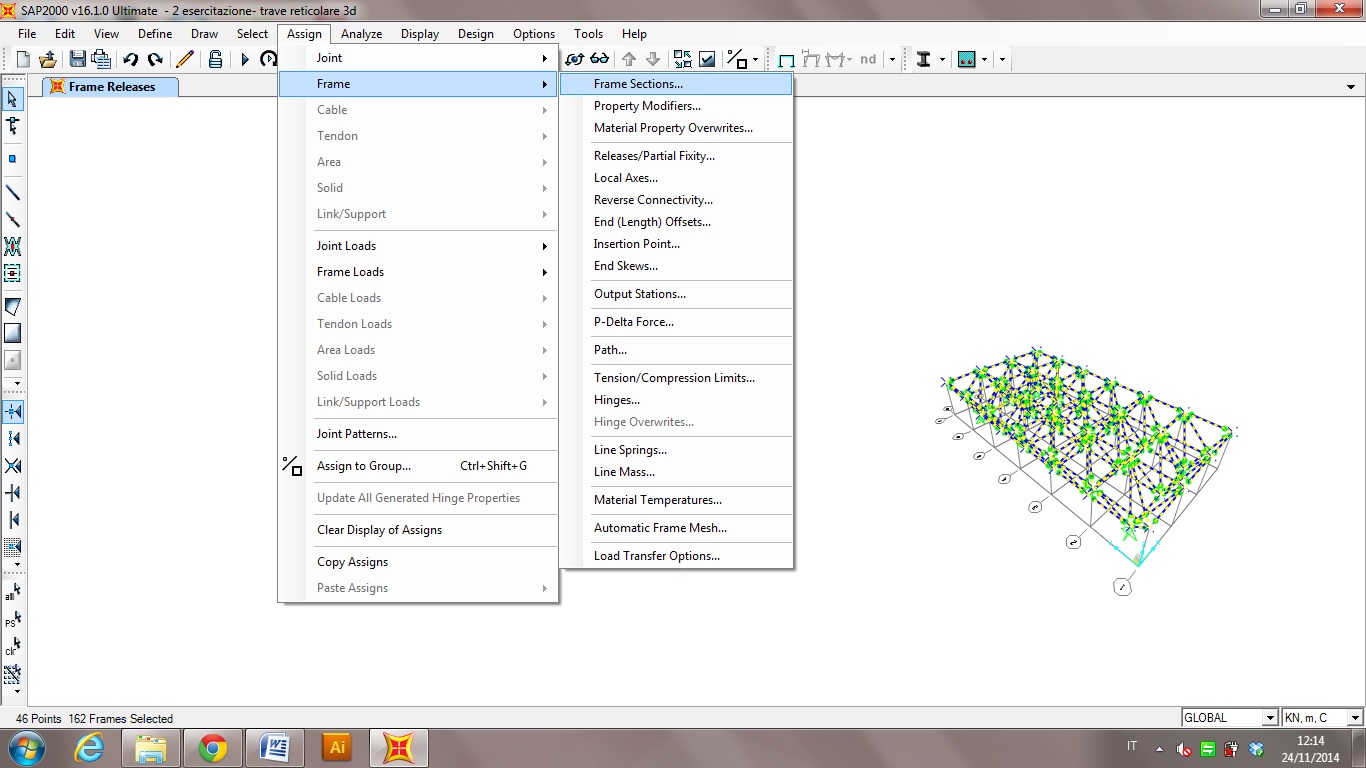
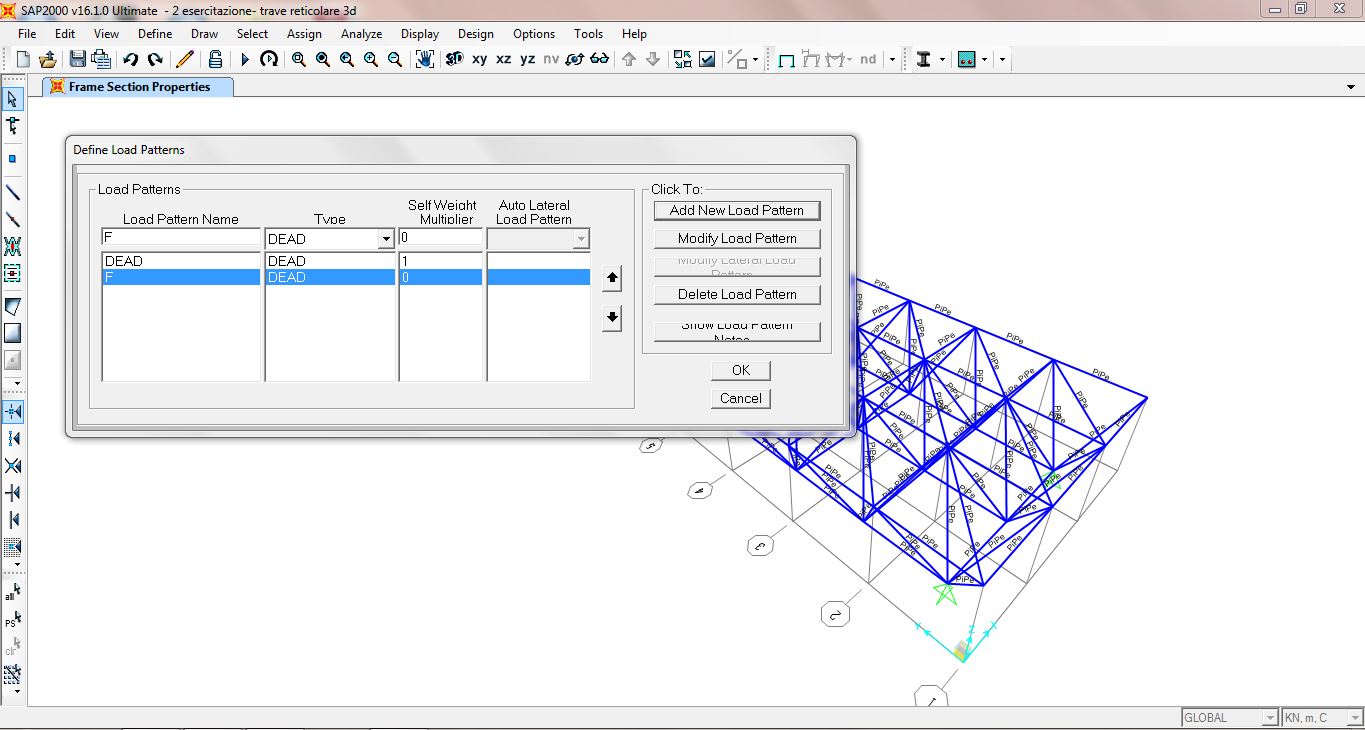
4- Andiamo a crearci il carico che poi assegneremo alla struttura: DEFINE→LOAD PATTERN,

nella finestra in Load Pattern Name  chiamo i carichi F e in Self Weight Multiplier (coefficiente del peso proprio) inserisco il valore di 0 e clicco Add New Load Pattern

5-Andiamo a questo punto ad assegnare il carico puntuale F sui nodi superiori della struttura: seleziono le aste superiori, ASSIGN→JOINT LOADS→FORCES

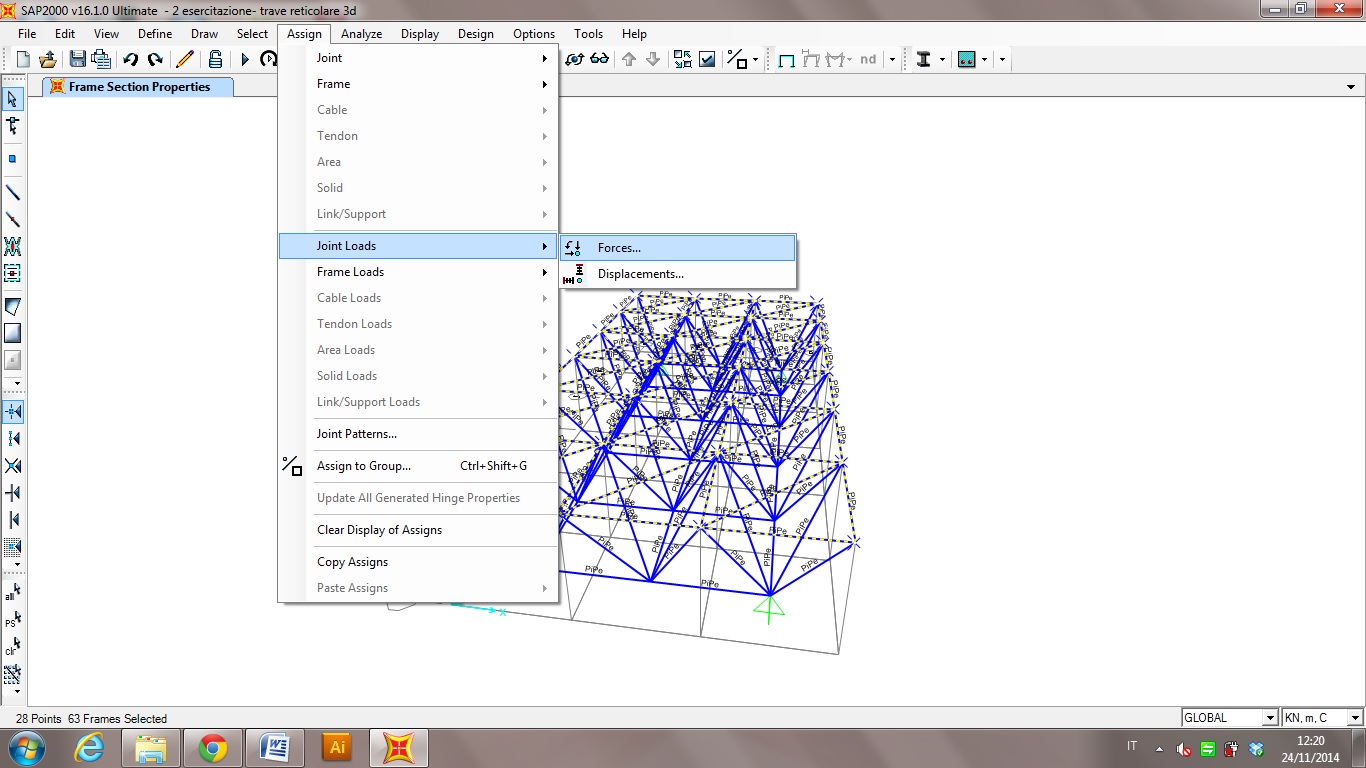
Dal menù a tendina scelgo il carico creato F, essendo un carico verticale verso il basso (asse z) andrò ad assegnargli in Force Global Z un valore di -50 KN.

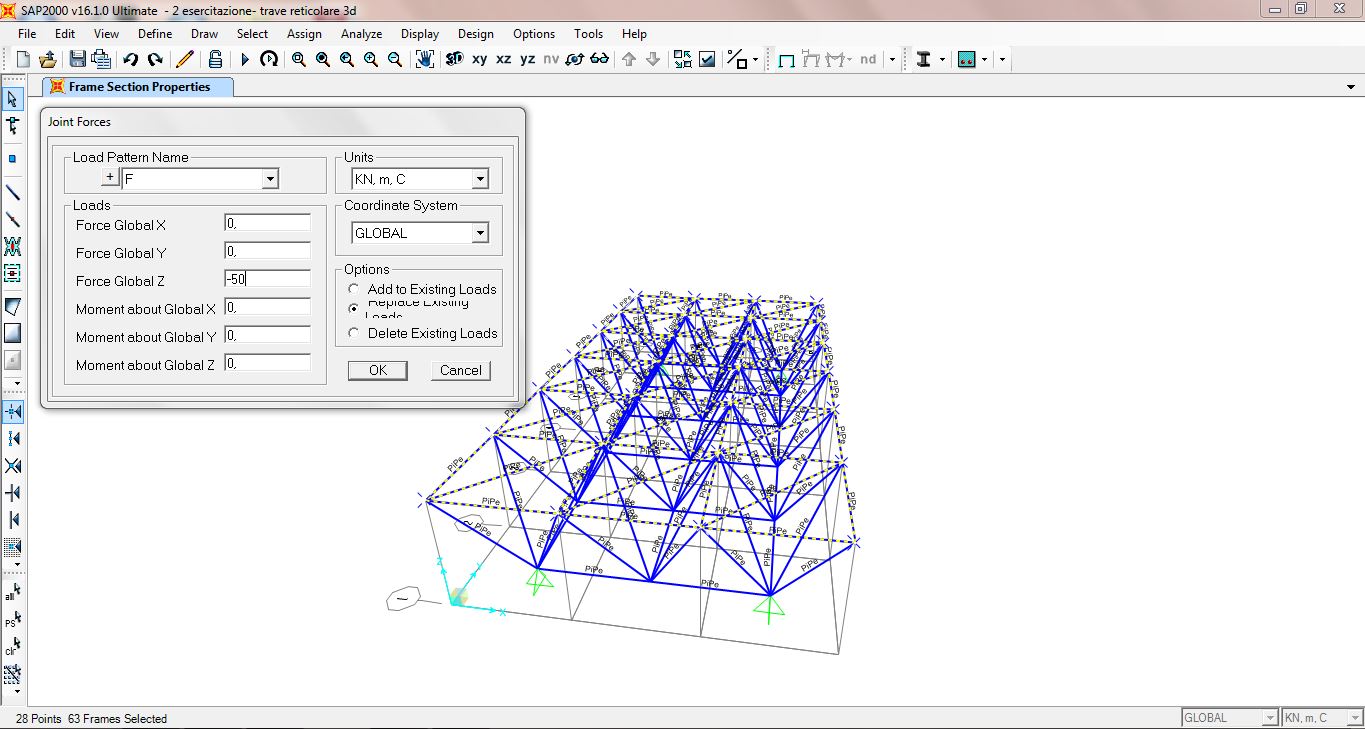
6- E’ ora possibile analizzare la struttura avendo fornito al software tutti i dati necessari:

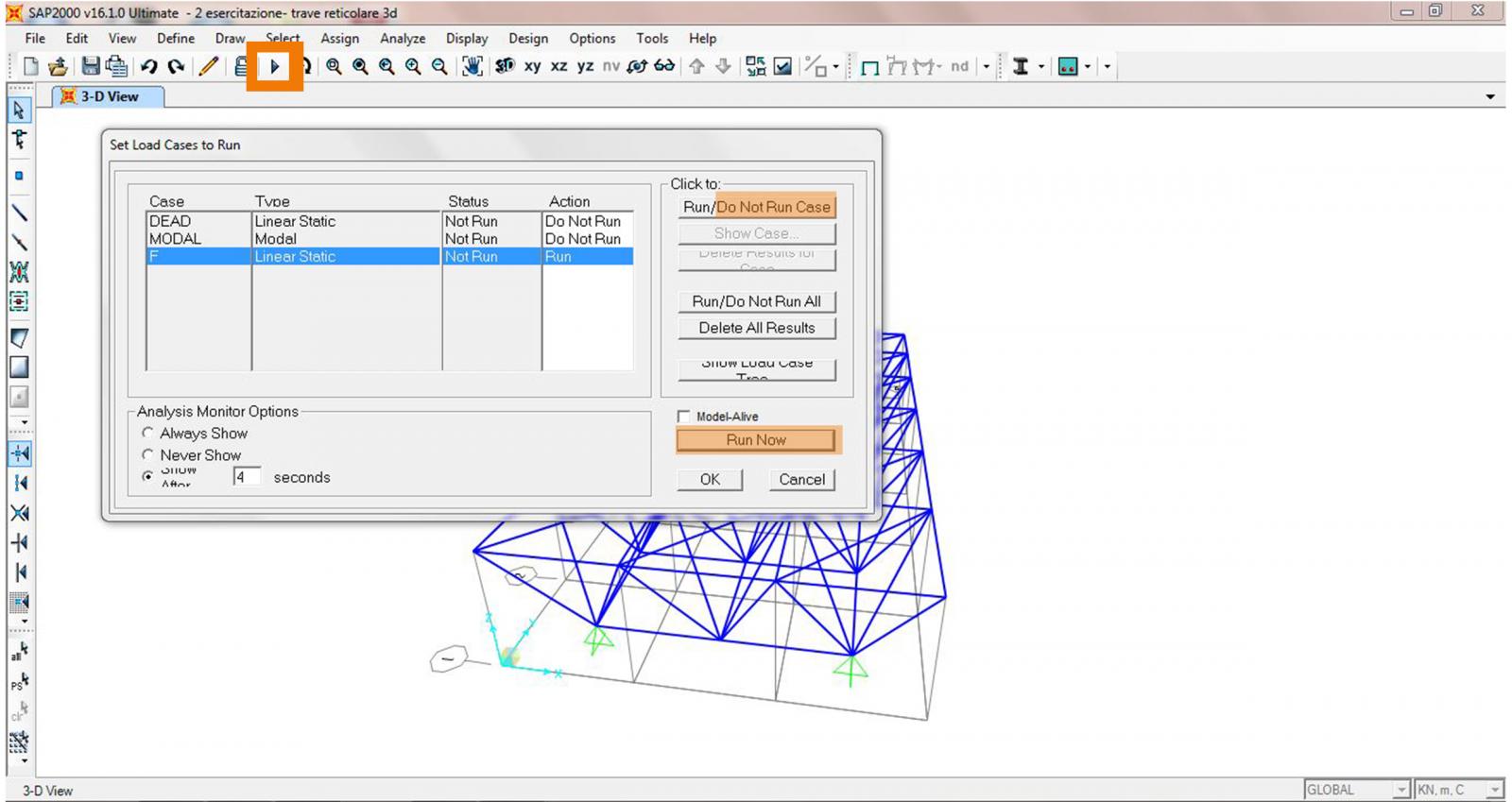
faccio partire l’ analisi cliccando sul tasto evidenziato in arancione, seleziono i carichi che non prendere in considerazione e clicco su Do Not Run , al contrario seleziono F (il carico che agisce sui nodi) e schiaccio Run Now.

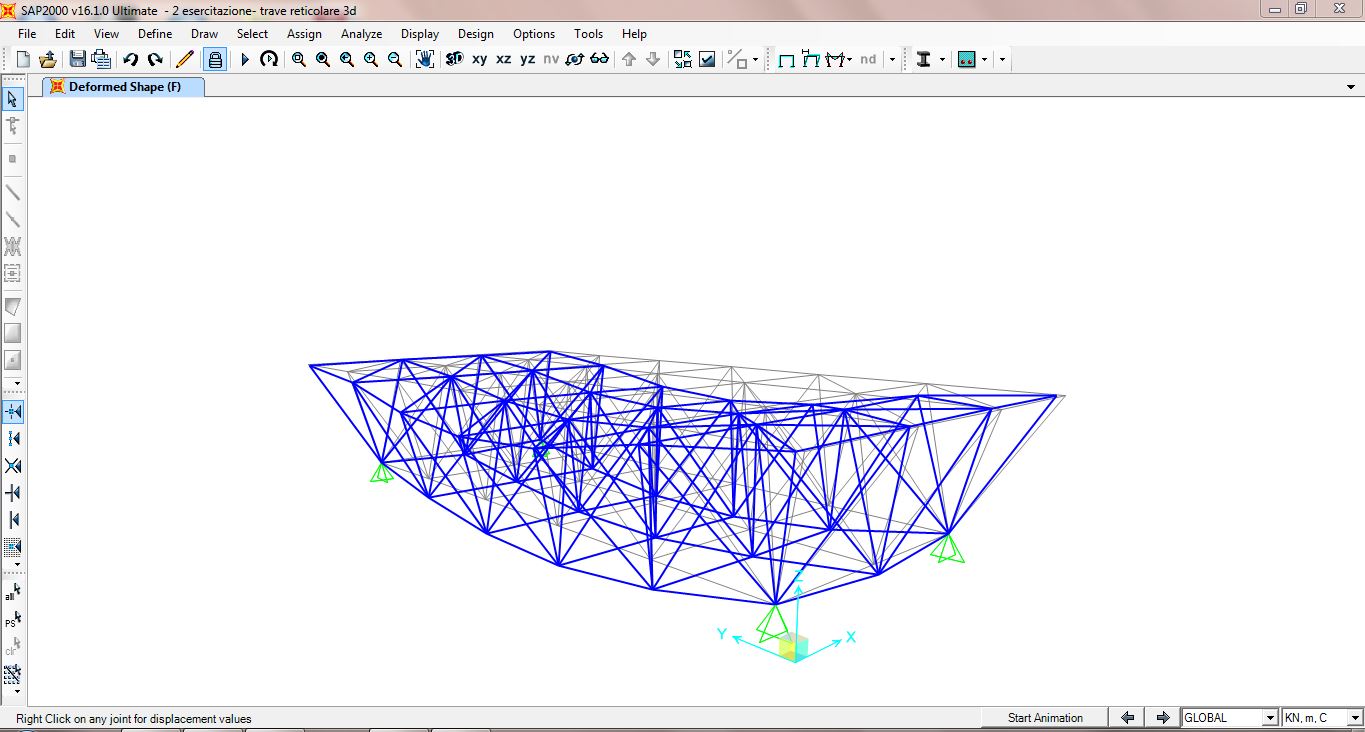
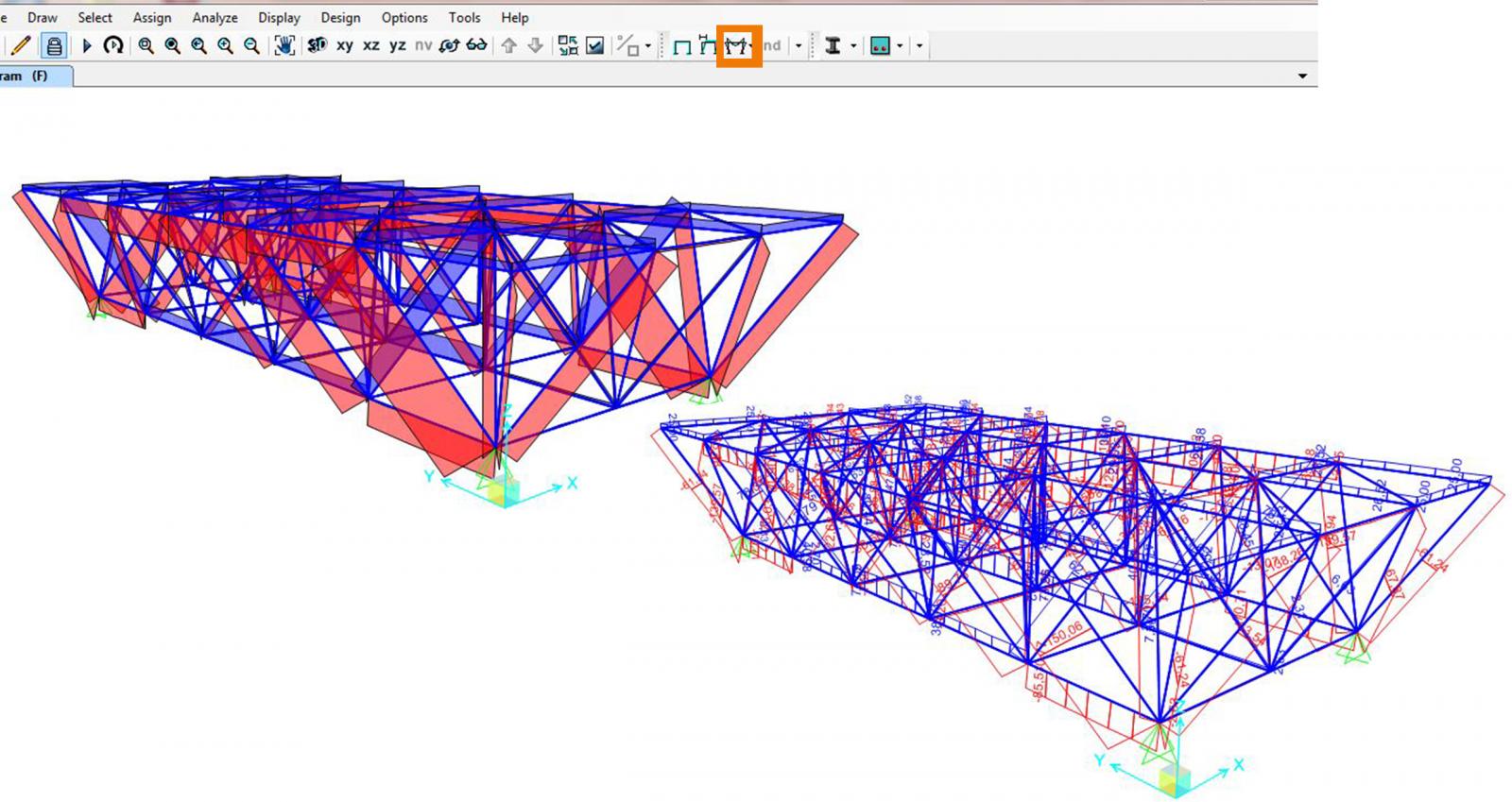
La prima informazione fornitaci dall’analisi è quella della configurazione deformata della struttura soggetta ai carichi F.

Dalle reazioni vincolari invece come ben sappiamo per quanto riguarda le travi reticolari sono soggette solo a SFORZO NORMALE di trazione se sono tese o di compressione se compresse, i diagrammi rappresentano in blu la trazione e in rosso la compressione.

7- il programma mi tabella tutti i valori di sforzo normale della struttura, con la possibilità di visualizzare delle tabelle ogni asta associata allo sforzo cui è soggetta: DISPLAY →SHOW TABLES 

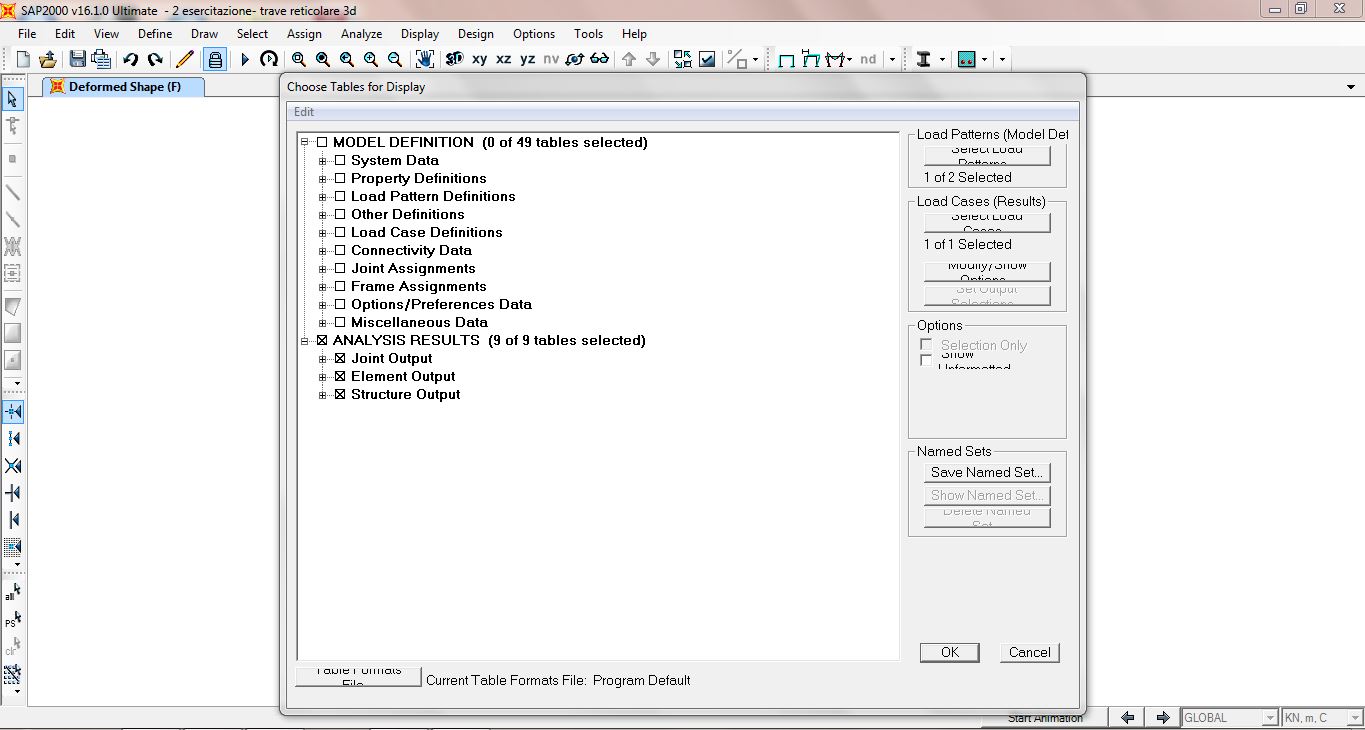
Il programma ci chiede ora ciò che effettivamente vogliamo inserire all'interno delle tabelle dei risultati; spuntiamo ANALYSIS RESULTS e diamo l'ok .

Dalla finestra che si apre mi seleziono la tabella che a me serve di visualizzare, in questo caso Element Forces-Frame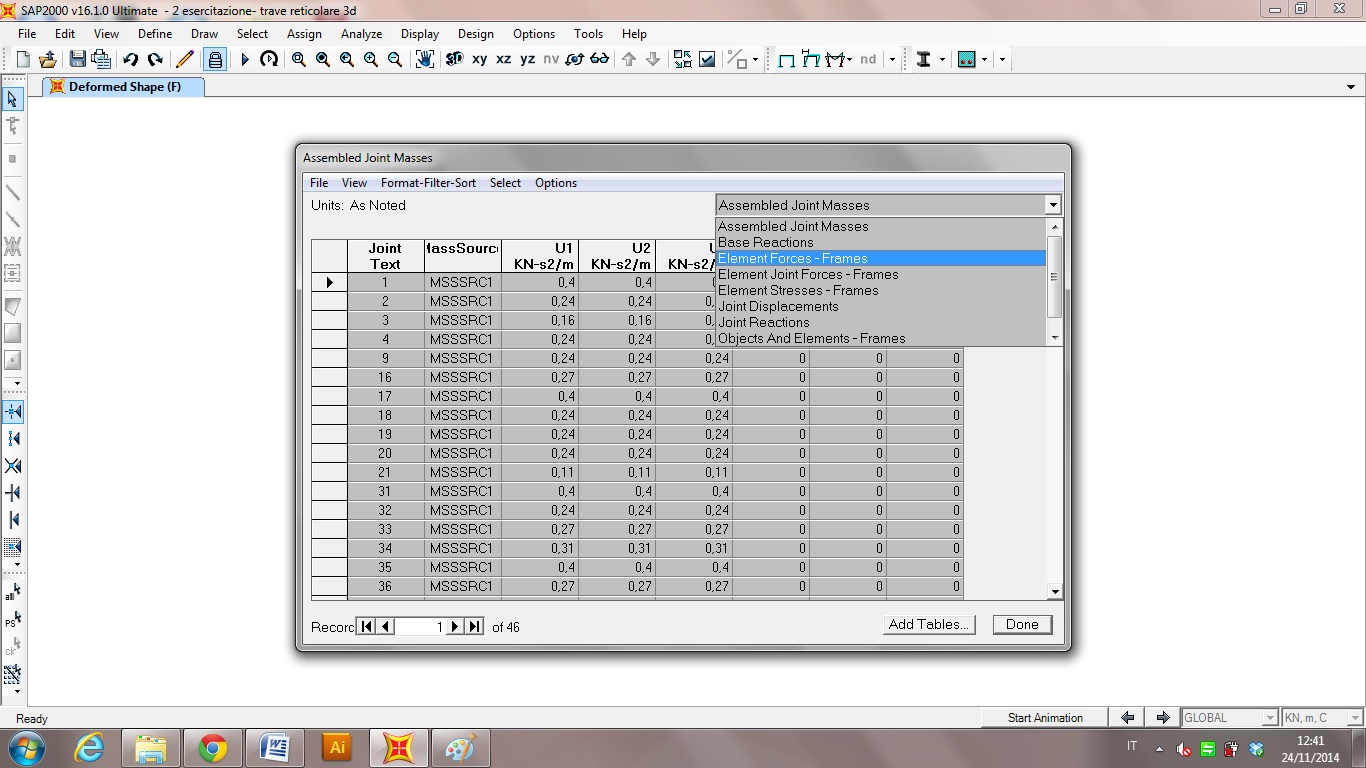

La esporto ora su Excel in modo da andarla a pulire dalle informazioni a me non necessarie: FILE→EXPORT CURRENT TABLE→TO EXCEL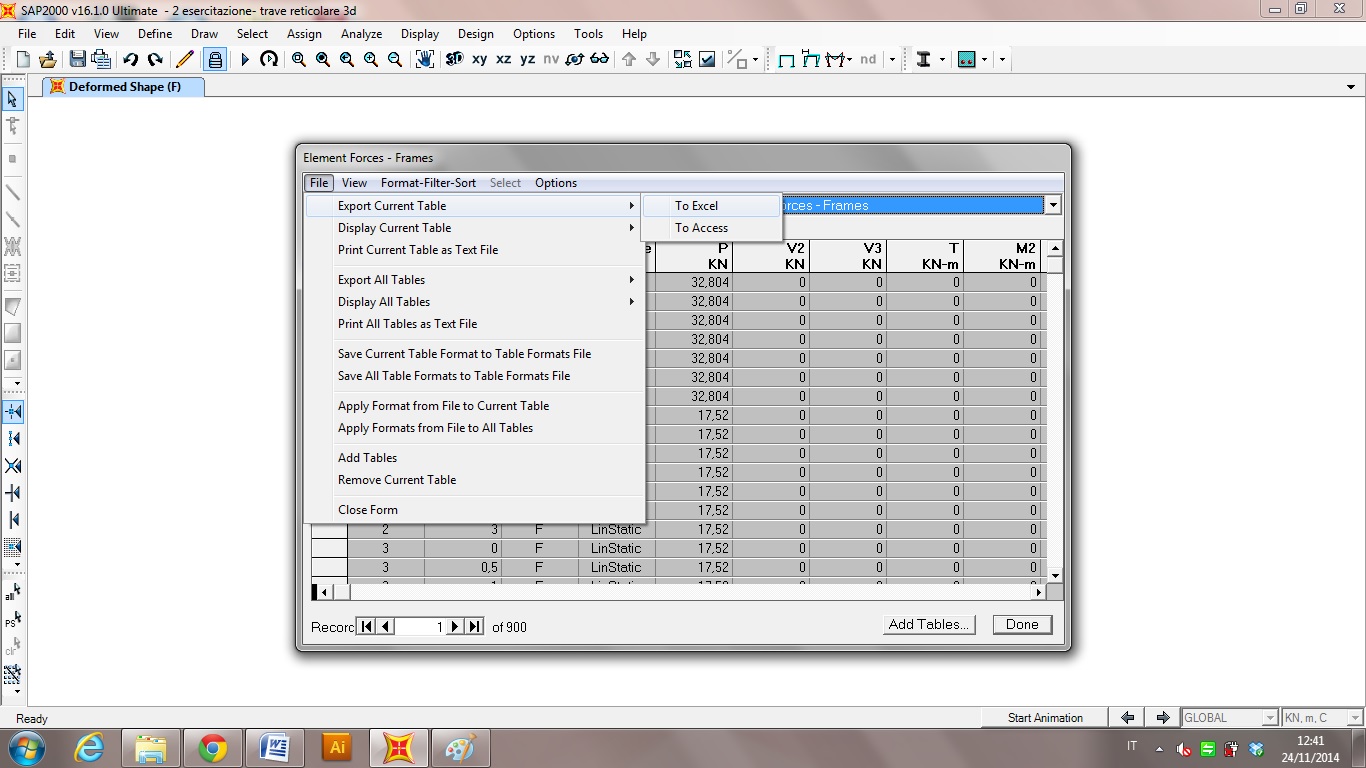

8- una volta esportata la tabella la “sistemo” seguendo questi passaggi:

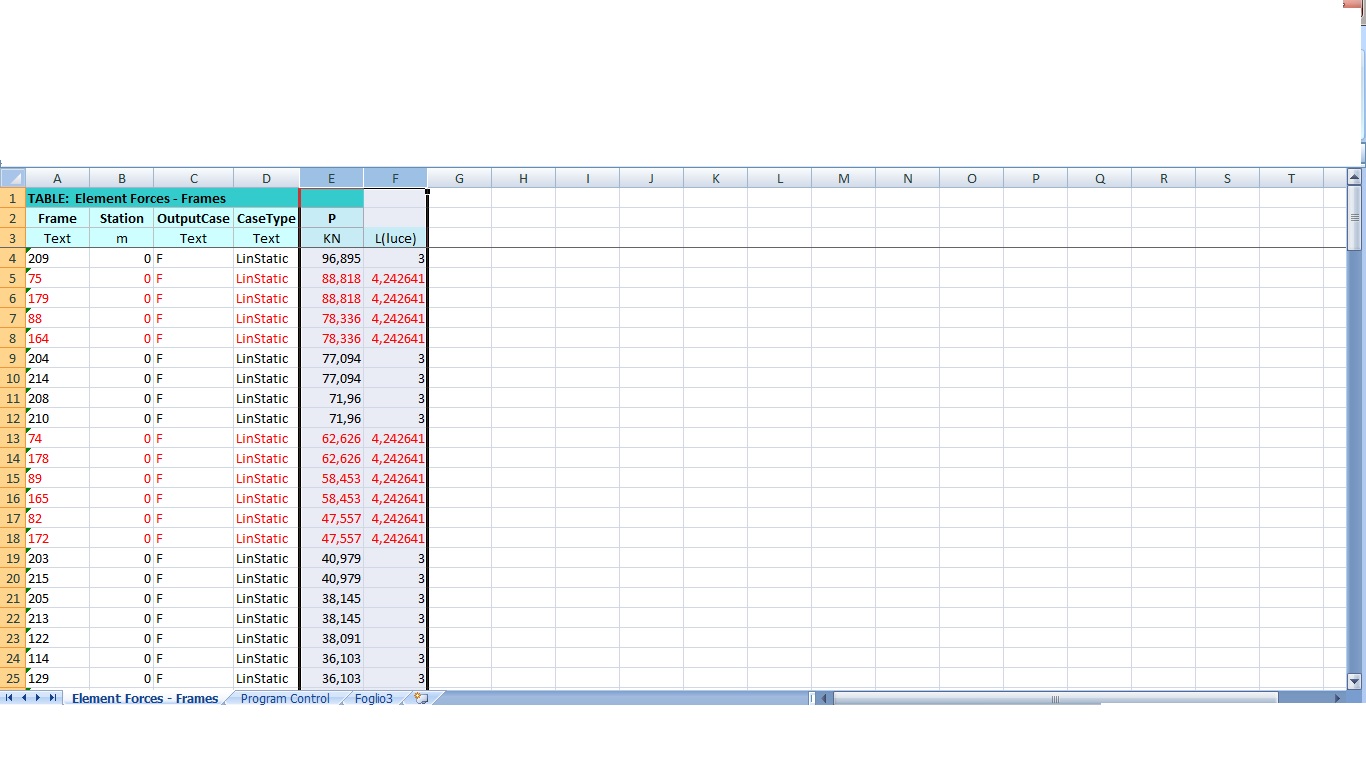
-cancello tutte le colonne dopo la lettere E;

-inserisco una nuova colonna per la luce delle aste;

-individuo in rosso le aste diagonali che valgono 3√2;

-cancello i doppioni delle aste con Rimuovi duplicati secondo Frame

-Ordino la tabella secondo lo sforzo normale P  in modo decrescente, avendo prima i valori positivi di TRAZIONE e dopo i valori negativi di COMPRESSIONE.

-infine copio nel file EXCEL della professoressa, che ci servirà per dimensionare le aste) i valori di dello sforzo normale di trazione nella trazione e viceversa.

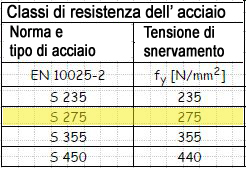
9-Nel file excel del dimensionamento dell’asta reticolare in acciaio nella sezione TRAZIONE dopo aver inserito i valori di sforzo normale in N, insieriamo l’Fyk che è la resistenza caratteristica dell’acciaio: ricordo che l’acciaio ha lo stesso valore di resistenza sia a trazione che a compressione.

Nel mio caso ho scelto un acciaio S275

Inserisco poi γ_m , un coefficiente di sicurezza pari a 1.05, il foglio mi calcola così Fd, la tensione di progetto e infine l’area minima che mi serve per la mia asta. A_min me la calcolo dividendo lo sforzo normale per la tensione di progetto.

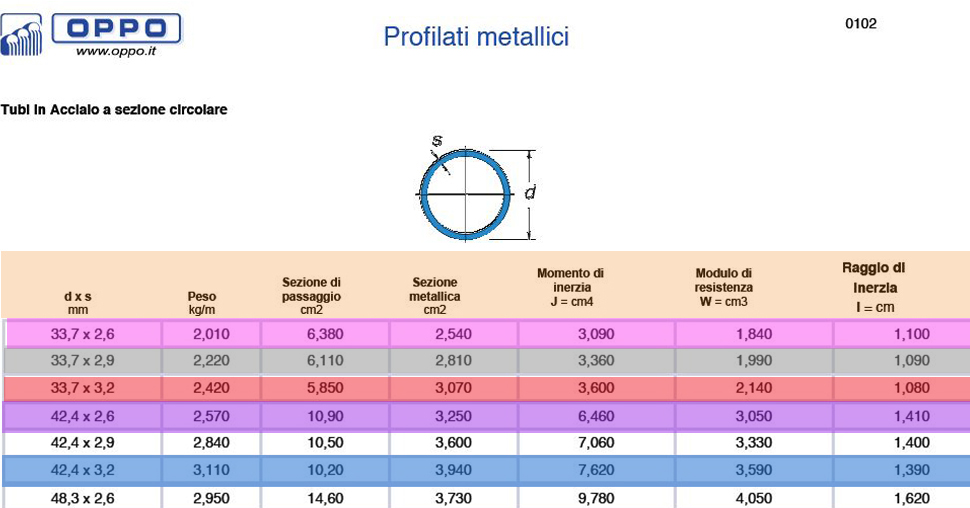
Vado ora ad” ingenierizzare” l’area minima dell’ asta maggiormente sollecitata affinchè il materiale possa resistere allo sforzo maggiore. Nella trazione l’area minima dall’ asta maggiormente sollecitata è di 3.70cm², cerco il profilo nelle tabelle Oppo dei tubi in acciaio a sezione circolari trovando un’ area di design e ripeto l’operazione per tutte le aste tese.

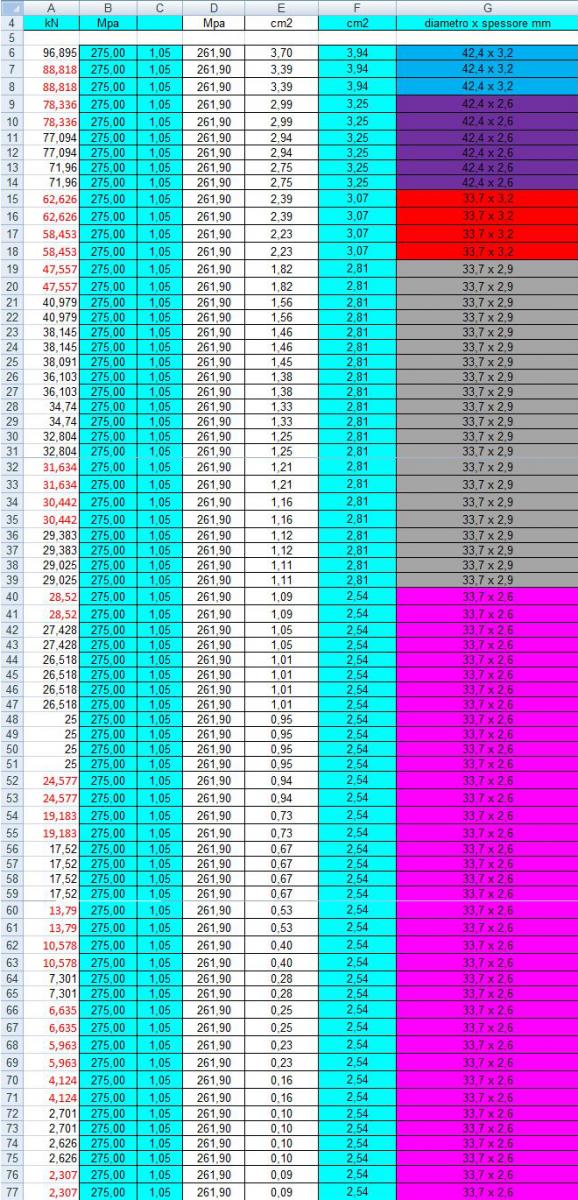
10- Passo ora all’area riservata al dimensionamento dell’area delle aste soggette a compressione:

inserisco anche qui sotto N i valore di sforzo normale in ordine crescente in questo caso così da avere l’asta più compressa in prima riga.

In questa sezione oltre ad inserire i valori precedenti vado ad inserire innanzitutto la luce associata ad ogni asta.

Anche qui il foglio di calcolo mi individua l’area minima ma non posso ancora ingenierizzarla poiché nella compressione devo tener conto di due importanti fenomeni di INSTABILITA’ che si possono verificare quali il CARICO DI PUNTA e LA FLESSO TORSIONE .

Aggiungo il modulo di elasticità E che è uguale per tutti gli acciai strutturali a 210000 Mpa e  un coefficiente che dipende dai vincoli esterni delle aste; in questo caso essendo cerniere esterne corrisponde a beta=1.

Avendo questi dati a disposizione il foglio mi calcola λ Lambda, la snellezza dell’asta, I il momento di inerzia minimo e Rho il raggio di inerzia minimo, valori che mi servono per contrastare i due fenomeni di instabilità e necessari per il dimensionamento delle aste.

Infatti sulle tabelle dei profilati a sezione circolare cava dovrò scegliere una serie di profilati che soddisfano tutti e tre questi requisiti oltre all’area minima.

 Posso procedere ora al dimensionamento delle aste facendo attenzione che il lambda finale risulti sempre  < 200

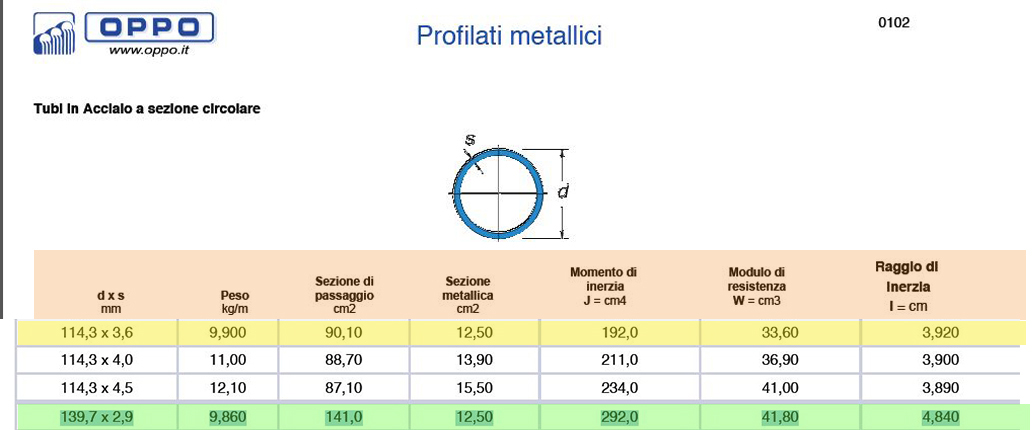
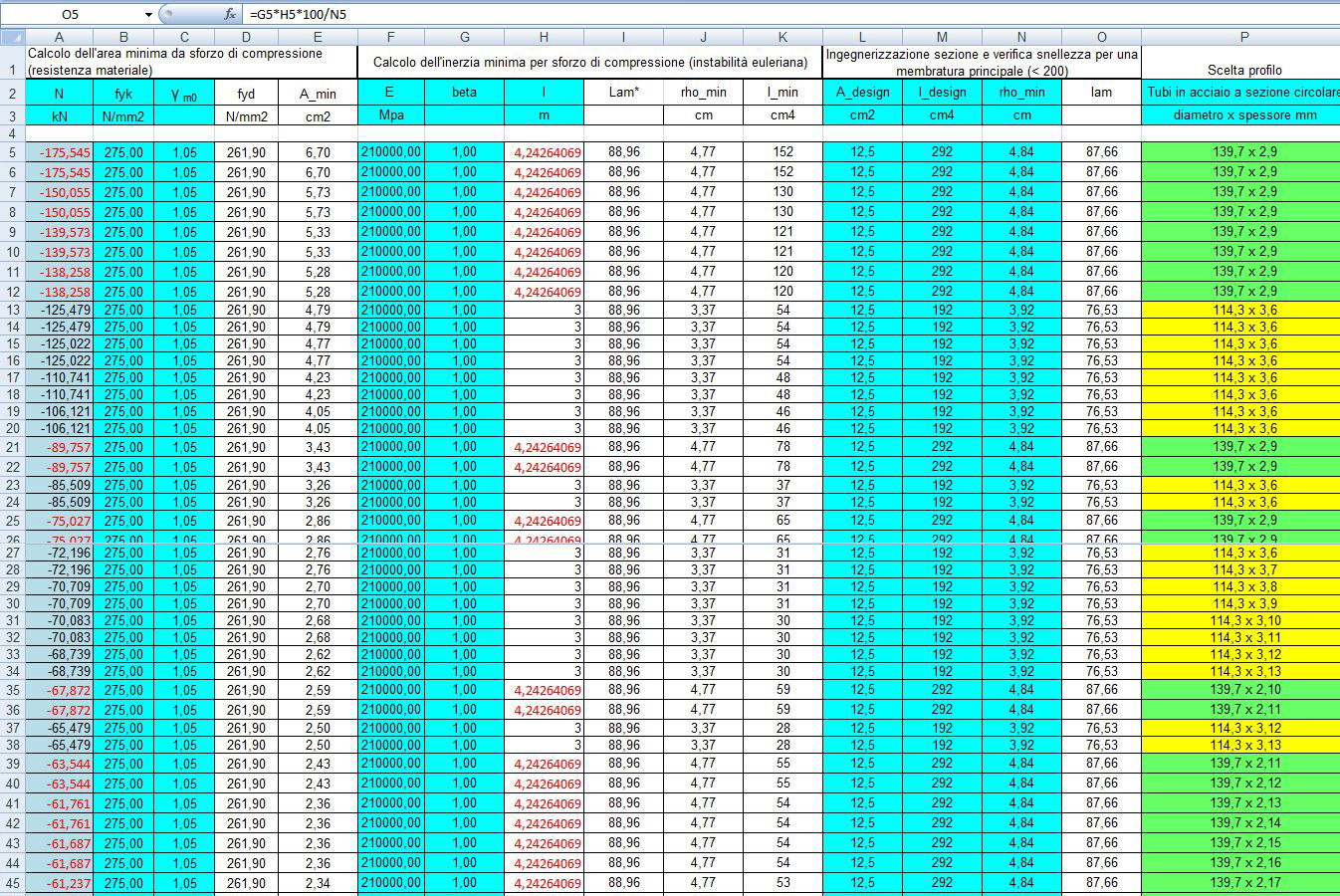
Per la compressione come si può vedere ho scelto solo due profili di aste uno per quelle diagonali (in verde), uno per quelle verticali e orizzontali (in giallo). Questo perché non devo solo considerare l’aria minima per la scelta ma anche il Raggio di inerzia che nel mio caso si diversifica per quanto riguarda la lunghezza delle aste.

Questa terza esercitazione consiste nel verifica della deformazione della mensola più sollecitata di un telaio in tre differenti tipologie: legno, acciaio e cemento armato.

La mensola sottoposta a maggiore carico nella struttura presa in analisi è quella evidenziata in rosso: su di essa infatti grava il carico di solaio maggiore.

Luce: 3m

Interasse: 6m

Area di influenza: 18m²

LEGNO

Prima di calcolare e verificare la deformazione di una mensola è necessario dimensionare l’altezza della stessa. Consideriamo lo stesso pacchetto di solaio della prima esercitazione e, come nel caso della trave inflessa, inseriamo nel foglio i dati inerenti all’interasse, al carico strutturale, permanente e accidentale. In questo modo otteniamo il carico ultimo. qu = [(qs x 1.3) + (qp x 1.5) + (qa x 1.5)] x i

Inserendo la luce il foglio ricava il momento massimo: nel caso della mensola pari a Mmax= (qu x L²)/2

Una volta inserita la resistenza caratteristica (nel caso del legno lamellare GL24h pari a 24 Mpa), il coefficiente di sicurezza del materiale (per il legno lamellare γm=1.45) e il coefficiente correttivo per umidità e durata del carico (consideriamo una classe media con kmod=0.8) il foglio ricava la resistenza di progetto

fd = (kmod x fmk)/γm.

Impostando la base della trave, si determina l’altezza minima come nel caso della trave inflessa. Scegliamo dunque un’altezza ingegnerizzata.

Ora possiamo procedere al calcolo e alla verifica della deformazione.  Con i dati già presenti del foglio si ricava il momento di inerzia che, nel caso di una sezione rettangolare, è Ix= bh³/12. Possiamo anche calcolare il carico di esercizio pari alla somma dei carichi maggiorati con i relativi coefficienti di sicurezza (1 nel caso dei carichi strutturali e permanenti, 0.5 nel caso dei carichi accidentali) per l’interasse.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i

Nel caso di una semplice mensola con carico uniformemente distribuito sappiamo che:

v(s) = 1/(EI) x [- (ql²s²)/4 – (qs⁴)/24 + (qls³)/6]

Poiché il massimo spostamento in una mensola avviene nell’estremo libero (cioè s=l) possiamo anche scrivere che

vmax= - (ql⁴)/8EI.

In realtà questo valore di spostamento massimo è un approssimazione: infatti esso viene associato ad una vera mensola mentre, in questo caso, la struttura si configura come aggetto di una trave appoggiata. Poiché la luce della trave appoggiata è 8m e l’aggetto è 3m (<8m/2) il vmax calcolato è maggiorato.

Dunque inserendo il modulo di elasticità E proprio del materiale nella tabella possiamo ricavare questo valore considerando come carico quello di esercizio (qe).

Affinchè la mensola sia verificata vmax < (1/250) x l. Dunque devo verificare che:

l/vmax >250.

In questo caso 439.70 > 250 dunque la mensola in legno è verificata!

ACCIAIO

Come nel caso del legno dobbiamo innanzitutto dimensionare l’altezza della mensola.  Inseriamo i dati inerenti l’interasse, la luce e i carichi del pacchetto di solaio considerato nella prima esercitazione. Il foglio di calcolo ricava carico ultimo e momento massimo della mensola come sopra. Inserendo la resistenza caratteristica del materiale (fyk=275Mpa per un acciaio S275) si ottiene la resistenza di progetto fd moltiplicando fyk per il coefficiente di sicurezza γm=1.05. Come nel caso della trave appoggiata imponendo σmax = fd e utilizzando la formula di Navier sappiamo che

Wxmin = Mx/fd

Dunque scegliamo nel sagomario una trave IPE con modulo di resistenza a flessione W immediatamente superiore. In questo caso un IPE 400. Dunque riportiamo sulla tabella i relativi valori di momento d’inerzia Ix e di peso della trave IPE 400 e il modulo di elasticità E proprio del materiale.

A differenza del legno il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave (nel caso del legno il peso della trave viene trascurato trattandosi di un materiale leggero). Dunque

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

Con la stessa formula precedentemente utilizzata per il legno ricaviamo lo spostamento massimo: vmax= - (ql⁴)/8EI     (anche in questo caso maggiorato).

Anche in questo caso il rapporto l/vmax = 440.082 > 250 dunque la mensola in acciaio è verificata!

CEMENTO ARMATO

Anche per il cemento armato dobbiamo prima calcolare l’altezza della mensola. Inserendo interasse, luce e carichi del pacchetto di solaio in latero-cemento della prima esercitazione otteniamo carico ultimo e momento massimo. Una volta scelto il tipo di barre (B450C con resistenza caratteristica fyk= 450Mpa) e la classe del calcestruzzo (C60/75 con resistenza caratteristica fck = 60 Mpa) il foglio ricava le corrispettive resistenze di progetto corrette con i coefficienti di sicurezza.

Una volta impostata la dimensione della base della trave il foglio ricava l’altezza utile come nel caso della trave appoggiata. Questo valore sommato per il copriferro permette di ricavare un’altezza minima che possiamo ingegnerizzare. Il foglio ricava direttamente l’area (base per altezza) e il peso al metro quadro (area per peso specifico del cls).

Nella riga sottostante il foglio ricalcola il valore del carico ultimo aggiungendo a quello precedente il peso della trave moltiplicato per il coefficiente per carichi strutturali pari a 1.3. Viene ricalcolato dunque il momento massimo e, mantenendo i valori delle resistenze e delle dimensioni scelte nel progetto, ricalcola l’altezza minima. Anche con il peso della trave l’altezza minima rimane inferiore al valore di altezza ingegnerizzata che avevamo scelto dunque l’altezza è verificata.

Ora possiamo procedere con il calcolo e la verifica dello spostamento massimo della mensola. Come nel caso dell’acciaio il foglio calcola il carico di esercizio sommando ai carichi maggiorati e moltiplicati per l’interasse anche il peso della trave.

qe= [(qs x 1) + (qp x 1) + (qa x 1.5)] x i + (peso trave x 1)

Inserendo il valore del modulo di elasticità E proprio del materiale e calcolando il momento d’inerzia Ix per una sezione rettangolare (come nel caso del legno Ix= bh³/12) il foglio ricava lo spostamento massimo

vmax= - (ql⁴)/8EI    (anche in questo caso maggirato)

Anche in questo caso il rapporto l/vmax = 286.21> 250 dunque la mensola in cemento armato è verificata!

Questa seconda esercitazione si basa sul dimensionamento di una travatura reticolare tridimensionale. Attraverso il software SAP2000 è possibile disegnare la struttura e vincolarla esternamente tramite quattro appoggi.

Trattandosi di una struttura reticolare possiamo modellizzare i nodi come delle cerniere interne.

Una volta scelto il materiale (acciaio) e i profili delle sezioni (circolari cavi) sono state applicate forze concentrate sui nodi superiori della travatura.

 Il software permette di visualizzare la struttura deformata e i grafici relativi allo sforzo normale: in rosso le aste compresse (puntoni), in blu le aste tese (tiranti).

 È possibile poi esportare i valori numerici degli sforzi assiali delle singole aste in una foglio di calcolo.

Innanzitutto il file va pulito mantenendo solo i valori di station pari alla lunghezza effettiva dell’asta. Dunque nel caso di questa struttura è necessario mantenere le aste di 2m che corrispondono ai lati del quadrato di base (nere); le aste lunghe 2.82m che corrispondono alle diagonali dei quadrati di base (verde); le aste lunghe 2.44m che corrispondo ai lati della piramide (arancio).

Quindi è possibile ordinare la tabella in funzione dello sforzo normale dal valore maggiore al valore minore e quindi si possono individuare facilmente le aste più tese nella struttura (valori maggiori con segno positivo) e quali quelle più compresse (valori maggiori con segno negativo).

TRAZIONE

Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste tese.

Infatti, una volta inseriti i valori degli sforzi normali e scelto il tipo di acciaio (un acciaio S235 con resistenza caratteristica fyk = 235 Mpa), il foglio calcolerà la resistenza di progetto fd correggendo quella caratteristica con un coefficiente di sicurezza γm=1.05 e l’area minima dividendo lo sforzo normale per la resistenza di progetto appena calcolata

Amin = N/fd

Infatti abbiamo imposto che σ=fd.

Consultando la tabella dei profilati circolari cavi dovremmo scegliamo il profilo con area immediatamente maggiore per ciascuna asta, ma ciò comporterebbe un eccessivo costo e difficoltà di montaggio nella realizzazione della reticolare. Dunque si scelgono 4 profili che soddisfino le aree minime delle aste tese. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.

COMPRESSIONE

Un ulteriore foglio di calcolo ci permetterà di dimensionare i profili circolari cavi per le aste compresse.

Come nel caso della trazione, una volta inserito lo sforzo normale e il tipo di acciaio, è possibile ricavare la resistenza di progetto e dunque l’area minima imponendo nuovamente σ=fd.

Amin = N/fd

Nel caso della compressione, però, dobbiamo considerare anche l’instabilità euleriana. Dunque sarà necessario imporre σcrit = fd.

fd = σcrit = Ncrit/A = (π²E)/λ²

dunque λ = π/√(E/fyd)

Dove E è il modulo di elasticità dell’acciaio pari a 210000Mpa. Nella tabella possiamo aggiungere due ulteriori valori noti: β = 1 (trattandosi di un asta incernierata) e le luci delle aste. Con questi nuovi dati possiamo calcolare ρmin.

ρmin = L0/ λ

dove L0= β x l

Ora sapendo che ρmin²=Imin/A

Imin = ρmin²/A

Consultando la tabella dei profilati circolari cavi dovremmo scegliere il profilo con area e momento di inerzia immediatamente maggiori per ogni asta. Come per quelle tese sarà necessario scegliere un numero di profili limitati per semplificare il montaggio e ammortizzare i costi: sono stati scelti dunque 4 profili che soddisfino le aree e le inerzie minime delle aste compresse controllando che la snellezza λ sia inferiore di 200. Si aggiungono dunque due nuove colonne con il tipo di profilo scelto e il numero di asta corrispondente.

Si apre il programma e dopo aver impostato le unità di misura (KN, m, C), si imposta un nuovo modello Grid Only. Si impostano il numero di linee su ogni asse e la distanza tra di esse e in questo modo si verrà a creare una griglia di riferimento su cui poter disegnare la travatura reticolare.

Attraverso  lo strumento Draw Frame si iniziano a disegnare le aste e, completato il primo modulo, questo si copia Ctrl-C e incolla Ctrl-V  lungo gli assi X e Y fino a completare la griglia.

Si seleziona tutta la struttura e attraverso il comando Edit – Edit Points – Merge Joints si riuniscono i nodi che durante i passaggi potrebbero essersi spostati.

Si selezionano i nodi nei quali si vogliono inserire i vincoli e attraverso il comando Assign – Joint – Restraints  si assegna il vincolo di cerniera esterna.

Selezionare tutte le aste e attraverso il comando Assign – Frame – Releases/Partial Fixity spuntare Start e End ai Moment 22 e Moment 33, in modo tale da imporre che il momento all’inizio e alla fine di ogni asta sia uguale a zero.

A questo punto si assegna il materiale, quindi seleziono tutte le aste e poi Assign – Frame – Frame Sections – Add New Property. Poi Frame Section Type - Steel, Add a steel section – Pipe, Section name – Tubolare.

Con il comando Define – Load Patterns metto il nome “carico”, impongo Self Weight Multiplier uguale a zero (non si prende in considerazione il peso proprio della struttura) e Add New Property.

Ora si selezionano tutti i nodi su cui si vogliono inserire i carichi e poi si clicca il comando Assign – Joint Loads – Forces – Load Pattern Name si assegna “carico” e poi in Force global Z si inserisce -100, cioè un carico verticale rivolto verso il basso.

A questo punto si può avviare l’analisi tramite Analyze – Set Load Cases To Run, impongo a MODAL e DEAD Do Not Run in quanto non voglio farne l’analisi, mentre a “carico” impongo Run e poi Run Now.

Tramite il comando Show Forces/Stresses – Frames/Cables/Tendons si possono vedere i diagrammi degli sforzi assiali.

Per salvare i risultati bisogna premere Display – Show Tables, poi selezionare su Select Load Patterns e Select Load Cases il carico, in seguito spuntare la casella Analysis Results – Element Forces/Frames ed infine File – Export Current View – To Excel.

A questo punto sulla tabella Excel distinguiamo le aste tese da quelle compresse (segno negativo) e inseriamo i valori nelle tabelle di dimensionamento.

Per quanto riguarda le aste tese, una volta inseriti i valori di N e scelto il tipo di acciaio (S235 con resistenza caratteristica fyk= 235 Mpa), si può trovare l’area minima:

Amin= N/fd

Dalla tabella dei profilati circolari cavi si sceglie il profilo con area maggiore dell’area minima e in questo caso, avendo un numero importante di aste, si sono scelti 6 profili che soddisfano le aree minime.

Nel caso delle aste compresse, una volta calcolata l’area minima bisogna tener conto del problema dell’instabilità Euleriana. Vengono presi in considerazione il modulo elastico dell’acciaio E=21000 Mpa, la lunghezza delle aste e quindi L=2m o L=2,83m e beta che in questo caso è uguale ad 1 in quanto sono aste incernierate. A questo punto il foglio Excel calcola i valori di Lambda, Rho min e Momento di inerzia minimo. Dalla tabella dei profilati circolari cavi si sceglie il profilo con Area, Momento d’inerzia e Rho maggiori dei valori minimi trovati. Infine bisogna assicurarsi che la snellezza Lambda sia minore di 200. Anche in questo caso, avendo un numero importante di aste, si sono scelti 4 profili che soddisfano i requisiti minimi.

Allego il PDF dell'esercitazione.

L’esercitazione si basa sul progetto di una TRAVE A SBALZO

L (luce della trave a sbalzo)= 4.15m                                                                                                                                   I (interasse delle travi)= 4m

La trave più sollecitata è quella lungo il filo fisso 2, poiché l’area di influenza è di 16 mq.

SOLAIO IN ACCIAIO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave

• carichi strutturali qs = 0.078 + 1.44 +0.45 = 1.97 KN/mq
• carichi permanenti qp = 0.012 + 0.9+ 0.4 +1.5 = 2.81 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu

                                  (ricordando che qu =  qtot x A solaio influ trave / L)

Ora siamo in grado di calcolare il Momento massimo della mensola  M=  ql^2 /2  [KNm]

Scelgo il materiale di progetto:    Acciaio S275 con tensione caratteristica di snervamento fyk= 275 [ Mpa]; inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd = fyk/1.05  [Mpa]

Ricavo quindi il valore del Modulo di resistenza a flessione della sezione della trave  Wmin= Mmax/ fyd  [cm^3]

Una volta calcolato Wmin posso consultare la tabella dei profilati  IPE in acciaio scegliendo una sezione con Wx maggiore di quello derivante dal calcolo. Scelta la sezione della trave posso individuare la sua inerzia I ( molto importante nella verifica a deformabilità). La sezione è quindi completamente determinata. Posso inserire nel foglio di calcolo il peso della trave ( KN/m).

Tale procedimento mi ha permesso di progettare una trave con una sezione tale da resistere alle sollecitazioni di progetto (Mmax). Devo però verificare che la deformabilità massima che la trave progettata subisce sia conforme ai limiti imposti dalla normativa (Luce della trave / spostamento max >= 250).

Quando si progetta una sezione a deformabilità la verifica che si deve fare ricade nel campo dello SLE ( stati limite di esercizio): la deformabilità di un elemento infatti non pregiudica la sua funzionalità strutturale ma la possibilità di continuare a svolgere adeguatamente la funzione per cui l’edificio è progettato.

Pertanto devo ricalcolare i carichi agenti sulla trave ( inserendo anche il peso della trave che ora conosco) moltiplicandoli per i coefficienti di sicurezza dello SLE (combinazione dei carichi frequente).

Ora il foglio di calcolo mi permette di ricavare il valore dello spostamento massimo  vmax= qe L^4 /8EIx [cm]

Se tale valore è maggiore uguale a 250 la verifica è soddisfatta; in caso contrario devo cambiare uno o piu parametri che influiscono su Vmax : scegliere una sezione con inerzia più grande oppure diminuire la luce della trave a sbalzo.

SOLAIO IN LEGNO

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.16 + 0.15 = 0.31 KN/mq
• carichi permanenti qp = 1.08 + 0.012 + 0.72+ 0.4 +1.5 = 3.71 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Legno lamellare GL 32c con resistenza a flessione fmk= 32  [Mpa];            inserisco il dato sul foglio Excel che calcola la tensione di progetto fd =  Kmod  fyk/1.45  [Mpa]

A differenza della trave in acciaio, nel progetto in legno devo imporre per progetto la dimensione di una dei due lati della sezione: impongo la base e ricavo l’altezza che ingegnerizzo.

Ora devo verificare che la trave appena progettata non si deformi troppo. Trascurando il peso proprio della trave, che nel legno è un valore irrilevante, ricalcolo i carichi allo SLE.

Come per la trave in acciaio, ora il foglio di calcolo permette di ottenere il valore dello spostamento massimo Vmax.  La verifica è soddisfatta.

SOLAIO IN CLS

Dalla precedente esercitazione ho ricavato i carichi del solaio gravanti sulla trave che devono essere maggiorati da coefficienti di sicurezza allo SLU

• carichi strutturali qs = 0.76 + 1.20 + 0.73 = 2.69 KN/mq
• carichi permanenti qp = 0.012 + 0.72 + 0.4 + 1.5 + 0.18 + 0.09 = 2.90 KN/mq
• carichi accidentali qa = 2.00 KN/mq

Il foglio di calcolo permette di ottenere il valore del carico lineare agente sulla trave  qu e quindi anche il Mmax.

Scelgo il materiale di progetto:  Acciaio per le armature  B450C con tensione caratteristica  di snervamento     f yk = 450 [Mpa];  inserisco il dato sul foglio Excel che calcola la tensione di progetto fyd= fyk / 1.15 [Mpa]

                                                        Cls  classe  C60/75  con fck = 60 Mpa  da cui  fcd= 0.85 fck / 1.5 [Mpa]

Impongo quindi la dimensione della base della sezione e quella del copri ferro. Devo quindi calcolare l’altezza utile della sezione. Per farlo utilizzo lo stesso procedimento dell’esercitazione 1 calcolando attraverso il foglio Excel i valori di β e r e trovando quindi l’unica incognita hu.

Ricavo il valore dell’altezza minima che andrò ad ingegnerizzare. Ora devo verificare che lo spostamento massimo sia nei limiti consentiti dalla norma. Utilizzo lo stesso procedimento delle precedenti tecnologie.

La seconda esercitazione si basa sul dimensionamento di una travatura reticolare tridimensionale composta da aste sottoposte a trazione o compressione.  Per  riuscire a dimensionare questo elemento strutturale occorre utilizzare il programma SAP e il foglio di calcolo Excel.

Operazioni:

• Cliccare su file, new model, grid only selezionando una griglia su cui disegnare la reticolare
• Draw frame per disegnare le diverse aste che compongono la struttura. Decido di realizzare una struttura reticolare composta da cubi che dovranno essere controventati  su tutte le facce. Copiando la singola campata realizzo l’intera struttura.
• Seleziono i punti su cui mettere i vincoli; clicco su assign, join, restraint  per scegliere il tipo di vincoli.  (Vicoli scelti 4 cerniere)
• Selezionando l’intera struttura clicco su assign, frame, release: devo capire quali spostamenti sono ammissibile dal vincolo precedentemente scelto: nel mio caso la cerniera permette la rotazione, clicco quindi su Moment =0
• Clicco su assign, frame, frame sections, add new property, selezionando il materiale per le aste (steel, pipe)
• Nell’analisi delle sollecitazioni trascuro il peso proprio della struttura: define, load patterns, creo un nuovo elemento (A) inserendo 0 nel self weight
• Selezionando solo le facce superiori clicco assign, joint loads, forces (assegno carichi concentrati lungo l’asse z).
• Ora che la struttura è caricata posso far iniziare l’analisi, capendo come le aste rispondono alle sollecitazioni di trazione o compressione: run analysis, selezionando solo l’elemento da me creato (A).
• Clicco sul telaio show deformed shape per vedere la deformazione dell’elemento strutturale.
• Ora che ho le sollecitazioni devo esportare i dati sul foglio Excel: display, show tables, analysis result, select patterns, selezionando l’elemento da me creato A. esporto la tabella su Excel.

Dimensionamento delle aste tese

Dalla tabella esportata da SAP si è in grado di stabilire i valori di progetto degli sforzi di trazione N

Scelta del materiale: Acciaio S235 con tensione caratteristica di snervamento fyk= 235 Mpa. Con il foglio di calcolo si ottiene il valore della tensione di progetto fyd= fyk/1.05 Mpa

Conoscendo le caratteristiche del materiale e le sollecitazione si ottiene automaticamente il valore dell’area minima Amin= N/fyd [cm^2]. Sono ora in grado di ingegnerizzare la sezione. Decido di scegliere solo 2 dimensioni delle aste tubolari cave per una maggiore semplificazione: 4.53 cm^2 e  12.30 cm^2

Dimensionamento delle aste compresse

Stabiliti i valori di progetto degli sforzi di compressione e il materiale ( acciaio S235) posso procedere al dimensionamento delle aste compresse.

Dopo aver calcolato automaticamente l’area minima Amin (come il precedente caso)devo considerare nuovi parametri che entrano in gioco nell’instabilità delle aste compresse.

β è il parametro che dipende dal grado di vincolo. In questo caso β= 1 (asta doppiamente appoggiata)

L è la lunghezza delle aste ( paramento che influenza maggiormente l’instabilità): L= 4m e  L=5.65m ( per controventi)

 λ è la snellezza dell’elemento; è direttamente proporzionale a E (modulo di elasticità, nell’acciaio              E=210000 Mpa  e inversamente proporzionale alla tensione di progetto fyd

ρ è il rapporto tra la lunghezza di libera inflessione (β x L) e la snellezza λ

Imin è l’inerzia minima che la sezione deve avere Imin= Amin x ρ^2

Tutti questi valori sono calcolati automaticamente dal foglio Excel.

Ora posso ingegnerizzare la sezione andando a scegliere un’inerzia maggiore a quella calcolata. Come per il precedente caso, scelgo solo 2 dimensioni di profilo. La normativa impone che la snellezza λ= βL/ ρ  <200. La verifica è soddisfatta.

Inizio il predimensionamento di una travatura reticolare. Ipotizzata per una copertura che si estende per moduli di 2x2m definendo una maglia di 6x6 moduli.

Al fine di aumentare il numero di aste di lunghezza minore (nel mio caso proprio 2m) decido di utilizzare un modulo piramidale, a base quadrata di l 2m ed h= redice quadr (2). In questo modo tutti i lati della piramide avrenno lunghezza pari a 2 m, mentre la diagonale necessaria per controventare il quadrato di base avrà lunghezza = 2xrad.quadr.(2)

Questa costruzione è disegnata direttamente sulla griglia di SAP attraverso il pannello di controllo parametrico che compare disegnando un punto (che permette di posizionare il punto nella terna di coordinate X,Y,Z).

Ripetendo il modulo con copia/incolla (facendo attenzione a non copiare barre che si possano sovrapporre nell'operazione) completo la travatura.

Mi accerto della corretta rappresentazione del modello, unendo eventuali sovrapposizioni e con il comando MERGE JOINTS (offset di 0,1) sono certo di chiudere ogni nodo correttamente.

Inserisco i vincoli. Scelgo di posizionare 4 cerniere  in modo da ottenere uno sbalzo della copertura pari a 2m.

Assegno alle aste un profilo tubolare in acciaio.

Assegno il vincolo di cerniera interna ad ogni nodo, Ottenendo così il modello di trave reticolare.

Adesso attribuisco ai nodi della parte sommitale della travatura una forza concentrata sui nodi pari a 120 KN (verso il basso), Così da iniziare a capire come reagisce la travatura.

Inizio l'analisi osservando la deformata che ottengo:

Nella parte inferiore della travatura, mi aspetto di avere aste progressivamente meno tese verso l'aggetto. della travatura. La deformazione risulta chiaramente simmetrica data la collocazione regolare delle 4 cerniere di appoggio. La parte più sollecitata è la parte centrale della maglia 6x6.

Estraggo i dati relativi all'analisi dei valori di trazione e compressione delle aste.

Ottengo dei valori tabellati in excel, che ordino eliminando i valori superflui al mio dimensionamento. Per praticità, data la natura reticolare delle aste, so già che lo sforzo normale su ogni asta sarà costante per tutta la sua estenzione. SAP agisce analizzando lo sforzo normale lungo ogni asta per "tappe" chiamate dal programma "station". Come se il programma campionasse lo sforzo Normale in 4/5 punti dell'asta così da verificare che N sia costante. Risulta semplice comprendere come il valore "station" pari o superiore a 2,83m sia relativo alle aste diagonali, dal momento che esse sono le uniche ad avere dimensione pari a 2 x rad. quard.(2).
Seguendo questo criterio, ordino la tabella:
- lasciando un solo valore di N per asta (elimino i valori relativi alle diverse "station")
- evidenziando in rosso le aste diagonali (di lunghezza differente)
- ordinando i valori di N in modo crescente: otterrò così in modo ben distinto una separazione tra aste tese e compresse.

Qiondi potrò lavorare sul dimensionamento delle aste a trazione:

Importo i valori delle analisi di N effettuate in SAP in un file excel 

La tabella lavora fornendo un'Amin neccessaria a tollerare la tensione di progetto Amin= N/fd ( agiamo su Mpa e moltiplicando x 10 otteniamo l'area minima in cm2).

Attribuisco 3 profili tubolari di acciaio, dividendo le aste in tre gruppi con un'Amin che possiede uno scarto di 4 cm2.
Scegliendo i profili da una tabella di un'azienda di profilati in acciaio e considerando un'area ingegnerizzata superiore al valore Amin:

Procedo con il dimensionamento degli elementi compressi.
I puntoni presentano una problematica relativa a deformazione (elastica) esercitata dal carico di punta. La forza che agisce a compressione tende a compiere lavoro (ovvero tende a compiere uno spostamento) che inflette l'asta. Questo fenomeno meccanico porterebbe all'inflessione dell'asta, e nel caso in cui tale inflessione non sia controllata, comporterebbe una curvatura che comprometterebbe il funzionamento della struttura. Per controllare il fenomeno in fase di progetto si può agire sulla sezione dell'elemento (così da considerare un momento di inerzia tale da permettere di tollerare l'Ncrit) o sulla lunghezza dell'asta (che determina la lunghezza libera di inflessione).

Dunque va considerato lo sforzo N cui è soggetta l'asta, da qui si considera l'area minima della sezione (come per le aste soggette a trazione) ma in più, una volta scelta la sezione dell'asta, vanno considerati: il raggio di inerzia minimo (che mette in rapporto Area e momento di inerzia), la lunghezza dell'elemento (che in rapporto al Raggio di inerzia determina la snellezza dell'elemento) e le proprietà del materiale (modulo elastico dell'acciaio).

Secondo le Norme la Snellezza dell'elemento deve essere < 200 per essere verificata.

Su questo ragionamento inserisco i parametri opportuni nel file excel determinando sezioni adeguate allo sforzo normale fornito dall'analisi in SAP:

Apriamo il programma SAP2000 ed impostiamo un nuovo modello GRID ONLY con unità di misura (KN,m,C)

Impostiamo una griglia di riferimento che poi andrà a rappresentare la nostra travatura reticolare

Avendo costruito la mia griglia, ora devo andare a ricalcare asta per asta con il comando DRAW FRAME, una volta realizzato un piccolo modulo si andrà a copiarlo per tutta la mia griglia sia verso l'asse x sia verso l'asse y.

Per assicurarci che non si hanno linee sovrapposte, utilizzerò il comando EDIT- MERGE DUPLICATES. 

Per correggere, invece, eventuali  imperfezioni utilizzerò il comando EDIT - EDIT POINTS - MERGE JOINTS - OK

Vado a selezionare i vertici dove saranno posizionati i miei vincoli esterni, tramite il comando ASSIGN -JOINTS - RESTRAINTS (Sono andata a selezionare una cerniera di appoggio)

Una travatura reticolare essendo soggetta solamente a sforzo Normale, quindi vado a considerare nulli i valori del taglio e del momento. Andando a selezionare tutta la mia struttura utilizzo il comando ASSIGN - FRAME - RELEASES e spunterò Moment 22 e Moment 33.

Adesso bisogna assegnare alle nostre aste un materiale ed una tipologia di profilato che andrò a nominare come  "tubolari". Adesso bisogna andare ad inserire i carichi che andranno a gravare sulla mia struttura attraverso il comando DEFINE - LOAD PATTERN - NEW LOAD PATTERN. Andrò a creare la mia forza  che nominerò F. Assegnerò ad essa un valore ( 100 KN)  tramite il comando ASSIGN - JOINT LOANDS - FORCES. Questo valore andrà trascritto nella casella ( FORCE GLOBAL Z) con il segno negativo poichè la forza ha il verso della gravità.

Prima di far partire l'analisi devo assicurarmi che sulla struttura andranno a pesare solamente le forze inserite da me, per questo, tramite la casella con il "PLAY" seleziono tutto ciò che non è la forza F e clicco su DO NOT RUN CASE. Rimanendo in uso solo la forza F posso iniziare l'analisi (RUN NOW). Attraverso il comando SHOW FORCES - STRESSES posso visualizzare il mio sforzo normale che viene rappresentato dal colore rosso quello a trazione e con il colore blu quello a compressione.

Tutti i file andranno salvati in una tabella attraverso il comando DISPLAY - SHOW TABLES, spuntare ANALYSES RESULTS. Quando si aprirà la nostra cartella andremo ad inserire ELEMENTS FORCES - FRAMES. Poi dovrò importare tutti i miei dati su EXEL attraverso i comandi FILE- EXPORT CURRENT TABLES- TO EXEL.

Adesso che ho trasportato tutti i miei file sulla tabella EXEL. Devo prima di tutto fare una pulizia eliminando i dati ripetuti attraverso DATI- RIMUOVI DUPLICATI , poi andrò ad evidenziare con il colore rosso tutte le mie aste diagonali che riconoscerò poichè la loro lunghezza massima sarà di  5,65685. In seguito ordinerò i miei sforzi dal più piccolo al più grande per poter avere prima tutti quelli a compressione (negativi) e poi quelli a trazione (positivi). Dividerò adesso i valori negativi nell appropriata tabella di compressione e i valori positivi in quella di trazione.

TRAZIONE: Si sceglierà un acciaio con resistenza caratteristica di S235 Mpa. Per ricavare la mia Fyd ( resistenza di progetto) la mia resistenza caratteristica dovrà essere divisa per un coefficente di sicurezza pari a 1,05. Cosi potremmo ottendere il valore dell'area min del mio elemento. Confrontandoci con la tabella dei tubolari dovrò scegliere un elemento con area maggiore rispetto al valore dell area minima risultante dalla mia tabella exel.

COMPRESSIONE: Nelle aste compresse bisogna considerare molti più fattori poichè entra in gioco anche l'instabilità. Va considerato nei calcoli per il progetto dell'asta, oltre ai passaggi precedenti,  il MODULO ELASTICO del materiale ( 210000 Mpa) , la LUCE della aste ( 4m per le aste verticali ed orizzontali e 5,65685 m per quelle diagonali che sono evidenziate in rosso), il valore BETA (equivale ad 1 ) , ed inoltre i valori che vengono calcolati automaticamente da exel ovvero, LAMBDA, RHO MINIMO , MOMENTO D'INERZIA MINIMO. Tutti questi ultimi valori dovranno essere presi in considerazione per il dimensionamento della mia asta e quindi per la scelta di un appropriato profilo attraverso la stessa tabella utilizzata precedentemente.