Portale di Meccanica

Si definisce una struttura a telai piani con la luce maggiore di 8m, la minore di 5m ed uno sbalzo di 4m sui lati corti; l’interpiano è di 4m.
Mentre il carico strutturale Qs sarà definito volta per volta,
 il carico permanente Qp è fissato a 3,05kN /mq composto sta:

• 0,5 kN/mq da impianti 
• 1kN/mq di tramezzi
• 0,5 per una finitura di ardesia
• 1 per il massetto
• 0,05 per un isolante

Qa è dato da normativa a 3kN/mq per gli uffici aperti al pubblico.

ACCIAIO

TRAVE
Si parte con la definizione dei travetti, orditi sul lato lungo e con interasse di 1m. Questi devono quindi sopportare un carico Qs definito da un solaio in acciaio composto da lamiera grecata con riempimento in calcestruzzo, mentre Qp e Qa fissi a 3,05 kN/mq e 3 kN/mq.
Si ricerca quindi il peso del solaio scelto, ritrovando un valore di 1,86kN/mq.

Si inseriscono quindi i valori nel foglio di calcolo e, ricercando nella tabella dei profilati IPE, si stabilisce un IPE 270 per i travetti.

A questo punto si definisce la trave più sollecitata dove i carichi restano i medesimi ma con l’aggiunta del peso del travetto. Con l’aiuto della tabella si stabilisce che la trave adatta risulta essere una IPE 500.

PILASTRO
Si determina il pilastro più sollecitato, ovvero uno centrale con un’area in influenza di 8m x 5m.

Si inseriscono i dati inerenti le luci e il peso delle travi, successivamente il peso del solaio, dato dalle tre componenti moltiplicato per i coefficienti da normativa. Si inserisce il numero di piani e il tipo di acciaio usato, un 235. Per tener conto della presso-flessione si divide l’fyd per due, di modo da avere già un’indicazione di massima. L’ultimo dato importante da mettere è il beta, fissato a 0,8 tenendo conto dell’incastro a terra. I dati che si ottengono orientano la scelta del profilo di acciaio, un HEA 450.
MENSOLA
Si ripete il procedimento analogo con la mensola, la quale ha una luce di 4m e dei carichi analoghi alle travi principali.
Inserendo il momento di inerzia resistente di una IPE 500 si vede che l’abbassamento risulterebbe circa 1/350 della luce; si prova quindi ad inserire il valore di una IPE 450, constatando come l’abbassamento massimo risulta ancora inferiore all’ordine del 200. Poiché una IPE 400 restituirebbe un valore maggiore, si determina la 450 come soddisfacente.

CALCESTRUZZO

TRAVE
Nel caso del calcestruzzo, il solaio scelto è un tipo predalles, come da figura. Il carico strutturale è quindi dato dai pesi specifici a mc dei singoli materiali moltiplicati per le loro dimensioni e per l’interasse. Si ottiene quindi:

• 0,013 kN/mq alleggerimento
• 1,66 kN/mq travetti
• 1,25 kN/mq (x2) calcestruzzo superiore e inferiore.
  Qs = 4,173 kN/mq  - Qp = 3,05 kN/mq -  Qa = 3kN/mq

  Il procedimento risulta essere pressoché il medesimo; l’unica accortezza è quella di prendere i valori della riga inferiore in quanto qui essi tengono conto anche del peso proprio della trave che, nel caso del calcestruzzo, risulta essere un carico non indifferente.

PILASTRO
Nel caso del pilastro, una volta inseriti i valori bisogna giocare con i valori di base e altezza della sezione: colpa anche la classe non particolarmente performante presa, se si prendono dei valori nell’immediato intorno dei valori minimi suggeriti dal foglio di calcolo si ottiene una tensione massima nella sezione che supera il valore massimo sopportabile dal materiale. In tal caso, sebbene bmin e hmin si attestino su 40 e 25cm, la sezione definitiva del pilastro è stata fissata ad un quadrato di lato 65cm, questo anche per evitare di avere valori di resistenza che differissero di molto sulle due coordinate.

 MENSOLA
 

LEGNO
TRAVE
Si definisce un solaio in legno con un Qs di 1,11Kn/mq, derivante dalla somma di un tavolato del peso di 0,11Kn/mq per un legno di conifere e di un massetto di allettamento del peso di 1Kn/mq.
Si ricava quindi la dimensione necessaria dei travetti e delle travi principali, prendendo come materiale un legno di classe C18 di conifera.

PILASTRO

MENSOLA

Ciao a tutti,

Ho allegato in PDF l'esercizio che abbiamo risolto oggi in aula. L'ho rifatto velocemente a mano per mostrarvi l'equilibrio a rotazione del nodo triplo.

Buona serata a tutti

ML

Esercitazione svolta in collaborazione con Martina Moreno e Francesca Rossetti.

La travatura reticolare spaziale è stata pensata per coprire una superficie di 24x16m che necessitava di una luce centrale di 20 m nella direzione maggiore, mentre si presentava più libera di ospitare vincoli nella direzione minore, e la quale doveva sorreggere 4 solai delle medesime dimensioni posti al di sopra.

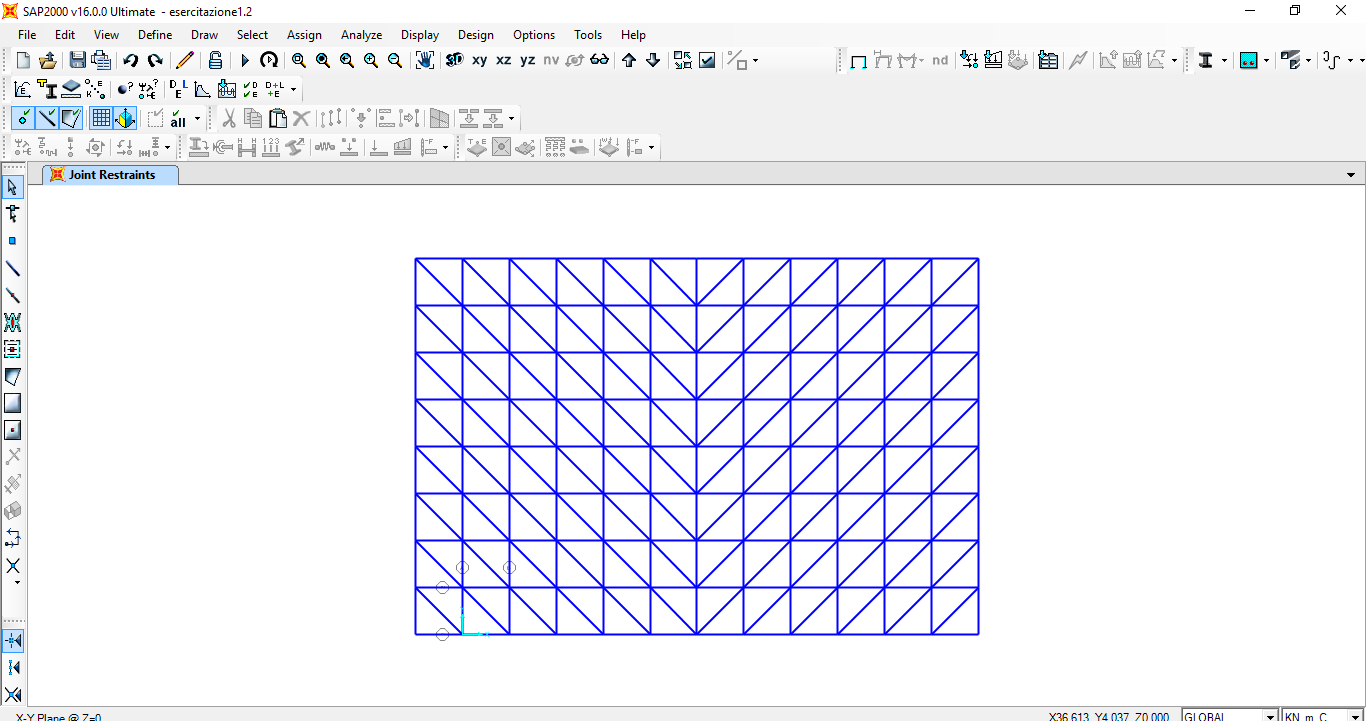
Si è scelto quindi di utilizzare un modulo quadrato di lato 2m corrispondenti ad 1/10 della luce maggiore da coprire. 

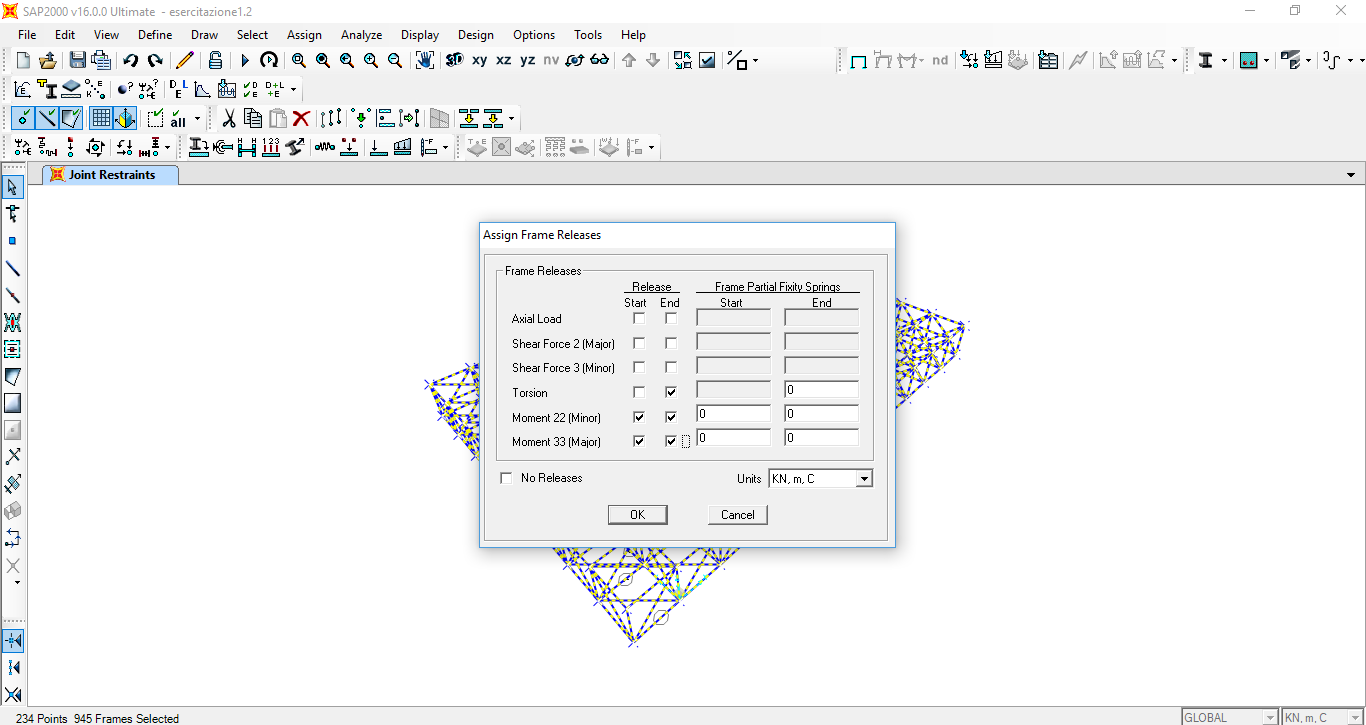
Dopo aver asseblato la struttura reticolare sono stati rilasciati i momenti nella direzione 2-2 e 3-3 ed una torsione

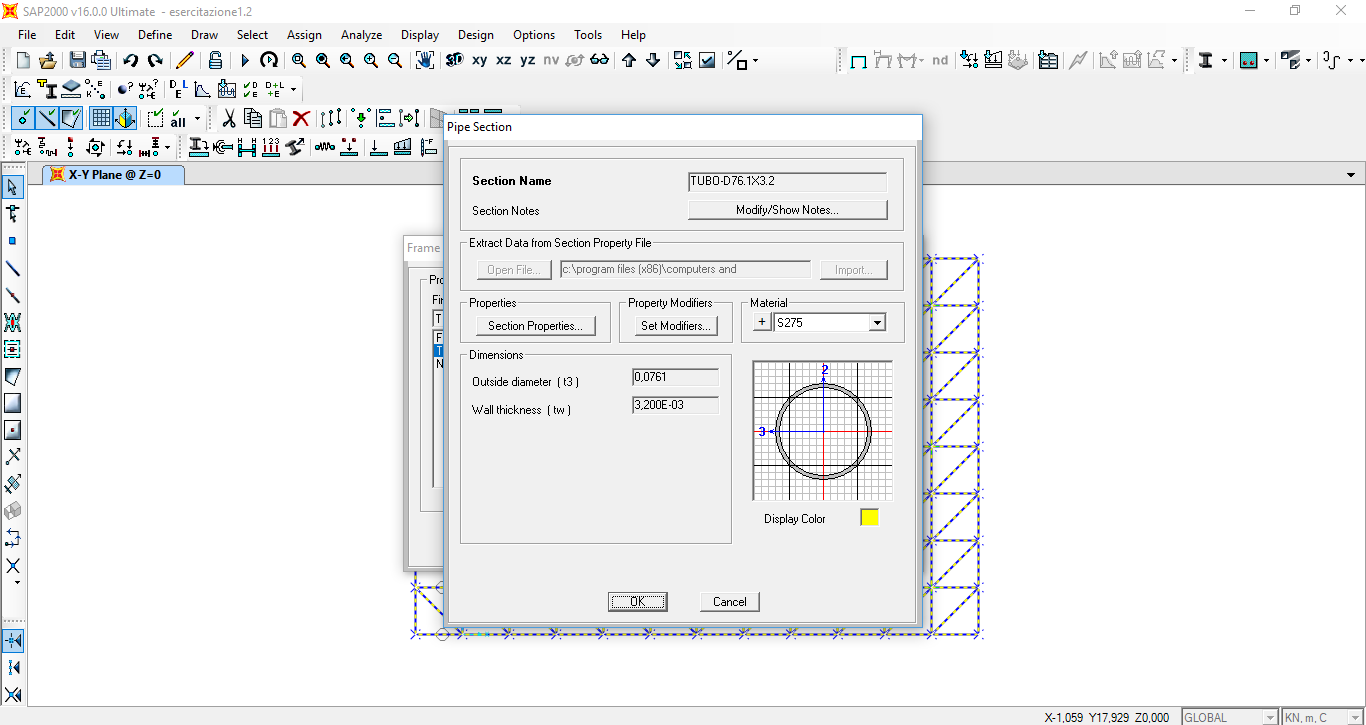
In seguito è stata scelta ed assegnata una sezione tubolare cava di partenza alla struttura.

Per completare il disegno della struttura sono stati quindi inseriti 6 appoggi (cerniere) disposti ad una distanza di 20m sul lato lungo e di 6 metri sul lato corto, lasciando quindi una fascia perimetrale a sbalzo di 2m (ovvero di un modulo), così da ottenere una migliore distribuzione delle sollecitazioni.

Si è passati poi al calcolo delle sollecitazioni agenti:

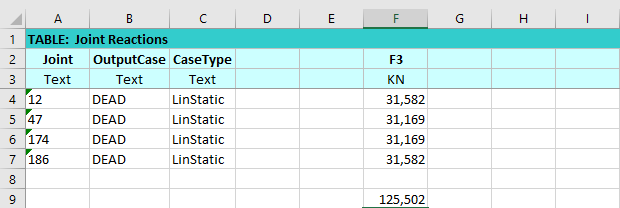
-si è calcolato il peso proprio della struttura attraverso il LOAD PATTERN DEAD ottenendo un valore di: 125,502(KN)/384(mq travatura reticolare) =  0,32 KN/mq

-si è stimato un valore portato relativo ai carichi dei solai superiori di 10( KN/mq )x 4 (n° solai) = 40 KN/mq

-il peso portato sommato al peso proprio della struttura ci ha fornito il carico per metro quadro che la struttura reticolare doveva sorreggere: 40,32 KN/mq

-si è stimato poi in base alle relative aree di influenza, il carico puntuale portato da ogni nodo definendo quindi tre valori di carico:

  -nodi angolari 40,32 KN (area di influenza 1 mq)

  -nodi laterali 80,64 KN (area di influenza 2 mq)

  -nodi centrali 161,28 KN (area di influenza 4 mq)

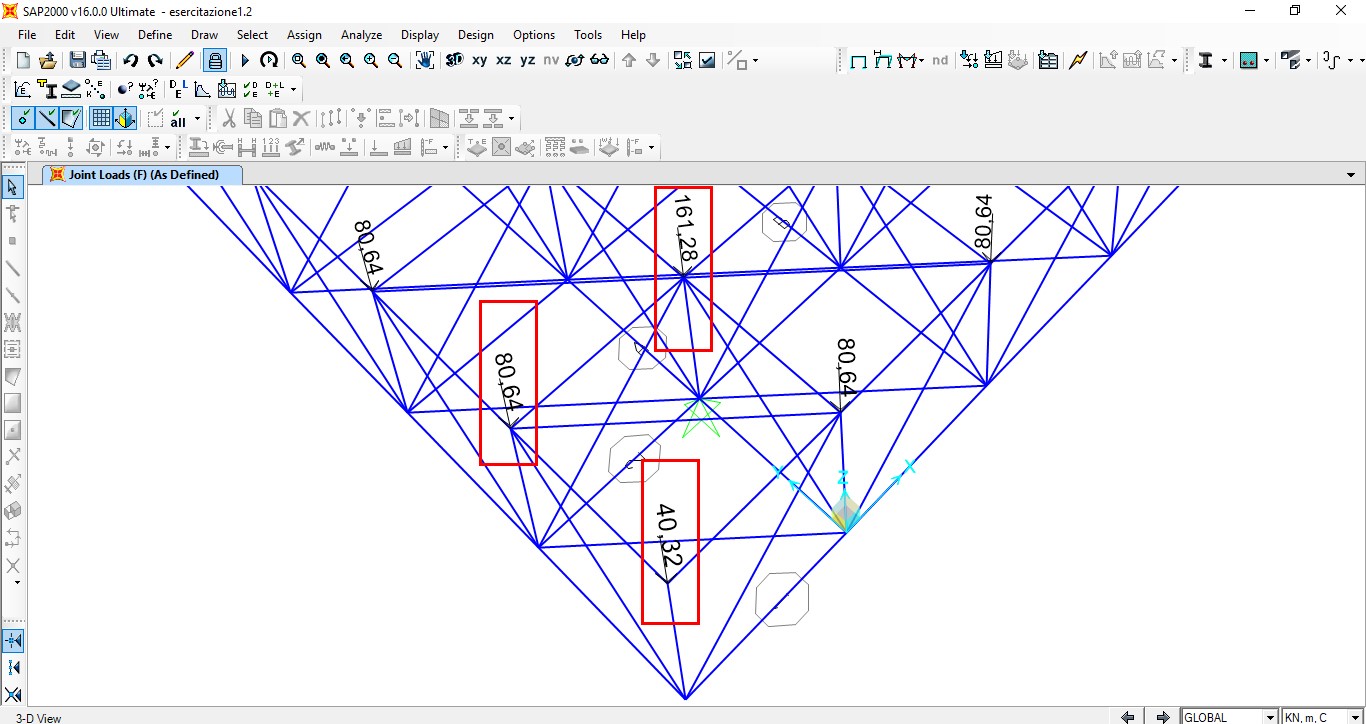
Dopo aver applicato i carichi sui nodi è stata effettuata l’analisi del modello utilizzando il caso di carico da noi creato, e i relativi dati sono stati esportati su excel.

Il modello excel ottenuto è stato poi ripulito dai dati superflui, e riordinato secondo un ordine crescente dello sforzo normale. Le aste soggette a sforzo di compressione sono state inoltre suddivise in aste rettilinee di lunghezza 2m, e aste oblique di lunghezza 2,8m per un dimensionamento più accurato di quest'ultime.

Le aste compresse sono state raggruppate poi, in categorie in base all’area minima associata ai rispettivi valori di sforzo normale, tenendo in considerazione anche il raggio di inerzia minimo e il momento di inerzia minimo. A questo punto, dopo aver selezionato due profilati  minimi di partenza per le aste rettilinee e quelle oblique che rispettassero il ρ minimo, sono stati assegnati i successivi profilati alle altre aste procedendo per intervalli di Area minima.

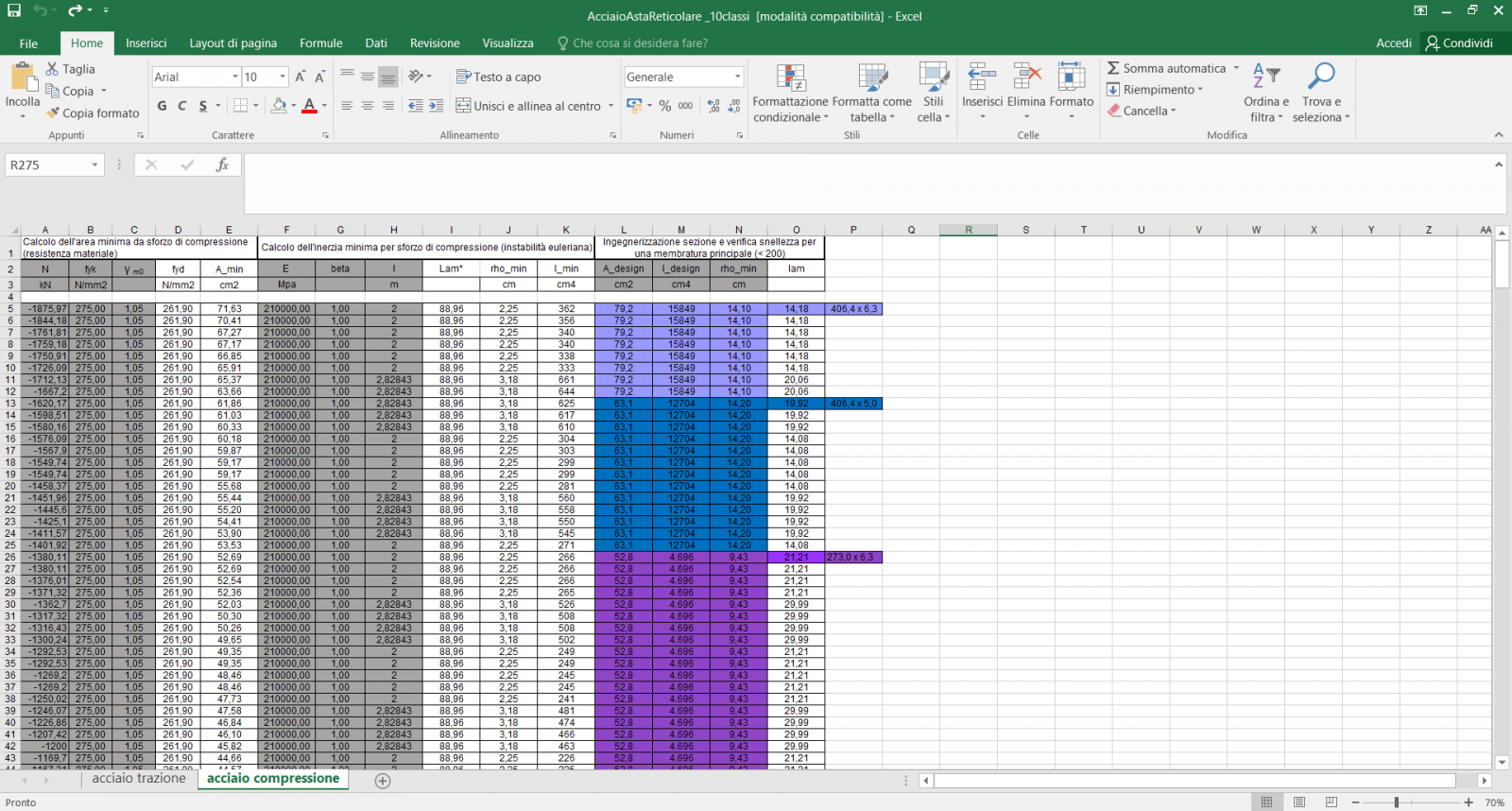
Dopo un primo tentativo di suddivisione, che prevedeva un numero troppo elevato di profilati, si è deciso di ampliare gli intervalli di A min per ottimizzare il progetto. 

La tabella seguente riporta le aste con valore di sforzo normale di compressione massimo per ciascuna categoria e i relativi profilati assegnati.

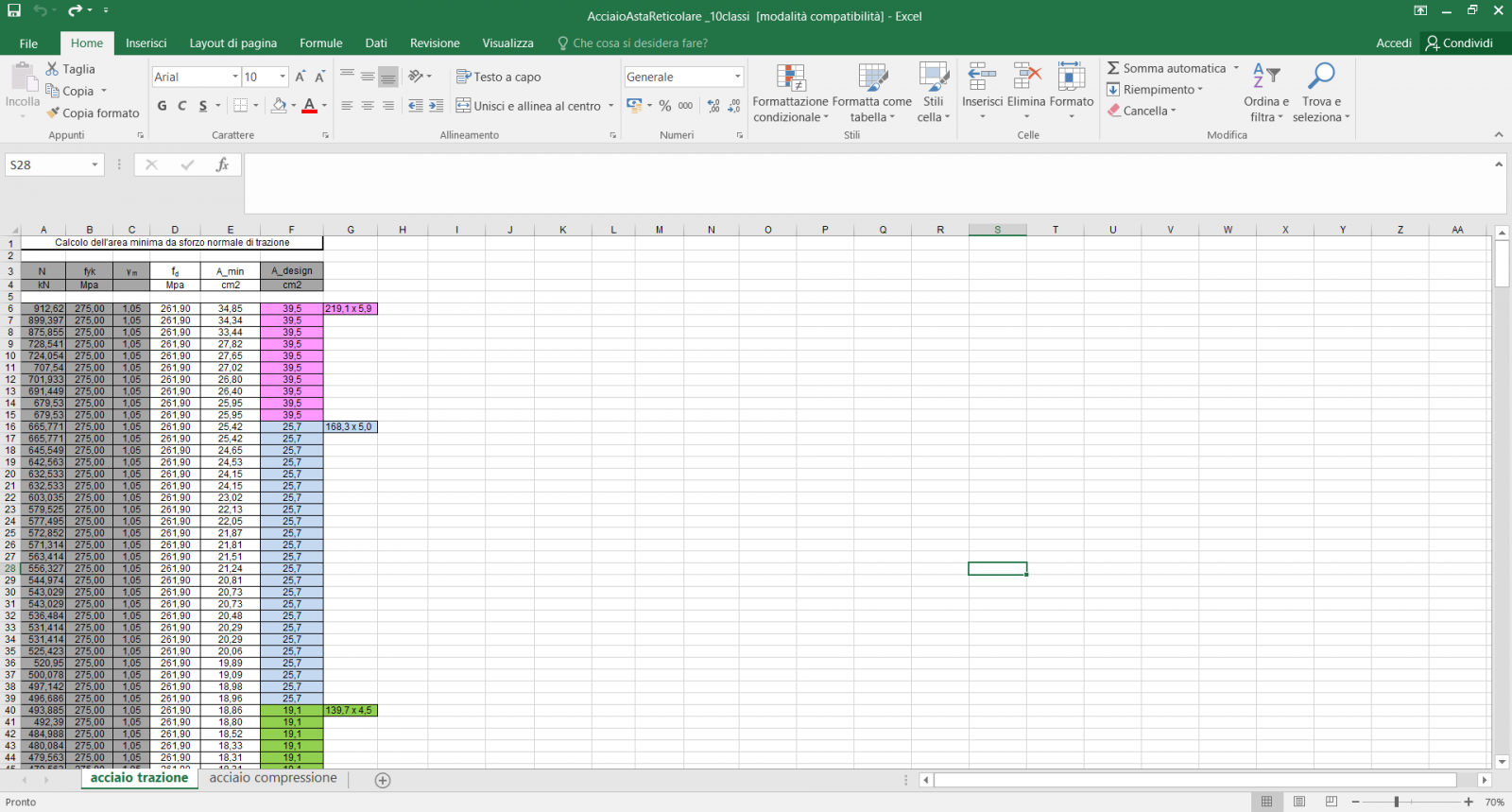
Anche le aste tese sono state raggruppate in base alle aree minime, associate agli sforzi di trazione, cercando però in questo caso di adattare gli stessi profilati scelti per le aste compresse. 

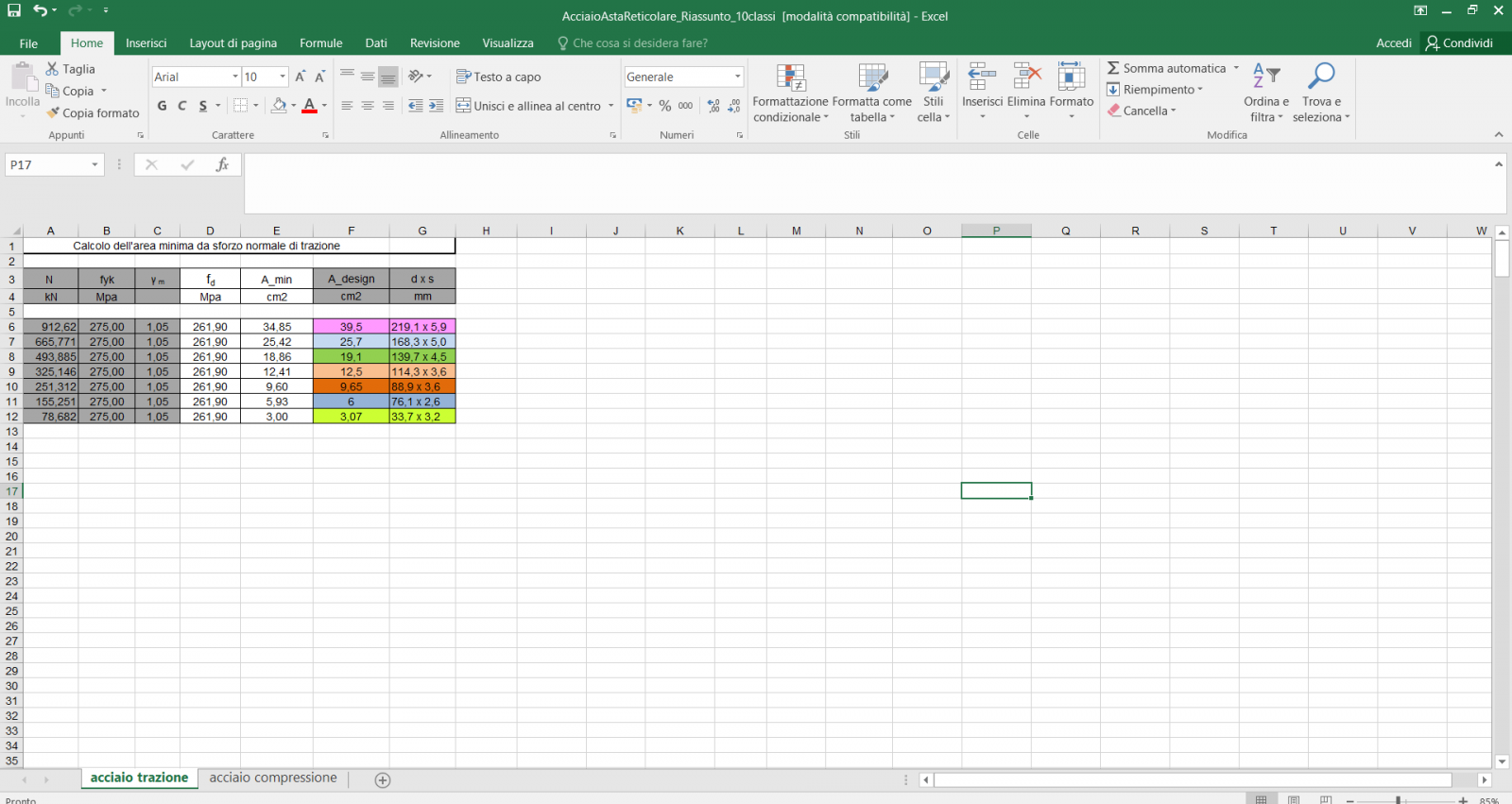
Sono stati infine riassunti nella seguente tabella le aste con valore di sforzo normale di trazione massimo per ciascuna categoria ed i relativi profilati.

Allego il PDF con l'esercitazione.

In allegato il Pdf con l'esercitazione

Per il progetto della travatura spaziale ho immaginato che la struttura sostenesse un edificio rifondato di 3 piani. Le dimensioni della struttura sono 20x20m. La spiegazione è nell'allegato

Il progetto che volevo realizzare era una travatura reticolare che potesse permettermi di sospendere un edificio di notevoli dimensioni (60mx20m) lasciandomi relativamente libero il piano terra.

Posto che potevo permettermi per il progetto che avevo in mente di fare 3 vincoli per lato lungo e 2 per il corto (6 vincoli in tutto) la luce massima che mi trovavo ad affrontare era di circa 27m.

Facendo perciò un calcolo approssimativo per l’altezza della trave ho ipotizzato un’altezza di 3,75m.

Ho quindi disegnato la trave in SAP2000. Ho assegnato i rilasci alle aste per imitare i comportamenti delle cerniere interne e i vincoli esterni.

Per procedere con i calcoli ho dovuto innanzitutto calcolarmi il peso proprio della mia struttura: per fare ciò oltre a scegliere un materiale, e personalmente mi sono orientato sul S235 data la sua duttilità, ho dovuto ipotizzare una sezione da affidare a tutte le aste. Sapendo che la snellezza massima consentita dalla legge è λmax≤200 e sapendo che λ=l₀/ρ abbiamo ottenuto che la sezione minima per legge al fine di evitare l’instabilità nelle aste compresse dovrà avere un raggio d’inerzia ρ=l₀/200. La lunghezza libera d’inflessione l₀=β*l dove β è un coefficiente che tiene conto della condizione al vincolo dell’asta considerata che nel caso di aste incernierata è β=1. Perciò nel nostro caso il raggio d’inerzia minimo è ρ=l/200. Per mettermi in sicurezza ho considerato le aste inclinate che avranno lunghezza l=3,75*√2. Quindi posso ottenere il raggio d’inerzia minimo ρ=2,65cm. Consultando il prontuario sceglierò la sezione 88,9x2,6.

Per calcolare il peso proprio faccio girare le analisi in caso di carico DEAD e sommo le reazioni vincolari verticali ottenendo il peso proprio di tutta la struttura in KN

Bisogna adesso stabilire le forze che agiscono sui nodi per reggere la struttura sovrastante: bisogna perciò calcolare l’area d’influenza considerando che i nodi centrali avranno un’area di influenza A1=3,75^2 mq quelli ai lati un’area A2=A1/2 e quelli agli angoli A3=A1/4

Considerando un carico di 10 KN/mq per piano e il peso proprio della struttura al mq moltiplicandoli per l’area d’influenza dei nodi,ottengo il carico da applicare sui singoli nodi

Vado quindi ad applicarli su SAP2000. Inserendoli in un load pattern che non consideri il peso proprio della struttura

Eseguo l’analisi per il nuovo caso di carico e mi estrapolo la tabella delle forze interne. Quindi scremo i dati rimuovendo le colonne sui tagli e sui momenti uguali a 0 per tutte le aste poi riduco ad una singola riga i dati per la singola asta. Una volta ordinati i dati in ordine crescente per le forze assiali mi accorgo di aver un carico di compressione particolarmente alto

Decido perciò di provare ad aumentare la resistenza della sezione aumentandone l’altezza e provo con una trave alta 5m. Ripetendo tutti i passaggi precedenti

Gli sforzi sono diminuiti notevolmente anche se rimangono piuttosto alti.

Vado quindi a effettuare il dimensionamento delle aste.

Inizio dimensionando le aste compresse. Sapendo che le aste compresse hanno un raggio d’inerzia minimo da rispettare per non incorrere in instabilità mi calcolo innanzitutto quale siano le sezioni minime che potrò usare. Sapendo che la tensione critica euleriana è σ(cr)=π^2*E/λ^2 allora eguagliandola alla tensione di snervamento(fyd) del materiale posso ottenere la snellezza critica per la quale la trave raggiunge l’instabilità prima che lo snervamento λ*=π√(E/fyd). Sapendo che la snellezza equivale come già detto λ=l₀/ρ posso ottenere il raggio d’inerzia minimo da dare alle sezioni compresse ρ=l₀/λ*.

Ottengo così due raggi d’inerzia minimi uno per le aste dritte da 5m e un altro per le aste inclinate da 7,07m

Scelgo perciò le mie 2 sezioni minime per le aste compresse

E le userò fino a quando mi rispettano i miei requisiti di area per le aste compresse dovuti allo sforzo normale A=N/fyd

Per gli sforzi assiali seguenti ho scelto dei profilati con aree maggiori scegliendo sezioni maggiori ogni volta che i requisiti non venivano soddisfatti.

Per dare una panoramica delle scelte oltre le immagini di seguito allego anche il foglio di calcolo su cui ho effettuato i dimensionamenti

Per quanto riguarda il dimensionamento delle aste tese ho deciso di riusare i profilati proposti per le aste compresse con l’unica accortezza di usare dei profilati più leggeri che coprissero le parti con un area minima minore di quella di partenza per le compresse.