Esercitazione svolta con Francesca Di Gregorio.
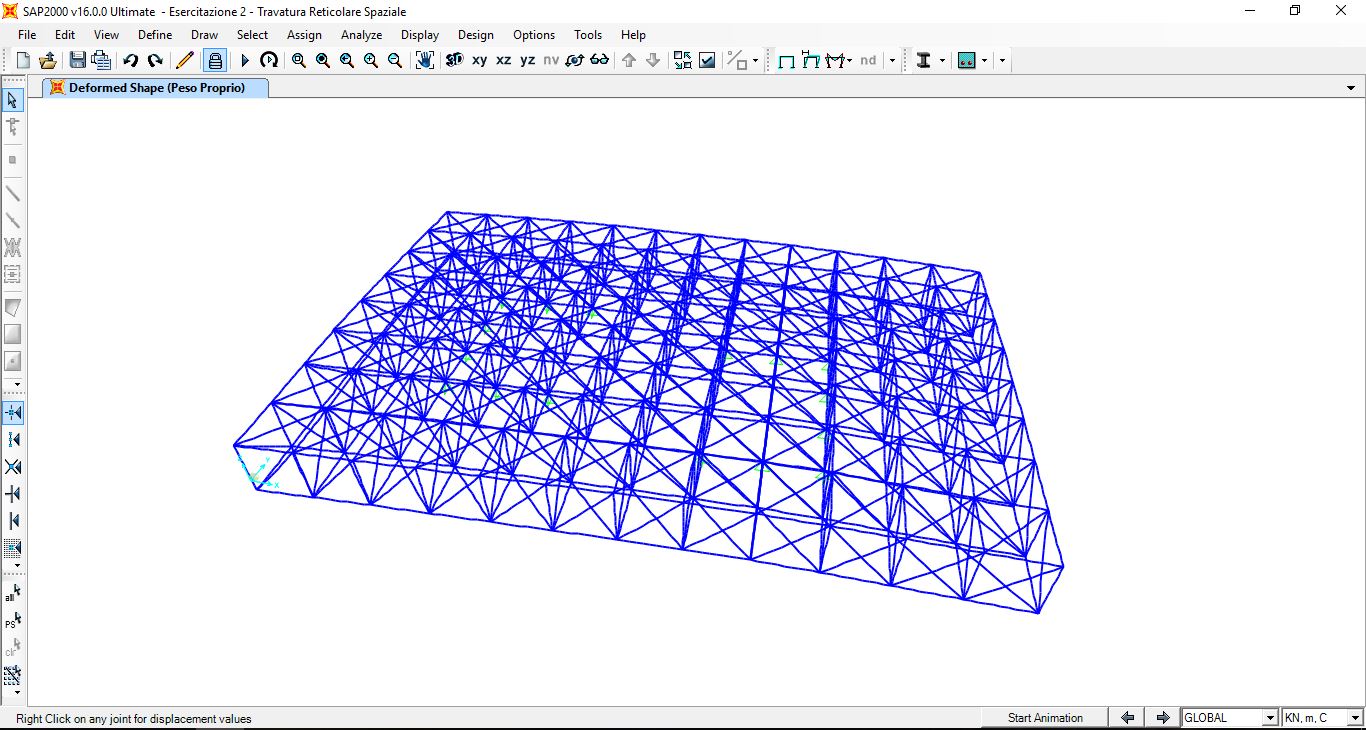
Disegnata su SAP200 una travatura reticolare spaziale di dimensioni 24x16m, di modulo 2 m, abbiamo assegnato alle aste della struttura una sezione tubolare di acciaio di dimensioni arbitrarie.
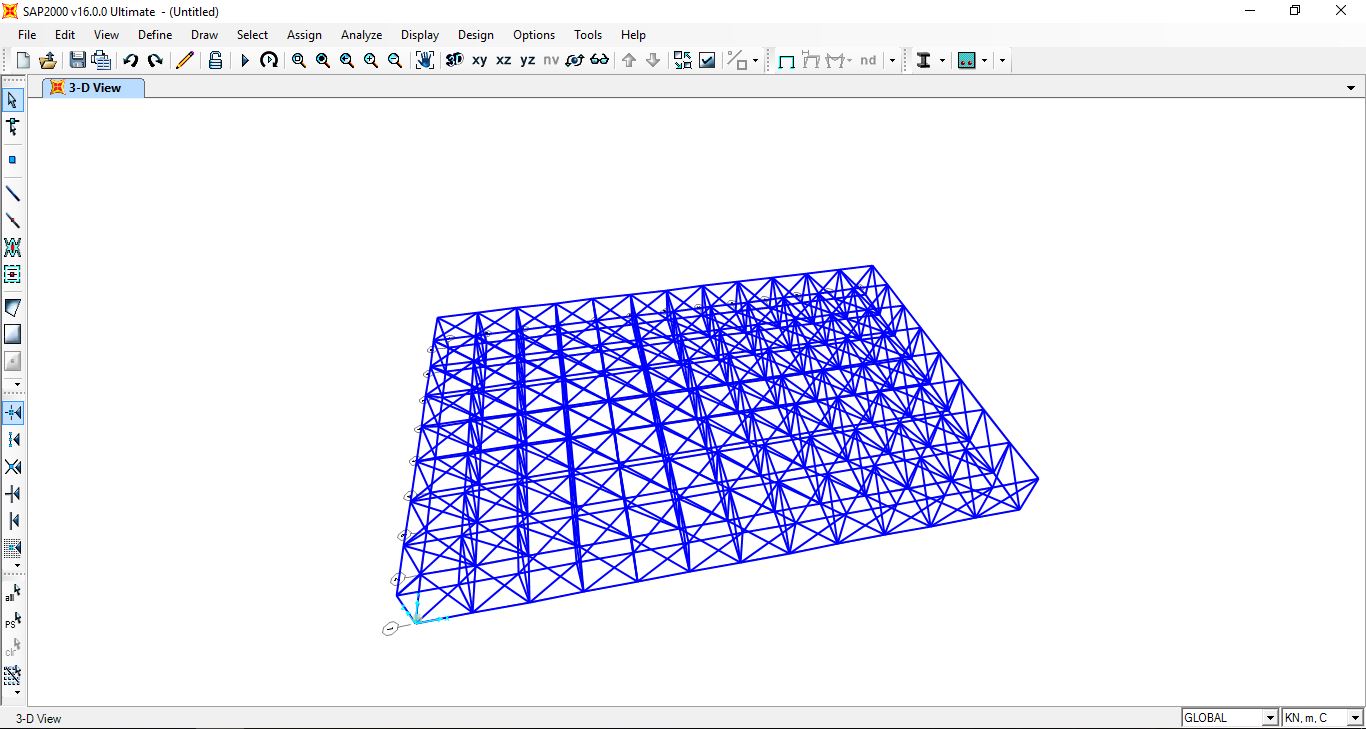
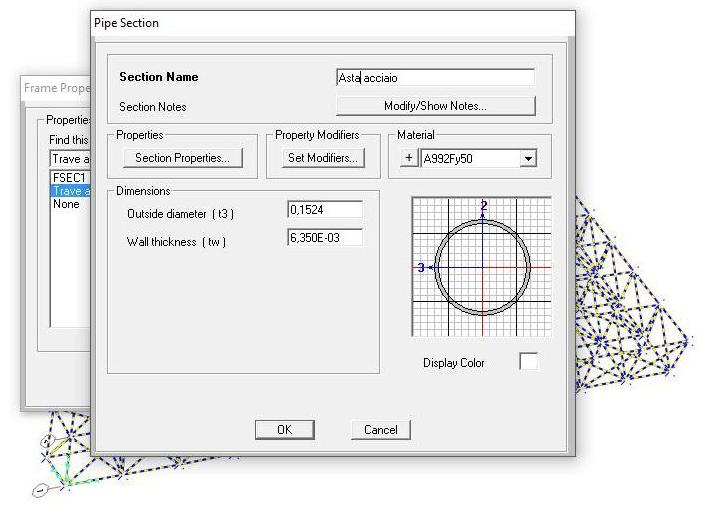
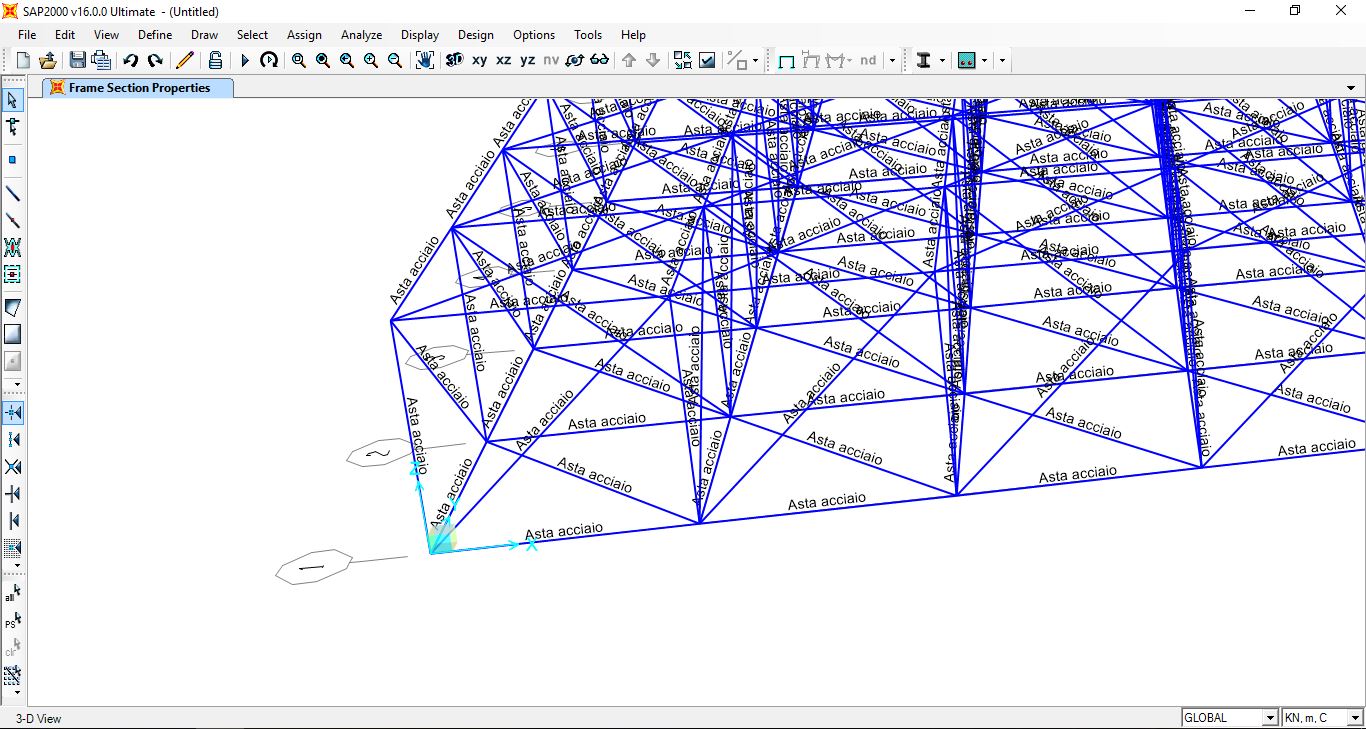
Assegnata la sezione, abbiamo impostato che i nodi fossero cerniere affinché le aste non trasmettano momento, assicurandoci che la travatura sia reticolare, ovvero che funzioni a solo sforzo normale. 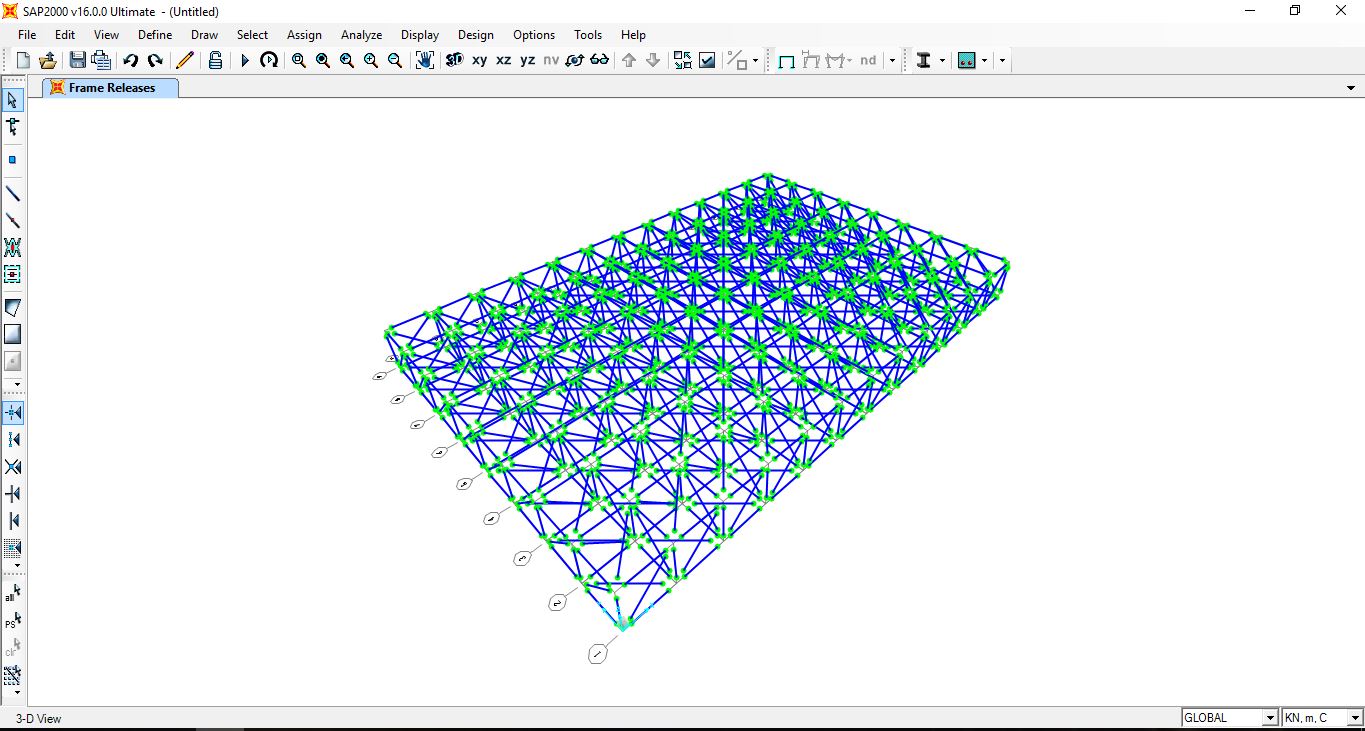
Abbiamo poi aggiunto le cerniere esterne, in corrispondenza di alcuni nodi, dove la travatura si poggierà alla struttura che scaricerà i carichi a terra.
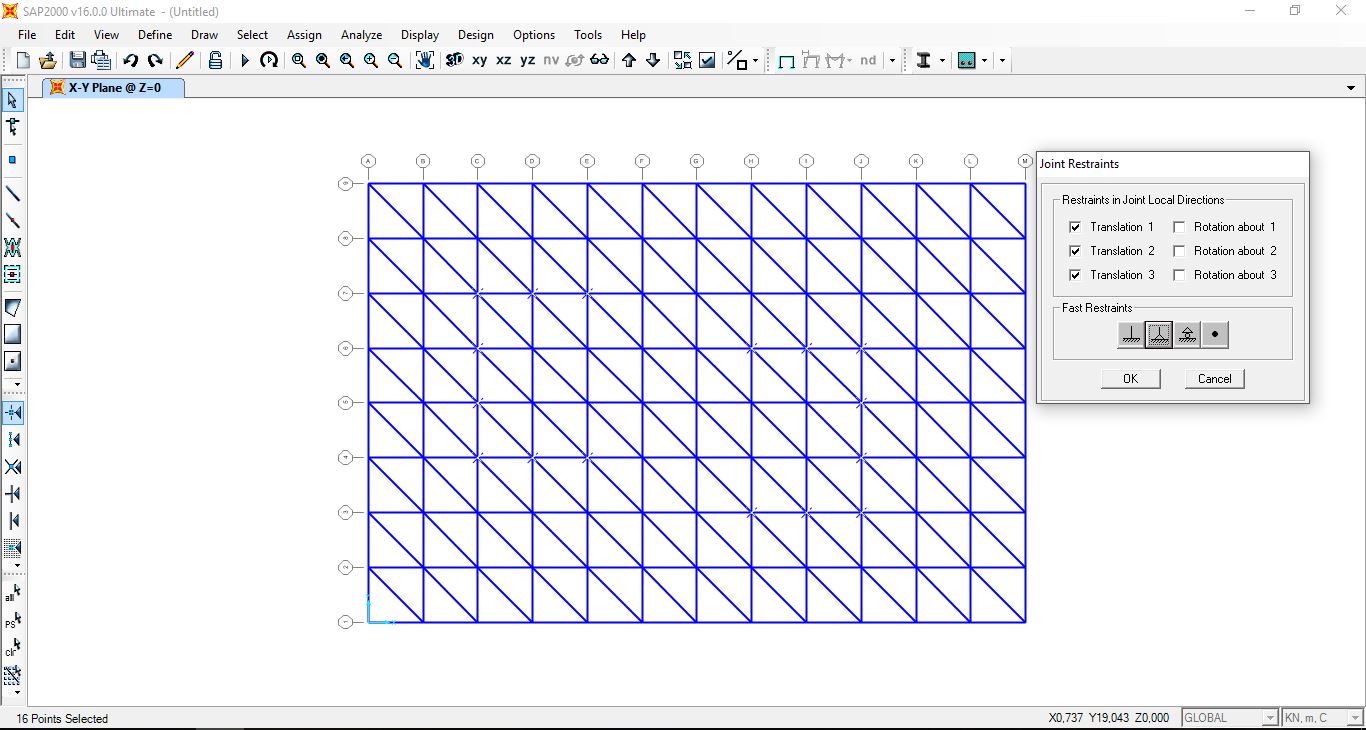
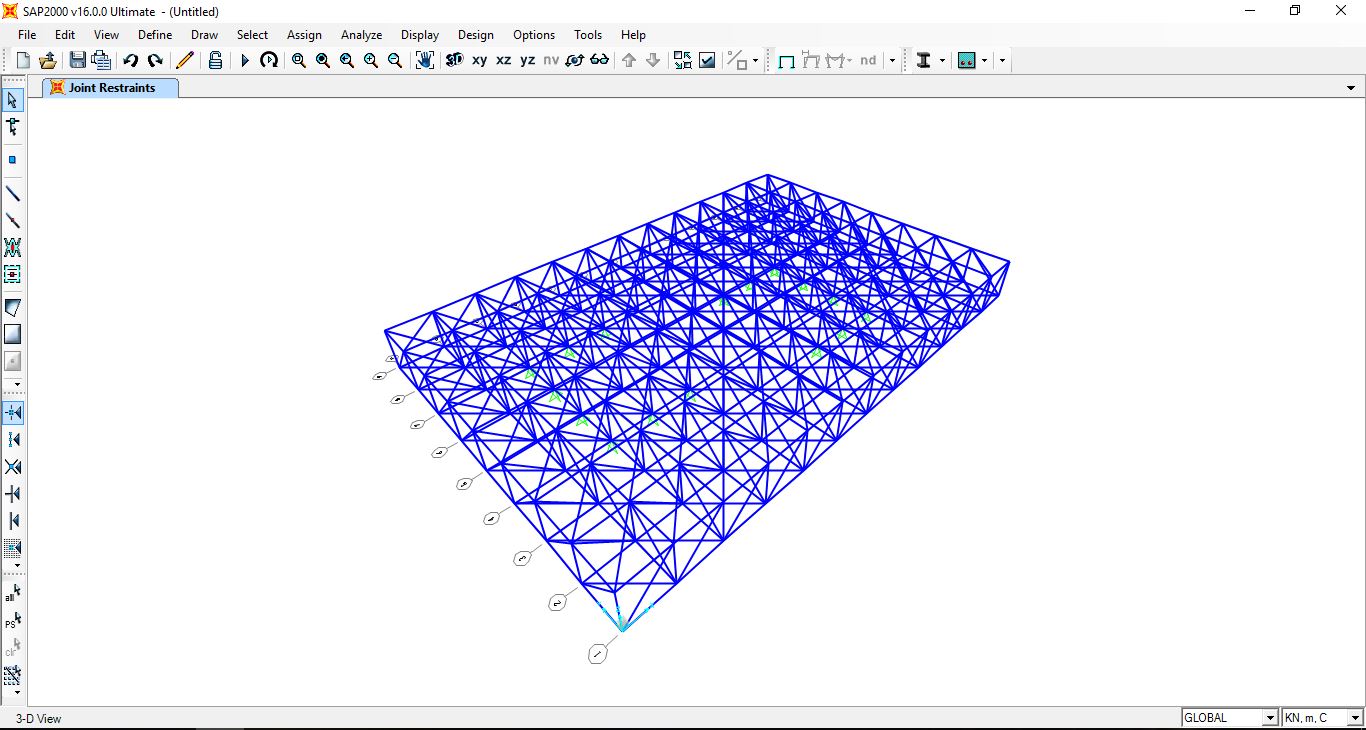
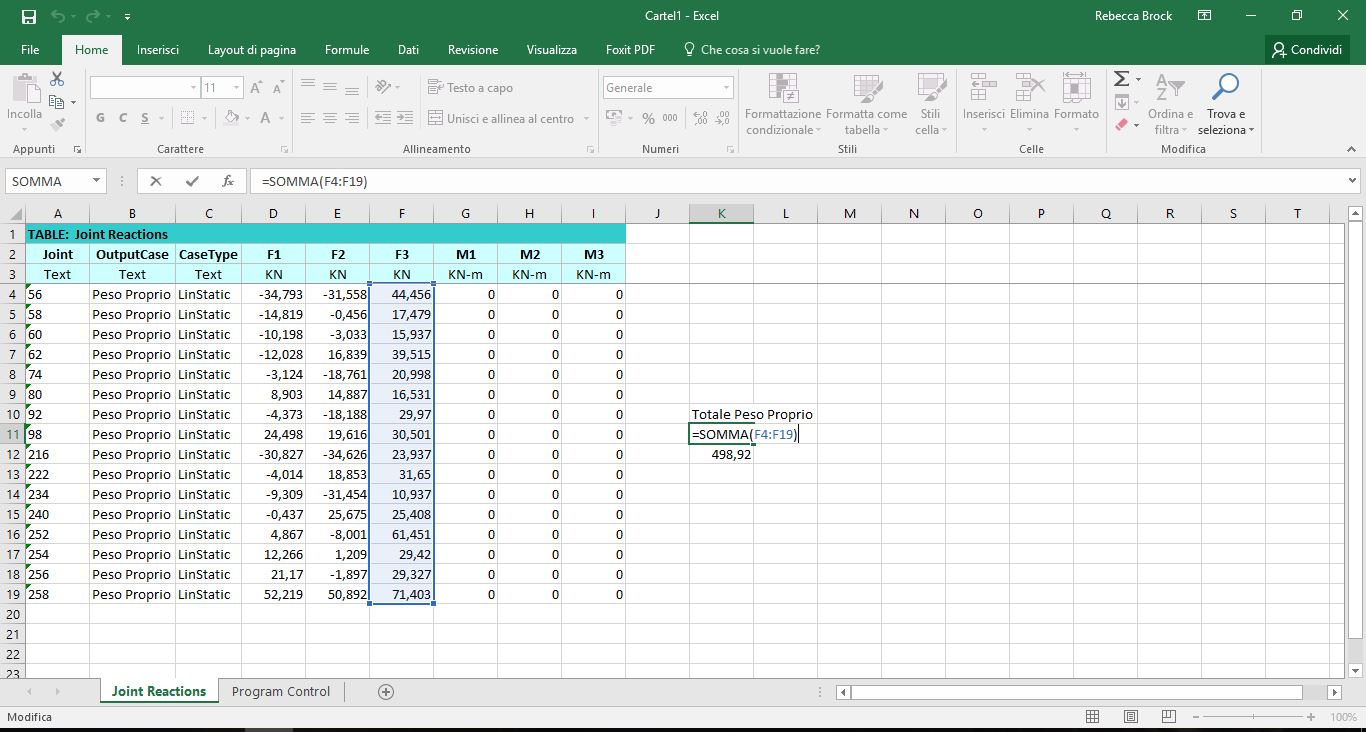
Aggiungendo un carico con il moltiplicatore di peso proprio pari a 1, abbiamo fatto gravare sulla struttura il peso di essa, che abbiamo ricavato sommando le reazioni verticali delle cerniere esterne su Excel.
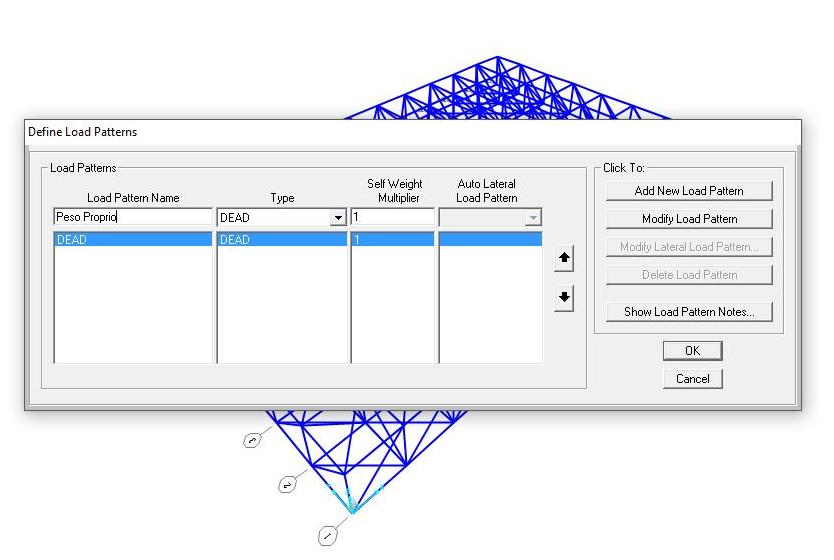
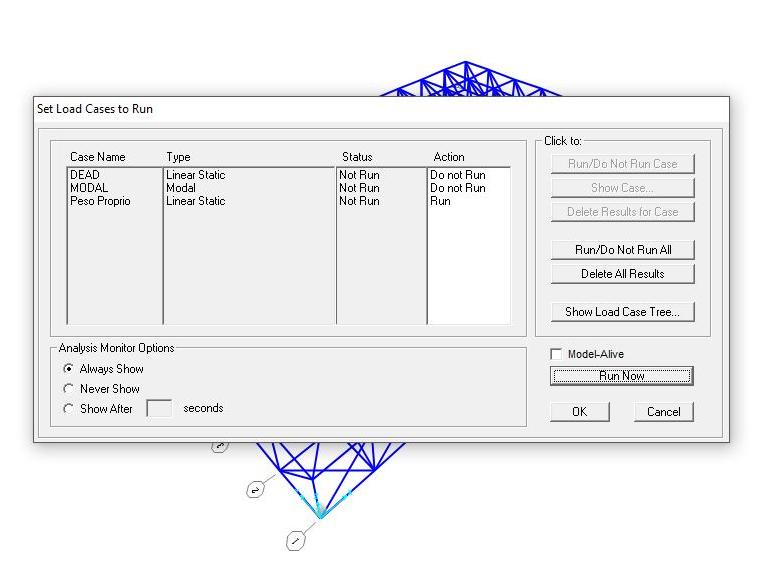
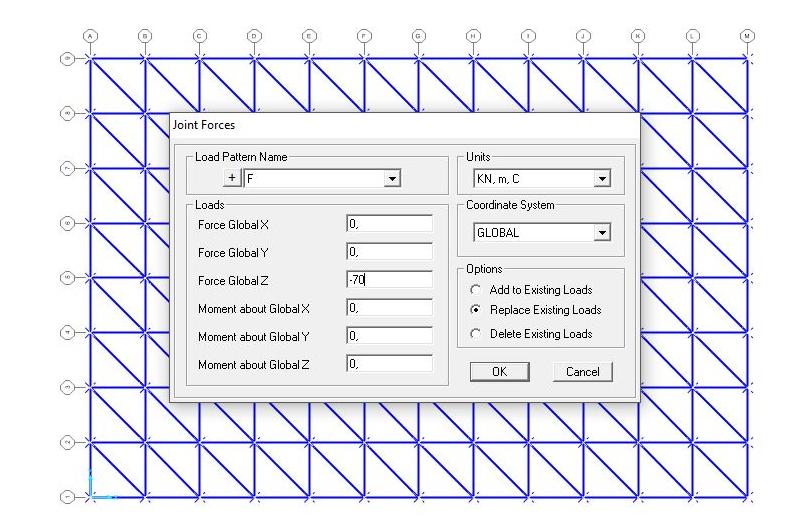
Supponendo che la travatura reggesse due solai, abbiamo calcolato il carico complessivo, compreso del peso proprio, e l'abbiamo applicato ai nodi.
Peso Proprio = 498,92 kN
q = 10 kN/m2
Area = 384 m2
Carico solai = 384 m2 x 10 kN x 2 = 7680 kN
Carico totale = 7680 + 498,92 = 8178,92 kN
Numero nodi = 117
F (carico concetrato sui nodi) = 8178,92 / 117 = 70 kN
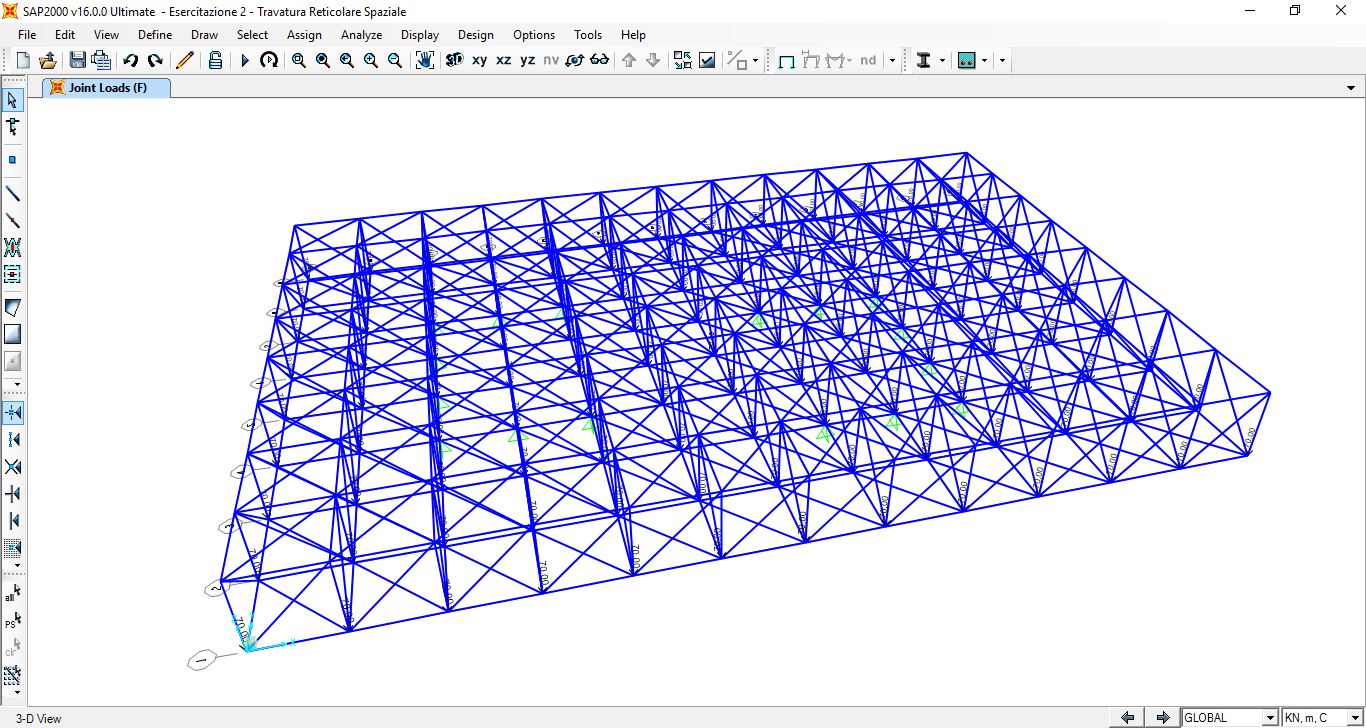
Struttura deformata Sforzo Normale
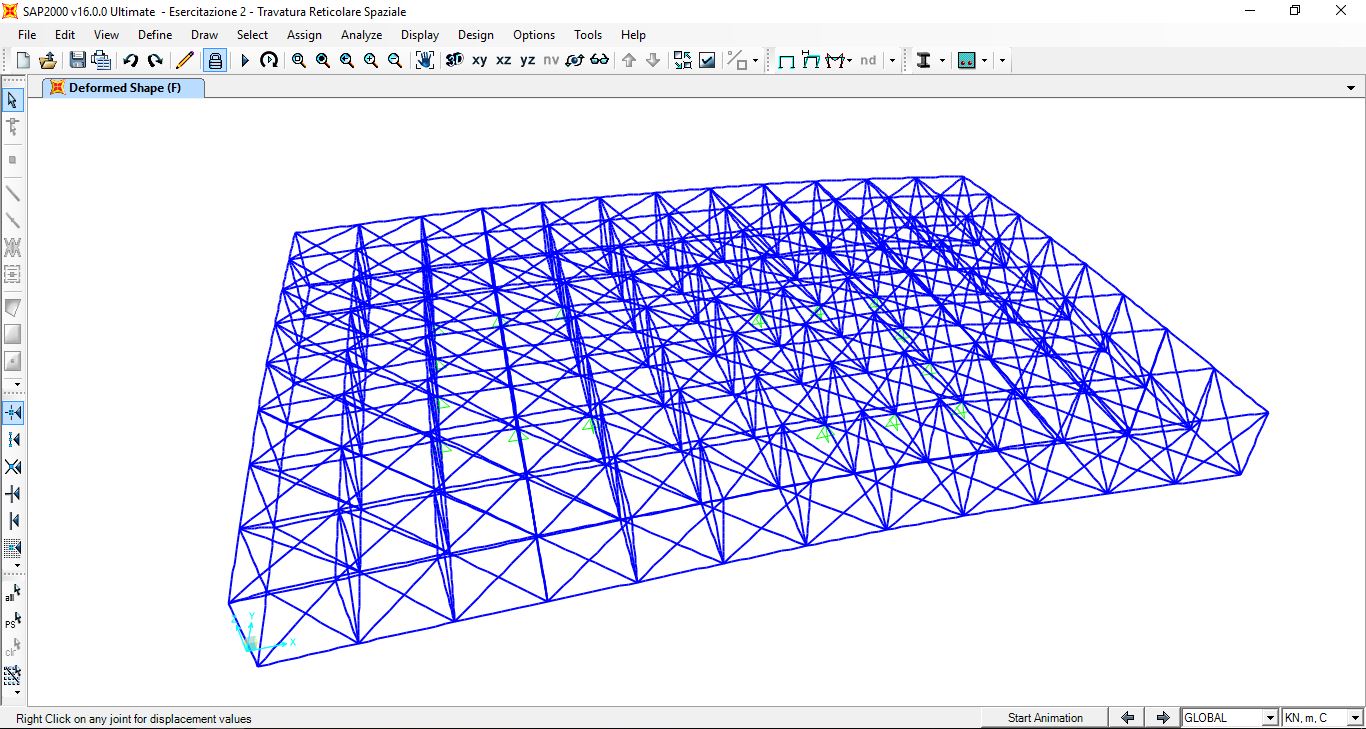
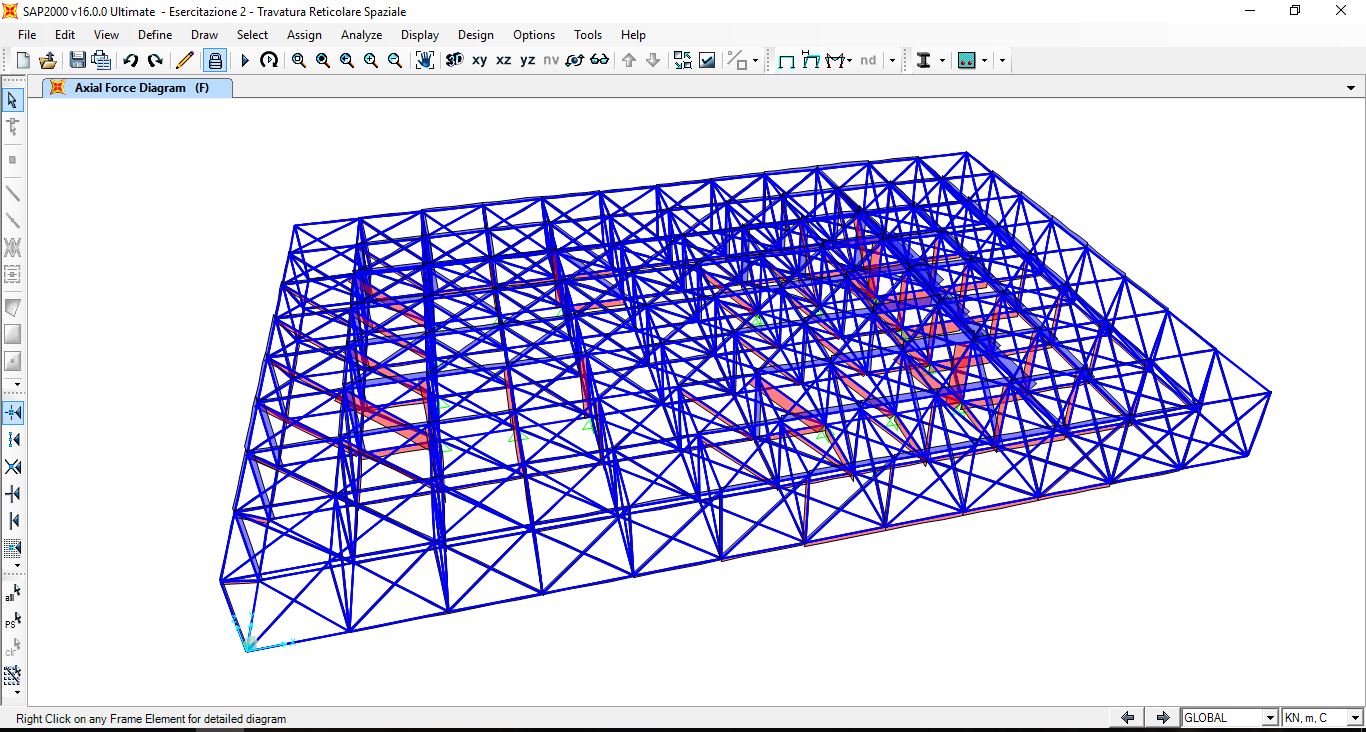
Abbiamo verificato che i momenti flettenti fossero nulli
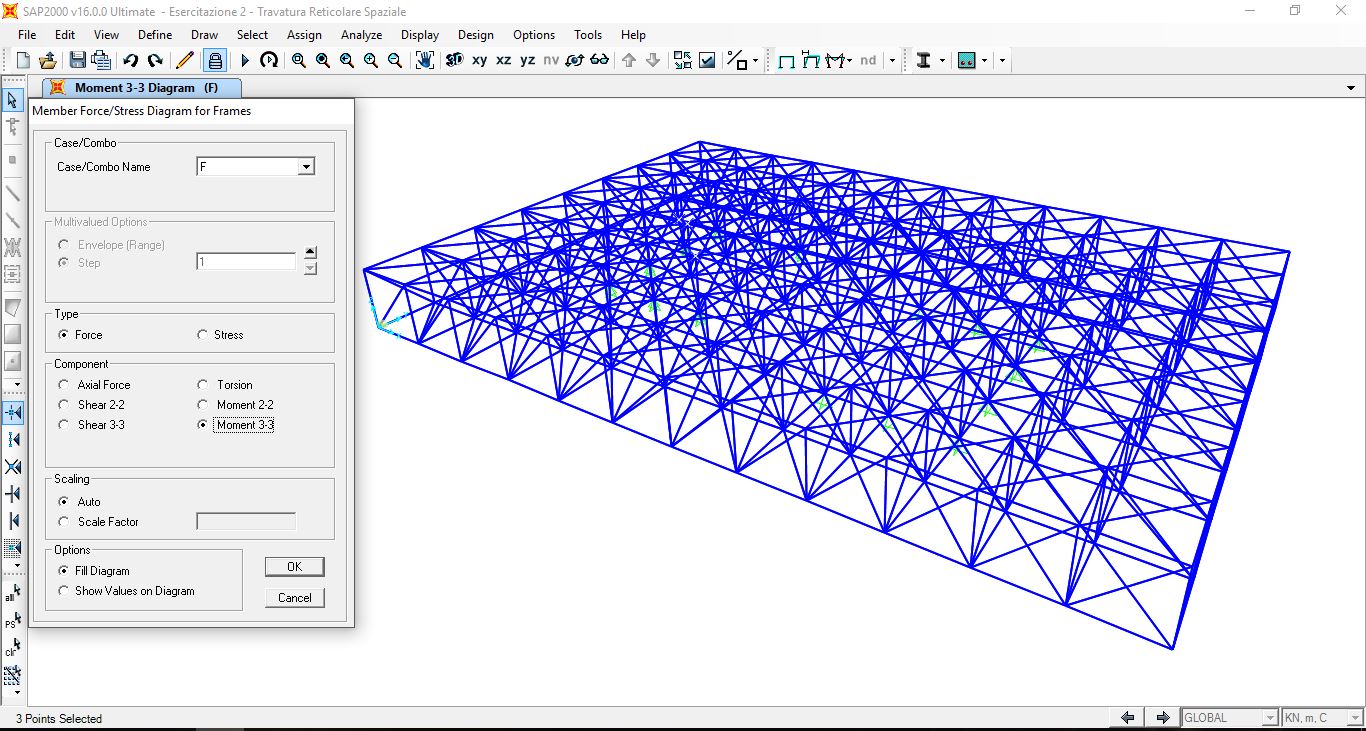
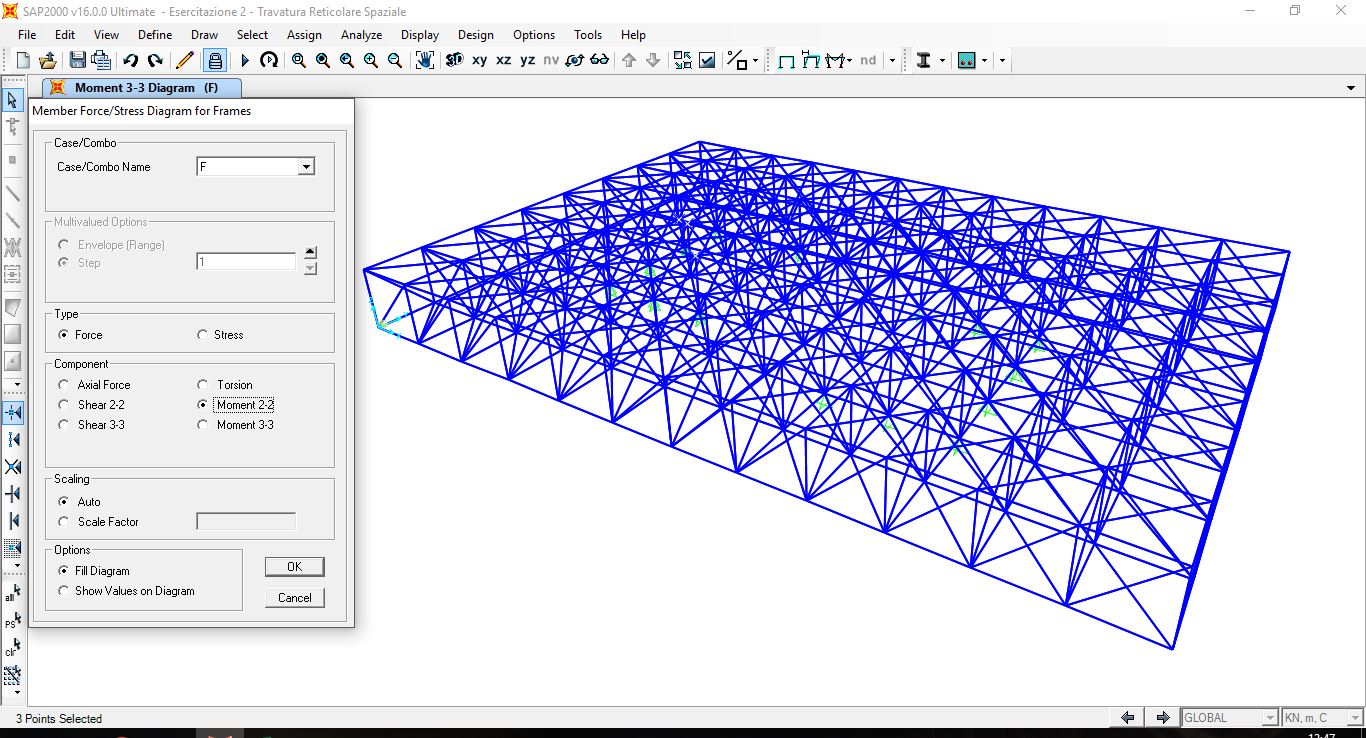
Ed abbiamo esportato i valori dello sforzo normale su Excel, dividendo le aste compresse da quelle tirate e ordinandole per valore dello sforzo nomale.
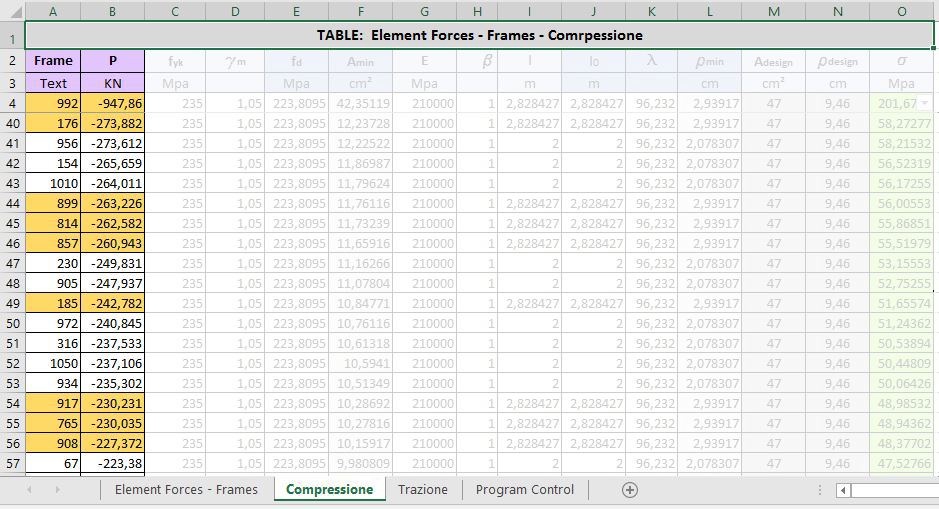
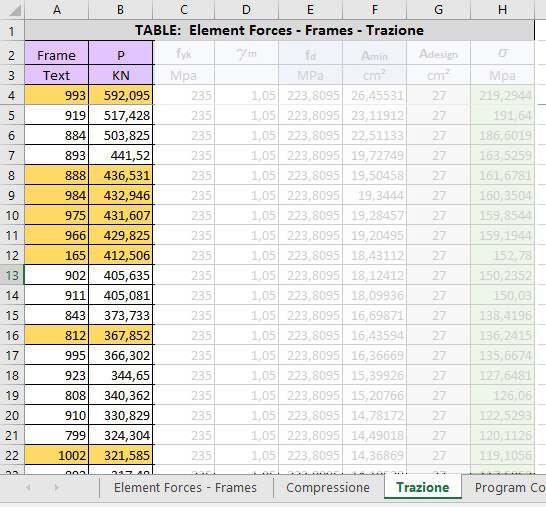
Abbaimo poi calcolato la tensione di design fcd=fck/γm
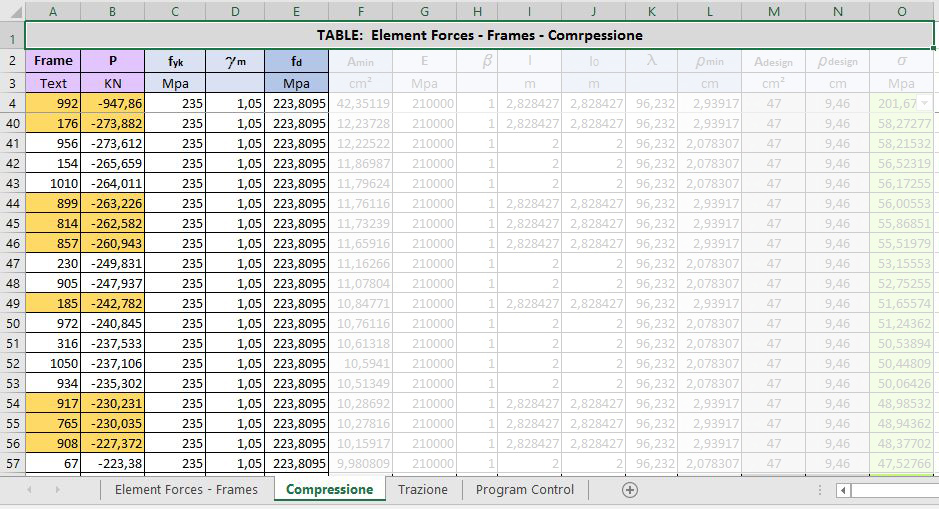
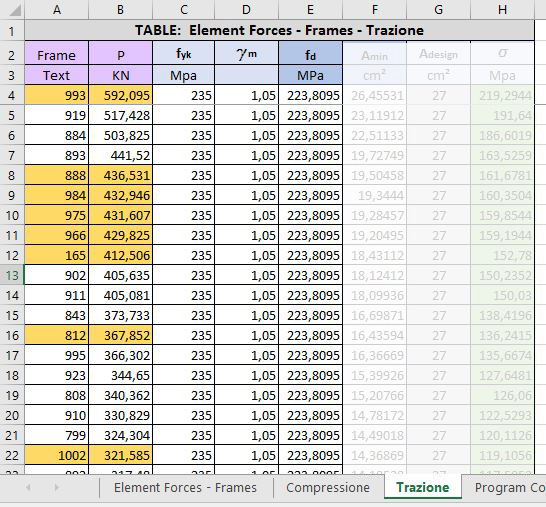
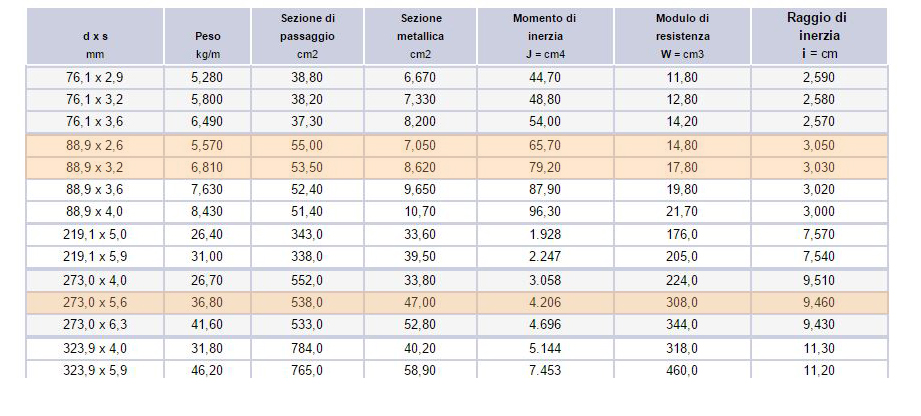
Per le aste tirate abbiamo usato fcd per calcolare l'area minima data da: Amin = N/fcd. Sono così stati scelti due profilati di area maggiore di quella trovata, così non da non sovradimensionare troppo le aste. Abbiamo verificato che le tnsioni non superassero fd.
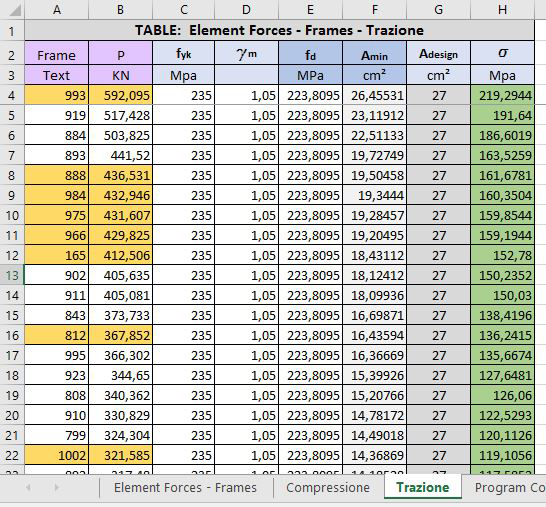
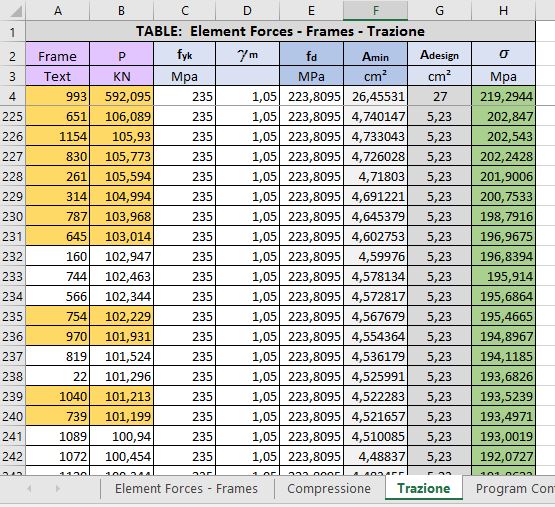
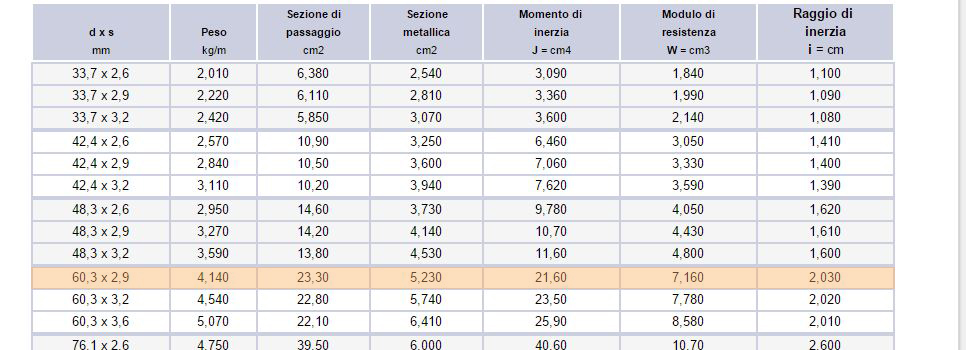
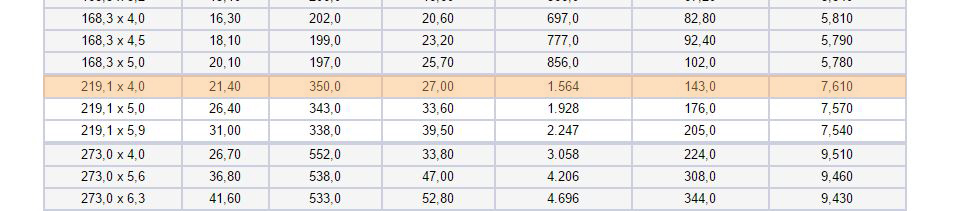
Le aste comrpesse invece sono state dimensionate non solo a rottura (A>Amin) ma anche tenendo conto dell'instabilità euleriana con ρ>ρmin. ρ è dato da l0/λ, con λ=(πE/fcd)1/2 e l0=lxβ. Abbiamo scelto tre diversi profilati e e verificato che il valore delle tensioni non superasse fd.
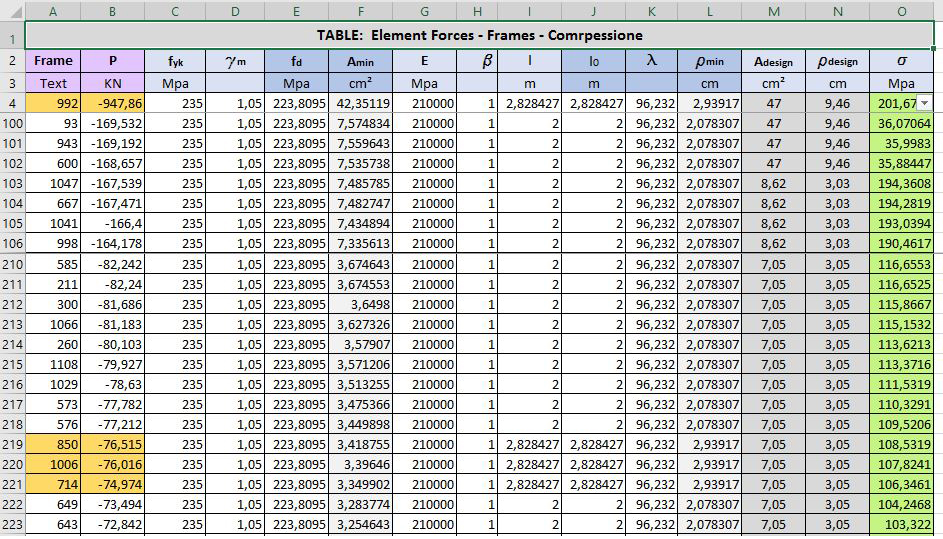
Dimensionata e verificata la struttura allo Stato Limite Ultimo l'abbiamo verificata allo Stato Limite di Esercizio, calcolando l'abbassamento e controllando che esso sia inferiore al limite imposto dalla normativa δ < l/200.
Abbiamo quindi esportato da SAP i valori dell'abbassamento dei nodi ed estratto su Excel il valore massimo (corrispondente in tabella al valore minimo poiché di segno negativo).
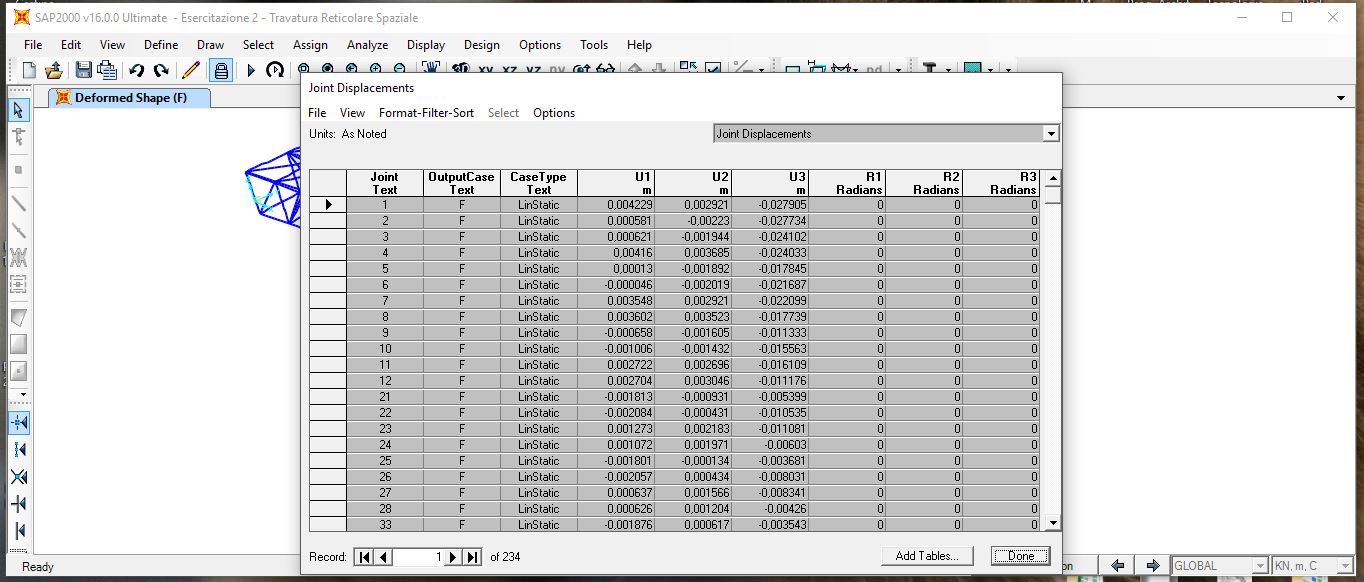
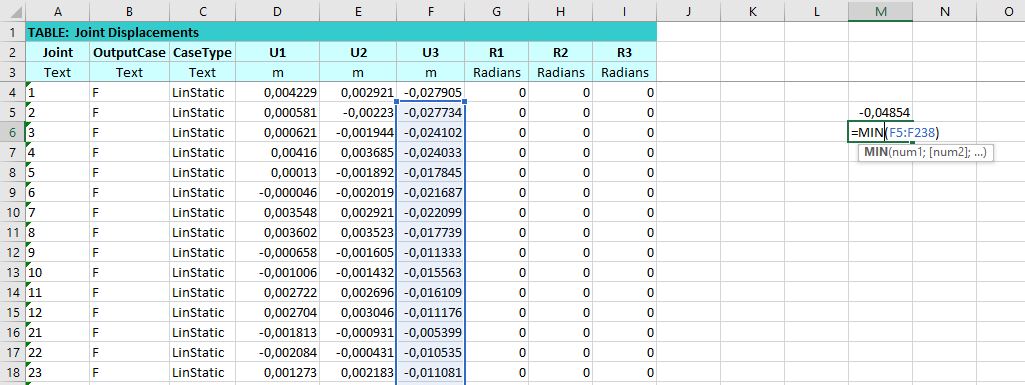
Abbiamo individuato il nodo corrispondente al valore
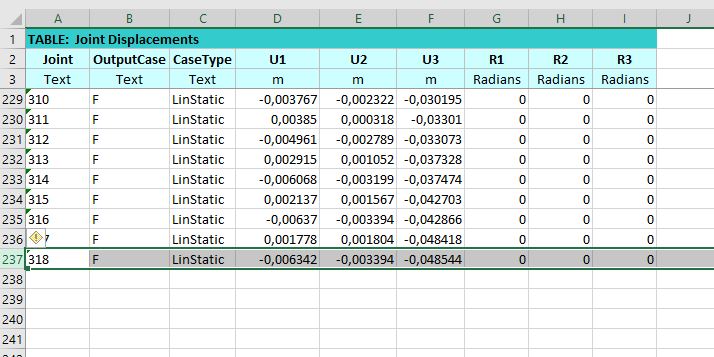
E misurato la luce. l = 7,2 m
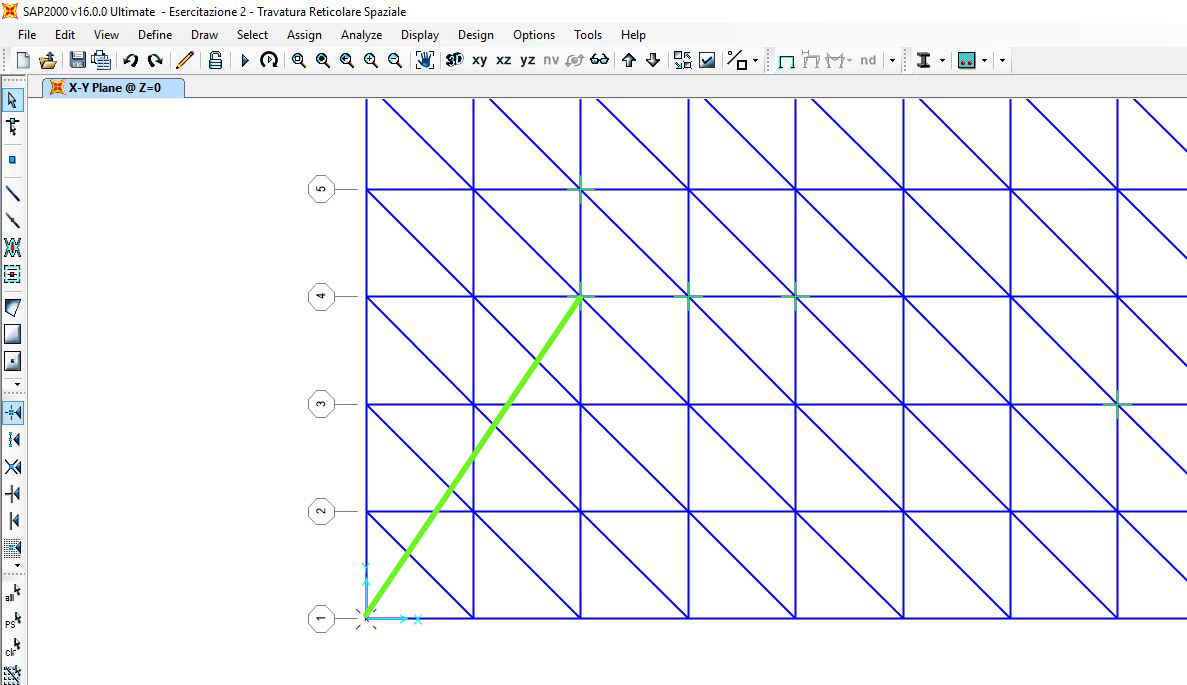
δ = 7,2 / 200 = 0,036
0,048 > 0,036.
La struttura non è quindi verificata allo SLE. Per ridurre l'abbassamento è necessario diminuire lo sbalzo (e di conseguenza la luce). Va considerato che con le nuove sezioni il peso proprio della travatura si ridurrà, per questo motivo andrà rifatto il calcolo delle forze applicate ai nodi che modificherà anche l'abbassamento.
Commenti recenti