Esercitazione

L'esercitazione è stata caricata in .jpeg perchè il blog non salva gli avanzamenti, ma solo una parte dell'esercitazione caricata.

CONSEGNA 2 - graticcio 

Paolo Burattini, Matteo Cavuoti

Abbiamo disegnato la struttura di un graticcio su Rhino di dimensioni 10x20m, con un interaase tra le travi che costituiscuino il graticcio di 1m.

Dopo aver esportato in sap il file dxf, con le dovute attenzioni, abbiamo inserito i vincoli esterni, in corrispondenza dei reali pilastri sottostanti.

Abbiamo caricato la struttura con un peso di 10 kN su metro quadro, che si traduce in 5 kN a metro per tutti i segmenti di trave interne, e 2,5 kN per i segmenti delle travi di bordo.

Otteniamo quindi quanto segue, deformata del graticcio, e i valori del momento su ogni segmento.

La tabella seguente è quella che sap ci fornisce con i valori del momento su ogni segmento di trave.

A seguito la abbiamo esportata su excel trovando il momento maggiore.

CONSEGNA 2 - graticcio 

Paolo Burattini, Matteo Cavuoti

Abbiamo disegnato la struttura di un graticcio su Rhino di dimensioni 10x20m, con un interaase tra le travi che costituiscuino il graticcio di 1m.

Dopo aver esportato in sap il file dxf, con le dovute attenzioni, abbiamo inserito i vincoli esterni, in corrispondenza dei reali pilastri sottostanti.

Abbiamo caricato la struttura con un peso di 10 kN su metro quadro, che si traduce in 5 kN a metro per tutti i segmenti di trave interne, e 2,5 kN per i segmenti delle travi di bordo.

Otteniamo quindi quanto segue, deformata del graticcio, e i valori del momento su ogni segmento.

Quelli di sopra è la tabella che sap ci fornisce con i valori del momento su ogni segmento di trave.

A seguito la abbiamo esportata su excel trovando il momento maggiore.

Considerando il momento maggiore, e riutilizzando le formule che già avevamo utilizzato per il dimensionamento di una trave in calcestruzzo a flessione, dimensioniamo la trave più sollecitata della piastra.

Dimensionamento di un graticcio in cemento armato

Il graticcio studiato copre un’area di 14x18 m e porta un solo piano adibito a biblioteca. I pilastri che sorreggono la struttura hanno una luce di 18 m, quindi sono stati posizionati lungo i lati corti. Le travi del graticcio sono state disposte con interasse di 1 metro ed hanno tutte la stessa sezione in entrambe le direzioni poiche’ non c’e’ gerarchia. 

Prima di inserire la struttura su SAP sono stati calcolati i carichi incidenti: considerando un solaio in latero cemento si definiscono i carichi qs= 3,05 kN/m², qp= 3,04 kN/m² e si considera un qa= 5 kN/m² per la categoria D2.

Dopo aver importato la struttura su SAP sono stati assegnati i vincoli di incastro nei nodi lungo il lato inferiore del graticcio e per il predimensionamento e’ stata assegnata una sezione 20x70 cm in calcestruzzo C40/50.

E’ stata creata una combinazione di carico in cui i carichi strutturali, sovraccarichi permanenti e accidentali sono stati moltiplicati per i loro coefficienti di sicurezza (qs*1,3+qp*1,5+qa*1,5) ottenendo il carico totale di un piano qu= 16,025 kN/m². Successivamente e’ stato assegnato il carico alle travi suddividendolo in entrambe le direzioni: in questo modo il carico e’ stato moltiplicato per l’area di influenza delle travi centrali, percio’ e’ stato assegnato un carico qu= 8,0125 kN/m alle travi centrali (con area di influenza 0,5 m) e un carico qu= 4,00625 kN/m per le travi di bordo (con area di influenza 0,25 m).

Avviando l’analisi e’ stato possibile avere la deformata della struttura e i risultati dei momenti flettenti.

Dopo averli importati su Excel e’ stato possibile trovare il valore del Momento massimo (di compressione) Mmax= 609,783 kN*m e, sempre attraverso Excel, verificare se la sezione assegnata fosse corretta. Con tale momento e mantenendo una base di 20 cm, l’altezza minima delle travi e’ risultata 75,7 cm quindi e’ stata scelta una altezza di 80 cm.

Avendo quindi modificato la sezione delle travi su SAP, analizzato la deformata e i diagrammi dei momenti, il valore del Momento massimo e’ risultato 636,679 kN*m e la sezione della trave su Excel e’ risultata corretta. 

A questo punto e’ stata verificata la deformabilita’ della struttura, in particolar modo l’abbassamento massimo risultato essere 0,022 cm e che deve essere inferiore a 1/200 della luce (quindi, in questo caso, inferiore a 0,09 m).

La trave piu' sollecitata a momento flettente, e con un maggiore abbassamento, e' quella centrale.

La progettazione di un graticcio prevede il dimensionamento di travi in calcestruzzo senza l’individuazione di una gerarchia. Il graticcio in esame, composto da travi con la stessa geometria, supera una luce di 15 m ed ha ha al di sopra un piano adibito ad uffici aperti al pubblico. 

Come primo passo definisco la geometria del graticcio su Autocad, creando una  griglia 15 m per 10 m, con interasse pari ad 1 m. Per l’esportazione su Sap è importante esplodere gli elementi creati (su un layer diverso dallo 0) e posizionare la griglia in prossimità dell’origine degli assi. 

Fig. 01 - L'immagine seguente mostra la griglia creata su Autocad importata su Sap. 

Definisco la tipologia di solaio in calcestruzzo, riportata nell’immagine seguente.

Fig.02 - Solaio

Questa scelta mi permette di calcolare i carichi strutturali q_s e i sovraccarichi permanenti q_p, agenti sul graticcio utilizzando la combinazione di carico, che include il carico accidentale q_a, legato alla funzione (questi valori sono moltiplicati per i coefficienti di sicurezza).  

La combinazione di carico segue la formula q_u=(q_s γ_s + q_p + γ_p + q_a γ_{a) * i} 

Importando il modello su Sap come prima operazione spezzo le linee che definiscono il graticcio in modo che si possa analizzare il comportamento delle travi considerandole disgiunte dalle altre poste perpendicolarmente. 

Dopo questo ipotizzo il posizionamento dei vincoli esterni (incastri) lungo i due lati corti e assegno la sezione in calcestruzzo, rettangolare e pari a 0,25 x 0,50 m. Successivamente assegno il carico agente distinguendo le travi di bordo da quelle interne: su quelle più esterne considero la metà del carico rispetto a quelle centrali in quanto l’area d’influenza è esattamente la metà rispetto alle travi interne, su cui calcolo il carico lineare moltiplicando q_u per 1m (quindi per quelle esterne farò q_u x 0,50 m). 

Fig. 03 - Griglia con vincoli e assegnazione della sezione 

Fig. 04 - Assegnazione del carico alle travi interne 

Fig. 05 - Assegnazione del carico alle travi esterne 

Assegnato il carico con questa distinzione, avvio l’analisi. Possiamo osservare la configurazione deformata e il diagramma del momento flettente. Il valore massimo del momento flettente lo ottengo come risultato di output delle tabelle generate su Sap e che utilizzo nel foglio di calcolo Excel per verificare se il dimensionamento ipotizzato sia corretto. 

Fig. 06 - Configurazione deformata 

Fig. 07 - Diagrammi del momento flettente 

Fig. 08 - Trave con sollecitazione di momento massimo 

Dalla tabella di Output di Sap possiamo trovare il valore massimo del momento flettente: 

 quindi possiamo utilizzarlo come dato di partenza nel foglio di calcolo Excel, come illustrato nell'immagine seguente (calcestruzzo C50/60) : 

Verificata la sezione analizzo la configurazione deformata ed esamino l’abbassamento massimo della trave centrale, verificando che questo sia minore di 1/200 della luce. 

0.0576 m < (1/200)*15 m = 0.075 m 

ESERCITAZIONE 2

Trave reticolare spaziale
Risoluzione tramite SAP2000

Dopo aver disegnato su SAP una travatura reticolare spaziale di un modolo 2mx2m

(1)

La prima cosa è indicare quali siano i punti in cui la reticolare si appoggia e quindi assegnare dei vincoli (per rendere la struttura isostatica) nella parte bassa della trave con il comando ASSIGN > JOINT >RESTRAINTS.

(2)

(3)

Poi si procede assegnando come materiale l’acciaio e scegliendo il tipo di acciaio per definire il modulo elastico E. Si sceglie come sezione Tubolare pipe. DEFINE>SECTION PROPERTIES>FRAME SECTIONS e poi assegniamo la sezione alla struttura.

(4)

(5)

Dato che in una struttura reticolare tutti i vincoli interni sono cerniere, dobbiamo fare un’operazione di rilascio del momento ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0.

(6)

(7)

Assegnata la sezione ho definito un caso di carico con delle forze concentrate nelle cerniere, per ricavare la forza concentrata ho tenuto conto di questi parametri:

Numero piani: 3

Peso proprio piano per mq: 5 KN/mq

Mq piano: 96 mq

Peso piano: 96 mq x 5 KN/mq = 480 KN

Peso per ogni nodo : (480 KN x 3 piani) / 35 =  41 KN

A questo punto carichiamo la struttura attraverso una serie di forze concentrate nei nodi strutturali: forze di entità maggiore nei nodi centrali ( 41 kN), e minore in quelli perimetrali ( 20,5 kN); questo perché le aree di influenza dei nodi laterali sono la metà di quelli centrali, ciò significa che saranno sottoposti a forze più piccole. Per aggiungere delle forze seleziono le frame che mi interessano e poi ASSIGN > JOINT LOADS > FORCES, da questa finestra di dialogo posso creare nuove forze con intensità e direzione variabile.

(8)

Possiamo ora avviare l’analisi. Il software mostra per prima cosa l’andamento della deformata.

Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE

(9)

(10)

Per visualizzare le tabelle di calcolo da esportare su Excel è sufficiente digitare Ctrl+T e spuntare ANALYSIS RESULT, cliccare su SELECT LOADS PATTERS e quindi selezionare F e dare OK. Dalla tabella apriamo il menù a tendina in alto a destra e selezioniamo ELEMENT FORCES > FRAMES e esportiamo su Excel.

(11)

(12)

Per prima cosa dimensioniamo le aste tese. In questo caso prendiamo in considerazione alcuni fattori, come la lunghezza dell'asta (l), il modulo di elasticità (E), resistenza di design(f_yd)e la tipologia del vincolo (β) , in quanto per le aste compresse dobbiamo calcolare il modulo di inerzia minima (Imin), l'area minima (Amin), ed il raggio di inerzia (ρ_min), ed inoltre verificare che la snellezza (λ) non dovrà superare il valore 200.

Per le aste compresse oltre ad f_yk, γ_m, e f_yd devo tener conto anche del momento di inerzia I_x e del raggio giratore di inerzia ρ_x

Come prima, inseriamo i valori dello sforzo normale (in questo caso il modulo in quanto i valori sono negativi trattandosi di compressione), il β (in questo caso equivalente ad 1 perché si tratta di aste incernierate) e la lunghezza espressa in metri di ciascuna asta. In base ai valori di Area Minima, Momento d’Inerzia minimo e raggio giratore di inerzia minimo scegliamo il profilato adatto da un sagomario e inseriamo i valori corrispondenti.  Fatto ciò controllo che il valore della snellezza λ non sia superiore a 200. 

Graticcio

Progetto un graticcio in CA, dimensioni 10x15 m, maglia 1x1 m. Incastrato,in appoggio, lungono i lati corti mi darà una luce libera di 15 m. Le travi avranno tutte la stessa sezione, poichè lo schema a graticcio non prevede gerarchia tra di esse.

La stratrigrafia del solaio mi darà i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²), il carico accidentale è definito dalla destinazione d'uso,in questo caso uffici e sarà q_a=3 kN/m²

q_s = 3,58 kN/m²            q_p = 2,264 kN/m²      q_a=3 kN/m²

La combinazione di carico si otterrà assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali.

                                                                q_u = 12,414 kN/m²   (1 piano)

Una volta definita la geometria e il carico importo il disegno fatto su Autocad in SAP.

Assegno i vincoli di incastro ai nodi nei lati corti (10m) e una sezione approssimativa a tutte le travi di 25x50 cm, considerando un cls di classe C 40/50.

Assegno poi il carico distribuito alle travi. Le travi ai bordi avranno metà del carico quindi 6,20 kN/m e le travi centrali il carico pieno 12,414 kN/m.

Avvio l'analisi e mi compare la configurazione indeformata.

Il diagramma dei momenti flettenti corrisponde a quello di una trave doppiamente incastrata. 

Estraggo dalle tabelle il valore del momento massimo che corrisponde a 260,58 kN·m e lo inserisco nella tebella per il dimensionamento corretto della sezione. Verifico, in questo caso che la sezione scelta è corretta. 

Dalla deformata trovo che l’abbassamento massimo δ si ha nella trave centrale e misura 0,0576 m. L’abbassamento deve essere inferiore all’abbassamento massimo ammissibile definito come 1/200 della luce: data la luce di 15 m, δ_max misura 0,075 m e quindi è verificato.

GRATICCIO IN CALCESTRUZZO ARMATO

Progetto il graticcio in calcestruzzo armato per coprire uno spazio di 14x18 m appoggiandolo (tramite incastri) sui lati corti e avendo, quindi, una luce di 18 m. Le travi avranno tutte la stessa sezione poiché non ci sono gerarchie all’interno della struttura.

Al di sopra del graticcio avrò un solo piano occupato quasi interamente da una piccola biblioteca, per cui il sovraccarico accidentale q_a sarà di 5 kN/m² come da normativa (Categoria D2).

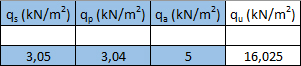
Definisco la stratigrafia di solaio e calcolo con il foglio Excel i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²).

Imposto una combinazione di carico assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali ed ottengo il carico totale q_u (kN/m²) di un piano.

Su Rhino disegno il graticcio con un interasse di 1 m tra le travi in entrambe le direzioni e lo importo su SAP.

Assegno ad ogni nodo dei due lati perimetrali lunghi 14 m il vincolo di incastro e assegno una sezione approssimativa di 30x70 cm a tutte le travi, utilizzando un calcestruzzo di classe C40/50.

In questo modo tengo subito conto, approssimativamente, del peso proprio delle travi che, trattandosi di calcestruzzo armato, è molto rilevante.

Assegno il carico q_u (kN/m²) suddividendolo tra le travi in entrambe le direzioni, quindi moltiplicandolo per 0,25 m per le travi di bordo e per 0,5 m per tutte le altre travi. I carichi distribuiti che avrò saranno, quindi, di 4,00625 kN/m per le travi di bordo e di 8,0125 kN/m per tutte le altre travi.

Avvio l’analisi e mi appare il graticcio nella configurazione deformata.

Osservando il diagramma dei momenti flettenti noto che corrisponde a quello di una trave doppiamente incastrata e dalla tabella degli sforzi trovo che il momento massimo si ha nella trave centrale e, precisamente, in corrispondenza dei due incastri e vale 701,952 kNm.

Sul foglio Excel inserisco il valore del momento flettente trovato per dimensionare correttamente la sezione della trave e, scegliendo un calcestruzzo di classe C40/50 e una base di 30 cm, ottengo un’altezza di 70 cm. È la sezione 30x70 cm usata già nel predimensionamento, è quindi verificata.

Stavolta osservo la deformata e dalla tabella degli spostamenti trovo che l’abbassamento massimo δ si ha nella trave centrale e, precisamente, al centro della campata e misura 0,024 m.

L’abbassamento deve essere inferiore all’abbassamento massimo ammissibile definito come un duecentesimo della luce: data la luce di 18 m, δ_max misura 0,09 m e quindi è verificato.