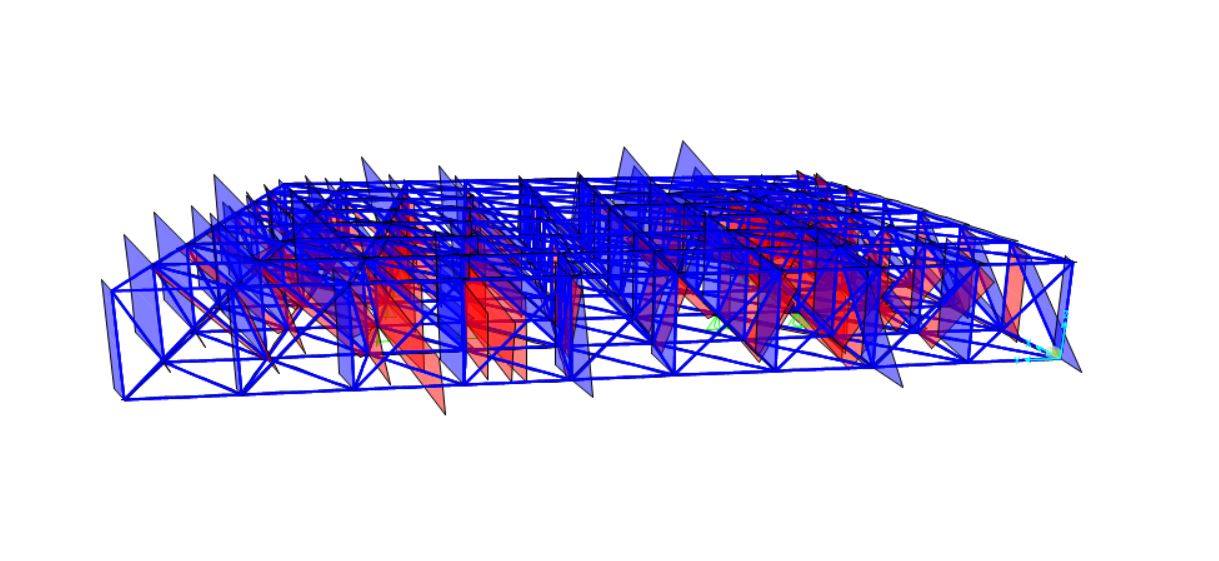
Questa esercitazione ha come scopo il dimensionamento e la verifica ad abbassamento la travatura reticolare spaziale dell’immagine sottostante, delle dimensioni di 27x21x3 metri, alla cui sono stati appesi i solai di 3 piani.
Il primo passo da compiere consiste nel disegno dello schema statico della struttura, in questo caso di modulo 3x3x3 m, su Sap 2000. Una volta disegnata la reticolare è necessario che ad essa vengano aggiunti dei vincoli esterni in corrispondenza dei punti in cui la reticolare è appoggiata. Attraverso i comandi ASSIGN > JOINT >RESTRAINTS sono stati inseriti i 12 appoggi collocati nella parte inferiore della struttura.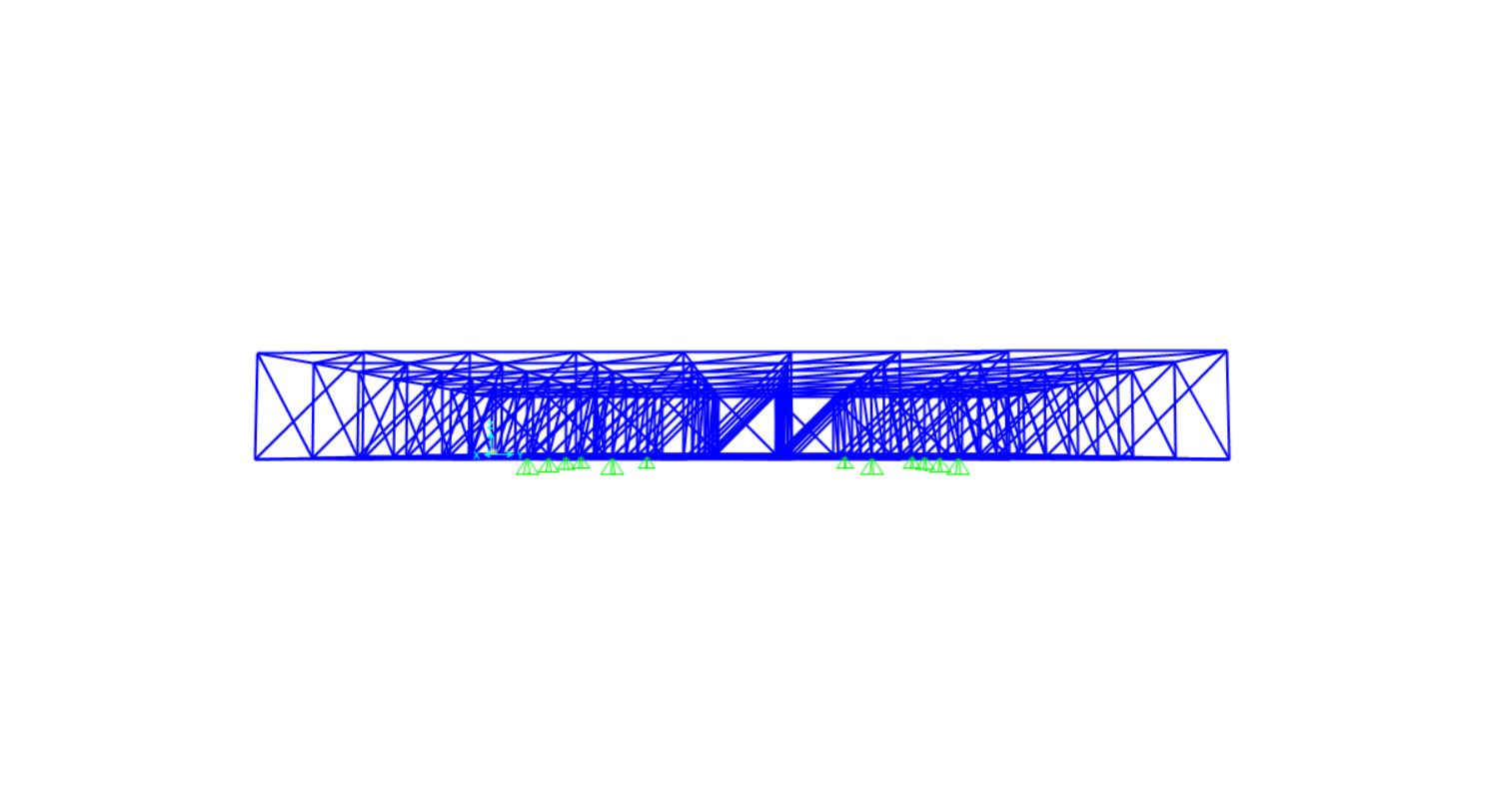
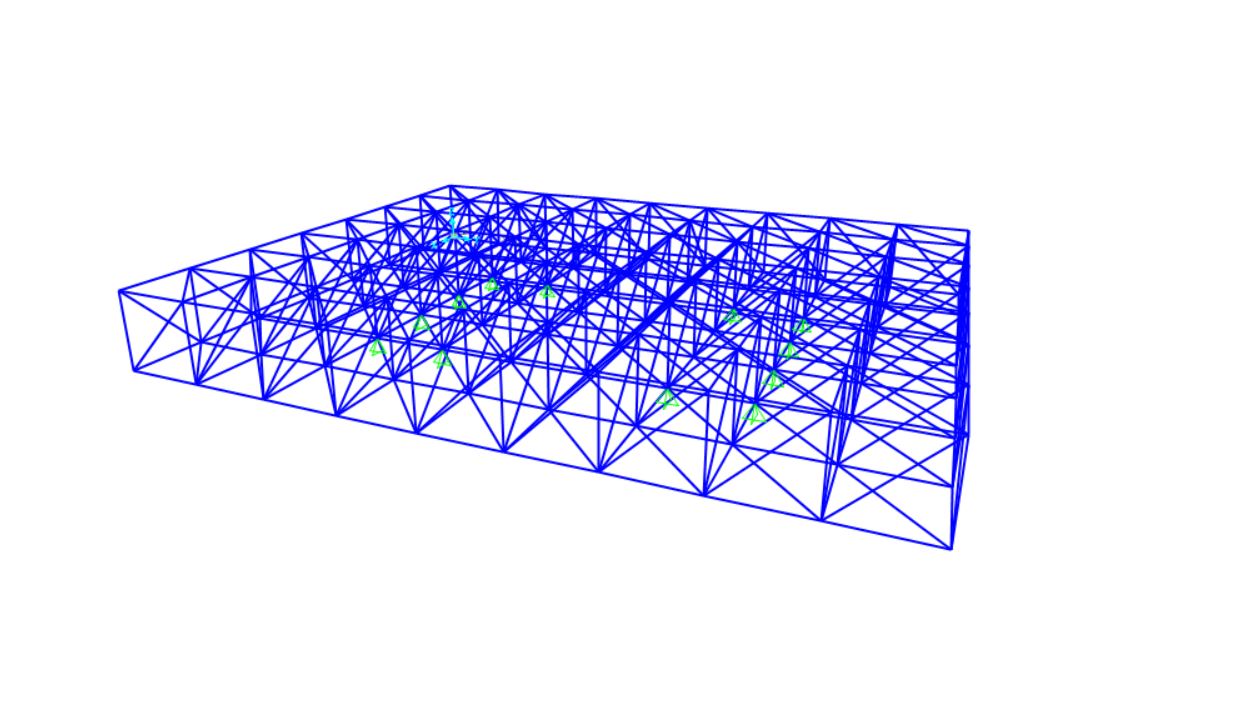
Gli elementi di cui è costituita la trave sono dei tubolari in acciaio S235, a cui è stata assegnata una sezione provvisoria per poter produrre le analisi. Per attribuire ad ogni asta dell’elemento questa sezione è necessario utilizzare i comandi DEFINE>SECTION PROPERTIES>FRAME SECTIONS per scegliere infine la sezione “tubular pipe”.
La travatura così schematizzata considera ogni nodo di connessione tra le aste come incastri mentre è necessario far sì che questi elementi si comportino come cerniere. A questo scopo, utilizzando i comandi ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0, è infatti possibile "rilasciare" il momento e mantenere soltanto le reazioni verticali e orizzontali dei vincoli interni.
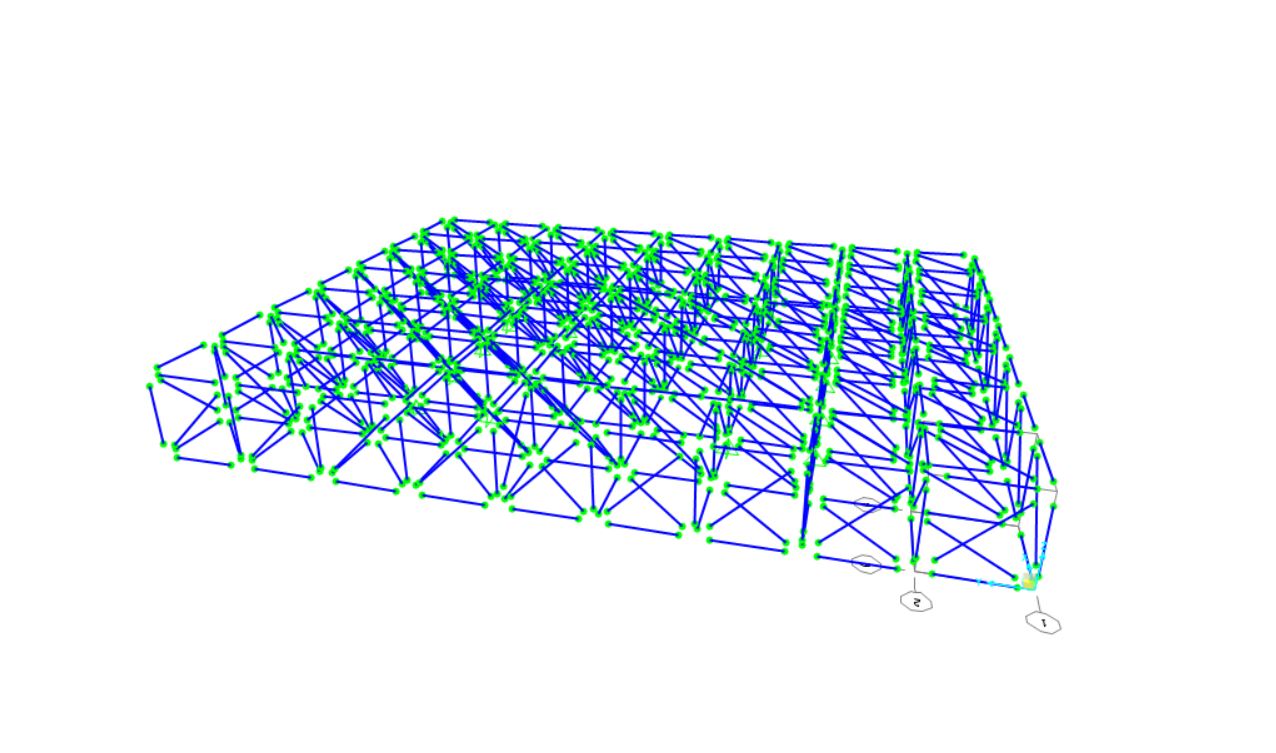
Come sappiamo la struttura reticolare è caratterizzata per essere composta da aste rettilinee, incernierate agli estremi e non soggette a carichi distribuiti lunga la propria lunghezza. Per far ciò, una volta calcolati i carichi distribuiti, si determinano gli equivalenti valori di carico concentrato agente sui soli nodi.
I carichi distribuiti sono la somma di due componenti: il carico dei solai appesi (come calcolato nella precedente esercitazione) e il peso proprio della struttura calcolato tramite Sap200.
Numero piani: 3
Peso proprio piano per mq: 8,72 KN/mq
Mq piano: 576 mq
Peso piano: 576 mq x 8,72 KN/mq = 4944,038 KN
Peso per ogni nodo: (4944,08 KN x 3 piani) / 80n nodi = KN
Per assegnare le forze vengono selezionati i frame da esse interessate e tramite la finestra di dialogo apribile tramite ASSIGN > JOINT LOADS > FORCES, è possibile creare nuove forze con intensità e direzione variabile.
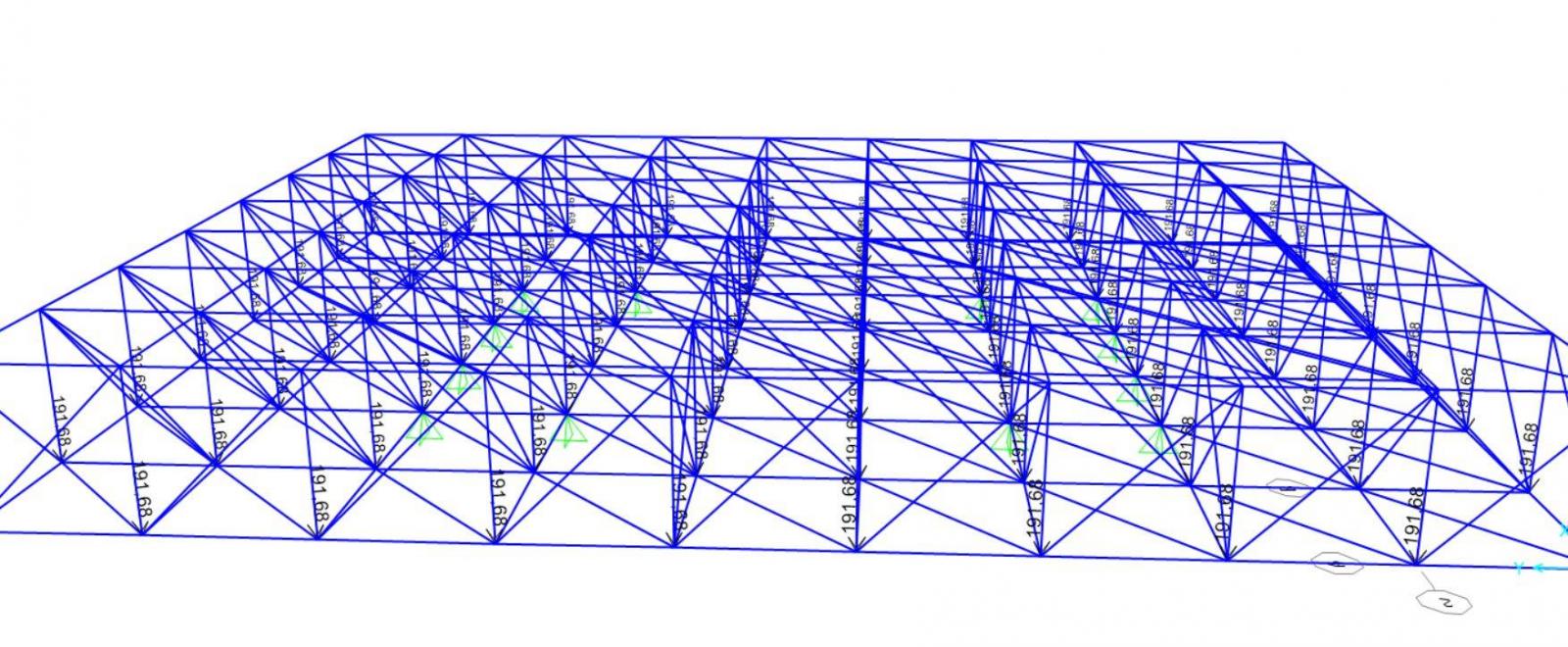
Avviata l'analisi, il programma mostrerà inizialmente l'andamento della deformata. Per far sì che esso fornisca informazioni rispetto l'andamento degli sforzi assiali è possibile utilizzare il comando SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE.
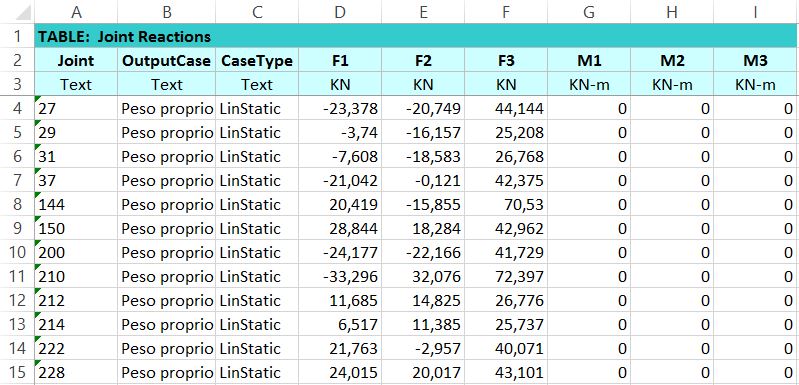
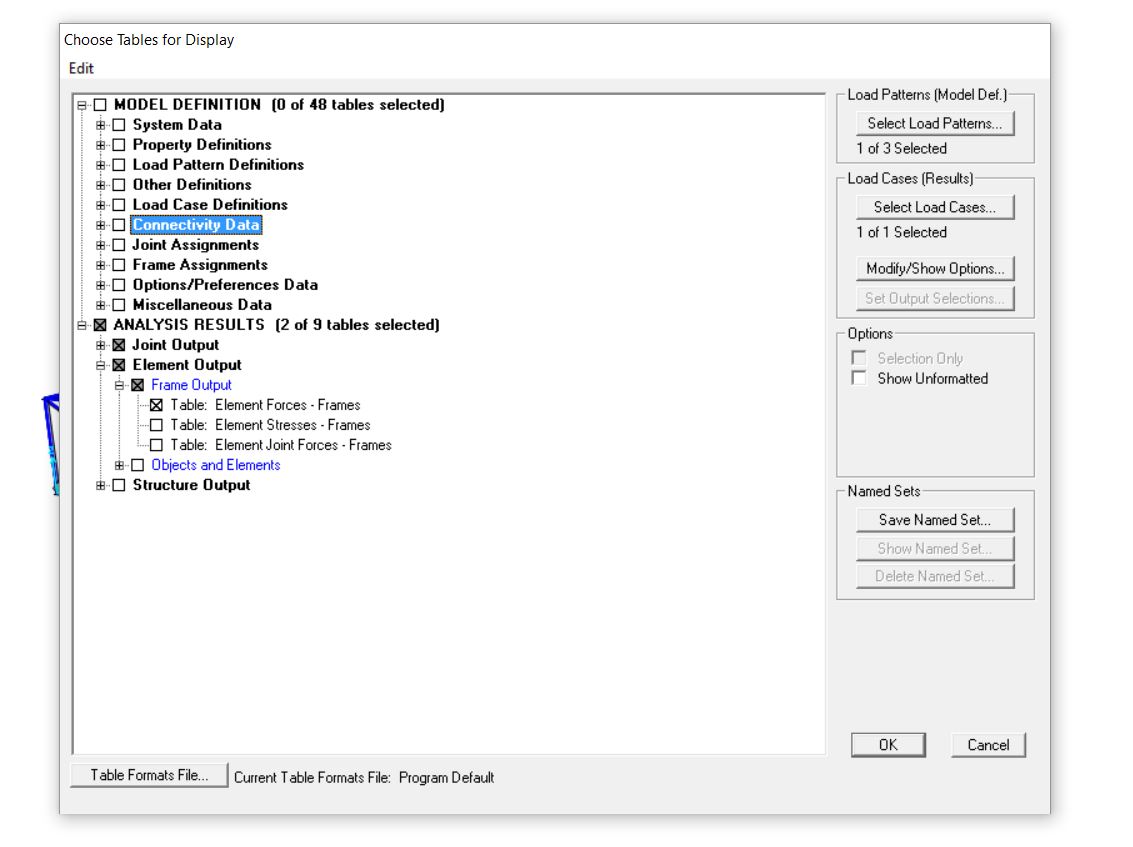
 Cliccando ctrl+T si apre una finestra di dialogo tramite la quale Sap 2000 dà la possibilità di ricavare dall’analisi delle tabelle esportabili in Excel. Aperta la finestra è necessario spuntare sotto ANALYSIS RESULTS le informazioni che si vogliono avere, cliccare su SELECT LOAD PATTERS e selezionare il nome assegnato al proprio carico, successivamente cliccare su SELECT LOAD CASE e anche qui selezionare il nome assegnato al proprio carico e infine dare OK. In ultimo per esportare la tabella una volta aperta, dal menù in alto a destra ELEMENT FORCES à FRAMES.
Cliccando ctrl+T si apre una finestra di dialogo tramite la quale Sap 2000 dà la possibilità di ricavare dall’analisi delle tabelle esportabili in Excel. Aperta la finestra è necessario spuntare sotto ANALYSIS RESULTS le informazioni che si vogliono avere, cliccare su SELECT LOAD PATTERS e selezionare il nome assegnato al proprio carico, successivamente cliccare su SELECT LOAD CASE e anche qui selezionare il nome assegnato al proprio carico e infine dare OK. In ultimo per esportare la tabella una volta aperta, dal menù in alto a destra ELEMENT FORCES à FRAMES.
 A questo punto essendo disponibili sul foglio Excel tutti I valori di sforzo normale su ciascuna asta è possibile dimensionare queste ultime. Questo passaggio differisce se l’asta è soggetta a trazione o a compressione.
A questo punto essendo disponibili sul foglio Excel tutti I valori di sforzo normale su ciascuna asta è possibile dimensionare queste ultime. Questo passaggio differisce se l’asta è soggetta a trazione o a compressione.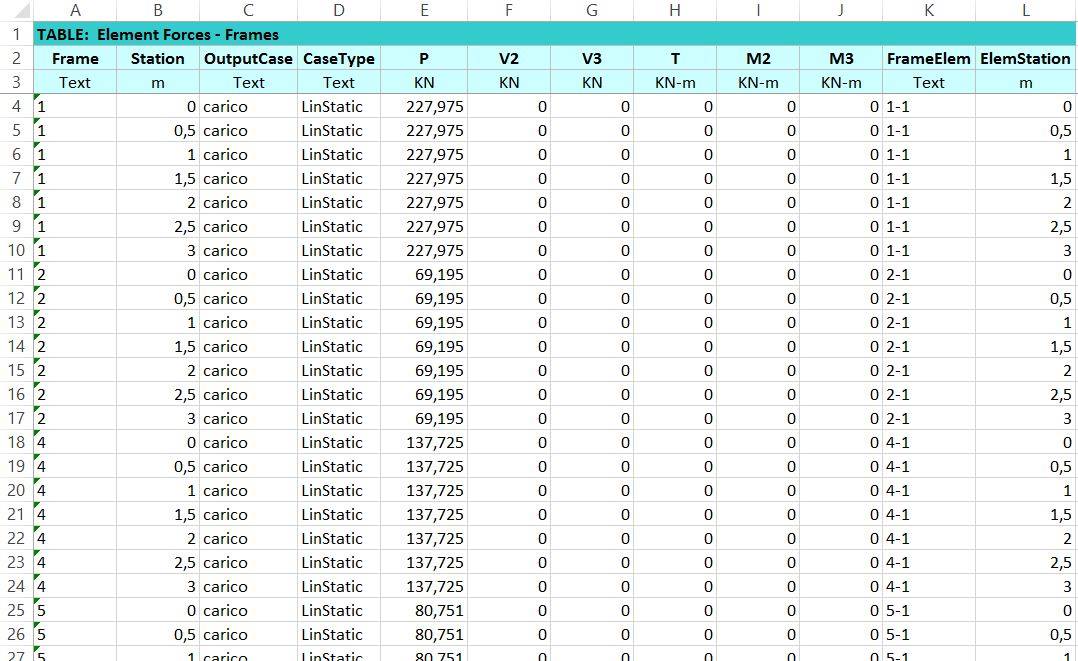
Avendo scelto precedentemente il tipo di acciaio di cui sono composti gli elementi della reticolare si è a conoscenza di alcuni dati quali il modulo di elasticità, la tensione di snervamento, la tensione di rottura ecc., nonché sono disponibili altre informazioni rispetto alla lunghezza degli elementi (3m) e alla tipologia di vincolo (β).
L’area minima dell’asta soggetta a trazione si calcola semplicemente come il rapporto tra la Forza Normale di trazione massima agente e a resistenza di progetto del materiale.
Amin= Nmax/fyd
Per le aste soggette a compressione invece, oltre a calcolare un’area minima resistente con lo stesso procedimento, si deve anche garantire che l’asta non vado incontro a fenomeni di instabilità euleriana.
Oltre a un’area minima si calcola dunque anche la snellezza massima da cui si ricava il giratore di inerzia minimo della sezione tramite il quale si può scegliere l’elemento della reticolare direttamente dal profilario.
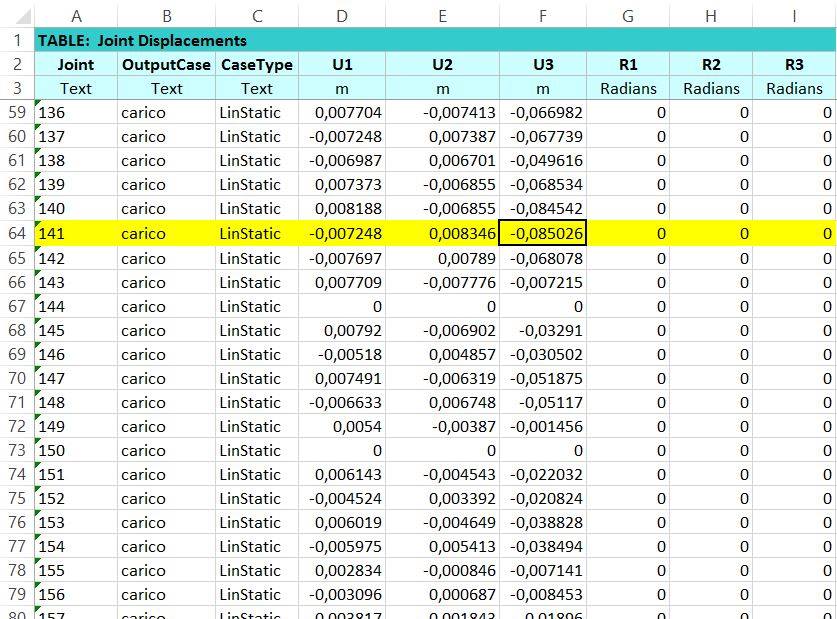
Ultimo passo da compire in Sap consiste nel verificare che l’asta maggiormente deformata non subisca un abbassamento superiore a L/200.
A questo scopo tramite Ctrl+T è possibile aprire la stessa tabella di cui sopra e chiedere al programma delle informazioni rispetto la deformazione di ogni asta. Aperta quindi la tabella vengono spuntati “Joint output”à “Joint displacements” e la tabella ottenuta può essere esportata in Excel, per leggere più facilmente il valore massimo della deformazione. A questo punto quindi si verifica che questo valore sia inferiore a L/200.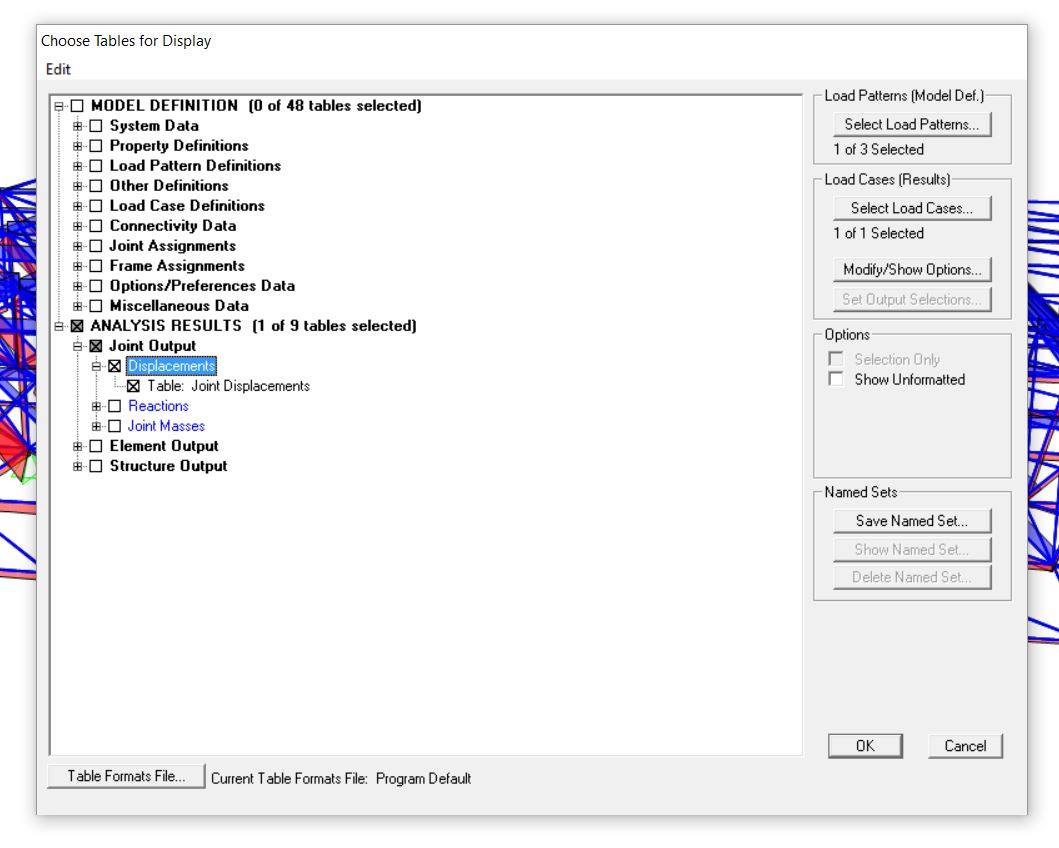
L'esercitazione è stata svolta insieme a Carlotta Contiguglia
Commenti recenti