Portale di Meccanica

TRAVE RETICOLARE SIMMETRICA

 

Le travi reticolari sono composte da aste rettilinee, collegate alle estremità mediante cerniere, soggette solo a sforzo normale.

 

 

STEP 1 VERIFICA DELL'ISOSTATICITA'

 Per verificare se la struttura è isostatica dobbiamo vedere se il numero dei vincoli è uguale al numero dei gradi di libertà della struttura. V sarà uguale alla somma dei vincoli interni più quelli esterni. Quelli esterni sono facili da individuare, sono 3, quelli interni li calcoliamo con una piccola formula: V_i = 2*(n -1) dove n è il numero di aste che arrivano alla cerniera interna.

Per ogni cerniera avremo:

 

A-H     2*(2-1) = 2

B-G     2*(3-1) = 4

C-D-E     2*(4-1) = 6  La somma dei vincoli interni è 30 quindi V= 33.

Ora bisogna confrontare il n. dei vincoli per i gradi di libertà della struttura (numero di aste presenti nella struttura X per il numero di gradi di libertà di ogni elemento)

V= 33 L =33 la struttura è ISOSTATICA!

STEP 2 CALCOLO DELLE REAZIONI VINCOLARI.

Considerando che la struttura è simmetrica le reazioni saranno anch'esse simmetriche.

Equilibrio alla traslazione verticale: V_A + V_B - 60 kN = 0

Va= 30 KN; Vb= 30 KN

STEP 3 CALCOLO DELLE AZIONI DI CONTATTO CON IL METODO DELLE SEZIONI DI RITTER

Calcolo gli sforzi lungo le aste usando il metodo delle sezioni di RITTER. Taglio la struttura in più parti tramite sezioni che prendono un numero di aste che non concorrono nello stesso modo; poi si dovrà vedere se le aste saranno soggette a compressione o trazione ( N>0 TIRANTE), (N<0 PUNTONE)

SEZIONE N 1

Faccio l'equilibrio dei momenti intorno a C

∑M (c) = 0      -30KN X 4m + 20KN X 2m - N₁ X 2m = 0

N₁ = -40 KN (negativo è un PUNTONE)

Per trovare N₃   faccio l'equilibrio intorno a B

∑M(b) = 0     -30KN x 2m + N₃ x 2m =0    N₃ = 30KN (positivo è un TIRANTE)

Per trovare N₂  lo scompongo come se fosse la diagonale di 1 quadrato.

∑y= 0    30KN -20KN - N₂ √2/2 = 0  N₂ = 10√2 KN ( N>0 )

SEZIONE N 2

∑y= 0    N₃ + N₄ √2/2 = 0        30KN + N₄ √2/2= 0   N₄ = -30√2 KN

SEZIONE N 3

∑M(d) = 0         N₆  x 2m + 20KN x 4m - 30KN x 6m = 0     N₆ = 50 KN

Trovo N₅       

∑y =0         30KN- 20KN + N₅ √2/2 = 0       N₅ = -10 √2 KN

disegno tutte le reazioni nelle aste.

STEP 4 ANALISI IN SAP

Una volta impostete le unità di misura (Kn m C) mi apro la trave reticolare del modello predefinito (n campate 3, ampiezza 2 altezza 1).

Definisco il materiale (DEFINE - MATERIAL -ADD NEW MATERIAL) e la geometria ( TUBOLARE) e assegno il materiale appena creato alla nostra struttura.

Ora la carico nei nodi 5 -6- 7 e faccio partire l'analisi.

la sua deformata

e i rispettivi diagrammi N,T,M

TRAVE RETICOLARE ASIMMETRICA

In questo esercizio la trave reticolare è asimmetrica e lo affronteremo, a differenza dell'altro, con il metodo dei nodi.

Come sappiamo una struttura è in  equilibrio se ognuno dei suoi nodi lo è. Facciamo quindi per ciascuno di essi l'equilibrio a traslazione.

Anche qua mi assicuro che la struttura sia isostatica, dopo di che mi trovo le reazioni vincolari.

 Equilibrio alla traslazione orizzontale

U_B - U_G = 0 ------------- U_B = U_G

 Equilibrio alla traslazione verticale

V_B - 2F = 0 -------------- V_B = 2F = 20 kN

- Equilibrio alla rotazione in B

- F*l - F*2l + U_G*l = 0 ----> U_G = 30 kN = U_B

Ora bisogna isolare ogni nodo e calcolarne l'aqeuilibrio.

NODO A

 Equilibrio alla traslazione orizzontale N₁ = 0

 Equilibrio alla traslazione verticale N₂ = 0

NODO B

 orizzontale 30 kN + N₄ + N₃* √2/2 = 0

 verticale 20 kN + N₃* √2/2 = 0 ----> N₃ = -20√2 kN

N₄ = - 10 kN

NODO D

 orizzontale 10 kN + N₆ = 0 ----> N₆ = 10 kN

 verticale N₅ = 0

NODO C

orizzontale 20 kN + N₈ + 10 kN = 0 ----> N₈ = -30 kN

 verticale 20 kN - 10 kN - N₇*√2/2 = 0 ----> N₇ = 10√2 kN

NODO G

orizzontale 10 kN + N₁₁*√2/2 - 10 kN = 0 ----> N₁₁ = 0

 verticale N₉ + 10 kN = 0 ----> N₉ = -10 kN

NODO H

 

orizzontale N₁₀ = - 30 kN

 

disegno tutti gli sforzi assiali per ogni asta, verifico in sap, e ottengo il mio diagramma delle N.

 

ESERCIZIO IN CLASSE

CALCOLO DELLE REAZIONI VINCOLARI:

Primo corpo

∑y=0       ya+yb=0   ya= -yb

∑M(a)=0    -50+yb x 6m    yb= 50/6 = 8,33    quindi  ya= -8,33

Secondo corpo

∑y= 0       -yb+yc=0    yb=-yc

∑M(b)=0    50 + Yc x 6m=0     yc= -8,33  quindi yb= 8,33

verifica in sap....

DIMENSIONAMENTO TRAVE IN CLS, LEGNO ACCIAIO.

PROGETTO A FLESSIONE

L'esercitazione verte nel dimensionare una trave (o travetti) in tre diverse tipologie con l'aiuto del nostro foglio exel.

Tutto ruota intorno alla formula di flessione (che può essere utilizzata come formula di verifica o di progetto)

                       σ = Mx      y

                          -------

                              Ix

 

Dove Mx è il momento flettente che agisce sulla sezione che la fa ruotare intorno all'asse x, Ix è il momento principale di inerzia intorno all'asse x e y è una variabile che varia sulla sezione.

Questa formula ci fa capire come nel materiale arriva la TENSIONE per effetto della flessione, cioè da l'indicazione, data una sezione, dell'andamento della tensione media.

A noi interssa però la σ max= Mx /Wx  dove Wx= Mx/ fd.

Nel momento in cui faccio il progetto di una sezione, impongo che la tensione massima sia proprio il valore che mi ha datola normativa in funzione del materiale che ho scelto.

fd è il valore di progetto della tensione massima del materiale che è legato al valore di crisi (la crisi va distinta da maeriale a materiale). Noi dobbiamo prendere distanza da questa crisi, grazie ai coeficienti di sicurezza che variano da materiale a materiale.

 

Le formule presenti in exel partono da dati ben precisi: LUCE DELLA TRAVE, MATERIALI E CARICHI.

Utilizziamo le formule come equazione. Tutti i dati che inseriamo nel foglio serviranno ad eliminare un'incognita, perchè abbiamo una sola equazione.

Questa incognita per la sezione di legno sarà L'ALTEZZA, per l'acciaio sarà il MODULO DI RESISTENZA A FLESSIONE  e per il cls sarà L'ALTEZZA UTILE.

 

L'impalcato in esame è un'abitazione ad uso residenziale.

ACCIAIO

DIMENSIONAMENTO TRAVETTI:

Luce della campata maggiore: 3,30 m

Interasse: 1 m

 

ANALISI DEI CARICHI: per progettare la sezione dobbiamo definire i carichi.

 

 - VARIABILI

Sovraccarichi accidentali Qa (legati alla funzione dell'edificio)  - un'abitazione ad uso residenziale 2KN/mq

Riporto qui la tabella con le categorie dei tipi di locali previste dalla normativa per la definizione di tali carichi.

 

 

- PERMANENTI

Sovraccarichi di natura permanente: Qp ( carico esercitato sulla struttura dal peso degli elementi costruttivi fissi all'interno del solaio)

                                     - pavimento in gres porcellanato 0,2 KN/mq

                                        - massetto 0,64 KN/mq

                                        - isolante 0,00072 KN/mq

                                        -  incidenza impianti che è 0,50KN/mq

                                        - incidenza tramezzi 1KN/mq

 

Pesi propri delle sturtture: Qs (peso proprio della struttura)  - soletta e la lamiera grecata (10 cm)1,86KN/mq

 

 

 

 

Per trovarmi il carico totale al metro lineare farò: Qa + Qp + Qs x 1 m = 6,21 KN/mq

 

Utilizzo il foglio excel per trovarmi Wx ovvero il modulo di resistenza che mi indicherà il tipo di profilo da utilizzare per i miei travetti.

 

 

Wx = 37,77 cm ³

 

 

N.B. Nel foglio exel c'è una differenza tra caselle azzurre e bianche. In quelle azzurre dobbiamo NOI mettere i dati, mentre le bianche ci danno il risultato. La colonna E ci da il risultato del Q totale, ottenuto moltiplicando la somma di Qa + Qs + e Qp per l'interasse, per trasformare il carico al mq in carico lineare. Nella colonna G compare il nostro momento massimo (per la trave appoggiata ql / 8, ma si può sempre cambiare la formula). Nella colonna H troviamo la classe di snervamento dell'acciaio che abbiamo scelto. Colonna I c'è il valore di progetto Fd.

 

 

 

Secondo la tabella devo utilizzare una IPE 120 con un peso di 0,104 KN/mq. Ora devo verificare che il modulo di resistenza che viene, sommando il Q con il peso dell'ipe, non sia superiore al modulo di resistenza dell'ipe stessa.

 

0,104 KN/mq + 6,21 KN/mq = 6,314 → Wx = 38,40 ‹ 52,96 LA VERIFICA è SODDISFATTA!

 

DIMENSIONAMENTO TRAVE PRINCIPALE:

 

 

Luce: 3,40 m

Interasse: 2,90 m

Qa: 2 KN/mq

Qs: 1,964 KN/mq (1,86 + 0,104 KN/mq)

Qp: 2,3472 KN/mq

 

Wx= 118,17 cm³ → IPE 180 che pesa 18,8 kg/m

 

Q + 0,188KN/mq = → Wx = 119,12 m³ < 146,3 m³ LA VERIFICA è SODDISFATTA

 

LEGNO

 

DIMENSIONAMENTO TRAVETTI:

 

Luce : 3,30 m

 

Interasse: 0,5 m

 

Qa: 2 KN/mq

 

Qs: tavolato: 350 kg/m³ (legno forte) x 0,035 m (spessore) = 12,25 kg/mq → 0,1225 KN/mq

 

Qp: pavimento (cotto 28 kg/mq) 0,28KN/mq; massetto (1800kg/mc x 0,05 m) 0,9KN/mq; impianti 0,50KN/mq e incidenza tramezzi: tramezzo 8 cm, intonaco 1 cm; peso specifico laterizio 800 kg/mc x 0,08m = 0,64KN/mq – peso specifico intonaco 2000 kg/mc x 0,01m = 0,2 x2 (intonaco da entrambe le parti del tramezzo) = 0,4 KN/mq

 

TOTALE TRAMEZZI: 0,64KN/mq + 0,4 KN/mq x H (altezza) / i (interasse) = 1,07 KN/mq

 

Qa + Qs + Qp = 2,32KN/mq

 

Inserisco i dati nel foglio excel e ipotizzo la base del mio travetto di 10 cm, otterrò un h di 15,13cm.

L'altezza che ho ottenuto la più piccola altezza della sezione della trave.

Quindi scelgo una sezione di 10x16 e un legno GL24h. Ora devo aggiungere il peso del travetto al Q e verificare che la nuova altezza risulti entro i limiti di quella ipotizzata.

 

Il legno GL 24h ha una massa volumica di 380Kg/m³, quindi per un travetto di 10x16cm avrò:

3,8KN/mc x 0,1m x 0,16m x 1m = 0,060KN/m x 2 (perchè in un metro ci sono due travetti) = 0,12 KN/m

Sommando il peso del travetto al Q iniziale ottengo un h di 15,52 che è < di 16 quindi la VERIFICA è SODDISFATTA!!

 

 

N.B nel valore di progetto del legno troviamo un coefficiente moltiplicativo Kmod ,che tiene conto dello scorrere del tempo,(molto basso tipo 0,7-0,6 0,5) in funzione della durata del carico. Se il carico in cui staimo facendo la verifica è permanente, stiamo ammettendo che quel legno deve durare 40-50 anni.

 

Fd = Kmod  Fk/ γ m → Kmod e γ m hanno lo stesso effetto: γ m essendo > 1 e stando al denominatore DIMINUISCE la resistenza, Kmod stando al numeratore e < 1 DIMINUISCE anch'esso la resistenza. Quindi Fk (che è il valore di crisi) viene abbattuto due volte.

 

DIMENSIONAMENTO TRAVE PRINCIPALE:

 

Luce: 3,40 m

 

Interasse: 2,9 m

 

Qa: 2KN/mq

Qp: 2,75 KN/mq

Qs: 0,1225 KN/m + 0,12KN/m = 0,2425KN/mq

 

Dal foglio excel, ipotizzando una base di 25 cm ho un h di 28,02 cm. Scelgo quindi una sezione di 20x30cm

Il legno GL 28h ha una massa volumica di 410 kg/m³. Mi calcolo il suo peso: 4,1KN/mc x 0,2m x 0,3m x 1m = 0,246 KN che vado a sommare a Q. Di seguito avrò la nuova h che è di 28,26cm < a 30 cm. LA VERIFICA è SODDISFATTA.!!

 

 

ES 1. Calcolo struttura reticolare simmetrica con il metodo delle sezioni di Ritter 

Ci troviamo di fronte ad una struttura reticolare, una struttura formata da elementi lineari, collegati da cerniere, soggetti a solo sforzo normale.

Passo 1

Per prima cosa dobbiamo verificare se la struttura è isostatica. Per fare ciò dobbiamo vedere se il numero dei vincoli è uguale al numero dei gradi di libertà della struttura.

Il numero di gradi di libertà è dato dal numero di aste presenti nella struttura moltiplicato per il numero di gradi di libertà di ogni elemento.

l = 11 (aste) x3 (gradi di libertà) =33

Il numero dei vincoli è dato dalla somma dei vincoli interni e esterni.

V = V_e + V_i

I vincoli esterni sono 3: la cerniera blocca 2 gradi di libertà, il carrello blocca la traslazione verticale perciò un grado di libertà.

Per calcolare i vincoli interni utilizziamo la formula: V_i = 2*(n -1) dove n è il numero di aste che arrivano alla cerniera interna. Calcoliamo perciò il contributo di ogni cerniera:

A-H --> 2*(2-1) = 2

B-G --> 2*(3-1) = 4

C-D-E --> 2*(4-1) = 6

La sommatoria dei vincoli interni sarà perciò: V_i = 2+2+4+4+6+6+6 = 30, che sommata ai vincoli esterni V_e = 3 dà V = 33

Perciò: V(33) = l(33) VERIFICATO!

Bene, ora abbiamo verificato l' isostaticità della struttura, passiamo al calcolo delle reazioni vincolari:

Passo 2

Equilibrio alla traslazione orizzontale: U_A = 0

Equilibrio alla traslazione verticale: V_A + V_B - 60 kN = 0

Essendo simmetrica la struttura: V_A = V_B = 30 kN

Passo 3: Metodo delle sezioni di Ritter

A questo punto utilizzando il metodo delle sezioni di Ritter calcoliamo gli sforzi assiali nelle singole aste.

Faccio l' equilibrio alla rotazione nel nodo C: -120 kNm + 40 kNm - 2N₁ = 0 ----> N₁ = -40 kN

 

Equilibrio alla rotazione in B: -30 kN * 2 m + 2m * N₃ = 0 ----> N₃ = 30 kN

Per calcolare N₂ faccio l' equilibrio alla traslazione verticale considerando la componente verticale di N₂:

30 kN - 20 kN - N₂ * radice2/2 = 0 -----> N₂ = 14,14 kN

Passiamo ora alla sezione n° 2:

Faccio l' equilibrio alla traslazione orizzontale per calcolare N₄:

30 kN + radice2/2 N₄ = 0 ----> N₄ = -42,4 kN

Faccio l' equilibrio alla rotazione in D: N₅*2m + 20 kN*4m - 30 kN*6m = 0 -----> N₅ = 50 kN

Faccio ora l' equilibrio alla traslazione verticale per calcolare la reazione restante N₆:

30 kN - 20 kN + radice2/2*N₆ = 0 ----> N₆ = - 14,14 kN

Sfruttando le proprietà della simmetria riesco a disegnare tutte le reazioni nelle aste:

A questo punto posso verificare i risultati trovati tramite il software SAP2000:

- disegno la struttura

- assegno i carichi

- avvio l' analisi della struttura

Diagramma dello sforzo assiale:

 

ES 2. Calcolo struttura reticolare asimmetrica con il metodo dei nodi

In questo esercizio ci troviamo di fronte ad una struttura reticolare asimmetrica.

Come fatto per l' esercizio precedente prima di tutto dobbiamo verificare che la struttura sia isostatica:

Passo 1

Per verificare l' isostaticità dobbiamo vedere se il numero dei vincoli (esterni e interni) e quello dei gradi di libertà è uguale:

V = l

Il numero di gradi di libertà è dato dal prodoto del numero delle aste per i gradi di libertà di ogni elemento:

l = 11 (aste) x3 (gradi di libertà) =33

Il numero di vincoli è dato dalla somma dei vincoli interni e esterni:

I vincoli esterni sono una cerniera, che blocca 2 gradi di libertà, e un carrello che blocca 1 gdl.

V_e = 3

Calcoliamo i vincoli interni con la formula: V_i = 2*(n -1) dove n è il numero di aste che arriva alla cerniera:

A-G = 2(2-1) = 2

B-D-E = 2(3-1) = 4

F = 2(4-1) = 6

C = 2(5-1) = 8

Avrò percio V_i = 30 che sommato al contributo di V_e da V = 33 = l VERIFICATO!

Passo 2

Calcolo ora le reazioni vincolari con l' equilibrio alla traslazione e alla rotazione:

Sostituisco i vincoli con le loro reazioni e imposto le equazioni di equilibrio:

- Equilibrio alla traslazione orizzontale

U_B - U_G = 0 ----> U_B = U_G

- Equilibrio alla traslazione verticale

V_B - 2F = 0 ----> V_B = 2F = 20 kN

- Equilibrio alla rotazione in B

- F*l - F*2l + U_G*l = 0 ----> U_G = 30 kN = U_B

Disegno ora la struttura equilibrata:

 

Passo 3

Calcolo ora le azioni di contatto con il metodo dei nodi. Isoliamo cioè ogni nodo e calcoliamo l' equilibrio:

Nodo A

- Equilibrio alla traslazione orizzontale N₁ = 0

- Equilibrio alla traslazione verticale N₂ = 0

Nodo B

- Eq. trasl. orizzontale 30 kN + N₄ + N₃* √2/2 = 0

- Eq. trasl. verticale 20 kN + N₃* √2/2 = 0 ----> N₃ = -20√2 kN

N₄ = - 10 kN

Nodo D

- Eq. trasl. orizzontale 10 kN + N₆ = 0 ----> N₆ = 10 kN

- Eq. trasl. verticale N₅ = 0

Nodo C

- Eq. trasl. orizzontale 20 kN + N₈ + 10 kN = 0 ----> N₈ = -30 kN

- Eq. trasl. verticale 20 kN - 10 kN - N₇*√2/2 = 0 ----> N₇ = 10√2 kN

Nodo F

- Eq. trasl. orizzontale 10 kN + N₁₁*√2/2 - 10 kN = 0 ----> N₁₁ = 0

- Eq. trasl. verticale N₉ + 10 kN = 0 ----> N₉ = -10 kN

Nodo G

- Eq. trasl. orizzontale N₁₀ = - 30 kN

Posso disegnare ora la struttura con gli sforzi assiali di ogni asta:

Possiamo notare come alcune aste nella struttura sono scariche.

Passo 4

A questo punto verifico se i calcoli sono giusti tramite SAP2000:

Reazioni vincolari.

Diagramma sforzo assiale.

 

ES 3. Dimensionamento trave (Legno,Acciaio,Calcestruzzo)

INTRO.

In questo esercizio andiamo a dimensionare la trave sottoposta a maggior carico dell' impalcato dell' edificio ad uso residenziale progettato nel Laboratorio di Progettazione 1.

 

 

Consideriamo la trave 2-3 nell' allineamento B. La trave ha una luce di 5 m e porta il carico di un' area di influenza di 3 m di interasse.

Primo passo nel dimensionamento della trave è l' analisi dei carichi che gravano sulla trave stessa. I carichi vengono classificati in 3 categorie:

- carichi strutturali permanenti (qs) : considera il peso proprio degli elementi strutturali permanenti come travi e travetti

- carichi non strutturali permanenti (qp) : considera il peso proprio degli elementi non strutturali che compongono il pacchetto solaio come massetti, pavimenti, impianti...

- carichi accidentali (qa) : è legato alla funzione dell' edificio in quanto considera la variazione dei carichi mobili all' interno dell' edificio come persone mobili, ma anche l' azione del vento, della neve...

Andiamo ora ad analizzare i carichi e dimensionare la trave per le tre tecnologie prese in considerazione: legno, acciaio calcestruzzo.

SOLAIO IN LEGNO

Consideriamo il seguente pacchetto di solaio:

PROGETTO DEL TRAVETTO

1.Carico strutturale(qs): -assito in legno P = volume x peso specifico = (0,035 m x 1 m x 1 m ) x 6 kN/mc = 0,21 kN/mq

2.Sovraccarico permanente(qp): -Sottofondo 0,54 kN/mq

-Isolante fibra di legno 0,072 kN/mq

-Caldana 0,28 kN/mq

-Impianti 0,5 kN/mq

-Tramezzi 1 kN/mq

qp = 0,54 + 0,072 + 0,28 + 0,5 + 1 = 2,33 kN/mq

3.Carichi accidentali(qa): - per civile abitazione 2 kN/mq

CARICO TOTALE

Q = ( qs + qp + qa ) x interasse = ( 0,21 kN/mq + 2,33 kN/mq + 2 kN/mq ) x 1 m = 4,54 kN/m

A questo punto scegliamo la classe di resistenza del legno per i travetti:

scelgo la classe GL24h con resistenza caratteristica a flessione di 24 N/mmq.

Per trovare la resistenza di progetto farò:

fD = Kmod x fk / γ_m = 0,5 x 24 N/mmq / 1,45 = 8,27 N/mmq

dove Kmod è un coefficiente correttivo che tiene conto dell' effetto, sui parametri di resistenza, sia della durata del carico sia dell' umidità della struttura.

Ora considerando il modello di una trave doppiamente appoggiata inserisco i dati nel foglio Excell:

--> TRAVETTO IN LEGNO GL24h 10X20 cm

PROGETTO TRAVE

Applico lo stesso procedimento per il dimensionamento della trave principale:

1.Carico strutturale(qs): -assito in legno P = volume x peso specifico = (0,035 m x 1 m x 1 m ) x 6 kN/mc = 0,21 kN/mq

-peso travetto (0,1 x 0,2 x 1) x 6 kN/mc = 0,12 kN/mq

2.Sovraccarico permanente(qp): qp = 0,54 + 0,0072 + 0,28 + 0,5 + 1 = 2,33 kN/mq

3.Carichi accidentali(qa): - per civile abitazione 2 kN/mq

CARICO TOTALE LINEARE: Q = (qs + qp + qa) x i = (0,32 + 2,33 + 2) x 3 m = 13,95 kN/m

Inserisco ora i dati nel foglio excell:

--> TRAVE IN LEGNO GL28h 20x40 cm

Verifico il dimensionamento aggiungendo il peso proprio della trave principale:

q_trave al metro lineare = (0,2 m x 0,4 m x 6 kN/mc) = 0,48 kN/m

q_trave al metro quadro = 0,48 kN/mq / 3 m = 0,16 kN/mq

qs = 0,32 kN/mq + 0,16 kN/mq = 0,48 kN/mq

La trave è verificata!

 

SOLAIO IN ACCIAIO

Consideriamo ora un solaio il lamiera grecata con travetti in acciaio:

 

PROGETTO DEL TRAVETTO

1.Carico strutturale(qs):

Il carico della lamiera grecata e del getto in cls è un valore tabellato. Ho scelto la lamiera A75/P570 con un carico di 2,50 kN/mq

2.Sovraccarico permanente(qp): -Pavimento in gres porcellanato 1 kN/mq

-Massetto 0,64 kN/mq

-Isolante fibra di legno 0,072 kN/mq

-Impianti 0,5 kN/mq

-Tramezzi 1 kN/mq

qp = 1 + 0,64 + 0,072 + 0,5 + 1 = 3,15 kN/mq

3.Carichi accidentali(qa): - per civile abitazione 2 kN/mq

CARICO TOTALE

Q = ( qs + qp + qa ) x interasse = ( 2,5 kN/mq + 3,15 kN/mq + 2 kN/mq ) x 1 m = 7,65 kN/m

A questo punto scelgo la classe di resistenza dell' acciaio dei travetti: S275.

La resistenza a flessione di progetto si ottiene dividendo il valore della resistenza caratteristica per il coefficiente di sicurezza

fy,K /1,05 = 275/1,05 = 261,9 N/mmq

Ora inserisco i valori trovati nel foglio di excel:

Nel caso dell' acciaio il foglio excel non ci dà l' altezza della trave ma il modulo di resistenza(Wx) minimo che la trave deve avere. A questo punto vado sul profilario e scelgo un profilo che abbia un modulo di resistenza maggiore di quello trovato a favore di sicurezza.

Scelgo il profilo IPE100 S275 con Wx = 34,2 cm³

PROGETTO DELLA TRAVE

Applico lo stesso procedimento per il dimensionamento della trave principale:

1.Carico strutturale(qs): -carico soletta 2,5 kN/mq

-peso travetto 0,08 kN/mq

2.Sovraccarico permanente(qp): qp = 1 + 0,64 + 0,0072 + 0,5 + 1 = 3,15 kN/mq

3.Carichi accidentali(qa): - per civile abitazione 2 kN/mq

CARICO TOTALE LINEARE: Q = (qs + qp + qa) x i = (2,58 + 3,15 + 2) x 3 m = 23,19 kN/m

Inserisco ora i dati nel foglio excel:

Scelgo la trave IPE240 S275 con Wx = 324 cm³

Verifico il dimensionamento aggiungendo il peso proprio della trave principale:

q_trave al metro lineare = 0,22 kN/m

q_trave al metro quadro = 0,22 kN/m/3 m = 0,073 kN/mq

qs = 2,58 kN/mq + 0,073 kN/mq = 2,65 kN/mq

Aggiungendo il carico della trave il Wx minimo rimane sotto i 324 cm³ della sezione scelta quindi la trave è VERIFICATA!

 

SOLAIO IN LATEROCEMENTO

Consideriamo ora un solaio in laterocemento con pignatte e travetti in cls:

ANALISI DEI CARICHI

1.Carico strutturale(qs): - pignatte 12 cm + caldana 4 cm = 2,36 kN/mq (valore tabellato)

 

2.Sovraccarico permanente(qp): -Pavimento parquet 0,18 kN/mq

-Massetto 0,64 kN/mq

-Isolante acustico 0,64 kN/mq

-Intonaco 0,3 kN/mq

-Impianti 0,5 kN/mq

-Tramezzi 1 kN/mq

qp = 0,18 + 0,64 + 0,64 + 0,3 + 0,5 + 1 = 3,26 kN/mq

3.Carichi accidentali(qa): - per civile abitazione 2 kN/mq

CARICO TOTALE

Q = ( qs + qp + qa ) x interasse = ( 2,36 kN/mq + 3,26 kN/mq + 2 kN/mq ) x 1 m = 7,62 kN/m

A questo punto scelgo la classe di resistenza dell' acciaio per barre da cemento armato. Posso scegliere tra due classi: la B450A e la B450C. Entrambe hanno lo stesso valore di tensione allo snervamento di 450 Mpa. Scelgo la B450C che essendo più duttile, viene utilizzata in zona sismica. Il coefficiente di sicurezza per barre da cemento armato è 1,15 e non 1,05 come nell' acciaio da carpenteria.

fy,K /1,15 = 450/1,15 = 391,3 N/mmq

Una volta scelto il tipo di acciaio scelgo il calcestruzzo e calcolo la tensione di progetto:

Le classi di resistenza del calcestruzzo vanno da C8/10 a C90/105, scelgo la classe C40/50 dove il primo numero rappresenta la resistenza cilindrica caratteristica (Fck) e il secondo la resistenza cubica caratteristica (Rck).

La tensione di progetto è data dalla formula:

Fcd = a_cc*Fck / g_C

dove : a_cc è il coefficiente riduttivo per le resistenze di lunga durata pari a 0,85;

g_C è l coefficiente di sicurezza relativo al calcestruzzo pari a 1,5;

Perciò:

Fcd = 0,85 x 40 / 1,5 = 22,6 N/mmq

A questo punto inserisco i dati all' interno del foglio excel:

Dal foglio elettronico ricavo una trave 20x35 cm.

Ora faccio la verifica della trave scelta: per fare ciò aggiungo al valore dei carichi quello proprio della trave:

q_trave al metro lineare = 1,61 kN/m

q_trave al mq = 1,61/3 = 0,54 kN/mq

qs = qs + q_trave = 2,36 + 0,54 kN/mq = 2,9 kN/mq

Dalla verifica viene fuori un hu della trave di 28,21 cm che sommata ai 5 cm da un' altezza minima di 33,2 cm al di sotto dei 35 cm della trave scelta.

VERIFICATA!

 

ES 4. STRUTTURA RETICOLARE SPAZIALE

Per prima cosa disegno la struttura reticolare spaziale su AUTOCAD:

Apriamo un nuovo file e creiamo un nuovo layer "aste" poichè se disegnassi con il layer 0 poi SAP non lo riconoscerebbe.

Disegno aste di 2 m con il comando polilineae assegno come origine il punto (0,0) della struttura.

Ora utilizzo il comando array andando ad impostare i valori della serie rettangolare con 1 riga e 4 colonne a distanza di 2 m. Infine chiudo la serie con un asta verticale.

Ora effettuo una rotazione 3d (comando Ruota3D) e passo alla visualizzazione isometrica trdimensionale.

A questo punto cambio l' UCS in modo da disegnare le aste sul piano y-z facendo attenzione a disegnare sempre un modulo aperto in modo tale da non sovrepporre alcun asta.

Utilizzo di nuovo il comando array per duplicare il modulo lungo l' asse x ad una distanza di 2m.

Utilizzo ancora una volta il comando array per moltiplicare la struttura disegnata fino a ora. Imposto nella serie rettangolare 1 riga e 7 colonne alla distanza di 2m lungo l' asse y. Infine calcello l' ultima colonna per ottenere una struttura reticolare spaziale composta da 4 moduli lungo l' asse x e 6 moduli lungo l' asse y.

Salvo in AutoCAD 2000/LT2000 DXF per poi importare il file su SAP2000.

CALCOLO DELLA STRUTTURA IN SAP2000

Importo il file disegnato con Autocad su SAP ricordando di impostare come unità di misura KN,m,C.

A questo punto assegno i vincoli ai 4 angoli inferiori della struttura. Assegna->Nodo->Vincoli Esterni

Ora seleziono tutta la struttura e rilascio i momenti, in modo che le aste lavorino solo a sforzo normale. Assegna->Frame->Rilasci, e spunto il momento 22 e 33 sia all' inizio che alla fine.

Definisco il materiale della struttura per poi assegnarlo a tutte le aste. Definisci->Materiali->Nuovo materiale->seleziono steel e lo chiamo ACCIAIO.

Ora vado ad assegnare all’acciaio un sezione tubolare, quindi vado su Definisci->Proprietà Sezione->Aggiungi Nuova Proprietà e su Proprietà Tipo Sezione Frame seleziono l’acciaio e gli assegno la sezione tubolare, poi come materiale gli assegno “acciaio” cioè il materiale che ho creato in precedenza.

Assegno la sezione tubolare a tutte le aste tramite Assegna->Frame->Sezioni Frame e seleziono FSEC1 creata precedentemente.

Sulle aste vedrò comparire il nome della sezione assegnata.

Ora vado a definire il carico concentrato che assegnerò sui nodi superiori della struttura. Definisci->Schemi di carico e creo un nuovo carico che chiamerò "forza concentrata". N.B. Devo ricordare di assegnare al nuovo carico 0 come "Peso Proprio Moltiplic."

Ora seleziono tutti i nodi superiori della struttura e assegno il carico. Devo fare attenzione a selezionare solo i nodi superiori della struttura perciò nelle "Opzioni di Visualizzazione" nella colonna "Nodi" deseleziono "Invisibile" e nella colonna "Frame" seleziono "Frame non in vista".

In questo modo SAP mi fa vedere solo i nodi che andrò a selezionare.

Mi assicuro di aver selezionato solo i nodi superiori passando alla visualizzazione del piano x-z.

PERFETTO! Assegno il carico precedentemente creato alla selezione. Caricherò la struttura con una forza concentrata di 40 KN.

Riaccendo le aste e visualizzo le forze concentrate nei nodi.

Posso finalmente lanciare l' analisi. Seleziono DEAD e MODAL e clicco "Non eseguire caso".

L' analisi mi fa visualizzare la deformata della struttura:

Per visualizzare il valore dello sforzo assiale su ogni asta faccio: Mostra sollecitazioni->Tensioni Frame->Sforzo assiale.

Ora devo individuare le aste con maggiore sforzo assiale sia di compressione che di trazione. Vado perciò su

Visualizza->Mostra Tabelle e in "Risultati Analisi" seleziono "Output Elemento".

Nella tabella scelgo l' asta con il maggior sforzo di compressione (-385,631 KN):

E l' asta con maggior sforzo di trazione (263,469 KN):

 

PROGETTO DELLE ASTE

-Progetto a compressione

Devo innanzitutto scegliere il tipo di acciaio con cui realizzerò le aste. Scelgo un S275 con tensione di snervamento di 275 MPa.

Sapendo che σ = fD = N/A posso ricavare l' area minima necessaria. Applico perciò la relazione:

A = N/fD dove fD è la tensione di design.

La tensione di progetto si ricava dalla formula: fD = fy/ϒm = 275/1,05 = 261,90 MPa

,dove fy è la tensione caratteristica di snervamento e ϒm è il coefficiente di sicurezza per acciaio da carpenteria pari a 1,05.

A = Nmax(compressione)/fD = 385631 N/261,9 N/mm² = 1472,436 mm² = 14,72 cm²

Ora prendo il profilario e scelgo una sezione che abbia un ' area maggiore di quella trovata:

Scelgo un tubolare con diametro di 11,43 cm e spessore di 4,5 mm con area di 15,5 cm².

 

-Progetto a trazione

Applico la stessa formula per il progetto a trazione, mantenedo il tipo di acciaio che ho scelto per le aste compresse:

A = Nmax(trazione)/fD = 263469 N/261,9 N/mm² = 1006 mm² = 10,06 cm²

Scelgo un tubolare con diametro di 8,89 cm e spessore di 4 mm e area di 10,7 cm².

VERIFICA SNELLEZZA

Nell’asta soggetta a compressione, inoltre, occorre verificare che l’asta non sia troppo snellaper non incorrere in uno sbandamento laterale. Attraverso la formula di Eulero posso calcolarmi il valore del carico critico per cui si innesca il fenomeno dello sbandamento:

• Se Nmax ≥ Pcrit → Asta instabile
• Se Nmax < Pcrit → Asta stabile

Pcrit = (∏² * E * Jmin) / l₀² dove: E = modulo elastico dell' acciaio

Jmin = momento d’inerzia minore

l₀ = lunghezza libera d' inflessione, che dipende dalla luce e dalla condizione di vincolo Nel nostro caso i vincoli sono costituiti solo da cerniere per cui l₀ = l, dove l è la lunghezza dell’asta quindi pari a 2,828m (poiché l’asta soggetta a massimo sforzo di compressione è una delle aste inclinate)

 

Pcrit = (3,14² * 210000N/mm² * 2340000 mm⁴) / 2828² mm = 605808N = 605,808 KN

 

Nmax = 385,631KN < Pcrit = 605,808 KN → la sezione è verificata.

 

 

ES 5. RIPARTIZIONE FORZE SISMICHE

 

Esercitazione trave reticolare 2d- Metodo delle sezioni di Ritter-

 

Nel modello di travatura reticolare consideriamo le aste soggette solo a sforzo normale, e non a momento e a taglio. Un metodo per calcolare una travatura reticolare isostatica è il metodo delle sezioni di Ritter.

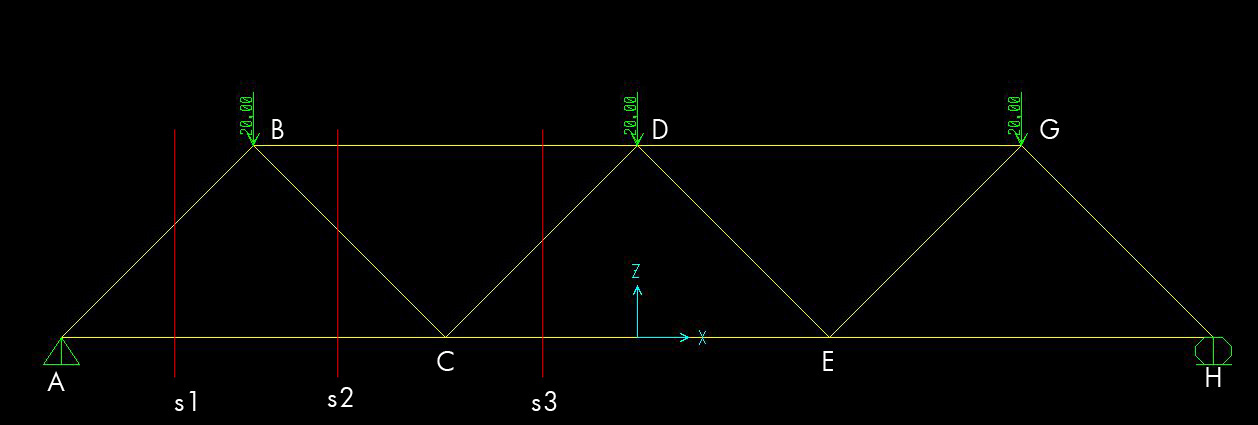
Prendo in considerazione quindi il modello di trave reticolare (AB= 2*sqrt2 m, AC= 4m) rappresentato in figura sopra. Come prima cosa ne verifico l'isostaticità. Illustro i due metodi per farlo:

1) l=V (con l: gradi di libertà e V= Ve + Vi: vincoli esterni + vincoli interni)

l= n_aste * 3= 11*3=33

Ve= carrello + cerniere= 2+1=3    Vi= 2(n-1) --> con n= numero di corpi che la cerniera collega

A-H= 2(2-1)= 2; B-G= 2(3-1)= 4; C-D-E= 2(4-1)=6; Vi=30 --> V= 30+3= 33= l (isostaticità verificata)

2) Ve + a = 2n ( dove a= numero aste e n= numero nodi) --> 3+11= 2*7 --> 14=14 (isostaticità verificata)

Calcoliamo ora facilmente le reazioni vincolari di carrello e cerniera tenendo a mente la simmetria della struttura. Faccio l'equilibrio a traslazione verticale: Va + Vb= 3F.                            Per simmetria Va= Vb= 3/2F

Il metodo delle sezioni di Ritter prevede di effettuare dei tagli virtuali che dividono in due la struttura sezionando le aste facendo in modo che tre di esse non convergano nello stesso nodo.

-primo taglio s1:

 

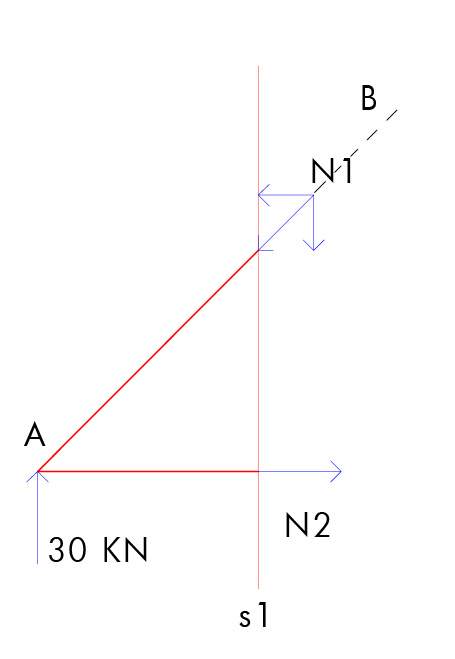
Scomponiamo N1 nelle sue componenti verticale e orizzontale entrambe con valore N1*(sqrt2)/2.

Per prima cosa facciamo l'equilibrio a rotazione con centro in B. Otteniamo quindi: 30*2 -2* N2= 0 --> N2= 30KN

Facendo poi l'equilibrio a traslazione verticale otteniamo N1*(sqrt2)/2=N2 --> N1=30*(sqrt2) KN

L'asta AB risulta quindi compressa (puntone). L'asta AC risulta invece tesa (tirante).

 

 

 

-secondo taglio s2:

 

 

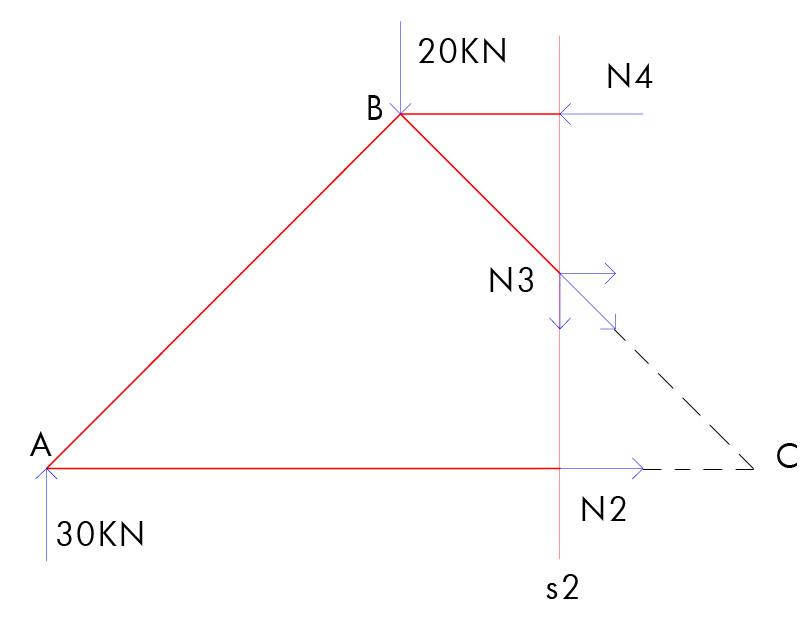
Scomponiamo N3 nelle sue componenti verticale e orizzontale entrambe con valore N3*(sqrt2)/2.

Facciamo l'equilibrio a rotazione con centro in C. Otteniamo quindi: 30*4 - 20*2 - N4*2 --> N4= 40 KN

Facendo poi l'equilibrio a traslazione verticale otteniamo: 30 - 20 - N3*(sqrt2)/2= 0 --> N3= 10*(sqrt2) KN

L'asta BD risulta quindi compressa (puntone). L'asta BC risulta invece tesa (tirante).

 

 

 

-terzo taglio s3:

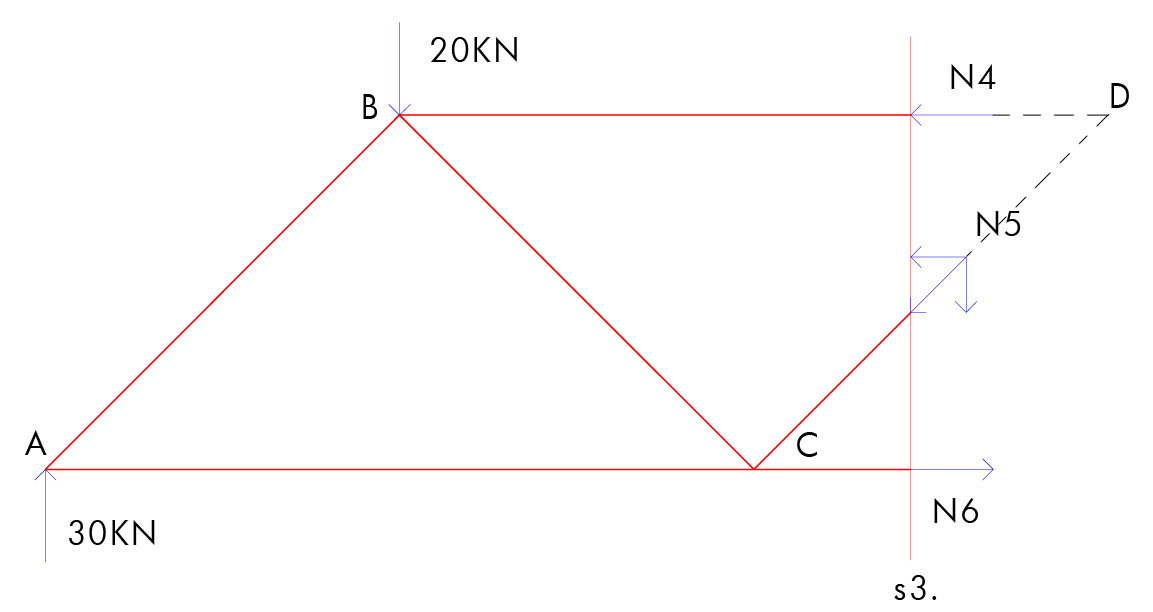
Scomponiamo N5 nelle sue componenti verticale e orizzontale entrambe con valore N5*(sqrt2)/2.

Facciamo l'equilibrio a rotazione con centro in D. Otteniamo quindi: 30*6 - 20*4 - N6*2 --> N6= 50 KN

Facendo poi l'equilibrio a traslazione verticale otteniamo: 30 - 20 - N5*(sqrt2)/2= 0 --> N5= 10*(sqrt2) KN

L'asta CD risulta quindi compressa (puntone). L'asta CE risulta invece tesa (tirante).

 

 

 

Per simmetria della struttura possiamo considerare i valori delle azioni di contatto trovati validi anche per il pezzo di trave speculare non calcolato.

 

Esercitazione trave reticolare 2d- Metodo dei nodi-

Un altro metodo per calcolare lo sforzo normale in una travatura reticolare isostatica è quello dei nodi. Partiamo dal presupposto per il quale una struttura si considera in equilibrio se ognuno dei suoi nodi è in equilibrio. Poniamo quindi per ciascuno di essi l'equilibrio a traslazione.

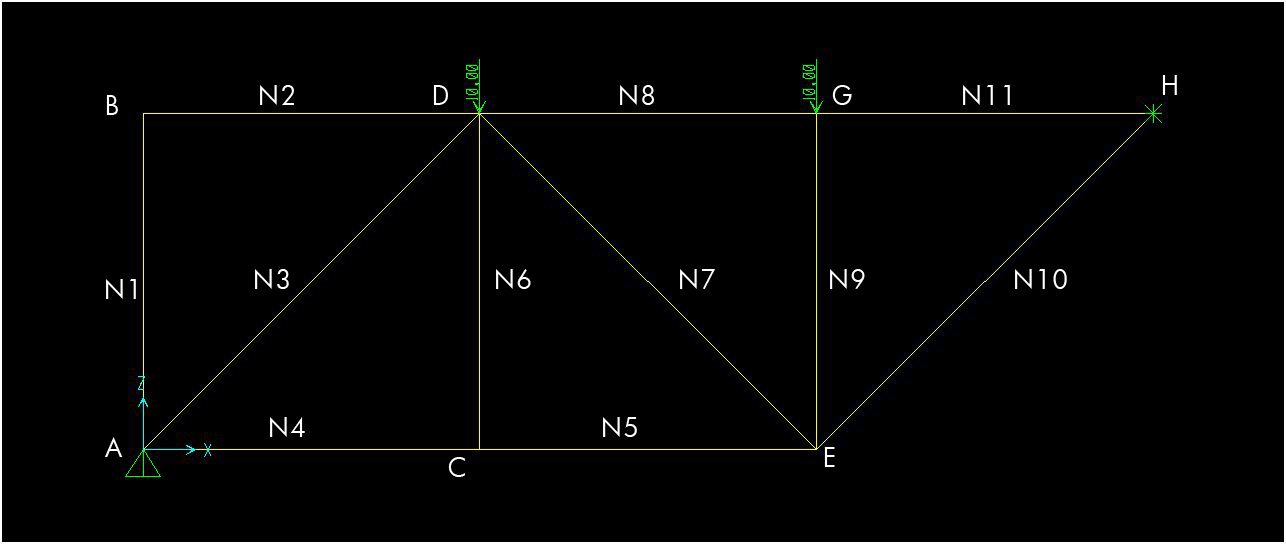
Il modello di trave reticolare preso in considerazione è rappresentato in figura sopra. (AB=AC= 1m). Come illustrato nel precedente esempio verifichiamo l'isostaticità della struttura.

l= 11*3= 33= V= 30+3=33 --> l=V

Calcoliamo facilmente quindi le reazioni vincolari di carrello e cerniera. Dall'equilibrio a traslazione verticale: Ya= 2F. Dall'equilibrio a rotazione: Xh= 3F. Dall'equilibrio a traslazione orizzontale: Xa= Xh= 3F.

-) nodo B:

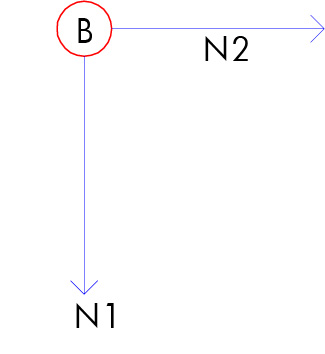
Non essendo presenti forze esterne agenti, dall'equilibrio a traslazione ricaviamo che N1=N2=0

Da cui: aste AB-BD scariche.

 

 

 

-) nodo A:

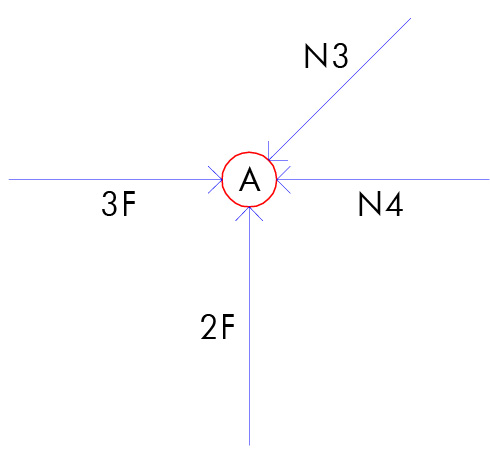Scomponiamo N3 nelle sue componenti verticale e orizzontale entrambe con valore N3*(sqrt2)/2.

Da Eq. Fy ricaviamo che: N3= 2F*(sqrt2)

Da Eq. Fx ricaviamo che: N4= F

Da cui: aste AC-AD compresse.

 

 

 

 

-) nodo C:

 

 

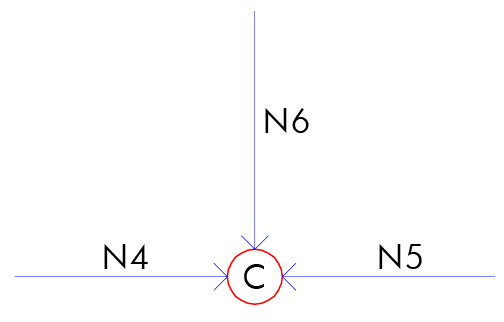
Da eq. Fy ricaviamo che N6=0

Da eq. FX ricaviamo che N5=N4= F

Da cui: asta CD scarica; asta CE compressa.

-) nodo D:

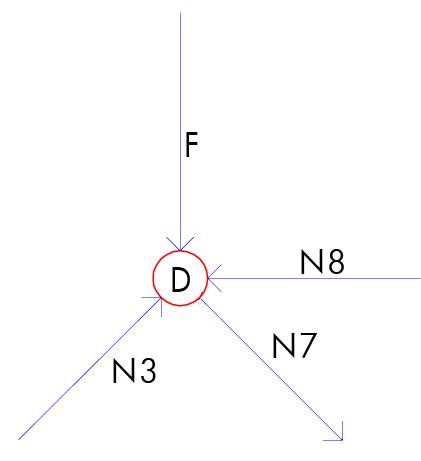Scomponiamo N7 nelle sue componenti verticale e orizzontale entrambe con valore N7*(sqrt2)/2.

Da Eq. Fy ricaviamo che: N7= F*(sqrt2)

Da Eq. Fx ricaviamo che: N8= 3F

Da cui: asta DG compressa; asta DE tesa.

 

 

 

 

-) nodo E:

 

 

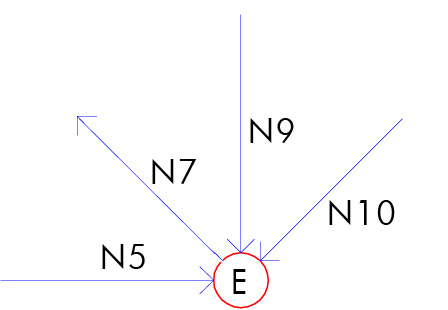
Scomponiamo N10 nelle sue componenti verticale e orizzontale entrambe con valore N10*(sqrt2)/2.

Da Eq. Fy ricaviamo che: N9= F

Da Eq. Fx ricaviamo che: N10= 0

Da cui: asta EH scarica; asta EG compressa.

 

 

-) nodo G:

 

 

 

 

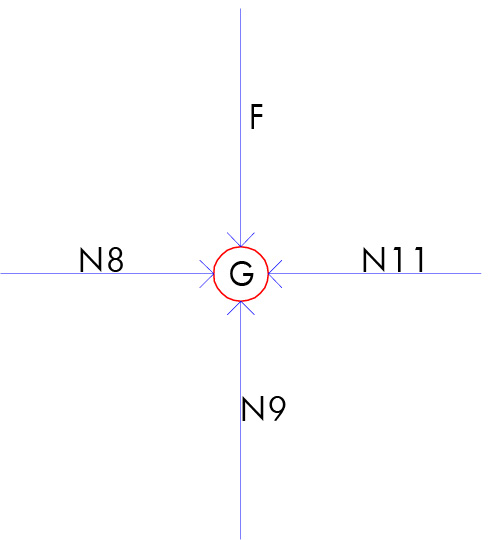
Da Eq. Fy ricaviamo che: N9= F

Da Eq. Fx ricaviamo che: N8= N11= 3F

Da cui: asta GH compressa.

 

 

 

-) nodo H:

 

Da Eq. Fx ricaviamo che: N11= 3F

Di seguito riportiamo i diagrammi dello sforzo normale elaborati in Sap:

 

 

 

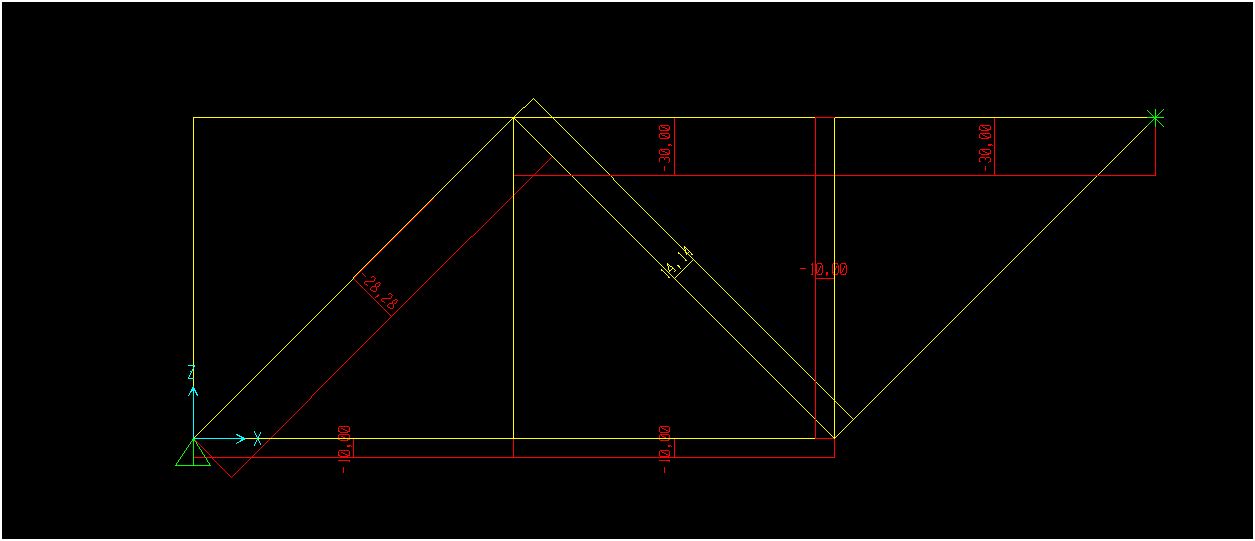
Esercitazione dimensionamento trave in legno, acciaio e calcestruzzo

Per svolgere l’esercitazione di dimensionamento di travi ho preso in considerazione la prima ipotesi di struttura che sto elaborando con il mio gruppo di laboratorio 2M (Forlani, Cardone, Dad Khan) per il progetto di un albergo a Garbatella. In particolare ho scelto come modello di impalcato da analizzare una porzione di piano tipo dell’edificio-albergo che comprende lo schema distributivo camera-ballatoio.

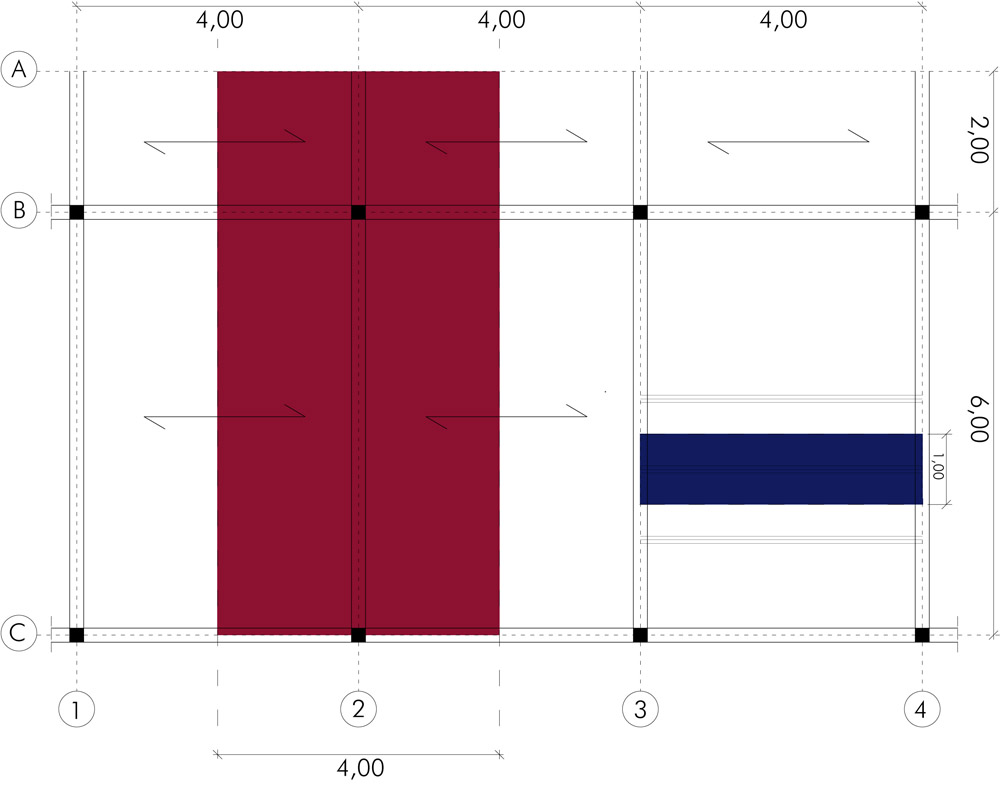
La struttura raffigurata nel disegno sottostante è caratterizzata da un interasse di 4 metri e una luce di 6 metri, con uno sbalzo (ballatoio) di 2 metri. La trave e il travetto di cui eseguirò il dimensionamento nelle tre tecnologie sono quelli evidenziati con il colore. L' area di influenza della trave è di 4,00m x 8,00m= 32 mq mentre l'area di influenza del travetto in legno e acciaio è 1,00m x 4,00= 4,00 mq, in calcestruzzo: 0,50m x 4,00m= 2mq. (Tutti i pesi specifici dei materiali sono stati presi da http://www.sanzioniamministrative.it/collegamenti/Testi/Tabelle/Tab_Pesi_Spec.htm ).

DIMENSIONAMENTO SOLAIO IN LEGNO

 

-)TRAVETTI:

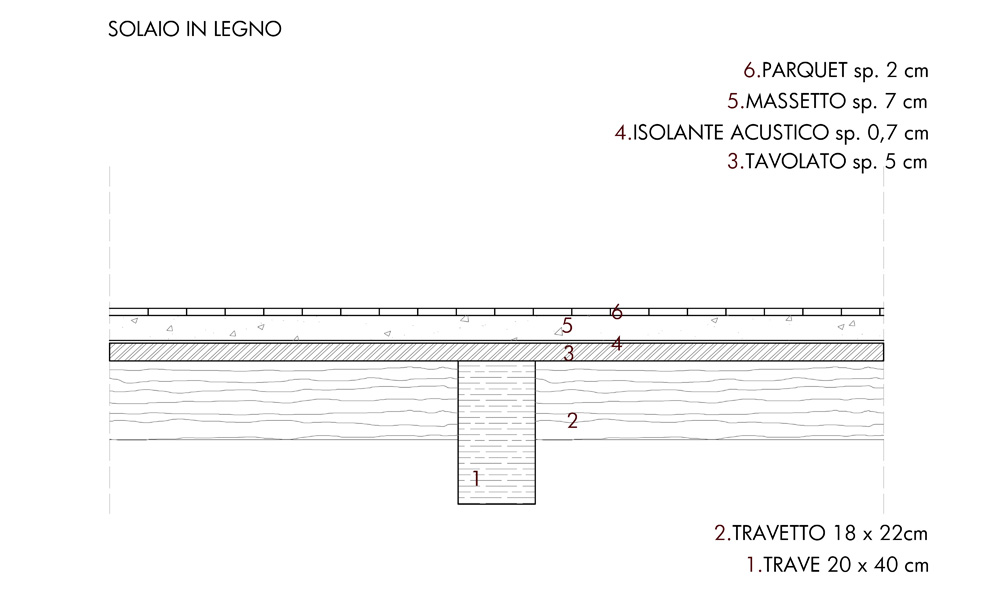
In primo luogo immagino che l’impalcato sopra descritto sia realizzato in legno, dunque rappresento di seguito un’ipotetica soluzione di pacchetto di solaio in legno. Subito dopo comincio a ragionare sui carichi che un solaio così realizzato deve sostenere. In base alle tre categorie in cui sono suddivisi i carichi annovero (per una porzione di solaio di 1mq) in:

-CARICHI STRUTTURALI (qs) le travi, i travetti, e il tavolato;

-SOVRACCARICHI PERMANENTI (qp) isolante acustico, massetto, parquet;

-SOVRACCARICHI ACCIDENTALI (qa) legati alla funzione dell’edificio, nel mio caso per l’albergo, considero il valore stabilito per un edificio mediamente affollato (2 KN/mq).

Calcolo ora nello specifico i carichi:              

-CARICHI STRUTTURALI (qs): tavolato in legno di noce, peso specifico: 700 kg/mc

                                           volume tavolato (per 1 mq): 0,05 m x 1,00 m x 1,00 m= 0,05 mc

                                           peso tavolato (per 1 mq): 700 x 0,05= 35 kg/mq= 0,35 KN/mq

 

-CARICHI PERMANENTI (qp): isolante acustico ACUSTIC SYSTEM 7, peso al mq (tabellato),  

                                             spessore  7 mm, peso: 3 kg/mq= 0,03 KN/mq

                                  

                                             massetto in cemento, massa volumica: 2000 kg/mc

                                             volume massetto (per 1 mq): 0,07m  x 1 m x 1 m= 0,07 mc

                                             peso massetto (per 1 mq): 2000 x 0,07=140 kg/mq=1,4 KN/mq

                                           

                                           

                                            parquet in ciliegio, peso specifico: 850 kg/mc

                                            volume parquet (per 1 mq): 0,02m x 1m x 1m= 0,02 mc

                                            peso parquet (per 1 mq): 0,02 x 850= 17 kg/mq= 0,17 KN/mq

                                           

                                            incidenza impianti: 0,5 KN/mq

                                            incidenza tramezzi: 1 KN/mq

 

-CARICHI ACCIDENTALI (qa): 2 KN/mq (edificio per civile abitazione)

 

-CARICO TOTALE: (qs + qp + qa) x interasse

                     ( 0,35 + 3,1 + 2 ) x 1= 5,45 KN/m

A questo punto inserisco i dati relativi ai carichi calcolati nel foglio elettronico fornito a lezione, viene quindi calcolato il momento massimo per una trave appoggiata appoggiata mediante la formula q*l^2/8. Scelgo poi la classe di resistenza del legno, ad esempio GL24H, con fm,k=24 N/mmq e inserisco il kmod (coefficiente legato alla durata del materiale) che per il legno lamellare vale 0,7.

Inserisco infine un valore per la base della sezione di 12 cm, ottengo un valore di altezza minima di 21,69 cm. Scelgo quindi un profilato, da una tabella di prodotti fornita da un’azienda produttrice trovata in rete (Kaufmann-Canducci), di 12 x 22 cm.

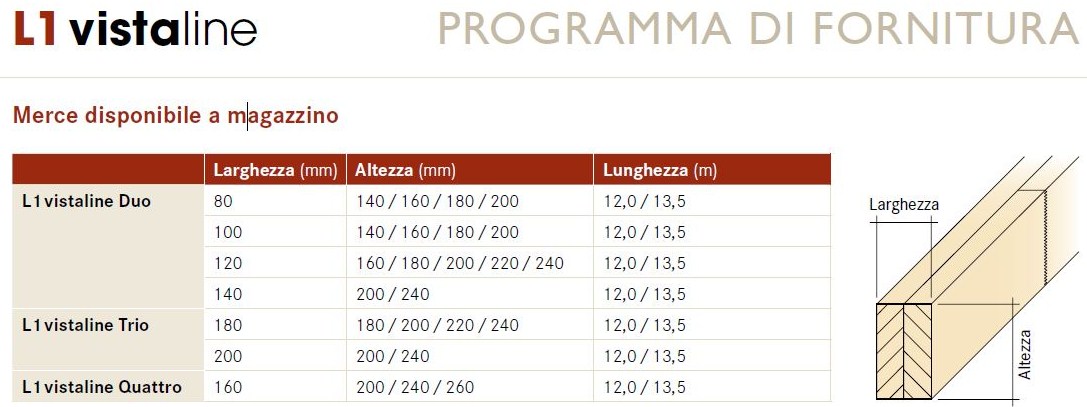
Verifico il progetto del travetto aggiungendo ai carichi strutturali precedentemente calcolati anche il peso del travetto progettato:

peso specifico legno lamellare: 450 kg/mc

volume travetto (per 1 mq): 0,12m  x 0,22m  x 1,00 m= 0,0264 mc

peso travetto (per 1 mq): 450 x 0,0264= 11,88 kg/mq= 0,

12 KN/mq

CARICO TOTALE: ( (0,35 + 12) + 3,1 + 2 ) x 1= 5,57 KN/m

Inserisco il nuovo valore di carico totale nel foglio elettronico, e ottengo un valore di altezza minima di 21,93 cm < 22 cm inferiore a quello della sezione progettata, che risulta quindi verificata.

-)TRAVE:

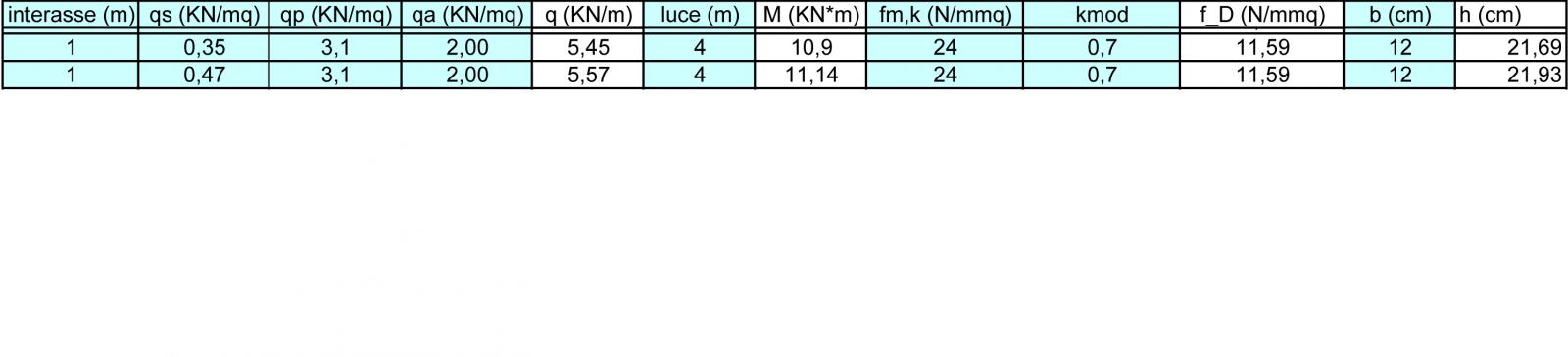
Dopo aver calcolato i carichi al mq nel progetto del travetto, il procedimento per il progetto della trave risulta analogo e velocizzato. Devo però ricordare che i carichi sono gli stessi eccetto il carico strutturale a cui devo aggiungere il contributo del travetto progettato, e l’interasse è ora quello della trave, 4 metri.

-CARICO TOTALE: (qs + qp + qa) x interasse

                             (O,47 + 3,1 + 2 ) x 4= 22,28 KN/m

Devo ora calcolare il momento massimo agente sulla trave. Stavolta non si tratta di una trave appoggiata appoggiata come nel travetto, ma di una trave appoggiata appoggiata con uno sbalzo di 2 metri (ballatoio). Per desumere rapidamente il momento massimo disegno il mio modello in SAP2000, assegnandogli il carico che ho calcolato. Trovato quindi il momento massimo lo inserisco nel foglio elettronico.

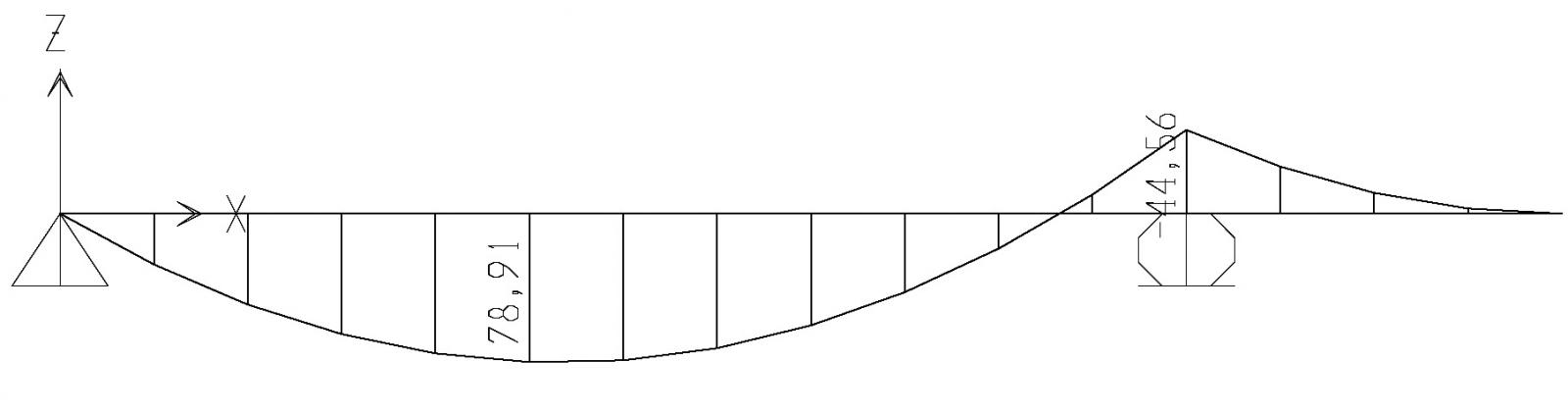
Scelgo la classe di resistenza del legno, stavolta GL36H sempre consultando i dati forniti dall’azienda produttrice, e inserisco un valore per la base della sezione di 20 cm. Ottengo quindi un valore di altezza minima della trave di 36,91 cm, scelgo dunque un profilato di 20 cm x 40 cm.

Verifico il progetto della trave aggiungendo ai carichi strutturali precedentemente calcolati anche il peso della trave progettata:

peso specifico legno lamellare: 450 kg/mc

volume trave: 0,20m  x 0,40m  x 8,00 m= 0,64 mc

peso trave: 450 x 0,64= 288 kg

peso distribuito della trave: 288/(8 x 4)= 9 kg/mq= 0,09 KN/mq

CARICO TOTALE: ((O,47 + 0,09) + 3,1 + 2 ) x 4= 22,64 KN/m

Avendo calcolato il nuovo carico totale comprensivo del contributo della trave progettata, mi ricalcolo il momento massimo modificando il modello già disegnato in SAP2000, e inserisco il valore trovato nel foglio elettronico.

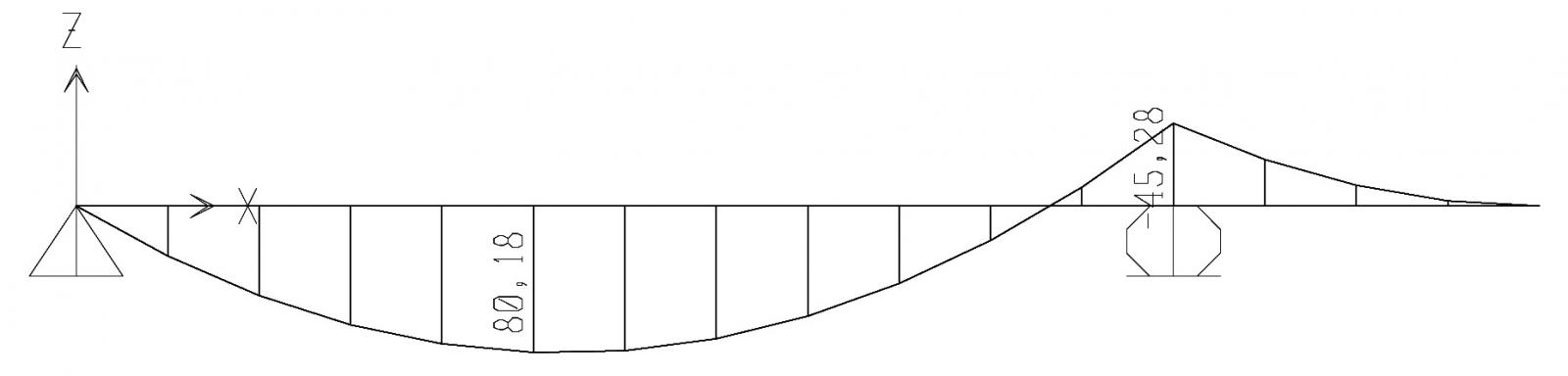
Ottengo un valore di altezza minima di 37,20 cm < 40 cm, inferiore a quello della sezione progettata, che risulta quindi verificata.

 

DIMENSIONAMENTO SOLAIO IN ACCIAIO

Prendo in considerazione lo stesso impalcato immaginando stavolta di realizzarne la struttura in acciaio. Ipotizzo che il solaio sia in lamiera grecata.

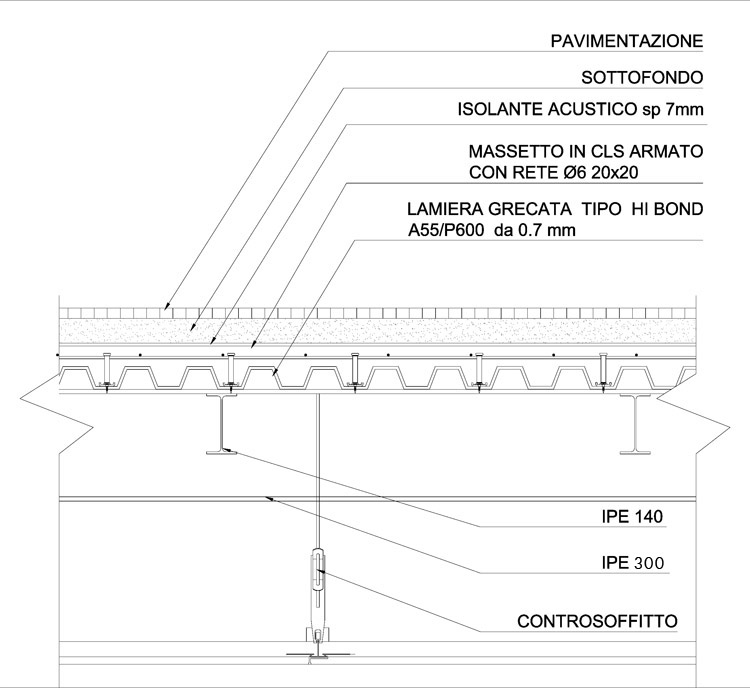
-)TRAVETTI:      

-CARICHI STRUTTURALI (qs): lamiera grecata tipo HI-BOND A55/P600, spessore: 0,7 mm

                                              peso: 9,16 kg/mq= 0,092 KN/mq

                                          

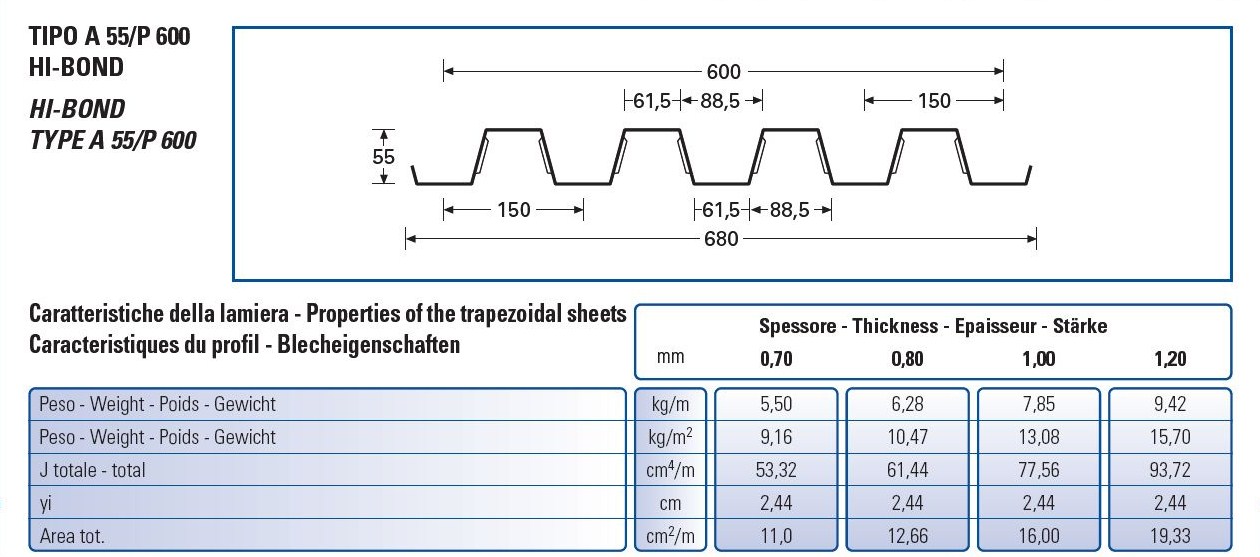
                                              soletta, spessore (Htot): 12cm

                                              peso: 240 kg/mq= 2,4 KN/mq  

                                      

 

-CARICHI PERMANENTI (qp): rete elettrosaldata ф6/20 cm, peso specifico acciaio: 78,50 KN/mc

                                            Volume 10 ф6 (per 1 mq): (πr^2*1)*10= 0,0011304 mc

                                            Peso rete (per 1 mq): 78,50 x 0,0011304= 0,0887 KN/mq

                                            

                                            isolante acustico ACUSTIC SYSTEM 7, peso al mq (tabellato)            

                                            3 kg/mq= 0,03 KN/mq

                                     

                                            Sottofondo in malta, peso specifico: 1900 kg/mc

                                            Volume sottofondo (per 1 mq): 0,06m  x 1 m x 1 m= 0,06 mc

                                            peso sottofondo (per 1 mq): 1900 x 0,06=114 kg/mq=1,14 KN/mq

                                           

                                            pavimento in marmo, peso specifico 2694 kg/mc

                                            volume lastra di marmo (per 1 mq): 0,02m x 1m x 1m= 0,02 mc

                                            peso pavimento (per 1 mq): 0,02 x 2694= 53,88 kg/mq= 0,54 KN/mq

                                           

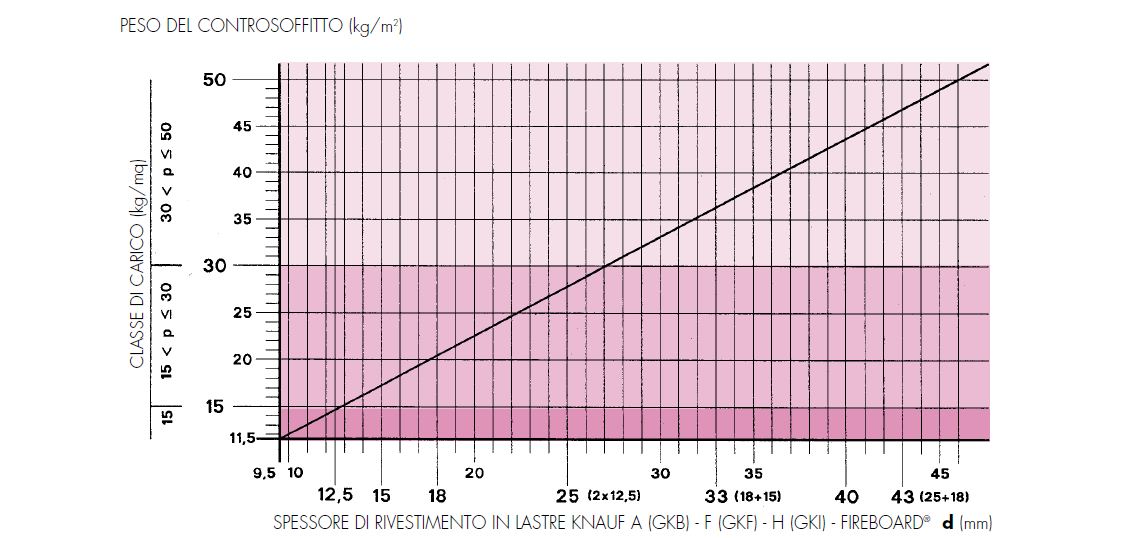
                                            controsoffitto in lastre di gesso tipo KNAUF,spessore di rivestimento:2,7cm

                                            peso controsoffitto: 30 Kg/mq

                                            peso sovraccarichi controsoffitto (materiali isolanti, lampade, plafoniere,                        

                                            impianti in genere…): 40 Kg/mq  

                                            peso totale controsoffitto: 70 kg/mq= 0,7 KN/mq

                                           

                                            incidenza impianti: 0,5 KN/mq

                                            incidenza tramezzi: 1 KN/mq

 

-CARICHI ACCIDENTALI (qa): 2 KN/mq (edificio per civile abitazione)

 

-CARICO TOTALE: (qs + qp + qa) x interasse

                     ( 2,492 + 3,9987 + 2 ) x 1= 8,4907 KN/m

Inserisco a questo punto i valori dei carichi calcolati nel foglio elettronico. Scelgo la classe di resistenza del ferro FE430S275 e ottengo un valore di Wx=64,84 cm^3. Dalla tabella trovata in rete, il profilo con valore di Wx immediatamente superiore risulta avere una sezione di 14 x 7,3 cm, con un Wx=77,3 cm^3.

 

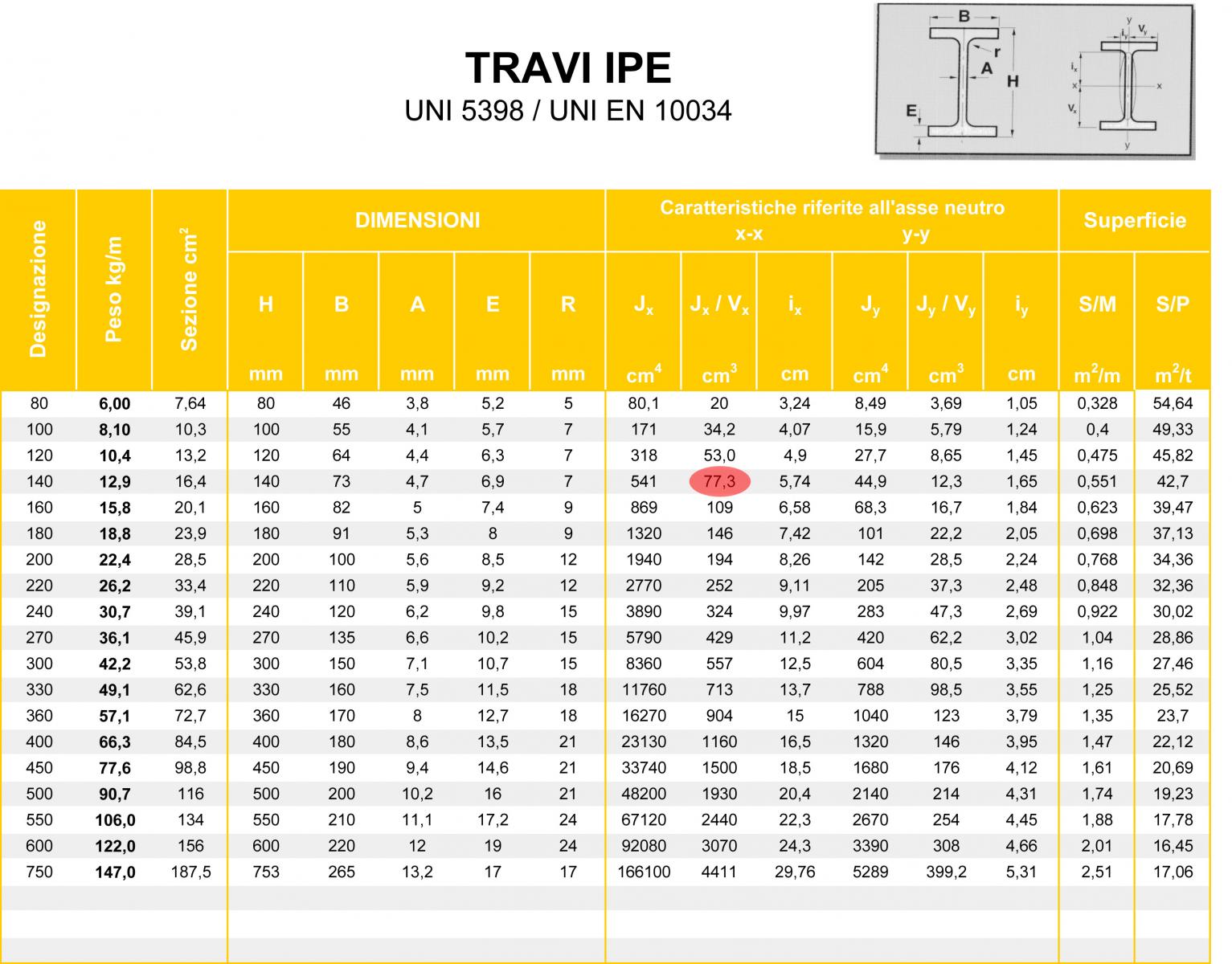
Verifico il progetto del travetto aggiungendo ai carichi strutturali precedentemente calcolati anche il peso del travetto progettato:

peso travetto (per 1 m): 12,9 kg/m (dalla tabella di riferimento trovata in rete)

peso travetto (per 1 mq): 12,9/1= 12,9 kg/mq= 0,13 KN/mq

CARICO TOTALE: ( (2,492 + 0,13) + 3,9987 + 2 ) x 1= 8,6207 KN/m

Inserisco il nuovo valore del carico strutturale (aumentato del contributo del travetto) nel foglio elettronico e ottengo un nuovo valore di Wx= 65,83 cm^3 < 77,3.

La sezione è dunque verificata.

-)TRAVE:

Anche in questo caso, dopo aver calcolato i carichi al mq nel progetto del travetto, procedo al progetto della trave principale. Aggiungo ai carichi strutturali il contributo dato dal travetto appena progettato, e considero che l’interasse è stavolta quello della trave, ovvero 4 metri.

-CARICO TOTALE: (qs + qp + qa) x interasse

                             (2,622 + 3,9987 + 2 ) x 4= 34,4828 KN/m

 

Calcolo ora il momento massimo agente sulla trave. Inserisco il mio modello di trave appoggiata appoggiata con sbalzo in SAP e ottengo il valore del momento massimo= 122,13 KN*m. Lo inserisco nel foglio elettronico.

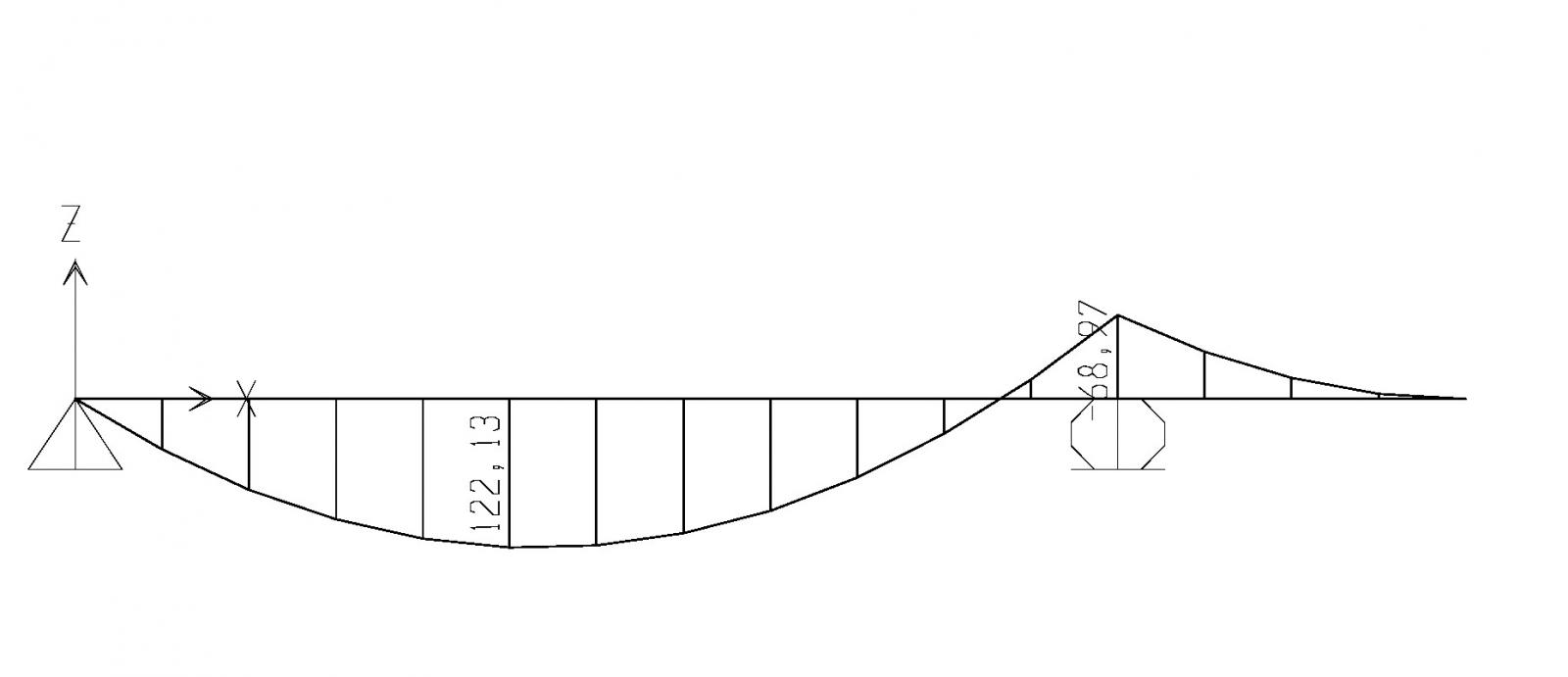
Mantenendo la classe di resistenza del ferro FE430S275 ottengo un valore di Wx minimo= 466,31 cm^3. Dalla tabella che ho preso come riferimento seleziono una sezione di dimensioni 30cm x 15cm e Wx= 557 cm^3.

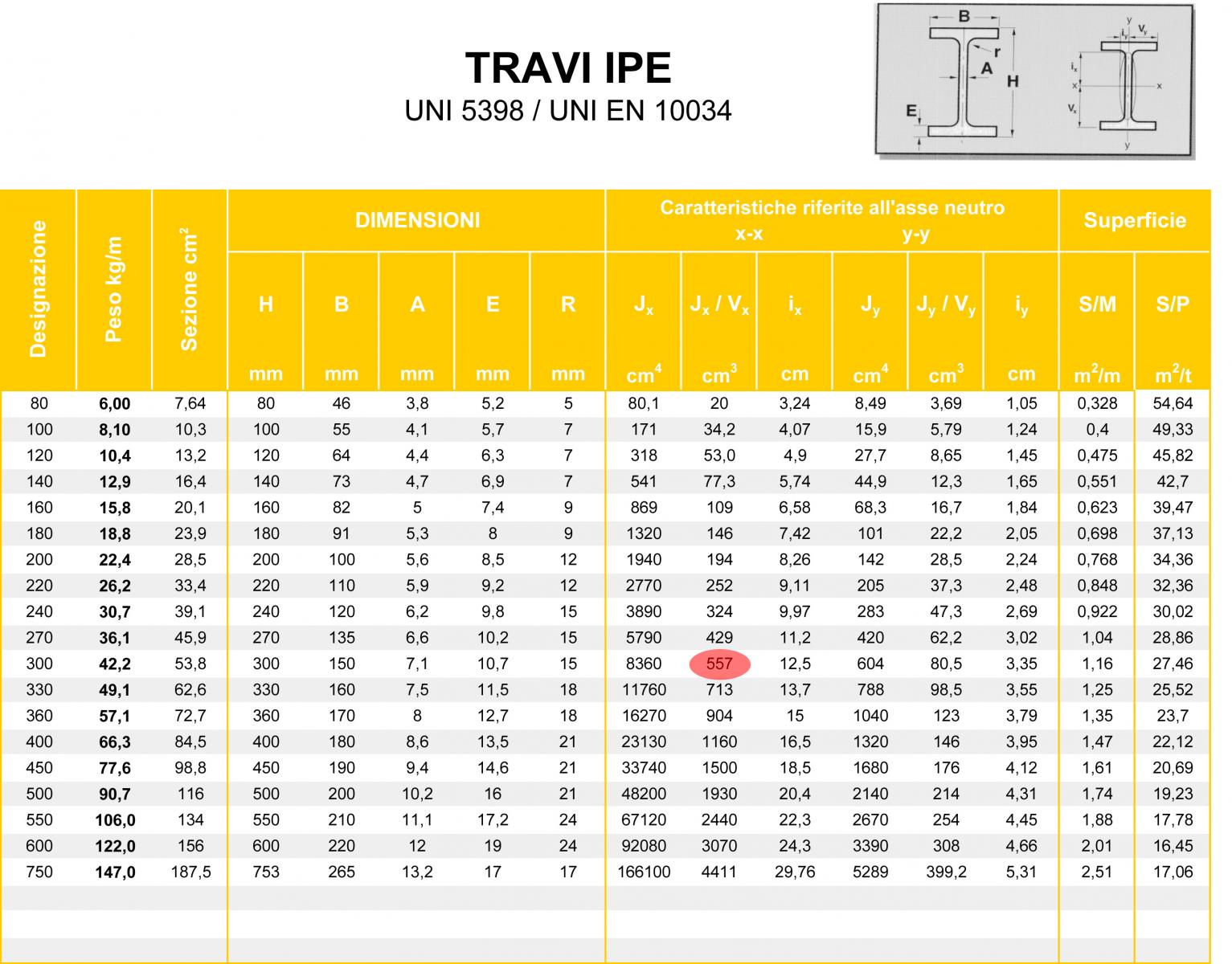
Verifico ora il progetto della trave aggiungendo ai carichi strutturali il peso proprio della trave:

peso trave (per 1 m): 42,2 kg/m (tabellato)

peso trave (per 1 mq): 42,2/4= 10,55 kg/mq=0,1KN/mq

CARICO TOTALE: ((2,622 + 0,1) + 3,9987 + 2 ) x 4= 34,8828 KN/m

Calcolo nuovamente in SAP il momento massimo agente sulla trave avendo modificato il carico. Il momento massimo risulta essere di 123,54 KN*m.

Inserisco il nuovo valore del momento nel foglio elettronico e ottengo un valore di Wx minimo= 471,70 < 557 cm^3.

La sezione risulta dunque verificata.

 

DIMENSIONAMENTO SOLAIO IN CEMENTO ARMATO

Infine prendo in considerazione ancora lo stesso impalcato immaginando stavolta di realizzarne la struttura in cemento armato. Analizzo quindi un solaio in latero cemento come mostrato nel disegno sottostante. 

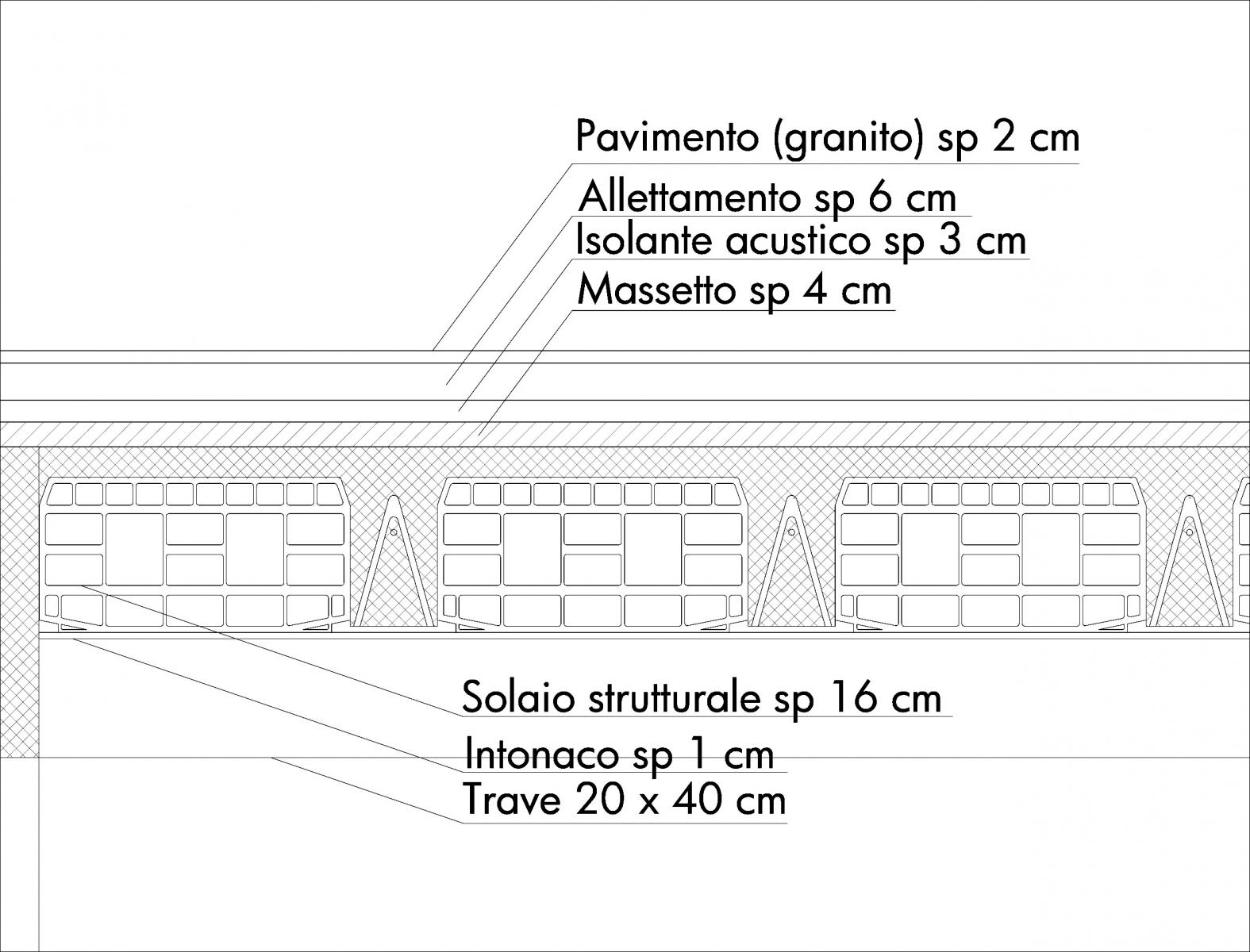
-)TRAVETTI:

Considero inizialmente il carico strutturale qs=0

Calcolo ora i carichi permanenti:

-CARICHI PERMANENTI (qp): massetto in cemento, massa volumica: 2000 kg/mc

                                            volume massetto (per 1 mq): 0,04m  x 1 m x 1 m= 0,04 mc

                                            peso massetto (per 1 mq): 2000 x 0,04=80 kg/mq=0,8 KN/mq

                               

                                            isolante acustico ACUSTIC SYSTEM 7, peso al mq (tabellato), spessore                                        

                                            7 mm, peso: 3 kg/mq= 0,03 KN/mq

 

                                            Sottofondo in malta, peso specifico: 1900 kg/mc

                                            Volume sottofondo (per 1 mq): 0,06m  x 1 m x 1 m= 0,06 mc

                                            peso sottofondo (per 1 mq): 1900 x 0,06=114 kg/mq=1,14 KN/mq

                                

                                            pavimento in granito, peso specifico 2500 kg/mc

                                            volume lastra di marmo (per 1 mq): 0,02m x 1m x 1m= 0,02 mc

                                            peso pavimento (per 1 mq): 0,02 x 2500= 50kg/mq= 0,5 KN/mq

 

                                            intonaco, sp. 1 cm, peso al mq per cm di spessore: 16 kg/mq= 0,16 KN/mq

                                           

                                            incidenza impianti: 0,5 KN/mq

                                            incidenza tramezzi: 1 KN/mq

 

-CARICHI ACCIDENTALI (qa): 2 KN/mq (edificio per civile abitazione)

 

-CARICO TOTALE: (qs + qp + qa) x interasse

                     ( 0 + 4,13 + 2 ) x 0,5= 3,065 KN/m

Inserisco a questo punto i valori dei carichi calcolati nel foglio elettronico. Scelgo la classe di resistenza del ferro: FE360S235 e del cemento: C32/40. Seleziono una sezione del travetto di base 12 cm e ottengo dal foglio elettronico un valore minimo di altezza utile di 9,50 cm con copriferro di 4 cm.

Seleziono da una tabella trovata in rete di una casa produttrice, un pacchetto di solaio in calcestruzzo con interasse 50 cm, travetti da 12 cm di larghezza e altezza 16 cm (12cm + 4cm).

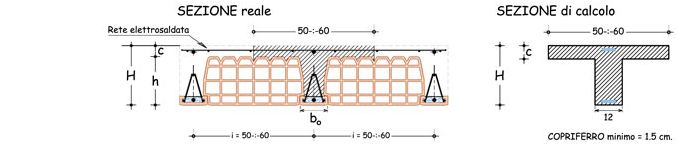
Verifico il progetto del travetto considerando il suo peso proprio come carico strutturale:

peso del pacchetto strutturale del solaio selezionato: 2,15 KN/mq (tabellato)

CARICO TOTALE: (2,15 + 4,13 + 2) x 0,5= 4,14 KN/m

Inserisco il valore nel foglio elettronico e ottengo un'altezza minima totale di 15,04 cm < 16 cm.

La sezione risulta dunque verificata.

 

-)TRAVE:

Anche in questo caso, dopo aver calcolato i carichi al mq nel progetto del travetto, procedo al progetto della trave principale. Aggiungo ai carichi strutturali il contributo dato dal travetto appena progettato, e considero che l’interasse è stavolta quello della trave, ovvero 4 metri.

-CARICO TOTALE: (qs + qp + qa) x interasse

                             (2,15 + 4,13 + 2) x 4= 33,12 KN/m

Calcolo ora il momento massimo agente sulla trave. Inserisco il mio modello di trave appoggiata appoggiata con sbalzo in SAP e ottengo il valore del momento massimo= 117,3 KN*m.

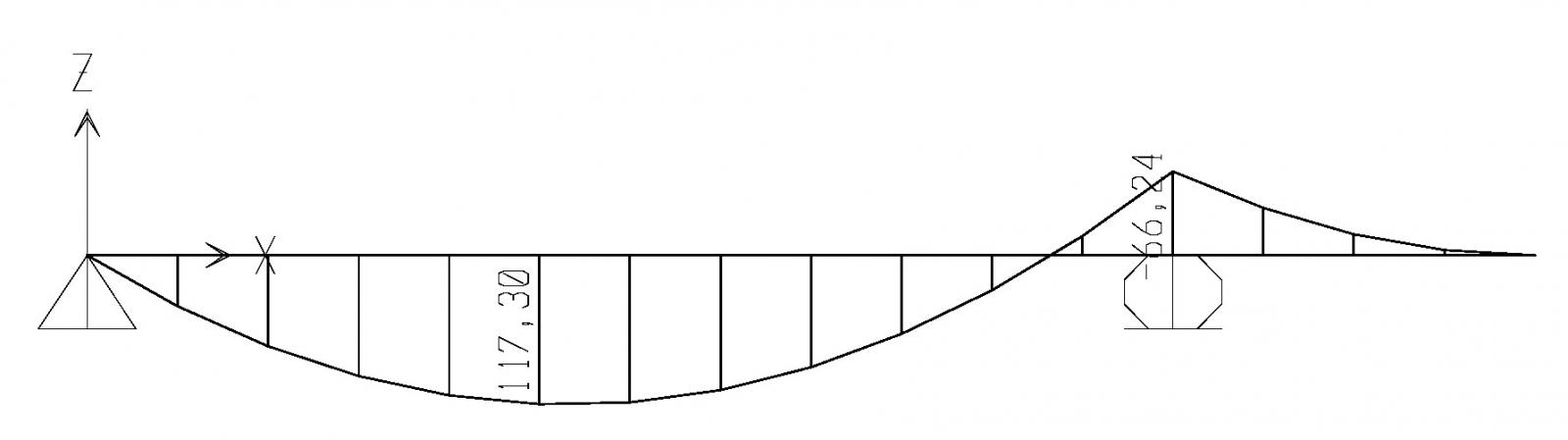
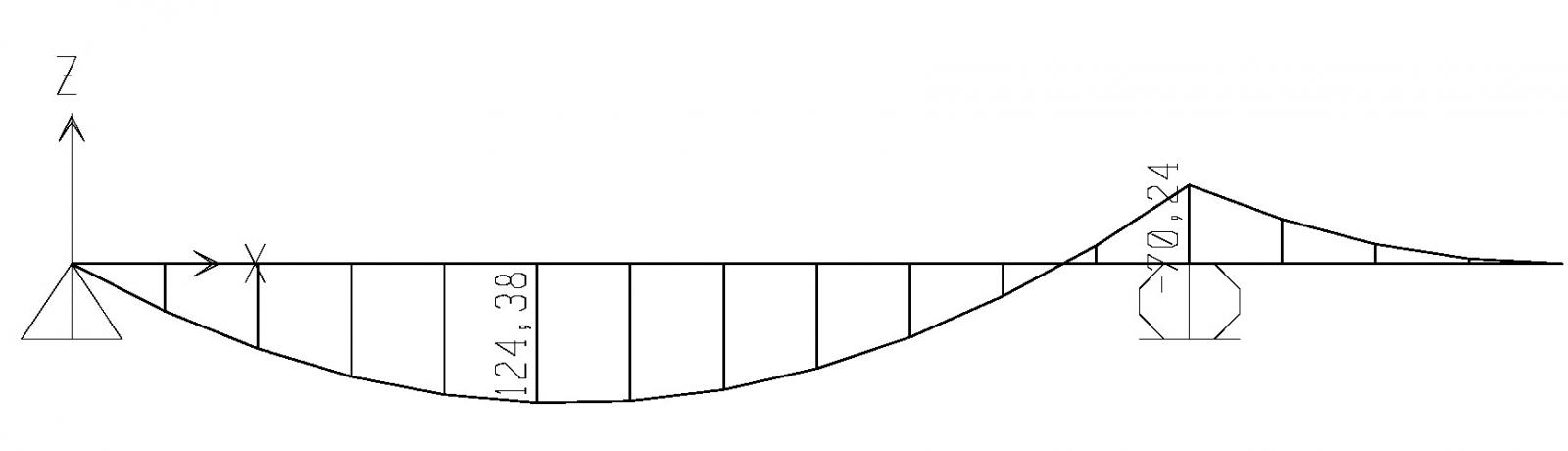
Scelgo la classe di resistenza del ferro: FE360S235 e del cemento: C32/40. Considero una sezione di base 20 cm e ricavo un valore di altezza utile minimo di 32,18 cm, considerando 5 cm di copriferro: 37,18 cm. Seleziono quindi una sezione di dimensioni 20 x 40 cm.

 

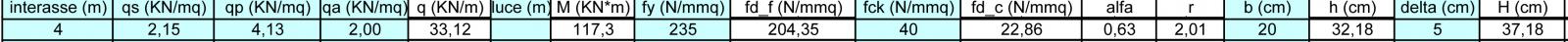
Verifico il progetto della trave aggiungendo ai carichi strutturali il suo peso proprio:

peso specifico cemento: 2500 kg/mc

volume: 0,2 x 0,4 x 8= 0,64 mc

peso trave per 1 mq: (2500 x 0,64)/32= 50 kg/mq= 0,5 KN/mq

CARICO TOTALE: ((2,15 + 0,5) + 4,13 + 2) x 4= 35,12 KN/m

Calcolo nuovamente in SAP il momento massimo agente sulla trave avendo modificato il carico. Il momento massimo risulta essere di 124,38 KN*m.

Inserisco il nuovo valore del momento nel foglio elettronico ottengo un valore minimo di altezza utile di 33,13 cm, altezza totale : 33,13 cm + 5 cm= 38,13 cm < 40 cm.

La trave è quindi verificata.

 

ESERCITAZIONE TRAVATURA RETICOLARE TRIDIMENSIONALE

 

Dopo aver svolto l’esercitazione sulla travatura reticolare tridimensionale in aula, ho provato a rifarne una rielaborando la struttura. Il modulo base e l’intera struttura sono rappresentati nelle immagini sottostanti.

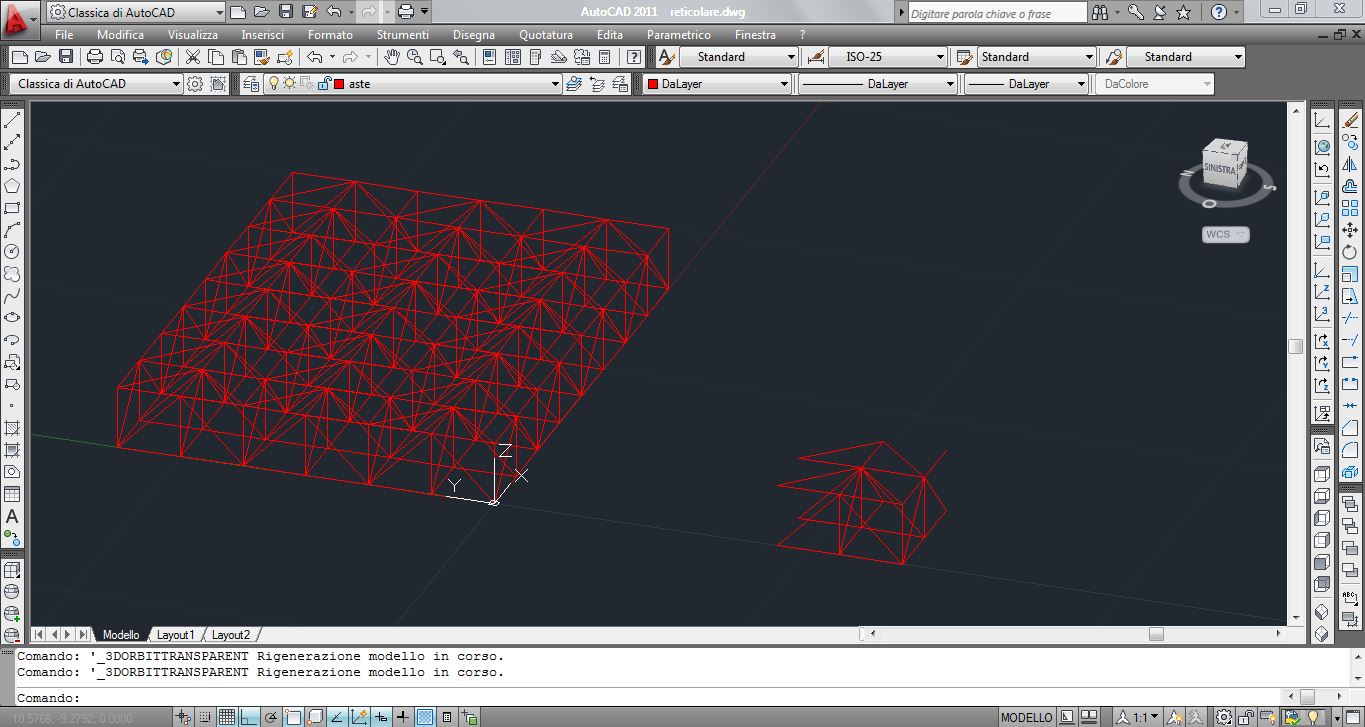
Quindi una volta disegnata la struttura reticolare tridimensionale in autocad la salvo in formato .dxf (possibilmente 2000 perché può dare problemi con le versioni successive).

Importo quindi il file .dxf appena disegnato in SAP2000 e in primo luogo assegno i vincoli esterni, cioè le quattro cerniere agli angoli.

Definisco quindi il carico concentrato, ponendo il moltiplicatore di peso proprio uguale a zero.

Assegno il carico concentrato solamente ai nodi superiori, di valore 100 KN. Per selezionare solo i nodi superiori imposto la vista sul piano xy e controllo di essere alla quota giusta tramite il comando “set 2d view”. Con il comando “set display options” disattivo la voce “invisible” sotto “joints” e attivo la voce “frames not in view” sotto “frames”. Ho reso così visibili solo i nodi superiori della struttura e posso selezionarli per assegnare la forza concentrata.   

Trattandosi di una travatura reticolare le aste sono collegate tra loro da cerniere interne, quindi seleziono tutte le aste e rilascio i momenti all’inizio e alla fine.

Eseguo quindi l’analisi.

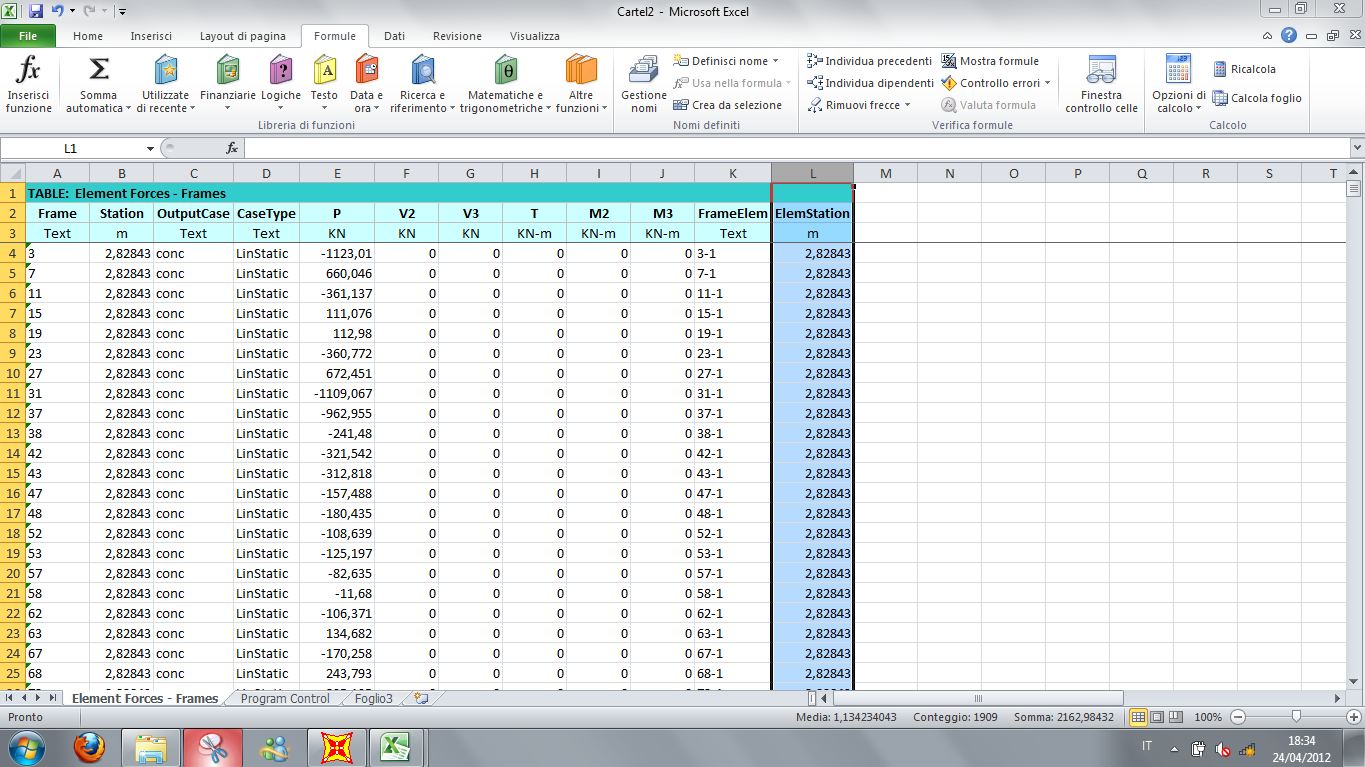
Mi serve visualizzare i valori dello sforzo normale per le singole aste, quindi clicco su “display”, “show tables”, spunto la voce “element output” sotto “analysis results”. Per esportare il file con i valori dello sforzo normale delle aste in excel seleziono “file”, “export current table”, “to excel”.

Per eseguire il dimensionamento delle aste mi occorre ottenere un file excel che mi comunichi le tre informazioni principali: numero dell’asta, lunghezza, e sforzo normale agente su essa.

So che Sap per ogni asta effettua più sezioni, essendo lo sforzo normale costante, e dato che l’ultima sezione corrisponde alla lunghezza dell’asta, posso ordinare la tabella excel in base alle sezione. Sapendo che nello schema strutturale da me disegnato ho precisamente due tipi di aste: di lunghezza 2 metri e di lunghezza 2,8 metri (aste diagonali), posso copiare su un nuovo file excel la tabella solamente con i dati relativi alle sezioni effettuate rispettivamente a 2 metri e a 2,8 metri.

Così facendo ottengo un file excel in cui ogni asta compare una sola volta con le tre informazioni principali: numero asta, lunghezza e sforzo normale agente.

Dimensiono in primo luogo le aste tese considerando lo sforzo normale massimo di trazione, e poi dimensiono le aste compresse considerando lo sforzo normale massimo di compressione relativo sia alle aste lunghe 2,8 metri e sia alle aste lunghe 2 metri, in modo da poterle verificare separatamente poi a instabilità euleriana.

Per trovare lo sforzo normale massimo di trazione utilizzo la funzione di excel che permette di trovare massimi e minimi di una serie di valori.

Una volta trovati i valori procedo al dimensionamento dei tubolari attraverso la formula: σ= N/A, quindi A =N/σ. In fase di progetto considero σ= Fyd= Fy/γ.

Scelgo il tipo di acciaio, Fe360s235, e considero γ=1,15.

 

Otteniamo per le aste tese un valore minimo di area di 32,9 cm^2, per le aste compresse lunghe 2,8 metri area minima di 54,9 cm^2 e per le aste compresse lunghe 2 metri area minima di 48,3 cm^2.

Una volta trovate le aree seleziono i tubolari da una tabella trovata in rete.

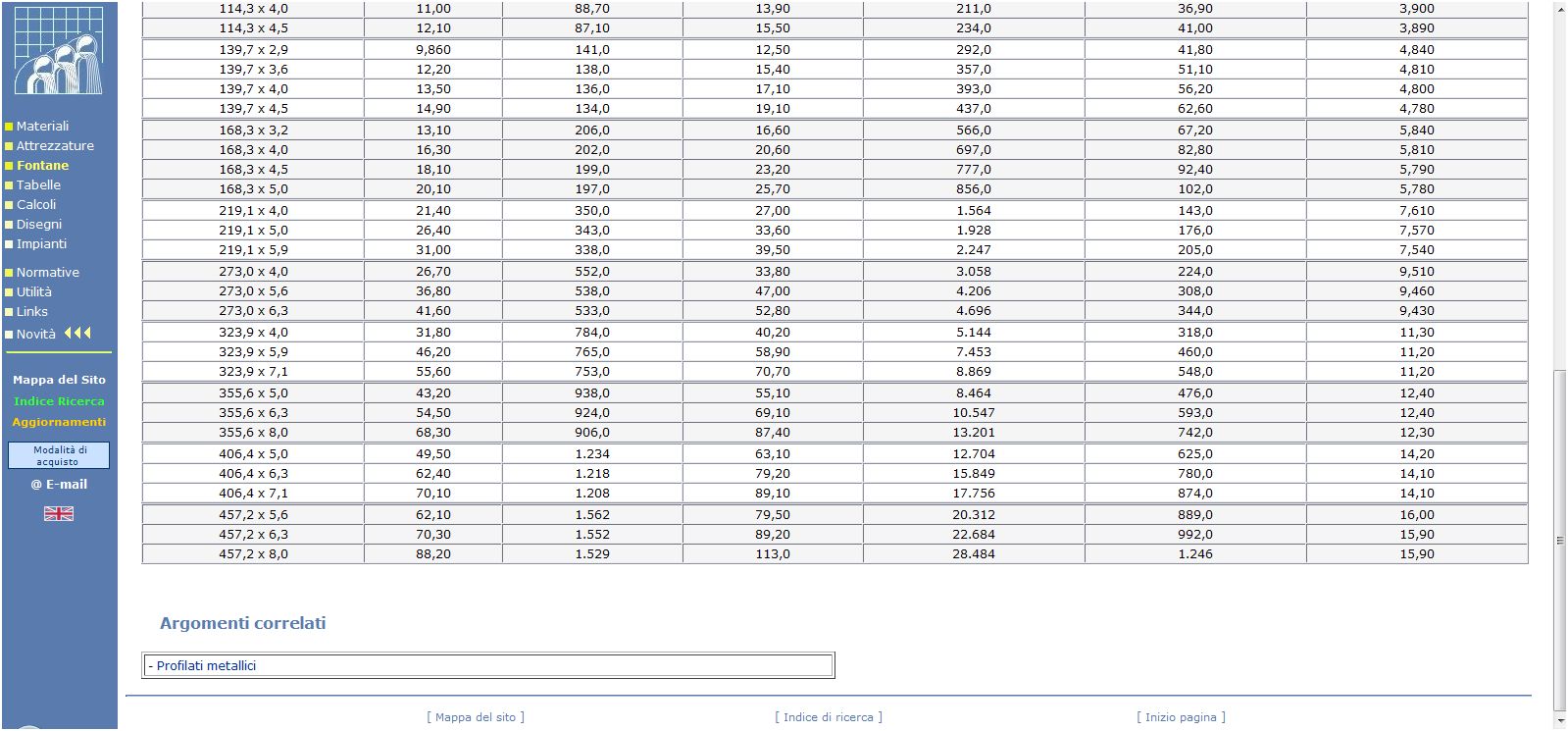
Per le aste tese seleziono tubolari di area 33,6 cm^2, per le aste compresse lunghe 2,8 metri scelgo tubolari di area 55,1 cm^2 e per le aste compresse lunghe 2 metri scelgo tubolari di area 52,8 cm^2.

Per le aste compresse calcoliamo poi il peso critico per la verifica a instabilità euleriana tramite la formula:

Pcritico= (π^2*E*Jmin)/l0^2

     l0= k*l, dove k dipende dalle condizioni di vincolo e l è la lunghezza effettiva dell’asta. Nel mio caso K=1 perché ho due cerniere alle estremità delle aste.

Quindi calcolo il peso critico per le aste lunghe 2,8 metri:

Pcritico= (3,14)^2*21000(KN/cm^2)*8464(cm^4))/(280cm)^2= 21906 KN

Confronto il valore con lo sforzo normale massimo di compressione agente=1123,01KN<<21906 KN

 

Calcolo poi il peso critico per le aste lunghe 2 metri:

Pcritico= (3,14)^2*21000(KN/cm^2)*4696(cm^4))/(200cm)^2= 24307 KN

Confronto il valore con lo sforzo normale massimo di compressione agente=986,654KN<<24307 KN

Entrambe le aste sono largamente verificate a instabilità euleriana.

Ho poi provato nel foglio excel ad aumentare la classe di resistenza dell’acciaio. Ho inserito prima un ferro FE430S275 e poi un ferro FE510S355. Ho notato che all’aumentare della classe di resistenza, diminuisce l’area della sezione, diminuisce il momento d’inerzia e di conseguenza diminuisce il valore del carico critico euleriano.

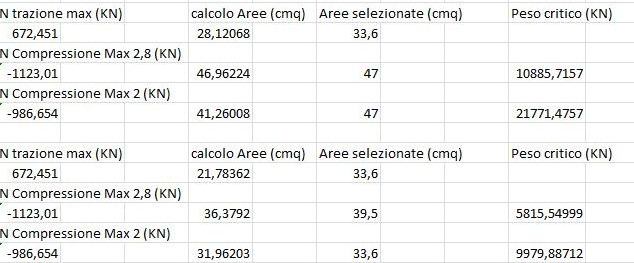
Le sezioni sono ugualmente verificate.

Circuiti chiusi

Consideriamo un circuito chiuso di travi di lunghezza l e forze F applicate a l/4 come mostrato in figura:

 

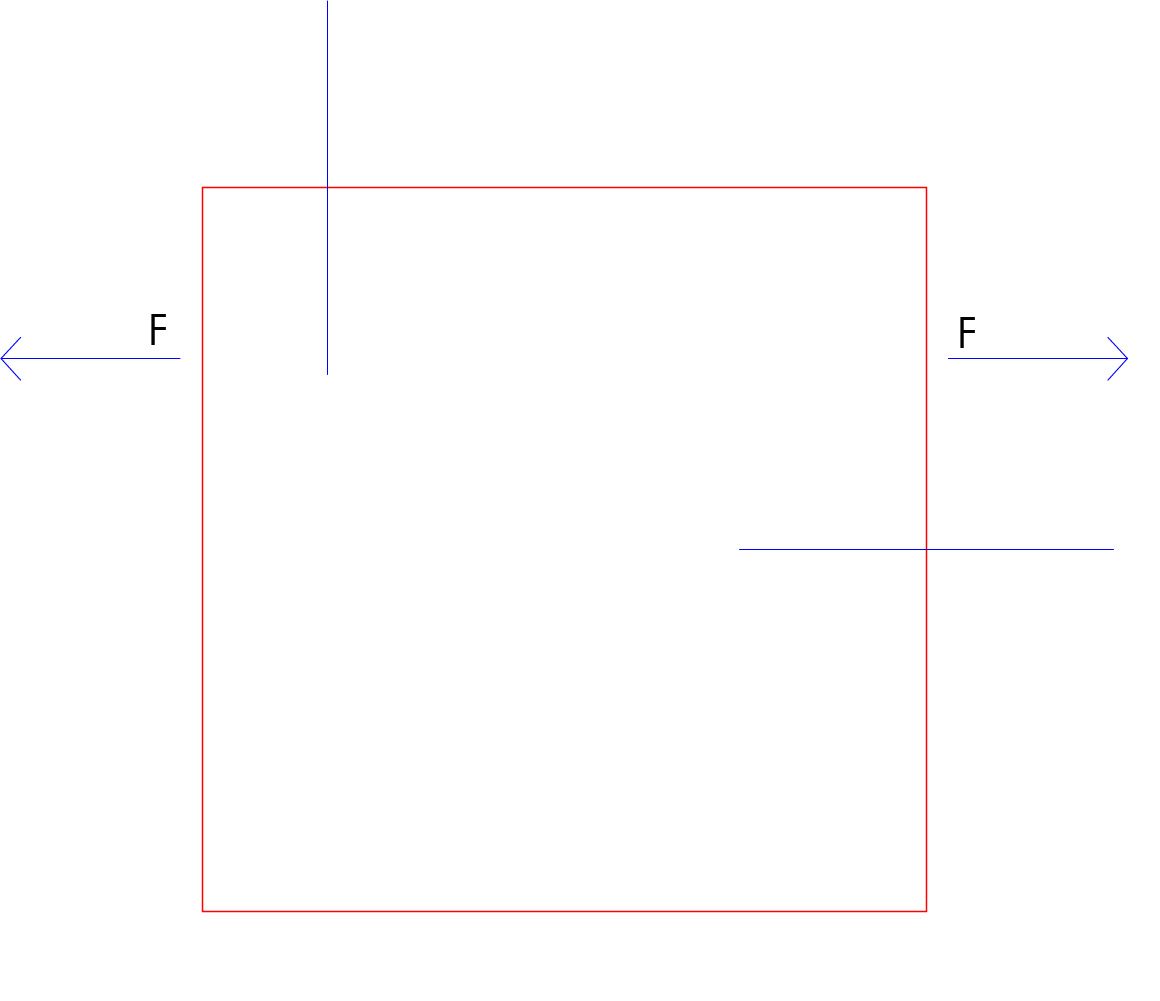
Con le sole equazioni di equilibrio a traslazione e rotazione questa struttura non è risolvibile in quanto in qualunque punto noi decidiamo di tagliare la struttura ci sono sempre sei incognite e solo tre equazioni. La struttura quindi è tre volte iperstatica. La situazione cambia notevolmente se inseriamo tre cerniere interne come mostrato in figura.

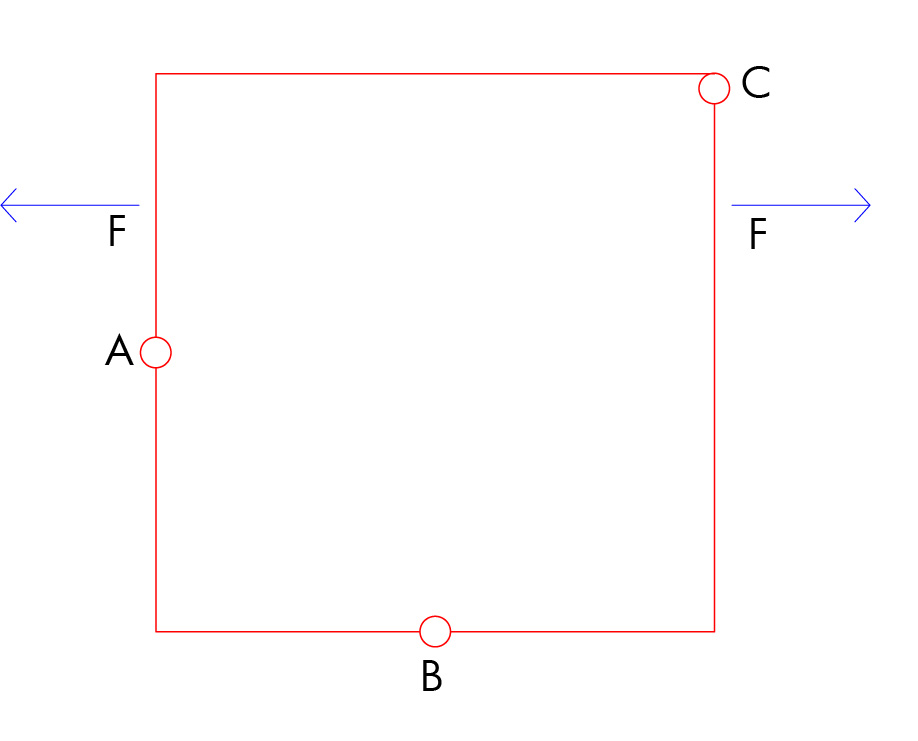
Conosciamo ora tre incognite interne e dunque la struttura è isostatica.

Per risolvere la struttura consideriamo i tratti che vanno da cerniera a cerniera e li poniamo in equilibrio.

 

 

 

 

 

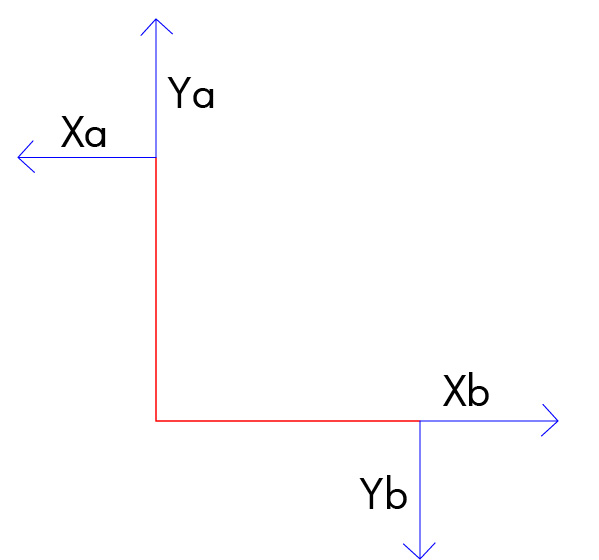
Tratto AB:

Xa=Xb

Ya=Yb

Xa*l/2= Ya*l/2

 

 

 

 

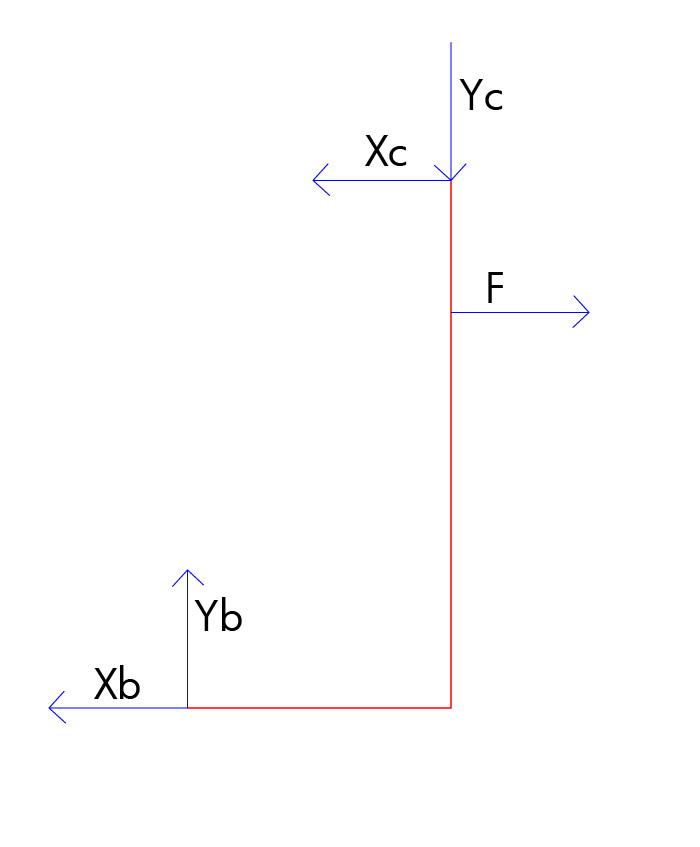
Tratto BC:

Xb + Xc - F= 0

Yb= Yc

-Xb*l - Yb*l/2 + F*l/4=0

 

 

 

 

 

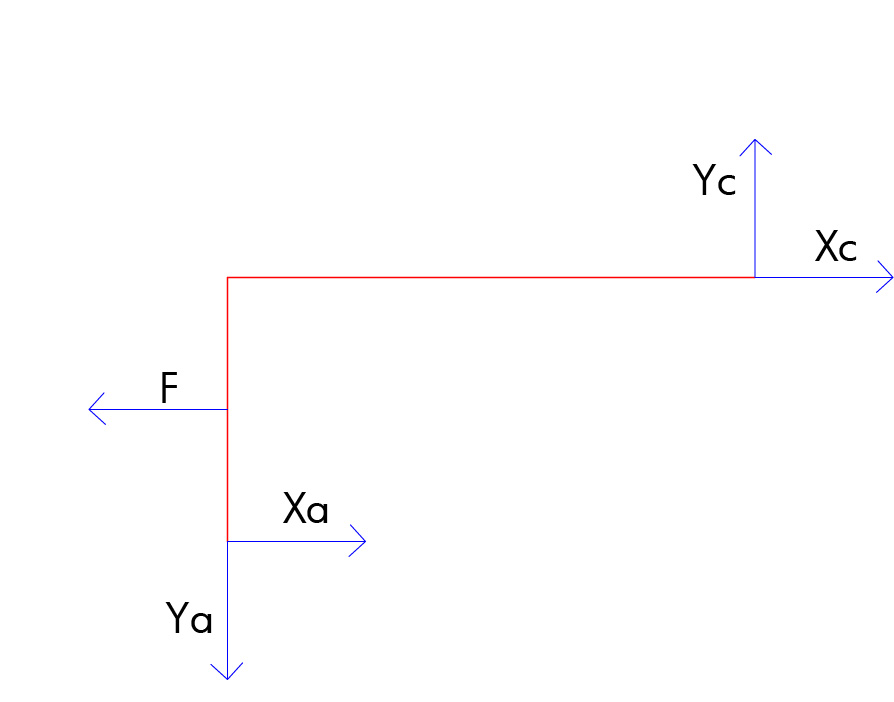
Tratto AC:

Xc + Xa - F= 0

Ya= Yc

-Xc*l/2 + Yc*l + F*l/4=0

 

Dai tre sistemi ricaviamo:

Yb=Yc=Ya=Xa=Xb= F/6 e Xc= 5/6 F

Dopo aver calcolato a mano i diagrammi delle sollecitazioni abbiamo effettuato la verifica in SAP2000 con una F=50 KN.

N)                                                                                  T)                                                                                 

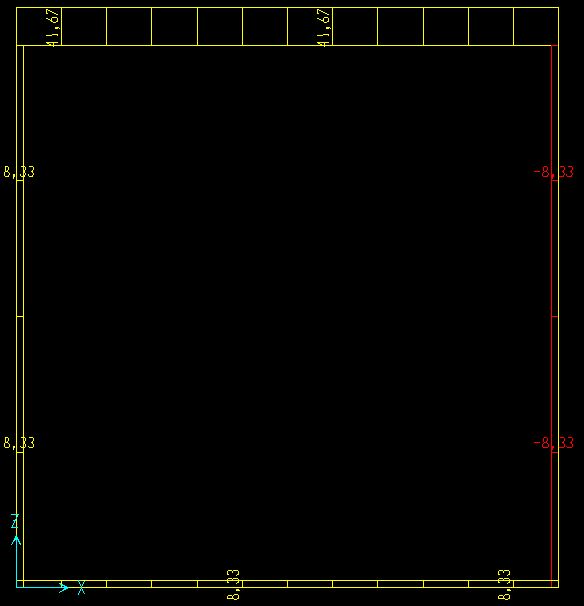
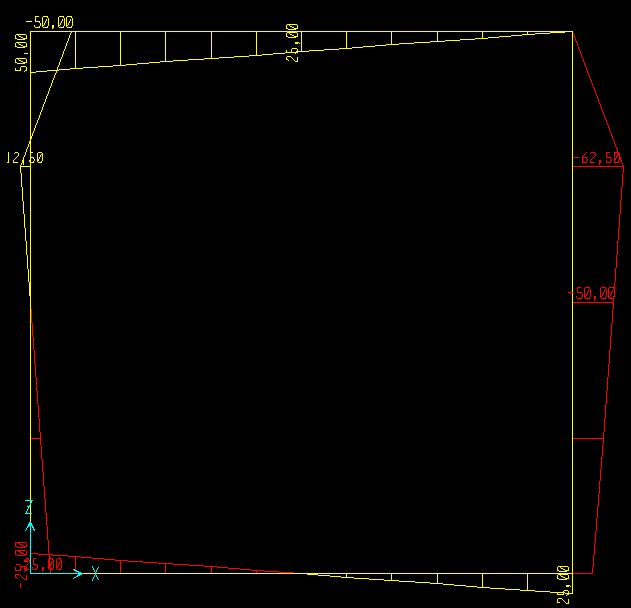
M)

 

 

 

 

 

 

Per prima cosa disegno la struttura reticolare spaziale su AUTOCAD:

Apriamo un nuovo file e creiamo un nuovo layer "aste" poichè se disegnassi con il layer 0 poi SAP non lo riconoscerebbe.

Disegno aste di 2 m con il comando polilineae assegno come origine il punto (0,0) della struttura.

Ora utilizzo il comando array andando ad impostare i valori della serie rettangolare con 1 riga e 4 colonne a distanza di 2 m. Infine chiudo la serie con un asta verticale.

Ora effettuo una rotazione 3d (comando Ruota3D) e passo alla visualizzazione isometrica trdimensionale.

A questo punto cambio l' UCS in modo da disegnare le aste sul piano y-z facendo attenzione a disegnare sempre un modulo aperto in modo tale da non sovrepporre alcun asta.

Utilizzo di nuovo il comando array per duplicare il modulo lungo l' asse x ad una distanza di 2m.

Utilizzo ancora una volta il comando array per moltiplicare la struttura disegnata fino a ora. Imposto nella serie rettangolare 1 riga e 7 colonne alla distanza di 2m lungo l' asse y. Infine calcello l' ultima colonna per ottenere una struttura reticolare spaziale composta da 4 moduli lungo l' asse x e 6 moduli lungo l' asse y.

Salvo in AutoCAD 2000/LT2000 DXF per poi importare il file su SAP2000.

CALCOLO DELLA STRUTTURA IN SAP2000

Importo il file disegnato con Autocad su SAP ricordando di impostare come unità di misura KN,m,C.

A questo punto assegno i vincoli ai 4 angoli inferiori della struttura. Assegna->Nodo->Vincoli Esterni

Ora seleziono tutta la struttura e rilascio i momenti, in modo che le aste lavorino solo a sforzo normale. Assegna->Frame->Rilasci, e spunto il momento 22 e 33 sia all' inizio che alla fine.

Definisco il materiale della struttura per poi assegnarlo a tutte le aste. Definisci->Materiali->Nuovo materiale->seleziono steel e lo chiamo ACCIAIO.

Ora vado ad assegnare all’acciaio un sezione tubolare, quindi vado su Definisci->Proprietà Sezione->Aggiungi Nuova Proprietà e su Proprietà Tipo Sezione Frame seleziono l’acciaio e gli assegno la sezione tubolare, poi come materiale gli assegno “acciaio” cioè il materiale che ho creato in precedenza.

Assegno la sezione tubolare a tutte le aste tramite Assegna->Frame->Sezioni Frame e seleziono FSEC1 creata precedentemente.

Sulle aste vedrò comparire il nome della sezione assegnata.

Ora vado a definire il carico concentrato che assegnerò sui nodi superiori della struttura. Definisci->Schemi di carico e creo un nuovo carico che chiamerò "forza concentrata". N.B. Devo ricordare di assegnare al nuovo carico 0 come "Peso Proprio Moltiplic."

Ora seleziono tutti i nodi superiori della struttura e assegno il carico. Devo fare attenzione a selezionare solo i nodi superiori della struttura perciò nelle "Opzioni di Visualizzazione" nella colonna "Nodi" deseleziono "Invisibile" e nella colonna "Frame" seleziono "Frame non in vista".

In questo modo SAP mi fa vedere solo i nodi che andrò a selezionare.

Mi assicuro di aver selezionato solo i nodi superiori passando alla visualizzazione del piano x-z.

PERFETTO! Assegno il carico precedentemente creato alla selezione. Caricherò la struttura con una forza concentrata di 40 KN.

Riaccendo le aste e visualizzo le forze concentrate nei nodi.

Posso finalmente lanciare l' analisi. Seleziono DEAD e MODAL e clicco "Non eseguire caso".

L' analisi mi fa visualizzare la deformata della struttura:

Per visualizzare il valore dello sforzo assiale su ogni asta faccio: Mostra sollecitazioni->Tensioni Frame->Sforzo assiale.

Ora devo individuare le aste con maggiore sforzo assiale sia di compressione che di trazione. Vado perciò su

Visualizza->Mostra Tabelle e in "Risultati Analisi" seleziono "Output Elemento".

Nella tabella scelgo l' asta con il maggior sforzo di compressione (-385,631 KN):

E l' asta con maggior sforzo di trazione (263,469 KN):

 

PROGETTO DELLE ASTE

-Progetto a compressione

Devo innanzitutto scegliere il tipo di acciaio con cui realizzerò le aste. Scelgo un S275 con tensione di snervamento di 275 MPa.

Sapendo che  σ = fD = N/A posso ricavare l' area minima necessaria. Applico perciò la relazione:

A = N/fD  dove fD è la tensione di design.

La tensione di progetto si ricava dalla formula: fD = fy/ϒm = 275/1,05 = 261,90 MPa

,dove fy è la tensione caratteristica di snervamento e ϒm è il coefficiente di sicurezza per acciaio da carpenteria pari a 1,05.

A = Nmax(compressione)/fD = 385631 N/261,9 N/mm² = 1472,436 mm² = 14,72 cm²

Ora prendo il profilario e scelgo una sezione che abbia un ' area maggiore di quella trovata:

Scelgo un tubolare con diametro di 11,43 cm e spessore di 4,5 mm con area di 15,5 cm².

 

-Progetto a trazione

Applico la stessa formula per il progetto a trazione, mantenedo il tipo di acciaio che ho scelto per le aste compresse:

A = Nmax(trazione)/fD = 263469 N/261,9 N/mm² = 1006 mm² = 10,06 cm²

Scelgo un tubolare con diametro di 8,89 cm e spessore di 4 mm e area di 10,7 cm².

VERIFICA SNELLEZZA

Nell’asta soggetta a compressione, inoltre, occorre verificare che l’asta non sia troppo snellaper non incorrere in uno sbandamento laterale. Attraverso la formula di Eulero posso calcolarmi il valore del carico critico per cui si innesca il fenomeno dello sbandamento:

• Se Nmax ≥ Pcrit → Asta instabile
• Se Nmax < Pcrit → Asta stabile

Pcrit = (∏² * E * Jmin) / l₀²                              dove: E = modulo elastico dell' acciaio

                                                                                 Jmin = momento d’inerzia minore

                                                                                 l₀ = lunghezza libera d' inflessione, che dipende dalla luce e dalla condizione di vincolo Nel nostro caso i vincoli sono costituiti solo da cerniere per cui l₀ = l, dove l è la lunghezza dell’asta quindi pari a 2,828m (poiché l’asta soggetta a massimo sforzo di compressione è una delle aste inclinate)

 

Pcrit = (3,14² * 210000N/mm² * 2340000 mm⁴) / 2828² mm = 605808N = 605,808 KN

 

Nmax = 385,631KN < Pcrit = 605,808 KN → la sezione è verificata.