La destinazione d’uso del progetto proposto è di tipo residenziale: l’edificio è composto di due piani con il medesimo schema strutturale. Per prima cosa analizziamo la pianta al fine di individuare la trave maggiormente sollecitata. Scegliamo quindi di dimensionare la trave che “porta” una superficie di solaio maggiore: nel nostro caso la trave “C”.

Considerando come dati la pianta e la sezione della nostra struttura, progetteremo tre differenti solai da associare al progetto dimensionale della trave scelta in tre differenti tecnologie costruttive : calcestruzzo armato, acciaio e legno.
-
CALCESTRUZZO ARMATO
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in latero cemento. Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.
 1a
1a
analisi dei carichi
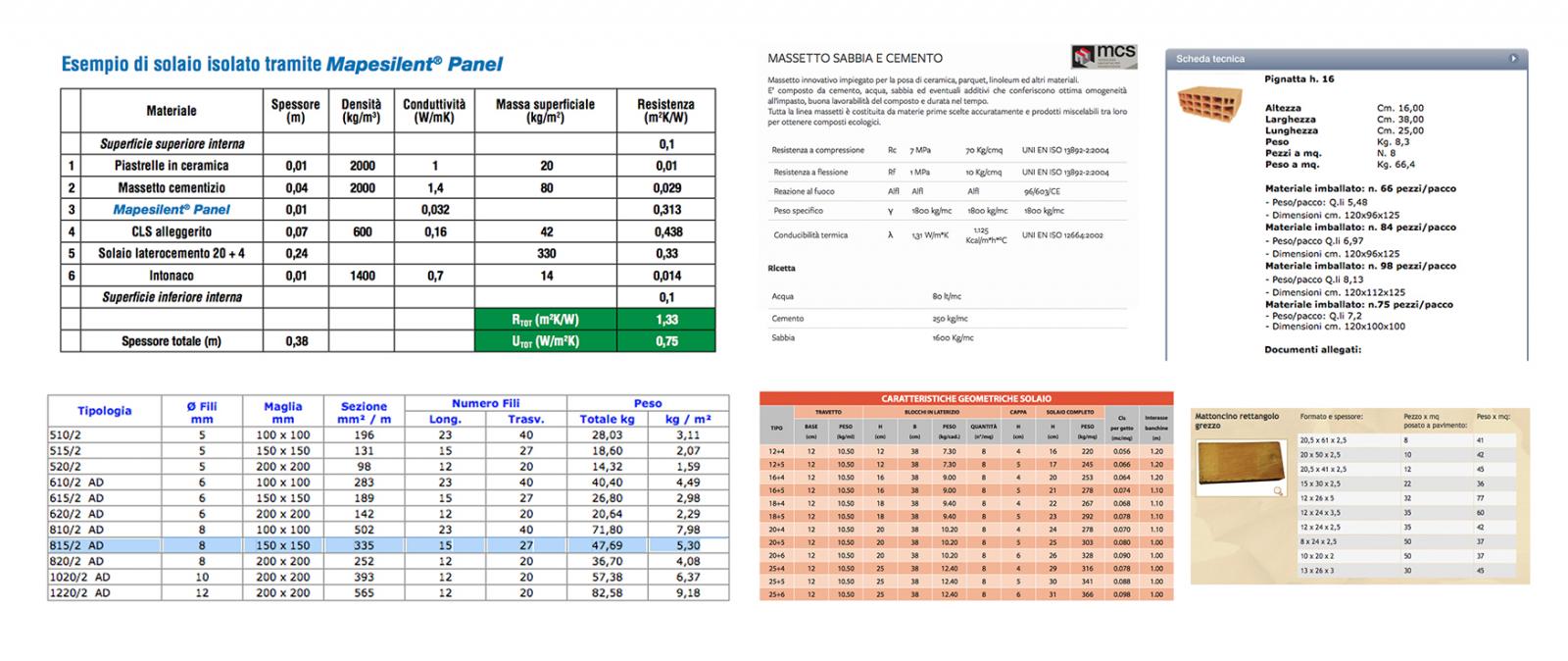
Per effettuare l’analisi dei carichi sono stati scelti dei materiali e degli elementi identificati dalle schede tecniche fornite dai produttori (figura 2a). Verrà calcolato tutto per una porzione di solaio pari a 1m2 (figura 3a).
figura 2a
 figura 3a
figura 3a
qs (carichi strutturali)
_caldana in calcestruzzo: [(0,04*1,00*1,00)m3 + (0,16*0,20*1,00)m3]/m2 * 2300kg/m3 = 165,60 kg/m2 = 1,66 kN/m2
_rete elettrosaldata (maglia 15cm*15cm ø8): 5,3 kg/m2 = 0,053 kN/m2
_travetti: 2,00ml/m2 * 10,50kg/ml = 21,00 kg/m2 = 0,21 kN/m2
_pignatte (8 pz/m2): 66,4 kg/m2 = 0,66 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qs = 2,58 kN/m2
qp (carichi permanenti)
_pavimento in cotto (10 pz/m2): 42,0 kg/m2 = 0,42 kN/m2
_massetto in sabbia e cemento: (0,04*1,00*1,00)m3/m2 * 1800kg/m3 = 72,0 kg/m2 = 0,72 kN/m2
_isolamento acustico: 5 kg/m2 = 0,05 kN/m2
_intonaco: 13,3kg/m2 = 0,13 kN/m2
_incidenza tramezzi: 0,5 kN/m2
_incidenza impianti: 1,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qp = 2,82 kN/m2
qa (carichi accidentali)
_carichi accidentali in ambiente residenziale: 2,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qa = 2,00 kN/m2
Il valore di carico da utilizzare per il progetto della trave non è dato dalla sola somma qs+qp+qa: i valori trovati devono ora essere moltiplicati per i rispettivi coefficienti stabiliti dalla normativa; i loro risultati poi andranno sommati e daranno come risultato qtot /m2 ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere qu /ml (cioè il carico agente su un metro lineare di trave) sarà sufficiente moltiplicare qtot /m2 per la misura dell’interasse: conosceremo così quindi il carico della superficie disegnata in blu più scuro (1m2 * interasse) in figura 1c.
qtot /m2 = ƔG1qs + ƔG2qp + ƔQ1qa ƔG1=1,3 ƔG2=1,5 ƔQ1=1,5
qtot /m2 = (1,3 * 2,58) + (1,5 * 2,82) + (1,5 * 2,00) = 10,58 kN/m2
qu /ml = qtot /m2 * interasse = 10,58 kN/m2 * 6m --------------------> qu /ml = 63,53 kN/m
Passiamo adesso al calcolo del momento flettente massimo della nostra trave: essendo una trave doppiamente appoggiata la formula del momento massimo è nota: Mmax = ql2/8.
Mmax = [(63,50 kN/m) * (6m)2]/8 ----------------------------------> Mmax = 285,89 kNm
Ora scegliamo il tipo di calcestruzzo e di acciaio che vogliamo utilizzare per sviluppare il nostro progetto. Entrambi saranno caratterizzati da una resistenza caratteristica: moltiplicando tali resistenze caratteristiche per i relativi coefficienti maggiorativi otterremo i valori delle loro resistenze di progetto (fcd per il calcestruzzo, fyd per l’acciaio: la “y” sta per yield = snervamento, la “d” per design = progetto).
fcd = αcc*fck/Ɣm = 0,85*(40 N/mm2)/1,5 ----------------------------> fcd = 19,83 N/mm2
fyd = fyk/ Ɣy = (450 N/mm2)/1,15 ----------------------------> fyd = 391,3 N/mm2
Adesso abbiamo tutti i dati necessari a ricavare la l’altezza della trave. Lo faremo sfruttando la relazione che intercorre tra il concetto di momento flettente (Bernoulli) e il concetto di tensione (Navier).
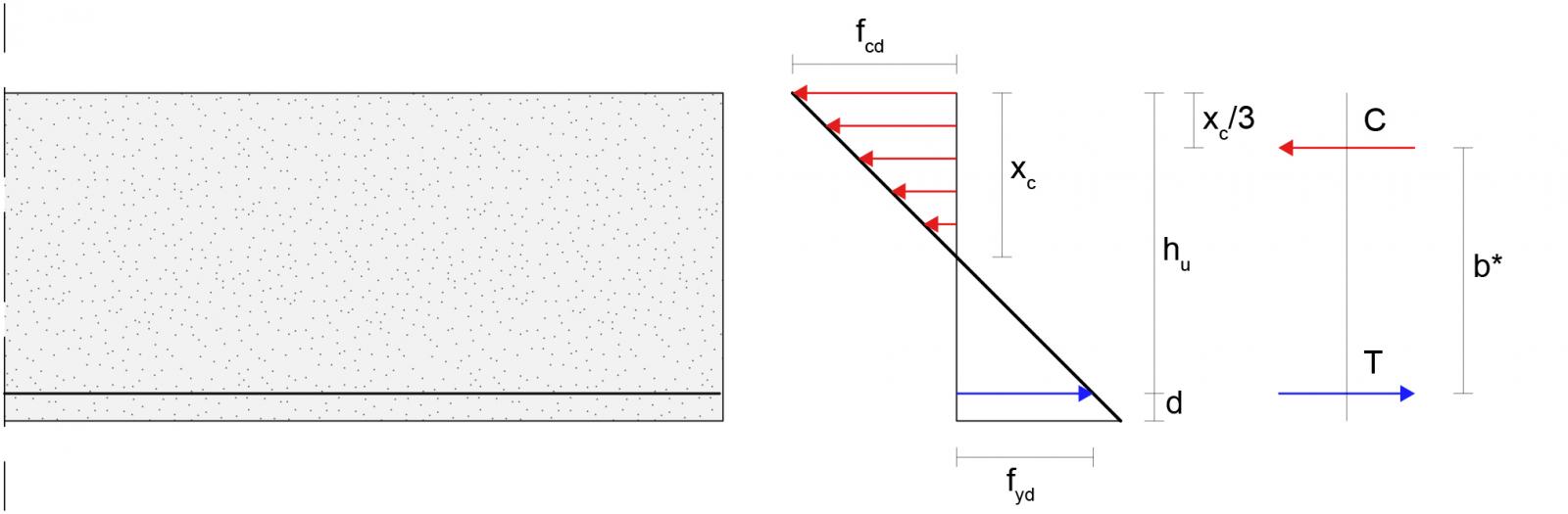 .figura 1d
.figura 1d
xc : hu = fcd : (fcd + fyd/n) ---> xc= hu* [fcd*(fcd + fyd/n)]
con α = fcd*(fcd + fyd/n) ---> xc = α * hu
Dalla figura 1d notiamo che la forza di compressione del calcestruzzo (C = (fcd*b*xc)/2) e la forza di trazione dell’acciaio (T = Af*fyd) costituiscono una coppia di forze parallele, con stesso modulo, verso opposto e braccio non nullo (b* = hu – xc/3). Generano quindi un momento:
M = C*b* = T*b*
Prendendo in considerazione solo la parte riguardante la compressione (e quindi l’azione generata sul calcestruzzo) possiamo giungere alla formula che ci permetterà di calcolare l’altezza utile (hu) che la nostra trave deve avere, fissando arbitrariamente un valore per la base (in questo caso scelgo b= 30cm).
M = [(fcd*b*xc)/2]*[hu – (α*hu/3)]
Sapendo che (xc = α * hu) continuiamo a sviluppare la formula esplicitando hu fino ad ottenere:
hu = √ 2/[fcd*(1-α/3)*α] * √ M/b con r = √ 2/[fcd*(1-α/3)*α] hu = r * √ M/b
Sommando al valore di hu trovato quello dell’altezza del copriferro “δ” otteniamo la nostra hmin. I calcoli effettuati hanno preso in considerazione la massima resistenza del materiale, quindi per i dati di carico e misura della base da noi scelti, l’altezza trovata è l’altezza minima resistente “hmin”. Le misure di progettazione del calcestruzzo sono espresse in multipli di 5 cm, per questo l’altezza che sceglieremo sarà un valore multiplo di 5 subito più grande dell’hmin trovata. Nel nostro caso:
hu = 50,98cm δ = 5cm ------> hmin = hu + δ = (50,98 + 5)cm = 55,98cm ----> H = 60,00 cm
Terminata la fase di progetto passiamo alla fase di verifica. Adesso andremo ad aggiungere il peso proprio della trave alla somma dei carichi portati dalla trave stessa, calcoleremo il momento massimo, e verificheremo poi se la sezione scelta sarà adatta anche a queste nuove carattristiche di carico.
pt/ml = 4,50 kN/m lo moltiplico per ƔG1 = 1,3
qu’ = qu + (4,50 kN/m*1,3) = (63,53 + 5,85) kN/m --------------------> qu’ = 69,38 kN/m
M’max = qu’ * l2 / 8 ------> M’max = (69,38 kN/m) * (6m)2 / 8 ----------> M’max = 312,21 kNm
M’ = C*B* = T*B* ------> h’u = √ 2/[fcd*(1-α/3)*α] * √ M’/b ----------> h’u = 53,28 cm
h’min = h’u + δ = (53,28 + 5)cm = 58,28cm -----------------------------> H’ = 60,00 cm
La sezione scelta risulta quindi verificata in quanto -----------------------> H = H’ = 60,00 cm

2. ACCIAO
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in lamiera grecata. Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.

analisi dei carichi
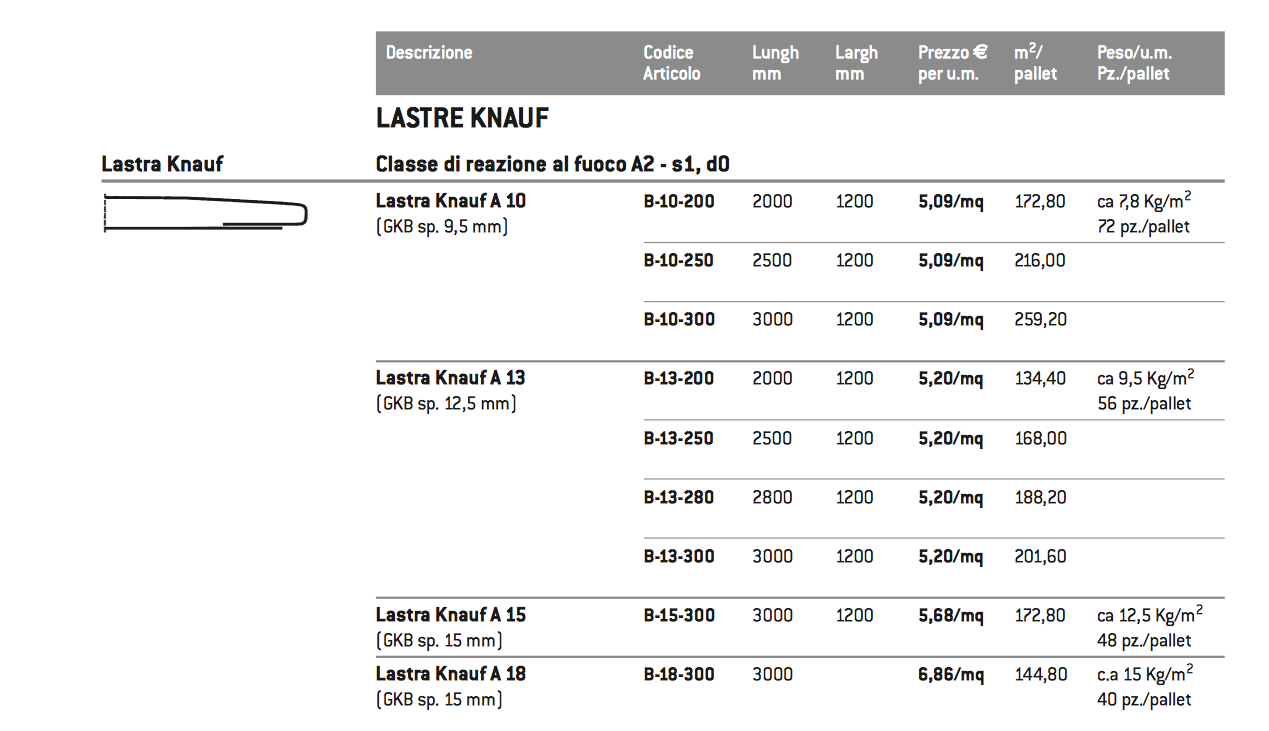
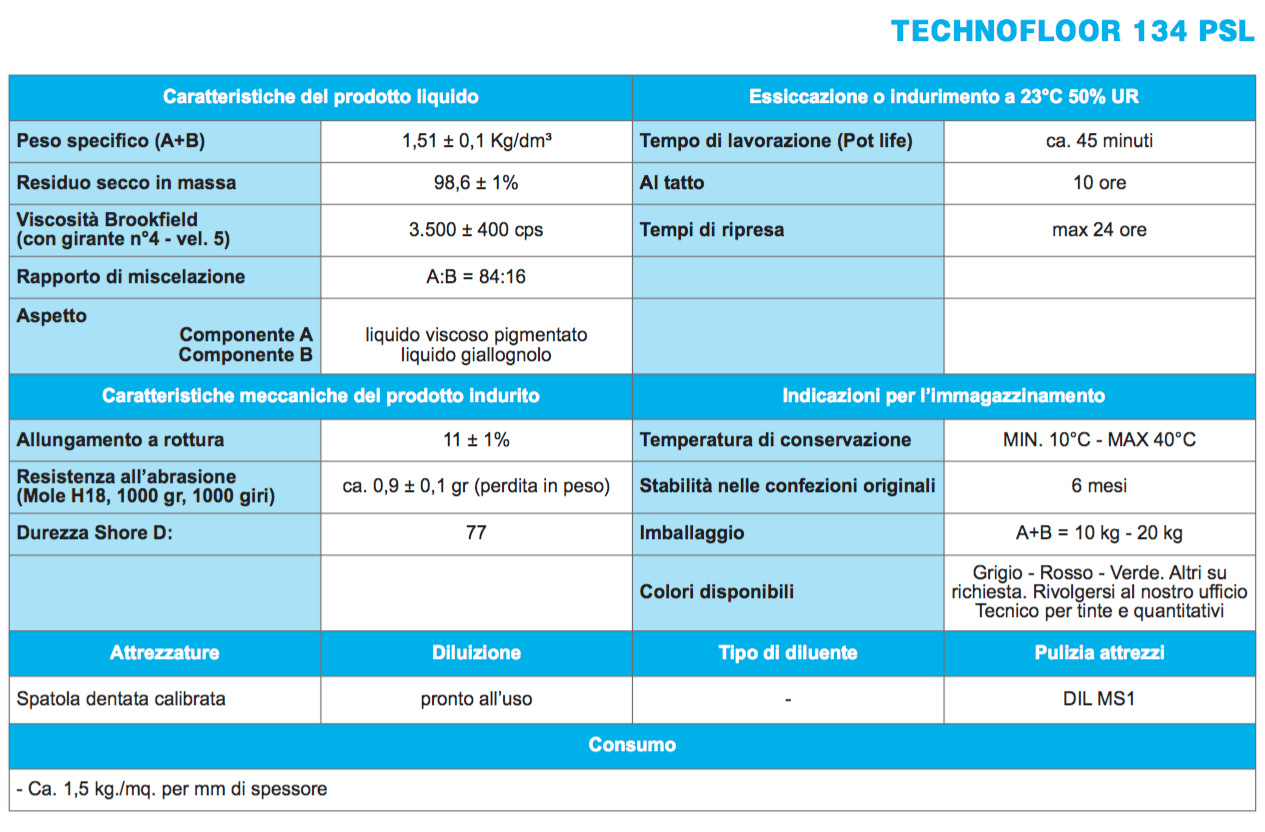
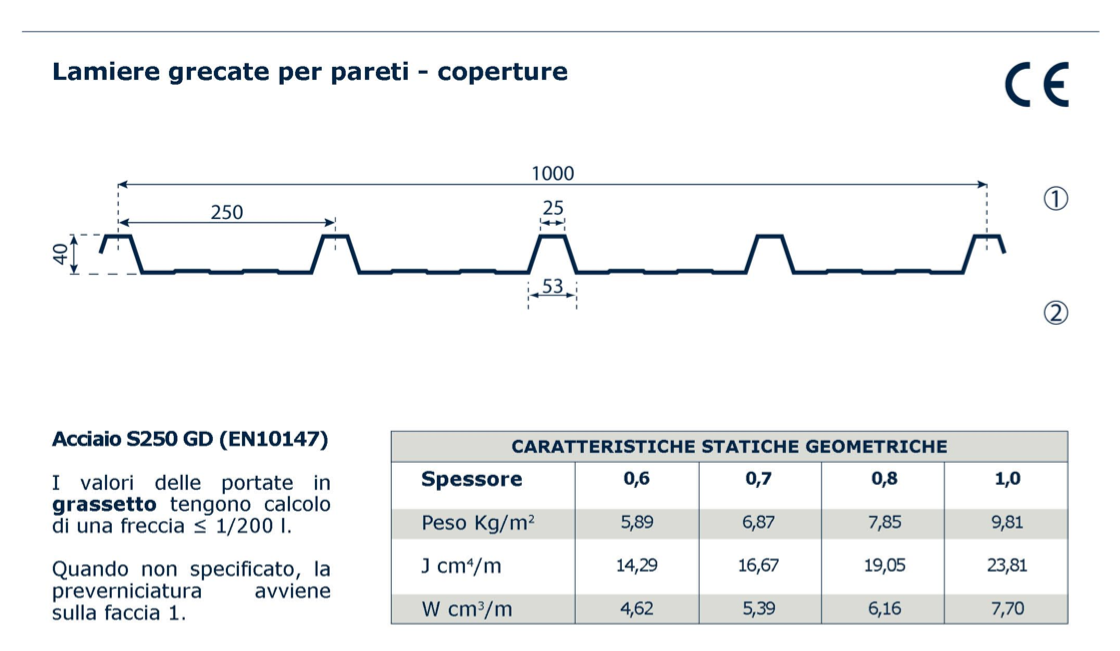
qs (carichi strutturali)
_caldana in calcestruzzo: [0,0538*1,00)m3]/m2 * 2300kg/m3 = 123,74 kg/m2 = 1,24 kN/m2
_rete elettrosaldata (maglia 15cm*15cm ø8): 5,3 kg/m2 = 0,053 kN/m2
_lamiera grecata: 2,37 kg/m2 = 0,024 kN/m2
_travetti in acciaio IPE 200: 0,24 kN/m * 1m/m2 = 0,24 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qs = 1,56 kN/m2
qp (carichi permanenti)
_pavimento in resina: 1610 kg/m3 * 0,015 m3/m2= 24,15 kg/m2 = 0,24 kN/m2
_massetto in sabbia e cemento: (0,04*1,00*1,00)m3/m2 * 1800kg/m3 = 72,0 kg/m2 = 0,72 kN/m2
_isolamento acustico: 5 kg/m2 = 0,05 kN/m2
_controsoffitto in cartongesso: 7,8 kg/m2 = 0,08 kN/m2
_incidenza tramezzi: 0,5 kN/m2
_incidenza impianti: 1,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qp = 2,59 kN/m2
qa (carichi accidentali)
_carichi accidentali in ambiente residenziale: 2,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qa = 2,00 kN/m2
Sommando i valori dei carichi ottenuti troveremo qtot /m2, ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere qu /ml (cioè il carico agente su un metro lineare di trave) sarà sufficiente moltiplicare qtot /m2 per la misura dell’interasse.
qtot /m2 = ƔG1qs + ƔG2qp + ƔQ1qa ƔG1=1,3 ƔG2=1,5 ƔQ1=1,5
qtot /m2 = (1,3 * 1,56) + (1,5 * 2,59) + (1,5 * 2,00) = 8,91 kN/m2
qu /ml = qtot /m2 * interasse = 8,91 kN/m2 * 6m ---------------> qu /ml = 53,48 kN/m
Passiamo adesso al calcolo del momento flettente massimo della nostra trave: essendo una trave doppiamente appoggiata la formula del momento massimo è nota: Mmax = ql2/8.
Mmax = [(53,48 kN/m) * (6m)2]/8 ----------------------------> Mmax = 240,65 kNm
Ora scegliamo un tipo di acciaio, osserviamo la sua resistenza caratteristica “fyk” e dividiamolo per il suo coefficiente di sicurezza ( 1,15 per l’acciaio) per ottenere il valore della resistenza di progetto “fyd” dell’acciaio utilizzato nella nostra struttura.
fyd = fyk / 1,15 = 275 N/mm2/1,15 ---------------------------> fyd = 239,1 N/mm2
Ora grazie alla formula per ricavare lo sforzo flessionale (formula di Navier), ricaveremo l’altezza della sezione della nostra trave.
σmax = Mmax/Wx ------> Wx = Mmax/σmax
Wx = (240,65 * 106) Nmm/(239,1 N/mm2) = 1’006’482,64 mm3 -----> WX = 1006,48 cm3
Avendo utilizzato nei calcoli il valore di resistenza massima a flessione, sceglieremo da tabella la sezione IPE con un valore Wx subito maggiore di quello da noi trovato: quindi una trave IPE 400 con Wx (ipe 440) = 1160 cm3.
Terminata la fase di progetto passiamo alla fase di verifica. Adesso andremo ad aggiungere il peso proprio della trave alla somma dei carichi portati dalla trave stessa, calcoleremo il momento massimo, e grazie al valore di Wx trovato verificheremo poi se la sezione scelta sarà adatta anche a queste nuove carattristiche di carico.
pt/m2 = 0,66 kN/m2 lo moltiplico per ƔG1 = 1,3
qu’ = 58,63 kN/m
M’max = qu’ * l2 / 8 ------> M’max = (58,63 kN/m) * (6m)2 / 8 -----------> M’max = 263,82 kNm
σmax = M’max/W’x ------> W’x = M’max/σmax
W’x = (263,82 * 106) Nmm/(239,1 N/mm2) = 1’103’387,70 mm3 ----> W’X = 1103,4 cm3
La sezione della trave scelta è verificata in quanto anche W’x risulta inferiore al valore di Wx (ipe 440).

3. LEGNO
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in lamiera grecata. Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.

analisi dei carichi
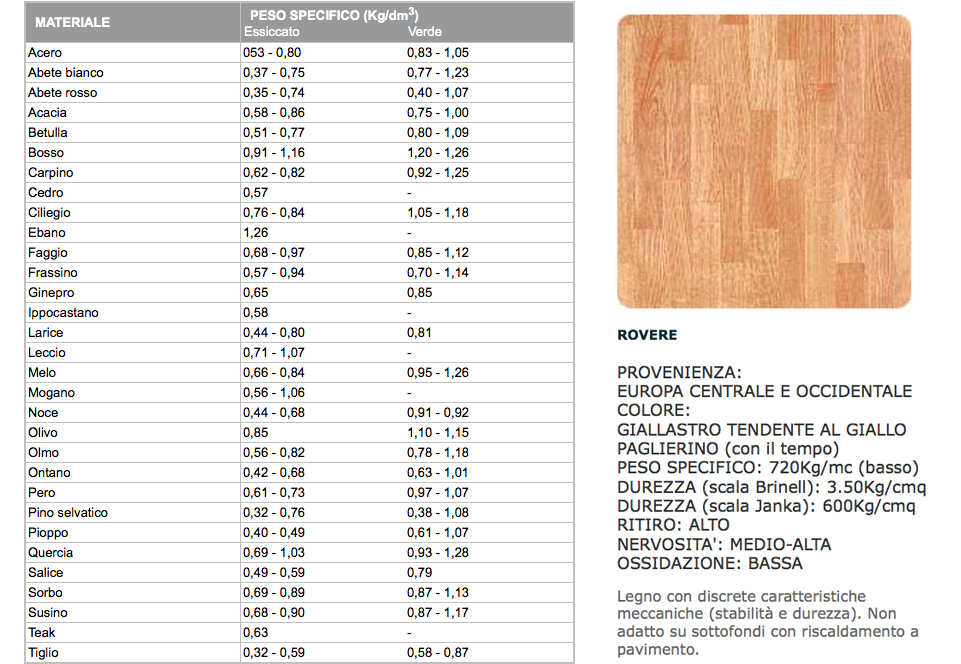
qs (carichi strutturali)
_caldana in calcestruzzo: [0,04*1,00)m3]/m2 * 2300kg/m3 = 92,00 kg/m2 = 0,92 kN/m2
_rete elettrosaldata (maglia 15cm*15cm ø8): 5,3 kg/m2 = 0,053 kN/m2
_tavolato di base in abete rosso: 740 kg/m3 * (0,03*1*1) m3/m2 = 22,2 kg/m2 = 0,22 kN/m2
_travicelli in abete rosso: 740 kg/m3 * (0,08*0,20*1) m3/m2 = 11,84 kg/m2 = 0,12 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qs = 1,31 kN/m2
qp (carichi permanenti)
_pavimento in parquet di rovere: 720 kg/m3 * (0,015*1*1) m3/m2 = 10,80 kg/m2 = 0,11 kN/m2
_massetto in sabbia e cemento: (0,04*1,00*1,00)m3/m2 * 1800kg/m3 = 72,0 kg/m2 = 0,72 kN/m2
_isolamento acustico: 5 kg/m2 = 0,05 kN/m2
_incidenza tramezzi: 0,5 kN/m2
_incidenza impianti: 1,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qp = 2,38 kN/m2
qa (carichi accidentali)
_carichi accidentali in ambiente residenziale: 2,0 kN/m2
-------------------------------------------------------------------------------------------------
_totale: qa = 2,00 kN/m2
Sommando i valori dei carichi ottenuti troveremo qtot /m2, ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere qu /ml (cioè il carico agente su un metro lineare di trave) sarà sufficiente moltiplicare qtot /m2 per la misura dell’interasse.
qtot /m2 = ƔG1qs + ƔG2qp + ƔQ1qa ƔG1=1,3 ƔG2=1,5 ƔQ1=1,5
qtot /m2 = (1,3 * 1,31) + (1,5 * 2,38) + (1,5 * 2,00) = 8,27 kN/m2
qu /ml = qtot /m2 * interasse = 8,27 kN/m2 * 6m ---------------------> qu /ml = 49,64 kN/m
Passiamo adesso al calcolo del momento flettente massimo della nostra trave: essendo una trave doppiamente appoggiata la formula del momento massimo è nota: Mmax = ql2/8.
Mmax = [(49,64 kN/m) * (6m)2]/8 ----------------------------------> Mmax = 223,37 kNm
Ora che abbiamo trovato il momento massimo Mmax possiamo ricavare la resistenza di progetto “fd” moltiplicando la resistenza caratteristica del legno “fmk” per il coefficiente di degradazione nel tempo “kmod”, e dividiamo per Ɣm che è il coefficiente di sicurezza del legno.
fd = fmk*kmod/Ɣm = 24 N/mm2*0,8/1,45 ---------------------------> fd = 13,24 N/mm2
Ora grazie alla formula per ricavare lo sforzo flessionale (formula di Navier), ricaveremo l’altezza della sezione della nostra trave.
σmax = Mmax/Wx ------> Wx = Mmax/σmax
Wx = (223,37 * 106) Nmm/(13,24 N/mm2) = 16’870’845,92 mm3 ----> WX = 16870,85 cm3
Wx = Jx/(h/2) Jx = b+h3/12 Mmax = q*l2/8
Wx = Mmax/σmax
Jx/(h/2) = (q*l2/8)/ σmax
(b+h3/12)/(h/2) = (q*l2/8)/ σmax
h = √(6*q*l2)/(8*b* σmax)
Ipotizzando una base b=30 cm, proseguiamo i calcoli ed otteniamo l’altezza della trave.
hmin = √[(6*49,64*(6*1000)2)/(8*(30*10)* 13,24)] mm = 580,8 mm = 58,08 cm
Scelgo quindi una sezione con una base di 30cm e un’altezza H = 60cm

Commenti recenti