Reference

ciao a tutti! Virginia

Come richiesto un bel ciao sul blog!

ciao!! Giulia :)
 

Ciao ragazzi,

voi siete riusciti ad aprire il file di Osvaldo? Se si, come? Grazie

Inoltre, Lunedì 02 Novembre sarà necessario portare il pc per la lezione di Struttuale?

Buon fine settimana a tutti

                                                                                                      F.R.

proviamo ad entrare nel sito!!!

Inserisco le immagini dell'Analisi fatta in Saap

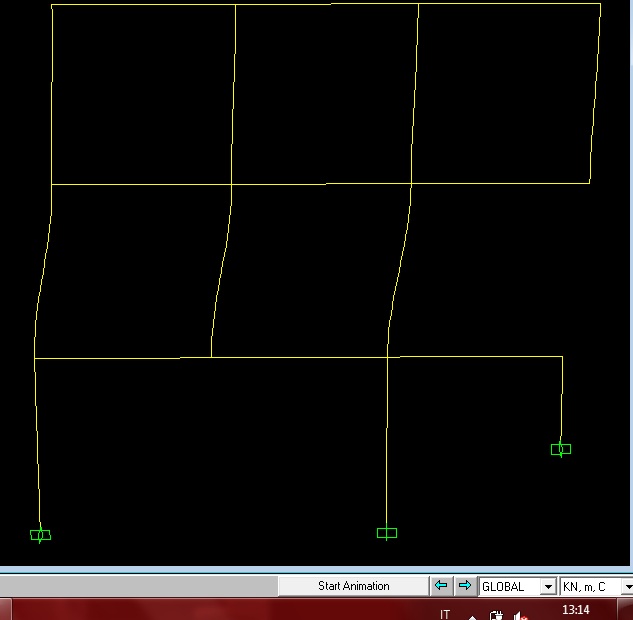
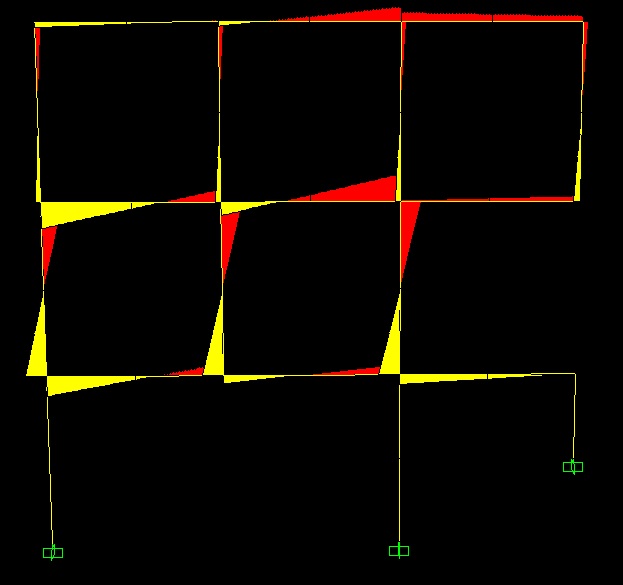
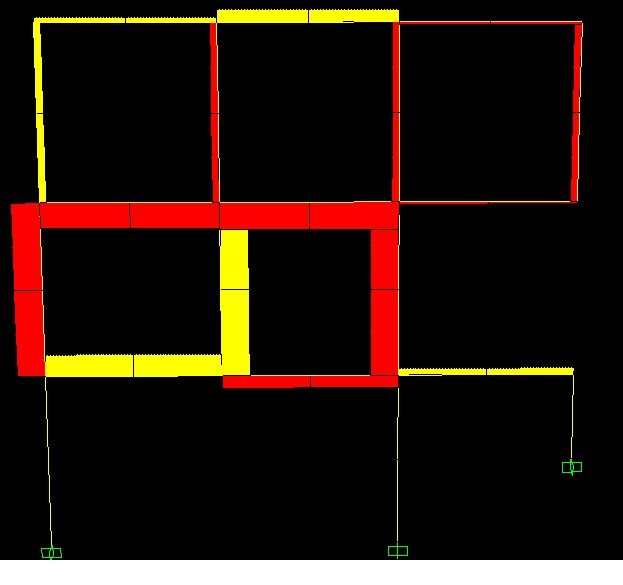
ESERCITAZIONE 2

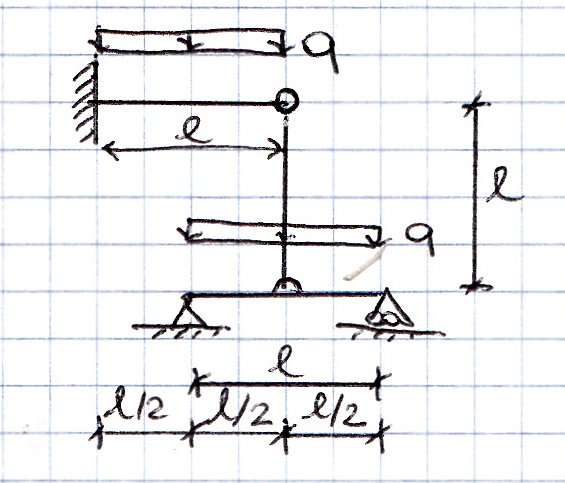
La struttura presa in esame è 1 volta iperstatica quindi per poterne studiare la deformazione le conferisco 1 GdL sostituendo l’asta BD con x, supponendo l’asta tesa. In questo modo ottengo due strutture isostatiche: la mensola con carico distribuito q e forza concentrata all’estremo B, x, e la trave appoggiata con carico distribuito q e forza concentrata in mezzeria x.
Dobbiamo porre come condizione v_B = v_C poiché abbiamo eliminato l’asta ma teniamo in considerazione la sua azione: impedisce l’allontanamento e l’avvicinamento dei punti B e D.

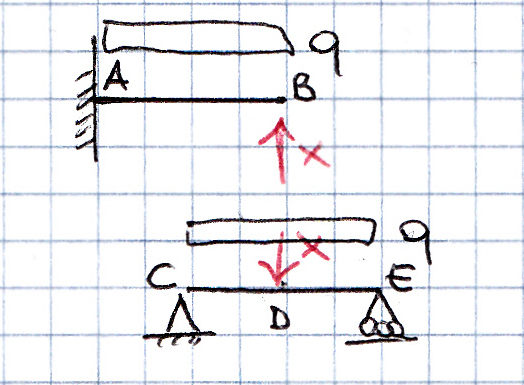
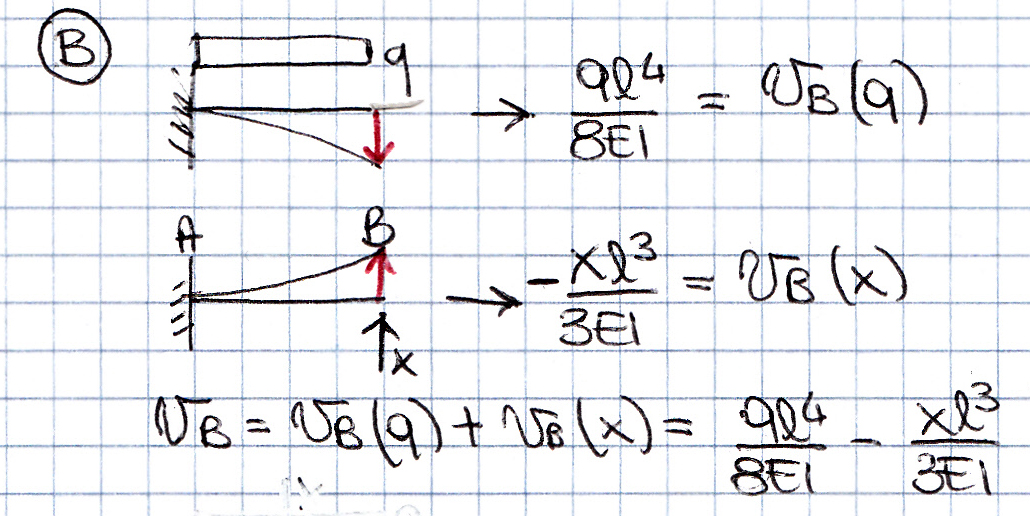
Punto B: lo spostamento relativo v_B = v_B(q) + v_B(x) Risulta quindi: v_B = ql⁴/8EI – xl³/3EI

Punto D: l lo spostamento relativo v_D = v_D(q) + v_D(x) Risulta quindi: v_D = 5ql⁴/384EI + xl³/48EI

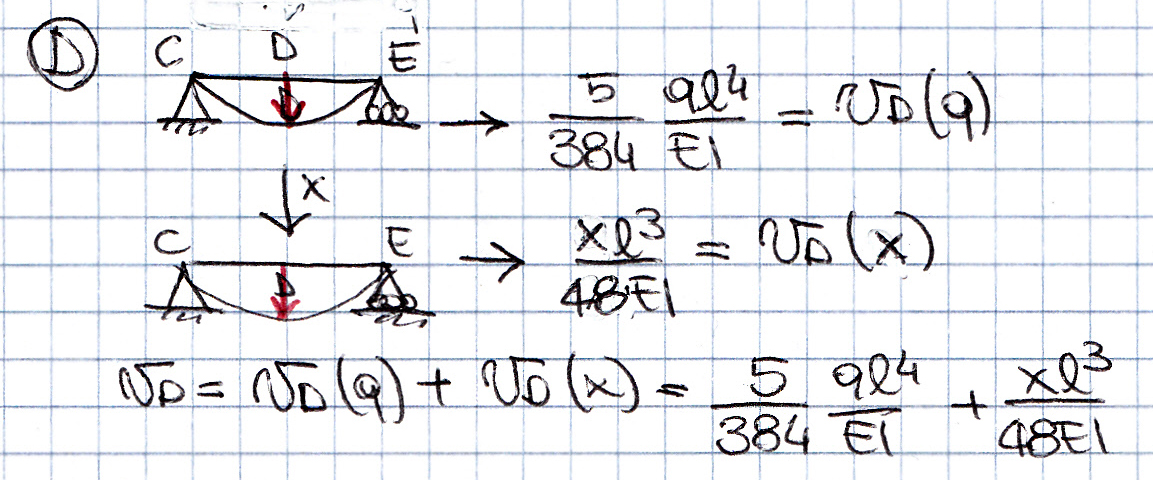
Posto v_B = v_D ottengo: x = 43ql²/136

DIAGRAMMA DEL MOMENTO

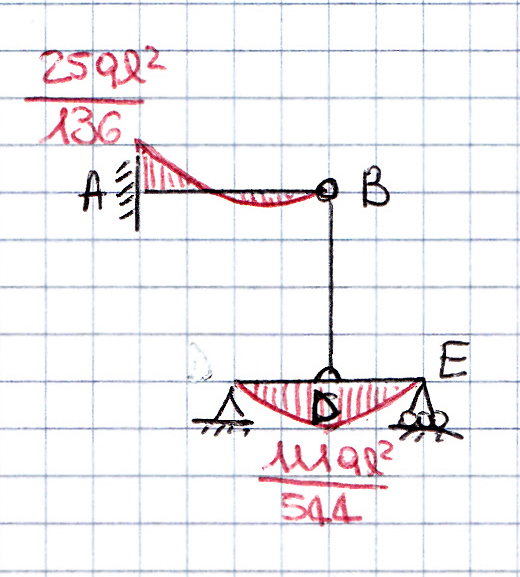
Verifica con SAP 2000

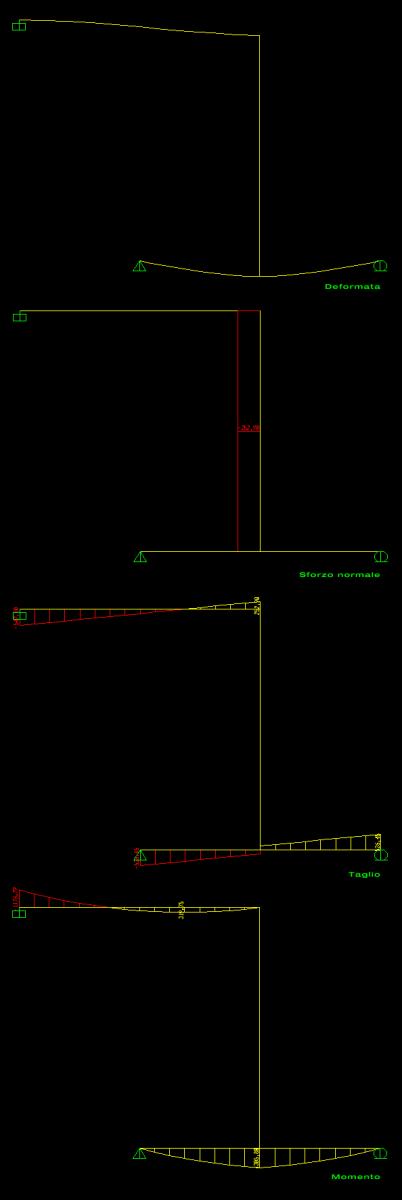
ESERCITAZIONE 1

La struttura presa in esame è 2 volte iperstatica quindi per poterne studiare la deformazione le conferisco 2 GdL consentendo la rotazione relativa nei punti B e C. Così facendo posso trovare il valore dell’azione esercitata dai vincoli in B e C, rispettivamente x₁ e x₂.

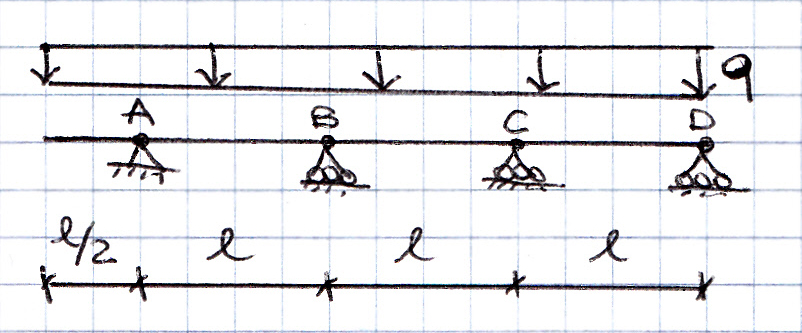
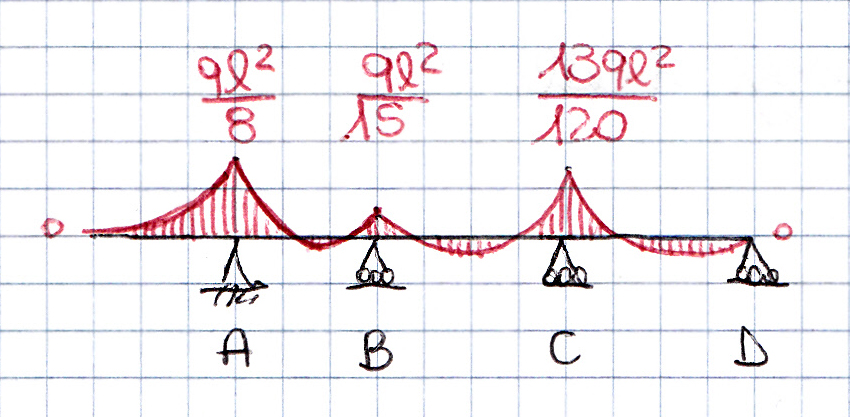
Inoltre per semplificare il calcolo sostituisco la mensola con il momento da essa prodotto: q(l/2)²/2 = (ql²)/8

Punto B: la rotazione relativa Δφ_B = Δφ_Bs - Δφ_Bd = 0 Risulta quindi: Δφ_B = ql²/16 -2x₁/3 –x₂/6 = 0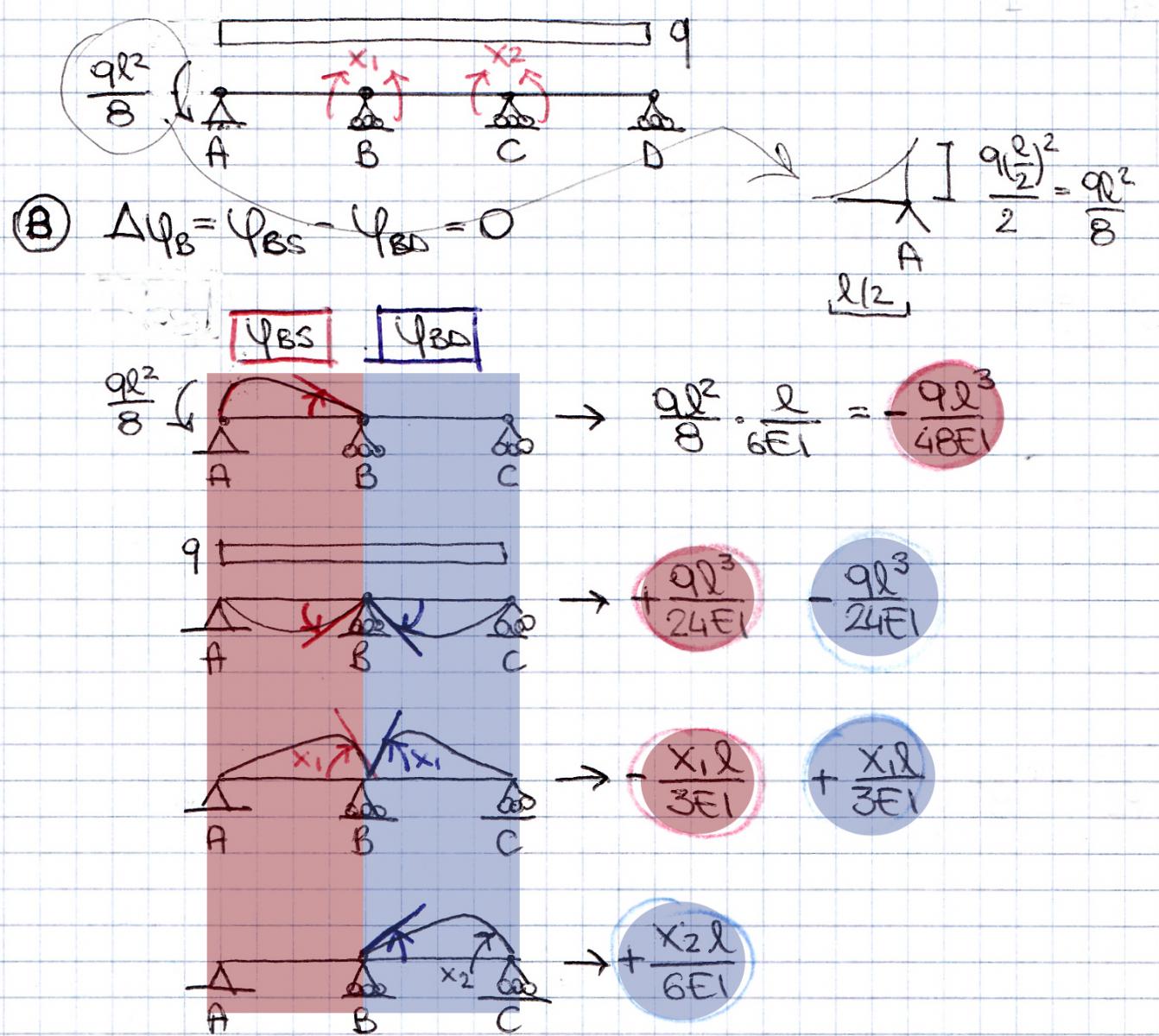

Punto C: la rotazione relativa Δφ_C = Δφ_Cs – Δφ_Cd = 0 Risulta quindi: Δφ_C = ql²/12 -x₁/6 –2x₂/3 = 0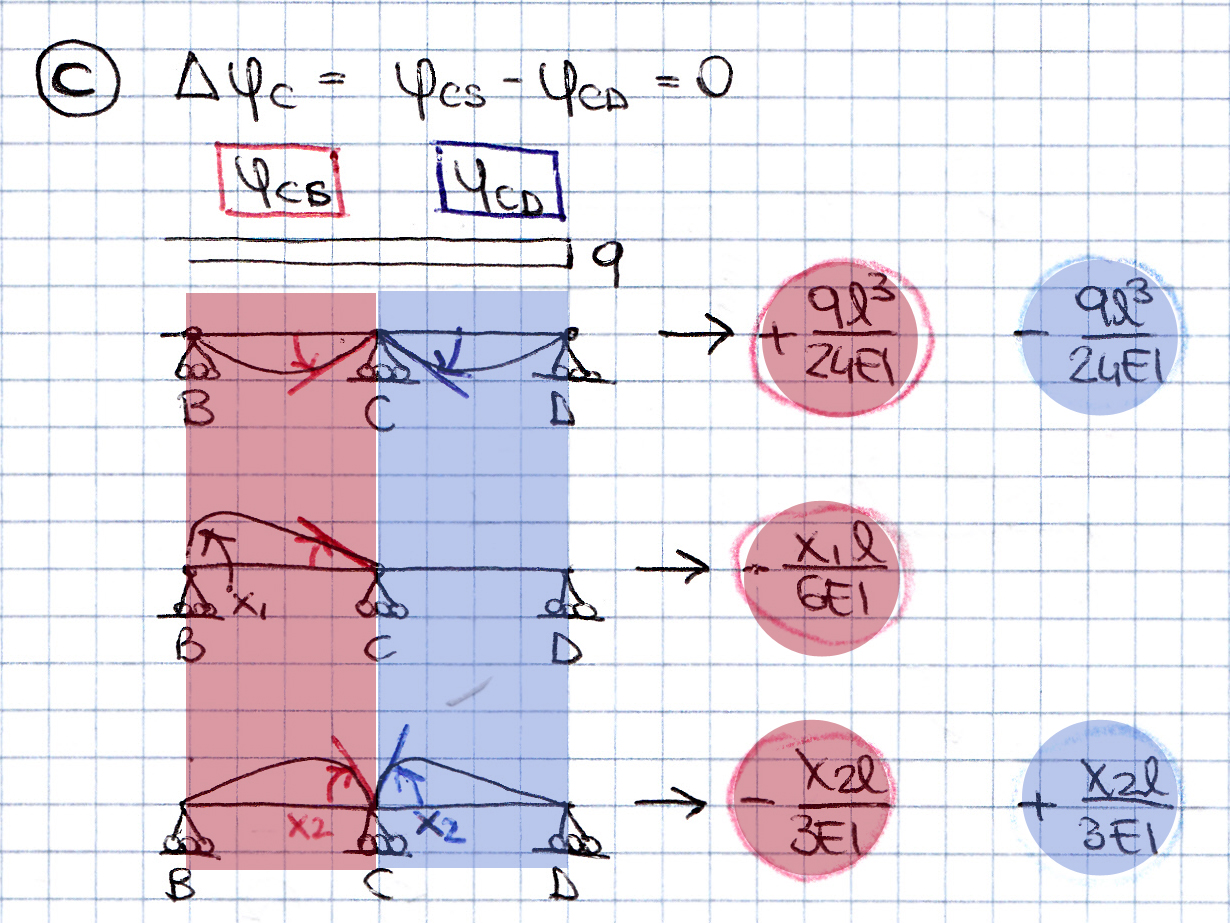

Mettendo a sistema le equazioni delle rotazioni relative ottengo x1 e x2:
x₁ = ql²/15
x₂ = 13ql²/120

DIAGRAMMA DEL MOMENTO

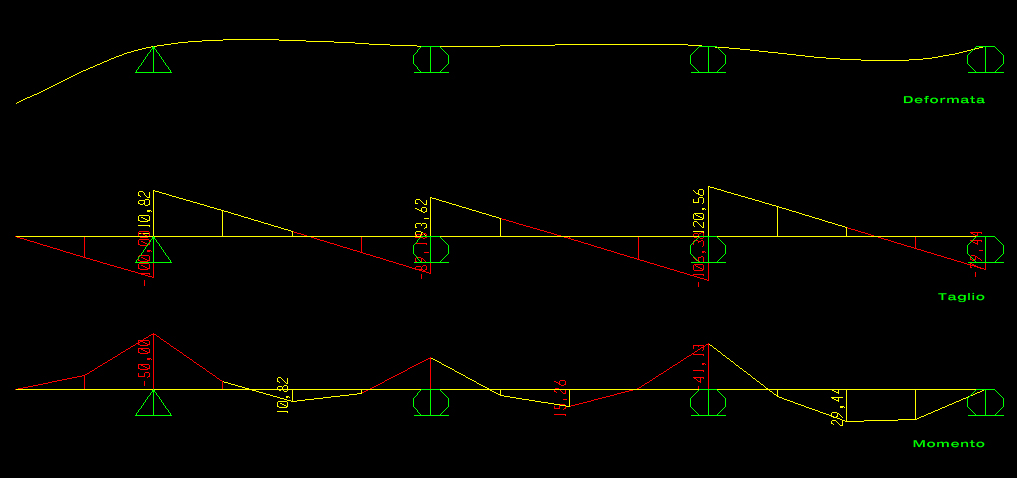
Verifica con SAP 2000