Per questa sercitazione ho considerato una pianta di carpenteria come quella riportata in figura

 

 

 

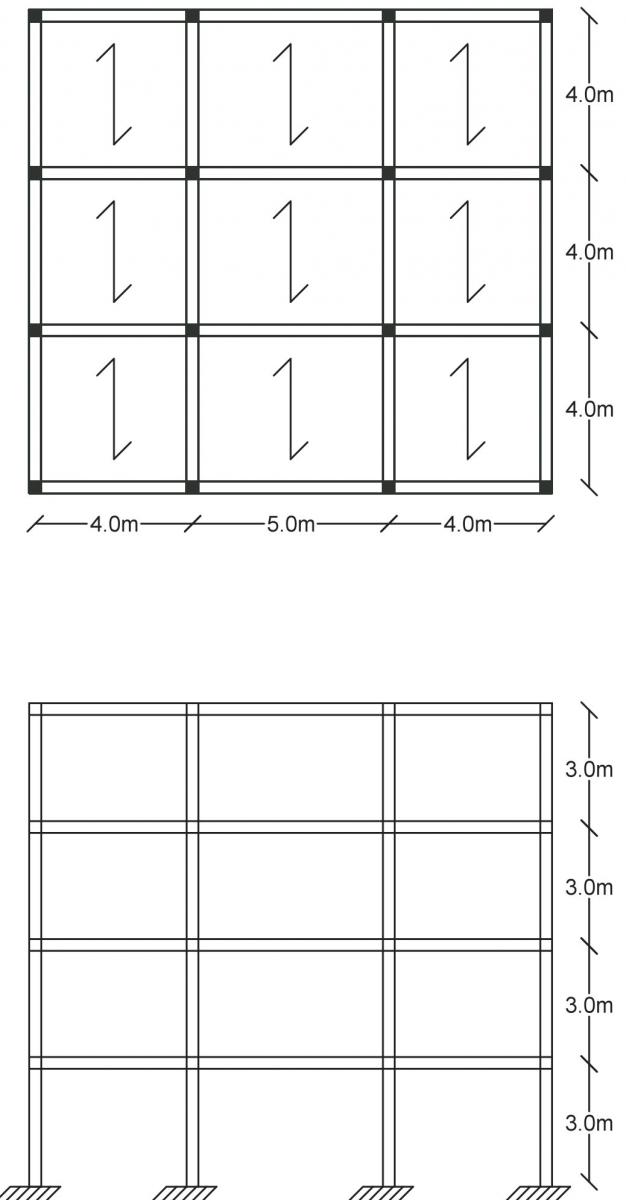
Lo scopo dell'esercitazione è quello di dimensionare la trave e il pilastro maggiormente sollecitati.

Questi ultimi sono individuati a partire dalla loro area d'influenza, che risulterà maggiore rispetto alle altre

 

 

 

 

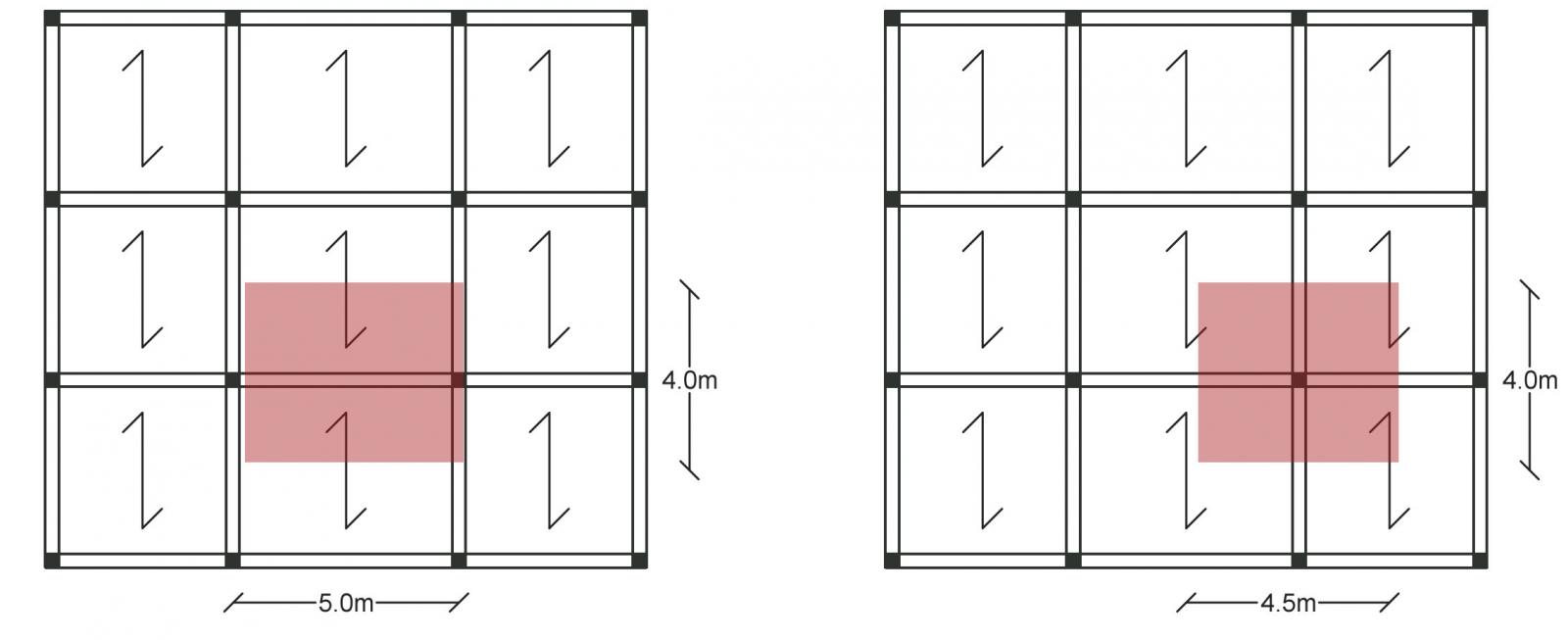
Per dimensionare la trave a flessione bisogna in primo luogo definire i carichi agenti sul solaio che ci permetteranno di trovare il carico di progetto della trave.

Il carico agente sul solaio si compone di tre parti:

- Il carico strutturale q_s

- Il carico permanente portato q_p 

- Il carico variabile qa

Questi carichi dipendono dalla tecnologia del solaio  e dalla destinazione d’uso dell’edificio.

 

ACCIAIO

 

Per quanto riguarda la struttura in acciaio ho considerato un  solaio  come quello in figura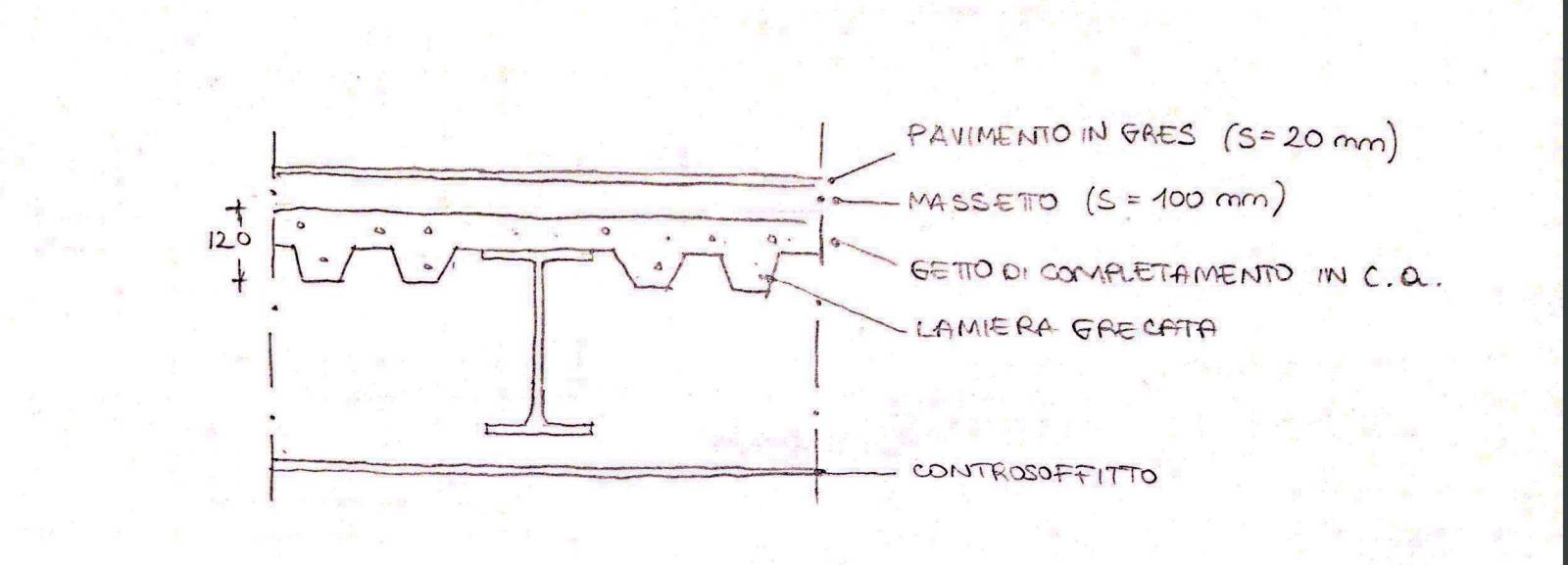

 

Carichi Strutturali q _s

  -peso proprio lamieta grecata = γ x s = peso specifico del materiale x spessore= 0,11KN / mq

  -getto di completamento = 25,00KN / m ^ 3 x 0,0925 m = 2,32 KN / mq

   q _s = 2,43 Kn / mq

 

 

Carichi Permanenti q _p

  -pavimento in gres ceramico = 0,40 KN / mq

  -massetto = 20,00 KN / m ^ 3 x 0,10 = 2 KN / mq

  -controsoffitto = 0,6 KN / mq

  -incidenza impianti = 0,10 KN / mq

  -incidenza tramezzi = 1,60 KN / mq

   q _p = 4,16 KN / m2

 

 

Carichi accidentali q _un

  -civile abitazione = 2,00 KN / mq 

   q a = 2,00KN / mq

 

Per trovare il carico al metro lineare sulla trave bisogna calcolare la combinazione di carico caratteristica.

La combinazione di carico dipende dallo stato limite che si intende considerare, in questo caso la verifica è stata effettuata allo SLU.

Combinazione di Carico Caratteristica = γ _G1 x qs + γ _G2 QP + 1 γ _Q1 qa = 14.301 KN / mq

Una volta trovata la combinazione di carico caratteristica si ricava il carico al metro lineare moltiplicando la combinazione di carico caratteristica per l’interasse della trave presa in considerazione. 

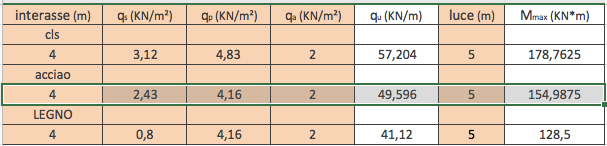
q _u = carico al metro lineare = 14.301 KN mq x interasse = 14.301 KN mq x 4 m = 57,2014 KN m

Trovato il carico al metro lineare si puo’ ricavare il momento massimo di progetto Mmax

Trattandosi di una trave doppiamente appoggiata il momento massimo sarà

M _{ma x} = ql ^ 2/8 = 154,98 KN / m.

 

            

 

Una volta determinato M _max bisogna definire il materiale di progetto.

Per questa esercitazione ho considerato un'acciaio S275. 

Questo ci permette di stabilire la tensione di progetto a flessione f_yd , che si calcola a partire dalla tensione di snervamento caratteristico dell’acciaio preso in considerazione, moltiplicato per un coefficiente parziale di sicurezza γ che nel caso dell’acciaio caso è pari a 1,05.

f _d = f _yk / γ

A questo punto è possibile definire il modulo di resistenza a flessione W _xmin tramite la formula 

W _xmin = M _max / f _d . 

essendo W _xmin il valore minimo che la sezione deve avere affinché il materiale non superi la tensione di progetto, si deve scegliere una sezione in cui il W_x sia maggiore del W _xmin .

La sezione adottata per le travi e: IPE330 .

       

 

Dopo aver dimensionato la trave  è stato possibile dimensionare il pilastro più sollecitato.

Per calcolare lo sforzo normale occorre  definire il peso di solaio portato dal singolo pilastro in base alla sua area d’influenza. Oltre al peso del solaio bisogna considerare il peso  delle travi scelte in precedenza, in quanto anch’esso grava sul pilastro. Essendo il  pilastro a terra quello più sollecitato bisogna infine moltiplicare il carico ottenuto per il numero dei piani, in questo caso tre.

Peso travi = (A _Trave xL _A + A _Trave xL _B ) x peso specifico acciaio

N1piano = q _u x A _inf + peso travi

Nmax = N _piano x numero piani = 681 KN.

 

Per dimensionare pilastro soggetto a compressione bisogna considerare che esso potrebbe collassare per schiacciamento o per l’insorgere dell’instabilità euleriana.

Per evitare il collasso per schiacciamento bisogna ricavare l’area minima della sezione utilizzando la formula 

A _min = N _max/ f _d

                         

Per quanto riguarda l’instabilità euereliana è fondamentale trovare un valore d’inerzia minimo dell’inerzia minima.

Per poter calcolare l’inerzia minima serve il modulo di elasticità del materiale E, l’altezza del pilastro e il coefficiente β (coefficiente che dipende dai vincoli del pilastro).

E = 210000 Mpa 

β = 0,8 (incastro-cerniera)

L = 3 m

Utilizzando questi valori è possibile calcolare la snellezza massima λ, il raggio minimo d’inerzia ρ  e  l’inerzia minima.

I _min = Ax (ρ _min ) ^ 2 = 189,5224 cm ^ 4

           

 

Con i valori trovati ho  potuto  scegliere una sezione di progetto facendo attenzione che l’area e l’inerzia fossero maggiori dei due valori minimi calcolati.

In questo caso è stata adottata un HEA140 .

Dopo aver dimensionato gli elementi che compongono la struttura ho effettuato una verifica con il programma SAP2000 .

Le analisi hanno mostrato che il momento sulla trave è minore del momento di progetto, mentre lo sforzo normale sul pilastro risulta maggiore di quello di progetto 

N _max = 681,957KN <N ed = -748,63KN 

                     

 

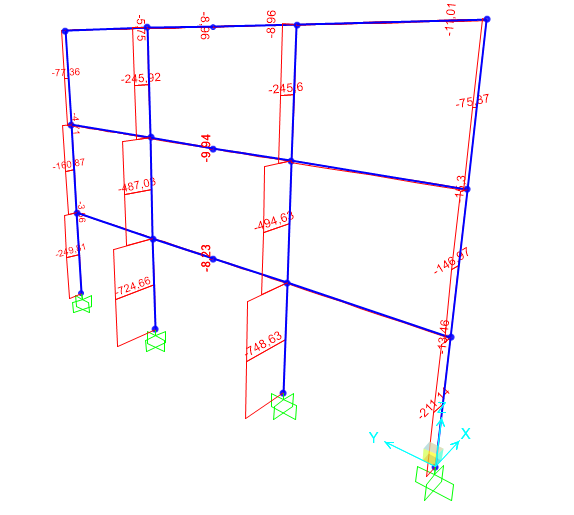
Ho effettuato un’ulteriore verifica adottando un profilato più grande HEA160 per il quale la struttura risulta verificata

N _max = 748,63KN > N _ed = -711KN

 

 

 

 

 

                       

 

 

CALCESTRUZZO

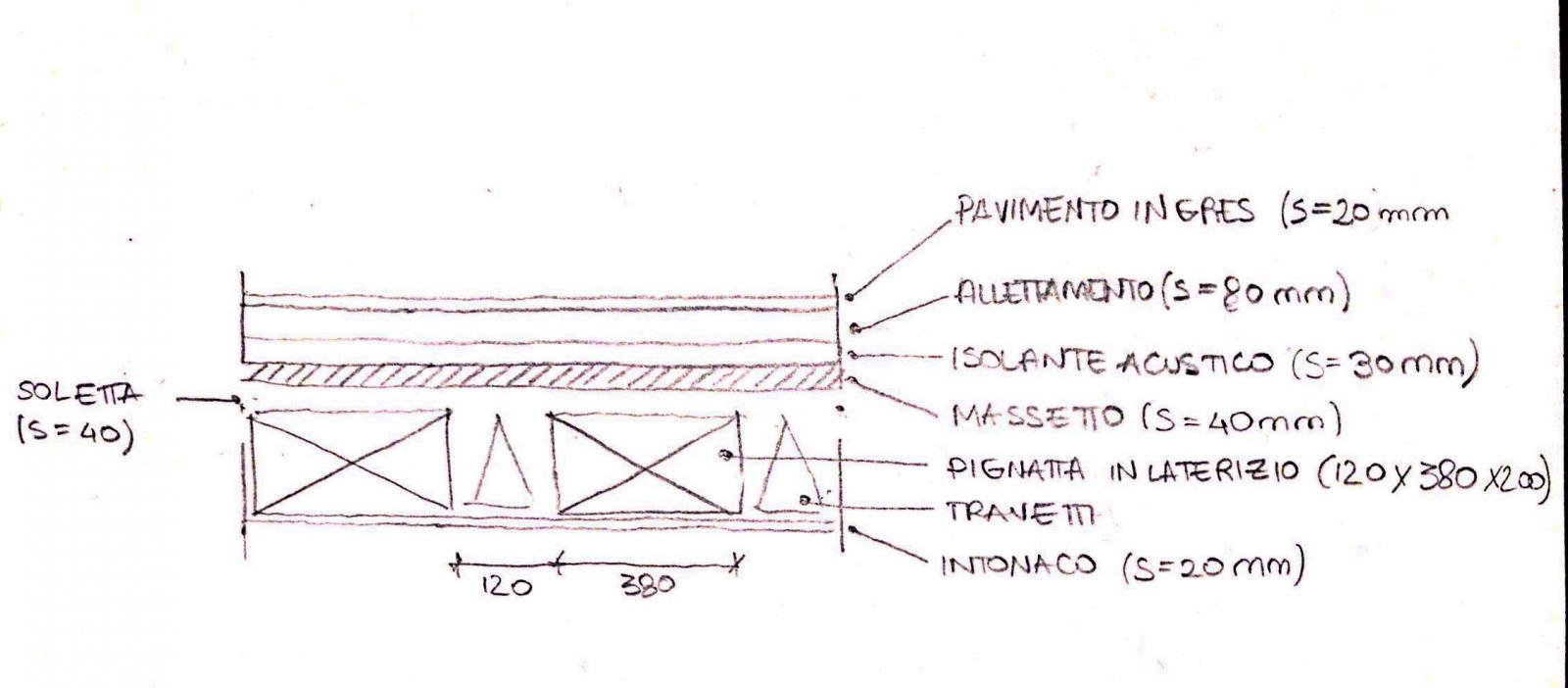
Carichi Strutturali q _s

 -Peso Proprio Soletta= 25,00 KN / m ^ 3 x 0,04 m = 1kN / mq

 -Peso Proprio travetti =25,00 KN / m ^ 3 x 0,12 x (0,24-0,04) m / 0,5 = 1,20 KN / mq

 -Peso Proprio pignatte= 6,00 KN / m ^ 3 x 0,38 x (0,24-0,04) m / 0,5 = 0,92 KN / mq

  q _s = 3,12Kn / mq

 

Carichi Permanenti q _p

 -Pavimento In gres ceramico = 0,4KN / mq

 -Allettamento + Massetto 20,00KN / m ^ 3 x 0,12m = 2,4KN / mq

 -Intonaco = 20,00KN ^ 3 X 0,02m = 0,40KN / mq

 -Isolante = 0,3KN / mq

 -Incidenza Tramezzi = 1,60KN / mq

 -ncidenza impianti = 0,10KN / mq

  q _p = 4,83KN / mq

 

Carichi accidentali q _a

 -civile abitazione = 2,00KN / mq

  q _a = 2,00KN / mq

 

    

 

Per prima cosa ho scelto  le classi di resistenza dei materiali che compongono la sezione.

Posso quindi ricavare la tensione di progetto dell’acciaio e del cls.

f _d = f _yk / γ_s

f _cd = α_cc xf _{CK /} γ _c

dove 

f _yk = 450 MPa

γ _s = 1,15 coefficiente di sicurezza dell'acciaio

f _ck = 25 MPa

α _cc = 0,85 coefficiente riduttivo

γ _c = 1,5 coefficiente di sicurezza del cls

 

 

Date le tensioni di progetto e scelta una base di design è possibile determinare l’altezza utile H_u della sezione. L’altezza minima della sezione sarà data dalla somma di H _u con lo spessore del copriferro δ.

δ  = 5 cm

H _min = Hu + d = 57 cm

H design = 60 cm

Infine ho ingegnerizzato l'altezza e scelto una sezione di 30x60cm . 

          

         

 

Per dimensionare il pilastro trovo lo sforzo normale di progetto.

Peso travi = (A _Trave xL _a+ A _Trave xL _b) x Peso specifico cls

N _piano = q _u x A_inf + peso travi

N _max = N _piano x numero Piani = 887.004 KN. 

 

 

Come nel caso dell’acciaio bisogna trovare un’area minima in modo che il pilastro non collassi per schiacciamento.

A _min = N _max / F_CD

A questo punto bisogna trovare la base minima di progetto della sezione.

Per trovare questo valore servono il modulo di elasticità del materiale, l’altezza del pilastro e il coefficiente β.

E = 21000 MPa

β = 0,5 (doppio incastro)

L = 3 m

Questi valori permettono di ricavare il raggio minimo d’inerzia, la snellezza massima (che per deve avere un valore <200) e  quindi la base minima della sezione.

B _min = 4,29 cm

B _{di design} = 30 cm

Trovato questo dato posso calcolare l’altezza minima necessaria. 

H _min = 20,87068cm

H _design = 30 cm

Infine ho ingegnerizzato la sezione ( 30x30cm ). 

 

   

 

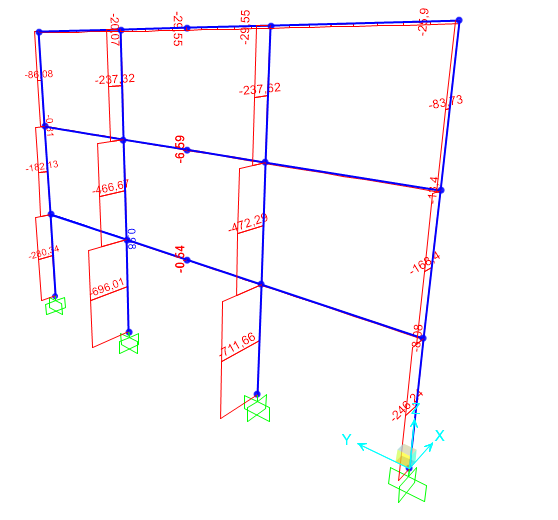
Effettuando le dovute analisi su Sap200 risultano verificati sia la trave che il pilastro.

 

M _max = 178,7625 KNm > M ed = 158,54 KNm

 

N _max = 887.004 KN > N _ed = -859,58 KN

 

 

        

 

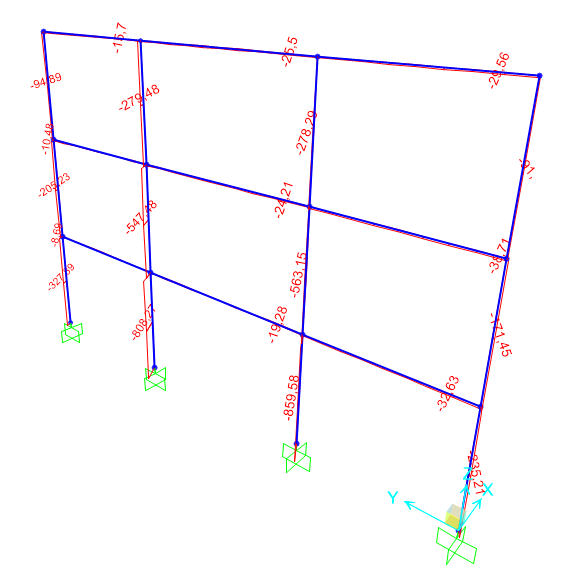
LEGNO

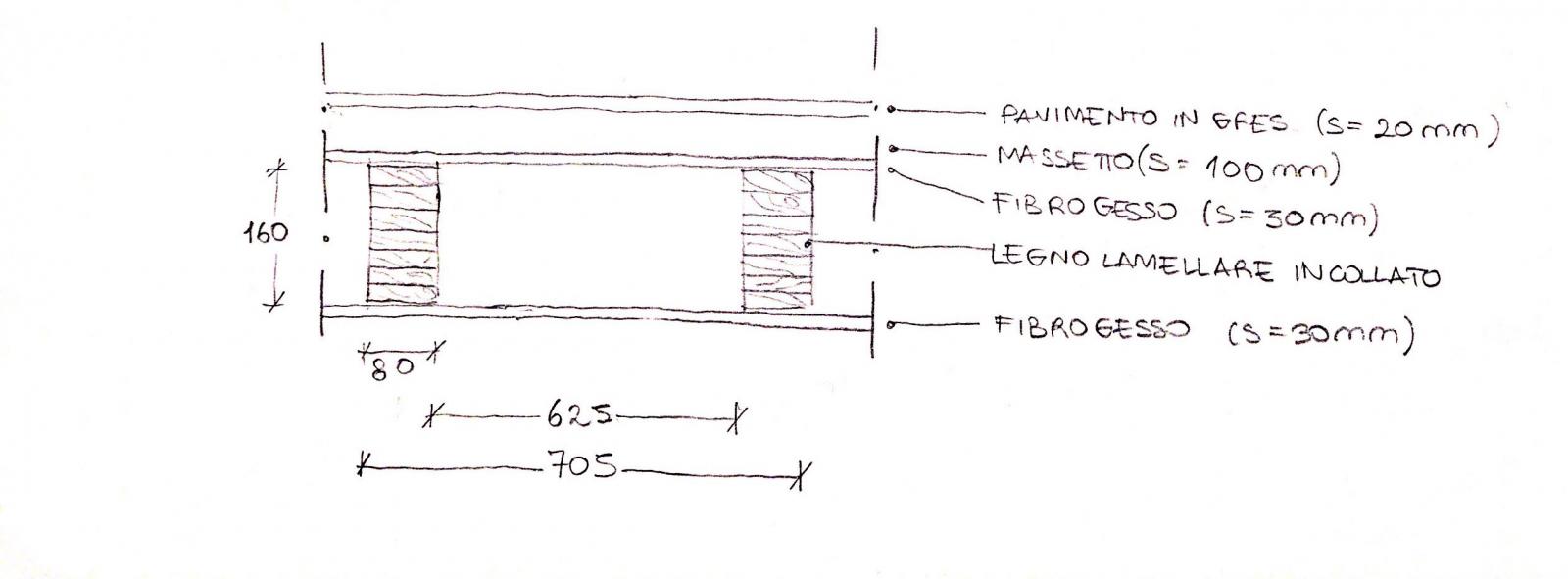
Carichi Strutturali q _s

 -peso travetti = 5,5 KN / m ^ 3 x (0,08 x 0,16) / 0,625 m = 0,11 KN / mq

 -soletta in fibrogesso = 11,5 KN / m ^ 3 x 0,03 m = 0,69 KN / mq

  q _s = 0,8 kNN / mq

 

Carichi Permanenti q _p

 -pavimento in gres ceramico = 0,40 KN / mq

 -massetto = 20,00 KN / m ^ 3 x 0,10 = 2 KN / mq

 -controsoffitto = 0,6 KN / mq

 -incidenza impianti = 0,10 KN / mq

 -incidenza tramezzi = 1,60 KN / mq

  q _p = 4,16 KN / m2

 

Carichi accidentali q _a

 -civile abitazione = 2,00KN / mq

  q _a = 2,00KN / mq

 

Per poter progettare a flessione la trave bisogna scegliere la tipologia di legno. 

In questo caso è stato utilizzato un legno di classe C24 . 

 

 

La tensione di progetto viene calcolata come

f _d = K _mod x f _mk / γ_m = 9,93 Mpa 

dove

Kmod = 0,6 (classe 1) coefficiente diminutivo dato dalla normativa che tiene conto l’effetto                                           della durata del carico e  delle condizioni di umidità in cui la struttura si                                       troverà ad operare

        

 

γ _m = 1,45 per legno lamellare incollato (da normativa) 

 

             

 

Trovata la tensione di progetto e definita la base della sezione è possibile trovare l’altezza minima.

B = 30 cm

H _min  = (M / b) ^ 0,5 x (6 / F _d ) ^ 0,5 = 50,8 cm

H _design = 55 cm

Infine ho ingegnerizzato l'altezza e adottato una sezione di 30x55cm.

 

Calcolo N _max

Peso travi = (A _trave xL _A + A _trave xL _B ) x Peso specifico legno

N _piano = q _u x A _inf + peso travi

N _max = N _piano x numero Piani = 584,5725 KN.

 

 

Per calcolare area minima di progetto bisogna conoscere la resistenza caratteristica parallela alle fibre del legno, il coefficientek _mod e il coefficiente di sicurezza del legno.

F_{C0, k} = 21 MPa

K _mod = 0,6

γ _m = 1,45

f _c0d = K _mod x F _c0k / γ _m

A _min = N _max / f _c0d = 672,7229 cmq

             

                    

 

Per calcolare la base  minima e l'altezza minima della sezione è necessario conoscere il modulo di elasticità del legno, l'altezza del pilastro e il coefficiente β.

E = 8000 Mpa 

β = 1 (cerniera-cerniera)

L = 3 m

Con questi valori determino la  snellezza massima λ, il raggio d’inerzia minimo ρ.

Conoscendo  λ e ρ trovo  il valore minimo della base.

B _min = ρ _min  x 2x (3) ^ 2 = 10,40021

H _min = A _min / B _min = 22,42

La sezione ingegnerizzata e di 30x55 cm.

 

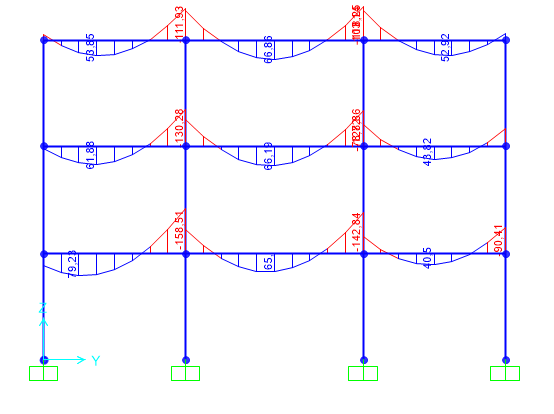
Eseguendo le analisi su Sap200 la sezione risulta verificara 

M _max = 128,5 KNm > M _ed = 96, 023 KNm

 

 

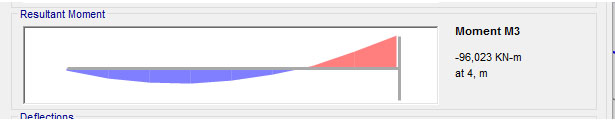
Lo sforzo normale agente sul pilastro risulta invece maggiore di quello di progetto.

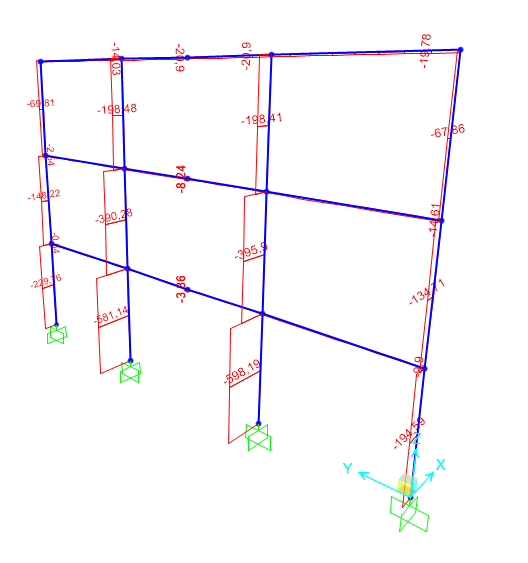
N _max = 584.573 KN < N _ed = - 606,82 KN 

           

 

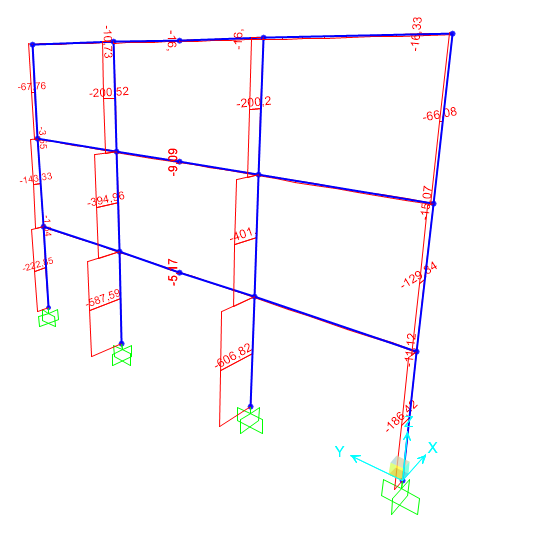
Ho effettuato un'ulteriore verifica su Sap2000 adottando un profilato più grande di dimensione 35x35cm con il quale la struttura risulta verificata.

N _max = 606,82KN <N ed = -598,19KN

Questa esercitazione viene svolta con l’obiettivo di individuare il metodo di ripartizione di una forza orizzontale, come quella sismica e del vento, sui diversi telai che costituiscono una struttura, applicando il metodo delle rigidezze.

Si prende in considerazione un edificio generico ad un solo piano, in cui struttura è composta da telai piani che, oltre a trasmettere i carichi verticali alla fondazione, possono costituire dei controventi per le azioni orizzontali. In particolare, i telai piani che compongono tale struttura sono realizzati sul modello del telaio Shear-type. I telai Shear-Type sono un modello teorico che hanno la capacità di possedere travi infinitamente rigide, questo fa si che le estremità dei pilastri non possono ruotare. La rotazione impedita porta a deformare i pilastri stessi come travi doppiamente incastrate. In questo caso la deformata si avvicina alla deformata di una trave deformabile per solo taglio.

Nell’ impalcato in figura si individuano 7 telai, 3 paralleli all’asse x e quattro paralleli all’asse y.

• Telaio 1 verticale: pilastri 1-5-9
• Telaio 2 verticale: pilastri 2-6-10
• Telaio 3 verticale: pilastri 3-7
• Telaio 4 verticale: pilastri 4-8
• Telaio 1 orizzontale: pilastri 1-2-3-4
• Telaio 2 orizzontale: pilastri 5-6-7-8
• Telaio 3 orizzontale: pilastri 9-10

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell’impalcato come molle.

In tutta la struttura sono presenti due tipologie di pilastro, uno rettangolare di dimensioni 50x30 cm e uno quadrato di dimensioni 30x30 cm. Pertanto otterremo tre momenti di inerzia distinti (bh^³/12), due per il pilastro rettangolare, uno rispetto ad x e l’altro rispetto ad y, e uno per il pilastro quadrato.

I₁xy= bh³/12= 67.500 cm⁴     I₂x= bh³/12= 31.2500 cm⁴    I₂y= b³h/12= 11.2500 cm⁴

Tramite la tabella excel, dopo aver inserito tutti i valori trovati dei diversi momenti d’inerzia, calcoliamo la rigidezza traslante associata a tutti i controventi, inserendo per ognuno di essi l’inerzia dei pilastri che lo compongono. Si parla di telai Shear type, pertanto, per trovare la rigidezza traslante di un telaio composto da n pilastri utilizziamo la formula:

Si ottiene anche una tabella riassuntiva in cui vengono riportate le rigidezze di tutti i controventi calcolati precedentemente. Nella stessa tabella, si devono inserire le distanze di ogni controvento, calcolate da un’origine O arbitraria, che per comodità collochiamo nell’angolo in basso a sinistra dell’impalcato.

Si calcola ora il centro di massa dell’edificio, che corrisponde al centro delle aree dato che si considera l’impalcato con densità di massa uniforme, suddividendo la struttura in tre figure elementari di cui conosciamo il centro in modo intuitivo.

Per farlo utilizziamo la formula derivata da quella per ottenere le coordinate del centro di un sistema di vettori paralleli:

Giunti a questo punto, si calcola la rigidezza totale orizzontale, data dalla somma delle singole rigidezze dei controventi orizzontali, e la rigidezza totale verticale, data dalla somma delle singole rigidezze dei controventi verticali. Così sarà possibile calcolare il centro delle rigidezze riadattando la formula precedentemente utilizzata per il centro di massa, e la rigidezza torsionale totale.

Si riesce così ad individuare sia il centro di massa G sia il centro delle rigidezze C, dell’intero impalcato.

Si effettua l’analisi dei carichi sismici per ricavare la forza che agisce nel centro di massa. Si calcola il carico totale permanente (G) e accidentale (Q) del solaio, partendo dal valore dei carichi per unità di superficie [kN/mq] e utilizzando le seguenti formule:

G = (q_s + q_u) A_tot      Q = q_a A_tot

In accordo con la normativa tecnica si utilizza la combinazione sismica per calcolare i pesi sismici:

W = G + ψ_2j · Q   in cui ψ rappresenta il coefficiente di contemporaneità indicato dalla normativa.

F = W c    moltiplicando W, ossia il peso sismico, per un coefficiente di intensità sismica c che tiene conto della sismicità del luogo di progettazione dell’edificio, si ottiene F, la forza sismica da applicare al centro di massa.

Ora si considera l’azione della forza sismica lungo x e poi lungo y. Si trova lo spostamento orizzontale, verticale e la rotazione tramite le seguenti formule:

Ora che abbiamo tale forza la andiamo ad applicare nel centro d’area creando 2 casi:

• forza applicata in direzione x, che comporterà ad possibile rotazione e traslazione orizzontale dell’impalcato
• forza applicata in direzione y, che comporterà ad possibile rotazione e traslazione verticale dell’impalcato